Mathematical Knowledge for Teaching the Area of Plane Surfaces: A Literature Review on Professional Noticing

Abstract

Mathematics teaching is a social practice, shaped by distinct ways of recognizing, interpreting, and responding to situations that emerge in the classroom. This professional noticing, however, requires a kind of mathematical knowledge that is specific to teaching. This study aims to identify discussions have taken place in Brazil regarding the mathematical knowledge necessary for teaching the concept of area of plane surfaces in Basic Education, based on a literature review conducted through the CAPES Theses and Dissertations Catalog. The theoretical framework is grounded in Moreira’s distinctions between school mathematics and academic mathematics, as well as in the body of literature concerning the concept of professional noticing. The analysis of the 17 selected studies revealed, among other aspects, that by understanding area as a magnitude through the lens of the Game with Frames—originally developed by Douady and Perrin-Glorian in the 1980s and later expanded by Brazilian researchers—it is possible to infer mathematical knowledge relevant to teaching the area of plane surfaces in Basic Education. This perspective supports the development of professional noticing of students’ errors, difficulties, and misconceptions observed both in classrooms and in teacher education contexts. Some elements of this knowledge are discussed in the present article.

1. Introduction

Teaching mathematics is a complex, situated, and often unpredictable social practice. Like other professional practices, it involves a specific way of observing and interpreting the context in which it takes place—an essential component of teacher professional development. In the classroom, teachers make decisions based on what they perceive as most appropriate for achieving the goals of mathematics instruction. In this regard, both lesson planning and instructional delivery are profoundly influenced by how teachers perceive their classes and interpret these perceptions. However, learning to notice professionally is neither straightforward nor does it arise naturally from initial training or teaching experience alone. This specialized way of attending to the classroom, students, and their actions also demands mathematical knowledge that is often absent from both initial and ongoing teacher education. Unlike academic mathematics—with its well-defined structure, language, and axiomatic foundations—the mathematics required for school teaching is less consolidated. Whether due to its emergent nature or its limited presence in discussions on teachers’ daily practices, training, and professional development, this type of knowledge often lacks accessible repositories or comprehensive texts that address the teaching of all mathematical topics. Thus, this article aligns with the efforts of scholars such as Moreira (2004), M. C. C. Ferreira (2014), Patrono (2023), Regis (2025), among others, in the pursuit of inferring and identifying mathematical knowledge directly associated with the schoolteacher’s work for teaching.

More precisely, it aims to investigate the mathematical knowledge required for teaching the concept of area of plane surfaces. As noted by Clements et al. (2018, p. 8),

Geometry and spatial reasoning are not only important in and of themselves, but lay a critical mental foundation for learning other topics in mathematics as well as other subject matter areas (Clements & Battista, 1992; Olkun et al., 2019; Sarama & Clements, 2009; The Spatial Reasoning Study Group, 2015; Vallortigara, 2012; Zacharos et al., 2011; Zorzi et al., 2002). Despite its importance, geometry and spatial thinking do not play a significant role in research.

In this context, given the limited attention that school geometry has received in educational research, and considering that both national and international literature have, for decades, emphasized the persistent difficulties associated with teaching and learning the concept of area of plane surfaces, this study adopts that notion as its central focus. This study consists of a bibliographic review with a qualitative approach, aiming to generate new insights through a critical analysis of the results presented in each study. This review is guided by the following research question: What discussions have taken place in Brazil regarding the mathematical knowledge necessary for teaching the concept of area of plane surfaces in Basic Education? To address this question, a review of Brazilian academic production was conducted using the Catalog of Theses and Dissertations of the Coordination for the Improvement of Higher Education Personnel (CAPES1).

The scope of the review is delineated, with a specific focus on the mathematical knowledge required for teaching the concept of area of plane surfaces in Basic Education2. From the perspective of school mathematics, this study specifically addresses the mathematical knowledge related to the concept of the area of plane surfaces. To this end, each selected study was carefully analyzed, with particular attention to how the concept was defined, substantiated, and discussed, as well as how it was connected to professional teaching knowledge and teaching practice.

The investigation is theoretically grounded in the work of Moreira and collaborators regarding the distinctions between school mathematics and academic mathematics, as well as in scholarly literature concerning the notion of professional noticing. The article begins with a brief presentation of the theoretical frame that underpins the study, followed by a description of the methodological approach adopted. Subsequently, the results derived from the analysis of the research comprising the survey corpus are presented, with particular emphasis on the mathematical knowledge required for teaching the concept of area of plane surfaces. Special attention is given to the knowledge associated with the construction of this notion, as discussed in the works of Douady and Perrin-Glorian (1989), Bellemain and Lima (2002)3, Bellemain et al. (2017), among others.

2. School Mathematics as a Core Component in the Development of Teachers’ Professional Noticing

The notion of professional noticing has been the subject of extensive discussion in the literature for over two decades (Mason, 2002; Jacobs et al., 2007; Sherin et al., 2011; Llinares, 2013a; Schack et al., 2017; Llinares et al., 2019, among others). Its foundations, however, can be traced back to earlier conceptual developments, notably in the work of Goodwin (1994 as cited in Jacobs et al., 2007) and Stevens and Hall (1998 as cited in Jacobs et al., 2007).

Like Mason (2002 as cited in Rhodes, 2007, p. 7), we understand that “every act of teaching depends on noticing: noticing what children were doing, how they respond, evaluating what is being said or done against expectations and criteria, and considering what might be or done next”. However, “intentional or professional noticing differs from everyday noticing as to what is attended to and how it is interpreted is influenced and focused by the professional experience and knowledge of the individual.” (Melhuish et al., 2015, p.748).

Professional noticing refers to a structured and reflective attentiveness to events that unfold in mathematics classrooms. It involves the ability to perceive and identify significant features of teaching situations, as well as to interpret and take decisions to them (Jacobs et al., 2010). This process is characterized by the interrelation and cyclical nature of these actions—perceiving, interpreting, and decision-making—which are typically influenced and refined through teaching experience. Nonetheless, at its core, “professional noticing is a knowledge-based process” (Llinares et al., 2019). Following Llinares (2013a, p. 119), we understand professional noticing as an integral component of the mathematics teacher’s professional practice. A key feature of this interpretative perspective is its connection to the teacher’s mathematical knowledge—that is, the interdependence between the teacher’s understanding of mathematics and their ability to notice professionally. To ensure professional noticing,

the teacher not only needs to have an interpretive viewpoint toward math teaching and learning, but theoretical knowledge as well. Having the theoretical background that allows one to interpret or “professionally notice” is what justifies the use of the word “professional”. In this context, the teacher must assess to what extent her knowledge is relevant to the professional task at hand. In order for knowledge to become “relevant” to a professional task, the teacher must be aware of how his/her own knowledge dovetails with the task to be carried out.

(Mason, 2002; Llinares, 2013b, p. 84)

Therefore, experience and motivation alone are insufficient to develop the disciplined attentiveness required for effective professional noticing in the classroom. While it is acknowledged that mathematics teachers construct and refine professional knowledge through their teaching practice, such knowledge is not necessarily informed by educational research. This is primarily due to the fact that the mathematics that predominates in teacher education—whether initial or continuing—is generally academic mathematics or some form of didactic adaptation thereof.

Historically, undergraduate mathematics programs in Brazil have been shaped by a view of mathematics as a universal discipline. This form of mathematics is regarded as foundational knowledge, from which other types of professional knowledge are expected to emerge (Moreira & David, 2005, p. 15). This foundational knowledge, often referred to as ‘specific knowledge’ or ‘disciplinary knowledge’, corresponds to academic mathematics. It is defined as “a set of practices and knowledge associated with the constitution of a scientific body of knowledge, as produced by professional mathematicians and socially recognized as such” (David et al., 2013, p. 57). “Although the other components are recognized as complex and important, they constitute a body of knowledge that is essentially ancillary to the process of transmitting school knowledge. This categorizes the teacher’s professional knowledge as fundamentally non-mathematical” (Moreira & David, 2005, p. 15).

So, teaching practice differs significantly from the professional practice of mathematicians. The teaching of mathematics in Basic Education requires a distinct form of mathematics, one that is specific to the practice of teaching, grounded in the professional demands of teachers who teach the subject in Basic Education, involves understanding mathematical concepts from a perspective that enables the teacher to interpret students’ responses, identify their difficulties and, when present, misconceptions, as well as to design instructional strategies that support students in overcoming them. School mathematics is also reflected in teachers’ responses to students’ “why” questions and in their selection of concept representations that best serve specific teaching purposes—such as justifying the validity of a mathematical statement (Moreira & Ferreira, 2021, p. 20). It permeates all dimensions of mathematics teaching practice. Therefore, the development of this body of knowledge is essential for cultivating a professional vision.

In line with Moreira (2012, p. 1145), we understand that “the teacher’s mathematics constitutes the teacher as a professional, while also being historically constructed through the interactions between the teacher and their students within the classroom context.” In this view, “the teacher’s mathematics is intrinsically tied to school education, which, in turn, is inseparable from teaching and learning processes.” Although “teaching and education are distinct concepts—neither reducible to the other—education cannot exist without teaching, and teaching cannot occur without some form of education, whether positive or negative” (Moreira, 2012, p. 1145). Thus,

the teacher’s mathematics cannot exist independently of people—especially those engaged in the processes of teaching and learning within educational relationships. For this reason, teacher’s mathematics is not merely the sum of two distinct components: content and pedagogy. It is, rather, a form of knowledge that emerges from the dynamic and relational nature of classroom practice.

(Moreira, 2012, p. 1145)

Moreover, although the dichotomy between ‘content knowledge’ (academic mathematics) and ‘didactic knowledge’ underpins the current structure of undergraduate mathematics programs, it has proven insufficient for adequately preparing future teachers to meet the demands of teaching in Basic Education. Teacher education curricula should be organized around professional practice as their central axis—both to comprehend it and to enable prospective teachers to develop a deep and critical understanding of it. This includes recognizing its underlying conditions, challenges and possibilities, existing knowledge and gaps, shortcomings and potential solutions, as well as the factors that constrain differentiated and context-sensitive pedagogical performance (Moreira, 2012, p. 1145). It is important to emphasize that

the practice of mathematics teachers in Basic Education unfolds within a specific educational context, which demands a fundamentally different perspective from that of academic mathematics. Within this context, descriptive definitions and alternative, more accessible approaches to demonstrations, arguments, and the presentation of concepts and results become essential values associated with school-level mathematical knowledge.

(Moreira & David, 2005, p. 21)

Considering the points discussed above, this article adopts the perspective that school mathematics constitutes

a body of knowledge encompassing both the knowledge produced and mobilized by mathematics teachers in their pedagogical practice, and the findings of research related to the teaching and learning of mathematical concepts, techniques, and processes. This perspective departs from the traditional view of school mathematics as merely the content taught in schools, and instead frames it as a body of knowledge intrinsically linked to the teaching profession.

(Moreira & David, 2005, p. 20)

In this article, the concept of school mathematics, as defined by Moreira and collaborators, will be understood as synonymous with mathematical knowledge for teaching. Both concepts refer to the mathematical knowledge required for teaching in basic education.

3. Methodology

This study consists of a literature review of qualitative research, aiming to generate new insights through a critical analysis of the findings presented in each study. The scope of the review is delineated, with a specific focus on the mathematical knowledge required for teaching the concept of area of plane surfaces in Basic Education. From the perspective of school mathematics, this study specifically addresses the mathematical knowledge related to the concept of the area of plane surfaces. To this end, each selected study was carefully analyzed, with particular attention to how the concept was defined, substantiated, and discussed, as well as how it was connected to professional teaching knowledge and teaching practice.

Between April and June 2025, a systematic search was conducted in the CAPES Catalog of Theses and Dissertations to identify Brazilian academic literature related to the teaching of mathematical knowledge concerning plane surfaces. No specific time period was delimited; that is, the review encompassed the entire body of work in the repository that met the criteria detailed below. The following inclusion criteria were established: (i) the study explicitly addressed the concept of area of plane surfaces and/or its teaching; and (ii) the study was situated within the field of research on mathematical knowledge inherent to teaching. In other words, for a study to be included in the review corpus, it had to involve teachers or prospective teachers engaged in training or professional development, or address aspects of their professional knowledge, and present a theoretically grounded discussion of the concept of area.

At this stage, the following searches were carried out:

“mathematical knowledge for teaching” AND “Area of plane surfaces”;

“mathematical knowledge for teaching “ AND plane surfaces”;

“knowledge for teaching “ AND plane surfaces;

“ knowledge for teaching “ AND areas;

“mathematical knowledge for teaching “ AND area, and

teaching AND area AND plane surfaces.

After excluding duplicate entries, approximately 170 studies were identified. Among these, only 47 made reference to both teachers and the concept of area. However, the majority did not engage in a substantive discussion of the concept, merely mentioning it in passing. Several studies were excluded due to a misalignment with the focus of this review—for example, those centered on information and communication technologies (ICT) or those that did not examine the concept of area within the context of professional teaching knowledge or teacher education. Studies that focused exclusively on textbook analysis or on students—without involving teachers and/or their professional knowledge—were excluded from the corpus. Additionally, four studies were excluded due to unavailability: they were not authorized for access in the CAPES Thesis Catalog and could not be located in institutional repositories, program websites, or through targeted Google searches. Ultimately, only nine studies met all inclusion criteria (Chiummo, 1998; Fraga, 2019; Gomes, 2018; Moura, 2019; J. A. S. Santos, 2011; M. R. Santos, 2015; Silva, 2016, 2022; Teles, 2007).

During an initial reading of the nine selected studies, we identified in Fraga’s (2019) reference list a study by Oliveira (2019) that met the inclusion criteria. However, this study had not been retrieved in the initial searches because it did not use the terms “mathematical knowledge” and/or “knowledge for teaching,” but rather the term “professional learning.” This prompted a new round of searches, as described below:

“professional learning” AND “area of plane figures”;

“professional learning” AND “area and perimeter”;

“teacher education” AND “area and perimeter”;

“mathematics for teaching” AND “teacher education” AND “area”;

“area of plane figures” AND teacher;

teaching AND area AND “plane surfaces”, and

“professional knowledge” AND mathematics AND area.

Among the 57 studies identified (excluding duplicates), eight additional works were located—Braga (2019), Campos (2021), Conceição (2018), Fonda (2020), Imafuku (2024), Lessa (2017), Oliveira (2019), and C. A. B. Santos (2008)—which had not been found in the initial search but met the established inclusion criteria. With the inclusion of these studies, the final corpus for this review consisted of 17 works.

We consider this set to represent, to a certain extent, the Brazilian scholarly production concerned with the study of the notion of area of plane surfaces from the perspective of school mathematics, with particular attention to teachers and their professional knowledge. This assertion is supported both by the systematic nature of the search procedures and by the additional step of analyzing the literature reviews within each selected study, in order to identify potentially relevant works not yet included in the corpus. At this stage, no further studies were identified, thereby concluding the review process.

As discussed by Moreira et al. (Moreira & David, 2008; Moreira & Ferreira, 2013, 2021), as well as by Ball et al. (2008), the mathematical knowledge inherent to teaching comprises multiple dimensions. In this article, we concentrate on one specific dimension: knowledge of the concepts involved in defining the area of plane surfaces. This focus is justified by the observation that, although most studies concerning mathematics teachers and the teaching of area highlight difficulties, errors, and misconceptions, fewer than half of them seek a theoretical foundation to analyze these challenges or to propose strategies for addressing them and informing educational practice. We argue that understanding a mathematical concept from the perspective of school mathematics is inherently multifaceted and involves interconnected notions that are not always clearly understood by teacher educators or by teachers themselves. For this reason, identifying and articulating this type of mathematical knowledge constitutes, in our view, a central task in the effort to strengthen mathematics teacher education.

The analysis process entailed multiple readings of each study and the progressive completion of analytical tables through which our understanding was gradually refined. The first table compiled basic bibliographic and contextual information—such as author, title, advisor, institution, defense year, academic program, and link to the full text—alongside general details about the research, including its guiding question or objective, theoretical frame, methodology, and main findings. In the second stage of analysis, we concentrated on the theoretical frames adopted by the studies and the ways in which the notion of area was addressed. Drawing from these frames, we synthesized the main ideas presented in the research concerning the understanding of the concept of area from the perspective of school mathematics.

4. What Do Brazilian Studies Reveal About the Mathematical Knowledge Required for Teaching the Area of Plane Surfaces?

The corpus comprises six doctoral theses and twelve master’s dissertations, with the earliest defended in 1998 and the most recent in 2024, as can be seen in

Table 1. Basic information regarding the studies comprising the review corpus.

Reference	Purpose
Braga, L. The concepts of perimeter and area in a Pedagogy course and the mobilization of professional knowledge. 2019. Thesis Doctorate.	This study uses a qualitative perspective of research based on the interpretative paradigm, in the form of intervention research, in which the researcher assumes the role of trainer, situating herself in the development of an extension action with students of a Pedagogy course. […] In this investigative context, the present research seeks to answer the following question: “What elements of the context of initial formation of FPEM based on the resolution of perimeter and area tasks and the analysis of a multimedia case of a class from the perspective of Exploratory Teaching, offer opportunities of mobilization and constitution of professional knowledge?” (Braga, 2019, p. 9)
Campos, A. P. de M. Concept Study in Mathematics Teacher Education: A Collaborative Study on the Concept of Area for Teaching. 2021. Dissertation (Master’s degree).	“The research, with a qualitative approach, aims to analyze a continuing education based on the concept study, aiming to (re) signify teaching knowledge of the concept of area for teaching. For this investigation, in the second semester of 2019, an extension course entitled: “(Re) signifying concepts for the teaching of area and perimeter” was offered to teachers who teach mathematics”. (Campos, 2021, p. 10)
Chiummo, A. The concept of area of plane surfaces: Training for elementary school teachers. 1998. Dissertation (Master’s degree).	The study is grounded in the French tradition of Mathematics Didactics. The methodology employed consists of a historical and epistemological investigation, alongside an analysis of the didactic transposition of the concepts of area and perimeter, through the design, implementation, and evaluation of a didactic sequence. (Chiummo, 1998, p. 2)
Conceição, J. de S. The construction of the concept of area in the early years of elementary education: a continuing professional development. 2018. Dissertation (Master’s degree).	“The purpose of this study was to analyze the implications continued education has, in relation to the construction of the concept of area, on the pedagogical approach of a math teacher. The theoretical reference of this investigation involves education in math, in particular geometry, of teachers working in the initial years of Elementary School, and Schön’s work with respect to the concept of reflection.” (Conceição, 2018, p. 9)
Fonda, C. R. S. Organizações matemáticas para o ensino de medida de área de triângulos: o trabalho da técnica. 2020. Dissertation (Master’s degree).	“This study aims to present a proposal of didactic praxeologies for teaching area of triangles, using the Anthropological Theory of Didactics as a theoretical framework. […] In search of answers to the following research question: “Is it possible to build didactic organizations that allow working with different techniques for teaching the calculation of the measure of the area of triangles in the final years of elementary school and in high school?”, we examined official documents and textbooks to identify how the area of triangles is placed in our basic education.” (Fonda, 2020, p. 17)
Fraga, T. C. G. An analysis of the multimedia case “Exploring perimeter and area” for the teachers education who teach mathematics. 2019 Dissertation (Master’s degree).	“This qualitative research of theoretical and interpretative nature has as investigation context the multimedia case “Exploring perimeter and area”. A multimedia case brings together a set of media that can be used to train teachers who teach mathematics (PEM). Thus, this investigation seeks to answer the following general question: “What elements of the multimedia case ‘Exploring perimeter and area’ can be problematized in the formation of PEM?”.” (Fraga, 2019, p. 8)
Gomes, J. O. de M. A educational process for mathematics teachers: (Re)signification of knowledge for teaching. 2018. Doctoral Dissertation.	“The purpose of this research is to analyze, in a formative process, the knowledge necessary for teaching area and perimeter of flat figures of a group of teachers who teach for the initial years of Elementary School.” (Gomes, 2018, p. 10)
Imafuku, D. B. S. Teachers’ knowledge about the area of plane surfaces through the use of dynamic geometry and manipulative materials. 2024. Doctoral Dissertation	“This thesis investigates aspects of the development of professional knowledge of fourth and fifth-grade teachers at a private school in São Paulo. This development was examined during a continuous professional development program aimed at reflecting on the use of a sequence of activities on the area of plane figures with the use of different teaching resources.” (Imafuku, 2024, p. 8)
Lessa, L. F. C. F. Construction of a reference epistemological model considering the analysis of institutional relations regarding the mathematical object area. 2017. Dissertation (Master’s degree).	“This research’s main goal is to contribute with the process of teacher training through the construction of an Epistemological Model of Reference that considers the incompleteness of institutional work regarding mathematics’ object of Area and seeks to integrate elements from this model into the praxeology baggage of teachers of mathematics in the 6th grade of elementary school.” (Lessa, 2017, p. 8)
Moura, A. P. de. The area of plane surfaces in the 6th grade of Elementary School: A study on the approximations and distances between Taught Knowledge and Learned Knowledge. 2019. Dissertation (Master’s degree)	“This thesis aims to analyze distances and approximations between the knowledge taught and learned in connection with the object area of flat figures in the 6th grade of elementary school under the perspective of the Anthropological Theory of the Didactics, developed by Yves Chevallard and his collaborators.” (Moura, 2019, p. 8)
Oliveira, J. N. de. Teaching Mathematics in the Initial Years of Fundamental Teaching: area and perimeter. 2019. Dissertation (Master’s degree).	“This research seeks to investigate which aspects of the professional learning of teachers who teach mathematics in the initial years of Elementary Education can be mobilized in a formation context that involves the discussion of the concepts of area and perimeter.” (Oliveira, 2019, p. 9)
Santos, C. A. B. dos. Teachers’ formation of mathematical: didactic theoriescontributions in the notions study of area and perimeter. 2008. Dissertation (Master’s degree).	“The present work goals are to accomplish a study in order to verify as the notions of area and perimeter are introduced in documents curriculars official and in the class books and to analyze the knowledges of a teachers’ group to teach these notions, contemplating the three knowledge slopes considered for Shulman (2005), that consist in knowledges curriculars, content didactic and mathematical the taught being.” (C. A. B. Santos, 2008, p. 8)
Santos, J. A. S. dos. Teaching and Learning Problems in Perimeter and Area: A Case Study with Mathematics Teachers and 7th Grade Elementary School Students. 2011. Dissertation (Master’s degree)	This research “sets out to discuss the problems of both teaching and learning problems relating to the Geometric Quantities perimeter and for the area of plane figures. This investigation has been based on the research question: What are the student errors in solving area and perimeter problems of plane figures and how can mathematics teachers analyze them?”. (J. A. S. Santos, 2011, p. 7)
Santos, M.R. The Didactic Transposition of the Concept of Area of Plane Geometric Figures in the 6th Grade of Elementary School: A Perspective Based on the Anthropological Theory of the Didactic. 2015. Doctoral Dissertation.	“This thesis aimed to analyze the gap between the teaching practice of mathematics teacher and the textbook approach adopted by him, in the sixth grade of elementary school, according to the concept of area of plane geometric shapes.” (M. R. Santos, 2015, p. 10)
Silva, S. M. F. da. Teacher Education in the Early Years: An Investigation into Knowledge for Teaching Area and Perimeter of Plane Figures. 2016. Dissertation (Master’s degree).	“The purpose of this study was to investigate, during sessions of teachers studies that teach math to the early years of a private school of the big São Paulo, the development of professional teaching knowledge about the concepts of area and perimeter and its teaching.” (Silva, 2016, p. 9)
Silva, S. M. F. da. The Development of Teachers’ Professional Knowledge in a Group Studying the Area and Perimeter of Polygons and Their Teaching. 2022. Doctoral Dissertation.	“This study sought to investigate teachers’ professional knowledge of the concepts of area and perimeter and their teaching in the light of the BNCC and research in the area during study sessions of teachers who teach mathematics for the early years in a private school in the Greater São Paulo.” (Silva, 2022, p. 6)
Teles, R.A.M. Interconnections between Conceptual Fields in School Mathematics: A Study on Area Formulas for Plane Geometric Figures. 2007. Doctoral Dissertation	The Theory of Conceptual Fields served as the central theoretical framework of this research, whose general objective was to investigate interconnections among the conceptual fields of measurement, geometry, number, algebra, and functions within school mathematics, particularly in the formulation and treatment of problems involving the area formulas for the rectangle, square, parallelogram, and triangle. (Teles, 2007, p. 18)

.

Of the 17 studies, 13 were defended in and after 2015, suggesting that scholarly interest in this topic is relatively recent. The participants of the studies include in-service and prospective teachers of the early years of elementary education (Fraga, 2019; Silva, 2016, 2022; Gomes, 2018; Chiummo, 1998; Oliveira, 2019; Braga, 2019; Imafuku, 2024; Conceição, 2018), as well as teachers of the later years of elementary and secondary education (M. R. Santos, 2015; Moura, 2019; J. A. S. Santos, 2011; Lessa, 2017; C. A. B. Santos, 2008). Some studies involve both early and later years elementary teachers (Campos, 2021). One of the investigations (Teles, 2007) is theoretical in nature.

All studies adopt a qualitative research approach. The majority focus on teacher education initiatives and the analysis of their contributions (Chiummo, 1998; Silva, 2016, 2022; Gomes, 2018; Conceição, 2018; Braga, 2019; Oliveira, 2019; Fraga, 2019; Campos, 2021; Imafuku, 2024). Some investigate teachers’ knowledge in relation to teaching the topic and/or in interpreting students’ responses (C. A. B. Santos, 2008; J. A. S. Santos, 2011), while others address the theme from a more theoretical standpoint (Teles, 2007; M. R. Santos, 2015; Lessa, 2017; Moura, 2019; Fonda, 2020). For instance, Teles (2007, p. 18) investigated “interconnections between the conceptual fields of magnitudes, geometry, numerical, algebraic, and functional aspects in School Mathematics, in the formulation and treatment of problems involving the formulas for the area of a rectangle, square, parallelogram, and triangle.” Similarly, M. R. Santos (2015) aimed to “analyze the gap between the mathematics teacher’s instructional practice and the approach presented in the textbook he adopted for the 6th grade of elementary school, with regard to the concept of area of plane geometric figures” (author’s summary). Moura (2019) analyzed “the gaps and alignments between the knowledge taught and the knowledge learned regarding the concept of area of plane figures in the 6th grade of elementary school” (author’s summary). Fonda (2020), in turn, proposed “a set of didactic praxeologies for teaching the area of triangles, using the Anthropological Theory of the Didactic as the theoretical frame” (author’s summary).

In 11 of the 17 studies, the concept of area of plane surfaces is approached through the notion of area as a magnitude, within the frame of the Game with Frames, developed by Régine Douady (1987), Régine Douady and Perrin-Glorian (1989), and later refined by Brazilian researchers (Baltar, 1996; Bellemain & Lima, 2002). Two studies discuss the notion of area drawing on the work of Duval (Oliveira, 2019; Fraga, 2019); however, these refer to broader theoretical ideas related to the cognitive processes involved in geometric thinking, rather than to a specific discussion of the concept of area of plane surfaces. Imafuku (2024) is based on the studies of Clements and collaborators. The remaining studies merely mention ideas from selected authors on the teaching of area, offering brief literature reviews without establishing a theoretical frame for the topic.

The process undertaken to make these inferences involved multiple thorough readings of each text, with particular focus on the theoretical frames employed and the findings reported. It is important to note that our intention was not to provide an exhaustive account of the mathematical knowledge required for teaching the area of plane surfaces that could be inferred from the corpus, as such an endeavor would have demanded considerably more time than was available. Below, we present the mathematical knowledge for teaching this topic inferred through a more in-depth analysis of the theoretical frames and results of the selected studies.

5. Mathematical Knowledge for Teaching the Area of Plane Surfaces Inferred from the Survey

The studies included in the corpus of this article—as well as many of the works referenced during the review process but not incorporated into the final selection—point to the difficulties encountered by both students and teachers in the teaching and learning of plane surfaces, along with the most frequent errors and misconceptions observed. Bellemain et al. (2018, as cited in Fraga, 2019, p. 54) identify several of the most recurrent issues:

confusion between different types of quantities (such as area and perimeter, or mass and capacity); the incorrect use or omission of measurement units (e.g., expressing area in centimeters or perimeter in square centimeters); and the application of inappropriate formulas (such as multiplying the side lengths of a non-rectangular parallelogram).

In addition to these common errors, other difficulties have been identified—for instance, understanding that the area of a figure can vary depending on the unit of measurement adopted (L. F. D. Ferreira, 2010, as cited in Fonda, 2020) and misconceptions also reported, such as

believing that “the area of a polygonal figure is proportional to the length of its sides—that is, if each side of the figure is doubled, then its area also doubles”; or that “figures with the same area necessarily have the same perimeter” (L. F. D. Ferreira, 2010, as cited in Fonda, 2020, p. 29); or even that the only way to compare magnitudes is through numerical values (de Brito & Bellemain, 2004, as cited in Braga, 2019), among others.

Kospentaris et al. (2011, as cited in Morais, 2022) administered a written test involving problems on the conservation and comparison of areas of plane surfaces to Greek high school seniors and first-year mathematics undergraduates. The results revealed several misconceptions, such as: “area equivalence is the same as congruence,” “non-congruent plane geometric figures cannot have the same area,” “the longer the sides of a plane geometric figure, the greater its area,” and, consequently, “the greater the perimeter, the greater the area” (pp. 51–52). Overall, the study indicated “that the concept of area conservation was not sufficiently consolidated among the students studied” (p. 52).

It is evident that the scientific community has expressed concern for decades regarding the teaching and learning of this topic. Nevertheless, persistent difficulties and misconceptions remain. The causes of these challenges are varied and complex. One possible way to address them and to develop strategies for overcoming such obstacles lies in a deeper understanding of the concepts underlying the construction of the notion of area. From this foundation, it becomes possible to design learning environments that are more appropriate to both the students’ developmental stage and the context of teacher education.

The most frequently adopted theoretical approach within the corpus is grounded in the work of Douady and Perrin-Glorian (1989) and subsequent research, particularly that developed by Bellemain and collaborators. This frame also stands out for the depth and consistency with which it is discussed across the studies. In what follows, we present a synthesis of the core ideas derived from this body of work, with the aim of analyzing its potential contributions to the development of professional noticing regarding the teaching and learning of plane surface area. While this synthesis is primarily based on the studies included in the corpus, in certain instances it was necessary to consult the original sources to clarify or elaborate on specific elements.

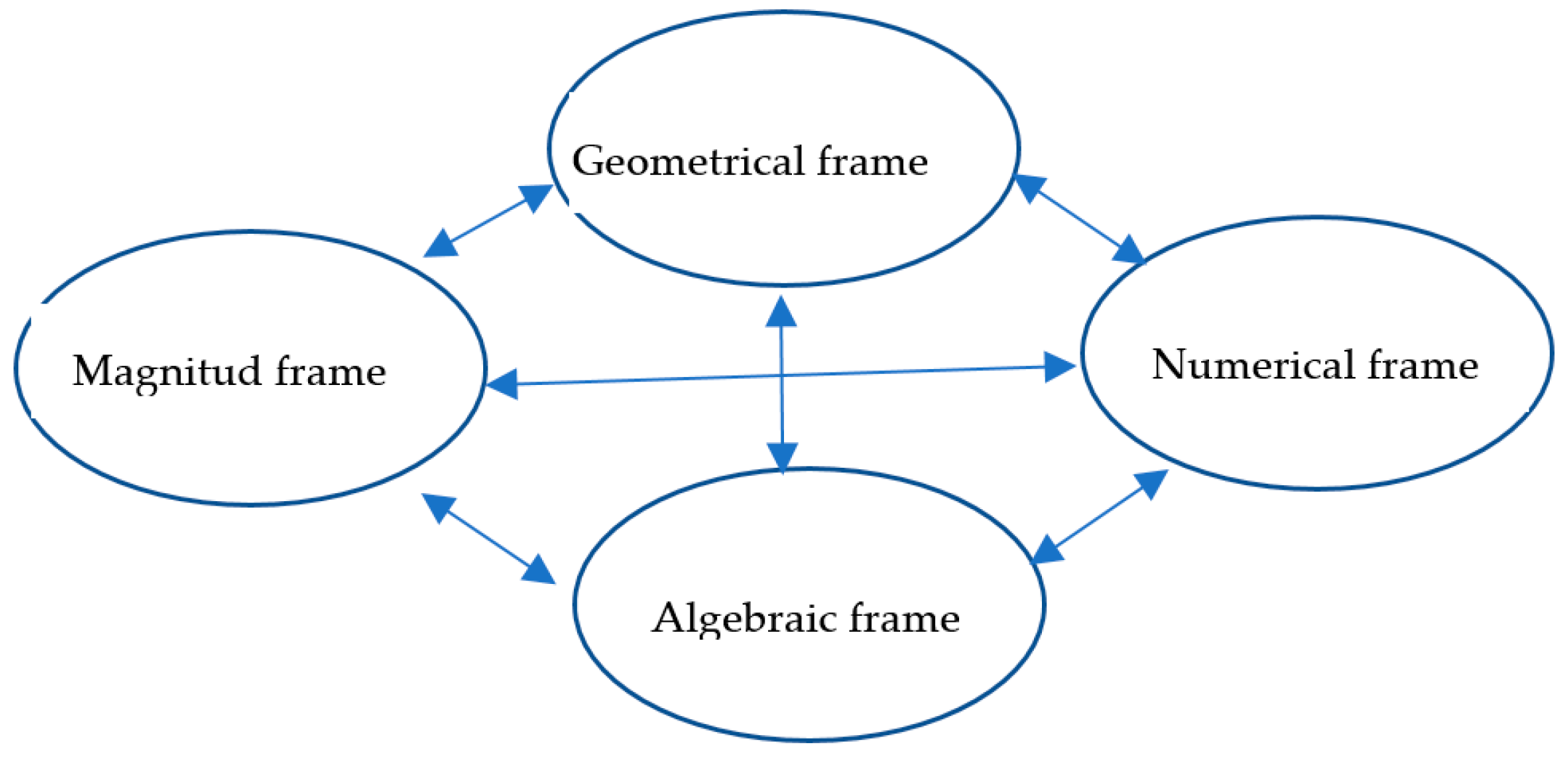
5.1. Approaching Area as a Magnitude from the Perspective of the Game with Frames

Professional noticing of students’ mathematical thinking when solving mathematical problems involving the concept of the area of plane surfaces requires mathematical knowledge specific to the teaching profession. Consequently, if teachers or prospective teachers possess only a formal, academic understanding of this concept, they are likely to have limited resources to comprehend and respond to their students’ reasoning and actions. In this context, school mathematics (Moreira, 2004) provides the most appropriate framework and tools to support teachers in professionally navigating such instructional situations.

In the case of the area of plane surfaces, approaching this notion as a magnitude can be understood from a mathematics perspective specific to teaching—namely, school mathematics—since it seeks to address the demands of the Basic Education classroom. Thus, considering area as a magnitude through the lens of the Game with Frames, as proposed by Douady and Perrin-Glorian (1989), provides, in our view, valuable elements for understanding this concept from the standpoint of school mathematics, thereby fostering the development of professional noticing. The following discussion will present this approach based on the research constituting the corpus of this study, along with some complementary references.

According to Deriard (2018), for more than a decade, Régine Douady supervised mathematics classes in the early years of basic education and implemented and analyzed teaching proposals in partnership with primary school teachers in Melun and Montrouge (France). In this process, she developed the notions of tool-object dialectics4 and the Game with Frames. This work culminated in her doctoral dissertation, defended in 1984. In it, Douady explains that she uses the term Frame (Cadre, in the original) because she understands that it “regroups, for a problem, the objects and their linked relationships, theorems, methods, diverse representation systems: figures, symbolic notations, formulas, tables, graphs. It is a part of a mathematical domain related to what we want to study” (Douady, 1984, translated by Deriard, 2018, p. 1098). In this sense, the Game with Frames involves

a transition from one frame to another allowing different formulations of a problem and a different approach to it. The Game with Frame allows a change in perspective in relation to the object. This new perspective allows the use of instruments that were not usable in a previous frame. […] A Game with Frame consists of working on the same mathematical question in two different domains. This allows one to move from one frame to another, facilitating the resolution of the problem. Then, one can return to the original frame after solving it.

(Deriard, 2018, p. 1099)

In 1989, in collaboration with Marie-Jeanne Perrin-Glorian—her research partner since 1975 in school-based studies (Deriard, 2018) Douady co-authored the article “Un processus d’apprentissage du concept d’aire de surface plane,” which is frequently cited in many of the studies forming the corpus of this research and serves as the theoretical foundation for several of them. In this work, the authors begin by examining the persistent difficulties commonly encountered by basic education teachers, concluding that

when addressing questions related to area, students sometimes conflated area with surface area (a characteristic the authors identified as geometric conceptions), at other times, they focused solely on the elements involved in the calculation, which was modeled as numerical conceptions. Furthermore, students often oscillated between these two types of conceptions without being able to effectively articulate the geometric and numerical knowledge required to solve area problems. These two conceptual poles (geometric and numerical) provided a frame for interpreting the common errors observed by teachers and documented in research.

(Bellemain et al., 2017, pp. 15–16)

This approach continues to predominate in Brazilian education. Morais (2022, p. 166) argues that “the conception of magnitude as number, developed by mathematics and other institutions,” should not serve as the primary reference in schools, as “the presentation of a definition, the abandonment of practical problems, the disregard for associated phenomena, and the dissociation between magnitude and number have proven unproductive from a teaching and learning perspective.” Moreover, although common pedagogical strategies based on visualization and manipulation are valuable and contribute to the construction of an understanding of the concept of area, they are not, in themselves, sufficient. In addition,

it is essential that the mathematical concepts associated with physical objects, drawings, and images be taught and learned simultaneously and progressively. These concepts and their interrelationships serve as abstract models of physical objects or as graphic representations thereof.

(Lima & Bellemain, 2010, as cited in Campos, 2021, p. 61)

According to Rogalski (1982, as cited in Bellemain et al., 2017, p. 17), understanding the relationships between different geometric magnitudes is a complex and long-term process. For example, in the relationship between length and area, “a dual process of differentiation and coordination is involved. One must simultaneously differentiate properties that are present within a figure (such as the length of its perimeter and the area of its surface) and coordinate these same properties when appropriating the formulas” (p. 17).

In this regard, Douady and Perrin-Glorian (1989, p. 138) argue that a powerful approach to overcoming such difficulties involves addressing the notion of area as an “autonomous magnitude, distinguishing area from surface, as well as area from number.” According to the authors, it is important to

differentiate between area and length even before introducing a method for measuring area—in particular, to distinguish between area and perimeter, which students tend to confuse. In fact, for many students, perimeter is perceived as another “measure” of surface. We postpone the identification between area and number based on the hypothesis that an early association between magnitudes and numbers fosters confusion between the different magnitudes involved (in this case, area and length).

(Douady & Perrin-Glorian, 1989, p. 138, our translation)

Considering area as a magnitude involves “distinguishing between area and figure (since different surfaces may have the same area), as well as between area and number (since measuring the area of a figure using different units yields different numerical values, although the area itself remains unchanged)” (Teles, 2007, p. 32). This perspective is also closely related to the notion of conservation. “Area conservation allows the individual to acknowledge that qualitatively different figures may be equivalent in terms of area. According to Kordaki (2003), understanding this concept requires the coordination of visual, numerical, and symbolic representations” (Teles, 2007, p. 41). For Kordaki (2003, as cited in Teles, 2007, p. 41), area—understood as the space enclosed by a figure—and the notion of area conservation “are preliminary concepts necessary for understanding the broader concept and measurement of area.” Thus, area can be understood as “a stable attribute—a definitive measurable dimension of the plane surfaces enclosed by figures. The notion of area conservation, framed in this way, is articulated with the idea of polygon equidecomposition and allows us to speak of area as a magnitude” (Teles, 2007, p. 41).

Teles (2007), drawing on Douady and Perrin-Glorian (1989), explains that understanding the concept of area as a quantity requires distinguishing and coordinating three distinct frames: geometric, numerical, and magnitude. According to the author, the geometric frame pertains to plane figures “such as triangles, squares, and figures with curvilinear boundaries; the numerical frame involves the measurement of surface area, interpreted as positive real numbers; and the magnitude frame refers to the construction of equivalence classes formed by figures that share the same area” (Teles, 2007, p. 32).

In addition to these, Bellemain and Lima (2002, as cited in Fonda, 2020, p. 67) propose the functional algebraic frame, which involves “formulas that express area in terms of lengths related to geometric figures.” According to the authors, the first three frames proposed by Douady and Perrin-Glorian (1989) allow for the analysis of situations in which the concept of area is understood as a one-dimensional magnitude. However, “area is also a two-dimensional magnitude in relation to length, and when the relationship between these two geometric magnitudes is addressed more directly, it becomes necessary to include length—like area—as an object within the frame of magnitudes” (Bellemain & Lima, 2002, p. 45). In this sense, it would be coherent to also consider the formulas that express area as a function of lengths related to geometric surfaces—what the authors term the functional algebraic frame. This expanded model could thus be represented as follows in Figure 1:

Bellemain et al. (2017, p. 4) emphasize that, in addition to distinguishing the frames represented in the diagram, it is essential to “establish meaningful connections between them.” That is, when measuring the area of a rectangular figure, we draw on geometric knowledge through the recognition of the object associated with the attribute being measured (surface), on magnitude-related knowledge through the selection of an appropriate unit of measurement (cm², m², etc.), and on numerical knowledge through the values obtained in the measurement process.

Thus, for example, the transition between the numerical and magnitude frames can be expressed by the pair (number, unit of measurement); that is, depending on the chosen unit, different pairs would represent the same surface, even though the surface itself does not change5. Similarly, the transition from the geometric to the magnitude frame occurs through the notion of equivalence—that is, by comparing surfaces with equal area. Observing these transitions enables students to recognize that two convex surfaces may have the same area without overlapping when compared, thereby highlighting the distinction between area and surface (L. F. D. Ferreira, 2010, as cited in Campos, 2021).

According to M. R. Santos (2015, p. 82), the frames are distinct but “intertwined with one another and represent some of the key foundational elements for the development of studies on the concept of area.” He offers the following examples: the equivalence relation, i.e., “having the same area” is the mathematical object that “enables the transition from the geometric frame to the magnitude frame. Likewise, the units of area measurement allow for the passage from the magnitude frame to the measurement frame, and the functions enable the transition from the geometric frame to the numerical one” (M. R. Santos, 2015, p. 82).

Frame shifting occurs when one transitions from one frame to another while solving a problem, whether spontaneously or not. However, according to Bellemain (2025, personal communication), frame shifts are the result of intentional teaching. In other words, the notion of frame shifting involves more than a spontaneous shift in perspective. Bellemain (2025, personal communication) explains, “in the very elaboration of the problems to be proposed to students, a priori analysis involves identifying the possibility and interest of shifting from one frame to another in order to objectify a different view of the problem and advance toward its solution”.

According to Douady and Perrin-Glorian (1989 as cited in Campos, 2021), transitions between frames facilitate a deeper understanding of the situation at hand and promote diverse problem-solving approaches, as well as the ability to distinguish between the object and the magnitude. As Campos (2021, p. 59) points out, “this distinction is fundamental, as it is possible to associate different magnitudes with the same object.” For instance, when employing different unitary surfaces that correspond to the same unit, the measurement remains unchanged. What does vary is the choice of area unit. As noted by Bellemain (2025, personal communication), “a small square with 1 cm sides constitutes a different unitary surface than a rectangle measuring 0.5 cm by 2 cm; however, both represent the same unit of area, namely one square centimeter.”

All the above highlights several central elements for developing situations that give meaning to the concept of area:

-

Surfaces (objects of the geometric frame), understood here as “geometric objects of which area is an attribute. In relation to surfaces, an important aspect to emphasize is the frequently overlooked distinction between concrete objects (e.g., the surface of a table) and abstract objects (square, rectangle, …)” (Bellemain et al., 2017, p. 46).

-

The equivalence relation “having the same area” (an object that allows for transition from the geometric frame to that of quantities).

-

Areas (objects of the frame of quantities), understood as “a type of quantity that relates to other types of geometric quantities: length, volume, angle aperture. This term will designate both the type of quantity and a particular value of that type of quantity (e.g., the area of a given square)” (Bellemain et al., 2017, p. 46).

-

Units of area (an object that enables the transition from the frame of quantities to that of measurements).

-

Measures of areas—positive real numbers (objects of the numerical frame) (Bellemain & Lima, 2002, apud Fonda, 2020, p. 66).

Baltar (1996, as cited in Campos, 2021) proposed three categories of situations that confer meaning to area as a magnitude: comparison, measurement, and production. This frame is theoretically grounded in the Theory of Conceptual Fields developed by Gérard Vergnaud and has served as the foundation for numerous studies conducted in Brazil.

According to Bellemain and Lima (2002, as cited in Fonda, 2020), comparison situations are fundamentally situated within the frame of magnitudes. Thus, when comparing two surfaces, although the geometric and numerical frames are often necessary to carry out the comparison, their role can be regarded as secondary to the frame of magnitudes, since it is essential to determine whether the surfaces belong to the same equivalence class. In measurement situations, the numerical frame and the transition from magnitude to number, achieved through the selection of a unit, are particularly prominent. “The expected result in a situation of this type is a number followed by a unit” (Bellemain & Lima, 2002, as cited in Campos, 2021, p. 60). Production situations differ from comparison and measurement situations in terms of the cognitive demands placed on the student. While in the first two types there is generally only one correct answer per situation, production situations often allow for multiple correct solutions. Moreover, although the expected outcome in a production situation is a surface (a geometric object), the involvement of other frames can be just as significant as that of the geometric frame (Bellemain & Lima, 2002, as cited in Campos, 2021, p. 60).

In summary, conceiving area as a magnitude and adopting the “Game with Frames” (along with its developments informed by Brazilian research) as a frame for teaching the concept of area on plane surfaces are powerful pedagogical approaches. These perspectives enable a more nuanced interpretation of the errors and difficulties encountered by students, as well as by teachers and prospective teachers. Furthermore, they offer valuable insights for the design of instructional strategies aimed at addressing such challenges. In this sense, they may be regarded as essential mathematical knowledge for teaching area and can significantly contribute to the development of a professional and reflective stance on this subject.

5.2. Implications for the Development of Professional Noticing on the Concept of Area of Plane Surfaces

The notion of area of plane surfaces is usually addressed in initial mathematics teacher education from the perspective of academic mathematics. That is,

Given an area function f, defined on a set of measurable surfaces, there exists a subset of surfaces such that all sur-faces belonging to it have the same area. This subset is called an equivalence class of surfaces with equal area.

The set of measurable surfaces can thus be partitioned into disjoint equivalence classes, each consisting of surfaces that share the same area. Importantly, these classes are independent of the specific area function chosen. The collection of these equivalence classes, denoted by S, constitutes the set of all possible areas.

Given a surface A, its corresponding equivalence class, denoted by [A], represents the area of A, that is, the set of all surfaces that possess the same area as A, regardless of the area function used. Typically, an element of this set is represented as U, where u denotes the numerical measure of the area and U represents a chosen unit surface. The area of the unit surface U is referred to as the unit of area, while u indicates the measure of the area of A relative to that unit.

Within the set of equivalence classes thus defined, it is possible to establish an order relation and define two operations: the addition of two classes and the multiplication of a class by a real number. These operations satisfy properties analogous to those of a one-dimensional vector half-space over the real numbers. The set S therefore constitutes a mathematical structure that enables the abstract treatment of the concept of area, representing, in fact, a particular instance of a quantity domain.

(Bellemain & Lima, 2002, p. 124)

This understanding of the notion of area aligns with the discussions characteristic of academic mathematics. Given its axiomatic structure, all definitions are derived from an exceptionally precise formulation, since ambiguities in the characterization of a mathematical object may lead to contradictions within the theory (Moreira, 2004, p. 23). “Formal definitions and rigorous demonstrations constitute essential elements both in the development of the theory itself […] and in the systematic presentation of the theory once it has been established” (Moreira, 2004, p. 24). However, in the context of mathematics education at the basic level, the primary concern does not lie in the validity of mathematical results—given that such validity is, a priori, ensured by the discipline of academic mathematics. Rather, the central issue involves the development of a pedagogical approach that promotes students’ understanding of mathematical facts and the construction of justifications that enable them to apply these concepts coherently and appropriately in both academic and everyday contexts (Moreira, 2004, p. 24). Nevertheless, in the context of mathematics teaching at the basic education level, the central concern is not the validity of mathematical results—since such validity is already established a priori by academic mathematics itself. The central pedagogical challenge, rather, lies in developing teaching practices that foster students’ understanding of mathematical facts and in constructing justifications that enable them to employ such knowledge coherently and appropriately in both their academic and everyday lives (Moreira, 2004, p. 24).

In the context of Brazilian basic education textbooks, the notion of area can be presented in different ways. Amaral et al. (2025, p. 9) aims to understand the different approaches to the concept of area presented by ten collections of mathematical textbooks for high schools. According to the authors,

Regarding conceptualization, most books define Area as the numerical result of comparing a region to a unit of measurement. There are other perspectives, such as in book E5 (p. 24), for example, which defines Area as a positive real number: “The portion of the plane occupied by a polygonal surface corresponds to a single positive real number A called area, obtained by comparing the portion occupied by the polygonal surface with the portion occupied by a unit of area measurement.” In addition, we also find area as a sum of other areas, specifically unit squares (e.g., B2, p. 116); unit squares as a unit of measurement, using the notation u! (e.g., E5, p. 24); and the use of formulas or approximation methods to determine area (e.g., I10, p. 31).

(Amaral et al., 2025, p. 9)

However, the analyzed corpus revealed that not only students in basic education exhibit errors, difficulties, and misconceptions related to the concept of area of plane surfaces. Several studies have also identified significant challenges among in-service and prospective teachers, particularly those working in the early years of schooling. According to Baturo and Nason (1996, as cited in Braga, 2019, p. 20), neither practicing teachers responsible for teaching mathematics in the early grades nor future primary education mathematics teachers (FPEM) possess adequate knowledge about the topics of area and perimeter, the concept of measurement, or “the role of formulas in learning the concept of area.”

In her literature review, Braga (2019, p. 21) found, among other things, that

Many (FPEM) have a limited repertoire of knowledge related to the study of these concepts, and such difficulties are not adequately addressed in initial teacher education programs.

(Baltar, 1996; Baturo & Nason, 1996; Bellemain, 2003; Figueiredo & Silva, 2019; Huang & Witz, 2013)

Such difficulties persist over time. Reinke (1997, as cited in Braga, 2019, p. 20), in analyzing the problem-solving strategies adopted by prospective teachers, observed that they were “as naive as those of ninth-grade students” and drew attention to the fact that “there were few studies investigating how these future teachers approach or learn perimeter and area, how they understand the nature of these concepts, and how they explore and diagnose the use of strategies.” Slightly more than twenty years later, Figueiredo and Silva (2019, as cited in Braga, 2019, p. 20) observed in their studies that

the analysis of the collected data revealed gaps in both common and specialized knowledge regarding area and perimeter. In addition, it was noted during the course that it was necessary to introduce the topic from the perspective of measurement and to promote reflections on research findings as well as on different strategies and methodologies related to the teaching of area calculation for plane figures.

If we consider the main difficulties related to learning about the area of plane surfaces as identified in the literature, we can establish a solid starting point for reflecting on the implications of adopting the ideas proposed by Douady and Perrin-Glorian (1989), as well as by Baltar (1996) and Bellemain and collaborators, for developing a professional noticing technique for students’ thinking regarding this topic. Understanding area as a magnitude whose comprehension is built through the interplay of different frames (geometric, numerical, magnitude-based, and algebraic) opens up meaningful possibilities for observing how students approach situations involving the area of plane surfaces and for making sense of their responses and written work. Moreover, a deeper interpretation of these responses, grounded in an understanding of the concept of area, would also support the design of strategies aimed at overcoming errors, difficulties, and misconceptions.

Some findings from this review could directly contribute to the design of tasks and the creation of a more productive learning environment. For example, in the empirical part of their studies, Douady and Perrin-Glorian (1989) sought to develop the notion of area with children in a way that was meaningful to them. To this end, they made “didactic choices based on games involving numerical frames, surfaces, areas, and numbers, in which the frames differed in terms of their objects” (p. 417). Some proposed tasks “aimed to make the comparison of areas conceivable without recourse to measurement,” while others “focused on the comparison and calculation of areas using measurement in the case of pavable surfaces with ‘foreign’ elements (non-overlapping or not derived from the subdivision of one of them)” (p. 417). They observed that this type of approach facilitated students’ understanding of the topic by allowing them to “expand the range of surfaces they knew how to measure with a given unit to include surfaces that could not be tiled with that unit,” as well as to realize “that it is possible to express the area of a triangle, a parallelogram, or another surface in cm², and that cm² represents the area of a surface that can take on very diverse shapes” (pp. 417–418). In other words, these didactic choices enabled a “distancing from the conception of area tied solely to shape” (Douady & Perrin-Glorian, 1989, p. 418).

This study and several others have highlighted tiling/paving and “cutting and pasting” without loss or overlap as interesting (and perhaps even necessary) strategies for the process; however, these strategies alone proved insufficient. Although area conservation was observed in both classes that participated in the study, Douady and Perrin-Glorian (1989, p. 418) found, following the development of the didactic sequences, that

this progression is not necessarily an immediate outcome following instruction. At this stage, in CM1, appropriate cutting and pasting for comparing the areas of familiar surfaces served as merely an operational tool for about half of the students. In both classes, some students still confused area with perimeter. Others relied excessively on numerical values by using the lengths of dimensions. Finally, some strongly employed a “deformation” perspective, transforming familiar surfaces (in this case, parallelograms) into more familiar shapes with which they felt comfortable working (rectangles). The deformation in the context examined could either preserve area (sliding one side of the parallelogram along its base) or not preserve it (hinging two lines around the vertices).

The experience demonstrated that the planned frame games were insufficient and that it was important to consider both the static and dynamic dimensions. According to Morais (2022, p. 36), drawing on Douady and Perrin-Glorian (1989), the static–dynamic relationship “expands the geometric frame by introducing different perspectives on surfaces, where the former privileges the descriptive aspect, while the latter focuses on the effects of actions upon them.” This expansion produces “a new type of object, a family of surfaces, which, by enabling new questions, helps students reject erroneous conceptions” (p. 36). For example, consider an articulated parallelogram represented in the Figure 2 below. If we assume its dimensions are rigid bars (of fixed length) that can be rotated around the vertices, how would the lengths of the sides, diagonals, perimeter, and area vary? (Morais, 2022).

According to Morais (2022, p. 42), “the continuous transformations described above occur within a dynamic frame.” By moving from a static viewpoint to a dynamic one—where the figure “deforms” while preserving its characteristics (in particular, areas and side lengths in the case of (a) sliding and (b) articulation)” (p. 42)—students are internally challenged. For example, some students perceive a parallelogram merely as a tilted rectangle and attempt to “straighten” the parallelogram to obtain a rectangle of the same area. These students become even more convinced of their approach because the parallelogram appears to them as a slightly ‘deformed’ rectangle (with sides slightly inclined). In doing so, students deviate little from the initial situation, which provides them with an illusion of stability. To move beyond this perspective, it is necessary to dissociate the initial and final states, considering them as two deformation states that can be pushed to limiting cases in order to amplify their effects: a highly elongated parallelogram in case (a) and a very flattened one in case (b). This perception compels doubt but does not immediately require the abandonment of initial beliefs (Morais, 2022, p. 42).

This is just one example of the mathematical knowledge specific to teaching regarding the construction of the concept of area of plane surfaces, which can be inferred from the studies comprising the corpus of this review, as well as from the literature underpinning them. The conceptualization of area as a magnitude, as well as its treatment through the Game with Frames, can be understood as a form of school mathematics. This characterization is justified by the fact that these ideas were primarily developed through studies centered on the mathematics classroom and the teaching practices of educators operating within that context. Furthermore, they reflect an effort to construct a perspective on mathematics that is responsive to the specific demands and realities of the basic education setting. Thus, by promoting an understanding of the concept of area that is more closely aligned with the demands of its teaching and learning, this approach also contributes to the development of professional noticing regarding students’ responses to tasks related to the topic.

6. Conclusions

Developing professional noticing techniques for students’ responses and records related to situations involving the concept of area of plane surfaces requires mathematical knowledge specific to teaching. This idea is strongly supported by the research comprising the corpus of the present study. For example, Lessa (2017, p. 181), upon “observing the praxeologies of participating teachers,” noted that, essentially, their practice involved “applying formulas without an explicit justification of the reasons that led them to develop such techniques”. This choice emphasizes the predominance and valorization of the numerical aspect and tends to potentially “hinder the understanding of the concept of area as a magnitude” (Lessa, 2017, p. 181).

However, findings from Lessa (2017), Fraga (2019), Campos (2021), among others, provide evidence that formative actions aimed at expanding the understanding of the concept of area—particularly perceiving it as a magnitude—as well as the study of the frames involved in constructing this notion and their embodiment in the collective development of tasks and teaching proposals, contributed significantly to the teachers participating in the study.

The theoretical frames adopted in the studies that comprise the corpus of this article are varied and, in some cases, reflect perspectives on appropriate mathematics for teaching that differ from the one adopted here. Nonetheless, we recognize that these frames provide valuable contributions that can be interpreted and analyzed from a specific viewpoint. Grounded in the premise that the mathematics appropriate for teaching is school mathematics (Moreira, 2004), we examined the findings of each study with the aim of inferring mathematical knowledge for teaching plane surfaces that may support the development of professional noticing regarding the topic.

In this regard, we understand that the theoretical frame briefly discussed here has the potential to be recognized within the perspective of school mathematics as mathematical knowledge specific to teaching and, consequently, could contribute to the development of professional noticing regarding students’ responses and records.

We understand certain limitations—for example, the fact that most of the studies have been conducted with teachers from the early grades. Nevertheless, the discussion presented here can serve as a starting point for future research. Furthermore, this article opens an interesting window by creating connections between theories and theoretical frames that are not often brought together in research. Thus, although the conception of mathematics present in French Didactics tends to differ from school mathematics (Moreira, 2004), we believe it was possible to indicate potential intersections or, at the very least, opportunities for dialogue between these two approaches. Similarly, other frames may also engage in dialogue to contribute to the formation of bodies of knowledge related to the various domains involved in school mathematics, thereby benefiting both initial and ongoing teacher education as well as the professional development of mathematics teachers.