Using a Multi-Agent System and Evidence-Centered Design to Integrate Educator Expertise Within Generated Feedback

Abstract

Generative AI (GenAI) can support mathematics teacher learning by automating parts of teacher rehearsals, or opportunities for teachers to practice specific mathematics teaching skills, receive feedback, and refine their approaches. However, little is known about how to design GenAI solutions that incorporate the expertise of mathematics teacher educators into the design of GenAI solutions. This article proposes a three-part design framework: first, by building on the modeling logic from evidence-centered design (ECD) to develop design templates that capture the complexity of mathematics teaching; second, by translating the expertise from these templates into prompts for GenAI; and third, by sharing how a multi-agent system that uses GenAI to simulate teacher rehearsals and feedback can keep the complexity of that expertise by splitting it across agents. We explore how this framework could serve as a general approach for designing simulations—both in its theoretical foundation and technical implementation—that support complex, interactive rehearsals intended to enhance teacher learning.

1. Introduction

Enacting the key skills of mathematics teaching (such as posing purposeful questions) is contingent upon variables that make each teaching decision slightly different (National Council of Teachers of Mathematics, 2014). For instance, what a teacher says during a class period depends on the focal mathematical content that day and the mathematical task (or discussion-worthy problem) the teacher assigns to their students to engage with that content. Further, a teacher responds to the student ideas that emerge during the specific class period. When a teacher poses purposeful questions, the types, phrasing, and sequence of those questions change in relation to which student ideas emerge about a mathematical task (B. A. Herbel-Eisenmann & Breyfogle, 2005; Jacobs et al., 2010; Smith & Stein, 2011). Although a teacher may teach that lesson multiple times a day, there are limited moments where a teacher gets to pose purposeful questions with the same combination of mathematical content, tasks, and student ideas. The rarity of moments to enact key skills of mathematics teaching, compounded with the fact that each moment consists of a different combination of mathematical content, tasks, and skills, makes it challenging for teachers to improve (Ball & Forzani, 2009; Franke et al., 2007; Smith & Stein, 2011). To become better at teaching, teachers need opportunities to repeatedly try such skills under similar conditions outside of the classroom.

The field of mathematics teacher education emphasizes using rehearsals to help teachers improve their implementation of key teaching skills. Rehearsals are carefully designed scenarios that address the complexity of classroom settings by allowing teachers to enact essential components of mathematics teaching skills and receive feedback outside of the classroom (Grossman et al., 2009a, 2009b). To make rehearsals more accessible, digital simulations, or rehearsals in computerized settings, allow teachers to practice skills by responding to digital actors (such as a student or coach) with pre-designed knowledge and behaviors within a simulated classroom environment (Cohen et al., 2020; Mikeska et al., 2024a; Thompson et al., 2019). Although digital simulations may differ visually, they generally involve verbal exchanges between a teacher practicing a skill, students responding to the teacher and each other, and a coach providing feedback—all within a specific classroom context (Figure 1). The ability to design these components enables integration of different mathematical content, tasks, and student ideas within a specific setting, thereby facilitating opportunities for teachers to rehearse important mathematics teaching skills (Grossman et al., 2009a; Kavanagh et al., 2020b). For this reason, digital simulations have increasingly been endorsed and adopted by mathematics teacher educators and instructional coaches, offering teachers opportunities to rehearse key mathematics teaching skills using online platforms (Cohen et al., 2020).

Generative AI models (GenAI) are used to automate specific verbal and text-based parts of digital simulations (henceforth simulations), supporting mathematics teachers’ learning and making rehearsals more accessible. Before advances in foundation models (i.e., GenAI models like ChatGPT-4o and Gemini-2.5-pro, which are pre-trained on vast datasets covering many purposes and use cases to generate multimodal outputs through prompting), some simulation platforms used few-shot training of GenAI models with large, context-specific large language datasets to automate pre-designed feedback based on how a teacher’s response was categorized (e.g., Hillaire et al., 2022; Thompson et al., 2019). Simulations with fine-tuned GenAI models trained on even larger datasets provided feedback on a teacher’s responses within a simulation and/or generated how a student might respond to a teacher’s response. (e.g., Copur-Gencturk & Orrill, 2023; D. Lee & Yeo, 2022; Mikeska et al., 2024b; Son et al., 2024). However, developing few-shot and fine-tuned simulation tasks is both time-consuming and expensive (Alier et al., 2024). There is a need to understand how GenAI can provide expert-level feedback to a teacher’s verbal rehearsal without the need for prior data and model training (Aperstein et al., 2025; U. Lee et al., 2023). Foundation models offer a promising opportunity to expand access to simulations for teachers to practice key mathematics teaching skills by using prompt engineering to automate parts of rehearsals.

However, the flexibility of prompt engineering raises concerns about how to address the complexity of teaching mathematics in simulations that use foundation models. Current simulation designs using this approach offer direct and focused opportunities for teachers to practice foundational teaching skills, such as using prescribed talk moves (e.g., “Can you say more?”) within pre-designed scenarios. These opportunities use simple prompt engineering techniques to incorporate cognitive and behavioral elements that generate student responses (e.g., Bhowmik et al., 2024; U. Lee et al., 2023; Mikeska et al., 2025). Some designs have even expanded this structure to include creating mentors who provide real-time feedback (e.g., Aperstein et al., 2025; Bywater et al., 2019). While essential for teachers to rehearse initial teaching skills, these simulations often limit opportunities for teachers to practice ways that more authentically reflect the complexity of classroom life, especially regarding the connections between mathematical content, tasks, and student ideas (Barno et al., 2024). Although early-career teachers benefit from rehearsals that decompose and simplify, there remains an open question about how to best incorporate the complexities of teaching into simulations that leverage foundation models.

Our goal in this paper is to propose a design method that draws on content-based expertise to translate pedagogical and disciplinary frameworks into prompts within GenAI-powered simulations. We address this simulation design challenge with a three-part approach: first, by using a design framework that draws directly from research in mathematics, educational pedagogy, and learning to populate design templates; second, by translating the information in the design templates into clear prompts to assign actors within a simulation to function appropriately; and third, by illustrating how a multi-agent system, when serving as the back-end of a simulation, can offer feedback and student responses to teachers rehearsing specific teaching skills that leverage the above expertise and prompting.

We view this design approach as an important contribution that proposes a formal process integrating the types of pedagogical knowledge needed to effectively conduct mathematical teaching practices (Ball & Bass, 2002) and the design of GenAI-powered simulations focused on mathematical teaching practices. This process leverages design logic by focusing attention on the content knowledge teachers need to use in practice, how they use this knowledge to teach mathematics, and how GenAI components influence that usage within a simulation (Mislevy & Haertel, 2006). We see this theoretical and design work as a critical first step toward supporting the field in designing simulations that can be used for future empirical work that explores the extent to which simulations perform as design, to what extent the simulations provide teachers opportunities to practice and receive appropriate feedback, and how these practice opportunities can be used to support professional learning.

To share our approach, we describe a mapping process that translates the expertise above into design templates, which are then converted into GenAI prompts. By applying best practices in prompt engineering alongside disciplinary expertise embedded in the design templates, the prompts are crafted to include disciplinary specificity, making the information easier for GenAI to interpret and act upon within simulations without compromising the epistemological foundation. Finally, we connect each template to a specific agent prompt that embodies the domain knowledge within the actions of the multi-agent system, ensuring clear communication of these details through the agents’ behavior.

2. Literature Review

Below, we outline how much teachers must learn about mathematics and its pedagogy to deliver content-specific instruction. We also highlight the challenges faced by teacher educators who support mathematics teachers in improving their teaching practices, especially during classroom rehearsals. This information provides context for recent efforts to create tasks that allow teachers to rehearse small components of mathematics instruction, particularly in digital formats. Together, these sections show the importance of rehearsals in supporting teacher learning, the challenges in how rehearsals use GenAI, and the potential for specific ways that foundation models can enhance the theoretical and practical aspects of teaching.

2.1. The Complicated Work of Mathematics Teaching

When entering the classroom, teachers are expected to implement high-leverage mathematics teaching practices (MTPs), which are specific skills identified by mathematics education research as effective in enhancing students’ mathematics learning (National Council of Teachers of Mathematics, 2014). Enacting MTPs in the classroom is a complex process that requires deep knowledge and skill. In preparation for the interactive nature of teaching, a teacher must select a mathematical task (or discussion-worthy mathematical problem) that intentionally emphasizes a central idea within grade-level mathematics standards, while also preparing for how students might respond or struggle with the task to support them in achieving a related learning objective (National Council of Teachers of Mathematics, 2018; Smith & Stein, 2011). Moreover, a teacher needs to understand examples of MTPs and consider ways to use them to encourage students to share their mathematical ideas related to the task. These behind-the-scenes decisions foster student-centered discussions, where a teacher’s use of MTPs promotes students’ argumentation and collective reasoning by carefully sequencing and responding to students’ ideas (Smith & Stein, 2011). Enacting MTPs involves a teacher synthesizing students’ work across various levels of mathematical precision or fluency and valuing a range of students’ thinking by thoughtfully connecting different representations (such as drawings, tables, algebraic expressions, or verbal descriptions). This occurs when a teacher uses MTPs to facilitate a whole-group discussion focused on students’ contributions, guiding them toward an intended learning objective. Enacting an MTP requires a teacher to interpret a task, anticipate possible student responses across all representations, and employ MTPs throughout a mathematical discussion in a way that encourages students to engage with and understand a mathematical idea.

After enacting one MTP, teachers face additional work to connect to and enact the next MTP. Because MTPs involve responding to students’ ideas about a particular task, enacting a sequence of MTPs requires teachers to re-synthesize their understanding of mathematical content with pedagogical strategies specific to teaching mathematics (B. A. Herbel-Eisenmann et al., 2013; Kavanagh et al., 2020a). Deciding which MTP to use means that, at a baseline, a teacher must grapple with key ideas behind a mathematical content area, the task presenting that content, and the students’ ideas during that class period (B. Herbel-Eisenmann & Wagner, 2010; Smith & Stein, 2011). However, deciding how to enact an MTP reveals the relational complexity between the mathematical content, the way that content exists within a particular mathematical task (such as the problem itself or the discussion surrounding that task), and interpreting and elevating student ideas. In other words, each singular utterance made by a teacher that is an MTP indicates that the teacher is considering, unpacking, and acting upon those components before the teacher speaks again. Knowing that a teacher can utilize many MTPs in a whole-group discussion, enacting an MTP requires more than simply knowing what an MTP is and the content being taught.

Because MTPs are intricately woven into the mathematical content being taught, the task that presents the content, and the students’ ideas shared during a specific classroom moment, a teacher usually has only one (or, at most, a few) chances to improve their use of MTPs within those same or slightly varied components. Teachers have limited opportunities to implement, receive feedback on, and practice MTPs outside of actual classroom interactions (Grossman et al., 2009b). Teachers aiming to improve their use of MTPs benefit from multiple chances to practice MTPs with the same components before they need to adjust to different combinations of content, tasks, and ideas (Ghousseini, 2015; Lampert et al., 2013).

2.2. The Complicated Work of Supporting Mathematics Teacher Learning

To improve their use of MTPs, teachers benefit from multiple opportunities to practice them and receive feedback, which can guide and enhance their decision-making. Unfortunately, classroom observations and professional learning often lack chances to practice, reflect on, and refine the MTPs they are using (Ball & Forzani, 2009). When teachers do get feedback on their instruction, it is often too complicated, confusing, or so infrequent that it fails to lead to real improvements (Grossman et al., 2009b; Reich, 2022). Despite the known difficulty of enacting MTPs, teachers typically lack chances to develop their skills before they are expected to implement them seamlessly during classroom instruction (Barno et al., 2025; Benoit et al., 2025).

This challenge has encouraged mathematics teacher educators to develop rehearsals for teachers to experiment with, reflect on, and deepen their understanding of how to use MTPs in ways that are closely aligned with mathematical content standards. One form of rehearsals includes digital simulations, which have been used for teachers to practice skills by making decisions within animations and choose-your-own adventure online scenarios containing classroom contextual elements, or in response to human-controlled avatars (Herbst et al., 2014; Mikeska et al., 2023; Reich, 2022). Rehearsing and receiving actionable feedback while enacting an MTP within a digital simulation breaks down the complexity of mathematics teaching into smaller, more manageable parts (Grossman et al., 2009b; Shaughnessy et al., 2019). In other words, teachers can practice small teaching components within a specific context, get targeted feedback, and immediately work on refining those components multiple times to improve. Simulations give teachers opportunities to experiment with, reflect on, and build their understanding of how to effectively use MTPs in ways that are closely tied to content standards.

2.3. Using Foundation Models to Support the Complicated Work of Mathematics Teacher Learning

Foundation models, which have drastically improved in the past two years, have been named as a potential solution for efficiently implementing simulations at low cost (Alier et al., 2024). However, there is an ongoing tension between the potential of foundation models for generating simulations that support teachers to rehearse MPTs and receive feedback and the concern that GenAI misrepresents and oversimplifies the complexity of teaching (Chiu et al., 2023). This tension stems from the disconnect between the complexity of classroom teaching, the many detailed components of teaching, and how that complexity is represented and used in prompting foundation models within simulations. In mathematics teacher education, the essential information included as components within any enactment of an MTP involves mathematical content, tasks, student ideas, and student utterances within a specific context (Ball et al., 2008). If a prompt to a foundation model aims to appropriately guide the behavior of generated students and provide feedback, the details within each prompt must rely on some iteration of these variables. The output, therefore, aligns with expertise in mathematics teaching (U. Lee et al., 2023). The continuous generation of student responses and feedback needs to be produced while considering what a teacher says to initiate a rehearsal, as well as what is generated as the student replies and pedagogical feedback. Addressing the complex interactions within a generated conversation guided by prompts is possible if such necessary details behind the mathematical content, tasks, and student ideas are included in the prompts and are understandable by the foundation model (Park et al., 2023).

One way to develop GenAI simulations that accurately reflect the complexity of MTPs is through a prompting structure that serves as a container for the essential domain expertise needed for the rehearsal. A prompt can specify what a rehearsal aims to evoke or encourage a teacher to do, such as enacting an MTP. Since a rehearsal provides an opportunity to enact that MTP, a designer must understand the key features a teacher needs to demonstrate in response to the contextual elements of a classroom scenario. This understanding involves recognizing how students should behave during such a rehearsal—including how they solve the task and articulate their work in response to the teacher’s questions—ensuring that teachers’ enactment of an MTP contextualizes the mathematical content, task, and student ideas. Collectively, these challenges offer an opportunity to design rehearsals that give teachers new practice experiences and immediate, targeted feedback by utilizing foundation models.

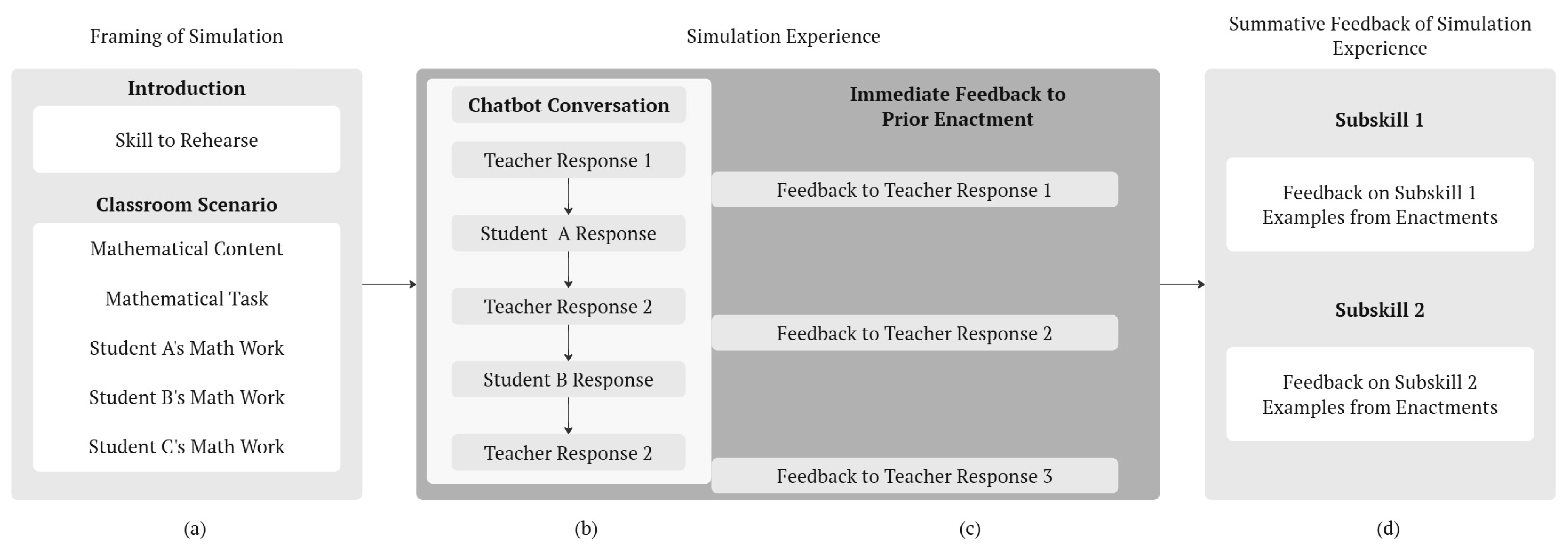
3. Evidence-Centered Design Modeling Logic to Design Templates

Here, we present a key component of our design argument for how simulations can utilize foundation models with specially designed prompts to generate targeted and controlled content. We introduce a framework inspired by evidence-centered design (ECD) that delineates the mathematical and pedagogical expertise that needs to be represented within prompts (e.g., Mislevy et al., 2004). The prompt, which serves as a container for this expertise, provides the domain expertise to perform specific tasks necessary for creating a theoretically sound simulation. This structure addresses the need to understand mathematics teaching and the theoretical perspective that a rehearsal for teachers cannot be effectively designed without a deep understanding of what teaching involves.

3.1. Overview of Evidence-Centered Design

ECD, although typically a process for assessment development, contains a useful logic to structure the design of simulations using GenAI. ECD specifies the nature of opportunities within an assessment that elicit evidence of a user’s ability. This evidence, in turn, is used to make inferences about a user’s capabilities. To depict a scenario or assess actions within it accurately, ECD provides a method for modeling complex activities within components that are both digestible and detailed. First, ECD focuses on simplified structures to handle the complexity of practices like mathematics teaching. These structures, referred to as models, highlight the key elements of the intricate parts, ensuring they are broken down and presented clearly. Modeling builds on ECD’s foundational understanding that to depict a scenario or assess actions within it accurately, an assessment designer must consider such details within a given model. Together, ECD clarifies the importance of laying out what inferences an assessment designer can make about a user, what evidence they need from the user’s performance within the assessment to make such inferences, and how a particular assessment task design would elicit that type of performance. To use the logic behind modeling, simulations should intentionally attend to the detailed reasoning that shapes and organizes all components, particularly those generated from prompting a foundation model, to understand actions within it accurately.

As ECD emphasizes the integration of expertise within models, incorporating ECD modeling logic into the design of simulations could help the design attend to essential theoretical aspects of mathematics teaching. First, the expertise needed for simulations to create opportunities for teachers to enact MTPs includes knowledge of mathematical content and specific student work on a particular math task. These components, deeply integrated within full-group discussions about a mathematical task, influence how a teacher implements MTPs. Any simulation using GenAI creates novel details influencing specific enactments of MTPs from teachers as a demonstration of their complex understanding. The directions within a GenAI prompt, therefore, should incorporate that expertise into both the design and the resulting generated components. Consequently, to determine whether an enactment of an MTP is a high-quality enactment within a simulation using GenAI, the enactment must be evaluated based on all present elements that should guide how a teacher implements an MTP. Those elements, due to their influential nature, must be crafted to create opportunities for teachers to demonstrate high-quality enactments of MTPs throughout a simulation. The complexity of classroom contexts and the enactment of MTPs offer chances to rehearse MTPs in an equally sophisticated manner, as the design of a simulation may better address that complexity using ECD modeling logic.

3.2. Relevance of ECD’s Modeling Logic to Simulation Design

To illustrate how modeling logic from ECD is useful within simulation design, consider the general steps to model the expertise within a teacher’s enactment of MTPs. A designer first should break down the complex prerequisites for enacting a specific MTP or sub-skill. To illustrate, consider the MTP of posing purposeful questions (National Council of Teachers of Mathematics, 2014, 2018). Posing purposeful questions requires synthesizing specific mathematical content as represented in a mathematical task and described within student thinking. So, a simulation meant to elicit a teacher’s enactment of posing purposeful questions should contain these elements of a whole-group mathematics discussion, in a similar sequence to a real classroom (e.g., accessing the mathematical content and task before enacting MTPs within a discussion with students). To do this, a designer should ensure these components are not only present within static components of a simulation (e.g., being shown the mathematical content and task before enacting an MTP), but also change across the simulation (e.g., enacting MTPs in response to a sequence of student ideas that respond to each enactment). With access to these static and changing components within a simulation, a teacher has an opportunity to enact an MTP in response to student work on mathematical features stemming from a specific task. Finally, evidence, or enactments by a teacher, can be elicited within a simulation and shape potential claims about the mathematical discourse. For example, if a simulation does not allow teachers to draw mathematical diagrams as part of their questioning or view visual diagrams of students’ work, then a teacher’s enactment of posing purposeful questions will only focus on the verbal discourse they use or the student’s response. Although this limits some aspects, the constraints on a teacher’s response shape the types of claims that can be made, focusing only on the interaction between a teacher’s response, the feedback generated, and the student’s response.

When simulations incorporate GenAI, it is important to pay close attention to the domain-specific expertise included within a prompt. Remember that a teacher’s specific enactments of MTPs within a simulation are intended to showcase their complex understanding. Any simulation that uses foundation models should be designed so that a teacher can demonstrate an MTP by breaking it down and including relevant details in the prompts for generated components. This approach indicates that the MTP skill being demonstrated can be considered within a context that incorporates domain expertise in both the design and the GenAI components of the simulation. Therefore, to judge whether an enactment of an MTP is high-quality, it must be evaluated based on all pertinent elements within the simulation that inform how a teacher applies an MTP. Because of their influential nature, these elements should be designed to create opportunities for teachers to demonstrate high-quality enactments of MTPs throughout the simulation. The complexity of classroom environments and the enactment of MTPs provide opportunities to rehearse MTPs in a similarly sophisticated way, as the design of a simulation leveraging foundation models can address this complexity using ECD modeling logic.

3.3. Constructing Design Templates from ECD Modeling Logic

To address the complexity of teaching mathematics, we use design templates to align with ECD modeling logic and outline aspects of mathematical teaching and learning within specific classroom scenarios (e.g., Shaughnessy & Boerst, 2018; Shaughnessy et al., 2019; Stein et al., 2022; Smith & Stein, 2011). Each design template is based on a specific research framework that highlights students’ rich mathematical thinking through discourse facilitated by teachers. Task and response templates break down the learning outcomes of mathematical tasks to connect them within a sequence of student ideas, drawing from research at the intersection of mathematical content knowledge and pedagogy. Student profile templates expand these ideas to include how students would respond to teacher-led mathematical questions, informed by research in rehearsals for pre-service teachers. Rehearsal skill templates outline specific “look fors,” or observable components of an enacted teaching skill related to a particular mathematical task, drawing from literature on high-quality mathematics instruction that emphasizes teacher facilitation of student discourse about their mathematical inquiry. The integration of these research areas—within the prompting of a foundation model within a specific agent—centers the expertise of teacher educators in providing effective feedback.

The task & response template and student profile templates include the logic necessary to respond to student thinking when asking purposeful questions during a whole-group mathematics discussion. Posing purposeful questions, an MTP, requires teachers to ask their students questions that “assess and advance students’ reasoning and sense making about important mathematical ideas and relationships” (National Council of Teachers of Mathematics, 2014, 2018). Asking purposeful questions has often been interpreted as repeating specific phrases such as “Can you build on?” or “What do others think?” This approach generally leads to classroom discussions where the teacher does not need to notice, interpret, or respond to students’ thinking, even though they are facilitating a discussion with students. While this method of posing purposeful questions is easier to implement and often serves as a solid starting point for novice teachers to facilitate discussions, moving from this approach to asking purposeful questions that are responsive to the mathematics and the students in front of the teacher requires greater awareness of student thinking and knowledge of the mathematical content needed for implementation. Rehearsing how to ask purposeful questions involves a teacher interpreting and responding to the mathematical content being taught, how it is presented within a mathematical task, and the students’ work related to that task (both in written form and when students verbally explain their thinking). Therefore, the task & response template and student profile templates delineate the specific student thinking about a task for the teacher to interpret and respond to when enacting an MTP.

The rehearsal skill template includes the logic necessary to understanding the quality of how a teacher posed a purposeful question. Asking purposeful questions takes various forms depending on the mathematical tasks and the students engaging with those tasks. Because asking purposeful questions directly comes from student ideas observed in the classroom and how the teacher interprets them, any instance of a purposeful question depends on those variables. This variation is not only in the actual words teachers use when asking purposeful questions but also in the style of those questions. These styles, or subskills that represent methods of asking purposeful questions, include “advancing student understanding that builds on, but does not take over or funnel, student thinking” (National Council of Teachers of Mathematics, 2014). A question that does this differs from one that demonstrates the subskill of “going beyond gathering information to probe thinking and requires explanation and justification.” While both subskills are strategies for asking purposeful questions, they show how a teacher enacting an MTP of asking purposeful questions can either apply a different subskill or receive feedback on a particular subskill. Together, the rehearsal skill template contributes to the immediate feedback generated to a teacher’s response, in relation to the task and student profile details.

4. An Illustrative Example of a Design Template

To illustrate, the upcoming sections show the design templates used to identify relevant expertise for a GenAI simulation involving facilitating a whole-group mathematical discussion with three 8th-grade students about a system of linear equations task. In this task, a teacher is trying to practice the MTP of posing purposeful questions. Although each design template includes information specific to this situation, the templates are adaptable based on the type of MTP elicited concerning a particular classroom discussion scenario. We demonstrate this by describing the deep pedagogical and content expertise needed to complete the templates, which help organize such complexity within prompts to a foundation model without losing any details. We aim to show how this example supports our design framework by emphasizing the importance of domain expertise and the power of templates to organize it for use in prompting.

Crosswalking ECD Modeling Logic to Design Templates

First, the task and response templates (

Table 1. Task and response template (Template adapted from Smith & Stein, 2011).

Mathematics Topic: Systems of Linear Equations Focal Task: Consider the equation y = 2/5x + 1. Write a second linear equation to create a system of equations that has exactly one solution. Key Learning Objective of Focal Task: A line that creates a system with exactly one solution, where the line y = 2/5x + 1 is any line without a slope of 2/5.
Anticipated Student A Understanding	Anticipated Student B Understanding	Anticipated Student C Understanding
The students’ understanding of the ideas involved in the problem/process: The student conceptually understands that opposite-reciprocal slopes mean that two linear equations will intersect exactly once, as they are perpendicular. The student also understands that having the same y-intercept means that two lines will intersect exactly once.	The students’ understanding of the ideas involved in the problem/process: The student conceptually understands that two lines with the same y-intercept must cross at the location of the y-intercept. The student also understands that for those lines to intersect only once, at the point of the y-intercept, their slopes must be different.	The students’ understanding of the ideas involved in the problem/process: The student conceptually understands that any two linear equations with different slopes will intersect exactly once. The student also understands that having the same y-intercept means that any two lines will also cross only once; however, they note that this condition is not necessary if the slopes are different.
Other information about the student’s thinking, language, and orientation in this scenario: The student may not be confident that having either the opposite-reciprocal slope or the same y-intercept ensures the system has one solution, as opposed to both. However, this might be because the task only asks for a line that creates a system with exactly one solution, which the student’s solution satisfies, albeit with additional conditions.	Other information about the student’s thinking, language, and orientation in this scenario: The student may not be confident about the difference between two lines with the same y-intercept but different slopes, as having one solution in comparison with two lines with the same y-intercept and the same or equivalent slopes, as having infinite solutions. However, because the task requires a line that forms a system with exactly one solution, the student’s proposed conditions—having the same y-intercept and different slopes—meet the task’s condition.	Other information about the student’s thinking, language, and orientation in this scenario: The student’s response does not specifically clarify that having different slopes includes the condition of having non-equivalent slopes (e.g., noting that having two linear equations with slopes of 2/5 and 4/10 does not mean the lines will intersect only once due to those “different” slopes being equivalent fractions).

) include student responses to the mathematical task that gradually support the specified learning outcomes. Our approach starts by understanding how students’ conceptual and procedural understanding connect to achieve the desired learning outcome in a step-by-step manner. Building on the selection and sequencing of students’ mathematical work (Stein et al., 2022; Smith & Stein, 2011), we reframe these building blocks as expected student responses to a task, aiming for the teacher to use questioning to connect these responses and support students’ mathematical understanding within the context of a mathematical discussion. Since the domain we aim to observe relates to the intersection of a teacher’s understanding of mathematical content and MTP, breaking down the learning outcomes into expected student responses prepares the foundation for the teacher’s decision-making during a simulation to gather evidence of how their response addresses the mathematical content knowledge in students’ responses and uses questioning to highlight aspects of that students’ content knowledge while connecting it to other students’ content knowledge, where the sequence collectively shows evidence of a path toward a learning objective.

Next, we connect expected student responses to student profile templates (

Table 2. Student profile template (adapted from Shaughnessy & Boerst, 2018; Shaughnessy et al., 2019).

Sample Student A Responses
“This works, y = −5/2 x +1. You have to have a line with a flipped and opposite slope for it to cross only once, with the same b.” “Well, with those slopes, they are going perpendicular to each other, so they have to cross. And they definitely cross at (0,1) because they have the same b.”
Student’s Process and Understanding	Student’s Way of Being
The student’s process: The student is using the slope and y-intercept of the original line to create a system with one solution. They achieve this by finding the opposite reciprocal slope and leaving the y-intercept unchanged. The students’ understanding of the ideas involved in the problem/process: The student conceptually understands that opposite-reciprocal slopes mean that two linear equations will intersect exactly once, as they are perpendicular. The student also understands that having the same y-intercept means that two lines will intersect exactly once. Other information about the student’s thinking, language, and orientation in this scenario: The student may not be confident that having either the opposite-reciprocal slope or the same y-intercept ensures the system has one solution, as opposed to both. However, this might be because the task only asks for a line that creates a system with exactly one solution, which the student’s solution satisfies, albeit with additional conditions.	The student is confident that their solution satisfies the task’s condition. When asked to explain their process, the student explains how their solution is a method that will always work. When it is brought to their attention, the student realizes that they did not have to have the specific conditions of the opposite-reciprocal slope and same y-intercept and connects their condition of the opposite-reciprocal slope to be a subset of any slope that is not 2/5.

). We first include the student’s original solution to the mathematical problem, and information on how they understand their approach (e.g., student’s process and understanding). Since a teacher’s actions during a simulation lead to inferences about their ability to implement MTP in a mathematics classroom, it is important to reexamine expected responses in a real classroom setting. Therefore, we provide a specific anticipated student response that, through effective implementation of an MTP, can support that student and connect their mathematical understanding to others’ (e.g., student’s way of being). Expected responses involve designing and selecting two to three examples that give teachers opportunities to demonstrate their understanding of the mathematical content, how that content appears in students’ immediate responses, and how choosing an MTP clarifies those understandings.

Finally, we draw inferences about a teacher’s choice or enactment of a specific MTP in response to a particular student’s input, considering their student profile, as rehearsal skill templates (

Table 3. Rehearsal skill template (adapted from National Council of Teachers of Mathematics, 2014, 2018; Shaughnessy et al., 2019).

Posing Purposeful Questions
Subskill of MTP	Evidence	Non-Evidence
Advancing student understanding by asking questions that build on, but do not take over or funnel, student thinking	Asking questions that build on students’ thinking about… ○ Role of y-intercept ○ Role of slope ○ Potential conditions ○ Definite conditions ○ Overlapping conditions to satisfy the task	Asking questions that take over or funnel students’ thinking about… ○ Role of y-intercept ○ Role of slope ○ Potential conditions ○ Definite conditions ○ Overlapping conditions to satisfy the task
Making certain to ask questions that go beyond gathering information to probing thinking and requiring explanation and justification	Asking questions that probe thinking and require an explanation and justification about… ○ The selection of a particular slope ○ If their selection of a slope is a specific part of a line that is the only solution, or part of a set of potential lines that would serve as a solution	Asking questions that gather information about… ○ The selection of a particular slope ○ If their selection of a slope is a specific part of a line that is the only solution, or part of a set of potential lines that would serve as a solution
Asking intentional questions that make the mathematics more visible and accessible for student examination and discussion	Asking intentional questions that make mathematics more visible and accessible for student examination and discussion about… ○ Slope to graphing feature ○ y-intercept to a graphing feature ○ Same slopes to a graphing feature ○ different slopes to a graphing feature ○ y-intercepts to a graphing feature ○ different y-intercepts to a graphing feature ○ pairing different slopes and the same y-intercept to a graphing feature ○ pairing different slopes and different y-intercepts to a graphing feature	Asking questions that focus on procedure or non-visual representations about… ○ slope to graphing feature ○ y-intercept to a graphing feature ○ Same slopes to a graphing feature ○ different slopes to a graphing feature ○ Same y-intercepts to a graphing feature ○ different y-intercepts to a graphing feature ○ pairing different slopes and the same y-intercept to a graphing feature ○ pairing different slopes and different y-intercepts to a graphing feature

). As designers, we hypothesize what teachers might say or do and connect those responses to what they reveal about the teacher’s current abilities regarding a particular MTP within a specific mathematical content area (Mislevy et al., 2004). A simulation can use the student profile to create opportunities for teachers to demonstrate how they can interpret: first, the mathematical content within a student’s immediate response; second, the mathematical content in the students’ previously observed responses when selecting an MTP; third, how the chosen MTP addresses students’ immediate responses; and finally, how the chosen MTP relates to students’ real-time responses to previously observed work. Together, these components evaluate a teacher’s skills at the intersection of content knowledge and core teaching competencies. It is important to focus on understanding the mathematical content, the choice of MTP, and the immediate and future implications of enacting the MTP. For example, if a teacher selects an MTP suitable for a specific scenario, they still need support if the enactment of the MTP does not engage with the particular mathematical content or discussion relevant to that scenario. Consequently, the intersection of these three components represents a balance that both assesses and guides a teacher’s professional development experience in a simulation.

5. Translating Design Templates into Multiple Prompts

Although the design templates outline the essential details needed for building a simulation that uses foundation models, it is crucial to break down and rewrite parts of each template to ensure clarity within specific prompts. While using design templates that help the designer break down and thoroughly address the pedagogical and content expertise, translating this information into prompts explicitly attends to and incorporates those details into the simulation. Therefore, regardless of the content area used to fill out the design templates, that expertise is integrated into the prompt structure.

Below, we explain the second part of our design process—designing a prompting structure to contain the material within the design templates within prompts sent to a foundation model (Google, 2024b). While the previous sections aim to initiate the development of specific requirements needed to create a theoretically sound and pedagogically supportive rehearsal for students, we now introduce a framework that applies this expertise to be digestible beyond interpretations within a single prompt (e.g., Liu et al., 2024). Again, we demonstrate this process through our illustrative example of a whole-group mathematical discussion with students about systems of linear equations for a teacher to demonstrate posing purposeful questions.

5.1. How and Why Design Templates Shape Prompting

ECD modeling logic provide a common framework for breaking down classroom scenarios into models that provide a basis for developing specific prompts, which in turn support foundation models appropriately generate components that can be clearly described and understood with respect to the fully enacted simulation. Since simulations offer a space for teachers to practice, the information conveyed in feedback and student responses must acknowledge the complexity of the decompositions. To facilitate this, each piece of information within the design templates—aligned with the general steps of ECD modeling logic—is divided into individual prompts. Each prompt then performs those instructions to produce content focused solely on those specific directions, ensuring that these details receive proper attention.

A simulation using foundation models involves dynamic objects that change—such as generated feedback and student responses—based on how they are prompted. Elements within a prompt that guide each generated output can be adjusted if they do not directly influence the prompting instructions of another element. However, what is produced from the directions within individual prompts ultimately interacts with how feedback is provided and how student responses are generated. Consequently, changes within each component influence how an enactment of an MTP is carried out. Ideally, a high-quality enactment would specifically address the components that exist and are created from the designed and executed prompts. Since the templates reflect a situated view of mathematics teaching proficiency, what is generated from templates aims to encompass the elements influencing and involved in making high-quality instructional decisions. In other words, these components cannot exist without a specific context in which an MTP is enacted. Distributing these elements across templates and prompts helps mitigate the risk of a mismatch between the perspectives that support high-quality mathematics instruction.

5.2. Prompt Engineering for Generated Students and Feedback

The components of a prompt provide essential details about what the prompt guides a foundation model to generate. First, the components of a prompt include the objective (or what you want your prompt to achieve) and instructions (or the steps and details of how you want the generated content to perform the given objective). Additional components encompass the objective and persona given to what is generated, constraints on what the agent can produce, context related to information that should be referenced when generating a response, and constraints that guide the structure of the generated content (Google, 2024b). These details, along with the instructions, correspond to the components listed in the student response template when writing the prompt for generated student responses. To generate feedback responses with this prompt construction, these details correspond to the components listed in the rehearsal skill template.

6. An Illustrative Example of a Design Template to Prompt Structure

To describe the mapping process, we explicitly show the translation between the student profile template to create a prompt that guides the responses of a student, and the translation between the rehearsal skill template to create a prompt that guides the response of feedback. The task and response template, in turn, influences individual components of each prompt and serves as a contextual basis for the other two templates.

Table 4. Model of translating student response template components into prompt components for student agents within a multi-agent system.

Student Response Template Component	Example of Prompt Component
Student A: Mathematical Process	<OBJECTIVE_AND_PERSONA> You are an 8th-grade student about to share your mathematical ideas about a problem. The user is your teacher, who is going to ask you and your classmates questions about your different solutions to the problem. Your task is to answer the user’s questions when they ask about a general solution to the problem and only answer the questions in relation to your solution. Your solution is using the slope and y-intercept of the original line y = 2/5 x + 1 to create a system with one solution by finding the opposite-reciprocal slope and leaving the y-intercept the same.
Student A: Mathematical Ideas & Student A: Language and Orientation	<CONTEXT> To perform the task, you need to consider the mathematical problem that the user is talking about with you and your classmates, and how it relates to your solution. This is the problem: <Given the linear equation y = 2/5 x + 1, write a linear equation that, with the first equation, makes a system of linear equations with one solution.> To perform the task, you need to answer only using the ideas listed below. You conceptually understand that opposite-reciprocal slopes mean that two linear equations will intersect exactly once due to them being perpendicular. You understand that having the same y-intercept means that two lines will intersect exactly once. You are not sure that you can either have the opposite-reciprocal slope, or the same y-intercept ensures the system has one solution, as opposed to both, even though you do know that your solution satisfies the conditions of the task.
Student A: Mathematical Way of Being	<CONSTRAINTS> Dos and don’ts for the following aspects. You only respond with one or two sentences at a time like an 8th grader describing their work. You are confident that your solution satisfies the condition of the mathematics problem. When asked to explain your process, you will share your solution and explain how it is a method that will always work. When brought to your attention or said by a classmate, you will realize that you did not have to have the specific conditions of the opposite-reciprocal slope and same y-intercept to solve the problem When brought to your attention or said by a classmate, you will connect your condition of the opposite-reciprocal slope to be a subset of any slope that is not ⅖.

illustrates how each part of the student profile template directly corresponds with an element that aligns with high-quality prompt engineering to guide a generated student response. Outside of these components, the instructions outline the expectations for when a response should be generated during a simulation (as supported by the additional information within the prompt). Consider the instructions intended to guide the responses of a student, labeled student A, generated within the simulation.

To complete the task, you need to follow these steps:

• Speak when the user asks the first question.
• Speak when the user asks a specific follow-up to your question.
• Speak if the user asks for a summary of three solutions. When you respond at this moment, adjust your thinking to reflect the thinking shared by your classmates.

These instructions guide when student A responds in the simulation. Further, the instructions guiding student A’s responses draw from the fact that student A’s mathematical solution was the first of three meant to be sequenced in a discussion, as represented in the task and response template. The rest of the prompt utilizes information from the design templates to generate student A’s responses, as written in Table 4. Critical here is the alignment of what is provided to each part of the prompt (seen in the right-hand column of Table 4) relative to the design template (listed in the left-hand column). The prompt structure, acting as a container, holds each component of the student profile template as written but reorganized within the components of the entire prompt. Although not explicitly mentioned, the expertise within the student response template is present within the prompt instructions to guide each response with the specific mathematical and pedagogical ideas in the student profile template.

Similarly,

Table 5. Model of translating rehearsal skill template components into prompt components for feedback agents within a multi-agent system.

Task and Response Template Component	Example of Prompt Component
Immediate Feedback: MTP and Subskills of MTP	<OBJECTIVE_AND_PERSONA> You are a friendly coach to the user who is practicing how to ask questions to students during a whole-group mathematics discussion. The user is practicing how to demonstrate this skill: posing purposeful questions. Your task is to identify whether the user has demonstrated the following subskills when speaking, and provide feedback on what they did well, what they could improve, and what they should consider in order to demonstrate the following subskills if they were to repeat the conversation again.
Immediate Feedback: Look Fors for Subskills of MTPs	<CONTEXT> To perform the task, you need to consider the mathematical problem that the user is talking about with their students, and how it relates to demonstrating a subskill: <Given the linear equation y = 2/5 x + 1, write a linear equation that, with the first equation, makes a system of linear equations with one solution.> To perform the task, you need to identify if the user completed any of the following subskills: Asked a question that built on student thinking about role of y-intercept, role of slope, potential or definite conditions to satisfy the problem; Asked a question that surfaced why a student chose a particular slope, or asked if the student’s slope was the only slope that would work or was an example of a set of potential slopes; Asked a question that explicitly connected the slope and/or the y-intercept as a feature within a graph of that line and/or a feature of that line and another line within a system of linear equations Asked a question to discuss and explain one of the following strategies: a. how a new line with the opposite-reciprocal slope and the same y-intercept of the original linear equation can make a system of linear equations with one solution, b. how a new line with the opposite-reciprocal slope of the original linear equation can make a system of linear equations with one solution, c. how a new line with the same y-intercept of the original linear equation can make a system of linear equations with one solution, d. how a new line with a non-equivalent slope of the original linear equation can make a system of linear equations with one solution.
Immediate Feedback: Subskills of MTPs	<CONSTRAINTS> Dos and don’ts for the following aspects. Do specifically reference what the user said in their response as evidence or non-evidence of demonstrating a subskill Do specifically refer to quotes of what any student agent said as evidence or non-evidence of a user demonstrating a subskill Do specifically talk about the mathematical problem being discussed in the conversation as it relates to the user demonstrating a subskill. Don’t provide specific quotes for the user to try in the next part of the conversation.

maps the components of the rehearsal skill template to specific components of a prompt. Consider the instructions intended to guide how immediate feedback is generated to a teacher’s enactment of an MTP, labeled immediate feedback, generated within the simulation.

To complete the task, you need to follow these steps.

• Identify how the user’s statement shows evidence of any of the subskills.
• If the user’s statement has evidence of at least one of the subskills, provide 1–2 sentences of feedback about how what they did showed evidence of that subskill. Then encourage the user to keep going.
• If the user’s statement does not have evidence of at least one of the subskills, provide 1–2 sentences of feedback to the user of how they could respond again in a way that would better align with one of the subskills that makes the most sense at that moment in time.

Following these instructions, the rest of the prompt interprets and utilizes information from the rehearsal skill template to generate immediate feedback each time a teacher enacts an MTP within the simulation. Like the construction of the prompt for student A, the expertise held within the rehearsal skill template exists across the different components of a prompt aligned with strong prompt engineering across contexts. So, although the expertise is different, as written in different design templates, both types of design templates can be translated into a similar prompting structure while maintaining the original pedagogical and content expertise present in the original template.

7. Connecting Multiple Prompts to a Multi-Agent System Design

Our process of translating from design templates to prompts makes it possible to generate components within a simulation, giving teachers the chance to engage with students’ mathematical thinking and ask important questions. To harness this complexity in the technical aspects of a simulation, we propose using a multi-agent system to allow a simulation to utilize the detailed information outlined above within prompts. A multi-agent system is a computer system composed of multiple interacting agents that make autonomous decisions and act in a digital environment based on individual prompts provided to a foundation model. A simulation designed as a multi-agent system offers rehearsal opportunities along with generated feedback and student responses to teachers. Before explaining how the above prompting structure is used within a multi-agent system simulation, we will highlight the need to move beyond a single prompt when using foundation models to capture the complex nature of teaching within simulations. We will then demonstrate how each prompt aligns with components of a multi-agent system and how this design addresses the challenges of managing the complexity of teaching theoretically through a technical approach that leverages foundation models to decompose that complexity.

7.1. Adjusting the Back-End of Simulations to Suit the Design Needs

The arrival of foundation models offers a promising way to automate teacher rehearsal and feedback in simulations. As mentioned earlier, foundation models let anyone create parts of a simulation by providing instructions, questions, or constraints through prompting. This ability to prompt means digital activities like simulations can be designed and operated without designer supplied data and can be adjusted by the designer through prompt engineering. Note that, although this process allows for iterative improvements to what is generated through prompting, it does not involve training or changing the architecture of the foundation model itself. In other words, a simulation where a teacher enacts an MTP receives immediate feedback along with a student response generated by a foundation model based on the prompt. Using foundation models solely with prompting to design simulations is more user-friendly than modifying the core architecture with large, context-specific datasets.

The benefits of simulations using foundation models also raise concerns when considering their design. When trying to use these models for complex tasks, such as creating a simulation for teachers that provides feedback and responds to students, logistical problems quickly appear. As mentioned earlier, the amount of domain-specific expertise needed in a prompt becomes significant because of the complexities of teaching and the difficulty of accurately representing it within a simulation. Even with better prompt engineering, the complexity within a simulation indicates that ongoing prompt design with detailed instructions is already necessary for generating individual actions (Liu et al., 2024). Therefore, there is a natural tension between simplifying this complexity into a single prompt and maintaining it by adapting the use case of one prompt to address the need for multiple prompts that can better capture the full scope of teaching.

7.2. Multi-Agent Systems to Handle the Complexity of Simulations

To handle the complexity of the pedagogical and content expertise, we propose using a multi-agent system within a chatbot environment to facilitate discussions with students and collect feedback, where each student and each type of feedback is generated by individual prompts to a foundation model. A multi-agent system spreads the work of a foundation model across agents, or “self-contained execution units designed to act autonomously to achieve specific goals” (Google, 2024a) (Figure 2). Prompting foundation models can be distributed among different autonomous agents, such as a student agent or a feedback agent. Each agent operates based on a specific instruction and goal supported by a foundation model, guided by a root agent, or the main agent responsible for coordinating when and how a group of autonomous agents should respond (Figure 3). Using a root agent to delegate when other agents reply, with responses guided by their own prompts, is a technical design that goes beyond simply prompting a foundation model to perform multiple roles at once within a single prompt. This approach allows each design template to serve as prompts that instruct individual agents, with each prompt given to a foundation model to generate responses by a single agent, as directed by the root agent. In other words, the information within each design template populates one prompt, which instructs an individual agent. Therefore, a multi-agent system links the information in each design template to be structured within a prompt to its own agent, in a way where the information translated from template to prompt is still detailed and specific to the pedagogical and domain expertise.

What makes this approach unique is the role and design of the root agent within a multi-agent system simulation, which decides which other agents are deployed after the teacher’s response. The root agent is prompted to select a student to respond and then directs the other agents to participate within the chat interface based on specific conditions. The way the root agent chooses which students to select depends on their profiles. Consider the following prompt used for the root agent that aligns with the expertise within the above design templates.

Based on the information that the user provides, select the student to respond that forces the user to connect the procedural and conceptual background of the math idea. You have three specialized sub-agents. 1. Student_A: Delegate to this student when the user asks for a broad solution. Student_B: Delegate to this student when the user asks for someone to correct Student_A, or to add an additional solution. Student_C: Delegate to this student when the user asks for the minimum requirements to solve this task.

In this scenario, there is a logical sequence involving Student A, Student B, and Student C to facilitate a whole group discussion. Student A solves the task correctly, using the maximum number of conditions, while Student B achieves this with a condition that is sufficient but not necessary. In contrast, Student C addresses the problem with the minimally viable conditions. While all students’ solutions are correct, this sequence allows the teacher to facilitate a discussion that builds on all students’ ideas and connects them in a way that helps students understand the learning objective.

The simulation’s generated components, guided by the design templates and their information translated into prompts, allow a user’s response to a generated students’ response to receive feedback. Since the design templates focus on content-based problems and related student work, carefully shaping the student’s work aims to elicit certain responses from teachers. Designing to provoke specific teacher responses through the structure of the templates enables the generated feedback, more broadly, to provide appropriate scaffolding and context-specific next steps. Because the feedback is based on specific prompts across two agents, it is tailored to both a teacher’s immediate response to a particular moment in the chatbot interaction and the overall collection of enactments of MTPs.

7.3. The Relationship Between Theory and Technology

A multi-agent system tackles the challenge of managing the complexity of teaching while using technological advancements based on foundation models. First, designing student agents (based on student profile templates developed through application of ECD modeling logic) creates specific moments for teachers to practice their responses. Instead of prompting a foundation model to generalize a student’s reply, student agents are made with specific knowledge profiles. When called upon to respond, they offer opportunities for teachers to rehearse an MTP in ways that might not happen frequently in a classroom—or, if they do, are unlikely to be repeated. Second, the design of feedback agents (based on rehearsal skill templates) describes precise and context-relevant ways for teachers to improve and try again immediately. Feedback agents can be customized to suggest improvements on components of MTPs within different timeframes, thereby dividing the work among various agents. As a result, a teacher can receive instant feedback on their enactment of an MTP from one agent, allowing quick understanding and reattempt, or get comprehensive feedback on all their enactments in a simulated environment from another agent. This helps teachers reflect on their overall performance and try the entire process again with that feedback in mind. These details, in turn, provide material for teachers to enact MTPs that specifically incorporate those variables and receive feedback that addresses them, either in real-time or across the simulation.

We explicitly designed the templates and used agents to highlight and connect with examples of student thinking, enabling teachers to face cognitive challenges related to selecting and applying MTPs. By adapting the ideas within design templates using ECD modeling logic, we create deliberately strong prompts for each student agent, tailored to a unique mix of content problems, goals, and student understanding profiles. This alignment allows teachers to demonstrate MTPs while tackling the cognitive challenges inherent to daily teaching tasks. First, a multi-agent system simulation can prompt student agents to generate reflective responses based on grade-level ideas from a grade-level task to a user’s input. The responses teachers give can then be used to evaluate their ability to enact MTPs in response to students’ thinking on content-related problems. The opportunities afforded within a multi-agent system simulation, built on a design using ECD modeling logic, not only highlight the enactment of an MTP but also emphasize specific mathematical content, pedagogical context, and the careful selection and structuring of student ideas.

8. Discussion

This paper argues for an approach that leverages ECD modeling logic and multi-agent system structures to shape the design of simulations using foundation models to address the complexity of teaching. Our design argument highlights a three-part framework as part of a new approach to design GenAI-powered simulations. First, it emphasizes the need for pedagogical and content expertise when using GenAI. Despite GenAI’s ability to create interactive components, we argue the need to model such expertise, particularly as it relates to the generated components of a simulation. Second, our approach directs foundation models, based on specifically designed prompts guided by pedagogical and content-based expertise, to generate responses within a simulation. Finally, it manages the interactive nature of a simulation using GenAI within a multi-agent system guided by the specifically designed prompts, thus providing opportunities for teachers to practice enacting MTPs in dynamic ways. The interactive nature of what our design argument highlights—being the iterative enactments of MTPs in conversation with students describing their thinking about a mathematical idea—becomes promising because the dynamic components are shaped by domain expertise, as organized and delineated across design templates and prompts. Our paper, therefore, describes how to model pedagogical and domain-specific expertise within prompts to agents to create opportunities for teachers to enact MTPs within dynamic multi-agent system simulations.

While parts of this work already exist in the field of simulations, there is a need to combine the design of ECD modeling logic and the design of prompts acting within a multi-agent system. Current work in the field utilizes foundation models to prompt generated components within simulations (e.g., Mikeska et al., 2025; Son et al., 2024) but uses technological structures outside of multi-agent systems that cannot manage the complexity beyond one-to-one interactions with a single generated entity. Such an approach raises questions about the type of opportunities presented to teachers to enact MTPs. Other work uses multi-agent system structures to separate prompts to foundation models (e.g., U. Lee et al., 2023; Park et al., 2023) but underspecifies the design and prompting frameworks used to guide foundation models, raising questions about the attention given to the pedagogical and content expertise. Despite using existing prompt engineering structures to generate clearer outcomes from a foundation model, and using modeling logic to clarify the domain expertise needed to create opportunities to demonstrate one’s ability to enact an MTP, there has not been work that models how that domain knowledge is translated into prompts and used within a technological structure that maintains that domain expertise across prompts.

While we see the design approach we have presented as providing a much needed and critical foundation for the future design of GenAI simulations, the real potential for this work is in the next stages of research and development. Building on our theoretical and technical approach, we see the need to design additional simulations that establish the utility of the design process across multiple teaching contexts and MTPs. Associated studies could be designed to investigate the functionality of these simulations and to assess practical considerations including the cost and feasibility of simulation development, administration, and reporting. Other studies might investigate additional ways the prompt can provide parameters to direct what is generated by GenAI foundation models and variation in the types of opportunities that are provided for teachers to enact MTPs. Related studies could examine whether the GenAI simulations are sufficiently sensitive to differences in teachers’ performance competencies and whether the feedback is appropriately targeted to their specific learning needs. Ultimately, the design process laid out in this paper sets the stage for research on teachers’ enactment of MTPs, their learning trajectories as they rehearse across multiple simulation iterations, and the impact of these practice opportunities on teacher learning and the quality of classroom mathematics instruction.