Updating Calculus Teaching with AI: A Classroom Experience

Abstract

In the context of mathematics education, the integration of artificial intelligence (AI) in teaching calculus is revolutionizing instructional methodologies and enhancing learning experiences both inside and outside the classroom. This study explores the use of specific AI tools, including ChatGPT, MathGPT, Gemini, and Wolfram Alpha, to deepen students’ understanding of key mathematical concepts such as derivatives and rates of change through continuous interaction with a virtual tutor. By employing well-designed prompts, these tools facilitated problem-solving exercises that were verified and refined by AI, fostering both precision in calculations and conceptual clarity. Observations from the classroom implementation reveal that students not only improved their accuracy in performing derivative calculations but also developed a clear understanding of the distinctions between average and instantaneous rates of change. The AI tools created a dynamic, adaptive learning environment, providing immediate feedback and simulations that significantly boosted student engagement and motivation. These findings underscore the potential of AI to transform mathematics education by making learning more personalized and accessible, ultimately enhancing educational outcomes and preparing students for future academic and professional challenges. Furthermore, this study introduces an innovative approach to refining AI prompts and interactions, highlighting the importance of iterative improvement to enhance the quality of AI feedback. This approach is crucial for developing better problem-solving skills and ensuring a comprehensive understanding of mathematical concepts.

1. Introduction

Artificial intelligence (AI) has become a transformative force in various fields, including education. Its integration into the educational sector, particularly in mathematics, promises to revolutionize teaching methodologies and improve learning outcomes. Recent studies have shown that AI can significantly enhance the learning experience by providing adaptive learning environments tailored to individual student needs [1]. For instance, Fahimirad and Kotamjani [2] demonstrated that AI-assisted teaching can improve student outcomes in basic mathematics education. Furthermore, Hjelte et al. [3] and Wang et al. [4] highlight the potential of AI to offer personalized support and immediate feedback, which are crucial for mastering complex mathematical concepts. The authors described the application of AI in education, including adaptive learning, teaching evaluation, and virtual classrooms, and analyzed its impact on teaching and learning, highlighting its positive effects on both teachers and students. Tan [5] highlights the role of AI and big data-driven systems in optimizing advanced mathematics education through adaptive algorithms. By leveraging these technologies, educators can create personalized learning environments that cater to the individual needs of students, thereby improving the quality and effectiveness of instruction. Similarly, Voskoglou and Salem [6] discuss both the benefits and limitations of integrating AI into traditional mathematics education, emphasizing its ability to provide immediate feedback and tailored learning experiences, which are crucial for student engagement and understanding. Despite these promising advantages, there is still a need for empirical evidence on the practical implementation of AI in teaching differential calculus, particularly in understanding derivatives and rates of change.

The value of artificial intelligence in education, particularly in the classroom for teaching calculus, is increasingly recognized. Research indicates that AI can help improve mathematics learning in various ways. Personalized training promises greater conceptual understanding and better assessment techniques, which are some of the advantages of integrating AI in the classroom [7]. AI technologies have many applications in education, including STEM education, mathematics education, and higher education [8,9]. According to Chen et al. [10], using AI in education is considered a way to improve student learning and adapt to changes in the work environment. This technology can adapt content and instruction to the individual needs of students, i.e., personalization of learning, which can help students learn more effectively and overcome difficulties [11]. Additionally, individualized and real-time learning can be facilitated by the advancement of AI, virtual reality, and learning analytics, which can be especially useful when teaching challenging courses such as calculus [12].

AI can also provide students with immediate feedback on their work, helping them understand their errors and improve their performance [11,13]. Additionally, AI can generate interactive content, such as games and simulations, to help students learn more actively and engage more effectively. It has been suggested that AI be used in medical education to familiarize students with AI-based clinical applications and introduce mathematical principles at various educational levels, such as probability, calculus, and linear algebra [14]. For AI to be smoothly implemented, it must be integrated into all facets of the curriculum [15].

Regarding AI-enabled adaptive learning systems (AI-ALS), while AI can improve students’ mathematical learning experiences, it should not be completely relied upon. Teachers are essential in addressing any conceptual gaps that students may have [16]. To ensure successful adoption across disciplines, integrating AI into mathematics education requires an effective strategy [17]. Furthermore, students’ favorable opinions of AI-based mathematics teaching suggest that AI has the potential to enhance the educational process [18]. The use of cutting-edge algorithms, such as particle swarm optimization, can also help improve resource management and sharing in mathematics teaching [5].

Salcedo [1] presented a review of the literature on the use of AI in the teaching and learning of mathematics. The author identified the main uses of AI in this area and discussed the challenges and opportunities it poses. Orhani [19] demonstrated that AI technologies can help diagnose individual learning problems, provide personalized support, and improve teaching and learning performance.

The Pedagogical AI Research Group [20] reports on the state of the art in the use of AI for teaching and learning mathematics, identifying key research areas and future trends. Kamalov, Santandreu, and Gurrib [21] investigate the potential impact of AI in education through a review and analysis of the existing literature, focusing on applications, advantages, and challenges. They emphasize the use of AI in collaborative learning between teachers and students, intelligent tutoring systems, automated assessment, and personalized learning. Lodge, Thompson, and Corrin [22] discuss the impact of large linguistic models and associated applications on tertiary education, highlighting areas that require further research and rethinking. They also outline the position of the Australasian Journal of Educational Technology (AJET) regarding the use of generative AI tools such as ChatGPT in research and writing.

The Office of Educational Technology of the United States Department of Education [23] underscores the need to share knowledge and develop policies for AI, a rapidly advancing class of capabilities increasingly integrated into educational technology systems and accessible to the public. The report’s recommendations aim to engage teachers, leaders, policymakers, researchers, and educational technology innovators in addressing pressing policy issues arising from the use of AI in education. Beyond typical classroom environments, AI supports theorem development, guides human intuition in mathematical inquiry, and enhances learning through adaptive learning systems [24]. Machine learning, a branch of AI, has proven essential in improving computer performance in various applications, including mathematics teaching [25]. The research reviewed offers a promising outlook on the potential of AI to improve teaching and learning by saving educational expenses, providing feedback, creating guided learning paths, and promoting mathematics learning [26]. However, challenges remain, including those related to research, policy formulation, educator participation, student support, and the integration of AI technologies for teaching and learning [27,28]. These authors emphasize the need to address these challenges to realize the potential benefits of AI in education fully.

Learning calculus poses significant challenges for students, particularly in grasping abstract concepts such as derivatives and their graphical interpretation. Recent studies have shown that students struggle with the cognitive processes involved in understanding these concepts, as evidenced by their performance in standardized assessments. For instance, Casalvieri et al. [29,30] used an eye-tracker tool to analyze the difficulties students face when solving calculus tasks involving derivatives and antiderivatives. Their research highlighted the distinct differences between the visual observation strategies of experts and non-experts, indicating that non-experts often misinterpret critical elements of the task, leading to incorrect answers. This finding underscores the importance of targeted instructional strategies that address these specific cognitive challenges. Moreover, the integration of AI in teaching mathematics, as discussed by Spagnolo et al. [31], offers promising avenues for addressing these challenges. By leveraging AI tools such as ChatGPT, teachers can provide real-time feedback and personalized support, helping students overcome common pitfalls in learning calculus. However, as these authors point out, the success of AI in education also depends on the effective design of AI prompts and the teacher’s role in guiding students through complex problem-solving processes. Additionally, the work by Segal et al. [32] emphasizes the importance of keeping the teacher involved in the learning loop, particularly when using AI to monitor group learning in real time. This approach ensures that AI serves as a complementary tool rather than a replacement for traditional teaching methods, allowing educators to address the nuanced difficulties students encounter in subjects such as calculus.

Motivating students to want to learn mathematical concepts is something that has always aroused the interest of researchers [33,34,35]. Thus, the integration of AI in the design and application of differential calculus learning activities represents an innovative step toward transforming mathematics education. AI offers tools and resources that personalize learning, adapt to each student’s pace and needs, and promote greater interaction and active participation in the knowledge acquisition process. Incorporating AI into calculus course activities has created more dynamic and engaging learning experiences through simulations, interactive visualizations, and intelligent tutoring systems. This approach allows students to explore the concepts of average and instantaneous rates of change more deeply, experiment with different approaches, and receive immediate feedback on their progress.

Although the integration of artificial intelligence (AI) in mathematics teaching has demonstrated significant benefits, there remains a gap in empirical research on the practical application of AI in learning differential calculus, particularly in the understanding of fundamental concepts such as derivatives and rates of change. Addressing this gap is crucial for developing effective AI-based educational strategies that can enhance student learning outcomes in complex mathematical subjects. To this end, this study formulates two key research questions: 1. How does interaction with an AI-based virtual tutor affect students’ understanding of average and instantaneous rates of change? 2. How do refined prompts improve the quality of feedback provided by AI and, consequently, student learning? These research questions guide the investigation, focusing on the impact of AI on students’ conceptual understanding and the effectiveness of tailored AI feedback in improving learning outcomes.

2. Methodology

This study was conducted at the [blinded], involving a classroom experience designed to integrate artificial intelligence (AI) in the teaching of calculus.

This study involved 22 students from the Bachelor of Mathematics program, who were intentionally selected based on their willingness to participate in this study actively. This selection process was designed to ensure that the results would be representative and relevant to evaluating AI tools in the context of learning differential calculus. This selection aimed to enhance the learning outcomes expected in the course and address the well-documented difficulties students face in learning mathematics both nationally and internationally [36]. Although this study did not focus on demographic variables such as gender, which were not deemed central to the research objectives, we acknowledge their potential importance and will consider including a more detailed population analysis in future studies.

This descriptive study assessed the effectiveness of using AI for learning differential calculus by collecting data on student performance and feedback. The analysis provided valuable insights into the advantages and disadvantages of AI in this educational context, informing future educational interventions that integrate AI.

2.1. Phase 1: Implementation and Intervention Procedure of AI Tools

This phase focused on integrating AI tools to facilitate the learning and appropriation of calculus concepts. The AI tools selected were aimed at providing personalized feedback and generating practice exercises tailored to individual student needs. The specific tools and their applications are as follows:

AI Tutoring System: Designed prompts were created to enable the AI to provide feedback on students’ work. Students used this tool to practice calculus problems, receive immediate feedback, and complete personalized exercises.

The intervention procedure was structured into several phases to integrate AI into the teaching process gradually. Initially, students were introduced to the AI virtual tutor through demonstration sessions to familiarize them with the technology. Following this, they participated in active learning sessions where they used AI tools—specifically ChatGPT, MathGPT, Gemini, and Wolfram Alpha—to solve calculus problems in real time. These AI tools were selected for their ability to provide immediate and personalized feedback, as well as their potential to generate adaptive exercises tailored to individual student needs.

2.2. Phase 2: Exercise Generation Prompts

These prompts were formulated to generate exercises for students to practice learned concepts and self-evaluate their understanding. This system ensured that students could continually refine their skills through repeated practice and feedback.

The prompts used in this study were carefully designed through a collaborative approach that involved both students and teachers. The design process was informed by the teachers’ extensive experience in teaching differential calculus, as well as the learning progress demonstrated by the students during their interactions with AI. This iterative process allowed the prompts to be refined based on real-time feedback from both the AI and the students, ensuring that they were not only technically accurate but also pedagogically effective. The goal was to create prompts that facilitated meaningful and productive interactions between the students and the AI, thereby enhancing the student’s understanding of key calculus concepts such as derivatives and rates of change. By integrating the expertise of the teachers with the observed learning needs of the students, the prompts were tailored to maximize the educational impact of the AI tools used in this study.

Throughout the intervention, technical terms such as “prompt” were clearly defined at the beginning of this study, and specific examples were provided to ensure all participants understood and correctly used these terms. For instance, ChatGPT was used to generate interactive problem-solving tasks, such as “Provide a step-by-step explanation of how to calculate the derivative of f(x) = 3x² + 2x − 5”. MathGPT offered detailed explanations for more complex mathematical problems, allowing students to explore alternative methods for solving these tasks. Each session was followed by group discussions to reflect on the experiences and optimize the interaction with AI technology. The AI tools were adapted to fit the learning styles of the students by adjusting the complexity of tasks and providing additional hints or alternative explanations when needed. This customization aimed to deepen the students’ understanding of differential calculus concepts, particularly derivatives and rates of change. Additionally, students were given the autonomy to choose which AI tools to use to solve the problems. Gemini was used for its capability to break down complex mathematical problems into smaller, more manageable steps, providing detailed explanations and facilitating a deeper understanding of the concepts. Wolfram Alpha was employed for its advanced computational abilities, allowing students to explore a wide range of mathematical problems, from simple algebraic equations to more complex integrals and derivatives. Students could choose between these tools based on their preferences and the specific requirements of the tasks. This autonomy was essential in fostering a sense of responsibility and encouraging students to engage actively with the AI tools, thereby enhancing their learning experience. The integration of these tools allowed students to work at their own pace, receiving personalized feedback and support as they progressed through the course.

2.3. Phase 3: Descriptive and Data Analysis

In this phase, a detailed descriptive analysis was conducted to evaluate the advantages and disadvantages of using AI in the students’ learning process. The analysis considered the work completed by the students and their performance in the activities, providing insights into the effectiveness of AI in promoting understanding and engagement with calculus concepts.

Data analysis was conducted using qualitative methods to obtain a comprehensive understanding of the effects of the intervention. The analysis focused on students’ interactions with AI tools during the problem-solving process, particularly in understanding key calculus concepts such as the average and instantaneous rates of change. The development and refinement of prompts to elicit effective AI feedback were also a critical focus. The analysis included reviewing records of student interactions with the AI, performance assessments, and questionnaires capturing student perceptions of the AI tools. The analysis included reviewing records of student interactions with the AI, performance assessments, and a general satisfaction questionnaire that captured student perceptions of the AI tools and their overall experience during the course. This holistic approach provided valuable insights into how AI tools can enhance the teaching and learning of calculus, particularly in improving student engagement, conceptual understanding, and overall learning outcomes.

2.4. Procedure

The main objective of this study is to evaluate how the implementation of AI tools can improve students’ understanding of key concepts in differential calculus, particularly average and instantaneous rates of change. Additionally, this study aims to investigate how the continuous refinement of the prompts used with AI can influence the quality of the feedback received and, consequently, the development of students’ problem-solving skills. These objectives are closely tied to addressing the research gap identified, which centers on the need for empirical evidence regarding the practical application of AI in enhancing learning outcomes in differential calculus. To achieve this study’s objectives, the following procedural steps were followed:

• Group Formation and Instruction:

• Students formed groups of four based on their criteria or affinity.
• Each group received instructions on using AI tools to develop the activities.

2.

Problem Presentation and Solution:

• Students were presented with problems or exercises related to the average rate of change or instantaneous rate of change.
• After solving the problem manually, students designed a prompt for the AI to verify the correctness of their solution.

3.

AI Feedback and Exercise Generation:

• The AI analyzed the students’ solutions and provided feedback, indicating whether the solution was correct or contained errors.
• If the solution was correct, the AI-generated a new practice exercise to further evaluate the student’s learning.
• If the solution was incorrect, the AI helped students identify and correct the errors.

4.

Iteration and Teacher Support:

• Steps 1 and 2 were repeated until students correctly solved the original problem or exercise.
• Throughout this process, the teacher reviewed the student’s work to ensure the prompts generated appropriate interactions and that the solutions or suggestions from the AI were correct and relevant.
• In situations where the AI provided incorrect solutions or failed to identify errors in the students’ procedures, the teacher, who has over 15 years of experience teaching differential calculus, actively intervened to address these issues. The teacher used these instances as opportunities to clarify the relevant concepts further and guide the students in refining their prompts to generate more accurate and effective AI responses. This intervention ensured that the student’s interaction with the AI remained pedagogically beneficial and that any misunderstandings were promptly corrected. The teacher’s extensive experience in mathematics education allowed for effective pedagogical strategies to be implemented, enhancing the overall learning experience for the students.

5.

Student Evaluation:

6.

At the end of the activity, students completed a general satisfaction questionnaire to evaluate their overall experience during the course. This questionnaire included sections designed to gather feedback not only on the development of the activity as a whole but also on the use of AI in the learning process. Therefore, while the students’ perceptions of the activity were collected, their feedback on the AI tools was also captured through this questionnaire.

2.5. Data Collection and Analysis

Each AI tool was integrated into the teaching process in a way that allowed students to work at their own pace while receiving personalized feedback. Students were given the freedom to select the AI tools they felt most comfortable with or that they found most effective for the specific problems they were tackling. This approach not only supported differentiated learning but also encouraged students to experiment with different tools, fostering a more profound understanding of the mathematical concepts being taught. The tools were also adapted to fit students’ learning styles by adjusting the complexity of the tasks and providing additional hints or alternative explanations when needed. This customization ensured that students could deepen their understanding of differential calculus through active engagement with AI-based resources. This study followed a rigorous data collection and analysis process. This included questionnaires to capture students’ perceptions of the AI tools, records of their interactions with the AI systems, and performance assessments to evaluate their progress in understanding key concepts in calculus. These data points allowed for a thorough evaluation of the effectiveness of AI tools in enhancing the teaching and learning of calculus, particularly in relation to improving student engagement and learning outcomes.

It is important to highlight that this study is not an experimental comparison between AI-enhanced learning and traditional methods, nor does it include pre- and post-tests. Instead, this study adopts a qualitative, descriptive approach, focusing on the interaction of the students with AI tools. Data were collected through observations, student performance records, and self-reported feedback to assess how AI can support the learning of key differential calculus concepts. Nevertheless, the results of this study have the potential to significantly impact mathematics education by demonstrating the effectiveness of AI in enhancing learning outcomes. The findings can be utilized by educators, educational technology developers, and curriculum designers to create new and improved learning experiences for students.

3. Results and Discussion

The implementation of Artificial Intelligence (AI) in a Differential Calculus learning activity, specifically in this study of the average rate of change, the instantaneous rate of change, and the derivative of a real function has proven to be an invaluable tool for optimizing the teaching and learning process. Through the design of interactive prompts between students and AI, significant progress was achieved in understanding mathematical concepts. AI, acting as an intelligent tutor, facilitated the correction of errors in real time, provided personalized feedback, and generated practice problems to consolidate the acquired knowledge.

The analysis presented in this section includes the interactions and outcomes for all student groups, not just Group 1. Although only images from Group 1 were included as illustrations, the results and feedback processes of all groups were thoroughly examined. This comprehensive analysis revealed variations in the effectiveness of AI use among the different groups. Some groups demonstrated more significant improvements in their conceptual understanding of differential calculus, particularly in grasping the concepts of average and instantaneous rates of change. These differences were largely attributable to the quality of the prompts formulated by the students and the level of teacher intervention during the learning process. For instance, groups that received more targeted guidance in prompt creation and benefited from more active teacher involvement tended to show better learning outcomes.

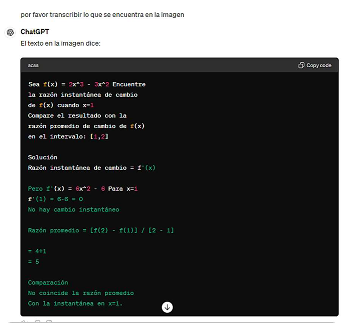
For example, when students were asked, “Given $f\left(x\right)={3x}^2-{2x}^3$, find the average rate of change in $f\left(x\right)$ over the interval [1,2] and interpret the results”, students from Group 1 solved the problem manually, took a photo, and created a prompt for the AI ChatGPT. This allowed them to verify the solution, review the steps, identify errors, and receive advice on solving the problem. Figure 1 illustrates the interaction of Group 1 with the ChatGPT AI in solving an average rate of change exercise.

The AI generated a response providing an explanation of what should be performed in the specific review of the task, mentioning the definition of the average rate of change based on the relation (Equation (1)):

$$Averagerateofchange={\displaystyle \frac{f\left(b\right)-f\left(a\right)}{b-a}}$$

(1)

Then, he described the solution presented in the image delivered by the students, displaying the calculations or operations recorded, comparing it with the solution obtained by applying the relation, and responding that “the solution and interpretation provided are correct; there is no error in the calculations, and the interpretation of the result is appropriate. An alternative method is not needed since the problem was solved correctly (Figure 2).

This iteration demonstrates the potential of AI as a tool for verification and feedback in learning Differential Calculus. The AI correctly identified that Group 1’s solution was accurate and provided a detailed explanation of the solution process. This likely helped students develop the skills to properly apply procedures to determine the average rate of change, corroborating the findings of Hwang and Tu [11] and Mohamed et al. [13]. These authors suggest that AI offers immediate feedback on the work of students, especially in situations that requiere the application of specific procedures, which helps students understand their errors and improve their performance. However, it does not necessarily guarantee a better understanding of the concept of the average rate of change. An important element of this interaction is the appropriate design of the prompts used by the students, which allows the AI to generate responses tailored to their needs.

Subsequently, the students were given the second exercise: “Given $f\left(x\right)=2x^3-3x^2$ find the instantaneous rate of change in $f\left(x\right)$ when $x=1$. Compare the results with the average rate of change in the function over the interval [1,2]”. This exercise aimed to help students identify the differences between the average rate of change and the instantaneous rate of change, thus introducing the concept of the derivative of a real function of a variable. In this situation, the students in Group 1 continued using the prompt and procedure from the previous exercise (Figure 3).

In Figure 3, it can be seen that the students solved the exercise manually using the derivative. However, they made an error in the calculation: “If $f\left(x\right)=2x^3-3x^2$, when $f’\left(x\right)=6x^2-6.$” Despite this, the numerical value of the instantaneous rate of change at $x=1$ was correct. They then took a photo of their solution and input the image into the AI, which checked the solution step-by-step, highlighted the errors, and provided an alternative solution method. The AI solved the exercise by correctly identifying that the instantaneous rate of change is essentially the derivative. It calculated the derivative accurately, evaluated it at $x=1$, and found that the answer matched the one provided by the students. The AI responded by stating that the solution matched the one provided in the image and added that the interpretation was consistent with the results of differential calculus. However, it did not identify the error made by the students in the procedure. See Figure 4.

This iteration highlights some limitations of using AI for verification and feedback in student learning, particularly in correcting procedures. While the AI was able to verify the students’ final answer, it failed to identify the error in their procedure. This oversight could have prevented the students from learning from their mistakes and improving their understanding of the concept, potentially leaving them with only the ability to obtain correct answers without grasping the underlying principles. In this case, the AI was unable to provide the students with the necessary feedback to learn from their mistakes. This demonstrates that while AI can be a useful tool for teachers in instructing students [5], it is crucial for the teacher to manually review the students’ solutions to identify procedural errors and provide appropriate feedback. Personalized training promises greater conceptual understanding and better evaluation techniques, which are just some of the advantages that can arise from the integration of AI in the classroom [7].

In response to this situation, the teacher intervened and suggested that the students improve the prompt, as the AI failed to identify the procedural error, resulting in inadequate feedback. The students then proposed a new prompt and restarted the process, as illustrated in Figure 5. In this interaction, the response of the AI did not change significantly, and it still did not detect the procedural error made by the students, as can be seen in Figure 6.

This iteration highlights the need to improve the ability of AI to identify and correct errors in students’ mathematical reasoning. While the AI was able to verify the students’ final response in the previous iteration, it failed to identify the error in their procedure, even when specifically asked to accomplish this task. This indicates that current AI still has limitations in identifying complex errors in students’ mathematical reasoning. Therefore, it is necessary to develop new AI techniques that can better understand the process of solving mathematical problems and detect errors at different stages of the process. Additionally, AI prompts must be carefully designed to provide clear and precise information about the error they are expected to identify.

To achieve adequate feedback from AI for students based on the provided solutions, the interaction steps with AI proposed in the methodology were restarted with the participation of all students and the support of the teacher. The image was provided again with new indications, as shown in

Table 1. Interactions with the AI to identify improvements in the prompt to obtain better feedback from the AI.

Image Provided by Students	AI Response
Prompt: “Please transcribe what is in the image”.	The AI makes a correct transcription of what is in the image.
Prompt. “Do you understand each symbol and what is presented in the text?”
The AI makes a proper explanation of what is contained in the text and its meaning.

.

Upon verifying that there are no errors in the response of the AI regarding the contents of the image, the prompt was changed to: “Now create two columns: one with the solution I propose and the other with the optimal solution. If errors are found, indicate them in the line where they occur, comment on them, and correct them”. 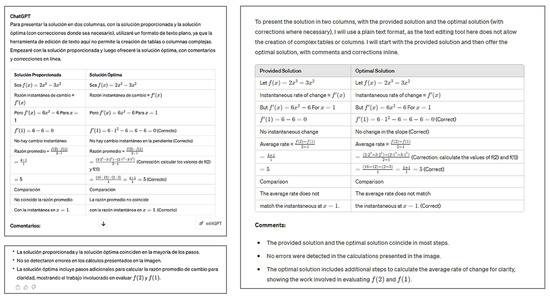This adjustment aimed to facilitate a more efficient analysis of the solution provided by the students, as illustrated in Figure 7.

As seen in Figure 7, the AI still did not detect the error made by the students in row 3. This indicates that, to improve the ability of the AI to identify errors in students’ mathematical reasoning, continued research into new AI techniques is necessary. These techniques should better understand natural language and mathematical reasoning.

In the ongoing search to find the most effective prompt for interaction, which would help students appropriate concepts and develop mathematical reasoning in differential calculus, the following prompt was provided to the AI (Figure 8).

Since the feedback is adequate, the prompt is maintained, but the exercise is changed to verify if it continues to identify errors and provide adequate feedback. To accomplish this, the solution presented by the students in Figure 8 is transcribed and included in the prompt to be reviewed by AI (Figure 9).

The AI response identifies the errors made by the students and makes the necessary corrections and suggestions for subsequent solutions. This interaction highlights and confirms the need to continue refining the prompts to generate appropriate feedback that contributes to the learning and appropriation of concepts.

These results suggest that AI can significantly enhance the learning experience in differential calculus by providing immediate, personalized feedback and generating practice problems. However, its limitations in procedural error detection indicate that teacher involvement remains crucial. Future research should focus on developing AI techniques that better understand and correct mathematical reasoning errors, thereby fully leveraging the potential of AI in mathematics education.

Integrating AI into the teaching of complex subjects such as differential calculus not only transforms mathematical pedagogy but, as research demonstrates, significantly improves the accuracy and depth of student understanding of fundamental mathematical concepts such as derivatives and rates of change. AI democratizes access to education through massive open online courses (MOOCs) and open educational resources (OERs), enabling the reuse and modification of resources under open licenses [37,38]. In calculus education, this offers students unlimited access to a diversity of problems and solutions, which is crucial for adaptive learning that personalizes instruction to individual student needs [39,40].

Gamification and game-based learning, which increases interactivity and student engagement [41], enhance decision-making and problem-solving skills, making them particularly useful in teaching complex mathematics such as calculus. Integrating these elements into calculus teaching using AI can significantly increase motivation and learning effectiveness [42,43].

Despite these advances, challenges in the application of AI in education, especially in detecting and correcting procedural errors, require attention. Current AI systems, although capable of providing immediate feedback, often fail to detect and correct errors in students’ procedures, which can impede deep and meaningful learning [44,45]. To maximize the capabilities of AI in mathematics education, it is crucial to develop technologies that can handle procedural and conceptual complexities, showing relevance and versatility [46,47,48,49], in addition to ensuring that these technologies are accessible and adaptive to changing educational needs. This requires ongoing collaboration between educators, technology developers, and students to ensure that AI interventions are effective, inclusive, and equitable, reflecting the principles of open educational resources and adaptive education. The integration of virtual reality and artificial intelligence with in-person instruction, known as blended learning, is reshaping educational environments. This allows for more dynamic teaching methods and enriched learning experiences that improve automation and intelligence in education and other fields [50,51,52,53,54].

The integration of AI tools into calculus teaching has been shown to significantly enhance students’ understanding of complex mathematical concepts, particularly average and instantaneous rates of change. By facilitating interactive problem-solving tasks and providing personalized feedback, AI tools such as ChatGPT and MathGPT have allowed students to engage more deeply with the material, resulting in improved conceptual clarity. This finding is consistent with the works of Casalvieri et al. [29,30], who highlighted the importance of tailored AI interactions in improving students’ grasp of derivatives through eye-tracker analysis. Similarly, Spagnolo et al. [31] demonstrated that the role of AI in problem-solving, when effectively guided by educators, can lead to better learning outcomes in mathematics.

Comparing our results with those of Fahimirad and Kotamjani [2], who explored the broader implications of AI in education, we find consistent evidence that AI can be a powerful tool in enhancing learning when appropriately integrated into the curriculum. However, this study goes further by focusing specifically on differential calculus and providing empirical evidence of how AI-driven prompts can be refined to optimize feedback quality. This aligns with Wang et al. [4], who showed that adaptive learning systems, when used in conjunction with teacher-led instruction, can outperform traditional methods in fostering student engagement and understanding.

Despite these positive outcomes, this study also revealed variability in the effectiveness of AI use across different student groups. This variation is attributable to differences in the quality of prompts formulated by the students and the level of teacher intervention during the learning process. Groups that received more targeted guidance in prompt creation and benefited from more active teacher involvement showed greater improvements in their understanding of calculus concepts. This finding underscores the critical role of the teacher in mediating AI interactions, as also emphasized by Segal et al. [32], who discussed the importance of keeping teachers involved in the loop when implementing AI in educational settings.

The practical implications of our findings suggest that for AI to be effectively integrated into mathematics education, continuous training for educators in AI technologies is essential. Teachers must be equipped not only with the technical skills to use AI tools but also with pedagogical strategies to guide and enhance student interactions with these technologies. Additionally, the development of AI-driven educational tools should prioritize adaptability and responsiveness to the diverse learning needs of students, ensuring that these tools can be customized to support individual learning paths. From a theoretical perspective, this study contributes to the growing body of literature on the use of AI in education by demonstrating the potential of AI to not only supplement traditional teaching methods but also to transform the learning experience. The insights gained from this research highlight the need for curriculum development that incorporates AI as a core component of mathematics education. Future curricula should consider the integration of AI tools as part of a holistic approach to teaching that balances technological innovation with human-centric pedagogy.

To provide a comprehensive understanding of this study’s findings, it is essential to acknowledge the following limitations. One notable limitation is the potential dependence of this study’s results on the specific features of the AI tools used. For instance, the effectiveness of the AI-generated prompts and exercises could be influenced by the unique capabilities of ChatGPT, MathGPT, Gemini, and Wolfram Alpha. These tools were selected based on their ability to provide immediate feedback, generate tailored problem sets, and support individualized learning pathways. However, the results may not be fully replicable with other AI tools that lack these specific features or have different functionalities or that may contain inherent biases or limitations in their training data or algorithms. Another limitation is the generalizability of the findings. This study focused on a small, intentionally selected group of 22 students from the Bachelor of Mathematics program, all of whom were willing to engage actively with the AI tools. While this selection process ensured a thorough evaluation of the role of AI in learning differential calculus, it may not fully represent the broader student population, particularly those who may be less motivated or have different learning preferences. Without a control group or pre- and post-tests, it is not possible to definitively attribute the observed improvements solely to the use of AI tools. Instead, this study provides qualitative insights into how AI can facilitate learning through personalized feedback and adaptive exercises. In this regard, Holmes et al. [55] emphasize the importance of using experimental designs to evaluate the effectiveness of AI in education, as self-reports and observational data may be limited by subjectivity and bias. These authors also pointed out that while AI offers powerful learning enhancements, it is important to complement these tools with teacher intervention. In this study, the teacher played a crucial role in guiding students through the process, verifying the accuracy of the AI-generated feedback, and providing additional support when needed. This combination of human oversight and AI-driven personalization created a balanced learning environment that facilitated student understanding. The involvement of the teacher ensured that AI did not replace traditional pedagogical methods but rather augmented them, a key point stressed by Holmes et al. [55] in their discussion of the role of AI in education. Similarly, Vanbecelaere et al. [56] underline the importance of adaptivity in educational systems, where feedback and learning content are dynamically adjusted based on the interactions of the students. In line with their findings, the results demonstrated how AI tools can provide personalized feedback, adjusting the difficulty and type of problems based on the progress of the students. For example, when students correctly solved a calculus problem, the AI generated more complex exercises to challenge them further. Conversely, when errors were detected, the AI provided corrective feedback and additional practice problems to help students refine their understanding. This adaptability is crucial for fostering an environment that continuously supports student learning, as highlighted in the work of Vanbecelaere et al. [56] on adaptive digital games. Future studies should aim to incorporate control groups and objective assessments to provide a more rigorous evaluation of the effectiveness of AI in mathematics education. Considering these limitations, this study offers important preliminary insights but calls for further experimental research with a control group and objective performance metrics to better understand the full impact of AI tools in education. Additionally, the intentional selection of highly motivated students may have contributed to the positive outcomes observed, as students who were already interested in mathematics were more likely to engage actively with the AI tools. As a result, the extent to which these findings can be generalized to other educational contexts or subject areas remains uncertain.

To build upon the findings of this study, future research should explore several key areas. First, long-term studies are needed to assess the lasting effects of AI on calculus learning. While this study provides valuable insights into the short-term benefits of AI integration, it remains unclear whether these benefits persist over time and how they might influence students’ long-term retention of calculus concepts and their overall mathematical proficiency. Additionally, future research should investigate the applicability of different AI tools in various educational settings and for diverse student populations. Studies could examine whether similar results can be achieved using other AI platforms or whether certain tools are more effective for particular types of learners. Comparative studies involving different AI tools could also help to identify which features are most beneficial for enhancing learning outcomes in calculus and other areas of mathematics. Moreover, exploring the potential challenges and barriers to AI adoption in educational institutions could provide valuable insights for educators and policymakers. Understanding factors such as teacher readiness, institutional support, student acceptance of AI tools, and the ethical implications of AI in education (for example, privacy, equity, and accessibility) will be crucial for successfully scaling the use of AI in education. By addressing these areas, future research can contribute to a more comprehensive understanding of the role of AI in mathematics education and help to refine and optimize its application for diverse learning environments.

In summary, while this study provides strong evidence for the benefits of AI in calculus education, it also points to the need for further research. Long-term studies are necessary to assess the lasting effects of AI on student learning and to explore the potential challenges of scaling AI integration across different educational contexts. By addressing these areas, educators and policymakers can better understand how to harness the full potential of AI in transforming mathematics education.

4. Conclusions

This study highlights the transformative potential of artificial intelligence (AI) in the teaching and learning of differential calculus. The practical implementation of AI tools in a real classroom setting provided valuable insights into their advantages and limitations. One of the original contributions of this work is the demonstration of how AI can be effectively integrated into calculus education to enhance students’ understanding of key concepts such as the average rate of change, the instantaneous rate of change, and the derivative of a real function.

The AI tools employed in this study facilitated real-time correction of errors, provided personalized feedback, and generated practice problems tailored to individual student needs. These tools significantly improved students’ accuracy and conceptual understanding, showcasing the utility of AI as an intelligent tutor. However, this study also revealed that current AI systems have limitations in detecting procedural errors in students’ mathematical reasoning. This finding underscores the necessity of complementing AI with manual feedback from teachers to ensure a comprehensive understanding of mathematical concepts.

An innovative aspect of this study is the iterative process of refining AI prompts and interactions. By continuously improving the prompts, this study was able to enhance the quality of AI feedback, which in turn helped students develop better problem-solving skills. This iterative approach highlights the importance of designing effective AI prompts to maximize the benefits of AI in education.

The integration of AI in the classroom created a dynamic and adaptive learning environment, increasing student engagement and motivation. This study demonstrated that AI can serve as a powerful tool to support personalized learning, allowing students to progress at their own pace and receive immediate feedback on their work. This personalized approach is crucial for mastering complex mathematical concepts and fosters a deeper understanding of the subject matter.

To fully realize the potential of AI in mathematics education, further research is needed to develop advanced AI techniques capable of better understanding and correcting errors in mathematical reasoning. Additionally, forming learning communities among educators specializing in AI can facilitate the sharing of experiences and the development of effective strategies for using AI in the classroom.

To ensure the successful integration of AI tools into mathematics education, educators should carefully evaluate their specific curricular goals and select AI tools that align with these objectives. Additionally, customizing AI tools to accommodate diverse student learning styles is essential for creating personalized learning experiences. Ongoing evaluation of AI tool effectiveness through various assessment methods is crucial to monitor their impact on student learning.

Pilot studies in different educational settings—ranging from traditional classrooms to online learning environments—could provide valuable insights into how AI tools perform under varying conditions and with different student populations. By leveraging the adaptability of AI, educators can provide tailored learning opportunities that cater to individual student needs, thereby enhancing engagement and understanding.

Educators should also receive comprehensive training on how to effectively integrate AI tools into their teaching practices, focusing on both technical aspects and pedagogical strategies. Moreover, successful implementation of AI requires collaboration among educators, administrators, policymakers, and AI developers to ensure that AI tools are designed and deployed in ways that meet the needs of both students and educators.

Overall, this study underscores the promising contributions of AI to mathematics education while acknowledging its limitations. The results advocate for a balanced approach, emphasizing the need for continued research, community building among educators, and the complementary use of AI and human feedback. By combining the strengths of AI and human instruction, we can create a more robust and effective educational environment that fosters both conceptual understanding and practical skills in mathematics.