Self-Regulation Profiles of Pre-Service Mathematics Teachers for Primary Education in Mathematical Problem-Solving Contexts

Abstract

Self-regulation in mathematical problem solving is of particular importance in the initial training of Primary Education teachers as it can contribute to improving their own competence in mathematics and at the same time enable them to teach effectively and in a personalized way. With this idea in mind, this study identifies self-regulation profiles present in university students in mathematical problem-solving contexts based on data from the application of a validated scale on a sample of 402 pre-service teachers of primary education at University of the Basque Country. The cluster analysis carried out made it possible to identify and characterize three profiles, labelled according to the level of self-regulation represented by each of them (low, medium, high). In view of the results obtained, we perceive a need to design didactic proposals that allow these profiles to evolve from the lowest to the highest levels.

1. Introduction

The importance of mathematics in education is recognized globally by organizations such as the United Nations Educational, Scientific and Cultural Organization (UNESCO) [1], which includes the promotion of mathematical competence as part of Sustainable Development Goal 4.4. This goal focuses on guaranteeing that students of all ages and educational levels acquire knowledge and skills in mathematics, which implies quality education for all.

Studies indicate that the quality of mathematics education depends to a large extent on the preparation and competence of teachers, as they are responsible not only for transmitting specific knowledge, but also for providing students with the necessary tools to develop critical thinking and creativity, enabling them to solve problems in everyday life [2,3].

Within this approach, recent research indicates that incorporating this objective requires special attention in pre-service teachers, especially in the area of mathematics [4,5].

However, research has shown that, in some cases, teachers do not have the necessary content knowledge, and this is reflected in below-average overall scores in mathematical and didactic-mathematical knowledge in pre-service teachers of primary education [6]. This lack specialized mathematical content knowledge in teachers was identified as one of the factors behind low student performance in international assessments such as the Programme for International Student Assessment (PISA) [7] and the Trends in International Mathematics and Science Study (TIMSS) [8].

Likewise, several studies point to motivational, affective and cognitive factors that affect students’ academic performance. For example, negative attitudes and beliefs towards mathematics and, in particular, towards mathematical problem solving, as well as emotions associated with this subject, such as anxiety, insecurity and frustration, were identified [9,10,11]. These factors influence students’ mathematics teaching and learning, and are, in turn, transmitted through instruction [12].

On the other hand, self-regulation of learning, increasingly present in the literature, is considered a key element for students’ academic success. This multidimensional construct refers to students’ ability to regulate their own thoughts, emotions and behaviours in order to achieve a goal [13,14]. From this perspective, motivational variables [15] and, in particular, self-efficacy [16] are considered crucial variables in the development of self-regulated learning.

With regard to [17] problem solving, one of the most important aspects of learning mathematics, is closely related to self-regulated learning. A study by Salangsang and Subia [18] points out that the problem-solving approach in mathematics education not only enables students to better understand mathematical concepts but also fosters the development of critical skills such as logical thinking, creativity and the ability to apply knowledge in practical contexts. In addition, by tackling problems, students improve their self-regulation skills, which include planning, monitoring and evaluating their own learning processes.

In this context, there exist specific measurement tools to assess self-regulation in mathematical problem-solving contexts, such as the one designed by Authors [19] for secondary school students or the one adapted and validated in the study by Authors [20] for university students.

Based on this latter scale, the study presented here is part of a broader investigation that aims to detect the impact of classroom experimentation based on cooperative learning on the self-regulation of pre-service teachers of primary education in solving mathematical problems; and, therefore, the aim of this study is to identify the self-regulation profiles, focusing our interest on certain variables associated with this construct, of pre-service teachers of primary education in this context.

2. Theoretical Framework

Self-regulated learning refers to the ability of learners to control and direct their own learning process; this involves setting learning goals, selecting and applying effective strategies, maintaining motivation, managing time efficiently, monitoring personal progress and evaluating their own performance [21].

From a socio-cognitive perspective in which we recognise that learning is not an isolated process, but is influenced by social, emotional and cognitive factors, the present study is based on the self-regulation model proposed by Zimmerman [22]. This model divides the process of self-regulation into three cyclical phases: anticipation, execution and self-reflection. It also identifies critical dimensions that students must regulate. Thus, we have motives, which direct students towards the goals they wish to achieve, with two important aspects in this dimension being goals and self-efficacy. Method refers to how self-regulated learning occurs. Here, the key processes are the strategies and routines that each learner uses to learn effectively. In the time dimension, the self-regulated learner chooses when and for how long to engage in a specific task. Time management is a key process in this dimension. The behaviour dimension refers to the outcomes or levels of competence that the learner wishes to achieve. Key self-regulatory processes in this dimension include self-observation, self-judgement and self-reaction. Finally, the social environment dimension focuses on the interactions and relationships with others that influence the learning process.

In addition to Zimmerman’s [22] model, which is widely recognised and used in educational research, this paper assumes Boekaerts’ [23] model, which complements the model above and states that one of the objectives of self-regulated learning is to redirect the path of well-being toward the path of learning. This idea serves as the basis for the construction of a new dimension, ethics, proposed by [24]. This holistic approach provides a solid basis for understanding how students regulate their own learning and achieve better academic results.

Focusing on self-regulation at the university level, we found the study carried out by Fernández et al. [25] with a sample of 552 first-year university students from different degrees at the University of Oviedo confirms that, in order for students to implement self-regulation strategies for learning, it is important that they feel capable of doing so, with self-efficacy for the use of self-regulation strategies with learning being the variable with the greatest predictive capacity in the use of these strategies. Thus, a poor sense of self-efficacy could be responsible for the academic problems of a large proportion of students [26]. Several studies suggest that self-regulation and motivational beliefs are significantly influenced by variables in the classroom environment [27,28]. This is evident in the study by Rojas-Ospina and Valencia-Serrano [29], which reveals that when students, at the university level and in the area of mathematics, perceive a positive classroom climate, where teachers promote a safe environment for participation and communicate clear expectations to students about their performance, they show greater motivation in class, as well as greater self-efficacy, more interest in the content, more commitment and more effort.

Previous studies have analysed various dimensions in which to categorise self-regulation, which is important for the present study since, based on categories of this construct, we try to identify self-regulation profiles that differentiate between learners. Thus, several studies show that students, in general, tend to use self-regulated learning strategies to moderate degrees [30,31]. However, we should not lose sight of the existence of self-regulation profiles that differentiate students. Xu and Corno’s [32] study categorizes students (918 Chinese students in grades 7 to 9) according to their strategies for managing mathematics tasks (i.e., organizing the environment, managing time, monitoring motivation, managing emotions, cognitively re-evaluating information, and handling both conventional and technological distractions). Five distinct profiles are identified that could be labelled as high in all strategies, moderate in all strategies, low in all strategies, low except for managing distractions and low in managing distractions. Similarly, the study by Cleary et al. [33] uses motivational, regulatory and contextual variables of secondary school students in mathematical tasks and, by means of cluster analysis, identifies four profiles that vary in two dimensions (self-regulated learning and perceived contextual supports) and levels (high and low). These profiles with well-defined characteristics are useful to subsequently test their evolution through the design of appropriate didactic proposals.

Restricting our focus to self-regulated learning and mathematical problem solving, we find several research papers that address this topic; the study by Schoenfeld [34] plays an important role, as it focuses attention on students’ resources, metacognitive strategies, as well as their beliefs about and affective behaviour to these types of tasks. Schoenfeld identifies three key metacognitive processes in self-regulation: planning, monitoring and evaluation. In addition, this study points out that beliefs can influence the way students approach a problem, the techniques they choose to use or avoid, and the time and effort they are willing to invest in the task. Schoenfeld [34] and later De Corte et al. [35] argue that self-regulation and motivational beliefs are key aspects of mathematical competence and of being a competent problem solver. Current models of self-regulation also stress the importance of both motivational and emotional processes in the context of mathematical problem solving [36,37].

Thus, in the study conducted by Cleary and Chen [38] with a sample of 880 students at the intermediate level of education, the level of performance in mathematics is investigated, as well as differences in self-regulation and motivation. The results of the analysis reveal that, as students progress through their education, they show a reduced ability to regulate their own learning and less favourable motivation toward mathematics, which may have a negative impact on their performance.

The research by Martínez and Valiente [39], on the other hand, explores the same problem in greater depth and shows that good performance in mathematics is not only associated with the use of appropriate strategies to solve problems but also with metacognitive competence, attributions of success to effort and a high perception of self-efficacy. In this study, as in others, the self-regulation and motivation profile turns out to be more maladaptive as the educational level increases, a result supported by other studies such as that of González-Pienda et al. [40].

At the university level, in particular, in the case of primary school initial trainers, as far as the authors of this paper are aware, there is not much research that addresses this issue. Even so, we find the work of Authors [20], which validates a scale to measure self-regulation in the context of mathematical problem solving. This scale presents good psychometric properties in terms of internal consistency and construct validity, and its factorial structure is composed of seven factors.

The Research Rationale and Goals

The literature review shows that self-regulation is a complex and multidimensional construct. In Mathematics Education, there are some consistent studies that establish self-regulation as a potential predictor of academic achievement in mathematics [38,41]; however, there is a shortage of specific scales to measure the level of self-regulation of university students in problem-solving contexts, which gives rise to the aforementioned scale by Authors [20] that would fill the detected gap.

Based on this scale, the aim of this study is to identify different self-regulation profiles in relation to the resolution of mathematical problems that characterize pre-service teachers with a Degree in Primary Education.

The identification of these profiles would be interesting to the research community, as it could provide information that would enable the design of specific interventions aimed at improving them.

3. Materials and Methods

This research is a non-experimental study aimed at identifying the self-regulation profiles of pre-service teachers of primary education in mathematical problem-solving contexts.

3.1. Sample

A non-probabilistic convenience or incidental sample was used to select the sample, as the students who participated in the study were selected on the basis of their accessibility and suitability for the study.

The study involves 402 pre-service teachers from the three campuses of University the Basque Country enrolled in the first year of the Degree in Primary Education in the 2021/2022 academic year. The choice of incoming students is a relevant decision, as we wish to obtain information on their level of self-regulation at the beginning of their training and, in particular, before the students have direct contact with the process of solving mathematical problems, a key area of the subject Mathematics Education, which is taught in the second term of the first year. This is why the data collection is carried out in the first term: it has the aim of capturing self-regulation skills in mathematical problem-solving contexts before students receive specific instruction in these concepts and practices. The characteristics of the sample are detailed in

Table 1. Sample data in the academic year 2021/2022.

	Academic Year
	2021/22
Variables	n = 402	%
Gender Identity
Woman	239	59
Man	148	37
Non-binary	6	1
NS/NC	9	2
Baccalaureate mode
Social Sciences	225	56
Science and Technology	169	42
Arts	3	1
Other	5	1

.

3.2. Instrument

The instrument used in this study is a scale on the self-regulation of learning in mathematical problem-solving contexts adapted for university students and duly validated [20]. The stages followed in the process of scale adaptation and validation are content validation, translation validation, face validity, internal reliability, and analysis of the factor structure of the scale (exploratory factor analysis). The content validity by experts who know the characteristics of this study sample and its sociocultural context implies the modification of some items. The process of validating the translation of the questionnaire into Basque is essential to ensure that students understand the items correctly and can respond appropriately, which contributes to obtaining valid and reliable data in the specific context of the study. The overall scale, in terms of internal consistency, obtains a value for MacDonald’s Omega ($\omega$) of 0.87, a particularly relevant coefficient when working with multidimensional scales. In relation to its factor structure, the KMO values (0.84 > 0.7) and the result of Bartlett’s test of sphericity (p = 0.000 < 0.05) are considered adequate. The questionnaire consists of 41 items (see Appendix A) grouped into seven interrelated factors, but each with their own factorial identity (see

Table 2. Distribution of items by factor.

Factors	Items
Factor 1: Learners’ perceptions of their ability and how this influences self-regulation of the resolution process	20, 21, 24, 28, 29, 30
Factor 2: Ethics	1, 2, 3, 4, 12, 22
Factor 3: Problem solving and personal growth	33, 37, 38, 39, 40
Factor 4: Attitude to the statement	5, 6, 7, 8, 9, 10, 11, 15
Factor 5: Negative self-efficacy beliefs and external causal attribution	14, 16, 25, 32, 35, 36, 41
Factor 6: Problem-solving method	17, 18, 19, 23, 27
Factor 7: Social Environment	13, 27, 34

Note: The wording of the items can be found in Appendix A.

), and corresponds to a Likert scale with 7 response levels where 1 = never or almost never; 2 = about one in ten times; 3 = about one in three or four times; 4 = about 50% of the time; 5 = about two in three times; 6 = between eight and nine times in ten; and 7 = always or almost always [20]. The reason for using 7 levels is that it gives students a greater ability to express subtleties in their answers, avoiding the tendency to choose intermediate or neutral answers. By having broader options, more precise and differentiated levels of agreement or disagreement can be captured, which provides greater richness in the information collected [42].

Table 2 shows the items that make up each of the factors.

3.3. Procedure

The fieldwork was carried out by means of the synchronous online application of the scale through the Forms application, with the presence of one of the researchers, after the participating students had signed the corresponding informed consent form in which they were informed of the objective of the study and the procedure, as well as guaranteeing the privacy and confidentiality of the data of the participants. Each student voluntarily responded to the online questionnaire in approximately 15 min, and this was without any notable incidents.

Finally, this project was approved by the Ethics Committee for research involving human subjects and their data or samples (CEISH-University of the Basque Country) with code M10_2021_087.

3.4. Data Analysis

Cluster analysis is based on the idea that the study sample, pre-service teachers of primary education, is organized into groups according to the scores obtained in the factors associated with self-regulation in mathematical problem-solving contexts. This statistical technique seeks to group students, aiming to achieve maximum homogeneity in each group and maximum difference between groups and, in this way, to be able to identify profiles with distinctive characteristics in relation to this construct [43].

Reference [43] states that cluster analysis is mainly used as an exploratory and descriptive technique, as is the case in this research. The solutions obtained in its application are not unique and depend on various elements of the chosen procedure. In this case, it must be taken into account that the variables are quantitative and that the interest of the study lies in the classification of profiles of a large sample of cases; therefore, a K-means cluster analysis was used, which is a non-hierarchical method that allows each participant assigned to a group in a certain step of the process to be reassigned to another group in a later step, if this optimises the selection criteria.

In order to identify such profiles, different cluster solutions are tested, including 3, 4 and 5 clusters [44]. Finally, a 3-cluster solution is chosen as the most appropriate according to the following criteria: (a) convergence in the first 10 iterations, suggesting that the analysis stabilizes quickly; (b) existence of significant differences between clusters in the seven self-regulation factors; (c) theoretical consistency, i.e., the solution reflects profiles that make sense from a theoretical perspective [43,44].

Finally, it is important to note that the use of cluster analysis suggests a lack of knowledge or incomplete knowledge about the classification of the data. Carvalho et al. [45] recommend using discriminant analysis to avoid subjectivity in the researcher’s choice of method. In addition, they consider this technique to be effective in validating the results obtained in cluster analysis. For this reason, once the profiles are identified, a discriminant analysis is used to verify the robustness of the clusters formed and to validate the grouping methodology used [45]. The data analysis is carried out with the statistical programme SPSS, version 28.0 for Windows.

4. Results

The non-hierarchical analysis mentioned in the previous section makes it possible to group pre-service teachers of primary education according to shared characteristics of self-regulation in problem-solving contexts, giving rise to three clusters. As can be seen in

Table 3. Clusters obtained.

Cluster No. K-Mean		Factor 1	Factor 2	Factor 3	Factor 4	Factor 5	Factor 6	Factor 7
1	Mean	3.83	4.51	3.81	3.8	4.12	4.17	5.06
	SD	0.75	0.75	0.78	0.72	0.63	0.71	1.05
2	Mean	4.67	5.37	4.46	4.68	3.94	5.27	5.98
	SD	0.63	0.61	0.74	0.77	0.78	0.61	0.73
3	Mean	5.61	6.06	5.21	5.47	4.55	5.98	6.62
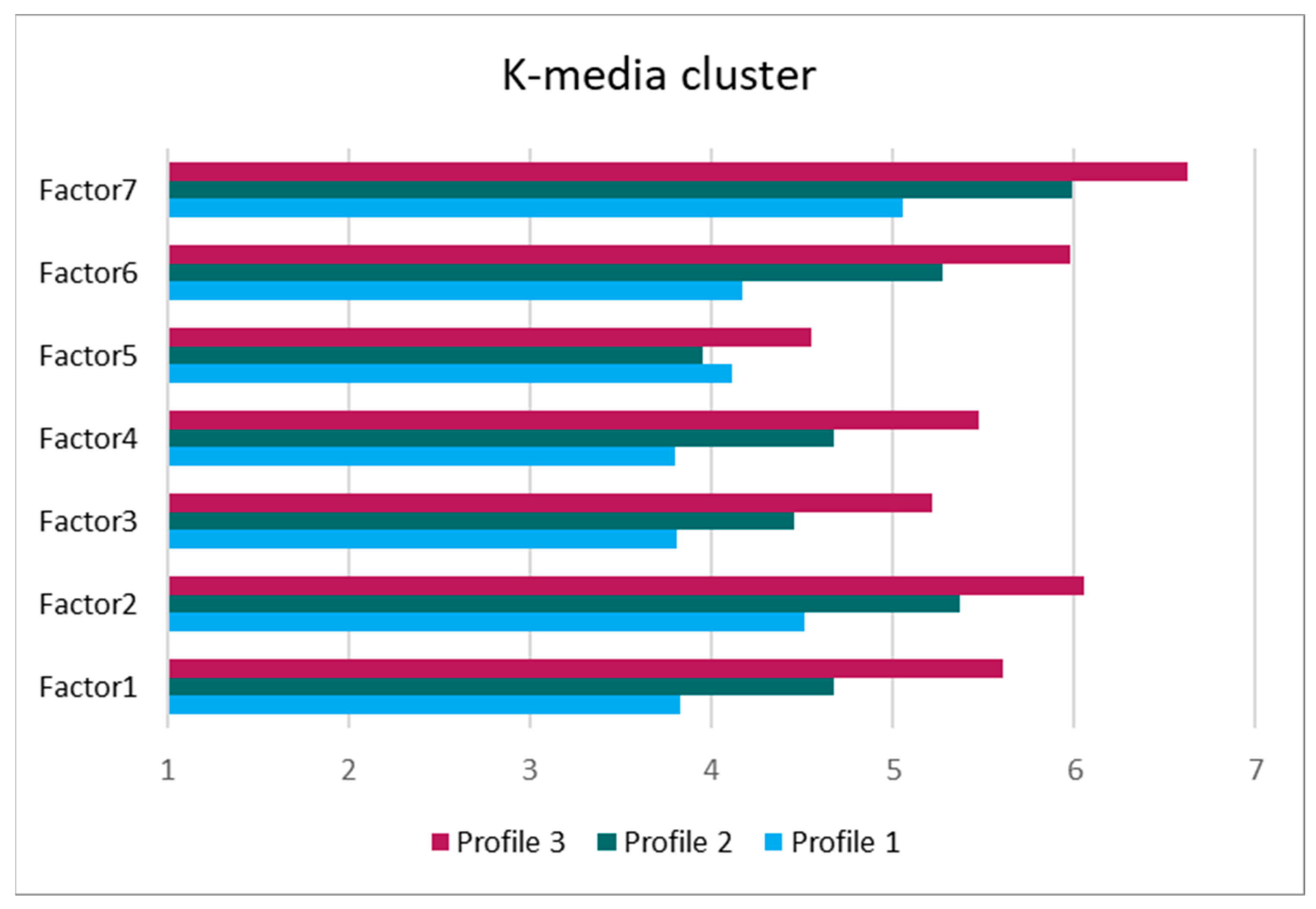
	SD	0.65	0.55	0.78	0.72	0.87	0.52	0.61

, the first cluster, to which we will assign, in view of its characteristics, the identity of Profile 1: low level of self-regulation, is composed of a total of 82 students, which corresponds to 20% of the sample and obtains a mean of 4.2 with a minimum value of 3.8 and a maximum of 5.06; the second cluster, which we label Profile 2: medium level of self-regulation, composed of 188 students, represents 47% of the sample, i.e., approximately half of the students are in this profile. This profile obtains a mean of 4.9 with a minimum value of 4 and a maximum of 5.98; and the third cluster, also endowed with its own entity, corresponds to what we agree to call Profile 3: high level of self-regulation, and is composed of 132 students, which represents 33% of the sample. In this case, this profile obtains a mean of 5.6 with a minimum value of 4.6 and a maximum of 6.6.

Then, based on the scores, mean and standard deviation, obtained in the factors under study and measurement, namely, Factor 1: “Students’ perception of their ability and how this influences the self-regulation of the resolution process”, Factor 2: “Ethics”, Factor 3: “Problem solving and personal growth”, Factor 4: “Attitude towards the statement”, Factor 5: “Negative self-efficacy beliefs and external causal attribution”, Factor 6: “Problem-solving method”, Factor 7: “Social environment” (See Table 3). Furthermore, it should be noted that Factor 5: “Negative self-efficacy beliefs and external causal attribution” consists only of negatively formulated items that were re-coded for analysis in order to maintain consistency in the interpretation of the responses, so that a higher mean value indicates a more favourable or positive result.

Below are the most relevant data and observations to categorize into the three aforementioned levels for self-regulation in problem solving:

Profile 1: Low level of self-regulation. Three factors (Factor 1, Factor 3 and Factor 4) score below 4. Therefore, students in this profile have a low perception of self-efficacy, do not value problems as opportunities for learning or personal growth, i.e., their motivation for the task is low and, around 70% of the time, they have a negative attitude towards the mathematical problem statement. Also, the value obtained for Factor 6 implies that around 50% of the time, they are not able to determine which strategies are most effective in solving the problem, nor when, how and why they should be applied. Finally, the highest value is obtained in Factor 7 which, with an average score of 5.06, indicates that students, when they have difficulty in solving the problem, approximately two out of three times, are able to ask their classmates for help.

Profile 2: Medium level of self-regulation. As in the previous case, the factors with the lowest scores are Factor 1, Factor 3 and Factor 4, these being below value 5; therefore, students in this profile have only a moderate, albeit positive, perception of self-efficacy. In general, students in this profile also have a relatively positive motivation, as well as a relatively positive attitude towards the statement. On the other hand, scores above 5 in Factor 2 and Factor 6 indicate that, when faced with obstacles, students in this group, on approximately two out of three occasions, try to solve problems by their own means, using effective strategies. The highest value, again, is obtained in Factor 7, whereby, when faced with the difficulty of solving a problem, students at this level, on 80% of occasions, are able to ask for help within their environment. Finally, it should be noted that, in this profile, Factor 5 obtains a score lower than 4, even lower than that obtained by students in Profile 1, although this is not a significant difference (p = 0.234 > 0.005, see Appendix B). This result suggests that students in this group, around 50% of the time, have negative self-efficacy beliefs and attribute failure or success to external causes such as the difficulty of the task, the teacher, etc.

Profile 3: High level of self-regulation. In this case, there are three factors that exceed the value 6—Factors 2, 6 and 7—which shows that students at this level, despite the difficulties, try to solve the problem with perseverance and by their own means, are able to maintain motivation over time, use some effective method to reach the solution to the problem 80% of the time and believe that it is very important to ask for help and learn from their classmates. The remaining factors, Factor 1, Factor 3, Factor 4, and Factor 5, obtain higher values than in the other two profiles, which implies that students at this level have a higher perception of self-efficacy, a better attitude towards problem statements and see challenges as opportunities to grow and develop.

In Figure 1, the three profiles are shown graphically on the basis of their mean scores obtained in the study factors (described in Table 3), in order to more easily observe improvements as one moves from one profile to another, except in the case of the controversial Factor 5. As can be seen in Figure 1, in Factor 5 there are no differences between the three profiles and Factor 7 has good scores in all of them. The rest of the factors show a positive evolution from one profile to another.

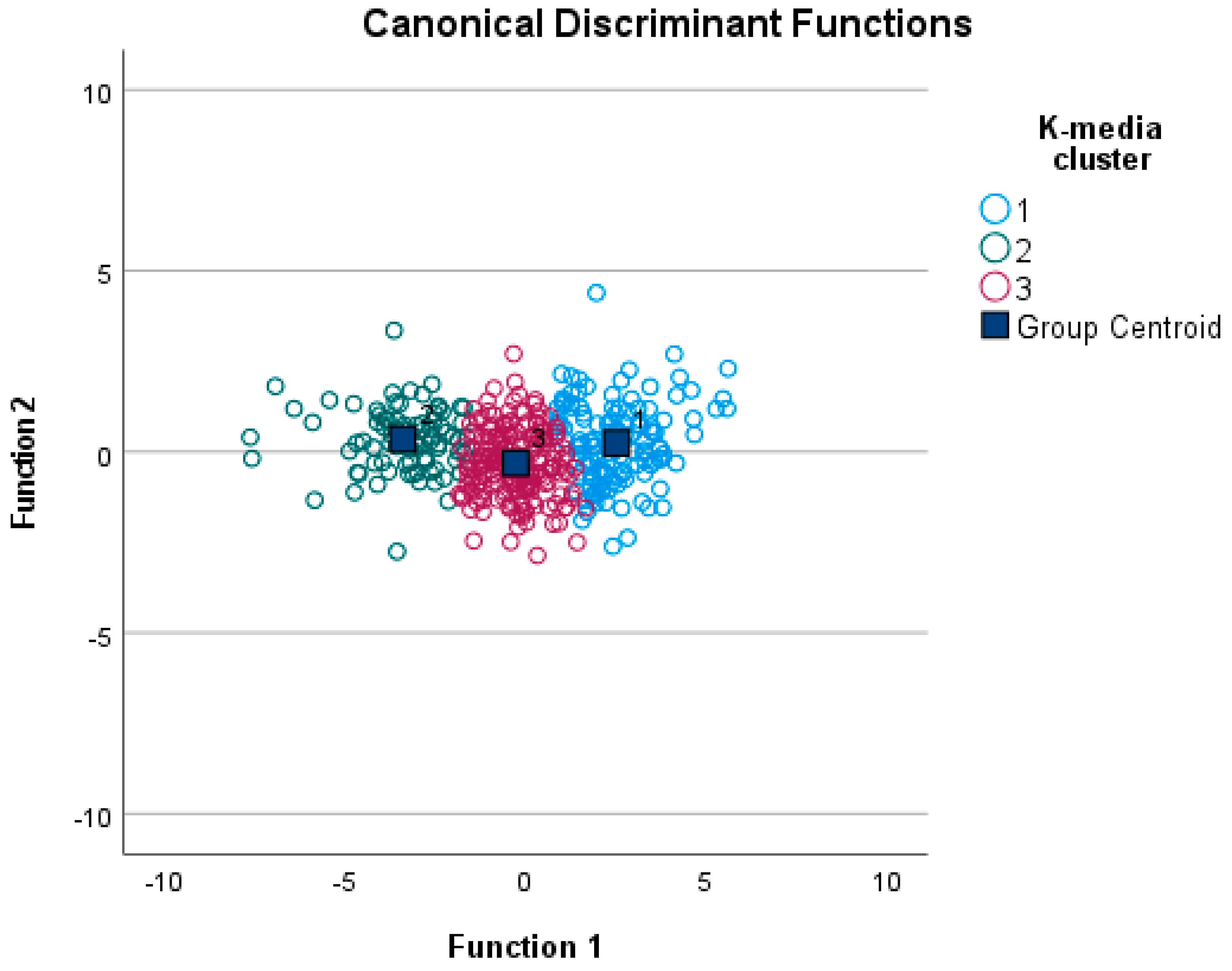
After the classification of the sample into clusters and their characterization into profiles, the quality of the classification procedure is assessed by means of discrimination analysis. First of all, the graphical representation of this three-cluster solution can be seen in Figure 2, where the position of each of the groups on the plane can be clearly distinguished. Based on the colours assigned by the SPSS, on the left we find Profile 1, in blue, which corresponds to the low self-regulation level; on the right, Profile 3, in red, which corresponds to the high self-regulation level; and finally, in the centre, Profile 2, in green, which corresponds to the medium self-regulation level. In addition, the centroid of each of the clusters is shown, which, as can be seen, relates appropriately to the centre of the clusters.

Second, the test of equality of means indicates that considering the factors individually, the significance values are less than 0.05; therefore, the means of the seven factors are different in the three groups (see

Table 4. Test for equality of group means.

	F	gl1	gl2	Sig.
Factor 1	188.26	2	399	<0.001
Factor 2	157.11	2	399	<0.001
Factor 3	91.15	2	399	<0.001
Factor 4	130.46	2	399	<0.001
Factor 5	23.01	2	399	<0.001
Factor 6	226.87	2	399	<0.001
Factor 7	104.27	2	399	<0.001

). Also, the high values of the F-statistic indicate that the variability between groups is much higher than the variability within each group, indicating that the clusters produced are homogeneous. Therefore, all the factors considered in the analysis can help to correctly classify each student into one of the three profiles.

Finally,

Table 5. Discriminant analysis with total scale scores.

Classification Results 1
			Predicted Group Membership
		Cluster Case Number	1	2	3	Total
Original	Count	1	129	0	3	132
		2	0	79	3	82
		3	3	0	185	188
	%	1	97.7	0	2.3	100.0
		2	0	96.3	3.7	100.0
		3	1.6	0	98.4	100.0

¹ 97.8% of original grouped cases correctly classified.

presents the percentage of cases correctly classified; Profile 1 achieves 97.7% of cases correctly classified, Profile 2 96.3% and Profile 3 98.4%. Overall, Table 5 shows a 98% success rate, i.e., according to this model, participants, based on the characteristics defined by their scores on the scale used, have a 0.98% chance of being placed in the correct group, indicative of a good consistency of the profiles identified in the cluster analysis.

5. Discussion

The results obtained in this study allow us to better detail the type of self-regulation of the sample and to determine different levels of self-regulation, in relation to mathematical problem solving, which characterize pre-service teachers of primary education, i.e., we found different profiles that explain the internal variability in self-regulation and determine certain traits of the sample depending on the cluster. From this perspective, specifically, three profiles were identified that were labelled as high, medium and low levels of self-regulation, respectively. These three profiles show significant differences in the seven measurement factors considered, showing, in general, improvements as one progresses from one profile to another. That is, the higher the students’ level of self-regulation, the higher their perception of self-efficacy and motivation is and, with it, their effort. Similarly, the attitude towards the statements, the search for help in the environment when necessary and the strategies used to solve problems improve, with the latter becoming more efficient.

The above results are consistent with other research that supports the idea that self-regulated learners understand when, where and why strategies are used, have a set of adaptive motivational beliefs and know how to seek help from their environment when they encounter difficulties [38,46]. These characteristics of self-regulated students coincide to a large extent with those of Profile 3: high level of self-regulation present in our work. However, with appropriate instruction, all the students in the sample could increase the degree of control, and so minimize the learning difficulties they present in the process of solving mathematical problems, particularly students with a low level of self-regulation [47].

In view of this state of affairs, the results of our research point to the need for designing and developing didactic proposals that would adapt to the diversity of the profiles present in the classroom. Specifically, in the case of Profile 1: low level of self-regulation, it is necessary to take measures both to improve motivational beliefs and the attitude towards the statement, as well as to increase the knowledge and appropriate use of strategies that help in the resolution of the problem.

To achieve these objectives, the direct teaching of learning strategies could be considered, explaining to students which strategies are most appropriate for specific problems: how, when, how and why they are used [48]. However, from a socio-cognitive perspective, based on Zimmerman’s motivational model [48], the theoretical framework of our work, the improvement of self-efficacy beliefs and affective reactions to tasks not only influence motivation to learn but also the way in which students use learning strategies; knowing the strategies would not be enough to implement them, a certain level of motivation would be essential to be able to put them into practice.

In the case of Profile 2: medium level of self-regulation, although there is a favourable evolution in certain aspects with respect to the previous group (perception of self-efficacy, motivation and attitude towards the statement), the scores are only moderate, which indicates that there is room for improvement. Similarly, students in this profile use more and better strategies in the solving process than students in Profile 1, so efforts should mainly focus on increasing motivation, as this can serve as a stimulus to improve other aspects of self-regulation in mathematical problem-solving contexts, such as attitude towards the statement [49].

Scaffolding instruction (Scaffolding) is a tool that improves student learning and motivation and where the teacher takes on the role of assistance and accompaniment which, in turn, leads to a change of role on the part of the students, i.e., adopting a proactive attitude to the learning process. In this framework, the teacher poses problems to be solved by the whole class and may propose group activities using different work techniques (collaborative, cooperative…) [50]. The ultimate goal is that the responsibility or control for generating, applying and evaluating strategies is progressively transferred from teachers to students [51].

In relation to Profile 3: high level of self-regulation, students belonging to this group obtain an optimal level of self-regulation. Even so, this is a group that also needs to be monitored since, as the results show, the line separating the different clusters is thin. There may be students with this profile who feel competent in mathematics and who, after repeatedly failing to solve mathematical problems, begin to rethink their competence in the subject. In this case, educational contexts that are sensitive to the assessment of the learning process rather than the evaluation of the product should be considered.

Self-reflective practice, as a goal of the didactic process, was put forward by various self-regulation programmes [52]; students would culminate the problem-solving process by discussing and reflecting on the steps followed, evaluating the effectiveness of the strategies and the performance achieved.

6. Conclusions, Recommendations and Limitations

As noted above, we detected different profiles that explain the internal variability of self-regulation. Although this research provides valuable information on self-regulation profiles of mathematical learning, particularly in the context of mathematical problem solving, it should be noted that there are limitations that need to be taken into account. As this is the first time this scale has been used to identify self-regulation profiles, it is suggested that further replication be carried out to test the robustness of these results in more detail. Moreover, the incorporation of new variables in future research may enrich our understanding of university students’ self-regulation in the context of mathematical problem solving.

In short, the results of this research work provide information from which to design and develop specific teaching strategies adapted to the needs of each student, according to their profile. The promotion of inclusive mathematical education would thus be ensured.

In addition to these educational practices, other methods of data collection should be considered, such as semi-structured interviews with students, classroom observations, etc., which would make it possible to explore how the profiles evolve and what factors influence these changes. Finally, researchers in the future may consider it interesting to examine how these profiles might influence the performance of future teachers of primary education and, ultimately, the quality of the mathematical education received by students.