More Evidence of Low Inter-Rater Reliability of a High-Stakes Performance Assessment of Teacher Candidates

Abstract

From 2010 to 2015, our school of education used the Performance Assessment for California Teachers (PACT), a summative assessment designed to assess preservice teacher competence. Candidate portfolios were uploaded to an evaluation portal, and trained evaluators assigned a final score of Pass or Fail to the work samples. Three consensus estimates of inter-rater reliability of 181 candidate portfolios that were either double- or triple-scored were computed. Two chance-corrected estimates of inter-rater reliability (Cohen’s kappa and Gwet’s AC₁) and percent agreement were computed and calculated within five content areas: elementary math, secondary history/social science, math, science, and English language arts. An initial Pass or Fail score was not more likely to be followed by either a Pass or Fail score given by a subsequent evaluator. Inter-rater reliability was interpreted as being low across all content areas that were examined. None of the percent agreement coefficients attained the minimum standard of 0.700 for consensus agreement. Increasing research access to proprietary double-scored data would lead to an increased understanding of, and perhaps improvement in, teacher performance assessments.

1. Introduction

Successful classroom teachers demonstrate a broad range of competencies and can have positive, life-long effects on their students. On an ongoing basis, preservice teacher competence is assessed within teacher preparation programs. To hold schools of education more accountable for the quality of teacher graduates, standardized teacher performance assessments were developed to also measure the skills and abilities associated with effective teaching. Performance assessments of teacher candidates is one possible way to increase the likelihood of placing skilled and competent teachers in K-12 classrooms. To be recommended for a preliminary teaching credential in California, teacher candidates must pass a state-approved teacher performance assessment (TPA).

In the current study, the inter-rater reliability (IRR) of Pass/Fail scores from the Performance Assessment for California Teachers (PACT) was examined, which is a standardized performance test of several content areas. The PACT, which is no longer used at our school of education, evolved into the edTPA [1,2,3,4,5,6,7], which is used nationally at several institutions, including our own. Both the PACT and edTPA originated at the Stanford Center for Assessment, Learning and Equity (SCALE) and share the same architecture [7] (p. 22). A major difference between the two TPAs is that the PACT was locally scored, whereas the edTPA is not.

Teacher performance assessments require candidates to construct their responses rather than select responses as in a true–false or multiple choice test. Even though evaluators are trained to fairly evaluate constructed response tests such as a teacher performance assessment, there will still be some subjectivity on the part of the evaluators. Because of the complexity of evaluating a multi-dimensional teacher performance portfolio across several tasks and components, rater variance in assessments has been noted by many researchers (e.g., [6,8,9,10]). Rating teacher performance assessments can be time-consuming, and a rater on a certain day may be tired. Some raters are more biased than others or have more difficulty discerning scale score differences than others. Some raters can be harsh, lenient, or overly inconsistent [8]. For example, depending on which rater was assigned to assess a candidate’s portfolio, or even on which day, one candidate could receive a stricter rater and not pass the performance assessment, whereas another candidate could receive a more lenient rater and pass the performance assessment. Because human judgment is involved, the main source of error in candidate scores in TPAs is typically from the rater [6] (p. 13). Eckes [8] noted that “rater variability is a general, notorious problem of rater-mediated assessments” (p. 93). Anderson et al. [9] noted that “Overall, raters differed substantially in their average ratings” (p. 30). Thus, rater variability seems more likely than rater homogeneity.

One way to try to increase reliability in rating is to train the evaluators to use scoring rubrics and to learn the distinction between scale scores (as was the case with the PACT). If it is consistently found that there is high inter-rater agreement, raters may be considered to be interchangeable, and the rating procedure can be streamlined and made more efficient with fewer rather than more raters doing the bulk of the ratings. If, however, low inter-rater agreement is observed, then the raters are not interchangeable. Maybe the test or the rubrics need to be altered (because of confusion about the rubrics), or raters could be more extensively trained. However, even with additional training, raters will tend to retain their scoring propensities. For example, Eckes [8] noted: “rater training that aims at achieving homogeneity within a given group of raters regarding their degree of severity or leniency, is, as a rule, highly unlikely to meet with success” (p. 93). See also [10].

Both reliability and validity are paramount to establish in high-stakes tests such as teacher performance assessments. Without reliability, a test cannot be valid [11]. “If we aren’t measuring something consistently, we cannot use that measurement to make an appropriate decision about the examinee” [11] (p. 2). In the current study, one form of reliability, inter-rater reliability (IRR), was examined, which is the extent to which different observers agree on what they are evaluating [2].

I wanted to examine the IRR in our candidates’ edTPA data, but when double-scored data were requested, access was not provided because the data are proprietary to Pearson Inc. In a prior study [12], IRR was assessed in the PACT during the last academic year (2014) of its use at our school. In the current study, the sample size has been expanded by over nine times, and the sample includes PACT data that were collected during the duration of its use at our institution, from 2010 to 2015, before its replacement by the edTPA. Because of the high-stakes nature of the TPA (receiving or not receiving your credential), examining IRR data was important for several reasons: (a) IRR data in TPAs have been reported as percent agreement without correction for chance agreement, and (b) double-scored data are not frequently reported and are even harder to obtain now that they are often proprietary to corporations such as Pearson [12].

Consensus Estimates of IRR

There are several methods that can be used to compute consensus estimates of IRR. Zhao et al. [13] discussed these many methods, including percent agreement, and noted the many paradoxes and abnormalities of the methods, ultimately calling for a new-and-improved agreement statistic to be developed. This ideal agreement coefficient is not currently available. With these limitations in mind, I chose three ways of examining inter-rater agreement (I use “agreement” interchangeably with “reliability”) in the present study: Cohen’s k, Gwet’s AC₁, and percent agreement.

I used two chance-corrected agreement coefficients: Cohen’s kappa (k) and Gwet’s AC₁. Kappa ranges from −1 to 1 (perfect nonagreement to perfect agreement) with chance agreement removed [14]. Kappa is a widely used measure of IRR, but it has known deficiencies, referred to as paradoxes [15,16]. One paradox is when there is high agreement between raters but the coefficient is low. I observed this in my own data. For example, the percent agreement between two raters was 0.833, even though the computation of k was 0. As shown in Table 19.12 of Zhao et al. [13] (p. 473), kappa is considered to be a more conservative measure of IRR than other coefficients.

I also chose to use Gwet’s AC₁ (like k, it also ranges from −1 to 1) as it is a relatively paradox-resistant agreement coefficient [16,17]. As shown in Table 19.10 of Zhao et al. [13] (pp. 469–470), it seems to have less paradoxes or abnormalities than other agreement statistics, and in Table 19.12 of Zhao [13] (p. 473), it is listed at the more liberal end of agreement coefficients. In my own work, I have observed that AC₁ is often larger than the corresponding kappa. In the above example where the percent agreement between two raters was 0.833 and k was 0, AC₁ was 0.803. Including both k and AC₁ will increase the precision of the IRR estimate. Finally, percent agreement, a measure of IRR that is not corrected for chance agreement, was computed. Of the three consensus estimates of IRR, percent agreement was expected to be the largest.

In most prior studies, IRR was determined by examining the individual rubric scores of an assessment (e.g., [6]). In the PACT, after evaluators assigned rubric scores, they gave a final score of Pass or Fail. It was this designation that was ultimately used to decide whether a teacher candidate passed or failed the PACT. In the current study, TPA data collected from 2010 to 2015 from a school of education at a large, private, west coast university were examined. Consensus estimates of the IRR of double- or triple-scored PACTs that were given final scores of Pass or Fail were computed. This study, therefore, is an examination of the PACT as an overall measure of teacher performance. The research question addressed in this study was as follows: What is the magnitude of the IRR based on final scores of Pass or Fail in a sample of PACTs from our teacher preparation program by content area as assessed by two chance-corrected agreement coefficients and percent agreement?

2. Methods

The PACT assesses teacher candidates’ abilities on five tasks: Planning, Instruction, Assessment, Reflection, and Academic Language [18]. Each of these five tasks includes two or three criteria (see

Table 1. Performance Assessment for California Teachers (PACT) tasks and criteria.

Task	Criteria
Planning	1. Establishing a balanced instructional focus; 2. Making content accessible; 3. Designing assessments;
Instruction	4. Engaging students in learning; 5. Monitoring student learning during instruction;
Assessment	6. Analyzing student work from an assessment; 7. Using assessment to inform teaching; 8. Using feedback to promote student learning;
Reflection	9. Monitoring student progress; 10. Reflecting on learning;
Academic Language a	11. Understanding language demands and resources; 12. Developing students’ academic language repertoire.

^a Assessed throughout the teacher performance event.

), which are each scored on a 4-point ordinal scale, with 1 = Fail, 2 = Basic or Pass, 3 = Proficient, and 4 = Advanced. These ordinal scores are derived from the evaluation of two types of evidence in PACT submissions: artifacts (evidence that candidates submit to show teacher competence, e.g., lesson plans, videos, student work samples) and commentaries (written responses to standardized questions that provide context and rationales for the artifacts submitted) [12].

During their time in a school of education at a large, private university in California, teacher candidates assembled a performance portfolio for the PACT. It took a substantial time commitment to assemble the evidence of their teaching prowess for the PACT [19,20]. This portfolio was uploaded by the candidates to an evaluation portal. Based on the content area of the candidate, the PACT coordinator would then assign an evaluator to evaluate the teaching event.

2.1. PACT Evaluator Training, Calibration, and Scoring

The evaluators consisted of full- and part-time school of education faculty members, K-12 administrators, and K-12 classroom teachers and were subject matter experts within their area of expertise. The evaluators underwent a 2-day training program to learn how to score the PACT and meet calibration standards. After initial training, the evaluators were required to attend annual re-calibration events. For more details about PACT evaluator training and calibration, please see [12].

The evaluators were trained to carry out the following:

• Start with a review of the background information provided by the candidate and review the PACT tasks in order—Planning, Instruction, Assessment, and Reflection— while addressing the use of Academic Language throughout.
• Identify evidence that met the criteria of a rating of “2” first (basic novice teacher competency), and then determine if the evidence was above or below this mark.
• Score the evidence submitted by the candidate without inferring what the candidate might have been thinking or intending.
• Assess PACTs using the rubrics only, take notes as they assess, refer consistently to a scoring aid document to provide a more in-depth explanation of rubric scores, and recognize their own biases [12].

The Pass/Fail rate of the PACT was examined to comply with state guidelines. Briefly, failing PACTs were double-scored, and 15% of passing PACTs were randomly selected to be double-scored. More information about the procedures involved with double-scoring initially passing or failing PACTs can be found in [12].

2.2. Passing or Failing PACTs

In addition to each candidate being individually scored on a 4-point ordinal scale on the 12 criteria (see Table 1; [12]), a final score of Pass or Fail was determined for each candidate based on the following rule: A candidate passed the PACT if they passed all five tasks (Planning, Instruction, Assessment, Reflection, and Academic Language), i.e., they had no more than one fail score (“1”) on any task AND had no more than two failing scores (“1” s) across all five tasks. Otherwise, candidates failed the PACT.

Examples of failing PACTs are shown in

Table 2. Examples of failed PACTs.

Cand.	P1	P2	P3	I4	I5	A6	A7	A8	R9	R10	AL11	AL12
1	2	2	1	2	2	2	2	2	2	1	2	1
2	1	1	2	2	2	2	2	3	2	2	2	2
3	2	1	2	1	1	3	2	2	2	2	2	2

Note. Cand = Candidate, P1 = Planning Criterion 1, P2 = Planning Criterion 2, P3 = Planning Criterion 3, I4 = Instruction Criterion 4, I5 = Instruction Criterion 5, A6 = Assessment Criterion 6, A7 = Assessment Criterion 7, A8 = Assessment Criterion 8, R9 = Reflection Criterion 9, R10 = Reflection Criterion 10, AL11 = Academic Language Criterion 11, AL12 = Academic Language Criterion 12.

. Candidate 1 failed because three “1”s were assigned across the 12 criteria. Candidate 2 failed because they failed the Planning task. Candidate 3 failed because they failed the Instruction task and also had three “1”s across all five tasks.

Because the final decision of whether a candidate passed or failed the PACT determined eligibility for licensure, these are the data examined in this study.

2.3. IRR Calculation

Consensus agreement occurs when evaluators agree on how the various levels of a rubric score have been applied to observed phenomena [21]. In the present study, a standard that consensus estimates “should be 70% or greater” [21] was used. Consensus agreement was examined in three ways. First, Cohen’s kappa coefficient of agreement, k, [14] was computed, which ranges from −1 to 1 and is calculated as the proportion of agreement with chance agreement excluded.

Table 3. Cohen’s kappa (k) and corresponding magnitude [22], with author’s modifications.

			k
−1 to <0	0 to 0.20	>0.20 to 0.40	>0.40 to 0.60	>0.60 to 0.80	>0.80 to 1
Poor	Slight	Fair	Moderate	Substantial	Almost perfect

shows the range of kappa and one way of interpreting its magnitude [22].

Second, IRR was estimated using the unweighted chance-corrected Gwet’s agreement coefficient, AC₁. AC₁ is considered to be a paradox-resistant agreement coefficient [16], and like k, it ranges from −1 to 1. Third, percent agreement was computed. It is instructive to see the three agreement measures side by side to see the effect of chance correction in k and AC₁. Using percent agreement alone does not adjust for chance agreement and therefore inflates the agreement estimate. Percent agreement is presented as a proportion to be more readily comparable to the chance-corrected agreement coefficients.

To compute IRR, data were formatted as shown in

Table 4. Data example showing scores for three candidates from two or three evaluators. Math content area.

Candidate	Eval1	Eval2	Eval3	Eval4	Eval5	Eval6	Eval7	Eval8
131					F	P
132				P	F
133	P			P	F

Note. Eval = Evaluator, P = Pass, F = Fail.

. The table shows Pass/Fail entries for three candidates, each evaluated by two or three evaluators (evaluators 5 and 6 for candidate 131, evaluators 4 and 5 for candidate 132, and evaluators 1, 4, and 5 for candidate 133).

For each content area, a candidate by evaluator matrix was uploaded and analyzed in agreestat360.com [23]. This program computed Conger’s kappa [16,24,25] (p. 30), a generalization of Cohen’s kappa, when more than two raters assessed the PACTs; Gwet’s AC₁; and percent agreement (as well as other agreement methods not reported in this study). The two chance-corrected methods and percent agreement were unweighted because the score categories were nominal (Pass or Fail). Also computed were the standard errors of the agreement methods, as well as the corresponding 95% confidence intervals.

It is one thing to compute an IRR estimate and another to interpret its magnitude. In agreestat360.com [23], a benchmarking method takes into consideration the standard error of the estimate [16]. For example, if two estimates were 0.360 but the first had a standard error of 0.28 and the second had a standard error of 0.04, the first estimate has less precision, and the corresponding 95% CI could show it spanning 0. Therefore, the first estimate would be benchmarked (and interpreted) as having a lower benchmark magnitude than the second, more precise estimate. I used the Landis–Koch cumulative benchmark method with a 0.95 critical threshold to interpret the magnitude of the coefficient estimate.

From 2010 to 2015 (the duration for which the PACT was used at our institution), 1542 candidate PACTs were evaluated. During this time, PACT submissions from 181 candidates that were either double- (n = 144) or triple-scored (n = 37) were used in the IRR calculations. Five content areas, each with their own rater pools, were examined for IRR: elementary math (22 evaluators, 47 candidates), single-subject history/social science (14 evaluators, 71 candidates), math (8 evaluators, 23 candidates), science (8 evaluators, 21 candidates), and English language arts (11 evaluators, 19 candidates). These are the data presented in this study. In the current study, 16 candidates (out of 181) were used in the computations of a prior study [12], but different methods were used to assess IRR. This study received IRB approval.

3. Results

After the evaluators assigned individual scores (ordinal four-point scale) to each of the 12 criteria (Table 1), the evaluator assigned a final score of Pass or Fail for the PACT (see Section 2, Methods). IRR estimates were based on the double- or triple-scored Pass/Fail data. The distribution of the final score of Pass or Fail, by content area, is shown in

Table 5. Distribution of Pass and Fail scores by content area.

Content Area	Candidates	Pass	Fail
Elementary math	47	34	66
History/Social science	71	56	105
Math	23	17	35
Science	21	15	29
English language arts	19	19	23

. There were roughly twice as many Fail scores assigned compared to the amount of Pass scores assigned, except English language arts, which had about 1.2 times more Fails than Passes.

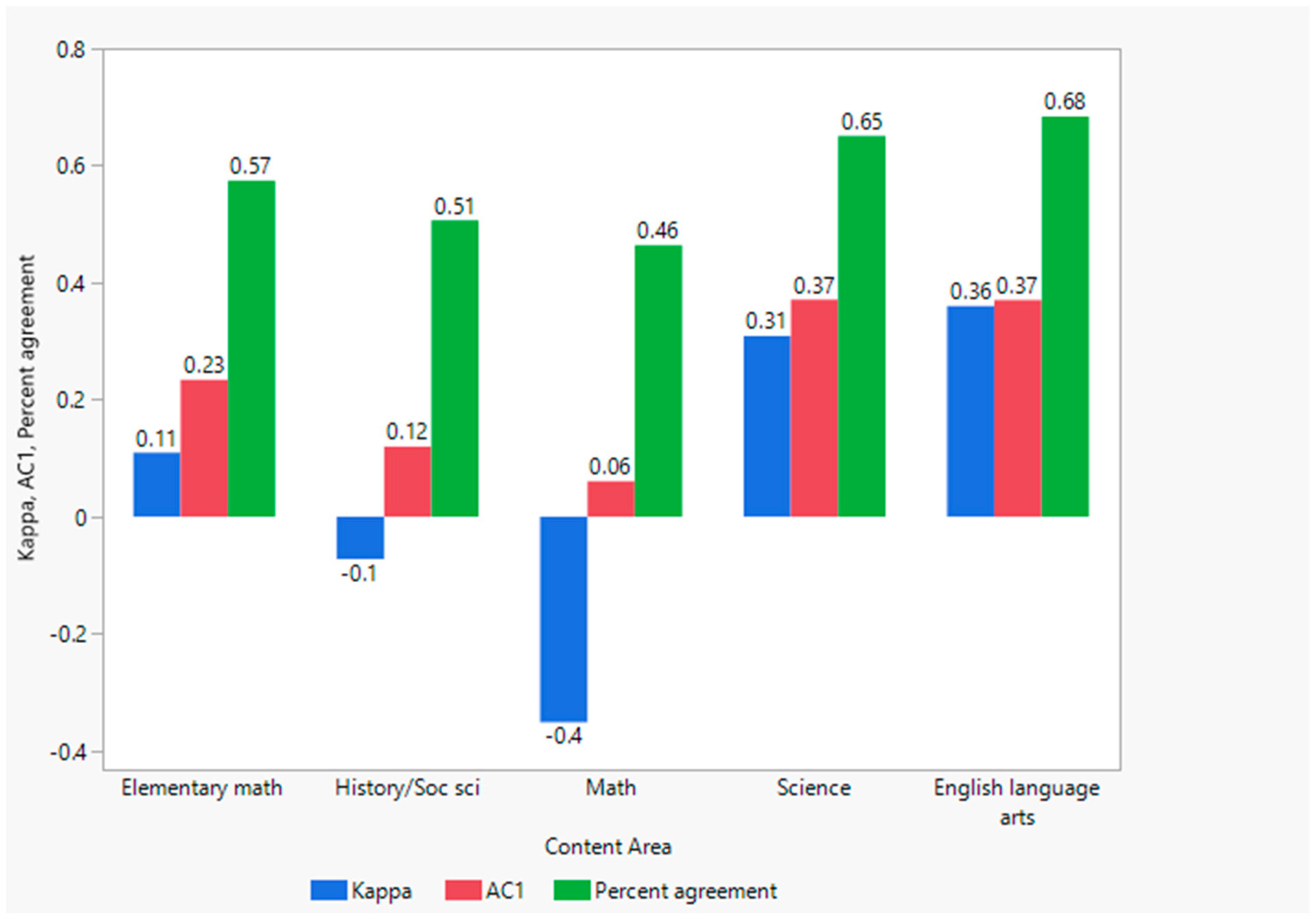
The IRR estimates for these double- or triple-scored Pass/Fail data are presented in Table 6 and Figure 1. Table 6 shows, for each content area, the number of candidates and evaluators, the IRR method and coefficient, corresponding standard error, 95% confidence intervals, and the Landis–Koch cumulative benchmark method of interpretation.

Table 6. Inter-rater reliabilities (unweighted Conger’s kappa, Gwet’s AC₁, and percent [proportion] agreement), with corresponding standard errors, 95% confidence intervals, and Landis–Kock benchmark magnitude interpretations, by content area.

Content Area	Cands	Evaluators	Method	Coefficient	Standard Error	95% CI	Landis–Koch
Elem math	47	22	Conger’s Kappa	0.110	0.135	(−0.162, 0.382)	Poor
			AC1	0.234	0.148	(−0.064, 0.532)	Poor
			Percent Agreement	0.574	0.069	(0.437, 0.712)	Moderate
History/SS	71	14	Conger’s Kappa	−0.072	0.096	(−0.264, 0.120)	Poor
			AC1	0.120	0.124	(−0.127, 0.367)	Poor
			Percent Agreement	0.507	0.053	(0.402, 0.612)	Moderate
Math	23	8	Conger’s Kappa	−0.351	0.151	(−0.664, −0.039)	Poor
			AC1	0.061	0.232	(−0.419, 0.541)	Poor
			Percent Agreement	0.464	0.095	(0.266, 0.662)	Fair
Science	21	8	Conger’s Kappa	0.309	0.194	(−0.096, 0.715)	Poor
			AC1	0.371	0.212	(−0.071, 0.814)	Slight
			Percent Agreement	0.651	0.102	(0.439, 0.863)	Moderate
ELA	19	11	Conger’s Kappa	0.360	0.208	(−0.076, 0.796)	Slight
			AC1	0.370	0.200	(−0.049, 0.790)	Slight
			Percent Agreement	0.684	0.100	(0.474, 0.895)	Moderate

Note. Elem = elementary, Cands = candidates, CI = confidence interval, ELA = English language arts.

Table 6. Inter-rater reliabilities (unweighted Conger’s kappa, Gwet’s AC₁, and percent [proportion] agreement), with corresponding standard errors, 95% confidence intervals, and Landis–Kock benchmark magnitude interpretations, by content area.

Content Area	Cands	Evaluators	Method	Coefficient	Standard Error	95% CI	Landis–Koch
Elem math	47	22	Conger’s Kappa	0.110	0.135	(−0.162, 0.382)	Poor
			AC1	0.234	0.148	(−0.064, 0.532)	Poor
			Percent Agreement	0.574	0.069	(0.437, 0.712)	Moderate
History/SS	71	14	Conger’s Kappa	−0.072	0.096	(−0.264, 0.120)	Poor
			AC1	0.120	0.124	(−0.127, 0.367)	Poor
			Percent Agreement	0.507	0.053	(0.402, 0.612)	Moderate
Math	23	8	Conger’s Kappa	−0.351	0.151	(−0.664, −0.039)	Poor
			AC1	0.061	0.232	(−0.419, 0.541)	Poor
			Percent Agreement	0.464	0.095	(0.266, 0.662)	Fair
Science	21	8	Conger’s Kappa	0.309	0.194	(−0.096, 0.715)	Poor
			AC1	0.371	0.212	(−0.071, 0.814)	Slight
			Percent Agreement	0.651	0.102	(0.439, 0.863)	Moderate
ELA	19	11	Conger’s Kappa	0.360	0.208	(−0.076, 0.796)	Slight
			AC1	0.370	0.200	(−0.049, 0.790)	Slight
			Percent Agreement	0.684	0.100	(0.474, 0.895)	Moderate

Note. Elem = elementary, Cands = candidates, CI = confidence interval, ELA = English language arts.

Figure 1. Conger’s kappa, AC₁, and percent agreement are shown side by side for each content area.

Figure 1. Conger’s kappa, AC₁, and percent agreement are shown side by side for each content area.

The results of Table 6 are displayed by content area in Figure 1.

As can be seen in Table 6 and Figure 1, the chance-corrected agreement coefficients are all lower than the percent agreement, as expected. The data also show the expected pattern of the AC₁ agreement coefficient, which is larger (more “liberal”) across all five content areas than the corresponding Conger’s kappa. Conger’s kappa ranged across the five content areas with a low of −0.351 in math to a high of 0.360 in English language arts. Because of the large standard error for English language arts (0.208) (and resulting large 95% CI, spanning 0), the cumulative probability Landis–Koch designation was “Slight”. For all other content areas, Conger’s kappa was designated as “Poor”.

For the AC₁ method, the chance-corrected coefficients ranged from 0.061 for math to 0.371 in science. Again, because of the large standard errors (and, subsequently, large CIs), the Landis–Koch interpretation for the magnitudes was “Poor” for all content areas except for science and English language arts, which were “Slight”. Thus, the chance-corrected coefficients (k and AC₁) were all consistently “Poor” or “Slight” in magnitude across all the content areas.

Finally, for the non-chance-corrected percent agreement method, the proportions ranged from 0.464 for math to 0.684 for English language arts. These proportions had smaller standard errors than the corresponding chance-corrected coefficients and were designated by the Landis–Koch cumulative benchmark estimation method as being mostly “Moderate” in size, with “Fair” for math. None of the percent agreements attained the suggested minimal standard of 0.700 for acceptable reliability [21].

The double- or triple-scored data (N = 181) were further analyzed to see if candidates who received an initial Pass (or Fail) were more likely to receive a subsequent rating of either Pass or Fail.

Table 7. Initial rating (Pass or Fail) of double- or triple-scored PACTs followed by a subsequent rating (Pass or Fail).

	Subsequent Rating
Initial Rating	Pass	Fail	Total
Pass	16	7	23
Fail	85	73	158
Total	101	80	181

shows the 2 × 2 contingency table for these data. Fisher’s exact test (2-tailed) showed that an association between the initial and subsequent ratings was not significant, p = 0.182, indicating that an initial score of Pass or Fail given by the initial evaluator was not more likely to be followed by a score of either Pass or Fail given by a subsequent evaluator.

Based on the 1542 portfolios that were examined in the present study, about 92% of the candidates initially passed the PACT, whereas about 8% of the candidates initially failed the PACT. Of course, the candidates who initially failed the PACT could re-submit either the entire PACT or sections of the PACT to see if they could ultimately pass.

4. Discussion

Based on the ultimate decision as to whether a candidate passed or failed (the “Final Score”), low consensus estimates of IRR were found on a teacher performance assessment for preservice teachers. Across all five content areas (elementary math, single-subject history/social science, math, science, and English language arts) examined in this study, IRRs, as determined by chance-corrected agreement coefficients, were found to be poor (mostly) or slight. These results were corroborated by the more conservative kappa and the more liberal AC₁. Non-chance-corrected percent agreement was interpreted as being mostly moderate and never attained the standard for acceptable reliability (0.700) [21].

Low estimates of IRR observed on the PACT suggest that the scores contain a large amount of measurement error [12,16,26], which was noted for the agreement coefficients in Table 6. The low IRR estimates could have resulted from “difficulty in observing or quantifying the construct of interest” [26] (p. 26). For example, in data collected in a prior study [12], trained evaluators stated in interviews that they had difficulty evaluating the rubrics in the Academic Language task (see also [27]). Evidence to suggest that the evaluators strayed from training protocol by, for example, not evaluating the PACT in the proper order, and frequently did not make use of an evaluation aid to help them discern the difference between rubric levels was also presented. In the present study, even though IRR was assessed on the final Pass/Fail scores that were ultimately assigned, these Pass/Fail scores were determined by a strict rule from the rubric-level scores (see Section 2, Methods). It is possible that the low consensus estimates of IRR observed in the present study resulted from a combination of these observations.

“The main source of error in edTPA scores [is] the rater” [6] (p. 17). “Rater variability is a general, notorious problem of rater-mediated assessments” [8] (p. 93). See also [9] (p. 30). As mentioned in the Introduction, variables such as rater strictness, or leniency, or bias have been hard to change [8]. Methods such as Rasch modeling [8] have been developed to try to account for issues of rater variability. About 88% of the TPAs in the present study were evaluated by a single rater. Low consensus estimates of IRR, however, demonstrate that the evaluators are not interchangeable.

Other studies have reported low IRR on teacher performance assessments. Most of these studies examined the individual rubric scores of the TPA, as opposed to using the methodology in the present study, where IRR was based on the final Pass/Fail scores that were ultimately used in licensure decisions. Relatively few studies of the IRR of TPAs were found in a literature search. Riggs et al. [28] computed IRR using the intraclass correlation coefficient (ICC) for the California Teaching Performance Assessment (CalTPA) and concluded that IRR was “inadequate” (p. 24).

In contrast to the results of Riggs et al. [28], Bhatnagar et al. [29] examined the IRR of the Observation of Field Practice (OFP) performance assessment, which consisted of four areas—professional knowledge, instructional delivery, assessment of and for learning, and learning environment—with 12 rubric items. Candidates were assessed on a 4-point scale: 4 = advanced, 3 = proficient, 2 = developing, and 1 = insufficient. IRR was computed using the intraclass correlation coefficient (ICC) from the average ratings of 42 instructors who evaluated six candidates. The ICC was 0.753, indicating a “good level of agreement”.

In an early IRR study of the PACT, Pecheone and Chung [18] reported percent agreement for two pilot studies. Percent agreement was based on exact plus adjacent agreement, a more liberal measure than exact agreement, and was reported as 90–91%. However, Stemler [21] noted that on a rating scale with a limited number of points, which was true for the PACT, “(e.g., a 1–4 scale)…then nearly all points will be adjacent, and it would be surprising to find agreement lower than 90%”.

Porter and Jelinek [30] examined the IRR of the PACT using Cohen’s kappa as well as percent agreement. Overall, they reported a kappa of 0.35, which they interpreted as a “fair” strength of agreement. They also reported the exact agreement among evaluators as 66%. In a prior study by Lyness et al. [12], we reported low inter-rater reliability on data collected during the 2014 academic year from our school of education. For each of the 19 candidates, pairwise agreement was computed on the ordinal four-point rubric scores, and the magnitude of the mean weighted kappa (0.17) was interpreted as being low.

Derham and DiPerna [31] reported that 30 preservice education students’ digital portfolios were assessed and IRR was computed using Cohen’s kappa. Two raters independently rated the teacher performance portfolios. The portfolios consisted of 11 components (the PACT consisted of 12 components), and each component was rated on a four-point scoring rubric (the PACT also had a four-point scoring rubric). The median kappa coefficient across the pairs of ratings was 0.14 and was similar to the results reported in [12].

In an IRR study of 136 preservice music teachers, Hash [32] estimated an exact mean unweighted kappa = 0.25. The estimated IRR was based on the average of kappas, ranging from 0.07 to 0.51 (“slight” to “moderate”), from 15 individual rubric scores. These estimates were “substantially below those reported” by edTPA. Hash asked the question whether his estimates were perhaps overly conservative because they were unweighted and suggested the possible use of a weighted Cohen’s kappa (the rubrics are ordinal) to be used for a proper analysis, as well as by edTPA. Gitomer et al. [6] also estimated IRR, average k = 0.231, and they observed, like Hash [32], that their computed kappa was lower than the kappa data reported in the edTPA.

It is worth noting that another measure of IRR was mentioned in the most recent edTPA report [33], namely, the intraclass correlation coefficient (ICC). The ICC estimates in the edTPA data (p. 10) for the same content areas examined in this current study were 0.65 for elementary math, 0.58 for history/social studies, 0.65 for math, 0.65 for science, and 0.59 for English language arts. In a reference provided in the edTPA report [34], these ICCs could be interpreted as being “moderate”. None of these data surpassed the minimal level for ICC deemed to be acceptable (0.800) in Graham et al. [35].

The edTPA sums the scores across the rubrics, and a cut score is determined by each state for passing or failing. It would be instructive to be able to determine the Pass/Fail results for the double-scored edTPA portfolios submitted from our school and compute IRR as was computed in the present study to compare results. Unfortunately, these data are proprietary to Pearson Inc., so such comparisons cannot be made.

Finally, I reviewed the international literature for teacher performance assessments of preservice teachers. Outside of the United States, most of the published research on TPAs is from Australia (e.g., [36,37,38,39,40]). Two TPAs mentioned were the Graduate Teacher Performance Assessment (GTPA) and the Assessment for Graduate Teaching (AfGT). Issues of reliability and concerns about outsourced scoring were discussed, but I was unable to find any data on IRR, possibly because the adoption of TPAs in Australia only took place relatively recently.

4.1. Study Limitations

Five study limitations were identified. First, limitations of Cohen’s kappa were noted (e.g., [15]). These limitations of Cohen’s kappa, however, were likely overcome by using Gwet’s AC₁ paradox-resistant agreement coefficient, which is not subject to the paradoxical problems that the kappa statistic is vulnerable to [15,16,17]. Limitations of AC₁ are also noted in Zhao’s [13] paper. Because k is considered to be a more conservative IRR estimate and AC₁ is considered to be a more liberal estimate, both chance-corrected agreement coefficients were used to obtain a broader picture of IRR in the present study. Second, the current study had a partially crossed design (i.e., not fully crossed) because all candidates within content areas were not rated by all the same evaluators. Fully crossed designs yield more accurate IRR estimates due to them having smaller standard errors than partially crossed designs [16] (pp. 17, 179). Third, regarding nominal ratings, “the small number of values that raters can assign to subjects increases the possibility of an agreement happening by pure chance” [16] (p. 26). Fourth, because not all of the candidates were randomly selected and the evaluators were not randomly selected, the generalizability of the findings of this study may be somewhat limited. Fifth, when the data were collected for Table 7 (see Section 3, Results), it was noted that the number of initial passing PACTs that were double-scored were under sampled. Only about 2% of the passing PACTs, instead of the goal of 15%, were included in the double scoring. This may have occurred because of time and personnel constraints. It is possible that with additional sampling, different results might have been observed in the present study. A reviewer pointed out that if more of the initially passed scores were sampled and included, more Pass–Pass observations would have been included in the IRR calculations. Therefore, the current IRR estimates are probably underestimated. However, “this doesn’t negate the fact that for those who are prevented from teaching on the basis of the test, the scores are very unreliable”.

4.2. Summary and Suggestions

In the present study, based on preservice TPAs being designated as Pass or Fail, mostly low consensus estimates of IRR were observed in the PACT for all five content areas that were examined. As pressure increases on schools of education to be held more accountable for producing high-quality teacher graduates, performance assessments should be held equally accountable. Accountability in teacher performance assessments would include greater transparency so that independent researchers could have access to double-scored data, because currently, we have to rely on the integrity of the testing companies to report a summary of these data. Increased transparency [2,6] from testing companies such as Pearson Inc. would likely lead to an increased understanding of, and improvement in, TPAs.

It is an issue worthy of discussion [2,5,6,41] whether the low to moderate IRR results reported here and in prior studies, including the edTPA report [33] (see Table on p. 10), should or should not be considered to be adequate for making high-stakes decisions such as granting licensure to a teacher candidate.