Misunderstanding Flight Part 2: Epistemology and the Philosophy of Science

Abstract

Flight has become a common everyday occurrence. We have engineered ever more efficient and reliable aircraft, facilitating safe transportation around the world. However, from the education literature on the topic of lift, online discussions, and YouTube, it becomes apparent that there are underlying pedagogical issues. The 2003 New York Times article by Chang and the 2020 Scientific American article by Regis conclude that no one really understands flight. These claims are made without regard for the underpinning science and engineering responsible for the modern aviation industry. Although, it does beg the question, why is there confusion about how wings work? Several factors have conspired together, resulting in this confusion. Fluid mechanics is a complex topic that stumped legends of physics and mathematics for centuries. It also contains paradoxes, exacerbating the complexity. However, the central thesis of this work is that knowledge about aerodynamics is not easy to construct due to two main factors. First, there are epistemological traps that directly lead to fallacious conclusions. Second, representativeness heuristics incorrectly apply behaviors of visible water to invisible air. While many assume they know how wings work, if they do not understand why there is confusion, rather than dismissing it, confusion will endure.

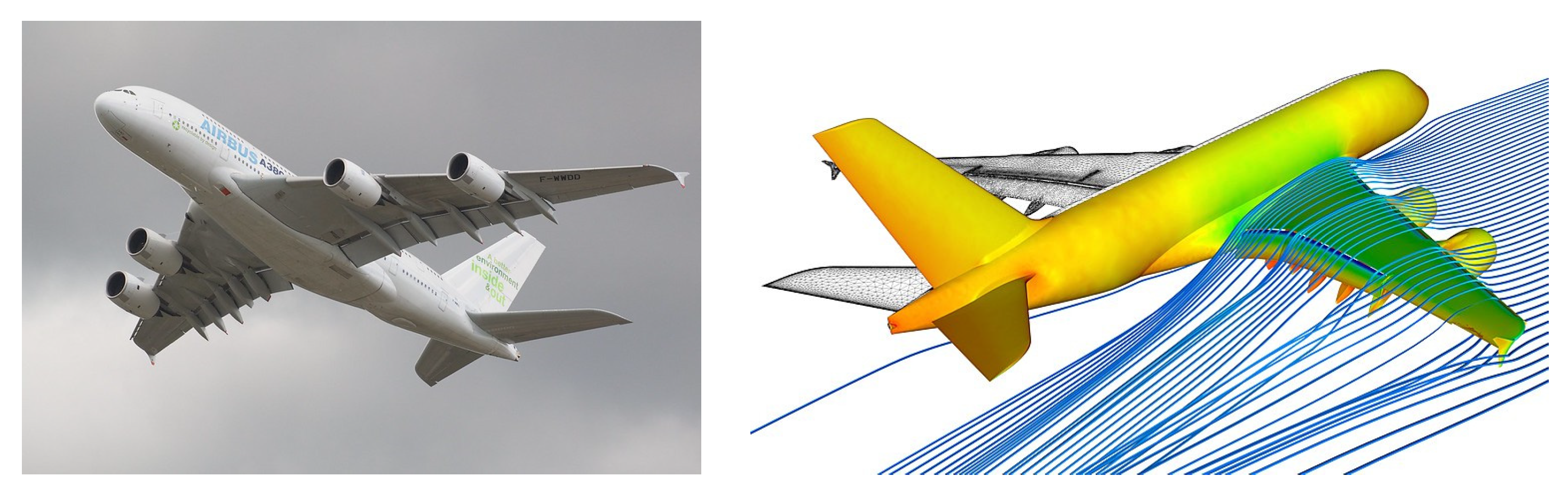
1. Introduction

The subject of aerodynamics is littered with great names. Euler was hugely influential, along with D’Alembert, as well as Newton before them and Prandtl after them [1]. Practical aviation involves great names such as Cayley, Lilienthal, Langley, and the Wright’s [2]. There has been a convergence of theory and practice that has given rise to modern aviation, on a foundation of aeronautical engineering. However, science education on the topic is inconsistent and rife with fallacies and misconceptions [3]. The standard texts for aerodynamics at a tertiary level correctly convey theoretical and practical knowledge [4,5]. Although, in science at a secondary and tertiary level, there is a problem. It is not surprising; D’Alembert’s paradox not only perplexed the inventor of partial differential equations [6], it could not be resolved by the great Leonard Euler, the “supreme geometer” [7]. The result is a devolving literature in science education looking for simple answers to a complex question in a landscape covered with paradoxes. Aerodynamicists may be confused why the complex topic that they have an intimate knowledge of is not understood by others. Meanwhile, science educators who have had their knowledge corrected at least once appear happy replacing one name with another in an attempt to escape the confusion. With such a complicated topic, it is unrealistic to assume that, from the top down, it is trivial to explain or, from the bottom up, that there is a simple explanation. Instead, by examining the sources of confusion a better understanding is possible for all.

The term aerodynamic lift, the force generated by an aerofoil or a wing, will be referred to simply as lift. The aim of this work is to answer the question, why is there confusion about how wings work? First, it will be clearly demonstrated that there is confusion about lift. This will be established through reference to the prior literature, a study of online media for science education/communication, and classroom reflections. Next, based on the observed features of these illustrated or animated understandings, the thesis of this study will explain the likely sources of confusion. Using analogous descriptions, a correct illustration and animation of airflow producing lift will be provided to give a complete and accurate explanation of this unintuitive phenomenon. This will be followed by an analysis of lift through the lens of the philosophy of science to further explore the case.

2. Confusion

2.1. Objective Reality

First, it should be noted that aerodynamicists understand lift and how wings work. The aerodynamic marvels that are modern highly efficient aircraft such as the Boeing 787 or the Airbus A350 are testaments to this fact (an A380 is shown in Figure 1). Anderson [5] is one of the standard texts used to teach aeronautical/aerospace engineering students about aerodynamics. The topic is taught at different levels constructively. Two-dimensional flow is followed by three-dimensional flow, flow without viscosity is considered before flow with viscosity, and compressible flow follows on from incompressible flow. The pinnacle is the Navier–Stokes equations. With modern computers, these complex equations can be applied to viscous compressible three-dimensional flow with relative ease, facilitating quantitative and qualitative assessment of aerodynamic effects and interactions (Figure 1 shows the result of a numerical simulation from computational fluid dynamics). While some consider these equations abstract in their application to explain lift and flight [8], they are the cornerstone of fluid mechanics and aerodynamics. However, presenting a set of coupled partial differential equations that describe fields is not a great way to explain lift to anyone and, worse, some suggest only an intuitive understanding is even possible [9]. As such, the abstraction of that knowledge to different levels is ultimately the true source of the confusion. The saying is, “you don’t need to be a rocket scientist to understand rockets, but you do to know how wings work.”

2.2. Literature

The education literature on lift and flight mechanics is highly varied [3]. There are many papers that purport “new” or “correct” explanations of lift. It must be stressed that fluid mechanics is a difficult subject within the complex field of engineering. In fact, many of the phenomena needed to understand aerodynamics are considered important but not well understood [10]. To quote Smith [11], when asked what he was doing after 25 years at Douglas Aircraft he replied, “still trying to understand aerodynamics”. This accounts for differences observed in the literature when looking at authors from a science context relative to an engineering context [3]. Top-down approaches are in the literature; Babinsky [12], an aerodynamicist, took a different approach, trying to explain lift at a secondary physics level, referring to the link between streamline curvature and pressure (Figure 2a). However, the simplification of a complex phenomenon is fraught with difficulties and, while Babinsky does offer a correct answer to “how” wings work, without Navier and Stokes, you cannot explain why. Bottom-up approaches are even more difficult. This occurs when non-subject-matter experts try to use constructivism coupled with knowledge of fallacies (incorrect theories of lift) to build an explanation based on basic observable phenomena [13]; examples are shown in Figure 2b,c.

Previous work looking at visualizations/illustrations of flow around an aerofoil or wing in the education literature indicates there is confusion about aerodynamic lift [14]. It was found that, of the 49 education articles on lift that provided flow visualizations, seven used known fallacies and 28% did not illustrate the flow ahead of the aerofoil/wing correctly, with more than 56% not showing key details. The study also indicated that more confusion exists for two-dimensional flow, with only 30% of illustrations correct, relative to three-dimensional flow, where 75% were correct. In Figure 2d,e, streamlines for 2D and 3D flow are shown; it is noted that 3D flow for wings exhibits downwash, which is why images of 3D flow tend to be more correct. Many 2D illustrations incorrectly include downwash.

2.3. YouTube Videos

To further prove that there is confusion, we can look at YouTube. For example, the video from Petter Hörnfeldt, known as the Mentour Pilot, entitled “Think you understand Winglets? Think again!!” (https://www.youtube.com/watch?v=2ieRwRnwqY8, accessed on 16 July 2023). In this video with 320k views, Petter states:

(…) you have to understand lift and you’ll be surprised to hear that actually how lift is created on the wing is not completely 100 percent understood (…)

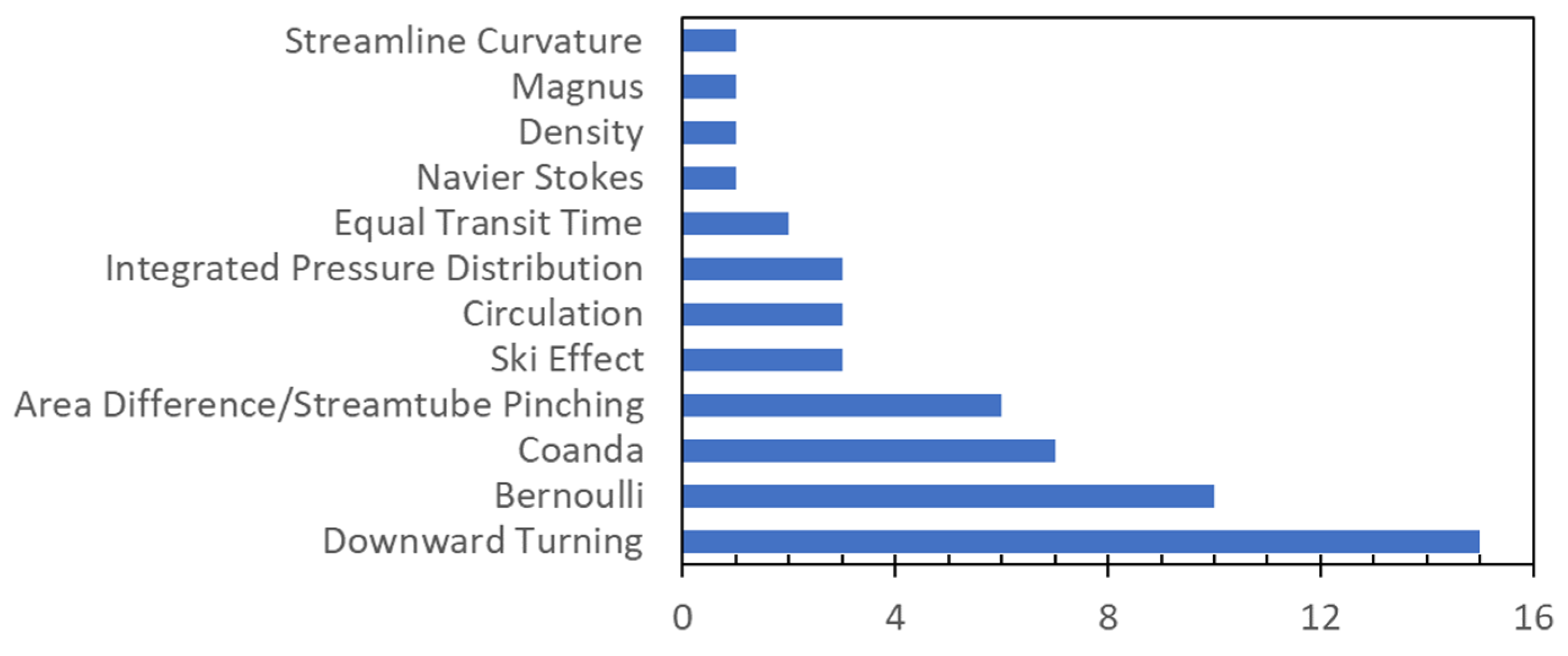
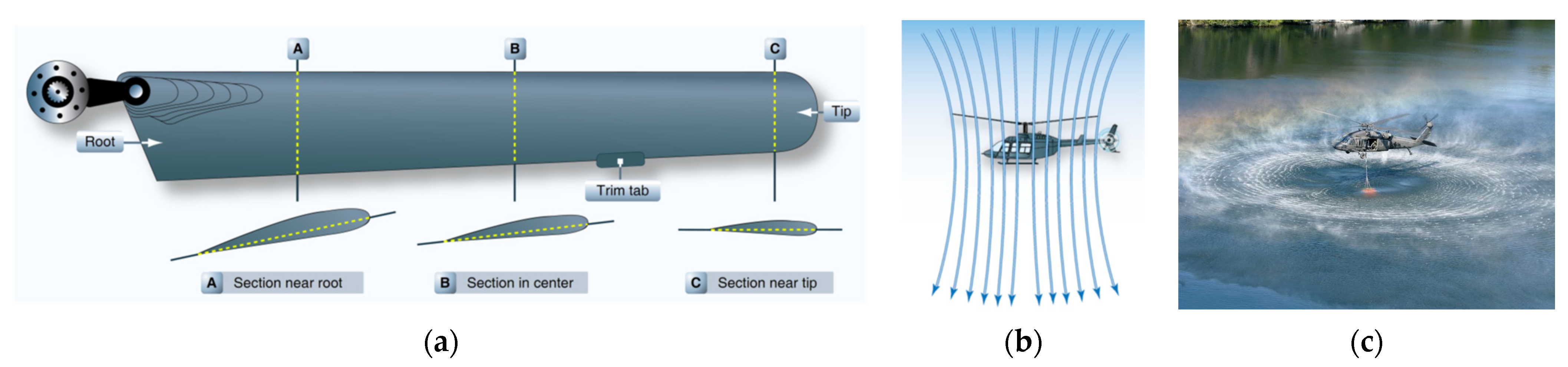
This quote illustrates the confusion presented in the introduction, while also not appreciating the objective nature of aeronautical engineering. Petter indicates that ongoing discussions are the evidence to support this statement; that is, there is a debate somewhere, so it must not be 100% understood. To objectively investigate this phenomenon, YouTube videos on the topic were examined to show the variety of theories and even fallacies used to explain lift. Key search terms used in YouTube included ‘lift’, ‘flight’, and ‘wing’, which were used along with other supporting terms, such as ‘aerodynamics’ and ‘aeronautics’, as well as ‘how’ and ‘why’. Applicable videos with more than 50,000 views were included (ranked by view count), giving a sample of 29 videos, with view counts ranging from 55,000 to 5 million views (770,000 average). The different concepts utilized in these were categorized, and the results are shown in Figure 3. The various explanations can be grouped into either momentum statements (“air goes down so wing goes up”) or pressure difference statements (lower pressure above relative to below); this coding results in a count of 19 each, with 10 of the videos using both explanations. Three of the momentum cases utilized the ski effect, where air bounces off the lower surface, a well-known fallacy (one of these videos had 2 million views). Two of the videos explained lift with the equal transit time fallacy [15]. One video used density instead of pressure, when we typically talk about basic lift in terms of incompressible flow, where density is constant; this mistake has also been made in the literature [16]. Furthermore, one video used the Magnus (Robins) effect, which explains the curved flight path of a spinning ball [17] or, originally, a spinning artillery shell [18], neither of which are directly related to wing lift.

2.4. Classroom Evidence

In the UNSW Canberra first-year course ZEIT1800 Introduction to Aviation Technology, students participated in weekly in-class pen-and-paper quizzes. The students were all recent high school graduates (median age of 18 years old). A practice quiz worth no marks was used in the first week, which included two relevant questions. The first question was:

1. 

Which “simple” theory of lift is your preference at this point in time?

(a) 

Equal transit time

(b) 

Area difference (stream tube pinching)

(c) 

Coanda

(d) 

Other:             

The intent of this question is to gauge the students’ current understanding from prior aviation or high school studies. Students were told that “other” can be anything, including names such as Newton or Bernoulli; anything they felt best summarized their current understanding. The results for Q1, Quiz 0, from 2021 (n = 39) and 2023 (n = 47) are shown here in Figure 4 (note, due to lockdowns, this was not possible in 2022). Surprisingly, the legacy equal transit time fallacy [15] is still the most common response, suggesting this is still taught in high school science classrooms. The most surprising result is the low 7% for Coanda, given how significant this has become in the education literature [3].

The second question relevant from Quiz 0 was based on screenshots shown in Figure 5. The question asked: “Examples of flow illustrations here show the air splitting in similar ways. Where do you think the air splits and why does it split there?” This was a short answer question, where students were given several lines to write a response. These responses were coded, giving the following themes: contact, hit, cut, push, pressure, and force. All these terms suggest that the students perceive a direct physical interaction between the leading edge of the wing and the airflow. In principle, this is a reflection of what the content creators have presented and what was previously observed in similar illustrations in the education literature [14]. This question was added to the quiz for 2023.

Based on the observed illustrations in the education literature [14], equivalent to those in Figure 5, an array of options for how air should split around an aerofoil was created. These are illustrated in Figure 6 below. This was added as a bonus question to the second quiz of 2023, with the following text:

In the images below, an aerofoil (wing) is placed in a wind tunnel. The dashed lines represent where the airflow is split; any air above this line will flow over the top while any air below will flow under. Which of the options do you think best represents how the airflow will split in reality?

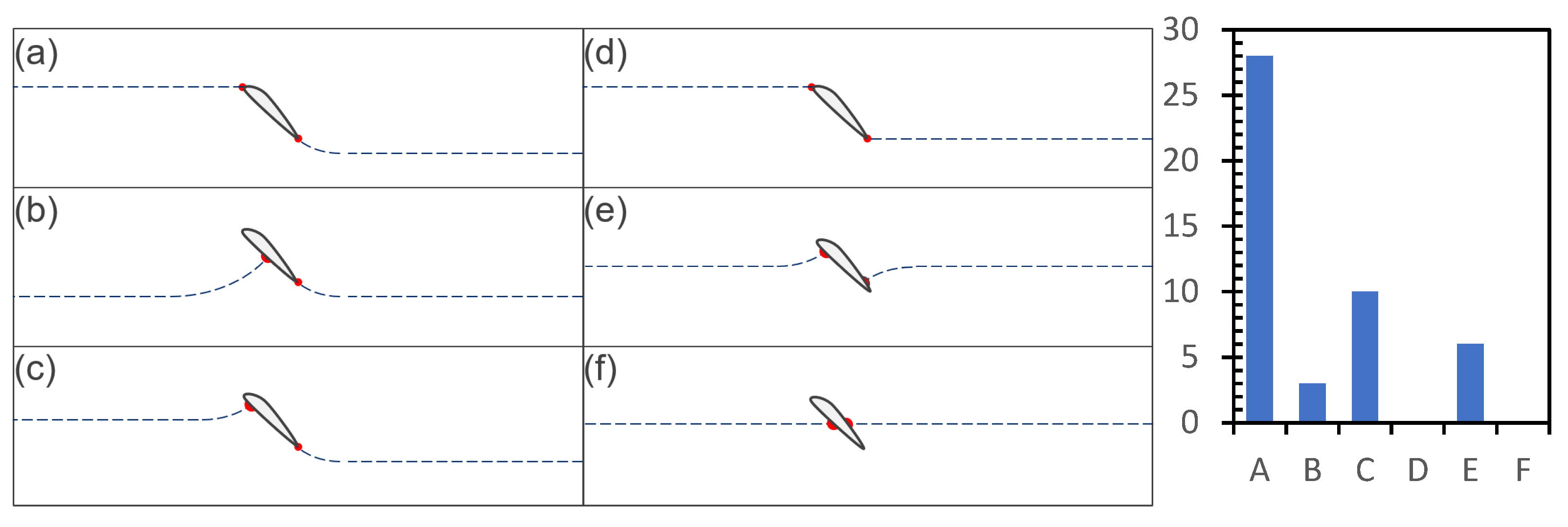
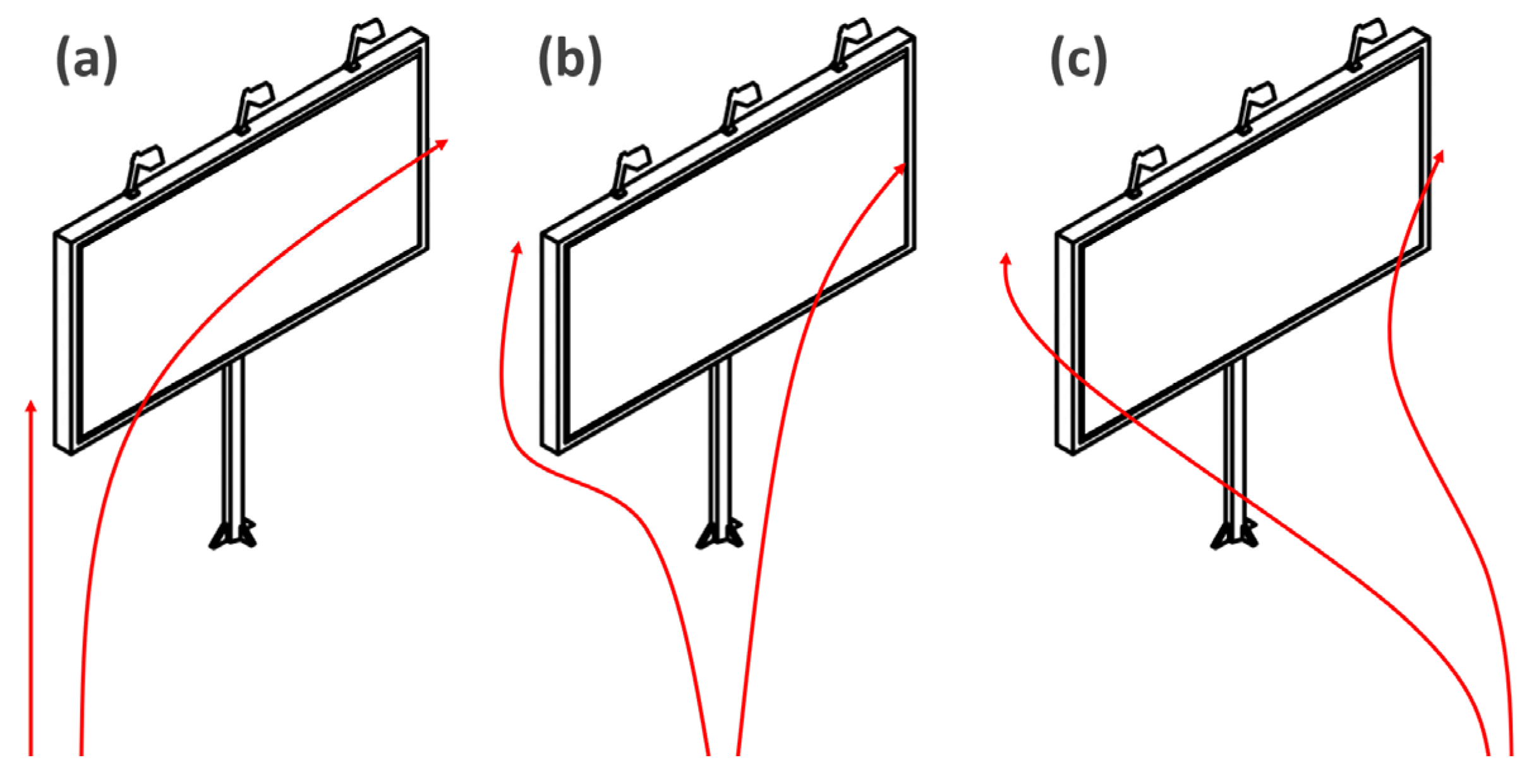
The correct response is Figure 6b. The figure also shows the distribution of the students’ responses. Looking at the distribution of responses, the concept that the leading edge dividing the flow is clearly the preference (a). Interestingly, the “sharp” departing lines (d) and (f) were not selected at all. The selection of (b), (c), and (e) suggests some students are aware of the need for upwash, although the correct amount of upwash given in (b) has the least number of responses.

2.5. Paradoxes

The paradox of Regis [8] and, to a lesser extent, Chang [19] is that two different theories to explain lift cannot be simultaneously correct. This is not really a paradox; it is a misunderstanding. Many things in physics can be explained in different ways. We could examine the swinging of a pendulum with force analysis or energy analysis or even using Lagrangian mechanics. Different ways to analyze a system does not imply that any or all forms of analysis are incorrect or even inconsistent. It simply implies that the methods are related. The same is true for the pressure difference and momentum conservation statements about lift; they are clearly related, not mutually exclusive [20,21,22].

In addition to the mathematical and technical complexities, a fundamental issue with fluid mechanics and aerodynamics is that the topic inherently includes a number of paradoxes [23]. These paradoxes include, D’Alembert’s paradox, the reversibility paradox, the fatness paradox, Eiffel’s paradox, and Dubaut’s paradox, to name a few. The most famous of these in aerodynamics is D’Alembert’s paradox. Although resolved, it was a concern when D’Alembert first applied Newton’s laws of motion to fluids and predicted no fluid force (drag or lift) which was clearly observable and measurable at the time. The equivalent null result by Euler is more commonly taught, and his equations are used as the basis for potential flow (Figure 6e). The paradox was resolved a hundred years later by Navier and then Stokes, who applied Newton’s laws of motion including viscosity.

There is an apparent paradox in Navier–Stokes [24], a singular perturbation problem, referred to as an asymptotic paradox [23]. This is exemplified first by Hoffren [25], who stated, “This kind of behavior in any physical phenomena is extremely rare, if known at all”, and later by Gonzalez and Taha [26], who stated “it would represent one example in nature where the physics is not continuous in the limit”; however, this is the defining feature of singular perturbation problems [27]. Consider the function y = ax² + bx + c; we set all the parameters (a, b, and c) to 1, but we vary a such that it becomes ever smaller (shown in Figure 7). Then, we observe the behavior of this function, y, as a goes to 0. If we have an infinite domain in x, for any positive non-zero value of a, as x goes to negative infinity, y will tend to positive infinity. However, if we change a to be exactly 0, then y goes to negative infinity. In aerodynamics, the singular perturbation problem applies to a differential equation, where “a” is viscosity. This means that the behavior of fluids with a very small viscosity is radically different to fluids with no viscosity; hence the reason why potential flows fail to explain lift without pseudo viscous effects (circulation) included.

2.6. Gettier Problems

2.6.1. Lift from Downwash

There is another paradoxical feature of aerodynamics, that of 2D versus 3D lift. What makes this interesting is that it is a Gettier problem [28]. A Gettier problem challenges the concept of “justified true belief” as the definition of knowledge [29]. When learners move from 2D flow to 3D flow, this requires the understanding of flow around a wing, not just an aerofoil. The flow around an aerofoil is constrained to be above and below, or ahead and behind. However, for a wing, the flow can also be along the wing, and more importantly, around the ends. The result of this spanwise flow is the formation of wingtip vortices [30]. These vortices can be seen growing and sinking behind passing aircraft (Figure 8). The key feature here is that the flow behind a wing has downwash, unlike 2D flow. In 2D flow, the downwash in the far field is zero (Figure 4b). There is a downward turning of the flow, but this is not downwash. If someone looks at the flow behind a wing, they are justified in their true belief that the downward velocity of the air has come about because of the passage of the wing; then, using Newton’s laws of motion they state justifiably that there is a momentum transfer. What makes this a Gettier problem, is that the net downward velocity imparted to the flow is not the momentum transfer responsible for lift, it is additional energy imparted to the flow that is wasted; hence, the correct name of this phenomena is induced drag [4]. As such, explaining lift in this way is a justified true belief that is not knowledge.

This Gettier problem of 2D versus 3D lift is responsible for a lot of misunderstanding. Some in online discussions (see Aviation Stack Exchange) and Anderson and Eberhardt [31] in their popular text “Understanding Flight” incorrectly state that 2D flow is not real. The lack of observed downwash is inductively used to support this hypothesis, and the induced conclusion is that lift is exclusively a 3D phenomenon. This is surprising because of how aerodynamics is taught. Aerodynamics students are first taught 2D lift and drag of aerofoils. These have been characterized and catalogued in a database of aerofoils by NASA (NACA) using a 2D wind tunnel [32]. Students are then taught about the effect the wingspan (aspect ratio) has on the lift from a wing relative to its constituent aerofoil. Hence, constructivistically, historically, in aerodynamics, 2D flow is taught first; then, corrections for 3D effects are incorporated [5]. However, since 2D flow lacks downwash, those that base their knowledge on the requirement for downwash to explain lift incorrectly conclude that 2D lift is not real.

2.6.2. Lift from Thrust

There is a second Gettier problem in aerodynamics, which we will call lift from thrust. Anderson and Eberhardt [31] incorrectly state that Prandtl [20,33] as well as McLean [22] are wrong in the assertion that the lift force is a reaction force of over-pressure at the earth surface (the earth itself is ultimately supporting all fixed wing aircraft, Figure 9c). Importantly, Prandtl is the father of modern aerodynamics, and many believe he should have been awarded the Nobel Prize in Physics for his contributions to aerodynamics [34,35]. As such, the over-pressure hypothesis is reasonable. To support this, consider the line from Star Trek: The Next Generation [36]:

Life is like loading twice your cargo weight onto your spacecraft. If it’s canaries, and you can keep half of them flying all the time, you’re all right.

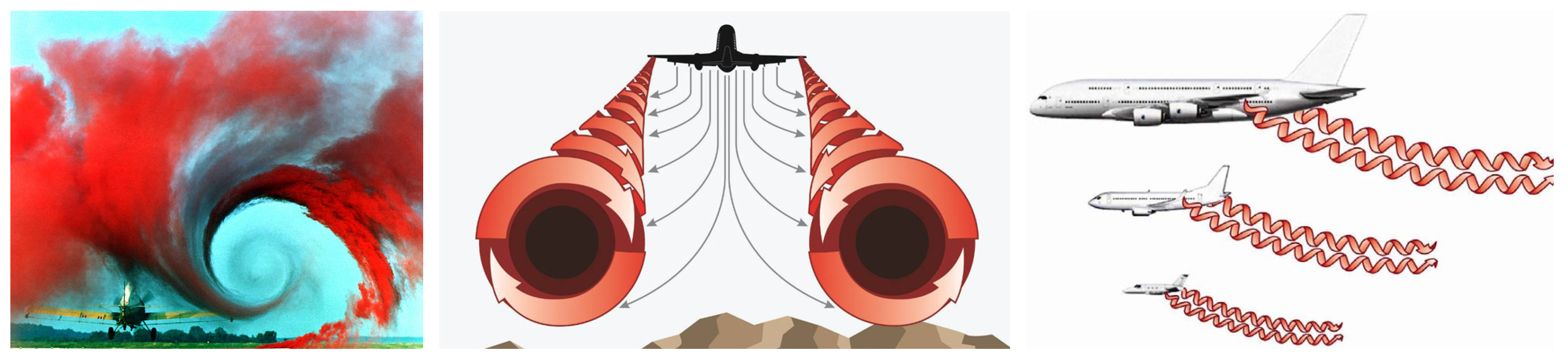
This idiom was tested on MythBusters [37] and, while journalistic sources appear to be saying there is a difference [38,39], it is clear that the time-averaged weight of any vehicle containing flying birds is constant. Similarly, the force of a wing in the atmosphere will react on the earth’s surface. Furthermore, consider the lift measurements by NASA (NACA) mentioned in Section 2.6.1. Those measurements made in a 2D wind tunnel, shown in Figure 9a, were taken from the integrated pressure difference between the top and bottom surface of the wind tunnel [32] (Figure 9b). That is, in the 1940s, we were measuring lift as the force pushing on the wind tunnel containing the aerofoil, not the pressure on the aerofoil itself. Applying Newton’s Third Law, the pressure difference on the surface of the wind tunnel is the reaction to the pressure distribution around the wing, or the lift force, the action. Although the force on a container containing forces is puzzling [40], the action/reaction in a wind tunnel is evident, and this is analogous to a wing in the atmosphere (Figure 9c).

How is lift from thrust a Gettier problem? This comes about because propellers and rotors are effectively wings. These objects have cross sections that are aerofoils. The aerodynamics that affect aerofoils are incorporated into the design and structure of propellers and rotors as twist and cord length changes over their radius (Figure 10a). However, the concept of how a propeller generates thrust is a statement of momentum transfer. The thrust equation is also taught to aeronautical and aerospace engineers, as well as to pilots [41]. The air leaving an “engine” is faster than the air entering. The product of the velocity difference and the mass of air per second gives the exact thrust. Although this will usually be taught for a jet engine, the same applies to a propeller being rotated by a gas turbine core. There is a mass flux across the propeller disk and a corresponding increase in velocity (Figure 10b). As such, propellers and rotors are imparting momentum to the air to produce thrust. For a rotor on a helicopter, this force, which is thrust, is now in the vertical direction, so it is called lift. Anderson and Eberhardt [31] conclude that, since the horizontal thrust force from a propeller is not supported by a physical structure (such as a vertical cliff), then the earth must not support a fixed wing aircraft. That is, since a rotor wing has the same shape as a fixed wing and a rotor wing produces lift by imparting momentum to the air, it is a justified true belief that all wings produce lift simply by imparting momentum to the air. The issue here is that, while rotor wings and fixed wings are similar in shape, they are producing a force in different ways. Consider blowing air over a wing or pushing a wing through air; relatively speaking, these are the same. However, rotating a wing such that it will cyclically interact with the flow it induces radically changes the dynamics. A further point of confusion comes about because propellers and rotors only exist in 3D, where there are tip effects, which further reinforces the 3D flow confusion.

At this point, it should be clear that aerodynamics is complicated, has many paradoxes, and there are epistemological issues. All these points coalesce, producing confusion and misunderstanding.

3. Resolution

A common feature of incorrect airflow over an aerofoil is a lack of upwash [14]. Instead of flow being drawn upwards ahead of the wing, it is typically illustrated as being split by the leading edge. All seven of the YouTube videos with over 1 million views have no upwash, showing air that is split at the leading edge (screenshots in Figure 5). It is hypothesized that the reason flow is illustrated this way, is because of our everyday observations of water motion, either as waves on ponds and lakes or as it flows along rivers and streams. This real-world visual experience is then utilized via constructivism as the foundation for our understanding of aerodynamics. In essence, the complexity of aerodynamics is bypassed with a representativeness heuristic [42]. The observed flows in water (Figure 11) are expected to be representative of flows in air, given that air as a fluid is like water in essential characteristics. The easing of one’s cognitive load is a feature of constructivism, where base knowledge is assumed correct and applicable; that is, there is a fundamental cognitive bias.

3.1. Hydrodynamics

What do we observe when we look at bodies of water with motion? The topic of water waves (also called gravity waves) is complex and there are differences between deep water waves [24] and shallow water waves [43]. First, it should be noted that the speed of water waves is typically on the order of 1 m/s at a wavelength of 1 m [43], with shorter wavelengths having a lower velocity and longer wavelengths having a higher velocity. There is also the effect of surface tension giving higher velocities to very short wavelength waves [24]. If an observed water wave has a wavelength of 0.1 m, its wave speed will be three orders of magnitude less than the speed of sound in water. As such, a boat moving through water has more in common with a supersonic aircraft. Similarly, the resultant flow of a rapidly moving river around rocks and branches is akin to looking at flow in a supersonic wind tunnel. The key difference is that surface waves (water waves and related phenomena such as earthquakes) are dispersive, where different wavelengths have different wave speeds (analogous to how white light becomes a rainbow). In contrast, the speed of sound in the atmosphere is effectively independent of wavelength. This explains the difference between bow waves for boats and ships compared to shock waves for supersonic aircraft [24].

Consider a situation where, in the middle of a river, there is a square pier (Figure 12a). This is angled at 45 degrees such that a single point, the leading edge, meets the oncoming water. If the water moves rapidly, it will build up at the leading edge such that the water raises up (where the kinetic energy of the flow is converted into potential energy at what is called a stagnation point); the flow will also divide evenly at this point, half flowing above and below. Suppose the pier was made of four walls and we remove three (it is unimportant which one remains due to symmetry). This single wall is geometrically equivalent to a flat plate. For this flat plate, there will be little change to the flow. The point at the leading edge still has a corresponding spike in water height. The flow is still split evenly at the leading edge. However, there is now a huge asymmetry in the pressure because there is water pushing on the front more than the back (in supersonic aerodynamics, we note there is an expansion fan, the opposite to a shockwave, responsible for this [41]). The underlying feature here is that the speed of the water flowing in the river is faster than the wave speed. We say this flow has a Mach number greater than 1 (M > 1). The Mach number is defined as the ratio of the flow speed to the wave speed. In air, the speed of sound is 340 m/s; hence, an aircraft with a speed of 340 m/s has a Mach number of 1.

3.2. Aerodynamics

In supersonic flow for aircraft, we observe the same features that we note above about rapidly moving water flowing around an obstacle. This is because supersonic flow is defined as M > 1, as it was above. However, when we talk about lift and flight, the misunderstanding and confusion comes at relatively low speeds, with Mach numbers less than 0.3 (the speed of the flow is approximately a third of the wave speed). Hence, the reason the representativeness heuristic fails is because our observations of water flow are effectively supersonic, and we are concerned with subsonic aerodynamics when we talk about lift in a science education context.

So, what happens to our square obstacle now in wind where the Mach number is less than 0.3 (the windspeed is 100 m/s or less)? For the initial square case, the result is somewhat similar (Figure 12b), except, at the stagnation point, there is no “build-up” of air, pushing the atmosphere higher. In fact, since sound is a pressure wave, pressure information is transmitted at the speed of sound back upstream. Given the wind is approaching at much less than the speed of sound, as the initial “blast” of wind reaches the leading edge, the pressure will start to increase (the flow will stagnate) but the air molecules near the leading edge will push back (due to this increasing pressure) on the molecules behind them (the concentric red, orange, and yellow regions in Figure 12b); that is, pressure information is transmitted back through the flow, upstream. Looking at Figure 12, the key difference is the geometry of the flow change. In supersonic flow, there are abrupt changes in flow direction because the pressure information cannot propagate upstream. For low speed flows the pressure information influences the flow very far back upstream. As such, if a molecule of air is above or below the centerline, it will start “accelerating” up or down, respectively, well before reaching the obstacle.

For the flat plate case, the resultant flow is much more unintuitive. In water (M > 1), it was noted that there would be a positive relative pressure on the front surface and less on the back. This is pressure information; since we are only really interested in flows with a Mach number less than 0.3, the pressure information can affect the flow well ahead of the obstacle. Consider a sudden gust of wind; it was zero and now it is 10 m/s, illustrated in Figure 13. At the leading edge of this flat plate there would be an initial increase in pressure (Figure 13a). However, since the plate is very thin, that pressure can easily spread out. That is, flowing above the plate is relatively easy, preventing the air from accumulating at the leading edge (unlike in the supersonic case). On the front side, the air molecules going down will push into neighboring molecules below them and, if that is too hard (a high enough pressure), they will flow up over the top where there is less pressure. It is tempting to say the molecules are sucked into the region of lower pressure, but suction is not a force; pressure is only a pushing force; it acts normal into the surface. So, we note a decrease in pressure above and an increase in pressure below (Figure 13b). Now consider the reciprocal point, the trailing edge. Since we noted that, initially, there will be a lower pressure behind the plate relative to in front, then there is nothing stopping flow at the trailing edge rounding the corner and spreading out into this region of lower pressure. In fact, the pressure gradient will be sufficient to push the flow partway back up the rear surface. However, if the fluid is pushing equally in all directions and flow is rounding the leading edge to the top surface as well as rounding the trailing edge to the top surface, there is symmetry (Figure 13c); this is D’Alembert’s paradox. Importantly, the result here is that the air flow is not splitting at the leading edge like it was in the M > 1 case.

Another illustrated feature in Figure 13 is the pressure information from the front stagnation point moving, which is illustrated traveling to the left along the streamline, and this would be at the speed of sound. The air that was below this line is accelerated upward above the line and will now flow above the plate. In this configuration, the stagnation point is located between the leading edge and the midpoint of the plate but, in the far field, the flow splits exactly at the geometric center. Assuming the midpoint of the plate is at the midpoint of the box, exactly 50% of the flow would go above and below the plate. This would be for any angle, or any geometry, and is a feature of D’Alembert’s paradox. This flow does not represent reality as it is what Feynman called “dry water” [24] or what mathematicians call a potential flow. This early type of abstract fluid had no viscosity. Dry water flowing around an inclined plate like this will balance the flow such that there is a symmetric flow field. That is, there will be a rear stagnation point at a location rotationally symmetric to the front stagnation point. Since the pressure distribution is rotationally symmetric, we can apply Bernoulli and state that the velocity distribution will be rotationally symmetric. This results in equal transit over the top or bottom surface [15]. However, it also means no lift!

There is an extra effect we have not considered; each molecule of air is sticky and, hence, is slightly adhered (attracted) to all the molecules around it. This is called viscosity, which provides the resolution to D’Alembert’s paradox via Navier–Stokes. The molecules that are pushed up, are helped, or pulled up by the viscous interactions with the molecules above. The plate is an obstacle, so there is going to be air pushing against it, slowing down. Eventually, there must be a point where it stops being easier to flow above. That is, there will be a new stagnation point where the flow splits into the flow above and below. Since viscosity acts to draw more air up over the plate, this moves the stagnation point lower down the front surface, illustrated in Figure 14.

More important is what happens at the trailing edge, illustrated in Figure 15. With the force of attraction added between air molecules this radically changes the flow at the trailing edge. Without viscosity, the lower pressure behind the plate would result in air molecules rounding the trailing edge being pushed backwards up the rear surface. Now, there is a competing force from viscosity. These backwards moving air molecules are trying to move away from neighboring molecules that they are attracted to. This is crucially different to the front flow going over the top. In that situation, the pressure gradient is favorable and accelerates the flow (in the converging and diverging section of Figure 14a, the pressure and viscous forces act mostly in the same direction). At the trailing edge, the 180-degree turn produces an instantaneous velocity that is zero and, hence, the viscosity becomes more significant. That is, the air now needs to move back up the rear surface from rest while being pulled along by neighboring molecules in the streaming direction (in the diverging section for Figure 15a, the pressure and viscous forces act in opposite directions). This forms a growing region of rotating flow at the end of the upper surface, and the center of curvature corresponds to a region of low pressure. This growing sticky low-pressure vortex will eventually become large enough to draw air down from the rear stagnation point and continue to grow, eventually forcing the stagnation point to the trailing edge (the Kutta condition) where the forces balance. This further affects the pressure distribution on the rear upper surface, such that it is even easier for more air to be drawn up over the plate at the leading edge (driving the front stagnation point lower).

The streamlines that correspond to stagnation points are critical. The sum of all forces at the trailing edge is such that (1) inertia wants the flow to continue ideally as horizontal as possible, (2) the viscosity wants it to stay cohesively together, and (3) the pressure gradient is away from the stagnation point (a point of high pressure). Therefore, the flow after the plate will be down and away in the near field, while returning to horizontal in the far field (for 2D flow), as shown in Figure 15c. Importantly, this rear stagnation streamline corresponds to where the flow splits; all flow above that streamline flowed above the aerofoil, while all flow below that streamline flowed below the aerofoil. That is, in the rear far field, the stagnation streamline is where the flow recombines to become horizontal again. If the aerofoil were exactly in the middle of a 2D wind tunnel, we can rationalize that the flow cannot split 50/50 above and below. This would require the streamline to be in the middle of the aerofoil in the far field. This is what happens in D’Alembert’s paradox (Figure 6e and Figure 13c). Since the streamline in viscous flow is below the aerofoil, more mass must flow above than below. The rationalization here is that the observed flow field into or out of the wind tunnel has a uniform velocity, which is horizontal, with constant density. The law of conservation of mass then necessitates that a greater area corresponds to more mass flow. That is, if the dividing streamline (those in Figure 6) is below the midline, then more of the air mass flows above than below. For the sake of discussion, consider a 60/40 split, illustrated in Figure 16. Here the stagnating streamline is the bold dashed line, and the other streamlines divided 60/40 are indicated as the arrows entering and leaving the control volume. Note the uniform velocity profile of the fluid is captured by the uniform distribution of the streamlines. That is, since the spacing between the streamlines is even, we know the velocity of the fluid is the same. If, in the rear far field, 40% of the fluid is below the stagnation streamline (Figure 16b), then conservation of mass requires 40% to have started below (Figure 16a). Similarly, if 60% is above the stagnation streamline, then all that fluid had to flow over the top. This imposes the condition that the front and rear stagnation streamlines must be colinear in the far field, ahead and behind, respectively [14] (Figure 16c).

The conclusion here is significant, since the flow at the trailing edge is down and back, with more air above than below, some of the air that was flowing along a path under the aerofoil flows above. That is, not only is the air not split by the leading edge (as incorrectly illustrated in Figure 5), some of the air that goes above the aerofoil originated below it. This is contrary to what we observe with everyday water flow. Figure 17 below further illustrates this case, assuming 2D flow ignoring edge effects at the top and bottom. Here, wind blows towards a billboard at an incident angle; intuition suggests the wind divides at the foremost point (a). D’Alembert’s paradox indicated that the flow would divide at the geometric center of the obstacle (b). The correct and unintuitive case (c) is that some of the air that was originally to the right of the billboard flows to the left. Viscous effects have generated a flow asymmetry, which then leads to an asymmetry of flow speeds and pressure, which can be used to explain (and calculate) lift.

3.3. Cause and Effect

What is presented above in this section is a causal chain of events. Looking at the literature, there are clear statements that this is, at best, difficult and, at worst, it is impossible to describe a causal chain of events [9,44]. Consider an ideal experimental setup, a wind tunnel, with pressure measurements around the aerofoil and along the surfaces of the tunnel; laser velocity measurements everywhere; and a six-axis force balance showing all the forces and torques. It is not possible to determine, for the steady state explained by coupled partial differential equations, what is a cause and what is an effect. Yes, changing something will change the flow but because everything is coupled. There is no starting point, so you cannot explain what came first. Then, how was the description in Section 3.2 possible? The key aspect of lift is that it requires an initial transient effect. This is the starting vortex which is coupled to the bound vortex of the wing (circulation). Initially, on the ground, the wing and wind are at rest relative to each other. In a wind tunnel, the air is accelerated relative to the wing, whereas in the atmosphere, a wing is accelerated relative to the wind. As such, the steady state solution to the partial differential equations does not exist to begin with and then there are things that happen sequentially before others, prior to the information propagating away, setting the status quo. This is exactly why, in computational fluid dynamics, you can specify a steady-state solution, which is much easier, or you can produce a transient solution, which requires much more computational power.

4. Philosophy of Science

McCarthy [45] appears to make it clear that the science education literature also possesses weaknesses in the philosophy of science. In response to criticism about the technical content presented to explain lift [46,47], McCarthy [48] states, “We, as science teachers, are left to decide…the explanation of lift that we wish our students to derive”. That is, it appears fundamental to assume that the underlying science is fact and the concepts such as skepticism are lacking.

Nietzsche [49] suggests that science can explain how but not why. This is a common trap that many trying to explain lift fall into; they only consider the how and, once they are satisfied, the line of inquiry stops. The philosophy of science compels us to go further. Instead, many on the topic of lift apply verificationism. The Gettier problems that trick many appear rooted in an adherence to verificationism, where those justified in their true belief of how lift is generated require the mechanism to be observable and, hence, verifiable with their senses; this is a common basis of the pseudoscience of flat-earthers, who demand proof using their own eyes [50]. This philosophy enables them to reject anything they cannot verify through visual observation [51]. The fact that multiple competing theories are used to explain lift means that the verificationist principle cannot be applied [52]. Rather, we must use falsificationism [53]. Coupled with skepticism, those who incorrectly claim that lift is produced via downwash must falsify lift in 2D flow where there is no downwash and not simply dismiss it. Given this is impossible, the correctly deduced conclusion is that lift is not exclusively a downwash or momentum transfer phenomena. As Popper [53] stated, “we have constantly to criticize our own theories, our own interpretations”.

Our pattern-seeking brain takes the representativeness heuristic cases and the other observable features that point to a justified true belief and uses them to construct a solution to the apparent puzzle. This is natural and understandable [54]; however, it is not science. Scientists must apply skepticism. One who does not employ skepticism is likely to come to fanaticism; if they do not adhere to Popper [53] and criticize their own theories, then they are blatantly misusing reason according to Kant [55]. This can be seen in online discussions about lift. Rather than applying skepticism, a person entrenched in their belief fanatically rejects reason and logic. Many believers of incorrect theories of lift appear to rely on underdetermination [56]. Here, the concept that there is insufficient evidence to disprove what they believe is central to their argument. However, there is sufficient evidence; it is just contrary to their preferred theory. This is analogous to anti-vaxxers and flat-earthers [51]. Flat-earthers have an impossibly high standard of evidence to renounce their belief [50]. This is in direct opposition to falsificationism and skepticism. Many of these believers also pursue what Francis Bacon called the crucial experiment [57]. For lift, there is no “crucial experiment”, as with other problems in physics; how the problem is framed is fundamental. The crucial experiment for lift would confirm a preferred theory and exclude all others. The pressure-based experiments used to characterize aerofoils by NACA have been previously explained, no experiment that shows downwash is going to counter that, because it cannot (there is a measurable pressure distribution which equates to the lift force).

Instrumentalism requires theories to produce empirical predictions [58]. While explanation is the goal for most of science, prediction is still an important output of science [59]. No theory of lift other than Navier–Stokes (or higher) is used in practical meaningful prediction applications. There is no Boeing or Airbus design team using a Coanda-based model to predict aerodynamic properties of an aircraft. In fact, the literature on the applications of Coanda does not claim anything other than providing additional lift when utilized [60]. Many in the education literature and in the YouTube videos, use Coanda as deus ex machina for lift; it is incorrectly used to define feature inherent to viscous flow [3]. While some corrections are possible for potential flow to give quick estimates, these are never the end of the process. That is, approaches such as vortex lattice methods or lifting line theory can approximate some aerodynamic properties [61,62,63]. However, modern predictive computational fluid dynamics is based on solving Navier–Stokes. This point is aimed at aerodynamicists that believe circulation is sufficient as a theory to explain lift, since it provides empirical predictions. The issue is that those predictions are limited and a more and more complicated tool needs to be constructed to provide more and more accurate and precise predictions; this is very reminiscent of the epicycles used in a Ptolemaic model of the solar system, which provided 1000 years of accurate predictions. The Cisotti paradox provides proof reductio ad absurdum why circulation is not a valid complete theory of lift [23]. Using a Tsien transform, the circulating flow around a cylinder can be conformally mapped to a flat plate at an angle of attack (see [15] for a visual explanation). As this is a conformal mapping of the same solution, the result is the same force with only a vertical component (lift). However, since inviscid fluids only interact with the surface through pressure normal to that surface, the resultant force is required to be perpendicular to the surface. Importantly, the surface is inclined at the angle of attack. This predicts a lift force that depends on the sin of the angle of attack, and not one that is linear, as observed in reality [11,64]. Therefore, circulation alone is not sufficient to explain lift.

In education, our ideas about a topic are interpellated; they are not something we arrive at on our own [65]. That is, ideas are internalized and accepted based on the information presented to us. The formal education system achieves this as what Althusser [65] calls Ideological State Apparatuses (ISA). Here, the government-funded (state) institute (apparatus) is responsible for the presentation of society’s ideas (ideologies). Of growing importance in modern education is what Weiner [66] analogously calls Ideological Corporate Apparatuses (ICA). In these, the state-funded institute is replaced by a corporate entity. As such, we can view YouTube as an ICA providing a platform for STEM influencers that are competing with traditional ISAs. Weiner [66] states that ICAs escape being called pedagogical because they are entertainment; however, we learn more when we enjoy what we are doing. He goes on to say that these ICAs must be held accountable “to the histories that they create and the futures that they imply.” Content creators driven by profit are not likely to be accountable. In the YouTube investigation above, the Minute Physics video (https://www.youtube.com/watch?v=Gg0TXNXgz-w, accessed on 16 July 2023) with two million views is based on the wholly incorrect ski effect. The creator of that video later helped in the creation of the Veritasium video (https://www.youtube.com/watch?v=aFO4PBolwFg, accessed on 16 July 2023), which, while admittedly better, invokes the incorrect use of Coanda and an incomplete momentum explanation. The point here is that the original video is still available to be viewed, even though its creator helped make a better video. The channel Lesics is similar (https://www.youtube.com/@Lesics, accessed on 16 July 2023); they have three videos on lift with significant view counts and, in each new video, the explanation has improved; however, the previous videos are also still available. Content which is created is only a source of revenue if it is consumed. This is radically different to the philosophy of science where we move on from outdated theories. To be fair, the same is true for more traditional corporate branches of ISAs, specifically publishing houses. At the end of this paper, it is hoped that it will be obvious that many textbooks printed for profit on this topic are inherently wrong; however, this will not stop them from being published and sold.

The issue of STEM influencers and ICAs as educational vectors is compounded by the algorithms used on social media platforms. If someone is entertaining, they will gain influence. Their ideologies are then propagated in a memetic way [67]. They have the dominant screen time; therefore, what they communicate as fact is what is accepted by others. That is, influencers influence because of prestige-biased social learning [68,69]. Our social nature means we tend to trust and learn from people who have gained attention, respect, and admiration from success [70]. It is an adaptive social learning strategy developed as a quick way to identify group members who are successful. In YouTube terms, what counts as successful is subscribers and views. This is a critical issue, because it has been suggested that anti-vaxxers and flat-earthers trust science, they just trust the wrong science [71]. Hume [72] suggests that changing people’s beliefs requires sympathy, reassurance, good example, encouragement, and art. The para-social relationships YouTube content creators have with their audience is, thus, a powerful tool to shape beliefs [73]; in the context of lift, the missing element is a correct understanding. An example of this is the episode of Hot Ones (https://www.youtube.com/watch?v=CJbP71RI-V4, accessed on 16 July 2023) on the channel First We Feast, with more than 5 million views; a general audience receives an unexpected aerodynamics lesson. In this, former NASA engineer Mark Rober incorrectly describes how a frisbee works, using a Newtonian ski effect coupled with the Coanda effect, incorrectly using water flowing along the curvature of a spoon as an example of Coanda [22]. He states, “it flies like a jet pack”, invoking an incorrect Newton’s Third Law argument, the Gettier problem of lift from thrust.

When reflecting on quantum theory, Einstein is quoted saying [74], “that all physical theories, their mathematical expressions apart ought to lend themselves to so simple a description ‘that even a child could understand them’”. This is in contrast to Derrida [75] and deconstruction, which criticizes the need for neat solutions to problems. Through deconstruction, we should dismantle the loyalty we have to our ideas and seek truths in aspects of their opposite. Theories of lift constructed from the bottom up that adhere to Einstein’s ideal reject Derrida, in that they do not accept the potential merits of other explanations. This is most significant with equal transit time theory [15], where a lack of knowledge about its historical context results in misunderstandings. Hence, while equal transit time theory should not be used, if it is carefully qualified, it may result in some simple pedagogical outcomes [76]. Even misunderstandings add value if we are ever skeptical and willing to question the positivistic knowledge we have. Simply by reflecting on those misunderstandings, we can hope to better explain fundamental knowledge.

Words have specific meanings in science, and we need to be careful not to allow people to play the politician or lawyer when it comes to words and their meaning. Consider the statement “Do Newton’s Laws of Motion explain how and why wings produce lift?” The answer to this is a conditional yes; this is technically a correct statement. The missing piece of knowledge here is that Newton has been applied several times by different people to explain fluid flow, most failing to do so [3]. As such, this statement is conditional because Navier and Stokes correctly included the viscous force to “the sum of all forces” in Newton’s Second Law. Could Newton himself answer those questions? No. Could Leonard Euler answer those questions without viscosity? No. So, can you technically say lift is a product of Newton’s Laws of Motion? Yes. However, is it a faithful representation considering how it is going to be misinterpreted? No. That is why Navier–Stokes is the critical thing, noting that Navier–Stokes are Newton’s Laws of Motion for fluids with viscosity. As is the role of courts and governments, the letter of the law must be considered in how it will be interpreted. Brevity in science is like brevity in a legal context; it must be avoided.

5. Discussion

Planck’s principle is [77]:

A new scientific truth does not triumph by convincing its opponents and making them see the light, but rather because its opponents eventually die and a new generation grows up that is familiar with it.

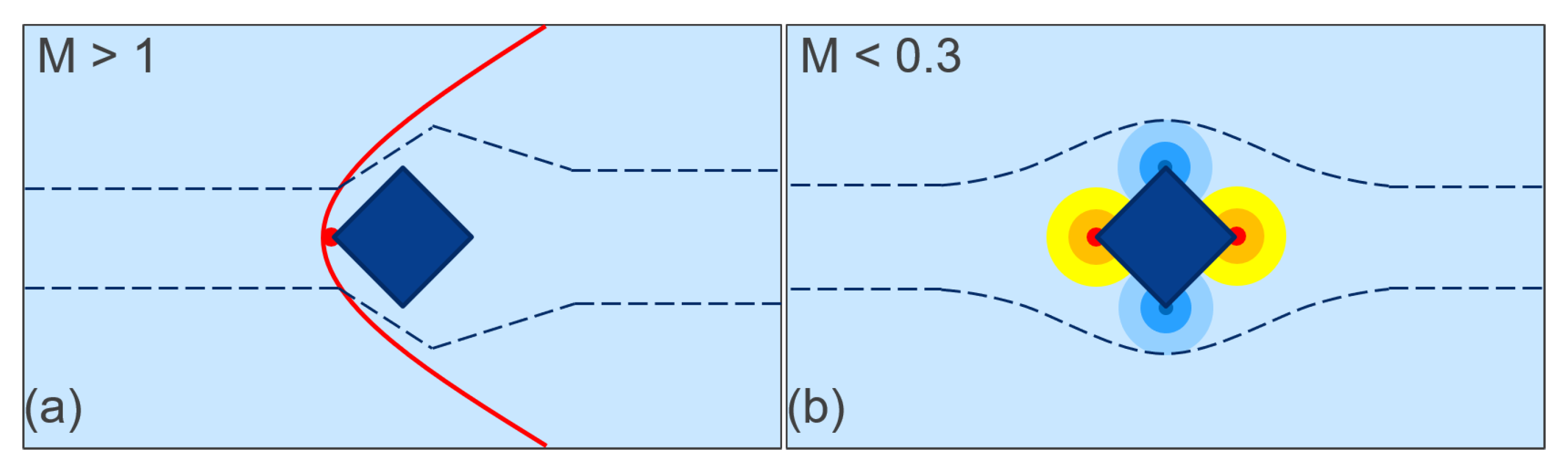
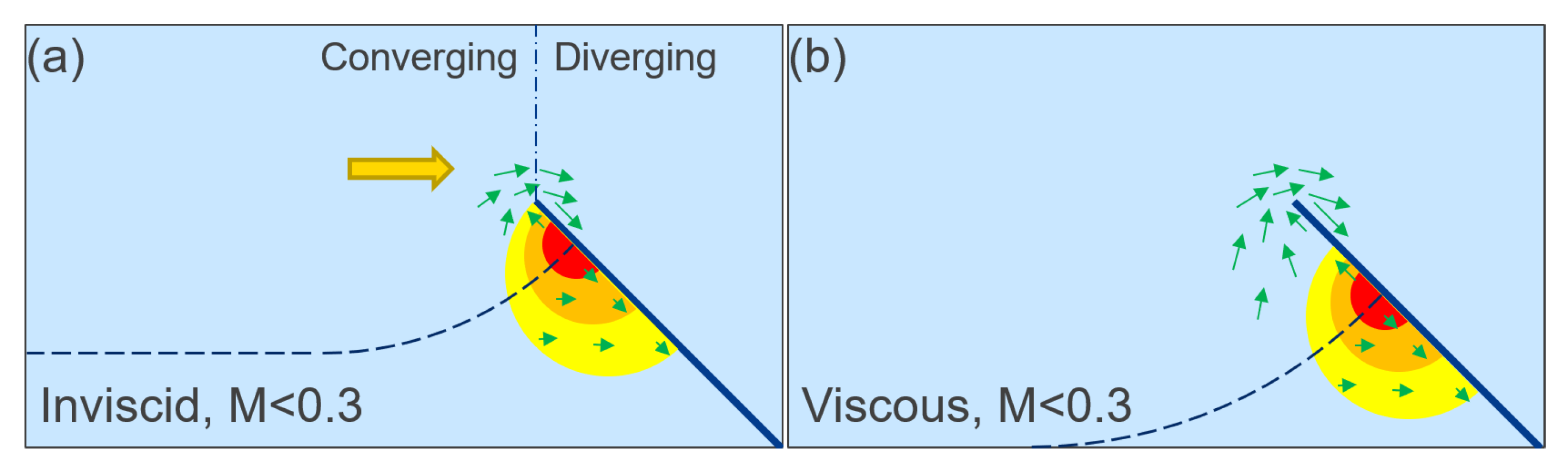
While the use of equal transit time theory has diminished, instead of being replaced with a useful correct explanation, Coanda has sprung up in its place. As noted, the Coanda effect, although real, does not apply to flow around an aerofoil. It is also used exclusively in concert with a pure momentum transfer statement, which is not possible in fluid mechanics terms. Because there is a reaction pressure on the surface of a wind tunnel or the earth, any control volume must have a pressure component on the control surface [20,21,22]. Therefore, any momentum difference calculated can only be part of the total lift. This was known to Prandtl prior to the 1920s [20] and, instead of this knowledge being abstracted in useful ways to educate people about lift, the relevant education literature shows a devolution of knowledge [3]; here, the approach was (1) there is a pressure difference, (2) only look at the flow outside the boundary layer, (3) apply Bernoulli, and (4) use D’Alembert’s equal transit time postulate to create a digestible explanation. Full of unstated assumptions and simplifications, this was easy to refute. However, those refuting that theory made other simplifying assumptions, such as circulation is enough, with no regard for why the flow is circulating, or, worse, simply apply Newton’s laws of motion, where action and reaction mean that, if a wing goes up, the air goes down. However, the correct application of Newton’s laws of motion to fluids is Navier–Stokes. As alluded to, these mistakes and incorrect assumptions are not unreasonable traps and there are paradoxes that are hard to avoid. That said, some fundamental aspects of the philosophy of science appear to be missing from many who profess to “know” how wings work.

An important take away from aerodynamics is that it mimics the wave–particle duality of light. The wave–particle duality is a key feature of quantum mechanics [78], and the wavelength is the important metric; that is, the longer the wavelength, the more wave-like and, the shorter the wavelength, the more particle-like. In fluid mechanics, the analogue is the continuum to free molecule flow spectrum. We inherently know that air is made up of tiny particles, and we expect particle-like things to happen, such as the ski effect where air molecules bounce off the bottom of an aerofoil, and, hence, the aerofoil is pushed upwards [79]. However, in incompressible aerodynamics, the important metric is the mean free path, which is orders of magnitude smaller than the size of the wing. Hence, continuum properties dominate, and these are not intuitive to visualize on a molecular scale. The Coanda effect is very similar in nature to this “hail of bullets” model of molecular interactions that produce the ski effect. Here, instead of individual molecules of air, there are confined tubes of fluid with greater momentum than the fluid around it. These visualizations exist in the majority of the 29 YouTube videos examined. However, around an aerofoil, there are no such jets of air. The unintuitive thing that is required for continuum flow is that a large domain of fluid must be considered. For example, in subsonic computational fluid dynamics, the boundary tends to be 10 cord lengths in front and 20 cord lengths behind. Similarly, the upper and lower surfaces are typically 20 cord lengths away (on this page, which is roughly 200 mm by 300 mm, an aerofoil would only be 6 mm long, at scale). While we might think 1% deviations are acceptable, computational fluid dynamics require much smaller variances to converge to a solution. The distribution of pressure information significant distances away from the wing is visible in these solutions because of the sensitivity and large domain. In a steady-state case, the information about the wing can continue to propagate forward in the flow at the speed of sound, without limit. In nature, once the level of pressure variation falls below that of the natural variance in the atmosphere, it will be indistinguishable.

In general, it appears that significant proportions of our collective knowledge on lift are flawed. This is a twofold problem. Top-down knowledge is difficult to transmit because Navier–Stokes is complex and bottom-up knowledge constructs erroneous explanations. This is not a flaw of constructivism; it is well known that “sometimes the old structures need to be replaced” [13]. The issue arises if there is a lack of correct raw materials; then, flawed structures can be constructed [80]. That is, people must be provided with appropriate materials to build their knowledge, which tends to be lacking in bottom-up explanations of lift.

In their work about physics studios, Yeo, et al. [81] claimed that students “alone must be responsible for their learning.” Herein, it has been demonstrated that, with complex topics, many cannot judge the quality of the raw materials needed to build new knowledge. Hence, as suggested by Swan [82], we must consider “Vygotsky’s zone of proximal development to maximize learning outcomes”. From Harland [83], the three-step process for the instructor is (1) identify the current level of developed knowledge, (2) provide learning activities to progress this to proximal (new) knowledge, and (3) repeat the process, reducing the level of teacher support while building independent and peer-based teaching and learning. A key tool in science education to support this is the predict–observe–explain (POE) process, which is essential to “encourage conceptual change” [82], and is demonstrated extensively by Lewin [84]. The correct challenges to knowledge need to be provided to learners with difficult concepts; that is, they need to be given opportunities to properly falsify incorrect theories. Those that believe that lift comes from downwash need to be challenged with the fact that lift is measured in 2D wind tunnels with pressure transducers on the top and bottom surfaces or around the aerofoil, not with particle image velocimetry to measure the vertical component of the flow before and after the aerofoil to determine the momentum flux.

As recommended by Wild [15], learners should be made aware of the historical development of aerodynamics. This historical context uses a constructivist approach based on history to demonstrate “the serial development of concepts” [85]. That is, it is essential to understand how we as a species have constructed our collective knowledge, one scientist standing on the shoulders of another, over centuries; or, as Newton [86] said, “if I have seen further, it is by standing on the shoulders of giants.” This underscores the evolution of knowledge, which is constructive, rather than the revolution of knowledge, which may be destructive. “History illuminates the process of science” [87]. For aerodynamics, it is critical that we have an awareness of the historical mistakes and flaws and how these were resolved. While D’Alembert’s paradox is taught, the true resolution of the paradox with the introduction of viscosity via Navier and Stokes is not appreciated. Rather, the arbitrary Kutta condition appears to be perceived as the resolution, facilitating the use of circulation to correct potential flow [88], noting this comes about due to the critical work of Prandtl with the boundary layer concept [20], a viscous effect.

Furthermore, the task of educating students about lift is made harder due to the perceived value of information, right or wrong, through avenues such as YouTube. Self-education is a key part of lifelong education [89]; however, a fundamental tenet is critical thinking [90] and, for scientific endeavors, this requires the correct application of the scientific method and the underpinning philosophy of science. At the intended level of this discussion, for secondary and tertiary science, it is critical that educators understand the correct underpinning theory (Navier–Stokes in the context of lift) and that they correctly use applicable observable demonstrations to predict–observe–explain the phenomena. To this end, future work will focus on experiments that facilitate the falsification of incorrect theories that can be performed in secondary science classrooms [64], as well as by expanding on simple flight simulation laboratories [61,62,63]. This will provide science educators with better tools to demonstrate science. Coupled with the detailed and complete qualitative understanding presented herein, it is hoped that future confusion will be avoided, although, according to Planck, it will take a generation to achieve a unified understanding.

Finally, Navier–Stokes (Newton’s laws for fluids) means that, at low angles of attack, the flow around a wing, due to viscosity, is asymmetric with a lower pressure above relative to below, resulting in lift. With regards to Newton’s Third Law, the lift force given by the pressure difference is equal and opposite to the pressure force on the earth’s surface (Figure 9c). Those statements should be a sufficient introduction. There will always be questions, and specific qualifying conditions have been given, but, at that point, it is time to consult Wild [88] (noting the lack of viscosity), Barnes and Potter [91], Wegener [92], Lissaman [21], McLean [93,94], or why not Prandtl [20]. If you need to teach students at a level you think is below this, the key term is simply aerodynamics. This is a beautiful, elegant word; it is the concept that the movement of air will result in forces on solid objects. That is, there is an exchange between the air and a rigid body in terms of energy and momentum. How does a curved piece of paper lift if you blow across it? Aerodynamics: the fluid motion is transferred to become motion of the rigid body. How does a hairdryer levitate a ball? Aerodynamics. It does not help at a low level to use names that are potentially wrong. But aerodynamics is objectively real; it does not need to be Bernoulli, Coanda, or Newton; it should be Navier and Stokes or maybe Prandtl, but it can just be aerodynamics. Labelling these observed phenomena with a scientist’s name does not help to understand the knowledge. What is important is that the observations prove that air can move solid bodies, and that is a statement that applies to fixed wing and rotor wing aircraft to give lift, as well as to propellers and jets to give thrust. This contrasts with aerostatics (more commonly hydrostatics), balloons, where the simple principle of buoyancy is at work. Does that need to be called Archimedes’ principle for the helium-filled balloon to float? No. Hence, for aerodynamics, such as a levitating ping pong ball or a lifting strip of paper, it really only needs to be called the aerodynamic reaction force [4]. So, an educator armed with a strip of paper which they blow across causing it to move should state, “I can move a physical object just using moving air. This is called aerodynamics. Aerodynamics is how a wing works; moving air interacts with the wing producing the force called lift, which overcomes weight, the force due to gravity.” If asked ‘how’, the educator would be correct to state, “it is complicated; there are pressure and viscous forces, with the air speeding up and slowing down, as well as it moving up and down. However, on the surface of the wing, it is about how the air pushes on it, and it pushes more in the upward direction.” The iterative loop of ‘why’ questions will likely only stop in tertiary aerodynamics, where Navier–Stokes can be appreciated as an explanation of aerodynamics.

6. Conclusions

The review of the literature presented in Part 1 highlighted that there are inconsistencies between the theories of aerodynamic lift describing how wings work in a science education context [3]. This is in stark contrast to engineering education, where aerodynamics is traditionally taught in a way that attempts to link the mathematical description of fluid mechanics to a conceptual understanding of the underpinning phenomena [4,5]. In aerodynamics, the coupled set of partial differential equations, the Navier–Stokes equations, are used to determine the fluid flow field around a wing, which can then be used to give the surface pressure on the wing, resulting in the lift force. In this context, an example from fourth-year aero engineering could have students use computational fluid dynamics to determine the air flow around a simple Cessna 172 wing. They would integrate the vertical component of the pressure on the external surface of the wing, giving the resultant lift force. To quote Anderson [4]:

No matter how complex the flow field, and no matter how complex the shape of the body, the only way nature has of communicating an aerodynamic force to a solid object or surface is through the pressure and shear stress distributions which exist on the surface.

(p. 57)

Of note here is that both the pressure and shear stress (due to viscosity) need to be considered. However, lift is dominated by the pressure term. It is true that, before engineering students learn computational fluid dynamics, they utilize approximations to analytically determine lift in 2D; although, these are simplifications to the actual underlying phenomena described by Navier–Stokes.

The result of the complex nature of lift, with Navier–Stokes the underlying “explanation”, is that there is a need to simplify presentations at school and in the media of this engaging subject which results in conflicting preconceptions observed in tertiary science students. This hypothesis is supported by the data collected from first-year students in their first week of university science study. The source of the students’ misconceptions is due to the different opinions and perspectives of the presenters as to what key elements a simplification should focus on. Did the presenters utilize a 2D inviscid theory as the source of the simplification and did that include a viscous correction (circulation) or not (Bernoulli)?

Tertiary teaching of lift should aim to point out the conflicting misconceptions first and not try to use them as a foundation for the aerodynamics learning of students. Educators should emphasize the importance of unlearning misconceptions and embracing a scientific approach that encourages constant refinement and updating of knowledge based on new evidence and research.

For secondary and primary school students, the concept of a “debate” should be eliminated and the “complex” nature of the topic should be stated as to why the current simple explanation given is incomplete. Armed with an appreciation that the current teaching is an oversimplification, students can be encouraged to dive deeper into the subject, fostering a sense of curiosity and critical thinking. By presenting the complexities of aerodynamics from the beginning, teachers can create a foundation that encourages students to question, experiment, and explore, leading to a more robust and accurate understanding of lift. By adopting this approach, tertiary, secondary, and primary educators can empower their students to develop a more sophisticated and nuanced understanding of aerodynamic lift, grounded in the scientific method, guided by the philosophy of science.