Abstract
We designed a teaching–learning sequence on relative motion in classical mechanics, based on the model of educational reconstruction and on the fundamental design principle of highlighting those conceptual elements which could be valuable in the future learning of special and general relativity. Thus, we propose an educational reconstruction strongly focused on the principle of relativity and the principle of equivalence. To highlight selected key concepts and motivate students in their exploration, we used a series of experiments based on video analysis and interactive simulations, which can be modified on the fly by the students. These tools are useful to stimulate autonomous investigation and to support the modelling of different physical situations. The sequence of activities was designed for students in introductory physics courses and was tested with a group of 24 undergraduate students in an online lab course, in which some distance learning techniques were also studied.
1. Introduction
Relativity of motion is a central concept in both classical mechanics and the modern theory of relativity. Both theories, rely on the concept of inertial frame of reference (FoR) to describe motion, and two fundamental principles can be presented to students already in the study of classical mechanics: the principle of relativity (PoR) and the principle of equivalence (PoE). The PoR is the starting point of special relativity as one of its postulates, while PoE is considered of high educational value in the introduction to general relativity [1,2,3].
In this work, we present the construction of a sequence of activities designed to address known students’ difficulties with the complex concepts involved in the description of relative motion in classical mechanics, as well as to help them advance towards representations of the above concepts and principles which are more productive for the subsequent study of special and general relativity. The teaching–learning sequence (TLS) proceeds by alternating real-world experiments and interactive computer simulations, so that these two aspects complement each other and contribute to improving students’ understanding, a design principle inherited from our previous work on teaching–learning sequences [4,5].
The design of the TLS is based on the model of educational reconstruction (MER) [6], and as in the tradition of German Didaktik, which is at the foundation of the MER [7], it places a strong accent on the significance of the knowledge gained for the learner, both at their current stage of education, and in view of their future learning and life. Thus, the initial choice of the subject matter for educational reconstruction and elementarization was driven by instructional inquiries and goals, such as What concepts are useful to help learners adopt a modern perspective on classical mechanics? What concepts are useful to facilitate the future adoption of a relativistic world view?
A relevant factor in the initial design of our learning environment has been related to the temporary closure of university laboratories due to the spread of coronavirus (COVID-19) in the spring of 2020. The event forced us to redesign the sequence by transforming the traditional face-to-face course in the lab into an online course. Therefore, while adopting a distance teaching methodology, we tried to offer students an authentic and meaningful laboratory experience, capable of providing the rigor required in a physics laboratory. Most of the experiments in the sequence are demonstrations performed by teachers (quantitatively analyzed by students) or experiments performed by students alone, simply using common objects available at home, a kind of experimental activity that we could define as “kitchen physics”. The removal of COVID-19-related restrictions presumably will allow us to revise the structure of the sequence, increasing student-to-student interactions and generally the inquiry character of our sequence.
The sequence was tested with a group of 24 university students of mathematics and physics who attended a course aimed at the training of future physics teachers. Our sources of data on students’ advancement and ideas include a questionnaire distributed before the activities (pre-test), a delayed post-test (about three months after the end of the sequence), discussions recorded during and after the experiments, responses to some teaching learning interviews made at the end of the course and some questions for the course evaluation answered after the activities.
2. Theoretical and Methodological Framework
In this section, we report on the research steps which led to the construction of our TLS, starting from the process of determining the content structure for instruction according to the MER (Section 2.1) and the development of the teaching–learning environment according to the principles of active learning and our previous research experience on TLSs (Section 2.2).
2.1. The Content Structure for Instruction
The MER [6] provides a methodological framework for physics education research and offers directions for combining empirical and theoretical education research for the design of teaching–learning interventions and educational materials [8,9]. The MER has proven extremely fruitful in physics education research and has been adopted as a theoretical foundation for the design of teaching–learning sequences and instructional materials by many authors in the past twenty years; for example, very recent works have adopted the model for designing educational reconstructions of general relativity [10], special relativity [11], nanotechnology [12].
The MER is based on the idea that three elements of educational research are strictly related. The first two, namely:
- (i)
- Analysis of science content (analysis from the perspective of theory),
- (ii)
- Analysis of students’ difficulties and assessment of the crucial features of students’ learning processes in this topic (analysis from the perspective of learners), contribute to the identification of the fundamental structure of the subject matter for instruction (i.e., the issue of elementarization) of the possibly fruitful strategies to improve learning outcomes and overcome student difficulties. From such outcomes, the third component of the MER stems:
- (iii)
- Construction and evaluation of learning environments and activities.
In the design of TLSs according to the MER, the above three elements are combined iteratively [6], in the sense that the educational outcomes, classroom observation and teacher reflection typical of action research contribute as new inputs to a revision of the processes of structuring the material for instruction and practically designing the learning environment and activities
2.1.1. Analysis from the Perspective of Theory
In this section, we report on our research work concerning the first element of MER discussed above; note however that the division in sections does not reflect a sequential relationship between the different kinds of analyses; in particular, the analysis from the perspective of theory and of students are constantly intertwined and dialectically juxtaposed.
Despite relative motion being an important topic in classical mechanics, it is not always highlighted in physics curricula. Taking as a reference the Italian curriculum for secondary school (which we consider since our students are future physics teachers, and the TLS we design is not only meant to improve their understanding, but to provide examples of activities and materials for their future teaching), we can read the following statement for the beginning of the second cycle of high school (grade 11): “The laws of motion [introduced in grades 9–10] will be reconsidered, in parallel with the discussion of inertial and non-inertial frames of reference and of the principle of relativity of Galilei” [13]. The principle of equivalence is never mentioned in the curriculum, and indeed it is our experience that a vast majority of students arriving at university never had the occasion to reflect on or problematize the identity between inertial and gravitational masses. However, we have seen two possible candidate key concepts explicitly mentioned in the Italian curriculum: the concept of frame of reference (FoR), with the classification of inertial and non-inertial, and the principle of relativity (PoR). We start our epistemological analysis of the subject matter, intended to define the boundaries of the educational reconstruction more precisely, from these two concepts.
The concept of FoR is at the heart of any description of relative motion in classical mechanics, and also forms the basis for the understanding of any concept in special relativity [14]. A significant conceptual revision is required for the concept of FoR within a learning trajectory in physics: for example, working within the theory of conceptual profiles [15], Ayala Filho [16] identified three different stages in the development of the conceptual profile of a frame of reference: the first one is the common sense profile, with the notion of absolute motion in a privileged reference frame and the identification of the concepts of observer and reference. The second is the one of Newtonian mechanics, in which physical quantities are associated with reference frames, but time is still a universal coordinate for all FoRs. Finally, the third stage is the one defined by special relativity, where it is only possible to establish a single scale of time for observers of the same FoR. According to a modern definition, inspired by relativity theory, “in a frame of reference, events are given spatial and temporal coordinates, as measured by an observer in relative rest to the frame of reference, by means of measuring rods and synchronized clocks” [17]. The three stages of conceptual development identified in [16] roughly correspond also to the historical evolution of the understanding of the concept of a frame of reference. Correspondingly, in the context of teaching classical mechanics, a primary educational goal should be to encourage first of all a transition towards a Newtonian point of view on FoRs, with the dismissal of the concept of absolute motion, deeply rooted in student thinking. But, consistently with the wider educational aims stated in the Introduction, we also wish to understand what aspects of the concept could be highlighted in order to make learning more fruitful for a future understanding of relativity. There are several ways in which this could be achieved. For example, according to [18], the transition towards a relativistic perspective on FoRs can be facilitated if the issue of simultaneity is brought up and problematized already in the context of classical mechanics. Although, in this case, the absolute character of simultaneity of events must be concluded, this setting could be ideal for clearly differentiating, already in classical mechanics, the time of an event from the time at which a given observer receives the time signal of an event, a confusion which is known to generate a wide number of difficulties in the learning of special relativity [14,19]. Another important element may be found in highlighting the connection between inertial frames and the PoR, and generally, the possibility of using the PoR as an auxiliary reasoning tool to deal with problems in classical mechanics which concern relative motion between inertial frames. This aspect will be addressed more extensively in the next paragraph.
The PoR of classical relativity grants the same status to all frame references in uniform relative motion, with respect to the laws of mechanics. The PoR can be taken as a postulate of classical mechanics [20], but this is not usually the case in university level textbooks, a more common approach [21,22] is to present it as a consequence of the definition of inertial FoRs, and the principle of inertia. Historically, the PoR was first formulated in an effort to explain why the motion of the Earth with respect to the stars, as postulated within the Copernican system, would not have been detectable through experiments performed on Earth. Note that, from a careful reading of Galilei’s “Dialogue Concerning the Two Chief World Systems—Ptolemaic and Copernican” [23], it is possible to argue [24] that what Galilei had in mind was that no experiment whatsoever (thus, not only limited to mechanics, within the boundaries of the known physics of Galilei’s time) could distinguish which one between two systems in relative uniform motion was ‘really’ at rest. But, as it is well known, a contradiction between the PoR and the laws of electromagnetism emerged towards the end the XIX century and the slowly rising concern in the physics community about such contradiction [25] grew into a research field, the electrodynamics of moving bodies. In the context of the construction of the special theory of relativity Einstein, following Lorentz and Poincaré, further generalized the PoR by assuming that all laws of physics must have the same form in inertial systems, and thus elevated the PoR to the status of a general principle for all physics. In this last form, the PoR, together with the invariance of the velocity of light, is one of the postulates of special relativity, and can be considered one of the most basic building blocks of our understanding of Nature. When reasoning within classical mechanics, the principle of relativity can be used as an auxiliary tool, allowing to solve a given problem in one’s preferred inertial reference frame and then, if necessary, translating the results to another by means of Galilean transformations. Take for example the following problem: “in the reference system of a cart moving horizontally at speed v with respect to the ground, a stone is thrown upwards with vertical speed w. Determine the distance at which it falls back to the floor in the frame of reference of the ground”. While it is possible to solve this problem entirely in the FoR of the ground, by initially performing a vector sum of velocities, it is arguably easier to solve it first in the cart FoR, and then translate it to the FoR of the ground by taking into account the invariance of time in the two FoRs. Note that a similar strategy would also work in special relativity, although rather than invariance of time intervals, which does not hold in such context, one would have to consider the invariance of four-distance between events.
From an educational point of view, several researchers (see, e.g., [26] as well as some textbooks as [27,28]) have identified the educational relevance of analysing situations similar to the gran navilio (large ship) which appears in Galileo’s Dialogue. The work in Ref [26], which investigated precisely the ability of students to use the PoR as an auxiliary tool for reasoning, is especially relevant and will be discussed in more detail in Section 2.1.2.
The relationship we have identified between relative motion in inertial FoR and the PoR has a rather evident counterpart in the relationship between relative motion involving non-inertial FoRs and the principle of equivalence (PoE). Consider, in fact, the following problem: “A support with a simple pendulum mounted on it is sliding without friction on an inclined plane with inclination α. The pendulum is oscillating. What is the direction of the axis passing through the pendulum’s pivot with respect to which the oscillation is symmetric? Is the duration of small oscillations longer or shorter with respect to the same pendulum oscillating on a fixed support in the laboratory?” Problems of this kind can of course be solved by distinguishing gravity from apparent forces, but they become much easier if the PoE is invoked to construct an “effective gravity”, combining real gravity and inertial accelerations [29,30]. Thus, by allowing an immediate translation from inertial to gravitational forces and vice versa, the PoE can operate as an auxiliary reasoning tool in the analysis of relative motion involving a non-inertial FoR.
Historically, the PoE has played an indispensable heuristic role in the conceptual transition from special to general relativity. However, there has been considerable debate on whether the PoE is actually a fundamental principle of general relativity, or indeed on whether it plays any part in the structure of general relativity at all [31,32,33]. Often, in an effort to reconcile the modern formulation of general relativity with Einstein’s own perspective on its foundations, several principles by the same name but slightly different content were formulated in later textbooks and articles [32]. As a consequence, the literature on the PoE has become extremely complex, with different formulations of the principle bearing different, sometimes contrasting, names. Using a rather common convention (used for example in [34,35]) we can distinguish at least (a) a “Newtonian” equivalence principle, stating that the ratio of inertial mass mI to gravitational mass mG is a universal constant, whose status within classical mechanics is simply that of an empirical fact; (b) the “Einstein” PoE, stating that “fundamental non-gravitational test physics is not affected, locally and at any point of spacetime, by the presence of a gravitational field”, by which it is meant that, given a sufficiently small region of spacetime, in which a non-gravitational experiment is performed, it is impossible to tell whether a gravitational field is present or not; (c) a “strong” PoE which further generalizes the previous formulation to any (gravitational or otherwise) physics experiment. From the last two formulations it can be seen clearly that the essence of the PoE is a generalization of the PoR to non-inertial frames, so that indeed understanding of the core content of the two principles can be considered interconnected. For example, the PoE states that experiments made locally in a reference frame uniformly accelerating with acceleration with respect to an inertial frame produce the same experimental results as in a frame of reference stationary with respect to an inertial reference frame, and immersed in a uniform gravitational field −, so that the observer cannot distinguish the two cases using the experimental result alone [36].
The historical studies of J. D. Norton [31,32,33] have shed much light on the role played by the PoE in Einstein’s thinking in the transition from special to general relativity, and especially [31] seems relevant from an educational point of view. In this work, Norton expresses the view that the PoE in the form used by Einstein between 1907 and 1912, during the painful elaboration of what would ultimately become general relativity, had actually no testable physical content going beyond special relativity. It essentially stated that those properties of space that manifest themselves in inertial effects should be more properly understood as the properties of a field structure in space: the same field structure which also governs gravitational effects [31]. In this sense, educational proposals focused on physical situations which can be most productively dealt with by computing an “effective gravity field”, comprising both gravitational and inertial effects [29,30], appear quite in line with the disposition of mind which led Einstein from special to general relativity.
The PoE is never mentioned in the Italian secondary school curriculum, and as reported previously, many students never encounter it before university. However, some—also at the high school level—textbooks [27,28] discuss it, sometimes in “special” pages devoted to more in-depth scrutiny of topics. Some international textbooks, even at university level [22] instead neglect to discuss the PoE and the equivalence between inertial and gravitational masses before the chapter about relativity. Notwithstanding this, we believe that both the considerations coming from the analysis of the scientific content of the theory, and those concerning the point of view of the learner, which will be presented in the next section, concur in making a case for the presentation of the PoE as integrated in the topic of relative motion, and as an additional key concept, leading to the structure proposed in Figure 1, which will be further refined in the next section.
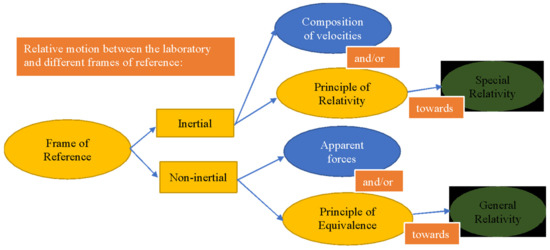
Figure 1.
Map of the proposed reconstruction. Yellow elements indicate key concepts which are stressed in our reconstruction, while blue elements indicate methods which are less stressed since students have already some familiarities with them.
2.1.2. Analysis from the Perspective of the Learner
2.1.2.1. Significance of the Subject Matter for Students
As mentioned in the Introduction, the significance of the subject matter for students, considering their intellectual and social development is of high importance within the MER [6]. Several authors have highlighted the importance not only to teach modern physics, but also to teach classical physics from a modern perspective, i.e., focusing on those overarching concepts and principles which may be productive for the future intellectual and cultural development of students [37,38]. For instance, these reasons were explicitly stated in [26], as a further motivation for studying the capability of students of reasoning using the PoR within classical mechanics. A reinforcement of these motivations is found in [39], where authors argue that some of the difficulties students have in assessing the plausibility of the special theory of relativity may stem from having no occasion to reflect on the true meaning of the PoR already during the study classical mechanics. Similar considerations are also put forward by authors arguing for a deeper clarification of the concept of mass, including the meaning of the PoE, already at the level of classical mechanics [40,41]. Providing a contribution to such efforts is one of the main motivations for the present research.
2.1.2.2. Research on Student Conceptions and Difficulties
Research on student difficulties on relative motion has a long history and several well-established results. In the classical work of Saltiel and Malgrange [42], the authors described the “natural” model of relative motion as having the following characteristics: (a) distances travelled by objects are made absolute, in the sense that their variation in different frames of reference is not considered; (b) relative motion between inertial frames of reference is attributed to the presence of forces, even if none are present. This model often is complemented by the idea of a privileged frame of reference of absolute rest. For example, many students stated that if a man is traveling on a moving pavement and throws a ball in the air, it will fall behind him, either for dynamical reasons (the ball will lose the force which was pushing it forward) or for geometrical reasons (presence of an absolute vertical direction connected to a frame of absolute rest). The presence of a frame of absolute rest is also connected to the distinction between ‘real’ and ‘apparent’ motion [42,43]: if relative motion cannot be explained in terms of forces (for example in the case of an observer within a train observing a moving landscape), then it is explained as ‘apparent’ motion, with the status of an optical illusion. The difficulties of students in analyzing the case of an object dropped from a moving carrier are also connected to naïve theories of inertia [44,45] and to the perceptual experience of observing the object fall in a straight line when the student herself was in the role of the carrier [46]. Note that this issue is the subject of two items of the Relativity Concept Inventory (RCI) [47], in which students are requested to choose the correct trajectory in both reference frames of the ground and the carrier. In the RCI test sample of first year undergraduates, these items are found of average difficulty, and among the most resistant to instruction. Overall, the presence of student difficulties with at least three possible originations (dynamical, geometrical, perceptual), resistance to instruction, and relevance for special relativity makes this classical problem a good candidate for the starting point of our sequence.
Student understanding of the concept of FoR was thoroughly investigated in [48,49] in which the authors worked with samples of physics undergraduates. In [48], which focuses on inertial frames of reference, the authors found that large percentages of students treat FoRs as concrete objects, or as inextricably connected to concrete objects, sharing the consequences of events which occur to those objects they are attached to. For example, authors report that about half the students believe that the FoR in which a plane flying with velocity v with respect to ground is at rest ceases to exist if the plane disintegrates. Students also think that FoRs are physically delimitated by the boundaries of object they are ‘attached’ to (for example about 40% of students believe that the FoR in which a ship is at rest does not extend beyond the boundaries of the ship) and share other physical properties of the object beyond its kinematic ones (for example, temperature). Several students identify certain events as ‘really’ taking place in certain FoRs and not in others, and some of them also develop a concept of pseudo-relativism, in which different observers, stationary with respect to each other in the same FoR, can provide different accounts of the same phenomenon, for visual/perceptual reasons. This appears to be connected with the well-known findings first reported by Scherr and coauthors in [14] and confirmed by other studies [17,50,51] which identify a significant obstacle in the learning of special relativity in the idea that the time of an event in a certain FoR corresponds to the time of reception of the light signal by an observer. This alternate conception, which often has the status of a global misunderstanding on the meaning of special relativity, is accompanied by the complementary misconceptions that (a) different observers stationary with respect to each other must be treated as different FoRs; and (b) different observers moving with respect to each other but placed in the same position at one instant of time must be regarded as being in the same FoR at that instant.
In [49] the authors investigate students’ understanding of non-inertial frames of reference, and the most important findings besides those already highlighted for inertial FoRs can be summarized as follows: (a) for many students (about 70% in the authors’ sample), the inertial or non-inertial character of a FoR must be judged externally, in the sense that for an observer stationary with respect to a FoR, that FoR is always inertial. Furthermore, for some students the judgement must be made by an ‘independent’ observer, by which it is typically meant one at absolute rest; (b) for many students (about 60% in the authors’ sample), the inertial or non-inertial character of FoRs is a relative property, i.e., two FoRs in relative uniform motion are inertial with respect to each other, while two FoRs in relative accelerated motion are non-inertial with respect to each other; (c) several problems arise with rotating FoRs, including the belief that centrifugal force acts on rotating objects but not on stationary objects in rotating FoRs, or that the presence of inertial forces must be judged subjectively (by the ‘feeling’ of a centrifugal force). Some of these difficulties with rotating reference frames have been reported in other studies (see, e.g., [52]). Note that difficulty (a) mentioned above corresponds to the finding reported in [26] that some students develop a ‘wider principle of inertia’ in which phenomena have the same form in all FoRs (inertial or not), with the sole specification that the environment in which the phenomenon is observed is stationary with respect to the observer.
In view of these research results concerning the concepts of FoR, the following points seem relevant for an educational reconstruction: (1) introducing a proper distinction between inertial and non-inertial FoRs, based on an accepted definition of an inertial FoR; (2) carefully distinguishing between FoRs and observers, and between FoRs and object/containers which are in rest with respect to them; (3) discussing explicitly the problem of an experimenter attempting to determine whether the FoR in which she is at rest is inertial or not, besides the subjective feeling of a centrifugal or other inertial force. Point (3) could also contribute to more in-depth understanding of the PoR and the PoE.
Research focusing specifically on the principles of relativity and equivalence has been less abundant than more general research on relative motion. In [26], the authors investigate the ability of undergraduate students to answer conceptual questions in classical mechanics by invoking the principle of equivalence. The questions posed by authors are all formulated in terms of the fundamental, and historical, content of the PoE, i.e., the impossibility of distinguishing, through an experiment performed within a FoR in relative uniform motion with respect to another inertial FoR, which one is ‘really’ in motion. Their most important finding of [26] is that students are completely unable to appeal directly to the PoR in answering these questions: most often their reasoning uses the principle of inertia, or the independence of the particular phenomenon at hand from velocity. This is related to the typical textbook presentation discussed in Section 2.1.1 which leads to the situation in which the PoR for students is an empty statement, equivalent to the law of composition of velocities for inertial systems, or even to the general idea that an experimental situation can be considered in different FoRs, and its actual content is never reflected upon. As mentioned in Section 2.1.2.1, this has consequences also in the capability of students of judging the plausibility of, and therefore accepting, special relativity [39]. Another relevant finding of [26] is that some students exhibit what the authors call relativistic noise, i.e., they expect that in FoRs that are moving at very high speeds, maybe close to the speed of light, the PoE may be violated because of relativistic effects. This finding resonates with some results of the RCI [47] in which students believe that experimenters on high-speed rockets or ships can assess the state of motion of their own FoR by observing relativistic effects (length contraction, time dilation, etc). Some of these items are among the most difficult within the RCI. In another important study [53], the author investigates undergraduate physics students’ ideas on the PoR through a questionnaire asking to agree or to disagree with several statements and providing comments and explanations. The results, which confirm and extend those of [26], can be summarized identifying three kinds of alternate meanings attributed by students to the PoR: (a) the PoR as equivalent to the Galilei transformations, while actually it is, conceptually and historically, independent of them [24]; (b) the PoR stems from reciprocity of the two systems involved (the first one sees the other as moving with velocity v, the second one sees the first moving with velocity −v); (c) the PoR stems from the stationarity of the observer with respect to its environment which makes it impossible for him to tell the state of motion. The author notes that both interpretations (b) and (c) could be extended to FoRs in relative accelerated motion, in agreement with the findings of [26].
We are aware of a single, recent study specifically targeted at students’ difficulties and alternate conceptions of the PoE [54]. The study sample was composed of advanced undergraduates and revealed a wide range of issues and vulnerabilities of students; among these, we consider here only those which do not require knowledge of general relativity. First of all, as we reported as anecdotical evidence from our own teaching experience, a significant percentage of students (about 40% in the authors’ sample) declared that the equality of inertial and gravitational masses requires no experimental confirmation, presumably because the distinction had never been introduced or problematized. Between 30% and 50% of students believed that the equality, rather than the proportionality, of mI and mG is stated by the PoE, and that there would be observable consequences if the constant of proportionality were different from unity. Finally, most students were unable to explain in detail the thought experiment of Einstein’s elevator from the point of view of the PoE, or to use the PoE as an accessory reasoning tool to deal with problems in which both gravity and inertial forces appeared, such as the one mentioned in Section 2.1.1 and those of [29,30]. These results of [54] have been of high importance in the development of our sequence. On the other hand, further issues reported in [54], many of which are related to the local character of the PoE and the appearance of tidal forces, have been excluded from our design.
2.1.2.3. Research on Effective Experimental Activities
In recent years several experimental activities based on low-cost, widely accessible technologies have been proposed to improve students’ understanding of relative motion, the PoR and the PoE. While these activities, as will be discussed in the next Section, must be presented in the context of immersive and active learning environments to be effective, the design of a novel way of experimentally introducing a concept using widely accessible materials and equipment has a value for practitioners and educators, and we took inspiration from some of them in the design of our sequence. Among these experiments many consist of demonstrations of Einstein’s elevator thought experiment [55,56] and the physics of free fall, such as [57] in which the author discusses a collection of experiments using techniques accessible to students and teachers with no especially advanced laboratory experience or skill. Many of these experiments integrate widely accessible technologies such as smartphone sensors [58,59,60] and video analysis techniques such as the free software Tracker (v6.0.3) [56,61].
2.2. Development of the Learning Environment
In the discussion above, we have defined the basis of the design of our learning environment, or the content structure for instruction as defined within the MER. Since a successful educational reconstruction must involve both content and design features, after the content structure is established, we now discuss the educational strategies and practical didactic choices which characterize the learning environment.
2.2.1. The Predict Observe Explain (POE) Strategy
In the design of a primarily experimental educational sequence, it is essential to choose a framework for conducting laboratory work. Predict-Observe-Explain (POE) [62,63] is not a very recent or particularly fancy strategy, but it has been our paradigm of choice for several reasons. First, it proved very effective in the past, in the context of teaching–learning sequences of our design, and with similar inspiration [5]. A second motivation is that our intervention concerns a topic in which student alternate conceptions are abundant and with high incidence (see Section 2.1.2.2). Thus, at least at the level of the initial cycles of experimentation of the sequence, we felt it important to adopt a methodology providing us with strong feedback on the extent of these difficulties for our students.
In POE, each experimental activity is characterized by three phases. In the initial “predict” phase, students are asked to make their own hypotheses about the outcome of the experiment. This step helps students bootstrap the learning process and start the construction of mental models relating theory to experiment. In the second phase, “observe”, the experiment is performed by students, often as a kitchen experiment or performed by the teacher as a video demonstration. In the latter case, however, the students had to quantitatively analyze the videos to acquire the data and carry out the measurements. Here, students are expected to link their observations and measurements to the previously hypothesized outcome and, as a result, confirm or reconsider their mental models, favoring meta-reflection and stimulating cognitive conflict [64]. In the final phase, “explain”, the experimental results are revisited through collective discussion between students and the teacher, and in this context the connection between theoretical and conceptual aspects and the outcome of the experiments is brought out.
The effectiveness of POE in eliciting and uncovering students’ misconceptions, and in provoking meta-reflection on them is, we believe, undisputed [65]. A third element we considered is that the sequence would have been tested at least partly in distance learning, using equipment students have at home, or provided in the form of an experimental kit [66], or even by analysis of a video experiment performed by the teacher. Predict-Observe-Explain, as a guided/structured inquiry strategy [67], may be not as effective in sustaining students’ engagement, motivating them to science, or improving critical thinking as more open inquiry learning models [68], but has a quite strong record of educational achievements in terms of conceptual understanding, and appears ideal to be adopted when students perform experiments remotely using home equipment or a kit, since does not require autonomous design of new experimental tests by students. Note, furthermore, that there is a long history of research on POE activities based on simulations rather than on actual experiments [69,70] that remote POE activities using videos or other materials in place of experiments have been proposed as a powerful strategy for the design of online learning environments [71,72].
2.2.2. Practical Choices for Creating a Productive Learning Environment
We made some fundamental decisions regarding the design of the teaching–learning sequence that can be summarized as follows:
- (a)
- Propose activities based on a combination of real experiments and interactive simulations. Measurements were taken via the open-source Tracker Video Analysis tool [61] while interactive simulations were designed and run within the freeware 2D simulation environment Algodoo (v2.1.0) [73]. Barring all educational considerations on these, the choice of free/open-source software in teacher education is motivated primarily by the importance of adopting tools that teachers can continue to use in their future school teaching.
- (b)
- Let students perform experimental activities even in the absence of specific equipment. The challenge facing remote education is the potential absence of practical interaction with measurement tools and experimental apparatuses. So, we asked students to use the resources they had at home, taking advantage of the spread of smartphones among them. When it was not possible for the students to perform the experiments themselves at home, the experiments were replaced by demonstration videos with experiments also performed with objects of common use by the teacher. Sometimes the real experiments were replaced or supported by Algodoo simulations, designed and realized by students, converted in video, and analyzed, thanks to Video Analysis, as if they were real experiments.
- (c)
- Let students perform the data analysis, modelling activities and explanation phase in groups, guided by the instructors who stimulated discussion about experimental results. Collaborative learning opportunities are at the heart of the socio-constructivist paradigm, and play an important part in our learning environment, on which they were made possible by exploiting breakout rooms in Zoom [74]. Within cooperative environments, students were guided in the construction of qualitative, conceptual mental models of phenomena connected with relative motion, which were refined reinforced with the progress of the experimental sequence.
- (d)
- In some cases, exploit the possibilities of Algodoo, to “break the rules” of POE and encourage students to more open and autonomous investigations starting from motivating questions. This strategy was used in the case of the thought experiment of Einstein’s elevator, with the stimulating question concerning the behavior of swinging pendulums and other objects after the start of free fall. Students in this case investigated the problem with fewer constraints by autonomously designing Algodoo simulations. In addition to the educational relevance of this strategy, observing the work of students and discussing the activity in groups provided us with crucial information on the role that the modeling activity has in scaffolding students’ knowledge.
3. Description of the Sequence
The central themes discussed in Section 2 are now investigated more in detail, focusing on the two principles of relativity. Schematically, the main aspects, key concepts, that we highlighted with the students were:
- -
- Inertial reference frame (PoR),
- -
- Non-inertial reference frame in accelerated motion with uniform acceleration: in the horizontal plane and on inclined planes, and
- -
- Non-inertial reference frame: Einstein’s elevator, free fall (PoE).
The sequence of activities is organized into six parts: (A) introductory examples and experiments: trajectories in different inertial reference frames; (B) non-inertial reference frame: trajectories in a linearly accelerated FoR; (C) free surface of liquids in non-inertial linear accelerated reference frame; (D) pendulum in a non-inertial reference frame (inclined plane): center and period of oscillations; (E) bottle of water in free fall and demonstration of Einstein’s elevator (interacting magnets and mass on the spring) and Pendulum in Einstein’s elevator.
Below, we describe the main features of the sequence, paying particular attention to the experiments and simulations involved. We also focus on students’ difficulties and, by discussing them, compare the known results of the literature with the results of pre-activity tests administered to students (summarized in Table 1).

Table 1.
The concepts tested by the pre-test and a summary of the activities. Although some questions are related to more than one concept, we have assigned each question to only one concept. Some questions (PT1, PT2, PT3) were administered only as a pre-test while the others (Q1, …, Q10) are also present in the post test The full text of the test is in the Appendix A.
3.1. Inertial Frame of Reference
Predict. It is known that students usually have difficulties in understanding the formal aspects of the change in reference frame while many researchers observed that the correct interpretation of Galilean relativity and reference frames is fundamental for a good conceptual understanding of special relativity, since the comprehension of classical relativity predisposes the student to the understanding of Lorentz transformations. We proposed two questions (Q1 and Q2) from the Relativity Concept Inventory [27] and the answers confirmed the students’ difficulties while visualizing the trajectory of objects in different reference frames, which is a common misconception [28]. Just half of our students answered the questions correctly. These data confirm the presence of the misconception that trajectories are often seen as free geometric shapes that do not depend on the reference frames. The results highlighted the difficulties in grasping the implicit initial conditions (position, speed, velocity), unavoidably different in different reference frames.
The difficulties in understanding the formal aspects of the change in reference frame is confirmed by students’ answers to the question Q3: if Alice observes the scene from a boat moving at a constant speed along the river, many students, 7 (28%), say that Alice will observe ‘a parabolic trajectory’ and just 9 (36%) give the correct answer. Then, just one-half 12 (50%) of the students recognize that there are no fictitious forces acting on the drone in the moving FoR (Q4).
Observe. With the aim of making students engage with these topics we encouraged them to design and realize some experimental and simulation activities. Usually, when the university laboratory was available, we used the Pasco ballistic chart accessory [29] showing a demonstration: a ball is thrown vertically upwards from a cart with respect to it while moving horizontally in uniform straight motion with any speed and it is shown that the ball lands again in the cart after the jump. In the face-to-face lessons, once the video of the experiment was acquired with their phones, the students analyzed the motion from two different reference frames (the cart and the Laboratory) using Tracker Video Analysis.
In the remote laboratory course, some students tried to make videos by themselves, as in the cases shown in Figure 2. The ball falls back into the student’s hand, i.e., there is no relative motion along the horizontal axis between the ball and the boy standing on the car. We can combine this qualitative analysis with a quantitative one using Tracker, which allows setting the FoR on the moving object, thus allowing to analyze the motion both from the observer at rest, and from the one moving at constant velocity. Here, one can see the Galilean transformation at work.
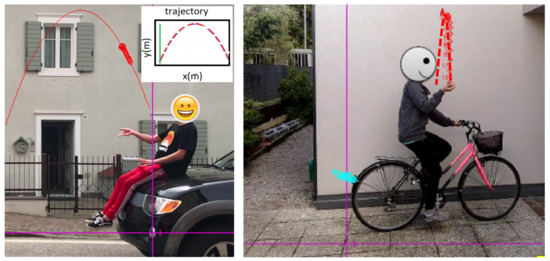
Figure 2.
Some students made a video on their own. Thanks to Tracker students can view the trajectories in the two different reference systems starting from the same video (video available https://youtu.be/hlxLNPzViGg, accessed on 10 July 2023): in the graph, two trajectories in the two different FORs are depicted with two different colors, green and red.
To explore the situation described by Q3–Q4 also in the distance learning environment, students were engaged in a computer aided activity by combining Algodoo simulations and Tracker Video Analysis (see Figure 3). They produced a video where the boat and the drone described in Q3–Q4 move according to the text of the questions. The simulated videos were analyzed using Tracker (see Figure 3) and the path followed by the drone in the two different frames was shown.
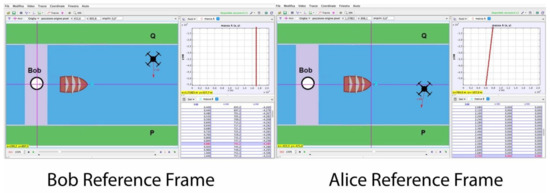
Figure 3.
Two frames from the video produced by students with Algodoo: Bob is sitting on a bridge on the river. Alice is standing on a boat moving along the river at velocity, a drone takes off from Q to P. The Tracker Analysis of the video shows the path of the drone for Bob (left) and for Alice (right).
Other activities. To reinforce the construction of the deep meaning of the PoR, we proposed to students the analysis of a set of videos derived from one showing a ball thrown upwards from a cart moving at constant speed (see the original at https://shorturl.at/hlyLU, accessed on 10 July 2023), digitally edited in such a way that the moving cart is maintained in a fixed position within the frame (https://shorturl.at/dsLS7, accessed on 10 July 2023). In this way, the same video can be convincingly shown to appear as a still cart, or as one moving in either direction, depending on background images which can be added or removed (e.g., a picture on the wall, either still or moving). This kind of strategy was directly borrowed from the PSSC [75]. Furthermore, we also produced, and proposed to students, a set of videos inspired from Galileo’s passage of the “gran navilio” showing the cart moving at uniform speed with either a (digitally added) bowl of fish (https://shorturl.at/buBQT, accessed on 10 July 2023), or a drop falling in a bowl from above (https://shorturl.at/abvx5, accessed on 10 July 2023). These videos are used to discuss the content of the PoR as stated by Galileo (the original videos without the digital manipulation at https://shorturl.at/cemC2, accessed on 10 July 2023 and https://shorturl.at/inKTV, accessed on 10 July 2023).
Finally, after the activities the concept of inertial FoR and the PoR are re-discussed with students; and it is highlighted how the pre-test examples (primarily focusing the attention on Q2) could be re-appreciated in view of the PoR. The effects of this work on students, both in terms of item performance, and of meta-cognitive reasoning on their understanding of the deep meaning of the principle, principle, can be seen in Section 4.1.1 and Section 4.1.2.
The answers provided by students in the post-test multiple-choice questions confirmed an improvement in their understanding of how to convert trajectories from one inertial frame to another using a simple transformation. Based on the interviews conducted however, it was observed that the principle of relativity is often replaced by the principle of inertia, which is typically considered sufficient. Additionally, students emphasized how the possibility to analyze simple videos and the option to change the frame of reference using Tracker software (v6.0.3) can greatly aid and enhance understanding in such situations.
3.2. Non-Inertial Reference Frame in 1D
Predict Students of introductory courses in physics have great difficulties in distinguishing the case of the inertial reference frame from the non-inertial one (see Q4). We introduce the experimental activity asking an open question (PT1).
Additionally, in this case, the ideas about the trajectories of a body are confused, even if someone has correctly predicted that, when the ball is thrown vertically upwards from a train while the train is accelerating, the ball will not land in the hands of the one who threw it. Therefore, unlike the inertial case, in the accelerated FoR, the ball has a velocity and an acceleration along the horizontal axis.
Observe To discuss the case of a non-inertial FoR with the students we proposed a video, acquired in the laboratory before the pandemic. The video shows that if the ball is thrown vertically upwards from the cart while the cart is accelerating, the ball will not land in the cart (https://shorturl.at/flmrF, accessed on 10 July 2023). Since carrying out such an experiment at home is quite difficult (or dangerous using the same apparatus as the previous one), we decided to analyze with students only a video recorded in the physics laboratory and based on PASCO equipment [29]. Additionally, in this case, it was therefore possible to analyze the motion both from the FR at rest, and from the one that moves by accelerated motion (https://shorturl.at/lEIL9, accessed on 10 July 2023). In Figure 4, we show the trajectories of the ball from the two FoRs.
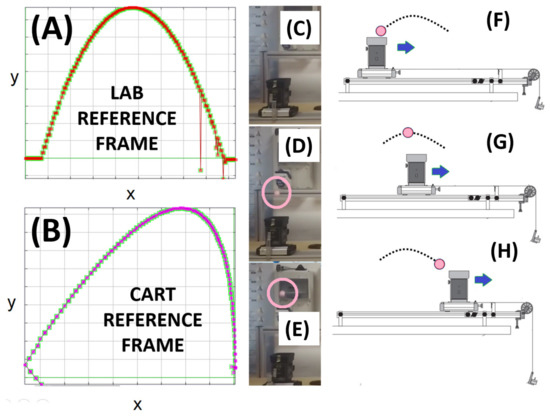
Figure 4.
The experimental apparatus, frames from the video and measurements with Tracker. On the left the trajectory of the ball in the reference frame of the laboratory (A) and the one of the carts (B). In (C–E) panels, three frames from the video before the ball is thrown, and in two snapshots of the uphill motion. In panels (F–H), three moments of motion: immediately after the launch, at maximum height and when the ball returns to the initial height.
For the quantitative examination students analyzed the video and on the left the graphs of the motion of the cart and the ball in the FoR integral with the laboratory are shown. According to graph (1), it is easy to estimate the horizontal acceleration of the cart as the ball moves at a constant speed. In non-inertial RF in motion, particle accelerations are also affected by transformations.
In the context of distance learning the production of a video with a ball thrown vertically upwards from an accelerating system is more difficult than the one reported in Figure 4. Thus, students realized a virtual simulation by using Algodoo to recreate the situation of the real experiment, exported the resulting video, and then proceeded to analyze, the path followed by the ball in the two different frames was displayed using Tracker (see Figure 4). While the trajectory seen in the laboratory is a parabolic path absolutely identical to that encountered in the inertial case, the trajectory in the FoR of the cart is something different and is described by a non-trivial equation:
This function can be used to interpolate experimental data measured using Tracker analysis. The quantitative analysis of the experiment allowed us to introduce the “fictitious force” and its relationship with the acceleration of the FoR in motion with respect to the laboratory. The explanation of this complex phenomenon within the context of accelerated motion emphasizes the usefulness of Galileo’s transformations in simplifying trajectory calculations for students. Additionally, we presented an alternative method involving the application of fictitious force, but it was observed that this approach becomes more challenging when addressing problems of this nature.
This experiment was useful as a valuable tool to introduce the concepts of non-inertial reference frames and fictitious forces, as well as to familiarize students with the PoE. By examining the trajectory of the ball in a moving frame of reference, students were able to identify it as a parabolic path achieved through axis rotation, effectively introducing an effective gravity in the direction of . Furthermore, this activity prompted students to reflect on the significance of fictitious forces, but also on the fact that introducing an effective gravity corresponds to adding two forces, one proportional to the inertial mass the other proportional to the gravitational mass.
At the end of the activities several students noted that a primary challenge lies in identifying the forces involved once the FoR has been changed. Generally, they expressed appreciation for both experiments and simulations, highlighting the value of video analysis in understanding them.
3.3. D Non-Inertial Reference Frame: Liquids’ Surface Shape in Accelerated Reference Frame
The shape of the surface of a liquid in an accelerated frame is a typical topic addressed in introductory physics courses and is useful for understanding and visualizing a complex and non-intuitive concept and improving the understanding of fictitious forces.
Predict. To introduce the topic, we ask students to answer two multiple choice questions (PT2-Q5, see Figure 5) in which the experimental situation that will be analyzed later is described.
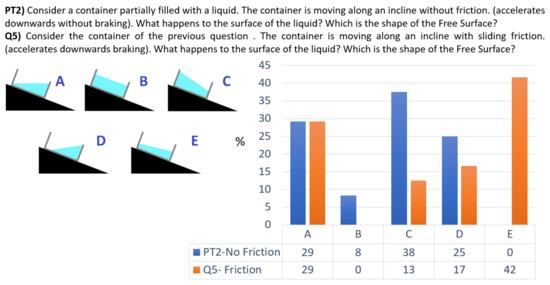
Figure 5.
The students’ answers percentages to questions PT2 and Q5.
We asked students to predict the shape assumed by the surface of a liquid in an accelerated system (in this case a liquid contained in a vessel that descends along a frictionless inclined plane), and what emerged is that ideas are confused. The most common answer, given by about one-half (13, 54%) of the students, is that the shape of the surface substantially will not change (A or D options) and only a small part (8%) of the students answered correctly. It is bizarre that students answered better in the case with friction (10 students (42%) of right answers, option E).
Observe. After collecting the students’ predictions, we asked them to make a video with everyday objects available at home, to reproduce the behavior of a tray containing liquid that descends along an inclined plane. In Figure 6C,D two frames of a video taken by a student at home showing a cart equipped with a tray, filled with colored water as it descends on an inclined plane of wood.

Figure 6.
Trolley with a transparent tray full of colored water at rest (top panels) and in descent mode along the inclined plane (bottom panel). In panels (A,B) frames from a video acquire in university labs, in panels (C,D) frames from a video acquired by a student at home. The student who recorded the video at home, proceeded to share his computer screen during the lesson and analyzed the motion and inclination of the surface of the water. We found that the frictional forces were negligible. In this situation the liquid surface will arrange itself to be parallel to the slope, far from being horizontal as it would be at rest. (E,F) Algodoo simulations to analyze the behavior of the surface shape of liquids, created using Algodoo. The top panel shows the car at rest (E) and then accelerates along the slope (F).
To perform more precise measurements, a demonstration video made by one of the instructors with commonly used objects available at home was also analyzed During the class students qualitatively analyzed this video focusing on the dependence on the inclination of the angle formed by the surface of the water. Thanks to the analysis tools offered by Tracker, the students measured the inclination of the liquid surface, the acceleration of the mass-trolley system and the inclination of the plane.
Since making a uniformly accelerated motion on the plane was not simple, the shape of the surface of the fluid in a non-inertial system was studied by means of some simulations performed using Algodoo. In Figure 6E,F, we show two simulations, one that exactly reproduces the situation of the pre-test and the experiment, with the tank descending without friction along an inclined plane, and the other that reproduces the motion in the horizontal plane with constant speed or with constant acceleration. In both simulations there was a pool of water pulled by a car and it was possible to control the motion of the car by accelerating, braking, and even reversing the direction of motion. The students were able to explore the simulations autonomously by collecting the observations and comparing them with the results of the experiment. Many students were highly surprised by the results observed during the experiment.
This experiment proved to be valuable in demonstrating to the students the superiority of reasoning based on the concept of effective gravity over reasoning in terms of fictitious forces. It effectively highlighted the effectiveness and advantages of employing the PoE in problem-solving and understanding physical phenomena. Nevertheless, after the TLS most students were still unable to accurately predict the changes in the shape of the free surface of a liquid when it fills a container that is being accelerated along an incline. They struggled to conceptualize the situation in terms of effective gravity.
3.4. Non-Inertial Reference Frame in 1D: Pendulum Oscillations
Predict. The motion of a pendulum in a non-inertial system is an extremely interesting and non-intuitive phenomenon, useful for stimulating students to think about the effective acceleration that acts in a non-inertial reference frame. We asked students to predict the center and period of small amplitude oscillations for a simple pendulum put in non-inertial system (here a car descending a frictionless inclined plane, Q6 and Q7). In this way, we wanted to test the students’ understanding of the fictitious force, which in this case modifies both the center of oscillation of the periodic motion and the period, changing the effective acceleration that acts on the bob.
Students’ ideas are confused. Although two-thirds (16, 67%) of the students understood that the presence of an acceleration of the car produces a change in the center of oscillation of the pendulum in the right direction, one-half of them (12, 50%) did not believe that the actual acceleration determines the period of oscillation and just 10 (40%) predicted that the period increases.
Observe. After the pre-test, we asked students to work with Algodoo simulations reproducing the system just described. Such simulations clearly show that the equilibrium point, which corresponds to the center of the oscillating periodic motion, moves away from the vertical and that the oscillation period increases.
The system simulated with Algodoo is shown in Figure 7, where the two oscillation centers are highlighted (for the constrained cart and for the one in descent motion). In Figure 7C, we observe the components that produce effective strength,
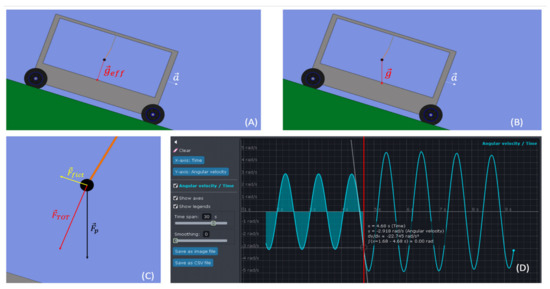
Figure 7.
(A,B) The Algodoo simulation that reconstructs the physical system present in the questions Q6 and Q7, with the force diagram (C). To investigate the dependence of the period on the acceleration of the cart, the students, working with Algodoo, can observe the graph (D) that represents the angular velocity with respect to time, for a pendulum placed in a cart, previously at rest, that begins to descend along an inclined plane. The red vertical line corresponds to the moment when the trolley began to move and helps us to visualize the different periods of oscillation: at rest and in motion downhill.
In Figure 7D, the students were able to observe that the oscillation period changes suddenly as soon as the cart begins the downward motion being the period function of effective acceleration
This experiment was useful to point out to the students how reasoning based on the introduction of effective gravity is more effective than reasoning in terms of fictitious forces. After the sequence, most students were able to identify the center of oscillation for a pendulum suspended from the ceiling of a car descending along an inclined plane. However, only a few of them understood that the period of the pendulum increases under such circumstances. Students emphasized the benefits of analyzing this phenomenon using Algodoo simulations, recognizing how it can assist and improve comprehension in similar scenarios.
3.5. Free-Falling Reference Frame: The Equivalence Principle and Einstein’s Elevator
Predict. Some past research has focused on some aspects related to students’ understanding of the PoE and FoR in free fall.
The first question concerns the free-falling bottle (Q8), cf. Figure 8: we can observe that only a small part (5 students, 20%) of the students is sure that during the free fall, the water will no longer come out the side holes of the bottle; most students think that the water will come out from the upper hole of the bottle.
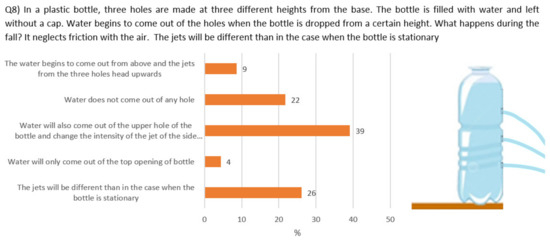
Figure 8.
Question about the elevator in free fall.
In the second question (Q9), we present an object moving along the horizontal direction in an elevator, initially at rest and suddenly starting to fall freely due to the gravitational field. We asked students to predict the motion of the object when the elevator begins to fall. Again, the ideas about what happens are really confused and most of the students replied that the cube will also move upwards respect to the elevator (13 students, 54%), probably referring to their personal experience in which, when an elevator starts to descend, we feel lighter.
As a motivating problem to engage students in inquiry activity, the motion of a pendulum in the free-falling elevator is studied. We proposed an open-ended question, concerning the motion of a physical pendulum in the free-falling elevator (PT3). The ideas of what happens in this case are many: some students think that the pendulum will remain still relative to the observer in the elevator, others that it will begin to move upward, others think that it will continue to swing but with greater amplitude.
Observe. The first experiment is a simple qualitative activity of kitchen laboratory: before the lesson we asked students to carry out the experiment of the free-falling bottle. Therefore, a student shared his computer screen, and analyzed the video, only qualitatively, in slow motion. The observation of the video makes it easy to answer to the pre-test question, in fact Figure 9 clearly shows that when the bottle begins to fall, suddenly no more water comes out. In addition, the water that has just come out of the bottle, moves horizontally with respect to the free-falling reference frame.

Figure 9.
Students’ homemade experiment reproducing the test question situation related to the free-falling bottle.
For the next question, related to an object moving along the horizontal direction in an elevator falling freely, the students worked with a virtual simulation, created using Algodoo, with which they represented exactly the physical system. By capturing a video of the simulation, they could then analyze it quantitatively using Tracker, as for a real system. In this way, they were able to visualize the motion from the two reference frames, the one integral with the laboratory and the free-falling one. Working in groups with the modelling software, students analyzed this complex problem in few minutes discussing all the different cases just by observing the phenomenon qualitatively. The students worked with an Algodoo simulation that exactly represents the situation of the pendulum in the elevator. The simulation was useful for them, to explore a vast scenario of events by changing the initial conditions, that is, changing the moment when the rope supporting the elevator breaks. For example, using the simulations, it becomes clear that, in the case in which the pendulum was at the inversion of motion point at the time of release, it would be absolutely at rest with respect to the elevator.
Thus, the spring-mass system and the oscillating pendulum in free fall were proposed to the students through some videos realized by one of the teachers of the course and then analyzed by the students with Tracker as reported in [76].
At first, the students analyzed the elevator at rest, when the two forces acting on the steel sphere, the gravitational and the elastic, are balanced. After the release, the elevator starts falling freely while the deformation of the spring disappears due to weightlessness condition in the falling elevator. So, the spring pushes the ball upwards with respect to the elevator and, after the very short time in which the spring relaxes, the ball moves by uniform motion. Students in this way understand that a body that falls freely in the gravitational field has no weight, even if the force of gravity acts on the body (video available https://youtu.be/c9jtOKSis28, accessed on 10 July 2023).
Thanks to the use of Tracker, as reported in [76], the students were able to build the graphs related to the motion of the elevator and the ball in the two different reference frames: the ball and the elevator move by accelerated motion in the laboratory system while the ball has a uniform motion in the reference frame integral with the elevator.
With the aim of showing the strange effects of weightlessness, we propose a demonstration based on other videos taken at home by the teacher and showing the pendulum in free fall. The behavior of this system can be grasped by applying the formula that describes the period of the simple pendulum as a function of the effective gravitational field, using the formula discussed earlier in the limit of angle of inclination 90°. In this case the weight disappears, and the period becomes infinite.
The subsequent analysis of the videos, which show the pendulum in circular motion, was carried out independently by the students during the lesson. Students noticed that at first the elevator model is stationary, and the pendulum swings. When the elevator begins to fall freely, the pendulum experiences a state of weightlessness, so in the FoR of the falling elevator the pendulum rod performs a uniform circular motion (in it is possible to neglect the friction between the rod and the pivot).
For the quantitative investigation of the free-falling pendulum, the students analyzed the video with Tracker and obtained the graph of the motion of the rod (angle as a function of time) in the FoR of the lift as reported in [76] (videos available at https://youtu.be/F_Ta53LuuGw and https://youtu.be/oh-HRTN83tc, accessed on 10 July 2023).
The exploration of various phenomena within a FoR in free fall provided the basis for reflecting on the PoE. The discussion regarding the two different perspectives, based either on fictitious forces or the PoE, is summarized in the two alternatives presented in Question 10. The approach based on fictitious forces appears much more complex when analyzing problems such as the pendulum (PT3) or the falling bottle (Q8).
In this context, the effectiveness of the educational intervention appears to be more significant, although it cannot be ruled out that the influence of memory of the recently conducted experiment and cognitive displacement may play a significant role in certain issues, such as the falling bottle. More in detail, after the sequence, almost all students successfully recognized that during free fall, the water inside a bottle experiences weightlessness and does not exert pressure through a hole in the side. They also correctly solved the question regarding an object moving horizontally inside an elevator in free fall. However, the PoE is not frequently mentioned spontaneously when discussing systems in free fall, where fictitious forces are commonly employed.
4. Results
4.1. Student Understanding of Key Concepts
As already mentioned, the sequence was tested with a group of 24 university students of mathematics and physics who attended a course oriented to the training of future physics teachers. During their previous studies they attended at least two courses of mechanics, a first introductory course on Newtonian mechanics and a second one on analytical mechanics, and they already passed the exams. The curricula of these courses include reference frames and relative motions.
Our sources of data on students’ progression and ideas include a questionnaire provided before the activities (pre-test), a delayed post-test given about three months after the end of the sequence, discussions recorded during and after the experiments, responses to some teaching learning interviews few days after the end of the course and some questions for course evaluation provided after the activities.
In the following we briefly summarize both quantitative and qualitative results.
4.1.1. Quantitative Results
The questionnaire, reported in the Appendix A, was intended to focus on some fundamental concepts underlying our teaching learning sequence (see Table 1) and had the function of stimulating students towards the investigation of each phenomenon by encouraging them to make predictions. The overall analysis of the difficulty of the test confirms the problematic nature of the topics addressed and, in particular, the difficulty that students have when predicting the behavior of simple mechanical systems in different reference frames in relative motion.
We previously mentioned those results from the initial questionnaire that were essential for the sequence design. In the following, we summarize the most relevant conclusions we drew from the pre-test to present a global picture of students’ ideas before the activity sequence. From the first questionnaire (24 responses):
- (i)
- Students showed big difficulties distinguishing between the trajectories of a projectile with respect to two inertial FoRs. Only six students (24%) identified the correct trajectory in the moving FoR while one-half of students recognized the path in the FoR of the Lab.
- (ii)
- Only a small fraction of students identified the real path of the drone of Q3 as seen by an observer sitting still on the bank of the river) at a constant speed with respect to a moving FoR (9 students, 36%) while just one-half recognize that there are no fictitious forces acting on the drone in this FoR.
- (iii)
- Most students (22, i.e., 92%) did not predict properly what happens to the shape of the Free Surface of a liquid which fills a container in accelerated motion along a slope.
- (iv)
- One-third of students did not identify what will be the center of oscillations of a pendulum hanging from the ceiling of a car descending along an incline and just 10 (42%) understood that the period of oscillations increases.
- (v)
- Only 5 (21%) students were convinced that during the free fall, the water in a bottle is in state of weightlessness and does not push through a hole in the side. Most students (13, i.e., 54%) predicted that an object moving horizontally in an elevator is deflected upward when the elevator starts to fall freely.
- (vi)
- 70% of students knew that a body in the ISS (International Space Station) in orbit around the Earth does not fall. Among them, a significant fraction (7, i.e., 28% of the total) believed that this happens because in the space station the gravitational field is negligible because of the great distance from the center of the Earth. Among the students who gave a correct answer one-half resorted to the presence of a fictitious force and one-half to the weightless due to the free-falling motion of the satellite.
The analysis of the answers provided by the students during the final exam showed us how the sequence of activities proved to be effective not only in understanding some concepts but also in developing a different approach to analyze physical phenomena. Many students have employed, in explaining the phenomena, Algodoo simulations produced and analyzed by themselves in various cases. All students were able to adequately address the proposed problems and demonstrated that they had metabolized the main concepts.
We analyze the data derived from a delayed post test administered to a group of 14 students. Compared to the pretest group, this sample is considered homogeneous, as indicated by the students’ average scores on the pretest aligning with those of the entire sample. However, given the limited size of the sample, the results do not provide statistically significant evidence to demonstrate an improvement in understanding resulting from the effectiveness of the teaching sequence. Nonetheless, the findings reveal varying levels of effectiveness across different topics within the sequence. Although the post test questions were identical to those in the pretest, it appears that the recollection of experimental results influences the responses to specific questions in the post test, particularly those related to the captivating demonstration involving a falling bottle (Q8), while the conditioning effect is less pronounced for other questions (e.g., Q5, Q7).
In Figure 10 we compare pre- and delayed post-test results for each item (see Table 1). Overall, in the post-test the percentage of incorrect answers was, for our students, nearly 25%. This result alone is an indication that that the sequence created a fruitful environment for the students’ learning, enabling them to address the most of their initial difficulties. More in detail:
- (i)
- Answers to the post-test (Q1–Q4) confirmed an improvement of students’ understanding of how trajectories in an inertial frame can be converted to trajectories in another by a simple transformation (correct answers, average of Q1–Q4, from 35% to 80%).
- (ii)
- Additionally, after the sequence most students did not predict properly what happens to the shape of the Free Surface of a liquid which fills a container in accelerated motion along an incline. However, if we consider the difficulty increased by the presence of friction, we can conclude that assuming as correct both B and E just 40% before while after 64%.
- (iii)
- Nearly 80% of the students, after the sequence, recognized what will be the center of oscillations of a pendulum hanging from the ceiling of a car descending along an inclined plane while, also after the sequence just 50% understood that the period increases.
- (iv)
- After the sequence a large percentage of students (90%) were able to recognize that during the free fall, the water in a bottle is in state of weightlessness and does not push through a hole in the side. Most students (80%) predicted correctly that an object moving horizontally in an elevator is not deflected by the gravitational force when the elevator starts to free fall.
- (v)
- All the students recognize that in the ISS in orbit around the Earth a body does not fall. Among them, nobody, after the sequence, believed that this happens because in the space station the gravitational field is negligible given the great distance from the center of the Earth. Most students (72%) resorted to the free-falling motion of the satellite.
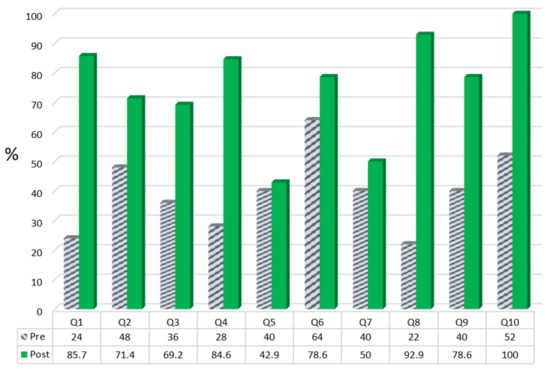
Figure 10.
Comparison of the result of the pre- and delayed post-test for each of the items.
4.1.2. Qualitative Results: Interviews
We conducted teaching–learning interviews with 11 of the students on different problems involving the principle of equivalence and the principle of relativity. We found that, although most students were able to address the proposed problems by providing correct solutions, recourse to the principles of relativity and equivalence is very limited. The problems proposed in the interviews mainly follow those of the pre-test. In the interviews the problems were addressed from a critical point of view trying to bring out both the difficulties encountered by each student and those that the student attributes to the students in general.
The principle of relativity and Galileo Transformation. As far as the principle of relativity is concerned, it is usually replaced by the typically adequate use of the principle of inertia. Students rarely approach problems by resorting to the Galilei transformations; only student S tends not to worry about the various forces (real or fictitious) that act on the object in question and to reduce the solution of the problem to a mere mathematical question by strictly applying Galileo’s transformations because they are reliable. Student F. emphasizes “the substantial equivalence between the principle of inertia and the “Galilean principle of relativity”. Many of the students, e.g., student FP, highlight that the main difficulty is describing the same situation in different FoRs. According to student G, the difficulty lies both in “visualizing the trajectory in mind by placing oneself in different references”, and in identifying the implicit initial conditions (position but above all velocity as a vector grasping both intensity and direction) of the problem in different reference frames. For example, in the case of the drone of Q2 and Q3, if we observe the scene from a boat moving at a constant speed along the river, for student G we will observe ‘a parabolic trajectory’. A few moments later, however, reasoning on the independence of the two uniform rectilinear motions and writing the equations, student G corrected himself by stating that the trajectory observed by the boat is straight. This shows us how difficult is to ‘imagine the trajectory’, but also how much the application of mathematics can help students in understanding. In any case, the students highlighted how the possibility of analyzing simple videos, and above all the possibility of changing FoR thanks to Tracker can help and facilitate understanding in these situations.
According to student S, the origin of students’ difficulties could arise from the difficulty in distinguishing the physical situation from a more “everyday” situation, i.e., students tend to treat reference frames as concrete objects and refer to real situations: “as if a ship and its reference frame were affected by the friction of water… In a real situation if you drop a ball “out” of the window of a running train, external forces such as air friction will act on it”. Some interviewees suggested, re-proposing Alice’s questions (Q1–Q2) on the train in two different situations: one where Alice is above the train, and one where Alice is inside a wagon, a case in which even instinctively one would probably tend not to consider friction with the air. However, it should be noted that in the various problematic situations of the pre-test it was clearly stated that the friction with the air should have been neglected; this shows how difficult it is for students to abstract themselves and ‘imagine’ an ideal situation in which these frictions (ubiquitous in real situations) are not present. It is clear how much more instinctive it is for students to trust their daily experience, as much as simple and clear laws, correctly known in a theoretical way, but not always applied correctly in the problem-solving phase. Additionally, the difficulty in this kind of questions could be related to the problem of identifying the reference frame with a concrete body or container (see Section 2.1.2.2).
Indeed, student V in several instances of his/her discourse displays such difficulty, although within the limit of the questions posed, he seems to be able to find workarounds and produce adequate solutions. Student S explicitly underlines how this kind of conception could be an obstacle to learning: “For example, considering a reference frame integral with a car, the body of the machine is the limit of the reference frame; outside this limit there is another reference frame”.
With some students we tried to reflect on the fact that they often do not consider the PR favoring explanations based on the application of the principle of inertia. Students usually identify the cause in the “way this topic is taught and reported by school textbooks” but also in the placement within the curriculum, particularly in high school. In fact, student SI says “in the Italian high school the principle of relativity is neglected and replaced by the principle of inertia, while the Galilean transformations and the rigorous approach are postponed to the 5th year if and when Einsteinian relativity is addressed”.
Non-inertial reference frames and apparent forces. With regard to the “non-inertial” FoRs FP underlines as the main difficulty to identify the forces at play once the FoR has changed and focus on the particularly counterintuitive case of the Coriolis Force. student FP says: “Fictitious forces create a problem because I see the effects of these forces, but I don’t see something acting”. However, through the typical example of a passenger in a braking bus student FP argues that “the fictitious force belongs to our experience, to our innate ideas, to our spontaneous physics”. So, student FP insists on the use of the term “Fictitious forces” which he tends, by his own admission, to always (or almost) treat as real forces, while student FS goes so far as to call these forces “a theoretical trick” by insisting on the relationship between fictitious forces and the presence of constraints.
Free fall, elevator, and the equivalence principle. The PoE is not so often mentioned spontaneously in dealing with the discussion of systems in free-fall, where fictitious forces are widely used. Student V seems to interpret the phenomenon without the need to resort to fictitious forces: “The system [falling elevator] is as if it were frozen, there is no force acting or rather I am not sure that there is a force acting. Since all bodies fall with the same acceleration, they maintain their position”. However, student V is a fairly isolated case.
Student FP states about the falling elevator that “The problem is not to understand that there are fictitious forces but to understand how these interact with the forces at play… For example, I may not understand that the fictitious force cancels out the weight force”. Despite this, he justifies the choice to consider the “fictitious” force with the “need to consider the real forces”.
Even student V, who showed a good knowledge of the PoE during the exam, when explaining what happens in the free-falling elevator immediately referred to the fictitious forces: “The elevator begins to fall with acceleration equal to g because it is a body in free fall… being an accelerated system, it is a non-inertial system thus, inside it, there will be fictitious forces and the fictitious force is exactly able to balance the weight… And the weight comes to be eliminated… this is telling us that having a body in free fall, that is, a reference frame in free-fall is equivalent to eliminate the gravity force and this pushes us towards the principle of equivalence… This works because the gravitational charge is equal to the inertial mass”.
If student V spontaneously emphasizes the difference between mass (inertial) and gravitational charge student FP admits “I have always considered inertial mass and gravitational mass as the same thing, I have always treated them as the same concept”. Even student N says “I can’t see PoE, I don’t think about it because I’m used to solve physics problems, the inertial and gravitational masses are equal and the fictitious force in a falling system equals gravity. It is obvious that mg = mi”.
Pendulum. While discussing the double problem of the pendulum (which descends along the inclined plane or falling freely), student FP states that “the origin of the students’ difficulties may arise from an inadequate knowledge of pendulum physics”. He also states that he has not grasped that the free-falling pendulum is the limit case of the pendulum on the inclined plane and considered the problem of the pendulum on the elevator simpler than that on the inclined plane. student V on the contrary, grasped this aspect “So the pendulum cannot swing, since […] its period is practically infinite. The important result is that in a free-fall reference, no physical experiment can highlight the presence of the gravitational field. Masses do not fall, pendulums do not swing, scales do not work”.
Bottle with three holes containing water. It should be considered that, because of the equality between inertial and gravitational mass, the common point between the gravity force and fictitious forces is their direct proportionality between force and mass of the object to which they are applied. This implies that as we well know, the gravity force and even fictitious forces accelerate all bodies in the same way, regardless of their mass.
Although the PoE in weak form is well known in a theoretical way, often operationally speaking it is not. In the case of the free-falling bottle, student S suggests that of the large number of incorrect answers is caused by the naïve idea that “water would have a certain INERTIA, in the sense that it takes over time to ‘understand’ that something has changed” (referring to the moment when the elevator cable is cut). For this reason, it is like it lags a bit with respect to the elevator, coming out of the hole of the cap. The misconception behind this reasoning is probably the common one whereof, even if we studied that all frictionless bodies fall equally, our experience suggests that “light bodies fall less quickly than heavy one”, as student A states. This misconception appears so well rooted that is really difficult to eradicate so student A suggests investigating further, re-propose the question of the falling bottle containing dust instead of water, expecting different results in the two cases.
Object moving horizontally on a table in the free-falling elevator. According to student C the problem of the table is not trivial and is “certainly the least intuitive… because here the free fall is combined with a motion, which takes place along a different direction (the horizontal). According to N “the mistake that many students make is to focus on the fictitious forces and forget the force of gravity, so they think that the cube rises” student FP thinks that this “forgetfulness” is linked to the feeling of lightness that we feel in the elevator “ it is a common experience to feel pushed upward in an elevator which starts moving downward” then student FP discusses how to attribute a different behavior of falling bodies in function of their mass (the heavy elevator falls with greater acceleration than the light cube) “objects fall with different speed, the small and light one rises”.
The orbiting station in free fall. While talking about free-falling systems with many students it’s natural to discuss what happens in an orbiting system (satellite, spaceship, or space station). According to student FP, to say that in this FoR there is no gravity suggests to the student “that the station is so far away that the gravity field is negligible”.
Student V points out that “often, erroneously, it is stated that the inhabitants of the ISS are in weightlessness. In reality they are in a constant condition of free fall, but from that perspective it is impossible to determine, being inside the inertial reference frame, if you are under the action of a gravitational field or if inside an accelerated FoR”.
Student MT states that “no (timid) forces act on an object in the ISS… That is, the sum of the forces is zero”. By specifically asking to choose between the two options ‘no force’ or ‘sum of forces equal to zero’ all students rely on the second option, confirming the need to consider at many forces instead of zero (which would be an application of the PoE).
The question is absolutely relevant: the path followed during the interviews consisted in the explanation of the principle of equivalence, and consequently in the analysis of a problematic situation (e.g., a body in an elevator in free fall, or in the ISS) solvable in an absolutely simple way with a rough application of the principle, for which ‘a reference frame in free fall is absolutely equivalent to an inertial reference frame without gravity’. Although this claim was well known by the students, during the resolution and explanation of various problematic situations, even the students who prefer a reasoning in terms of the Principle of Equivalence rather than one based on the introduction of fictitious forces, do not feel safe in stating that in these situations there are no forces acting, despite this would be an explanation more than satisfactory. Many students feel shy saying that “there are no forces”, and feel more confident affirming “… I mean, the weight is balanced by the fictitious force and their sum is zero”.
4.2. Evaluation of the Learning Environment: Student Ratings
With the aim of comparing the various types of activities, we first compare the evaluation of students on the various types of activities. We asked students to rate experiences in terms of three dimensions on a Likert scale from 1 to 5:
- -
- Effectiveness in terms of understanding a phenomenon thanks to the proposed activities (possible responses are presented in a range from 1 “not effective” to 5 “very effective”).
- -
- Enjoyment during each workshop activity (possible responses are presented in a sequence 1 boring, …, 5 very nice).
- -
- Engagement and personal interest during the activities (possible responses are presented in a sequence 1 unpleasant, …, 5 very engaging).
The results, in the sense of average scores, are shown in Table 2.

Table 2.
Evaluation of student experience in terms of three dimensions.
All activities were evaluated as very effective. The experiments performed by the teacher were considered more fun but less engaging, on the contrary the “kitchen” experiments designed and performed at home, although less fun, were evaluated more engaging. Algodoo simulations were preferred to experiment on each of the different dimensions, although in the comments reported by the students many of them point out that simulations can in no way replace real experiments.
We also asked the students interviewed for a comment on the didactic approach (POE), experiments and simulations. According to FP: “the experiments work and surprise the student” since “what you see is surprisingly different from what you would have expected”, and the same effect is attributed to the simulations used. N says, “if I see a phenomenon, it remains imprinted in me and I’ll never forget it” and reiterates the importance of “touching objects”.
Regarding the POE approach, N argues that the function of the test is to “make people think, arise interest and curiosity” while FP “The approach is really capable of activating a cognitive conflict” which is the right way to fight against misconceptions.
Despite these globally positive judgments, the students identified some weaknesses of the sequence: N says that sometimes the activity becomes dispersive, and the thread of the speech is lost while another student claims: “The activities are too guided and proposed too quickly, leaving not enough time to metabolize, so this limits the students in designing the freedom to design different problematic situations”. However, FP recognizes that “for this type of phenomena it is difficult to design and carry out real experiments autonomously by the student”.
5. Conclusions
The aim of this study was to describe and propose an educational reconstruction of classical relativity for upper secondary and undergraduate physics students. Following the framework of MER, we identified key features of classical relativity and studied learners’ difficulties based on an analysis of physics textbooks and relevant literature. Indeed, it can be assumed that the knowledge assessed in this study among the students primarily originates from their secondary school background rather than their university-level education. These results enabled us to turn the science content structure of classical relativity into a content structure for instruction. Thus, the sequence of activities was designed and tested with university students. Throughout the sequence, our goal was to assist students in supporting their knowledge of the Principle of Relativity and the Principle of Equivalence in classical mechanics. The results of the analysis of students’ preliminary reasoning suggests that this approach allowed them to gain a deeper and more precise understanding of the subject.
Activities based on video analysis were used to highlight experimental situations, while interactive simulations were essential to explore multiple variations of a given physical situation and provided the ideal environment for an investigation activity.
The main limitations of the study are that the sequence was tested with a relatively small sample of students with an uneven background, i.e., students of mathematics and physics. In the future we are planning a greater trial with a larger sample of university students, to assess whether the sequence is suitable for introductory physics courses.
Author Contributions
Conceptualization, A.M., P.O. and M.M.; methodology, P.O. and M.M.; investigation, A.M., M.D.M., T.R., P.O. and M.M.; resources, A.M., P.O. and M.M.; data curation, M.D.M., T.R. and P.O.; writing—original draft, A.M., M.D.M., T.R., P.O. and M.M.; writing—review and editing, A.M., M.D.M., P.O. and M.M.; visualization, A.M. and T.R.; supervision, P.O. and M.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Approval by the local research ethics committee was not required since no medical treatment was carried out and participants were anonymized. All participating students were over 18 years of age.
Informed Consent Statement
Informed consent forms were signed before the beginning of the activities by the student for study participation and research purposes, in order to fulfil the requirements of Italian law.
Data Availability Statement
Data used in this study are available under reasonable request from the authors.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A. The Pre-Post Test

Table A1.
The Pre Post Test.
Table A1.
The Pre Post Test.
| Inertial Reference of Frame | |
|---|---|
| Alice is standing in a train moving at velocity v from left to right relative to Bob, who is standing on a platform. As Alice passes Bob, she drops a bowling ball out of the train’s window: (Q1) Ignoring air resistance, which path of the ball would Bob observe, standing on the platform? (A) Path (A) (B) Path (B) (C) Path (C) | 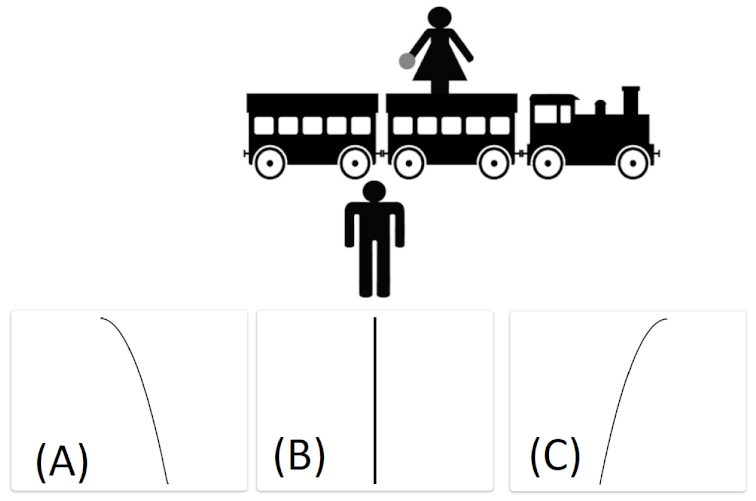 |
| (Q2) Ignoring air resistance, which path of the ball would Alice observe, standing in the train? (A) Path (A) (B) Path (B) (C) Path (C) | |
| (Q3) Bob is sitting on a bridge on the river. Alice is standing on a boat moving along the river at velocity v from left to right relative to Bob. As Alice passes the bridge, a drone takes off from point Q to reach point P flying at a constant speed. Which path of the drone would Alice observe, standing on the boat? (A) Path (A) (B) Path (B) (C) Path (C) (D) Path (D) (E) Path (E) | 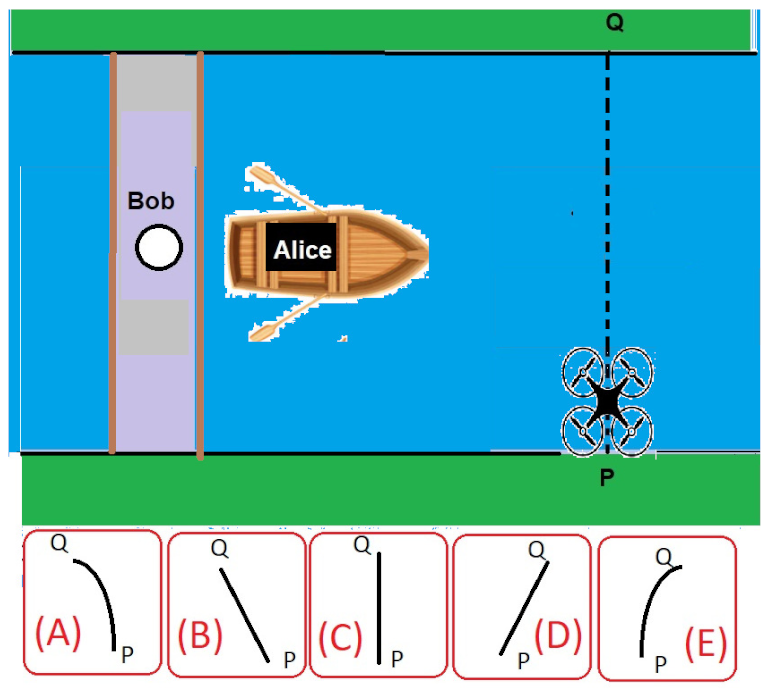 |
| (Q4) Thinking about the previous question: in Alice’s reference frame what will be the “fictitious” force acting on the drone (A) Constant towards the right (B) Not constant towards the left (C) There is no apparent force (D) Constant towards the left (E) Not constant towards the right | |
| Non-Inertial Reference of Frame | |
| (PT1) Open: Alice is standing in a train from left to right relative to Bob, who is standing on a platform. As Alice passes Bob, a ball is thrown vertically upwards from the train while the train is accelerating: Ignoring air resistance, what path of the ball would Bob observe, standing on the platform? What path of the ball would Alice observe, standing in the train? | 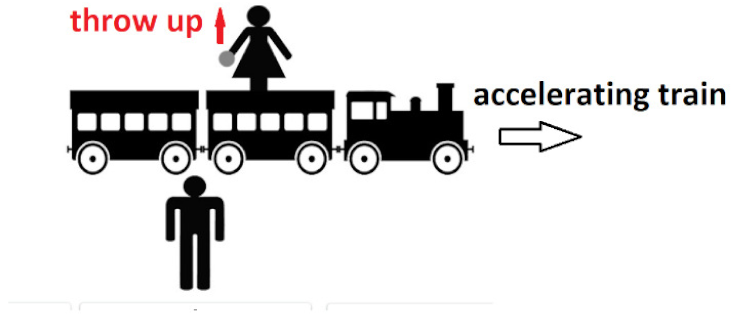 |
| (PT2) Consider a container partially filled with a liquid. The container is moving along an incline without friction. (accelerates downwards without braking). What happens to the surface of the liquid? Which is the shape of the Free Surface? A B C D E | 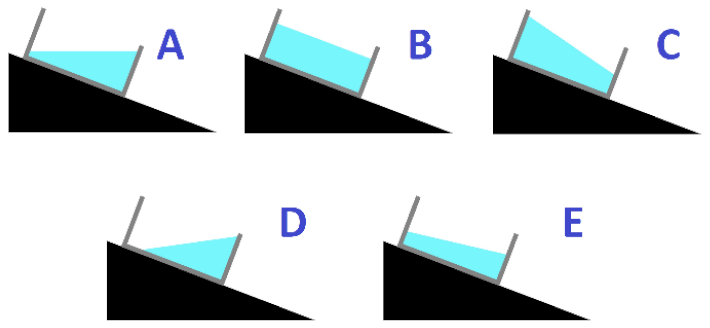 |
| (Q5) Consider the container of the previous question. The container is moving along an incline with sliding friction. (accelerates downwards braking). What happens to the surface of the liquid? Which is the shape of the Free Surface? A B C D E | |
| (Q6) A pendulum hanging from the ceiling of a car swings with small amplitudes, when the car starts to descend from an inclined plane without friction (accelerates downwards without braking). What will the pendulum center of oscillations be? A B C (Q7) Consider the pendulum of the previous question How will the period of the pendulum be while the car descends from the inclined plane compared to the period when the car is at rest?
| 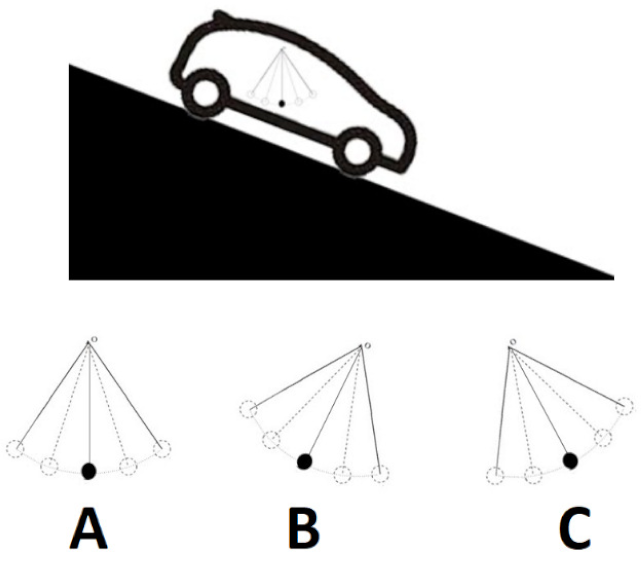 |
| Free-Falling Reference Frame | |
(Q8) In a plastic bottle, three holes are made at three different heights from the base. The bottle is filled with water and left without a cap. Water begins to come out of the holes when the bottle is dropped from a certain height. What happens during the fall? It neglects friction with the air.
|  |
| (Q9) Consider an elevator with a table anchored to it, as represented in the figure. A small cube is placed on the table, with an initial speed that allows it to reach the edge of the table, despite the friction with it. The elevator has a hole which would allow the cube to exit the elevator if it moved horizontally with respect to the surface of the table. After the cube is thrown, when it is in the center of the table, the cable that supports the elevator is cut. What happens? A B C | 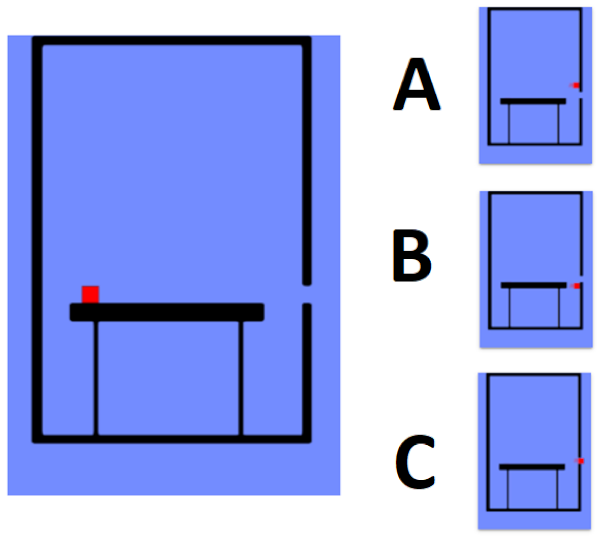 |
| (PT3) A rigid pendulum hanging from the ceiling of an elevator is swinging, when suddenly the cable supporting the elevator is removed. At the time of cable breakage the pendulum was at the point of equilibrium. Describe the motion of the pendulum observed by the reference frame S’ integral with the elevator, neglecting air friction. What happens if at the time of cable breakage the pendulum was at the point of maximum amplitude? | |
(Q10) Astronaut Samantha is on the ISS (International Space Station) in orbit around the Earth. Samantha has a small ball in her fist. Suddenly she opens her hand leaving the grip.
| |
References
- Kersting, M.; Henriksen, E.K.; Bøe, M.V.; Angell, C. General relativity in upper secondary school: Design and evaluation of an online learning environment using the model of educational reconstruction. Phys. Rev. Phys. Educ. Res. 2018, 14, 010130. [Google Scholar] [CrossRef]
- Levrini, O. Reconstructing the basic concepts of general relativity from an educational and cultural point of view. In Science Education and Culture; Springer: Dordrecht, The Netherlands, 2001; pp. 311–326. [Google Scholar]
- Bandyopadhyay, A.; Kumar, A. Probing students’ understanding of some conceptual themes in general relativity. Phys. Rev. Spec. Top. Phys. Educ. Res. 2010, 6, 020104. [Google Scholar] [CrossRef]
- De Ambrosis, A.; Malgieri, M.; Mascheretti, P.; Onorato, P. Investigating the role of sliding friction in rolling motion: A teaching sequence based on experiments and simulations. Eur. J. Phys. 2015, 36, 035020. [Google Scholar] [CrossRef]
- Onorato, P.; Malgieri, M.; De Ambrosis, A. Three years evaluation of a teaching learning sequence on rolling motion based on a blended learning environment. J. Phys. Conf. Ser. 2019, 1286, 012053. [Google Scholar] [CrossRef]
- Duit, R.; Gropengießer, H.; Kattmann, U.; Komorek, M.; Parchmann, I. The model of educational reconstruction–A framework for improving teaching and learning science. In Science Education Research and Practice in Europe; Brill: Leiden, The Netherlands, 2012; pp. 13–37. [Google Scholar]
- Klafki, W. Didactic analysis as the core of preparation of instruction (Didaktische Analyse als Kern der Unterrichtsvorbereitung). J. Curric. Stud. 1995, 27, 13–30. [Google Scholar] [CrossRef]
- Duit, R.; Komorek, M.; Wilbers, J. Studies on educational reconstruction of chaos theory. Res. Sci. Educ. 1997, 27, 339–357. [Google Scholar] [CrossRef]
- Niebert, K.; Gropengiesser, H. The model of educational reconstruction: A framework for the design of theory-based content specific interventions. The example of climate change. In Educational Design Research–Part B: Illustrative Cases; SLO: Enschede, The Netherlands, 2013; pp. 511–531. [Google Scholar]
- Kersting, M. General Relativity in Secondary School: Research-Based Development of Learning Resources and Analyses of Students’ Conceptual Understanding Using the Model of Educational Reconstruction. Ph.D. Thesis, University of Oslo, Oslo, Norway, 2019. [Google Scholar]
- Kamphorst, F.; Vollebregt, M.J.; Savelsbergh, E.R.; van Joolingen, W.R. An Educational Reconstruction of Special Relativity Theory for Secondary Education. Sci. Educ. 2023, 32, 57–100. [Google Scholar] [CrossRef]
- Metaxas, I.; Michailidi, E.; Stavrou, D.; Pavlidis, I.V. Educational reconstruction of size-depended-properties in nanotechnology for teaching in tertiary education. Chem. Teach. Int. 2021, 3, 413–422. [Google Scholar] [CrossRef]
- Italian Ministry of Education. Indicazioni Nazionali per i Licei Scientifici; Italian Ministry of Education: Rome, Italy, 2012.
- Scherr, R.E.; Shaffer, P.S.; Vokos, S. Student understanding of time in special relativity: Simultaneity and reference frames. Am. J. Phys. 2001, 69 (Suppl. S1), S24–S35. [Google Scholar] [CrossRef]
- Mortimer, E.F. Conceptual change or conceptual profile change? Sci. Educ. 1995, 4, 267–285. [Google Scholar] [CrossRef]
- Ayala Filho, Á.L. A construção de um perfil para o conceito de referencial em Física e os obstáculos epistemológicos à aprendizagem da teoria da relatividade restrita. Investig. Ensino Ciências 2010, 15, 155–179. [Google Scholar]
- Alstein, P.; Krijtenburg-Lewerissa, K.; van Joolingen, W.R. Teaching and learning special relativity theory in secondary and lower undergraduate education: A literature review. Phys. Rev. Phys. Educ. Res. 2021, 17, 023101. [Google Scholar] [CrossRef]
- Arlego, M.; Otero, M.R. Teaching basic special relativity in high school: The role of classical kinematics. In Contemporary Science Education and Challenges in the Present Society: Perspectives in Physics Teaching and Learning; FEUSP: São Paulo, Brazil, 2017. [Google Scholar]
- Scherr, R.E. An Investigation of Student Understanding of Basic Concepts in Special Relativity. Ph.D. Thesis, University of Washington, Seattle, WA, USA, 2001. [Google Scholar]
- Desloge, E.A. Classical Mechanics; John Wiley Sons: Hoboken, NJ, USA, 1982; Volume 1. [Google Scholar]
- Sommerfeld, A. Mechanics: Lectures on Theoretical Physics; Elsevier: Amsterdam, The Netherlands, 2016; Volume 1. [Google Scholar]
- Halliday, D.; Resnick, R.; Walker, J. Fundamentals of Physics; John Wiley Sons: Hoboken, NJ, USA, 2013. [Google Scholar]
- Galilei, G. Dialogo Sopra i due Massimi Sistemi del Mondo; Rizzoli: Milano, Italy, 2013. [Google Scholar]
- Browne, K.M. Galilei proposed the principle of relativity, but not the “Galilean transformation”. Am. J. Phys. 2020, 88, 207–213. [Google Scholar] [CrossRef]
- Norton, J.D. Einstein’s Special Theory of Relativity and the Problems in the Electrodynamics of Moving Bodies that Led him to it. In The Cambrridge Companion to Einstein; Cambridge University Press: Cambridge, UK, 2014; pp. 72–102. [Google Scholar]
- Pietrocola, M.; Zylbersztajn, A. The use of the Principle of Relativity in the interpretation of phenomena by undergraduate physics students. Int. J. Sci. Educ. 1999, 21, 261–276. [Google Scholar] [CrossRef]
- Mencuccini, C.; Silvestrini, V. Fisica: Meccanica e Termodinamica: Con Esempi ed Esercizi; Casa Editrice Ambrosiana: Milano, Italy, 2016. [Google Scholar]
- Amaldi, U. La Fisica di Amaldi; Zanichelli: Bologna, Italy, 2011. [Google Scholar]
- Múnera, H.A. The principle of equivalence: Demonstrations of local effective vertical and horizontal. Phys. Teach. 2010, 48, 131–133. [Google Scholar] [CrossRef]
- Fägerlind, C.O.; Pendrill, A.M. Liquid in accelerated motion. Phys. Educ. 2015, 50, 648. [Google Scholar] [CrossRef]
- Norton, J.D. What was Einstein’s principle of equivalence? Stud. Hist. Philos. Sci. Part A 1985, 16, 203–246. [Google Scholar] [CrossRef]
- Norton, J.D. General covariance and the foundations of general relativity: Eight decades of dispute. Rep. Prog. Phys. 1993, 56, 791. [Google Scholar] [CrossRef]
- Norton, J.D. Einstein’s Conflicting Heuristics: The Discovery of General Relativity. In Thinking about Space and Time; Birkhäuser: Cham, Switzerland, 2020; pp. 17–48. [Google Scholar]
- Di Casola, E.; Liberati, S.; Sonego, S. Nonequivalence of equivalence principles. Am. J. Phys. 2015, 83, 39–46. [Google Scholar] [CrossRef]
- Thorne, K.S.; Lee, D.L.; Lightman, A.P. Foundations for a theory of gravitation theories. Phys. Rev. D 1973, 7, 3563. [Google Scholar] [CrossRef]
- Krane, K. Modern Physics, 3rd ed.; Wiley: Hoboken, NJ, USA, 2012. [Google Scholar]
- Levrini, O.; Altamore, A.; Balzano, E.; Bertozzi, E.; Gagliardi, M.; Giordano, E.; Guidoni, P.; Rinaudo, G.; Tarsitani, C. Looking at the physics curriculum in terms of framing ideas. In Proceedings of the GIREP 2008 Conference, Nicosia, Cyprus, 18–22 August 2008; pp. 18–22. [Google Scholar]
- Giliberti, M.; Organtini, G. Reconsidering Physics Education for better understanding of modern physics. J. Phys.: Conf. Ser. 2021, 1929, 012046. [Google Scholar] [CrossRef]
- Villani, A.; Arruda, S.M. Special theory of relativity, conceptual change and history of science. Sci. Educ. 1998, 7, 85–100. [Google Scholar] [CrossRef]
- Doménech, A.; Casasús, E.; Doménech, M.T.; Buñol, I.B. The classical concept of mass: Theoretical difficulties and students’ definitions. Int. J. Sci. Educ. 1993, 15, 163–173. [Google Scholar] [CrossRef]
- Michelini, M.; Pugliese, E.; Santi, L. Mass from classical physics to special relativity: Learning results. In Proceedings of the World Conference on Physics Education 2012, Istanbul, Turkey, 1–6 July 2012; pp. 141–154. [Google Scholar]
- Saltiel, E.M.; Malgrange, J.L. Spontaneous ways of reasoning in elementary kinematics. Eur. J. Phys. 1980, 1, 73–80. [Google Scholar] [CrossRef]
- Maury, L.; Saltiel, E.; Viennot, L. Étude de la notion de mouvement chez l’enfant à partir des changements de référentiels. Rev. Française Pédagogie 1977, 40, 15–29. [Google Scholar] [CrossRef]
- McCloskey, M. Naïve Theories of Motion. In Mental Models; Gentner, D., Stevens, A.L., Eds.; Lawrence Erlbaum Associates: Hillsdale, NJ, USA, 1983; pp. 299–324. [Google Scholar]
- Nersessian, N.J.; Resnick, L.B. Comparing historical and intuitive explanations of motion: Does “naive physics” have a structure. In Proceedings of the Eleventh Annual Conference of the Cognitive Science Society, Ann Arbor, MI, USA, 16–19 August 1989; Erlbaum: Mahwah, NJ, USA; pp. 412–420. [Google Scholar]
- McCloskey, M.; Washburn, A.; Felch, L. Intuitive physics: The straight-down belief and its origin. J. Exp. Psychol. Learn. Mem. Cogn. 1989, 9, 636. [Google Scholar] [CrossRef]
- Aslanides, J.S.; Savage, C.M. Relativity concept inventory: Development, analysis, and results. Phys. Rev. Spec. Top. Phys. Educ. Res. 2013, 9, 010118. [Google Scholar] [CrossRef]
- Panse, S.; Ramadas, J.; Kumar, A. Alternative conceptions in Galilean relativity: Frames of reference. Int. J. Sci. Educ. 1994, 16, 63–82. [Google Scholar] [CrossRef]
- Ramadas, J.; Barve, S.; Kumar, A. Alternative conceptions in Galilean relativity: Inertial and non-inertial observers. Int. J. Sci. Educ. 1996, 18, 615–629. [Google Scholar] [CrossRef]
- de Hosson, C.; Kermen, I.; Parizot, E. Exploring students’ understanding of reference frames and time in Galilean and special relativity. Eur. J. Phys. 2010, 31, 1527. [Google Scholar] [CrossRef]
- Dimitriadi, K.; Halkia, K. Secondary students’ understanding of basic ideas of special relativity. Int. J. Sci. Educ. 2012, 34, 2565–2582. [Google Scholar] [CrossRef]
- Viennot, L. Spontaneous reasoning in elementary dynamics. Eur. J. Sci. Educ. 1979, 1, 205–221. [Google Scholar] [CrossRef]
- Bandyopadhyay, A. Students’ ideas of the meaning of the relativity principle. Eur. J. Phys. 2009, 30, 1239. [Google Scholar] [CrossRef]
- Bandyopadhyay, A.; Kumar, A. Probing students’ ideas of the principle of equivalence. Eur. J. Phys. 2010, 32, 139. [Google Scholar] [CrossRef]
- Mayer, V.V.; Varaksina, E.I. A simple demonstration of Einstein’s lift: A body thrown upwards moves rectilinearly and uniformly relative to a free-falling model of the lift. Eur. J. Phys. 2015, 36, 055020. [Google Scholar] [CrossRef]
- Kapotis, E.; Kalkanis, G. Einstein’s elevator in class: A self-construction by students for the study of the equivalence principle. Phys. Teach. 2016, 54, 404–407. [Google Scholar] [CrossRef]
- Bozzo, G. Free-Fall Demonstrations in the High School Laboratory. Phys. Teach. 2020, 58, 23–27. [Google Scholar] [CrossRef]
- Monteiro, M.; Cabeza, C.; Marti, A.C. Acceleration measurements using smartphone sensors: Dealing with the equivalence principle. Rev. Bras. Ensino Fis. 2015, 37, 1303. [Google Scholar] [CrossRef]
- Kuhn, J. Analyzing free fall with a smartphone acceleration sensor. Phys. Teach. 2012, 50, 182–183. [Google Scholar] [CrossRef]
- Kuhn, J.; Vogt, P. Smartphones as experimental tools: Different methods to determine the gravitational acceleration in classroom physics by using everyday devices. Eur. J. Phys. Educ. 2013, 4, 16–27. [Google Scholar]
- OSP, Tracker, Video Analysis and Modeling Tool. Available online: http://physlets.org/tracker/ (accessed on 10 July 2023).
- White, R.; Gunstone, R. Probing Understanding; Routledge: Abingdon, UK, 2014. [Google Scholar]
- Liew, C.W.; Treagust, D.F. A predict-observe-explain teaching sequence for learning about students’ understanding of heat and expansion of liquids. Aust. Sci. Teach. J. 1995, 41, 68–71. [Google Scholar]
- Treagust, D.F.; Mthembu, Z.; Chandrasegaran, A.L. Evaluation of the Predict-Observe-Explain instructional strategy to enhance students’ understanding of redox reactions. In Learning with Understanding in the Chemistry Classroom; Springer: Dordrecht, The Netherlands, 2014; pp. 265–286. [Google Scholar]
- Liew, C.W.; Treagust, D.F. The effectiveness of predict-observe-explain tasks in diagnosing students’ understanding of science and in identifying their levels of achievement. In Proceedings of the Paper Presented at the Annual Meeting of the American Educational Research Association, San Diego, CA, USA, 13–17 April 1998. [Google Scholar]
- Onorato, P.; Rosi, T.; Tufino, E.; Caprara, C.; Malgieri, M. Using smartphone cameras and ambient light sensors in distance learning: The attenuation law as experimental determination of gamma correction. Phys. Educ. 2021, 56, 045007. [Google Scholar] [CrossRef]
- Al Mamun, M.A.; Lawrie, G.; Wright, T. Exploration of learner-content interactions and learning approaches: The role of guided inquiry in the self-directed online environments. Comput. Educ. 2022, 178, 104398. [Google Scholar] [CrossRef]
- Jiang, F.; McComas, W.F. The effects of inquiry teaching on student science achievement and attitudes: Evidence from propensity score analysis of PISA data. Int. J. Sci. Educ. 2015, 37, 554–576. [Google Scholar] [CrossRef]
- Zacharia, Z.C. The impact of interactive computer simulations on the nature and quality of postgraduate science teachers’ explanations in physics. Int. J. Sci. Educ. 2005, 27, 1741–1767. [Google Scholar] [CrossRef]
- Alfiyanti, I.F.; Jatmiko, B. The Effectiveness of Predict Observe Explain (POE) Model with PhET to Improve Critical Thinking Skills of Senior High School Students. Stud. Learn. Teach. 2020, 1, 76–85. [Google Scholar] [CrossRef]
- Kearney, M.; Treagust, D.F.; Yeo, S.; Zadnik, M.G. Student and teacher perceptions of the use of multimedia supported predict–observe–explain tasks to probe understanding. Res. Sci. Educ. 2001, 31, 589–615. [Google Scholar] [CrossRef]
- Al Mamun, M.A.; Lawrie, G.; Wright, T. Instructional design of scaffolded online learning modules for self-directed and inquiry-based learning environments. Comput. Educ. 2020, 144, 103695. [Google Scholar] [CrossRef]
- Algodoo. Available online: http://www.algodoo.com/ (accessed on 10 July 2023).
- Zoom. Available online: https://zoom.us/ (accessed on 10 July 2023).
- Haber-Schaim, U.; Dodge, J.H.; Gardner, R.; Shore, E.A.; Walter, F. PSSC Physics, 7th ed.; Kendall/Hunt: Dubuque, Iowa, 1991. [Google Scholar]
- Marzari, A.; Rosi, T.; Onorato, P. Three experiments on the Einstein’s lift. Eur. J. Phys. 2021, 42, 045404. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).