Abstract
Computational thinking (CT) is increasingly incorporated into curricular planning across various educational levels in numerous countries. Presently, CT is being integrated into preschool and primary education. To effectively implement CT at the classroom level, the design and study of techniques and tasks are crucial. This research empirically evaluates a didactic sequence using programmable educational robots for problem-solving challenges rooted in mathematical concepts. The study consists of two sets of activities: computational localisation of elements on a regular grid, where students program robots to navigate, and problem-solving tasks involving sum calculations using distinct pre-operational strategies. The study sample is a class of 16 students at the preschool level. The results indicate an increasing complexity in the success of the designed sequence, with the ’counting all’ strategy demonstrating higher efficacy. These promising findings highlight the potential for further research, aiming to establish a strong foundation for early educational levels through the integration of CT via programmable robots and engaging problem-solving challenges.
1. Introduction
Computational thinking (CT), originally also introduced as algorithmic thinking in the 1950s, is a term that encompasses the notion of using programmatic or algorithmic thinking to produce an appropriate output to a given input [1]. In 2006, Wing [2] expanded on the definition of CT, defining it as an approach to problem-solving that involves the application of decomposition strategies, algorithm design, abstraction, and logical reasoning, drawing upon the fundamental principles of computer science. This definition, characterised by its generality, has gained widespread acceptance. However, its broad nature has also led to the demand for a more specific definition that can be employed in the context of CT Education (“CS for All” https://www.csforall.org/ (accessed on 15 June 2023)) (ISTE’s Standards for Students in Computational Thinking https://www.iste.org/explore/Solutions/Computational-thinking-for-all?articleid=152 (accessed on 15 June 2023) (Computer Science Teachers Association’s Concepts of Computational Thinking http://advocate.csteachers.org/2014/09/15/computational-thinking-and-beyond/(accessed on 15 June 2023)).
CT has emerged as a significant educational milestone, encompassing a set of skills and competencies that are accessible to all individuals. Its importance has been further accentuated by the integrative perspective known as STEM (Science, Technology, Engineering, and Mathematics), which emphasises the integration of science, technology, engineering, and mathematics in teaching and learning processes at the international level [3,4]. Within this context, computational thinking assumes a central role in various educational frameworks, particularly in preschool and primary school settings [5,6]. As an example, the Spanish preschool education curriculum has recently incorporated CT, acknowledging the need for sequential programming and instruction-based problem-solving in both analogue and digital tasks, thereby fostering the development of fundamental computational thinking skills (https://www.boe.es/eli/es/rd/2022/02/01/95/con (accessed on 15 June 2023)).
1.1. Computational Thinking and Mathematical Thinking
The connection between computational thinking (CT) and mathematical thinking (MT) has been widely studied, but less attention has been given to the kindergarten ages of 4 and 5 years old. Previous studies have explored the integration of CT and MT in mathematics education research. Wan-Rou et al. [7] conducted a literature review, finding that CT helps to develop mathematical concepts using software or programming, whereas MT improves problem-solving skills in CT, with or without programming. The reciprocal relationship between CT and MT embeds CT into mathematics learning and enhances MT performance in debugging and reflection. Lockwood [8] addressed challenges in counting problems and emphasised interventions to enhance understanding and problem type differentiation. Undergraduate students’ comprehension of outcome sets improved through Python programming, reinforcing conceptual understanding of combinatorial problem types. Zhihao et al. [9] used problem-based learning to design programming-based tasks for middle school students, co-developing CT and mathematical thinking across four mathematics domains. Tasks integrated various CT concepts and practices, promoting the application and generation of mathematical knowledge [9]. De Chenne [10] investigated challenges in counting problems and proposed interventions focusing on sets of outcomes. Tasks involving computer code enumeration fostered meaningful connections between counting processes and sets of outcomes, leveraging structure and connecting representations [10]. Ye et al. [11] reviewed the integration of CT in K-12 mathematics education, highlighting the need for clearer explanations of how CT supports mathematics learning. Geometry programming and student-centered instructional approaches were found to facilitate productive learning in CT and mathematics. CT-based mathematics learning involves a cyclical process of mathematical and computational reasoning, encompassing the construction of CT artefacts, interpretation of CT outputs, and generation of new mathematical knowledge.
These studies contribute to understanding the integration of CT and MT in mathematics education, providing recommendations for effective task design and highlighting the cyclical nature of reasoning mathematically and computationally [7,8,9,10,11].
1.2. Computational Thinking and the Role of Educational Robots
The incorporation of CT in the classroom is something that both the present and future society demand. However, this area remains largely unexplored, especially in the initial years of primary education, and this becomes more evident in preschool education. The study presented in [12] aims to assess whether the integration of unplugged activities promotes the development of CT in students in the early years of education. It explores the potential benefits of a blended approach that combines both unplugged and plugged-in activities. This study concludes that incorporating unplugged activities in instruction appears to be advantageous in terms of CT, motivation, and gender.
In [13], it is stated that computational thinking is emerging as a set of problem-solving skills that new generations of students must acquire to fully comprehend and participate in our computer-based world. Their findings demonstrate that students with computational talent can be identified during middle school, and these individuals have the capability to advance quickly in computer science education standards, surpassing regular learners by one to two years. This discovery could have significant implications for the development of computing curricula, which should consider these individual differences in computational ability and learning speed in coding to ensure appropriate progression for each student. These findings support the notion of introducing CT training to students at the earliest possible age, allowing them to engage with this increasingly important discipline.
The research in [3] establishes a connection between CT and creativity as essential skills for contemporary learners. In the past decade, there has been a growing body of research that explores the intersection of these skills within a single context. The findings indicate a geographic bias, with a dominance of research from the United States and a prominence of studies conducted in developed European countries. Additionally, there has been a focus on secondary education and STEM-related disciplines, which highlights the need to implement CT across other educational levels. The study emphasises the benefits of bridging the gap between CT and creativity, as creativity is a cognitive ability that enables innovative problem-solving and the creation of original and valuable products.
The authors of [14] conducted a systematic review of empirical studies with the objective of examining the use of robot-mediated activities to promote the development of CT in preschool-aged children. The study offers a comprehensive analysis of the robots utilised, proposed activities, and evaluation processes employed in this context. The research categorises the activities based on various features, including the context in which they take place, the modality of work, the type of activity, duration, and the role of adults, among others. Furthermore, the review scrutinises the evaluation process of CT, encompassing assessments used, conceptual assets, and research design. By providing a comprehensive overview of existing research, this work identifies gaps in the current literature and offers recommendations for future studies in this domain.
In the study conducted by Atmatzidou et al. [15], the authors conclude that students, regardless of their age and gender, achieve a similar level of development in CT skills. The research focuses on the development of CT skills in the context of educational robotics learning activities. The findings indicate that CT skills typically require time to fully develop, as evidenced by significant improvement in students’ scores towards the end of the activity. This study highlights the importance of providing sufficient time and opportunities for students to engage in CT activities, allowing for the gradual development of these skills.
Educational programmable robots have proven to be an effective educational tool for introducing CT to preschool children, as highlighted in the study by Bakala et al. [14]. These robots provide an adapted interface that makes it easier for children to engage with CT challenges. The study by Diago et al. [16] focuses on mathematical problem-solving in the early stages using educational robots. It involves three pairs of students, two from the final year of kindergarten and one from the first year of primary school. The objective is to observe and analyse the problem-solving strategies and heuristic techniques employed by these students as they program a robot to navigate a path from a starting point to an endpoint. This exploratory study not only examines differences in how students approach and manage mathematical problem-solving but also aims to introduce programming with technology and foster CT skills among kindergarten and early primary school students, thereby enhancing their problem-solving abilities. Moreover, Diago et al. [17] demonstrate that activities involving tangible programming on educational programmable robots, which provide a physical environment, not only result in significant improvements in CT skills but also improve the gains achieved through traditional instructional approaches.
The manuscript is organised as follows. The rest of this section presents the objectives of the study. In Section 2, we describe the theoretical framework of the experiment. It covers the different phases in both the acquisition (Section 2.1) and elaboration (Section 2.2) of the number sequence, and the theory needed to establish the pre-operational stage in preschool education (Section 2.3). Moreover, Section 2.4 provides insights into the learning with educational robots field. Section 3 deals with the materials used in the experiment, including the analysis and derived methodology. The proposed design for the didactic sequence is described in Section 3.1. Moving forward, Section 4 presents the results obtained from the experiment and offers a comprehensive discussion. Lastly, in Section 5, the overall conclusions of the study are presented, along with a discussion of ongoing and future work.
1.3. Objectives of the Study
Our specific work focuses on designing a didactic sequence of activities that integrate CT to promote mathematical problem-solving. To achieve this goal, we propose the use of programmable educational robots. These robots are particularly well suited for young students in the preschool stage, as they provide a user-friendly interface that simplifies engagement with the challenges presented in our study [15,18].
The tasks in our didactic sequence are focused on the number sequence, and some of them will require specific counting strategies (counting all and counting on) for their solution. We aim to investigate how the success rate varies across the different tasks, based on the students’ level of elaboration of the number sequence, as well as to identify the counting strategy that yields the highest success rate. Therefore, the main objectives of this study are threefold:
- O1.
- To develop a didactic sequence consisting of a series of activities with increasing complexity (The concept of complexity will be measured through features of the programming sequence which are detailed in Section 3.1) using educational programmable robots aimed at developing CT and mathematical problem-solving skills in early education.
- O2.
- To analyse the relationship between the students’ elaboration levels and their success rates in completing the various activities.
- O3.
- To investigate whether there are noticeable differences in success rates among activities of varying difficulty levels.
In particular, we aim to address the following research questions, which are closely linked to the previous objectives, in order to further our understanding:
- RQ1.
- Is there a relationship between the level of elaboration of the number sequence and the success rate in solving the tasks with our CT-oriented didactic sequence?
- RQ2.
- Are there variations in success rates between activities that utilise “counting all” and “counting on” counting strategies?
2. Theoretical Framework
In this section, we present an overview of the theory related to children’s learning about the sequence of number words. We shall also discuss different informal counting strategies and their requirements regarding the mastery of the sequence. We cover a theoretical framework that categorises the diverse applications of educational programmable robots within classroom settings. By adopting a learner-centric perspective, we describe how these innovative tools facilitate and enhance the learning experience.
2.1. Acquisition of the Number Sequence
The learning of the sequence has been described as having two distinct (but overlapping) phases. The first one is the acquisition phase, in which children learn to recite the sequence in the conventional order. The second one, which is called the elaboration phase, implies a deeper understanding of the sequence and the construction of equivalence and order relations and operations on it, together with being able to produce the sequence in more fluid and complex ways [19].
The acquisition phase, mainly focusing on the rote learning of the whole number sequence, can be divided into three milestones:
- Memorisation of number words that can not be obtained by algorithmic generation.
- Generation of tens from the elementary units of the base as a basic characteristic of the decimal numbering system (DNS).
- Learning the rules that allow the generation of new numbers by the combination of tens and units.
During the acquisition phase, Fuson [20] distinguishes three parts in the structure of children’s recitation of the sequence: an initial part, stable and correct, which adjusts to the conventional sequence; a second part, stable and incorrect, which does not follow the conventional order but is consistently repeated by the subject throughout different recitations; and a final part that is together incorrect and unstable.
The progress towards obtaining increasingly long conventional and stable parts of the sequence will be done in two steps:
- Progressively stabilising pieces of the third part (the non-conventional and unstable one), therefore making the second part (stable and non-conventional) bigger.
- Progressively correcting pieces of the second part (the stable and unconventional one), thus making the first part (stable and conventional) bigger.
2.2. Elaboration of the Number Sequence
In the elaboration phase, the student gradually builds relationships between the elements of the conventional and stable parts of the number sequence that has already been acquired. These relationships imply moving from a mere thoughtless recitation of the sequence to a more reflective one. More specifically, Fuson [20] divides the elaboration phase into the following levels.
String Level. This is the first level within this phase of elaboration, and is typically seen in students from the age of 2 years to almost 3 years. Mainly, both number-words and numerals are confused in the child’s mathematical thinking. The sequence is seen as a unidirectional whole structure; the pupil is only able to utter the sequence as if it was simply a single word without differentiating or pausing between the numerals, which always begin with the number 1. A student whose elaboration of the sequence is at string level is unable to count yet, since a one-to-one correspondence between numbers and objects can not be made without being able to separate the number words. However, according to [21], some children would still be able to determine small quantities of objects by means of subitisation. According to [22], subitisation is the “sudden” identification of certain small quantities without counting.
Unbreakable List Level. This is the second level, to which students between the ages of 3 and 4 generally belong. In this one, students try to establish the relationship between number words and their respective numbers. They are able to establish a one-to-one correspondence between objects and numbers and know how to distinguish different positions within the number sequence. The number sequence is correctly emitted but only in one direction (forwards) and they always need to start with 1. They are unable to recite the sequence backwards. However, this knowledge is enough to start using the number sequence for counting, successfully solving tasks of cardinal, ordinal, or measure contexts, and applying counting to find the solution to simple additive problems.
Fragmentary Chain Level. This is the third level, which is generally reached between 3 and 5 years of age. It is also known as the breakable chain level. At this level, students are able to recite the number sequence without having to start at the number 1. They can also count any interval they are asked to count, provided they are indicated the initial and final numbers. The ability to tell which number goes before or after a given one is also part of this level, thus being able to start reciting the sequence in descending order. This level allows facing tasks with a higher cognitive load since the student has to simultaneously manage the processes of reciting the sequence and checking if the end of a fragment has been reached.
Numerable Chain Level. This level, typically acquired between 6 and 7 years of age, is mainly characterised by the understanding that words can be converted into countable elements. The student can recite fragments of the sequence of a given length, answering questions such as “count 3 from 2”. This level also involves performing several cognitive operations at the same time, like the previous level, but now also allows to add the task of “double counting”. In the previous example, the student must continue from 2 and recite the fragment 3, 4, 5 while counting 1, 2, 3 at the same time. According to [16], due to the complexity of some tasks, the student often resorts to counting using their fingers to solve these kinds of questions. It is to be noted that using the fingers or any other objects can lower the elaboration level required to solve a task to a fragmentary chain level or even to an unbreakable list level, since it allows the student to divide the double counting into two separate processes.
Bidirectional Chain Level. This last level, which arises from the beginning of primary education, i.e., from the age of 6 years onwards, is characterised by the ability to count correctly in an increasing and decreasing order, showing the flexibility of being able to change in the middle of the count if necessary. In contrast to the rest of the levels, this one shows a clear speed of pronunciation and an exhaustive mastery of numerals. According to the studies of Fuson [20], the bidirectional level can sometimes be reached without going through the numerable chain level first.
In [16], it is pointed out that a child can have different levels of elaboration of the number sequence in a fragment of the sequence that he or she has already managed to acquire. For example, for an infant that has completely acquired the sequence from 1 to 15 (this fragment belongs to the stable and conventional part of his or her recitations), it is possible to have a numerable chain level of elaboration from 1 to 5 and a lower level (like fragmentary chain level) from 5 to 15. In fact, this is often the case, due to the higher amount of times the first numbers in the chain have to be recited, since the infant will usually start with 1 and then go through the sequence until reaching a number “x”, resulting in a better command of the initial parts of the sequence.
Summing up, the learning of the number sequence and its respective simultaneous phases, the acquisition phase and the elaboration phase, are developed mainly in the infant education stage and during part of the first years in primary education, culminating in the last levels, the numerable and bidirectional chain levels. This process constitutes one of the first experiences of children with a mathematical structure and will be the prelude to counting, a skill that will allow them to efficiently solve mathematical tasks in different contexts.
Table 1 summarises the characteristics of the five levels of the elaboration of the number sequence described above.

Table 1.
Summary of the number sequence categorisation according to K. C. Fuson [20]. Symbols ✓ and ✗ stand for concept acquired and not acquired, respectively.
2.3. Pre-Operational Stage
According to [16], the acquisition of the number sequence is parallel to the introduction of addition. Even before receiving explicit instruction, students are able to solve a variety of simple additive problems by using informal strategies for counting [23]. Over the last few years, the paradigm regarding the learning of basic arithmetic operations has undergone a profound change, moving from having its focus on the raw memorisation of number facts to an approach where the learning of those number facts arises from the use of informal strategies by the students in the context of mathematical problem solving [24].
In this sense, it is not necessary for the student to know the algorithms of the operations in order to solve many simple additive word problems as long as the size of the numbers involved allows it. It is not even necessary to have an understanding of the written representation of numbers. Students can deal with these simple additive problems by means of counting to find their possible solution, in a process that some authors call phase 1 of the acquisition of addition [25]. Of course, there are limitations in this phase, such as the representation of large numbers or the double counting process mentioned above, that children can circumvent by using their own fingers as an external tool to keep track of their count. The literature suggests that fingers may play a functional role in numerical development, and also a procedural tool that helps the development of mathematical cognition [26].
According to [27], the use of counting in addition allows the introduction of two types of counting strategies: “counting all” and “counting on”. Teachers need to be aware of the different demands and requirements of each strategy from the perspective of the level of elaboration of the number sequence. Let us explain how each of these two strategies work, and which level of elaboration the student is required to have to be able to use them.
Counting all. This strategy consists of constructing a set of objects for each one of the addends by counting, then joining both sets and counting the number of elements of the union set. Observe that this strategy can be performed by a student whose elaboration level of the number sequence has reached an unbreakable list level, since the sets associated with each addend can be counted starting with 1, and the union set can also be counted this way. Of course, to carry out this process, the child should have acquired at least the following counting principles: order stable, one-to-one correspondence, and cardinality [27].
Counting on. This strategy is based on taking one of the addends (usually the largest one) and then counting up from it as many units as the second addend has. The last number reached is the result of the sum. To apply this strategy, the student should at least be in the numerable chain level of elaboration of the sequence. In fact, observe that this counting strategy requires the following small skills to be performed [28]:
- Being able to start counting from a number other than 1.
- Understanding that the word that determines the cardinal of the first set can be used as an element in a counting process.
- Being able to start a count from a second set, starting from the numeral associated with the first set.
Note that children with a fragmentary chain level of elaboration of the sequence can apply this strategy if they use their fingers to split the double counting into two separate processes.
2.4. Learning with Educational Robots
According to [29], three types of paradigms directly related to robotics emerge behind this robotics-based learning add-on, and we cover them below.
Learning robotics. In this paradigm [30], students use a robot as a platform to learn robotics focusing mostly on the engineering components such as electronics and programming through a hands-on methodology and in a collaborative way.
Learning with robotics. Under this paradigm, students use robots accepting them as a complement and part of their learning [31]. The acceptance of robotics in education involves physical, cultural, behavioural, functional, social, and representational domains. This is the paradigm whose main function is to learn the usefulness and ease of use of each type of robot, and also to know its physical representation and its behavioural, social, and cultural function.
Learning by robotics. In this paradigm, students can learn through robots, acquiring transversal knowledge, in addition to the fact that the robot is used as a tool within the student-teacher-school material link [18]. Mainly, in this paradigm, thanks to robotic kits, it is possible to achieve curricular objectives, work on student–robot projects, and explore real-world problems. Robotic kits are normally made up of mechanical and electronic elements that are controlled by means of specific instructions in which the pupils program the robot’s functions, using a high-level language that can be verbal or graphic.
This last paradigm best captures our use of educational programmable robots as a tool to enhance mathematical problem-solving skills in preschool education. We advocate for the integration of these educational robots to facilitate the development of CT abilities by engaging students in mathematical challenges within a carefully designed sequence of activities outlined below.
3. Materials & Methods
In our study, we employ the Bee-Bot robot [32]. Figure 1a illustrates the type of educational robots used and Figure 1b shows a scheme of its control panel. This simple panel includes four arrows indicating the direction of the movement, a start button that initiates the sequence movement, a button to pause the sequence and a button to delete the programmed sequence that was stored in memory. These robots are programmable through this button-based interface and this allows to replicate a sequence of movements; they can move with precision in 15 cm steps, rotate in 90 degrees turns, and are able to remember up to 200 steps.

Figure 1.
In (a) the Bee-Bot [32], in (b) a general control panel scheme of educational robots.
We also used spatial orientation boards, which served as a platform for the children to engage with and manipulate the educational robot. The participants were tasked with designing a sequence of movements for the robot to navigate the grid with different goals. Firstly, a set of three activities in which students reach various objects distributed strategically on the board. Secondly, a set of two activities based on pre-operational strategies for solving sums.
3.1. Didactic Sequence Design
Our study relies on the design and analysis of a didactic sequence with increasing complexity. In particular, we have designed two main challenges explained below.
Activities 1, 2 and 3. This sequence of three different activities is based on finding an object in a regular grid of 15 cm × 15 cm squares. Here, students are advised to program a sequence on the robot situated at the same starting point which seeks to find the object, in that case, plastic toy animals, see Figure 2.

Figure 2.
Picture of the proposed activities related to finding an object through the robot in a regular 15 cm cm regular grid.
The number of objects distributed on the board and the number of turns and keys used to reach the goal served as an element of study to measure the complexity of these tasks. Table 2 summarises the features of the activities from one to three in this regard. It describes the total number of objects which students should find along the regular grid. It also reports the minimum number of turns which should be performed in order to find such objects. Finally, the minimum number of keys that should be pressed (or programmed) in order to achieve each proposed challenge. As it can be seen, the activities were designed in a way that each one contained either more objects to be found or required more turns or keys to be pressed than the previous one to be completed. Specifically, we set the number of turns as a strictly increasing variable from task to task, since dealing with rotations when programming the educational robots has been reported in the literature as one of the main sources of difficulties [17].

Table 2.
Summary of the features of each activity it represents the number of objects to achieve, the minimal turns for success of the activity, and the minimum number of keys necessary to achieve the task.
Activities 4 and 5. In these activities, from a set of marbles representing quantities, students should be able to represent each marble by advancing one square with the Bee-Bot to find out the final sum of all the marbles given to them by the teacher applying a certain counting strategy. Figure 3 illustrates the number sequence representation used. Specifically, the promoted addition strategy in activity four was counting everything, whereas activity number five is focused on the counting on strategy. Recall that these strategies were explained in Section 2.3. We decided to provide each child with a different number of marbles than the rest of their classmates. This decision was made because they tend to look at the results of the partner who is doing the test, even though they are doing another activity while waiting for their turn.

Figure 3.
Picture of the number sequence representation on the grid used to implement the pre-operational strategies related to the sum.
3.2. Participants
The study was conducted as part of the Internship III program in a second-cycle infant education classroom. The participant group consisted of 16 children, comprising 12 boys and 4 girls, with ages ranging from 4 to 5 years old. The selection of this specific age range aimed to capture the developmental stage where children are typically immersed in the early education curriculum and are actively engaged in the learning process. Although the gender representation was not balanced, both boys and girls were included to ensure a diverse sample.
A sample size of 16 participants was deemed suitable for the research scope, and convenience sampling was utilised as the selection criterion. The tutors in the classroom specifically chose students who had no prior experience with educational robots.
3.3. Data Acquisition
The first part of the acquisition process in this study consisted of assessing the level of elaboration in the number sequence. It was conducted individually and according to the elaboration levels of the number sequence studied by Fuson [20], explained in Section 2.2. The aim was to relate the elaboration level with the success in the designed tasks.
In addition to the study of the number sequence itself, the performance of the participants in the proposed activities was also measured by reporting their success or failure. It is important to highlight that each test was conducted in an entirely individualised manner, as the educational robot could only be operated by one student at a time. This approach ensured that the data acquired was specific to each participant’s actions and thought processes during the task. By capturing individualised data, the study aimed to provide a detailed understanding of the participants’ problem-solving abilities and their utilisation of computational thinking skills in the context of the number sequence elaboration.
4. Results and Discussion
In this section, we report the achieved results of our experiment and further provide a detailed discussion derived from them.
Table 3 summarises the elaboration level of the students in the study sample. Out of the four feminine students, one is at the string level, two are at the unbreakable list level and one is at the fragmentary chain level. As can be seen, the twelve masculine students are mostly at the unbreakable level (around 58%), whereas 25% are at the string level and two masculine students (which represent around 17%) are in the numerable chain level. These levels were explained in detail in Section 2.2. Regarding the total percentages, it is derived that 25% of students are at the string level, 56.3% are in the unbreakable list level, 6.3% are at the fragmentary chain level, and 12.5% are at the numerable chain level. Recall that none of the students were at the bidirectional level, which corresponds to the most advanced level, as it is habitual in this educational stage.

Table 3.
Participants’ elaboration level of the number sequence.
Figure 4 illustrates the success rate percentage for each activity and allows us to discuss objective O3. In (a) we show the activities regarding the object finding in the regular grid. As it can be seen, the regular trend is a decrease in success along the activity number. It can be also observed that feminine students performed worse in the more complex activity number three. In (b), the results of the pre-operational activities are presented. As can be seen, in activity four the success rates achieved in both genders are equal, and activity five reported small differences. Regarding our research question RQ2, the results obtained in this context are in line with what is usually stated in the related literature about counting strategies [28,33], since we observe that better results were achieved in activity four (counting all) compared to five (counting on) which supports the idea that counting all strategy is easier to the students compared to counting on strategy also in the setting of our experience.
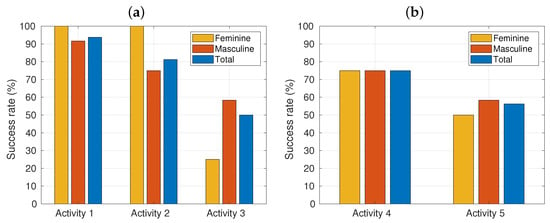
Figure 4.
Success rate in the proposed activities. (a) “Find on the grid” activities. (b) Pre-operational challenges.
Figure 5 presents a summary of the results obtained for objective O2 and research question RQ1. It depicts the success rates for tasks based on the level of elaboration of the sequence. In part (a), the results for tasks one to three are shown. Notably, the string level consistently achieved lower results in all activities, as expected, since students at this level struggle to separate individual word numbers when verbalising the number sequence. Activities 1 and 2 demonstrated the highest success rates across the different levels. Within each level, the results followed the expected trend, with success rates decreasing as the activity number increased. Interestingly, for activity 3, the results indicate that higher levels of sequence elaboration do not necessarily correlate with better task performance. This suggests that factors such as mental rotation or spatial skills [17,34] may have a stronger influence on success in these tasks compared to the mastery of the number sequence. It is important to note, however, that there was only one student in the fragmentary chain level and two in the numerable chain level. Activity 4 exhibited better results across all levels (except for the string level, which reported a 0% success rate) compared to activity 5, further highlighting the suitability of the counting all strategy for introducing counting. In activity 5, as in activity 3, a similar pattern emerges in terms of the success rate and the level of sequence elaboration.
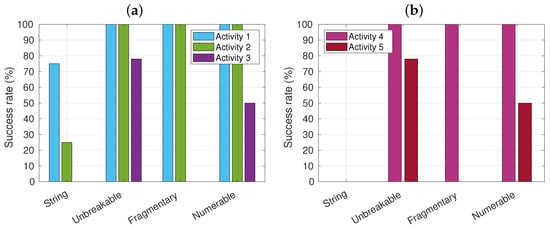
Figure 5.
The success rate (y-axis) of the students from each elaboration level (x-axis) in the proposed activities (a) find on the grid and (b) in the pre-operational challenges.
As previously mentioned, there is a clearly observable trend indicating that the success rate decreases as the activity number increases, both overall and within each level of sequence elaboration. This empirical observation provides confirmation for the design approach we intended to achieve in objective O1, which aimed to increase the complexity of the tasks progressively.
5. Conclusions & Future Work
The concept of CT has garnered substantial attention in recent years and is now widely acknowledged as a crucial element in educational curricula at various levels. Within the context of our study, which focuses on the integration of educational programmable robots, we devised and implemented two sets of activities characterised by increasing levels of complexity. These activities were designed to assess the effectiveness of our didactic sequence. The first set of activities revolves around programming sequences to locate objects within a regular grid, whereas the second set centers on solving sums using pre-operational strategies.
Our empirical findings provided valuable insights into the effectiveness of the designed didactic sequence, confirming the anticipated increase in task complexity and highlighting the correlation between students’ levels of sequence elaboration and success rates. These findings support the integration of educational programmable robots to promote computational thinking skills in early education, offering practical implications for curriculum design and fostering critical thinking from a young age.
Regarding the relationship between the success rate when solving the proposed tasks and the level of elaboration of the number sequence, it is noteworthy that in the most challenging activities of each set (activities 3 and 5), students with a higher level of elaboration of the number sequence did not always outperform those with a lower level, contrary to initial expectations. This suggests that factors such as spatial skills or mental rotation may exert a greater influence on the success of these tasks than those related to the sequence itself. In the second set of activities, which specifically target counting strategies, the findings indicate that the counting all strategy emerges as the most successful approach among preschool students when solving addition problems.
Looking ahead, it is crucial to conduct additional testing and validation to further establish the effectiveness of our didactic sequence. This can be achieved by including other preschool student groups and expanding the sample size, which would enhance the generalisability and robustness of the findings. Furthermore, an intriguing and ambitious direction for future research would be to extend the design of the sequence to encompass primary education, thereby establishing a seamless connection between preschool and primary education. This expansion would provide a more comprehensive understanding of the progression and continuity of CT skills across various educational stages.
Furthermore, we recommend considering the inclusion of students with high capacities and/or on the autistic spectrum in future studies. This would enable a more inclusive examination of the benefits and challenges of the didactic sequence for diverse learner profiles. By exploring these different contexts, we can attain a more comprehensive understanding of the impact and potential applications of our research findings.
The positive outcomes observed in this study serve as a strong motivation to further pursue research in this field and build upon our current findings. We are eager to explore further avenues of investigation and refine our didactic sequence, ultimately making significant contributions to the advancement of CT education in early education settings.
Author Contributions
Conceptualization, A.P.-S., I.G.-B., S.V.V. and A.B.P.-V.; methodology, A.P.-S., S.V.V. and A.B.P.-V.; software, A.P.-S. and I.G.-B.; validation, A.P.-S., I.G.-B. and A.B.P.-V.; formal analysis, A.B.P.-V., I.G.-B. and S.V.V.; investigation, A.P.-S., A.B.P.-V. and I.G.-B.; resources, I.G.-B., A.P.-S. and A.B.P.-V.; data curation, I.G.-B., A.P.-S. and A.B.P.-V.; writing—original draft preparation, A.P.-S., I.G.-B. and S.V.V.; writing—review and editing, A.P.-S., S.V.V., I.G.-B. and A.B.P.-V.; visualization, A.P.-S., A.B.P.-V., S.V.V. and I.G.-B.; supervision, A.P.-S. and S.V.V.; project administration, A.P.-S., A.B.P.-V., S.V.V. and I.G.-B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study has been developed following the code of good practice in research of the Universitat de València.
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
The data presented in this study is not publicly available due to privacy restrictions.
Acknowledgments
A.P.-S. wants to thant to the project AICO/2021/019, funded by the Regional Government of València (Spain).
Conflicts of Interest
The authors declare no conflict of interest.
References
- Denning, P.J. The Profession of ITBeyond Computational Thinking. Commun. ACM 2009, 52, 28–30. [Google Scholar] [CrossRef]
- Wing, J.M. Computational Thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Israel-Fishelson, R.; Hershkovitz, A. Studying interrelations of computational thinking and creativity: A scoping review (2011–2020). Comput. Educ. 2022, 176, 104353. [Google Scholar] [CrossRef]
- Van Vaerenbergh, S.; Pérez-Suay, A. A Classification of Artificial Intelligence Systems for Mathematics Education. In Mathematics Education in the Age of Artificial Intelligence: How Artificial Intelligence can Serve Mathematical Human Learning; Richard, P.R., Vélez, M.P., Van Vaerenbergh, S., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 89–106. [Google Scholar]
- Grover, S.; Pea, R. Computational Thinking in K–12: A Review of the State of the Field. Educ. Res. 2013, 42, 38–43. [Google Scholar] [CrossRef]
- Tsarava, K.; Moeller, K.; Román-González, M.; Golle, J.; Leifheit, L.; Butz, M.V.; Ninaus, M. A cognitive definition of computational thinking in primary education. Comput. Educ. 2022, 179, 104425. [Google Scholar] [CrossRef]
- Wu, W.R.; Yang, K.L. The relationships between computational and mathematical thinking: A review study on tasks. Cogent Educ. 2022, 9, 2098929. [Google Scholar] [CrossRef]
- Lockwood, E.; De Chenne, A. Enriching Students’ Combinatorial Reasoning through the Use of Loops and Conditional Statements in Python. Int. J. Res. Undergrad. Math. Educ. 2020, 6, 303–346. [Google Scholar] [CrossRef]
- Cui, Z.; Ng, O.-l.; Jong, M.S.Y. Integration of Computational Thinking with Mathematical Problem-based Learning: Insights on Affordances for Learning. Educ. Technol. Soc. 2023, 26, 131–146. [Google Scholar]
- De Chenne, A.; Lockwood, E. A task to connect counting processes to lists of outcomes in combinatorics. J. Math. Behav. 2022, 65, 100932. [Google Scholar] [CrossRef]
- Ye, H.; Liang, B.; Ng, O.L.; Chai, C.S. Integration of computational thinking in K-12 mathematics education: A systematic review on CT-based mathematics instruction and student learning. Int. J. Stem Educ. 2023, 3, 2196–7822. [Google Scholar] [CrossRef]
- del Olmo-Muñoz, J.; Cózar-Gutiérrez, R.; González-Calero, J.A. Computational thinking through unplugged activities in early years of Primary Education. Comput. Educ. 2020, 150, 103832. [Google Scholar] [CrossRef]
- Román-González, M.; Pérez-González, J.C.; Moreno-León, J.; Robles, G. Can computational talent be detected? Predictive validity of the Computational Thinking Test. Int. J. Child-Comput. Interact. 2018, 18, 47–58. [Google Scholar] [CrossRef]
- Bakala, E.; Gerosa, A.; Hourcade, J.P.; Tejera, G. Preschool children, robots, and computational thinking: A systematic review. Int. J. Child-Comput. Interact. 2021, 29, 100337. [Google Scholar] [CrossRef]
- Atmatzidou, S.; Demetriadis, S.N. Advancing students’ computational thinking skills through educational robotics: A study on age and gender relevant differences. Robot. Auton. Syst. 2016, 75, 661–670. [Google Scholar] [CrossRef]
- Diago, P.; Arnau, D.; González-Calero, J.A. Elementos de resolución de problemas en primeras edades escolares con Bee-bot. Edma Educ. Mat. Infanc. 2018, 7, 12–41. [Google Scholar]
- Diago, P.D.; González-Calero, J.A.; Yáñez, D.F. Exploring the development of mental rotation and computational skills in elementary students through educational robotics. Int. J. Child-Comput. Interact. 2022, 32, 100388. [Google Scholar] [CrossRef]
- Gaudiello, I.; Zibetti, E. Learning by Robotics: The Impact of Educational Robots on Learning. In Learning Robotics, with Robotics, by Robotics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; Chapter 3; pp. 87–141. [Google Scholar]
- Fuson, K.C.; Richards, J.; Briars, D.J. The Acquisition and Elaboration of the Number Word Sequence. In Children’s Logical and Mathematical Cognition: Progress in Cognitive Development Research; Brainerd, C.J., Ed.; Springer Series in Cognitive Development; Springer: New York, NY, USA, 1982; pp. 33–92. [Google Scholar] [CrossRef]
- Fuson, K.C. Children’s Counting and Concepts of Number; Springer: New York, NY, USA, 1988. [Google Scholar]
- Fuson, K.C. An analysis of the counting-on solution in addition. In Addition and Subtraction: A Cognitive Perspective; Carpenter, T.P., Moser, J.M., Romberg, T.A., Eds.; Erlbaum: Hillsdale, NJ, USA, 1982; pp. 67–81. [Google Scholar]
- Kaufman, E.L.; Lord, M.W.; Reese, T.W.; Volkmann, J. The Discrimination of Visual Number. Am. J. Psychol. 1949, 62, 498–525. [Google Scholar] [CrossRef]
- Baroody, A.; Baroody, A.J.; Coslick, R.T. Fostering Children’s Mathematical Power: An Investigative Approach to K-8 Mathematics Instruction; Routledge: New York, NY, USA, 1998. [Google Scholar] [CrossRef]
- Verschaffel, L.; De Corte, E. Number and Arithmetic. In International Handbook of Mathematics Education: Part 1; Bishop, A.J., Clements, K., Keitel, C., Kilpatrick, J., Laborde, C., Eds.; Kluwer International Handbooks of Education; Springer: Dordrecht, The Netherlands, 1996; pp. 99–137. [Google Scholar] [CrossRef]
- Baroody, A.J.E.A. Handbook of research on the education of young children. In Handbook of Research on the Education of Young Children; Spodek, O.N.S.B., Ed.; Lawrence Erlbaum Associates Publishers: Hillsdale, NJ, USA, 2016; pp. 187–221. [Google Scholar]
- Crollen, V.; Noël, M.P. The role of fingers in the development of counting and arithmetic skills. Acta Psychol. 2015, 156, 37–44. [Google Scholar] [CrossRef]
- Carpenter, T.P.; Hiebert, J.; Moser, J.M. Problem Structure and First-Grade Children’s Initial Solution Processes for Simple Addition and Subtraction Problems. J. Res. Math. Educ. 1981, 12, 27–39. [Google Scholar] [CrossRef]
- Secada, W.G.; Fuson, K.C.; Hall, J.W. The Transition from Counting-All to Counting-on in Addition. J. Res. Math. Educ. 1983, 14, 47–57. [Google Scholar] [CrossRef]
- Gaudiello, I.; Zibetti, E. Learning Robotics, with Robotics, by Robotics: Educational Robotics; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar] [CrossRef]
- Gaudiello, I.; Zibetti, E. Learning Robotics: Users’ Representation of Robots. In Learning Robotics, with Robotics, by Robotics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; Chapter 1; pp. 1–41. [Google Scholar]
- Gaudiello, I.; Zibetti, E. Learning with Robotics: Functional and Social Acceptance of Robots. In Learning Robotics, with Robotics, by Robotics; John Wiley & Sons, Ltd.: Hoboken, NJ, USA, 2016; Chapter 2; pp. 43–85. [Google Scholar]
- Group, T. Bee-Bot—The Story behind Our TTS Developed Award Winning Programmable Robot. 2019. Available online: https://www.tts-group.co.uk/blog/2019/01/25/bee-bot-the-story-behind-our-award-winning-programmable-robot.html (accessed on 26 April 2023).
- Maclellan, E. Counting all, counting on, counting up, counting down. Education 1995, 23, 17–21. [Google Scholar] [CrossRef]
- Sabena, C. Early Child Spatial Development: A Teaching Experiment with Programmable Robots. In Mathematics and Technology: A C.I.E.A.E.M. Sourcebook; Aldon, G., Hitt, F., Bazzini, L., Gellert, U., Eds.; Springer International Publishing: Cham, Switzerland, 2017; pp. 13–30. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).