Acceptance and Intentions of Using Dynamic Geometry Software by Pre-Service Primary School Teachers
Abstract
1. Introduction
2. Research framework
2.1. Technology Acceptance Model (TAM)
2.2. Perceived-Learning Fit Extension
- Visualization processes related to space representation for illustrating statements, heuristic exploration of complex situations, synoptic glances, or subjective verification;
- Construction processes using tools, where the construction of configurations can work like a model, relating actions on the representative and observed results to the mathematical objects being represented;
- Reasoning processes in relation to discursive processes for extending knowledge, providing proof, and offering explanations
2.3. Extended TAM
- (a)
- First-order latent variables related to the geometry reasoning model: Visualization Processes (VP), Reasoning Processes (RP), and Construction Processes (CP). These factors constitute the second-order latent factor Perceived Learning-fit (PLF). Specifically, it is hypothesized that PLF influences teachers’ intention to use DGS in geometry teaching.
- (b)
- Traditional TAM variables as first-order latent factors: Perceived usefulness (PU), Perceived Ease of Use (PEU), Attitude Towards Use (ATU), and Intention to Use (IU). It is hypothesized that teachers’ intention to use DGS in geometry teaching is directly influenced by their attitude towards the use of DGS and indirectly by the PU of DGS, the PEU, and the PLF, through their attitude towards the use of DGS, based on the assumptions of TAM theory. Finally, the proposed model suggests that PU and PLF have a direct effect on attitude, while PEU has both a direct and an indirect (through PU and PLF) effect on attitude.
- (c)
- External variables as first-order latent factors: Facilitating Conditions (FC), Computer Anxiety (CA), and Personal Innovation (PI). It is hypothesized that these external variables influence the latent constructs PEU, PU, and PLF.
3. Methodology
3.1. Participants
3.2. Instrument
3.3. Structural Equation Model
3.4. Software
4. Results
4.1. Descriptive Statistics
Differences between Groups
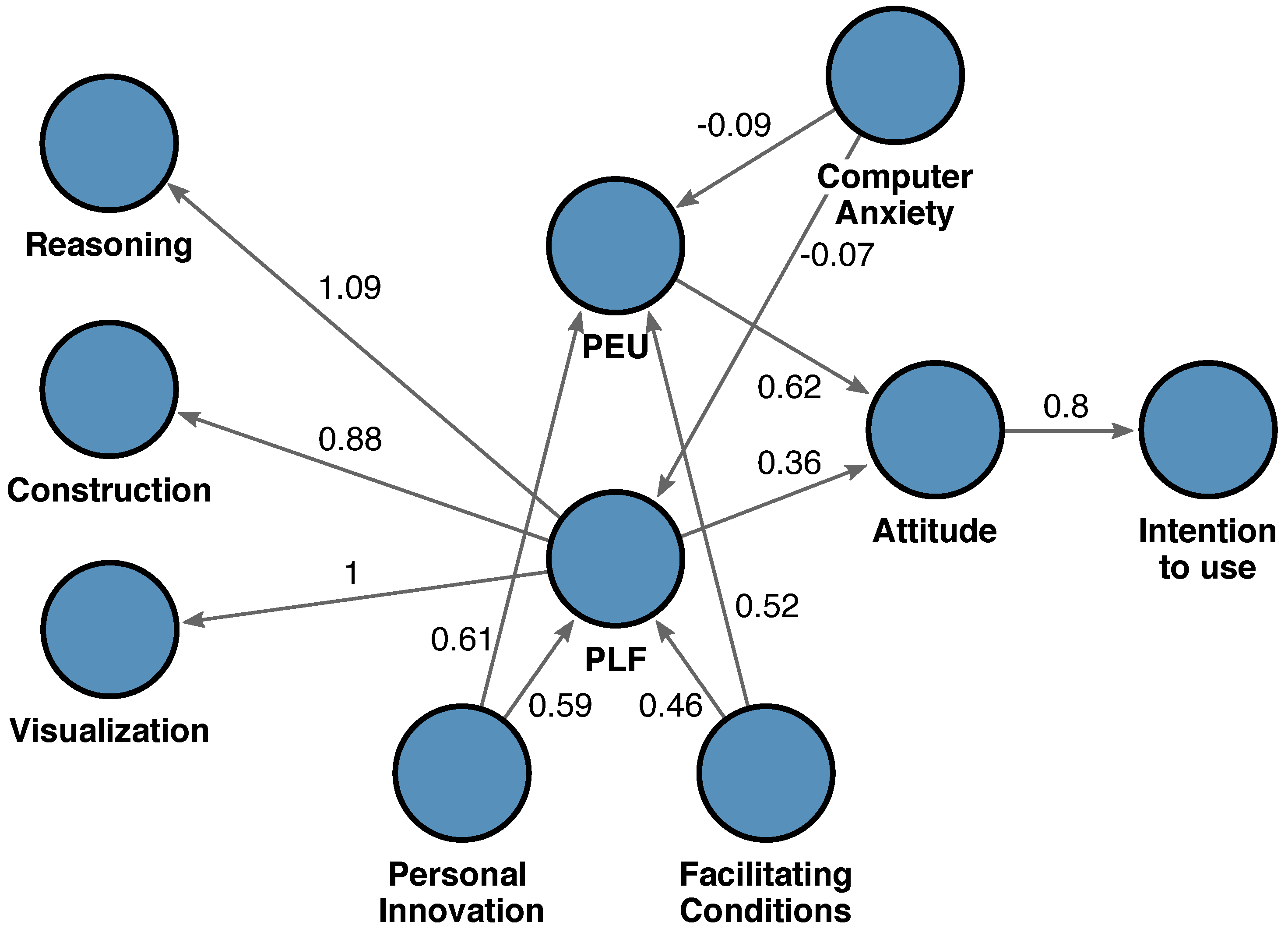
4.2. Structural Equation Model
4.2.1. Reliability and Validity of the Measurement Models
4.2.2. Assessment of the Structural Model Relationships
4.2.3. Evaluation of Model Fit and Predictive Power
5. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Straesser, R. Cabri-Géomètre: Does dynamic geometry software (DGS) change geometry and its teaching and learning? Int. J. Comput. Math. Learn. 2002, 6, 319–333. [Google Scholar] [CrossRef]
- Clements, D.H.; Sarama, J.; Yelland, N.J.; Glass, B. Learning and teaching geometry with computers in the elementary and middle school. Res. Technol. Teach. Learn. Math. 2008, 1, 109–154. [Google Scholar]
- Sinclair, N.; Bartolini Bussi, M.G.; de Villiers, M.; Jones, K.; Kortenkamp, U.; Leung, A.; Owens, K. Recent research on geometry education: An ICME-13 survey team report. ZDM 2016, 48, 691–719. [Google Scholar] [CrossRef]
- Hillmayr, D.; Ziernwald, L.; Reinhold, F.; Hofer, S.I.; Reiss, K.M. The potential of digital tools to enhance mathematics and science learning in secondary schools: A context-specific meta-analysis. Comput. Educ. 2020, 153, 103897. [Google Scholar] [CrossRef]
- Olivero, F.; Robutti, O. Measuring in dynamic geometry environments as a tool for conjecturing and proving. Int. J. Comput. Math. Learn. 2007, 12, 135–156. [Google Scholar] [CrossRef]
- Kovács, Z.; Recio, T.; Vélez, M.P. Automated Reasoning Tools with GeoGebra: What Are They? What Are They Good For. In Mathematics Education in the Age of Artificial Intelligence: How Artificial Intelligence can Serve Mathematical Human Learning; Richard, P.R., Vélez, M.P., Van Vaerenbergh, S., Eds.; Springer International Publishing: Cham, Switzerland, 2022; pp. 23–44. [Google Scholar] [CrossRef]
- Güven, B.; Kosa, T. The effect of dynamic geometry software on student mathematics teachers’ spatial visualization skills. Turk. Online J. Educ. Technol. 2008, 7, 100–107. [Google Scholar]
- Guven, B. Using dynamic geometry software to improve eight grade students’ understanding of transformation geometry. Australas. J. Educ. Technol. 2012, 28. [Google Scholar] [CrossRef]
- Stols, G.; Kriek, J. Why don’t all maths teachers use dynamic geometry software in their classrooms? Australas. J. Educ. Technol. 2011, 27. [Google Scholar] [CrossRef]
- Herbst, P.; Cheah, U.H.; Richard, P.R.; Jones, K. International Perspectives on the Teaching and Learning of Geometry in Secondary Schools; Springer: Berlin/Heidelberg, Germany, 2018. [Google Scholar]
- Mitchell, B.; Bailey, J.; Monroe, E. Integrating technology and a standards-based pedagogy in a geometry classroom: A mature teacher deals with the reality of multiple demands and paradigm shifts. Comput. Sch. 2007, 24, 75–91. [Google Scholar] [CrossRef]
- İbili, E. The use of dynamic geometry software from a pedagogical perspective: Current status and future prospects. J. Comput. Educ. Res. 2019, 7, 337–355. [Google Scholar] [CrossRef]
- Davis, F.D. Perceived usefulness, perceived ease of use, and user acceptance of information technology. MIS Q. Manag. Inf. Syst. 1989, 13, 319–340. [Google Scholar] [CrossRef]
- Scherer, R.; Siddiq, F.; Tondeur, J. The technology acceptance model (TAM): A meta-analytic structural equation modeling approach to explaining teachers’ adoption of digital technology in education. Comput. Educ. 2019, 128, 13–35. [Google Scholar] [CrossRef]
- Teo, T.; Lee, C.B.; Chai, C.S.; Wong, S.L. Assessing the intention to use technology among pre-service teachers in Singapore and Malaysia: A multigroup invariance analysis of the Technology Acceptance Model (TAM). Comput. Educ. 2009, 53, 1000–1009. [Google Scholar] [CrossRef]
- Fearnley, M.R.; Amora, J.T. Learning Management System Adoption in Higher Education Using the Extended Technology Acceptance Model. IAFOR J. Educ. 2020, 8, 89–106. [Google Scholar] [CrossRef]
- Sun, H.; Zhang, P. The role of moderating factors in user technology acceptance. Int. J. Hum.-Comput. Stud. 2006, 64, 53–78. [Google Scholar] [CrossRef]
- Teo, T.; Noyes, J. An assessment of the influence of perceived enjoyment and attitude on the intention to use technology among pre-service teachers: A structural equation modeling approach. Comput. Educ. 2011, 57, 1645–1653. [Google Scholar] [CrossRef]
- Dishaw, M.T.; Strong, D.M. Extending the technology acceptance model with task–technology fit constructs. Inf. Manag. 1999, 36, 9–21. [Google Scholar] [CrossRef]
- Pittalis, M. Extending the technology acceptance model to evaluate teachers’ intention to use dynamic geometry software in geometry teaching. Int. J. Math. Educ. Sci. Technol. 2021, 52, 1385–1404. [Google Scholar] [CrossRef]
- Nosek, B.A.; Errington, T.M. What is replication? PLoS Biol. 2020, 18, e3000691. [Google Scholar] [CrossRef]
- Davis, F.D. A Technology Acceptance Model for Empirically Testing New End-User Information Systems: Theory and Results. Ph.D. Thesis, Massachusetts Institute of Technology, Cambridge, MA, USA, 1985. [Google Scholar]
- Granić, A.; Marangunić, N. Technology acceptance model in educational context: A systematic literature review. Br. J. Educ. Technol. 2019, 50, 2572–2593. [Google Scholar] [CrossRef]
- Abdullah, F.; Ward, R.; Ahmed, E. Investigating the influence of the most commonly used external variables of TAM on students’ Perceived Ease of Use (PEOU) and Perceived Usefulness (PU) of e-portfolios. Comput. Hum. Behav. 2016, 63, 75–90. [Google Scholar] [CrossRef]
- Rondan-Cataluña, F.J.; Arenas-Gaitán, J.; Ramírez-Correa, P.E. A comparison of the different versions of popular technology acceptance models: A non-linear perspective. Kybernetes 2015, 44, 788–805. [Google Scholar] [CrossRef]
- Burton-Jones, A.; Hubona, G.S. The mediation of external variables in the technology acceptance model. Inf. Manag. 2006, 43, 706–717. [Google Scholar] [CrossRef]
- Laborde, C.; Kynigos, C.; Hollebrands, K.; Strässer, R. Teaching and learning geometry with technology. In Handbook of Research on the Psychology of Mathematics Education; Brill: Leiden, The Netherlands, 2006; pp. 275–304. [Google Scholar]
- Duval, R. Geometry from a Cognitive Point of View; New ICMI Study Series; Springer: Amsterdam, The Netherlands, 2012. [Google Scholar]
- Kline, R.B. Principles and Practice of Structural Equation Modeling, 3rd ed.; Guilford Publications: New York, NY, USA, 2011. [Google Scholar]
- Deegan, J. On the occurrence of standardized regression coefficients greater than one. Educ. Psychol. Meas. 1978, 38, 873–888. [Google Scholar] [CrossRef]
- Hair, J.F.; Risher, J.J.; Sarstedt, M.; Ringle, C.M. When to use and how to report the results of PLS-SEM. Eur. Bus. Rev. 2019, 31, 2–24. [Google Scholar] [CrossRef]
- O’Dwyer, L.M.; Bernauer, J.A. Quantitative Research for the Qualitative Researcher; SAGE Publications: New York, NY, USA, 2013. [Google Scholar]
- Carmines, E.G.; Zeller, R.A. Reliability and Validity Assessment; Quantitative Applications in the Social Sciences; Sage Research Methods: New York, NY, USA, 1979. [Google Scholar]
- R Core Team. R: A Language and Environment for Statistical Computing; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Rosseel, Y. lavaan: An R Package for Structural Equation Modeling. J. Stat. Softw. 2012, 48, 1–36. [Google Scholar] [CrossRef]
- Jorgensen, T.D. semTools: Useful Tools for Structural Equation Modeling; R Foundation for Statistical Computing: Vienna, Austria, 2022. [Google Scholar]
- Varela Mallou, J.; Lévy Mangin, J.P. Modelización con Estructuras de Covarianzas en Ciencias Sociales: Temas Esenciales, Avanzados y Aportaciones Especiales; Netbiblo: La Coruña, Spain, 2023. [Google Scholar]
- Bagozzi, R.P.; Yi, Y. On the Evaluation of Structural Equation Models. Journal of the Academy of Marketing Sciences. J. Acad. Mark. Sci. 1988, 16, 74–94. [Google Scholar] [CrossRef]
- Tentama, F.; Anindita, W.D. Employability Scale: Construct Validity And Reliability. Int. J. Sci. Technol. Res. 2020, 9, 3166–3170. [Google Scholar]
- Segal, R.; Oxman, V.; Stupel, M. Using dynamic Geometry Software to enhance specialized content knowledge: Pre-service mathematics teachers’ perceptions. Int. Electron. J. Math. Educ. 2021, 16, em0647. [Google Scholar]
- Chan, K.K. Salient beliefs of secondary school mathematics teachers using dynamic geometry software. Eurasia J. Math. Sci. Technol. Educ. 2015, 11, 139–148. [Google Scholar] [CrossRef]

| Factor | Items |
|---|---|
| Visualization processes (VP) | Q1. DGS facilitates the dynamic visualization and understanding of geometric theorems and proofs. |
| Q2. DGS functions (i.e., dragging) help students to ‘see’ the properties and characteristics of geometric shapes. | |
| Q3. DGS offers dynamic images that promote dynamic visualisation of geometrical concepts. | |
| Reasoning processes (RP) | Q4. Teaching geometry with DGS helps in developing students’ reasoning and conjecturing. |
| Q5. Manipulating shapes in DGS contributes to an understanding of the relations between geometric shapes. | |
| Q6. DGS measurement and dragging tools help students make generalisations. | |
| Construction processes (CP) | Q7. DGS tools make possible the construction of geometric shapes based on their properties. |
| Q8. DGS tools facilitate the construction of complex geometrical constructions, such as locus. | |
| Q9. Constructing geometric shapes in DGS is not a mechanical process, but it develops students’ construction abilities. | |
| Perceived usefulness (PU) | Q10. Using DGS in geometry teaching will enable me to accomplish my tasks more quickly. |
| Q11. Using DGS in geometry teaching will enable me to enhance my effectiveness in teaching. | |
| Q12. Using DGS in geometry teaching will enable me to increase my productivity in teaching. | |
| Perceived ease of use (PEU) | Q13. My interaction with DGS tools will be clear and understandable. |
| Q14. I will find the DGS tools to be flexible to interact with. | |
| Q15. I will find the DGS tools easy to use. | |
| Attitude towards Use (ATU) | Q16. I think it would be very good to use DGS in geometry teaching rather than traditional methods. |
| Q17. In my opinion it would be very desirable to use DGS in geometry teaching rather than traditional methods. | |
| Q18. Teaching geometry with DGS makes the lesson more interesting. | |
| Intention to Use (IU) | Q19. I will use DGS in geometry teaching rather than traditional methods of teaching geometry. |
| Q20. My intention is to use DGS in geometry teaching rather than traditional teaching methods. | |
| Q21. In geometry teaching, I would rather use DGS than traditional methods. | |
| Facilitating Conditions (FC) | Q22. When I need help in teaching geometry with DGS, one ofmy colleagues will help me. |
| Q23.When I need help in teaching geometry with DGS, one expert will help me. | |
| Q24. When I need help in teaching geometry with DGS, someone will provide me with additional material. | |
| Computer Anxiety (CA) | Q25. I am reluctant to use a computer because I am afraid that I will make mistakes that cannot be corrected. |
| Q26. When I use a computer I am scared that I might lose important data by clicking a wrong button. | |
| Q27. I feel uncomfortable when using a computer. | |
| Personal Innovation (PI) | Q28. When I am informed about a new technological tool, I find ways to experiment with it. |
| Q29. I like to experiment with new technological tools. | |
| Q30. Among my colleagues, I am usually the first person to try new technological tools. |
| Factor | Loadings | AVE | CRI | Cronbach’s |
|---|---|---|---|---|
| Visualisation Factor | 1 | 0.694 | 0.810 | 0.915 |
| Q1 | 1 | |||
| Q2 | 0.92 | |||
| Q3 | 0.92 | |||
| Reasoning Factor | 1.09 | 0.695 | 0.811 | 0.912 |
| Q4 | 1 | |||
| Q5 | 0.92 | |||
| Q6 | 0.81 | |||
| Construction Factor | 0.88 | 0.677 | 0.814 | 0.899 |
| Q7 | 1 | |||
| Q8 | 1 | |||
| Q9 | 0.98 |
| Factor | Loadings | AVE | CRI | Cronbach’s |
|---|---|---|---|---|
| Perceived ease of use | 0.692 | 0.809 | 0.915 | |
| Q13 | 1 | |||
| Q14 | 1.06 | |||
| Q15 | 0.99 | |||
| Attitude towards use | 0.707 | 0.802 | 0.930 | |
| Q16 | 1 | |||
| Q17 | 0.95 | |||
| Q18 | 0.85 | |||
| Intention to use | 0.8 | 0.726 | 0.819 | 0.936 |
| Q19 | 1 | |||
| Q20 | 1.01 | |||
| Q21 | 1.03 | |||
| Facilitating Conditions | 0.626 | 0.842 | 0.815 | |
| Q22 | 1 | |||
| Q23 | 0.97 | |||
| Q24 | 1.29 | |||
| Computer Anxiety | 0.642 | 0.833 | 0.850 | |
| Q25 | 1 | |||
| Q26 | 0.98 | |||
| Q27 | 0.91 | |||
| Personal Innovation | 0.677 | 0.814 | 0.881 | |
| Q28 | 1 | |||
| Q29 | 1.08 | |||
| Q30 | 0.88 |
| Standardised Estimates | ||||
|---|---|---|---|---|
| Outcome | Determinant | Direct | Indirect | Total |
| Intention to use ( | Attitude | 0.804 | 0.804 | |
| PEU | 0.496 | 0.496 | ||
| PLF | 0.292 | 0.292 | ||
| Computer Anxiety | −0.061 | −0.061 | ||
| Facilitating Conditions | 0.391 | 0.391 | ||
| Personal Innovation | 0.475 | 0.475 | ||
| Attitude ( | PEU | 0.617 | 0.617 | |
| PLF | 0.363 | 0.363 | ||
| Computer Anxiety | −0.076 | −0.076 | ||
| Facilitating Conditions | 0.486 | 0.486 | ||
| Personal Innovation | 0.590 | 0.590 | ||
| PEU ( | Computer Anxiety | −0.085 | −0.085 | |
| Facilitating Conditions | 0.516 | 0.516 | ||
| Personal Innovation | 0.611 | 0.611 | ||
| PLF ( | Computer Anxiety | −0.065 | −0.065 | |
| Facilitating Conditions | 0.462 | 0.462 | ||
| Personal Innovation | 0.588 | 0.588 | ||
| Variable | |
|---|---|
| VP | 0.945 |
| RP | 0.971 |
| CP | 0.830 |
| PEU | 0.510 |
| ATU | 0.589 |
| IU | 0.807 |
| PLF | 0.524 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Van Vaerenbergh, S.; Pérez-Suay, A.; Diago, P.D. Acceptance and Intentions of Using Dynamic Geometry Software by Pre-Service Primary School Teachers. Educ. Sci. 2023, 13, 661. https://doi.org/10.3390/educsci13070661
Van Vaerenbergh S, Pérez-Suay A, Diago PD. Acceptance and Intentions of Using Dynamic Geometry Software by Pre-Service Primary School Teachers. Education Sciences. 2023; 13(7):661. https://doi.org/10.3390/educsci13070661
Chicago/Turabian StyleVan Vaerenbergh, Steven, Adrián Pérez-Suay, and Pascual D. Diago. 2023. "Acceptance and Intentions of Using Dynamic Geometry Software by Pre-Service Primary School Teachers" Education Sciences 13, no. 7: 661. https://doi.org/10.3390/educsci13070661
APA StyleVan Vaerenbergh, S., Pérez-Suay, A., & Diago, P. D. (2023). Acceptance and Intentions of Using Dynamic Geometry Software by Pre-Service Primary School Teachers. Education Sciences, 13(7), 661. https://doi.org/10.3390/educsci13070661







