Abstract
Computational thinking (CT) has been accepted and embraced by educators and researchers alike, but many questions remain surrounding what concepts and topics have been used in CT, what tools have been used to help teach CT, and the current range of research on CT. In this paper, we address those questions and the state of professional development (PD) used to train teachers and preservice teachers in CT. Using a scientometrics analysis to map data from the scientific literature based on different kinds of published research, we found that most publications were published in education-related sources and that CT in relation to mathematics teaching was mostly about teaching computing skills and teaching computer programming using practice and algorithmic thinking in engineering and in STEM, mostly at the higher education level. Additionally, our results revealed that Scratch was the dominant tool used to teach programming skills at all school levels and in teacher education. Research on PD illustrated a main focus centred on improving computational thinking via programming skills in rural and urban areas of teaching. Lastly, we conclude that high-impact research outputs support the notion of computational thinking as a problem-solving process.
1. Introduction
Twenty-first-century learning necessitates positioning skill sets formed around innovation and creativity, flexibility, critical thinking, and so on. To that end, the 21st-century learner is to be equipped with many of these specific capabilities in order to align with the “…growing need to meet the increasingly complex challenges thrown up by rapid and escalating change in areas of the economy and work, technology, environment and the effects of globalisation” [1] (p. 799). In other words, equipping the 21st-century learner for the complex challenges ahead as part of the Fourth Industrial Revolution (4IR) defined in the main by technological developments through rapid connectivity, robotics, big data, artificial intelligence (AI), and so on. An important consideration in computational thinking (CT) and mathematics education is the extent to which computerisation and technology use facilitates the pedagogic relationship [2,3]. This, in many respects, is about assisting classroom teachers in learning more about the notion of CT and its applicability across a range of pedagogical contexts, both social and cultural.
The overarching purpose of this research study is to explore the capacity and applicability of practised and used methods/tools and approaches in the research literature for teaching CT through mathematics. The paper also aims to understand the range of professional development activities available for teachers on CT. We translate the data gained from our exploration by mapping the research literature to provide more practical information for classroom teachers and teacher educators to apply and use CT in their teaching practice. In addition, our paper seeks an understanding of teachers’ needs around practice in teacher programming so that researchers and educators can better assist classroom teachers with CT in the teaching of mathematics.
There is a great interest now in CT from major stakeholders (teachers, policy-makers, teacher educators, researchers, and so on) [4,5,6]. There are studies focusing on what CT is and how it is used [7,8]. Our study is geared towards the provision of practical and bibliographic perspectives on CT that we believe both editors of research journals and researchers will benefit from. The following research questions are investigated and guide the study:
- What is the range of research publications available presently aimed at teaching computational thinking?
- What are the main concepts and topics used in teaching computational thinking?
- What are the samples, methods/ways of teaching, and tools used for teaching computational thinking?
- What is the range of professional development activities for teachers and teacher training activities for preservice teachers on computational thinking?
In our paper, we acknowledge the relatively new territory of CT and how it links to mathematics education. This is to foster and build further interest around the implications of CT and its place in the mathematics classroom and school curricula more broadly. It is important that classroom teachers understand the processes of CT and how they can assist students when studying mathematics in making the necessary connections that are needed across numeric and conceptual processes. A large part of this is about helping students use CT when solving mathematical problems with the ultimate aim being the development of independent learners.
Our paper, then, is composed of six parts. Part one, the introduction, emphasises the importance of this research and includes the aim and research questions. Part two considers the notion of CT through the teaching of mathematics. It provides the background story around CT and its links to problem-solving approaches in mathematics. In doing so, key CT theorists and their contributions to the field are canvassed. Part three outlines the method undertaken in the exploration of CT and how to teach mathematics. The procedure undertaken, which includes the technique of data analysis, along with the results derived from the study, is presented in four parts. Part five is the discussion. The results obtained from the study are interpreted and links are made to the various CT approaches and mathematics teaching and learning. Part six concludes the paper. It provides a brief summary of the study and hints at possible pathways for future research around how to teach mathematics through CT.
2. Computational Thinking through Teaching Mathematics
2.1. Defining CT
In recent years, technological utilisation has accelerated at unprecedented rates, with classrooms being no exception [9,10]. This infusion of technology in both everyday lives and classrooms has impacted the ways in which teachers teach and students learn [11]. Computer science is a field that has grown alongside the technology boom. Computer science necessitates a modality of thinking that lends itself to problem solving, conceptualising, and abstraction. This type of thinking is called computational thinking (CT) and was first recognised by Dr Seymour Papert in 1980.
Papert [7] foregrounds CT to include instances when a “computer [is] used as a tool [to] effectively lead to a solution” (p. 116). He believed that concepts from computer science could be used to develop students’ mathematical thinking skills, but this notion did not gain traction until 2006 when Dr Jeannette Wing published an article in the Communications of the Association for Computing Machinery journal. Wing [8] outlined the importance of CT, noting that “computational thinking is a fundamental skill for everyone, not just for computer scientists” (p. 33). She expanded on Papert’s definition of CT when she stated CT “involves solving problems, designing systems, and understanding human behaviour, by drawing on the concepts fundamental to computer science” (p. 33). Wing’s emphasis on the importance of the thought process in systematically solving problems was reemphasised in 2011 when Wing [12] described CT as “the thought processes involved in formulating problems and their solutions so that the solutions are represented in a form that can be effectively carried out by an information-processing agent” (p. 20). In this reformed definition of CT, Wing detailed that an information-processing agent does not simply entail computers—this agent could also be a human or a combination of both. Barr et al. [13] similarly defined CT by emphasising that it is a problem-solving process that includes “formulating problems in a way that enables us to use a computer and other tools to help solve them” (p. 21). The authors also describe dispositions that are key aspects of CT, including the ability to deal with ambiguity and persist through challenging and complex problems. Most recently, Furber [14] offered a definition of CT that places the focus on interactions with the world around us: “the process of recognising aspects of computation in the world that surrounds us and applying tools and techniques from computer science to understand and reason about both natural and artificial systems and processes” (p. 29). Furber’s definition of CT recognises the situated nature of learning, a notion supported by several researchers that have explored CT through “computational participation” [15,16].
With numerous definitions of CT comes the opportunity and space for confusion. Aho [17] points out that as educators and researchers have used the word “computation” without qualification, the door for misunderstanding has swung open. What contributes to this problem is that “the nature of systems exhibiting computational behaviour is varied and the term computation means different things to different people depending on the kinds of computational systems they are studying and the kinds of problems they are investigating” [17] (p. 832). Mathematics has been historically viewed by many as a complex and challenging subject [18], and maths is certainly not immune to the issue highlighted by Aho [17].
Researchers have argued the importance of defining CT in mathematics, noting the reciprocal relationship of learning between CT and mathematics [19]. In mathematics, CT has been defined as “a problem-solving process” [20]. This mirrors the current attention given to CT in many education policy initiatives, standards, curricula and courses as a generic all-purpose skill and capacity that all students should possess once finished with formal schooling [21]. Whilst many nations across the globe have incorporated CT into curricula (Australia, New Zealand, Russia, South Africa, and the UK), much of it remains at a level that supports learning as part of a broader topic under study. This reflects the information-processing side of CT, which some suggest is not enough of a reason for it to be incorporated in formal school-based curricula as it is not seen as a general subject, discipline-specific enough, or multidisciplinary. There are questions surrounding its actual distinctiveness as a form of thinking amongst students [22].
2.2. CT in Mathematics
The incorporation of CT into mathematics education is not without its complications. Chief amongst them is formulating truly authentic student learning experiences that connect deep conceptual mathematical material with actual real-world scenarios [23]. Kallia et al. [24] suggest that the embedding of CT in mathematics education should hinge on three areas: problem solving, cognitive processes, and transposition. Their systematic literature review of CT in mathematics education revealed that student learning experiences that focus attention towards specific “thinking processes” provide the pedagogical link between the computational and mathematics disciplines. To this end, learning experiences that focus upon and foster “abstraction, decomposition, pattern recognition, algorithmic thinking, modelling, logical thinking and automation, followed by analytical thinking, generalisation and evaluation of solutions and strategies” [24] (p. 179) are of most value. This is because there is pedagogic flexibility inherent within CT that allows for its application “in a variety of ways that reflect authentic disciplinary contexts in which students connect learning and doing inside communities of practice” [24] (p. 180).
Across the world, CT in K–12 mathematics classrooms look quite different. In many countries, CT is not explicitly mentioned in curricula such as textbooks and standards, but Mannila et al. [25] detail that topics and activities with the potential to introduce CT may be widespread in K–12 classrooms. To better understand the landscape of curricula related to CT and teachers’ perceptions of this material, a survey was given to 961 primary and secondary teachers across five European countries. Mannila et al. [25] found that teachers reported the use of all nine aspects of CT as described by the International Society for Technology in Education and the American Computer Science Teachers Association in their teaching, with data collection, analysis, and representation being used the most in teaching. This finding indicates that many aspects of CT are being used by mathematics teachers from countries around the world. Not only do many teachers believe that aspects of CT are used frequently in their teaching, but teachers across many countries have expressed increasing amounts of enthusiasm for computer science education [26].
In mathematics, the computation aspect of CT was not strongly connected to the thinking element of CT until mathematics educators began emphasising how important it is for students to make sense of the mathematics they are doing, rather than simply computing or engaging in a more rote way of learning [27]. As a way to engage students in doing and learning mathematics, educational games such as Scratch have utilised CT to challenge and create learning opportunities in STEM [28,29]. Scratch, Alice, Frog Pond Evolution, and other educational games that utilise CT, many of which foreground coding and computer science-related topics, have benefits for students’ learning as they give students more ownership, agency, and freedom over their learning than traditional learning environments (see [30]). Four key elements utilised in educational games that employ CT, such as Scratch and Makey Makey, are freedom to fail, rapid feedback, progression, and storytelling [31]. By gamifying the learning experience, students are drawn to doing mathematics and engaging in CT. Prior research has found that as early as primary school, students can develop skills related to coding and benefit from early exposure to coding and programming languages [32,33]. Using coding as an access point to engage in CT can allow students to develop the skills and tools needed to deeply engage in mathematics.
2.3. CT in Teacher Education
In order to lessen the gap between interest and practice, Yadav et al. [26] assert the importance of redesigning teacher-education courses so that educational technology can be taught with a focus on CT and how to foster an environment conducive to CT. Several other researchers [9,34] have described how teachers can shape their instruction to encourage a CT perspective. Lye and Koh [9] report a constructionist environment, where problem-solving is emphasised, facilitating CT, and Csizmadia et al. [34] similarly foreground CT in algorithmic thinking and learning to generalise patterns. These researchers strongly put forward instructional methods teachers can use to assist students in developing CT skills. Other researchers have documented the ways in which CT instructional interventions and assessments have affected students’ proficiencies and skills related to algorithmic constructs [35,36]. Vourletsis et al. [36] employed a “CT instructional intervention on students’ testing and debugging proficiency level and strategy use” (p. 20), finding that multiple learning units in the CT instructional intervention significantly improved students’ testing and debugging skills. The study highlighted the ability of instructional practice to increase students’ engagement and, as a consequence, increase students’ proficiencies related to algorithmic concepts. Grover [35] explored the way assessments as part of Foundations for Advancing Computational Thinking (FACT), a middle school computing curriculum, captured students’ knowledge related to algorithmic thinking. The assessments, which included directed and open-ended assignments in Scratch as well as other formative and summative assessments, were able to address multiple facets of students’ understanding while also giving students various opportunities to showcase their learning and thinking. Students expressed enjoyment towards several assessments embedded in the FACT curriculum and noted that contextualised projects and assessments were especially fun.
Another portion of research on CT in teacher education has sought to better understand how workshops, professional development, and other training have helped increase in-service teachers’ understanding of CT [37,38]. Bort and Brylow [37] designed a computer science and CT workshop for high school teachers aimed at helping teachers integrate computer science and CT concepts into a classroom setting. To understand how the teachers planned to incorporate computer science and CT into their teaching, the researchers evaluated lesson plans, produced as an activity in a workshop. Bort and Brylow [37] found that teachers struggled to effectively integrate concepts of CT into lessons “that would hold any meaningful significance with the students in their classrooms” (p. 430). They also discovered that many teachers were unable to differentiate computer science and CT, a sentiment addressed by others [22]. Yadav et al. [38] designed a similar professional development course intended to help teachers support students in developing CT by examining how CT could be integrated into scientific inquiry. The research team found that the professional development course aided in teachers’ development of CT concepts and skills, with many teachers citing the role technology had in acting as a vehicle to engage students in CT. Yadav et al. [38] recommended the development of new assessments to capture teachers’ learning and understanding of CT to allow researchers to effectively design and implement professional development.
Now that we have briefly reviewed the literature on CT and illustrated how CT has been defined, used in mathematics, and integrated into teacher education, we will address our research questions by utilising an evaluative scientific mapping of CT in mathematics. We will turn to the methodology used to answer our research questions. We detail the steps taken in our scientometric analysis and lay out how data from the literature on CT were mapped using VOS.
3. Materials and Methods
3.1. Method
We used evaluative scientific mapping to answer the research questions of this study. The scientometrics analysis was used to map the data coming from the scientific literature based on different kinds of published research [39] (p. 9). We utilised the software VOSviewer using the network and density analysis based on a term co-occurrence map on text data along with an evaluative systematic review analysis [40].
3.2. Procedure and Data Analysis
We performed searches for peer-reviewed articles using Web of Science (WoS) Clarivate, which is a comprehensive and high-impact database in the Social Science Citation Index and Scimago Q1 and Q2 journals. We excluded review articles, book chapters, and editorials considering more empirical results can provide more information on the impact of research done in the computational thinking area in relation to mathematics education.
There are review papers on the concept of CT, the use of Scratch, CT in STEM, and CT in specific schooling years in the literature either using all publications from many databases or from years up to 2018 [9,41,42,43,44,45,46,47].
We sought to analyse published research specifically focusing on mathematics teaching but not a specific schooling level through CT between 2018 and 2022.
We started our search using the term “computational thinking” and “mathematics teaching/instruction” using the database of WoS Clarivate. The first search returned 248 publications. After excluding book chapters, review papers, and editorials, our search yielded 233 published research items, mostly papers, along with some conference papers.
In the results section, we will first provide the descriptive analytics for the publications followed by the analysis using VOSviewer for all 233 publications and, finally, the evaluation of the most cited publications. We will further analyse the most cited publications in detail by the utilisation of systematic and evaluative review analysis in relation to their methods of teaching and concepts and topics studied in teaching mathematics.
To broadly capture the picture of the research literature under study, we have not excluded articles incorporating mathematics teaching and other systematic review papers via other disciplines. There is also a focus on teaching mathematics in higher education.
4. Results
4.1. The Range of Research Publications Aiming to Teach CT through Mathematics
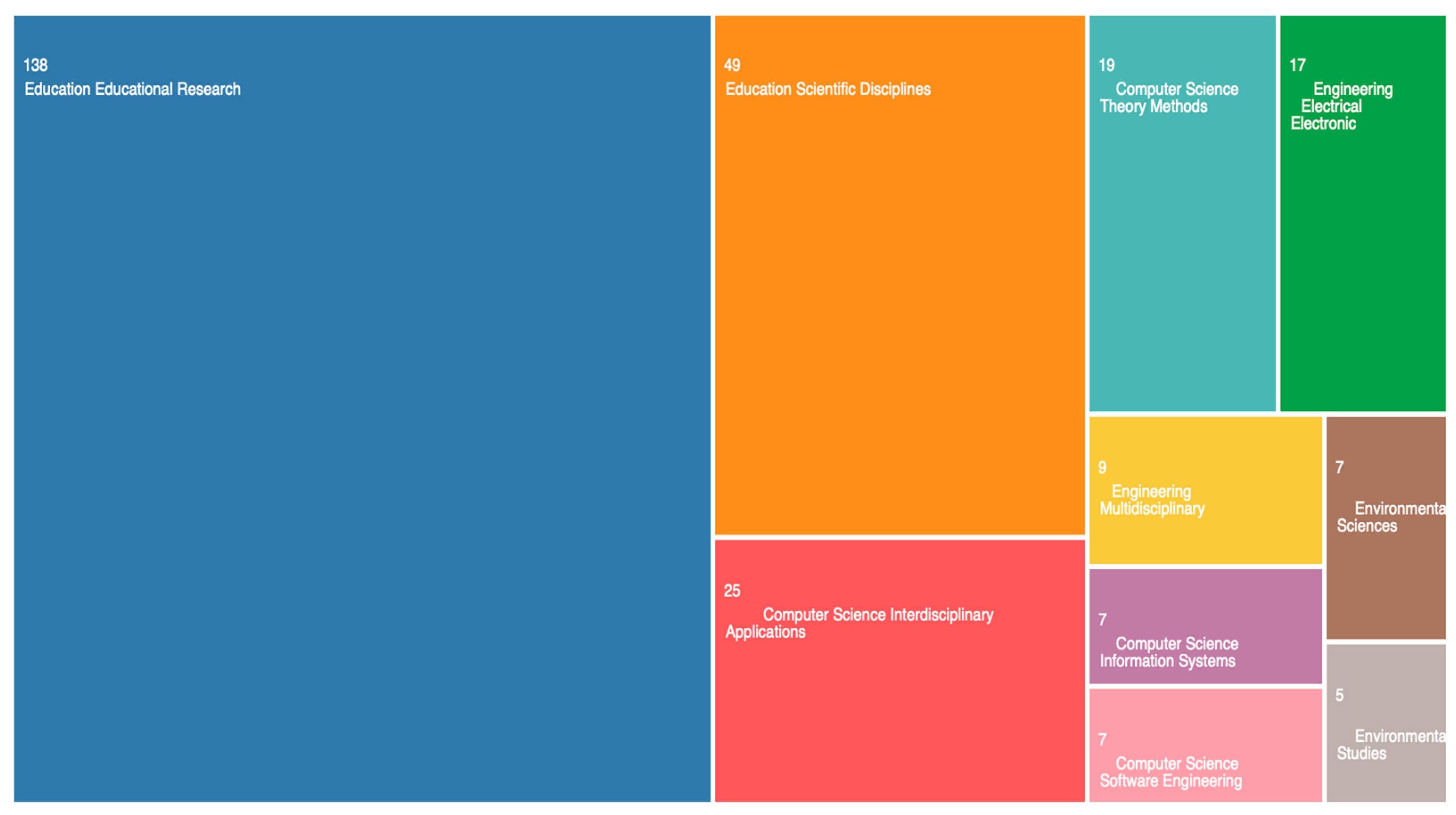
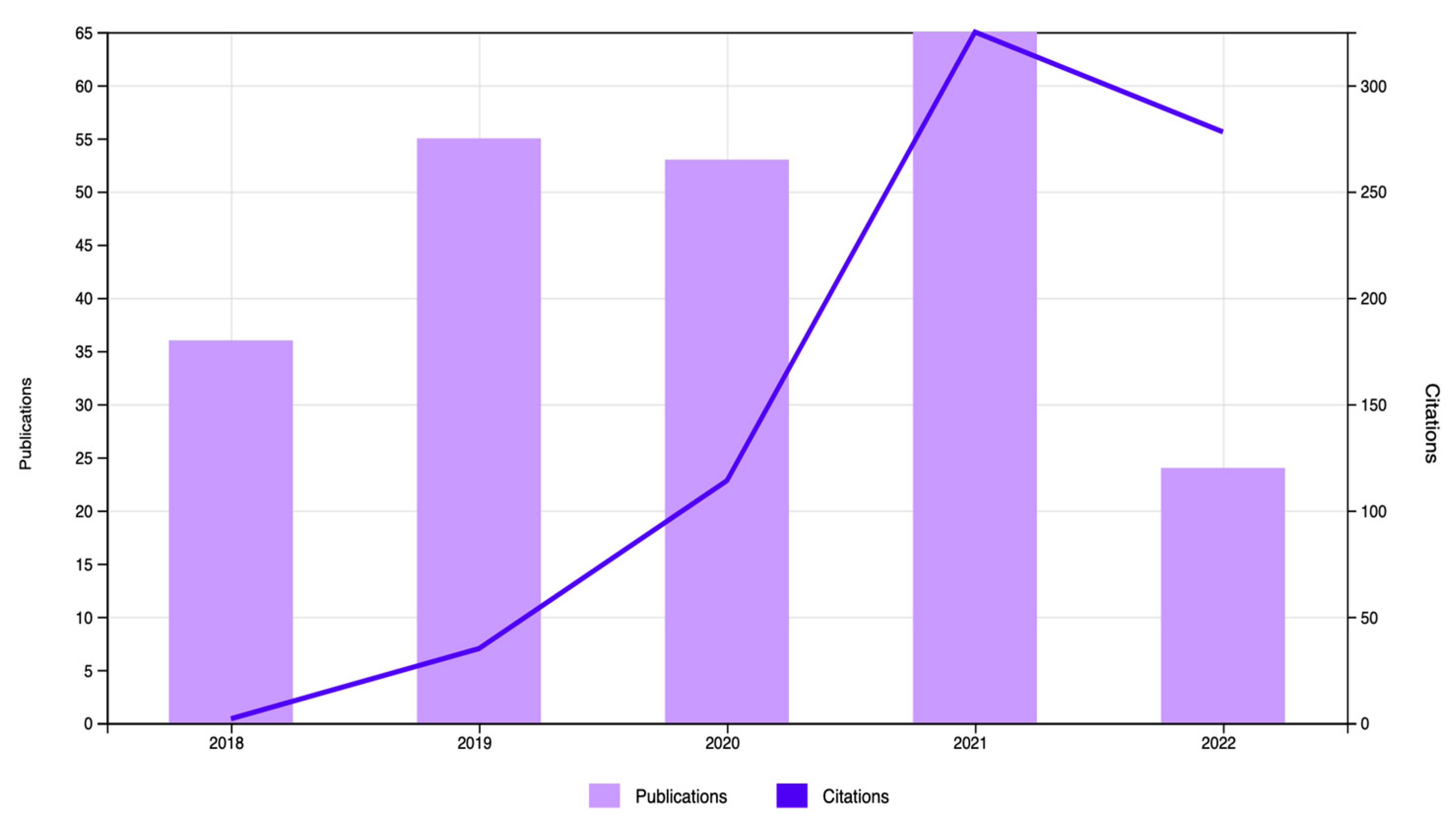
Queries were performed in July 2022, which yielded 233 publications classified by their authors, title, keywords, abstracts, and source titles. Below, Figure 1 from Web of Science website summarises the area of sources across the number of publications, and Figure 2 shows the publication trends based on years of publication and the number of citations each paper has.
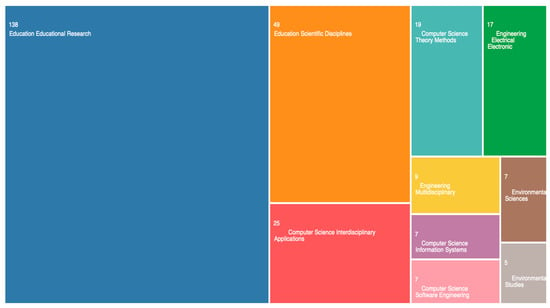
Figure 1.
Area of sources for all publications (The areas on the chart are not strictly proportional to the values of each entry).
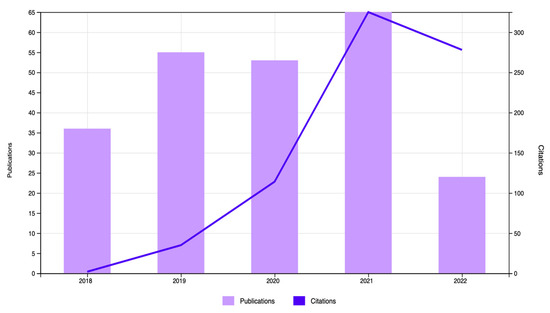
Figure 2.
Publication trends across years.
Figure 1 clearly shows that most of the publications were published in education-related sources (59% and 21%) even though some areas are related and intertwined. For example, some publications in the “education, educational research” (59%) category can also be considered in “educational specific disciplines” (21%), but education-related sources account for the largest area of the total shape. The largest areas not related to education were “computer science interdisciplinary applications (11%) and “computer science theory methods” (8%). As our focus was on using CT in teaching mathematics, we expected to see education-related areas as part of the larger whole. Figure 2, on the other hand, demonstrates the attention CT has had from researchers in recent years, especially since 2018, which was the focus of this study. The number of citations starts ascending in 2018 with fewer than 5 citations, picking up in 2021 with more than 65 citations, and then descending in 2022. The drop in 2022 should not be considered a decrease in the attention given to CT papers since this analysis was performed in the first half of 2022, so there is scope for an increase over the course of the year.
4.2. The Concepts and Topics Used in Teaching CT through Mathematics
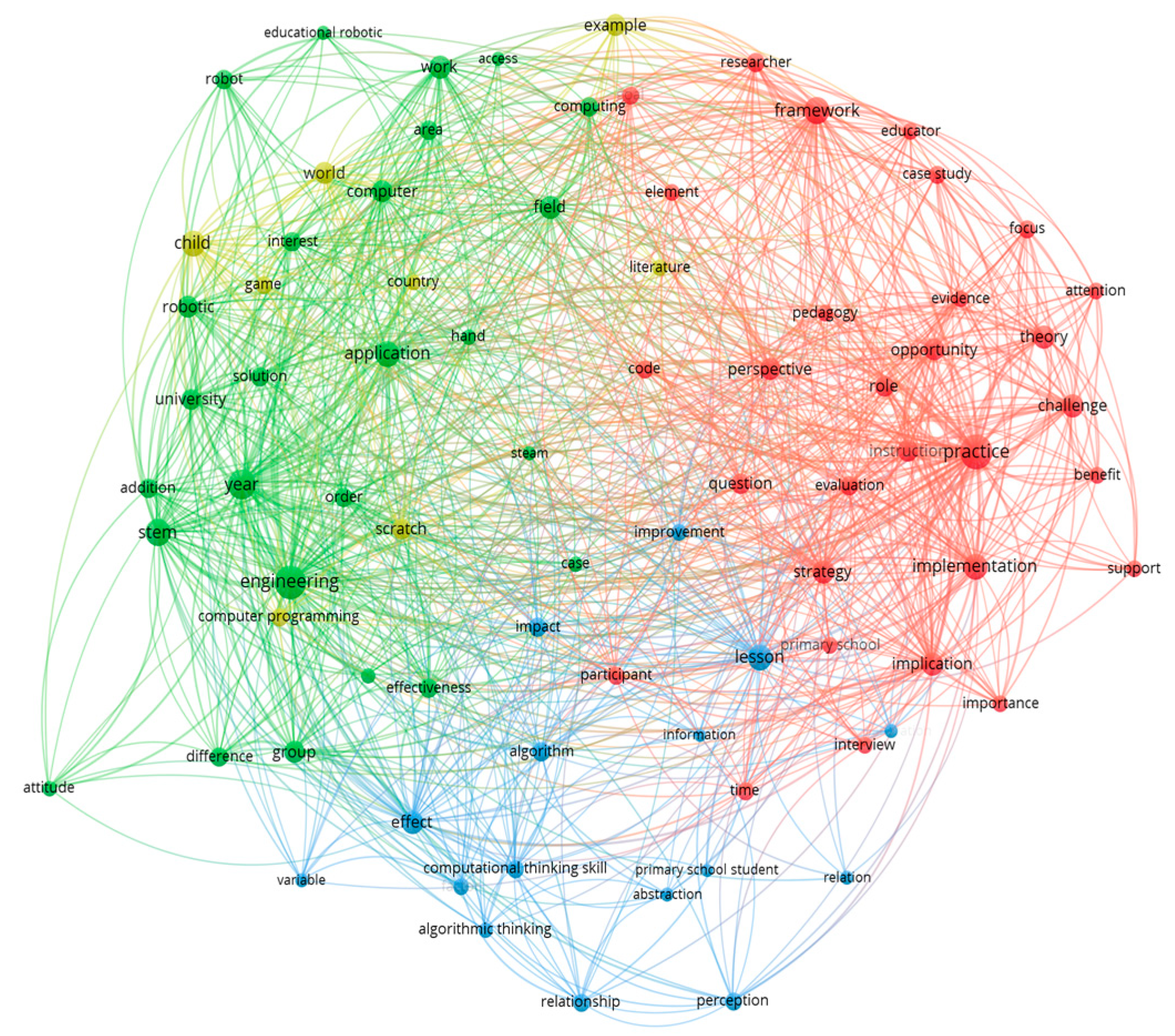
We utilised the VOSviewer visualisation tool to analyse the co-occurrences of keywords in clusters. The label and circle sizes of a term depend on that keyword’s weight and keywords are grouped together into clusters based on their shared characteristics, the heavier a keyword, the larger its label and circle. A keyword’s weight serves as a proxy for the cluster’s significance. When two keywords are connected by a line, that link between them and all other links the keyword has with other keywords is considered to be strong. The strength of a relationship reveals the proportion of publications where two keywords appear together [48].
The first cluster with 30 terms is represented by a red colour, cluster two by green with 26 terms, cluster three by blue with 16 terms, and cluster four by yellow with 8 terms. The bigger circles of terms show stronger links to other terms providing an indication of the most-used terms.
Based on network visualisations (Figure 3), CT in relation to mathematics teaching was mostly researched based on teaching computing skills, computer programming using practice, and algorithmic thinking in engineering and in STEM, mostly at the higher education level. There is also some research based on primary schools, focusing on using Scratch and games as part of teaching programming skills.
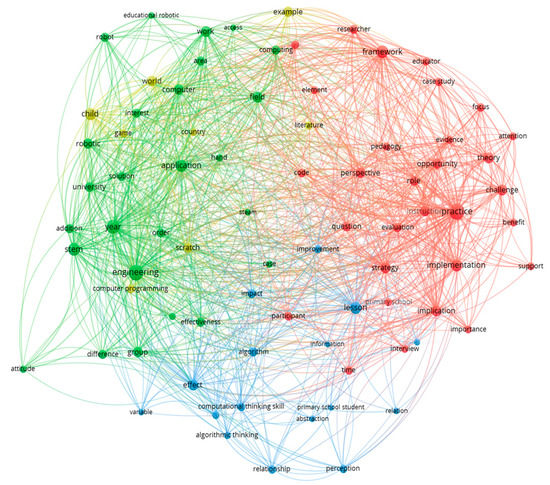
Figure 3.
Network visualisation of CT in mathematics teaching.
In Figure 4, it is clearly seen that the most important terms in clusters were: practice implementation, perspective, framework, challenge, instruction, and implication (first large cluster in red); engineering, application, effectiveness, lesson, algorithmic thinking, and computer (in the second large cluster in green); lesson, impact, effect, computational and algorithmic thinking, perception, and relationship (in the third large cluster in blue); Scratch, computer programming, and game in the fourth and final large cluster (in yellow), amongst some other terms.
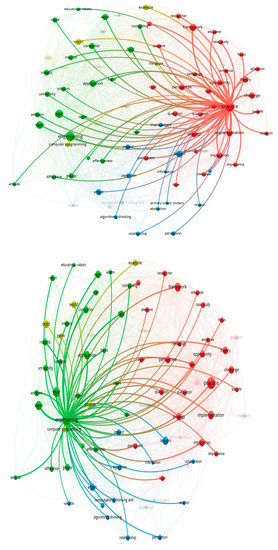
Figure 4.
Cluster visualisations in detail.
4.3. The Tools and Methods/Ways of Teaching CT through Mathematics
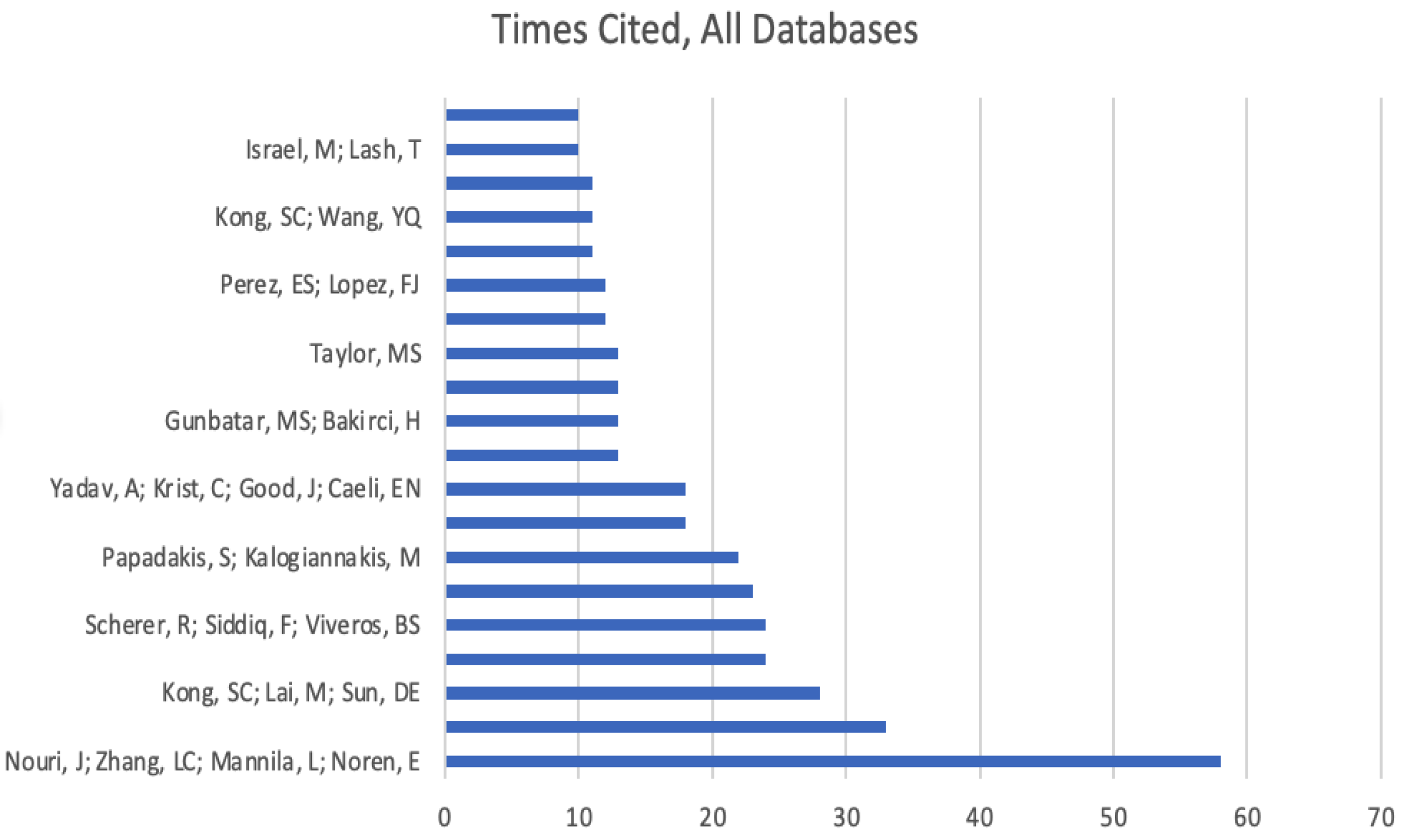
To answer research question 3, we first analysed the high-impact publications that are highly cited, with more than 10 citations. Our search returned 20 publications with 10 or more than 10 citations for each. Three of these articles were not specifically related to teaching computational thinking, they were either related to a framework study or the history of a tool and the maturity of engineering students. Hence, our analysis was focused on 17 articles, which are summarised below in Table 1, and Figure 5 presents the number of citations per author amongst the most highly cited research.

Table 1.
Research publications with citation numbers.
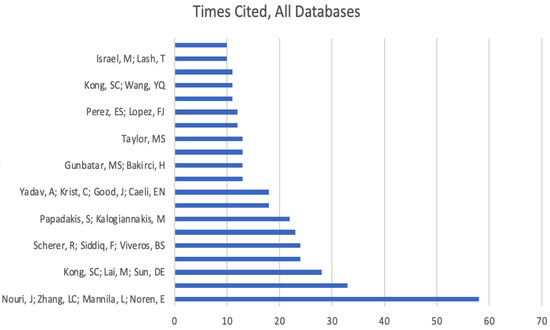
Figure 5.
Number of citations per author.
Table 2 maps the tools and methods/ways of teaching in the above 17 articles in detail. The papers were coded by their sample (1a–1d for “in-service teachers”; 2a–2b for “preservice teachers”; 3a–3f for “Primary School Students”; 4a–4c for “high school students” 5a–5b for “meta-analysis papers”, and 6a for “teachers”) and numbered with the same letters for similar samples. Based on their similarities and differences, we further analysed these data by clustering them according to their sample types to reveal their methods of teaching and tools to teach computational thinking skills in mathematics. The results for in-service teachers (1a–1d) were presented in the next section to respond to the fourth research question in detail. In Table 2, we presented a brief summary of the results, which are then discussed in the discussion section.

Table 2.
Summary of tools/methods/ways of teaching in research publications.
Our results revealed that Scratch was the dominating tool used to teach programming skills at all school levels and in teacher education. In primary years (3a–3f), code.org was also utilised to integrate science and mathematics disciplines and drawing spirolaterals was another method before introducing programming tools in teaching programming skills. For lower primary years (pre-K through grade 2), LOGO was the preferred tool since it is more age-appropriate for coding. For high school students, LightBot-type robotic games and smartphones were also used to teach programming. The LightBot app can be downloaded, and it introduces students to computational thinking basics (algorithms, iterations, and abstractions). It does not require students to create code; instead, it has a drag-and-drop function for programming. For initial teacher education (2a–2b), Scratch is the heavily used tool to introduce programming basics to preservice teachers so they can familiarise themselves with the basics of programming. In terms of methods and ways of teaching, in the primary years, instructional activities were mostly based on improving conceptual understanding of programming basics (e.g., using metaphors) and being familiar with programming tools through hands-on activities. In the high school years (4a–4c), teaching methods were structured around the subject matter rather than merely focusing on programming skills (e.g., learning electric circuits and the biological process function); hence, other apps and smartphones were included from time to time in the instruction process. Two large meta-analyses focused on the effectiveness of programming interventions, especially via visualisation tools and main instructional approaches. These meta-analysis papers (5a–5b) further revealed the tools and instructional methods. According to their results, short-term interventions, extra-curricular activities, and metacognitive instruction are the most effective methods of teaching, especially when used in group activities. Individual work and problem solving was a moderately effective method of teaching. Scratch and Arduni were the most effective tools used in students’ learning of programming. Lastly, a research paper (6a) mentioned understanding students’ skills while they are learning programming as important. The teachers were teaching computational skills via RoBots, block programming and text-based programming, and Scratch for approximately two years. Teachers were interviewed and asked what they thought about their students’ skills in programming based on their teaching experience. Teachers stated that they believed their students learned and developed skills of fundamental computational practices as well as dispositional skills while they engaged in learning programming.
4.4. Professional Development Activities for Teachers and Teacher Training Activities for Preservice Teachers on Computational Thinking
The research papers (1a–1c) in Table 1 address the professional development (PD) aspect. Some of these papers targeted providing PD to only primary teachers while others aimed to develop teachers from primary through secondary schools. The main focus of PD was improving computational thinking via programming skills in rural and urban areas of teaching. They also focused on the culturally responsive teaching of computational thinking skills. The main tool used in this PD was Scratch along with MINDSTORMS, AgentSheets and AgentCubes, and App Inventor. The results from this PD showed its effectiveness in developing teachers’ capabilities to devise programming education and practice via various methods and tools. Teachers also developed their understanding of programming and their teaching efficacy and outcome expectancy in teaching computational thinking skills to their students.
5. Discussion and Translation of Research Outputs for Teacher and Educator Practice
Through this research, we aimed to explore the capacity and applicability of methods/tools and approaches used for computational thinking through mathematics based on the research literature. Based on scientific mapping analysis, we found that core coding, computing skills, and related keywords were mostly used in higher education institutes such as engineering, teacher education, STEM disciplines, and high schools. In primary schools, the key concepts were around game-based learning in learning computational skills via text-based programming, RoBots, block programming tools, and especially Scratch and LOGO.
In terms of the tools used in teaching CT through mathematics, we found that Scratch was a heavily used tool in teaching programming skills at primary and secondary schools, teacher education, higher education, and professional development programs for teachers. In addition to Scratch, in high schools, there were other tools utilised, such as LightBot-type robotic games (LightBot introduces main concepts such as algorithms, iterations, and abstractions with a drag-and-drop function for programming). In lower primary, LOGO is the most preferred tool for teaching programming to younger children.
As the instructional method used for primary years, an integrated model was mostly used by combining science and mathematics disciplines to teach computational thinking/programming as well as making use of drawing spirolaterals through problem-solving tasks [49].
For younger children, metaphors were also used to improve their conceptual understanding as well as make use of hands-on activities through manipulatives [50]. For the high school years and preservice teacher education, there was a subject-based model rather than focusing on only programming skills (e.g., learning electric circuits and biological process functions, multimedia course); therefore, instructional methods varied where the concepts required explicit or project-based teaching [51,52].
In terms of the results from the most-cited and high-impact papers, students improved their computational practices such as abstracting/modularising, reusing code, and debugging code [53] and positive disposition skills such as building self-confidence and responsibility for their own learning in primary, middle, and high school years [54]. Teachers of these students saw their students acquire skills that they themselves might not fully possess. Students in high schools improved their confidence in programming subject-based activities such as programming microcontrollers using electrical circuits [52]. They also improved their understanding of AI systems [55] and the acquisition of computational concepts and the comprehension of mathematical ideas [54]. Some research results suggested that biology classes are excellent environments for CT because biological processes are systems that must be understood through algorithmic thinking and problem-solving abilities [53].
The results from two large meta-analyses [56,57] highlighted that short-term teaching interventions and extra-curricular activities, rather than a term- or year-long teaching mode, were more effective for students to learn programming skills. Metacognitive activities in teaching programming were also more effective than cognitive instructional activities such as problem solving, specifically when they were used as collaborative group activities. This research also pointed out Scratch and Arduni as the most effective tools in teaching programming.
In teacher education programs, Scratch was found to be a useful tool in teaching programming skills to Preservice teachers [51]. It is suggested that game development projects using Scratch enhance preservice teachers’ computational thinking abilities.
The PD focusing on improving computational thinking skills for in-service teachers was effective, and the workshops developed teachers’ efficacy beliefs and outcome expectancies in using programming in their teaching [58]. The teachers who had PD also improved their teaching of equitable STEM practices [47,59].
Some research using structural equation models has provided evidence that posing questions can directly promote computational identity formation during the primary school years through the ability to make connections [60]. For primary students, it is useful to integrate computer science, and computational thinking into mathematics instruction with increasing complexity to teach concepts such as sequencing, looping, and conditional logic. It is also suggested that the activities should flow from less integrated to more integrated with a discipline-specific conceptual understanding to build and develop programming skills [61]. High school activities should focus on modelling and simulation practices, focusing on problem-solving activities to promote computational thinking skills [53] and computational thinking in mathematics instruction with increasing complexity to teach concepts such as sequencing, looping, and conditional logic. It is also suggested that the activities should flow from less integrated to more integrated with a discipline-specific conceptual understanding to build and develop programming skills [61]. High school activities should focus on modelling and simulation practices focusing on problem-solving activities to promote computational thinking skills [53].
6. Conclusions
Computational thinking is a necessary skill that needs to be imparted to our students in today’s world. Researchers, educators and all stakeholders of education are aware of this and are working on how to frame and scaffold these skills for their students. We sought to explore what the research on CT has to say to practitioners and researchers in order to understand what CT is, why it is necessary, and how it can help students understand algorithms and data, especially in terms centred around activities utilising simulations. In this way, we can develop strategies to develop this important skill in students. We view CT as a problem-solving process and adopt [13] an operational definition advocated by Barr et al. (2011) because it supports the idea of developing CT skills and components across the curriculum through all grade levels and content areas. Barr et al. (2011) define CT as (i) “Formulating problems in a way that enables us to use a computer and other tools to help solve them, (ii) Logically organising and analysing data, (iii) Representing data through abstractions, such as models and simulations, (iv) Automating solutions through algorithmic thinking, (v) Identifying, analysing, and implementing possible solutions with the goal of achieving the most efficient and effective combination of steps and resources, and (vi) Generalising and transferring this problem-solving process to a wide variety of problems” (p. 21).
Our results suggest that some of these components are fully researched, and some are limited in their research, whilst others were not in top impact-factor journals, as detailed in the discussion section of this study. For example, formulating problems suitable for a computer and other tools to help solve them was used in most of the articles examined; however, automating solutions via algorithmic thinking was rarely researched. We conclude that CT is viewed in the current research literature as a problem-solving process that allows both human and computer-assisted approaches to aid in the understanding of complex problems. Future research should focus on developing practical frameworks to teach CT at any grade level and in any subject area.
Author Contributions
Conceptualization, Z.E.; writing—original draft, Z.E., M.S. and A.S.; writing—review and editing, Z.E., M.S. and A.S.; project administration, Z.E. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
This study did not require ethical approval.
Informed Consent Statement
Not applicable.
Data Availability Statement
The data is accessible via web of science data base.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Williams, C.; Gannon, S.; Sawyer, W. A genealogy of the ‘future’: Antipodean trajectories and travels of the ‘21st century learner’. J. Educ. Policy 2013, 28, 792–806. [Google Scholar] [CrossRef]
- Harris, J.; Hofer, M. Technological pedagogical content knowledge (TPACK) in action: A descriptive study of secondary teachers’ curriculum-based, technology-related instructional planning. J. Res. Technol. Educ. 2009, 41, 235–263. [Google Scholar] [CrossRef]
- Ertmer, P.A.; Ottenbreit-Leftwich, A.T.; Sadik, O.; Sendurur, E.; Sendurur, P. Teacher beliefs and technology integration practices: A critical relationship. Comput. Educ. 2012, 59, 423–435. [Google Scholar] [CrossRef]
- Australian Curriculum, Assessment and Reporting Authority. Australian Curriculum: Digital Technologies; Australian Curriculum, Assessment and Reporting Authority: Sydney, NWS, Australia, 2013. [Google Scholar]
- National Research Council. Report of a Workshop on the Scope and Nature of Computational Thinking; National Academies Press: Washington, DC, USA, 2010. [Google Scholar]
- European Commission. Opening up Education: Innovative Teaching and Learning for All through New Technologies and Open Educational Resources; European Commission: Brussels, Belgium, 2013. [Google Scholar]
- Papert, S. An exploration in the space of mathematics educations. Int. J. Comput. Math. Learn. 1996, 1, 95–123. [Google Scholar] [CrossRef]
- Wing, J.M. Computational thinking. Commun. ACM 2006, 49, 33–35. [Google Scholar] [CrossRef]
- Lye, S.Y.; Koh, J.H.L. Review on teaching and learning of computational thinking through programming: What is next for K-12? Comput. Hum. Behav. 2014, 41, 51–61. [Google Scholar] [CrossRef]
- Nouri, J.; Zhang, L.; Mannila, L.; Norén, E. Development of computational thinking, digital competence and 21st century skills when learning programming in K-9. Educ. Inq. 2019, 11, 1–17. [Google Scholar] [CrossRef]
- Law, N.; Pelgrum, W.J.; Plomp, T. (Eds.) Pedagogy and ICT Use in Schools around the World: Findings from the IEA SITES 2006 Study; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008; Volume 23. [Google Scholar]
- Wing, J. Research notebook: Computational thinking—What and why. Link Mag. 2011, 6, 20–23. [Google Scholar]
- Barr, D.C.; Harrison, J.; Conery, L. Computational Thinking: A Digital Age Skill for Everyone. Learn. Lead. Technol. 2011, 38, 20–23. [Google Scholar]
- Furber, S. Shut Down or Restart? The Way Forward for Computing in UK Schools; The Royal Society: London, UK, 2012; Available online: https://royalsociety.org/~/media/education/computing-in-schools/2012-01-12-computing-in-schools.pdf (accessed on 1 November 2022).
- Kafai, Y.B. From computational thinking to computational participation in K--12 education. Commun. ACM 2016, 59, 26–27. [Google Scholar] [CrossRef]
- Kafai, Y.B.; Burke, Q. Connected Code: Why Children Need to Learn Programming; Mit Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Aho, A.V. Computation and computational thinking. Comput. J. 2012, 55, 832–835. [Google Scholar] [CrossRef]
- Cornell, C. I hate math! I couldn’t learn it, and I can’t teach it! Child. Educ. 1999, 75, 225. [Google Scholar]
- Weintrop, D.; Beheshti, E.; Horn, M.; Orton, K.; Jona, K.; Trouille, L.; Wilensky, U. Defining computational thinking for mathematics and science classrooms. J. Sci. Educ. Technol. 2016, 25, 127–147. [Google Scholar] [CrossRef]
- Computer Science Teachers Association. Operational Definition of Computational Thinking for K-12 Education. Computer Science Teachers Association. 2011. Available online: https://cdn.iste.org/www-root/Computational_Thinking_Operational_Definition_ISTE.pdf (accessed on 1 November 2022).
- Kafai, Y.B.; Proctor, C. A Revaluation of Computational Thinking in K–12 Education: Moving Toward Computational Literacies. Educ. Res. 2021, 51, 146–151. [Google Scholar] [CrossRef]
- National Research Council. Report of a Workshop on the Pedagogical Aspects of Computational Thinking; National Academies Press: Washington, DC, USA, 2011. [Google Scholar]
- Pérez, A. A framework for computational thinking dispositions in mathematics education. J. Res. Math. Educ. 2018, 49, 424–461. [Google Scholar] [CrossRef]
- Kallia, M.; van Borkulo, S.P.; Drijvers, P.; Barendsen, E.; Tolboom, J. Characterising computational thinking in mathematics education: A literature-informed Delphi study. Res. Math. Educ. 2021, 23, 159–187. [Google Scholar] [CrossRef]
- Mannila, L.; Dagiene, V.; Demo, B.; Grgurina, N.; Mirolo, C.; Rolandsson, L.; Settle, A. Computational thinking in K-9 education. In Proceedings of the Working Group Reports of the 2014 on Innovation & Technology in Computer Science Education Conference, Uppsala, Sweden, 23–25 June 2014; pp. 1–29. [Google Scholar]
- Yadav, A.; Stephenson, C.; Hong, H. Computational thinking for teacher education. Commun. ACM 2017, 60, 55–62. [Google Scholar] [CrossRef]
- Li, Y.; Schoenfeld, A.H. Problematizing teaching and learning mathematics as “given” in STEM education. Int. J. STEM Educ. 2019, 6, 1–13. [Google Scholar] [CrossRef]
- Kalogiannakis, M.; Papadakis, S. Preparing Greek Pre-service Kindergarten Teachers to Promote Creativity: Opportunities Using Scratch and Makey Makey. In Children’s Creative Inquiry in STEM; Sociocultural Explorations of Science Education; Murcia, K.J., Campbell, C., Joubert, M.M., Wilson, S., Eds.; Springer: Cham, Switzerland, 2022; Volume 25. [Google Scholar] [CrossRef]
- Papadakis, S. Apps to Promote Computational Thinking and Coding Skills to Young Age Children: A Pedagogical Challenge for the 21st Century Learners. Educ. Process: Int. J. (EDUPIJ) 2022, 11, 7–13. [Google Scholar] [CrossRef]
- Erickson, A.; Lundell, J.; Michela, E.; Pfleger, I. Gamification. In The Students’ Guide to Learning Design and Research; Kimmons, R., Ed.; EdTech Books: London, UK, 2018; Available online: https://edtechbooks.org/studentguide/gamification (accessed on 10 December 2022).
- Stott, A.; Neustaedter, C. Analysis of Gamification in Education. Simon Fraser University. [Unpublished Manuscript]. 2013. Available online: http://clab.iat.sfu.ca/pubs/Stott-Gamification.pdf (accessed on 20 January 2023).
- Papadakis, S. The impact of coding apps to support young children in computational thinking and computational fluency. A literature review. Front. Educ. 2021, 6, 1–12. [Google Scholar] [CrossRef]
- Papadakis, S.; Kalogiannakis, M.; Zaranis, N. Teaching mathematics with mobile devices and the Realistic Mathematical Education (RME) approach in kindergarten. Adv. Mob. Learn. Educ. Res. 2021, 1, 5–18. [Google Scholar] [CrossRef]
- Csizmadia, A.; Curzon, P.; Dorling, M.; Humphreys, S.; Ng, T.; Selby, C.; Woollard, J. Computational Thinking-A Guide for Teachers; Commonwealth of Learning: Burnaby, BC, Canada, 2015. [Google Scholar]
- Grover, S. Assessing Algorithmic and Computational Thinking in K-12: Lessons from a Middle School Classroom. In Emerging Research, Practice, and Policy on Computational Thinking; Educational Communications and Technology: Issues and Innovations; Rich, P., Hodges, C., Eds.; Springer: Cham, Switzerland, 2017. [Google Scholar] [CrossRef]
- Vourletsis, I.; Politis, P.; Karasavvidis, I. The Effect of a Computational Thinking Instructional Intervention on Students’ Debugging Proficiency Level and Strategy Use. In Research on E-Learning and ICT in Education; Tsiatsos, T., Demetriadis, S., Mikropoulos, A., Dagdilelis, V., Eds.; Springer: Cham, Switzerland, 2021. [Google Scholar] [CrossRef]
- Bort, H.; Brylow, D. CS4Impact: Measuring computational thinking concepts present in CS4HS participant lesson plans. In Proceedings of the 44th Technical Symposium on Computer Science Education, Denver, CO, USA, 6–9 March 2013; ACM: New York, NY, USA, 2013; pp. 427–432. [Google Scholar]
- Yadav, A.; Krist, C.; Good, J.; Caeli, E.N. Computational thinking in elementary classrooms: Measuring teacher understanding of computational ideas for teaching science. Comput. Sci. Educ. 2018, 28, 371–400. [Google Scholar] [CrossRef]
- McBurney, M.K.; Novak, P.L. What is bibliometrics and why should you care? In Proceedings of the International Professional Communication Conference, Portland, OR, USA, 20 September 2002; IEEE: New York, NY, USA, 2002; pp. 108–114. [Google Scholar]
- Van Eck, N.J.; Waltman, L. Software Survey: VOSviewer, a Computer Program for Bibliometric Mapping. Scientometrics 2010, 84, 523–538. [Google Scholar] [CrossRef] [PubMed]
- Barcelos, T.S.; Muñoz-Soto, R.; Villarroel, R.; Merino, E.; Silveira, I.F. Mathematics Learning through Computational Thinking Activities: A Systematic Literature Review. J. Univers. Comput. Sci. 2018, 24, 815–845. [Google Scholar]
- Hickmott, D.; Prieto-Rodriguez, E.; Holmes, K. A Scoping Review of Studies on Computational Thinking in K–12 Mathematics Classrooms. Digit. Exp. Math Educ. 2018, 4, 48–69. [Google Scholar] [CrossRef]
- Lockwood, J.; Mooney, A. Computational thinking in education: Where does it fit? A systematic literary review. arXiv 2017, arXiv:1703.07659. [Google Scholar] [CrossRef]
- Nordby, S.K.; Bjerke, A.H.; Mifsud, L. Computational thinking in the primary mathematics classroom: A systematic review. Digit. Exp. Math. Educ. 2022, 8, 27–49. [Google Scholar] [CrossRef]
- Tang, X.; Yin, Y.; Lin, Q.; Hadad, R.; Zhai, X. Assessing computational thinking: A systematic review of empirical studies. Comput. Educ. 2020, 148, 103798. [Google Scholar] [CrossRef]
- Wang, C.; Shen, J.; Chao, J. Integrating computational thinking in STEM education: A literature review. Int. J. Sci. Math. Educ. 2022, 20, 1949–1972. [Google Scholar] [CrossRef]
- Zhang, L.; Nouri, J. A systematic review of learning computational thinking through Scratch in K-9. Comput. Educ. 2019, 141, 103607. [Google Scholar] [CrossRef]
- Van Eck, N.J.; Waltman, L. VOSviewer Manual; CWTS: Leiden, The Netherlands, 2022. [Google Scholar]
- Miller, J. STEM education in the primary years to support mathematical thinking: Using coding to identify mathematical structures and patterns. ZDM 2019, 51, 915–927. [Google Scholar] [CrossRef]
- Perez-Marín, D.; Neira, R.; Bacelo, A.; Pizarro-Romero, C. Can computational thinking be improved by using a methodology based on metaphors and Scratch to teach computer programming to children? Comput. Hum. Behav. 2018, 105, 105849. [Google Scholar] [CrossRef]
- Kalogiannakis, M.; Papadakis, S. Evaluating a course for teaching introductory programming with Scratch to pre-service kindergarten teachers. Int. J. Technol. Enhanc. Learn. 2019, 11, 231–246. [Google Scholar] [CrossRef]
- Pérez, E.S.; López, F.J. An ultra-low cost line follower robot as educational tool for teaching programming and circuit’s foundations. Comput. Appl. Eng. Educ. 2019, 27, 288–302. [Google Scholar] [CrossRef]
- Peel, A.; Friedrichsen, P. Algorithms, abstractions, and iterations: Teaching computational thinking using protein synthesis translation. Am. Biol. Teach. 2018, 80, 21–28. [Google Scholar] [CrossRef]
- Sáez-López, J.M.; Sevillano-García, M.L.; Vázquez-Cano, E. The effect of programming on primary school students’ mathematical and scientific understanding: Educational use of mBot. Educ. Technol. Res. Dev. 2019, 67, 1405–1425. [Google Scholar] [CrossRef]
- Estevez, J.; Garate, G.; Graña, M. Gentle Introduction to Artificial Intelligence for High-School Students Using Scratch. IEEE Access 2017, 7, 179027–179036. [Google Scholar] [CrossRef]
- Fidai, A.; Capraro, M.M.; Capraro, R.M. “Scratch”-ing computational thinking with Arduino: A meta-analysis. Think. Ski. Creat. 2020, 38, 100726. [Google Scholar] [CrossRef]
- Scherer, R.; Siddiq, F.; Viveros, B.S. A meta-analysis of teaching and learning computer programming: Effective instructional approaches and conditions. Comput. Hum. Behav. 2020, 109, 106349. [Google Scholar] [CrossRef]
- Kong, S.-C.; Lai, M.; Sun, D. Teacher development in computational thinking: Design and learning outcomes of programming concepts, practices and pedagogy. Comput. Educ. 2020, 151, 103872. [Google Scholar] [CrossRef]
- Leonard, J.; Mitchell, M.B.; Barnes-Johnson, J.M.; Unertl, A.; Outka-Hill, J.; Robinson, R.; Hester-Croff, C. Preparing Teachers to Engage Rural Students in Computational Thinking Through Robotics, Game Design, and Culturally Responsive Teaching. J. Teach. Educ. 2018, 69, 386–407. [Google Scholar] [CrossRef]
- Kong, S.C.; Wang, Y. Formation of computational identity through computational thinking perspectives development in programming learning: A mediation analysis among primary school students. Comput. Hum. Behav. 2020, 106, 106230. [Google Scholar] [CrossRef]
- Israel, M.; Lash, T. From classroom lessons to exploratory learning progressions: Mathematics + computational thinking. Interact. Learn. Environ. 2020, 28, 362–382. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).