Engaging Students in Mathematical Problem Solving with Technology during a Pandemic: The Case of the Tecn@Mat Club
Abstract
1. Introduction
- (a)
- What are the main design features of the Tecn@Mat Club, in terms of its structure, content, and organization?
- (b)
- What are the perspectives of the participants regarding problem solving and the use of digital technologies within the Tecn@Mat Club?
- (c)
- Which are the strengths, weaknesses, opportunities, and threats to the Tecn@Mat Club?
2. Theoretical Ideas on Solving Mathematical Problems with Digital Technologies
2.1. On the Role of the Digital Tools in Mathematical Activity
2.2. On Non-Routine Mathematical Problems
2.3. On Solving Non-Routine Problems and Expressing the Solutions with Digital Tools
2.4. On the Skills Needed to Succeed in Mathematical Problem Solving with Digital Tools
3. Research Methods
3.1. The Participants
3.2. Data Collection
3.3. Data Analysis
4. Results
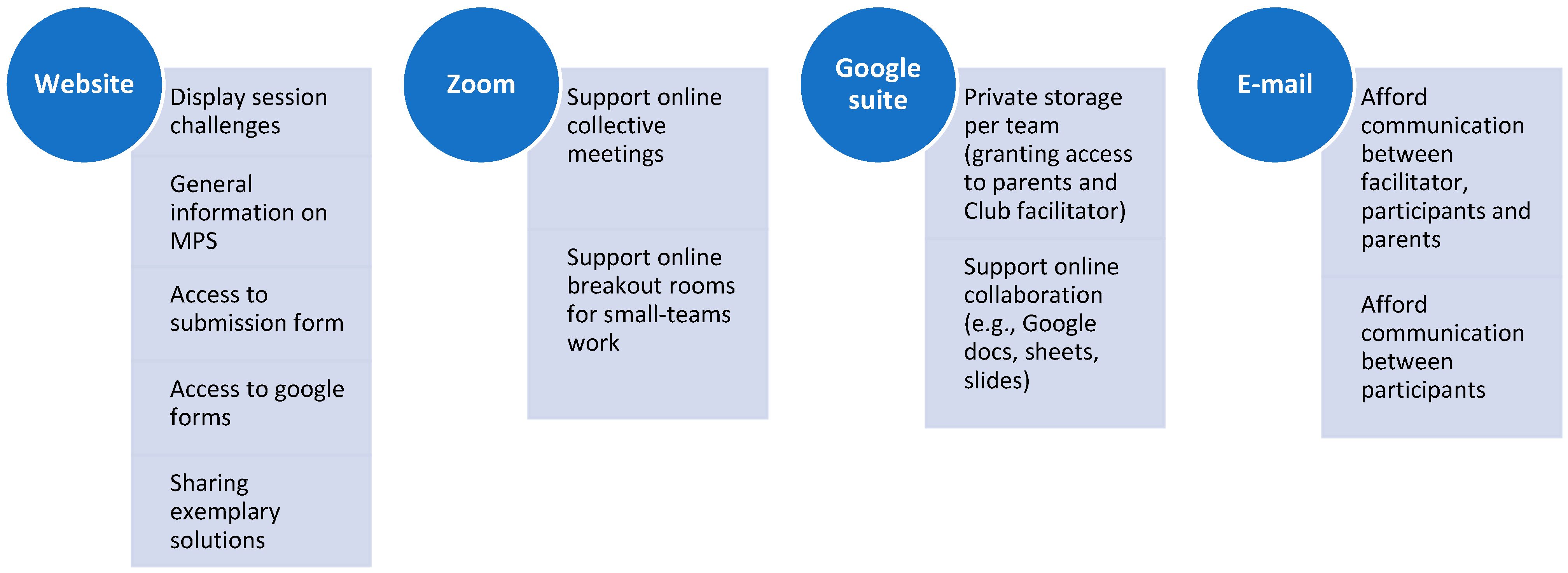
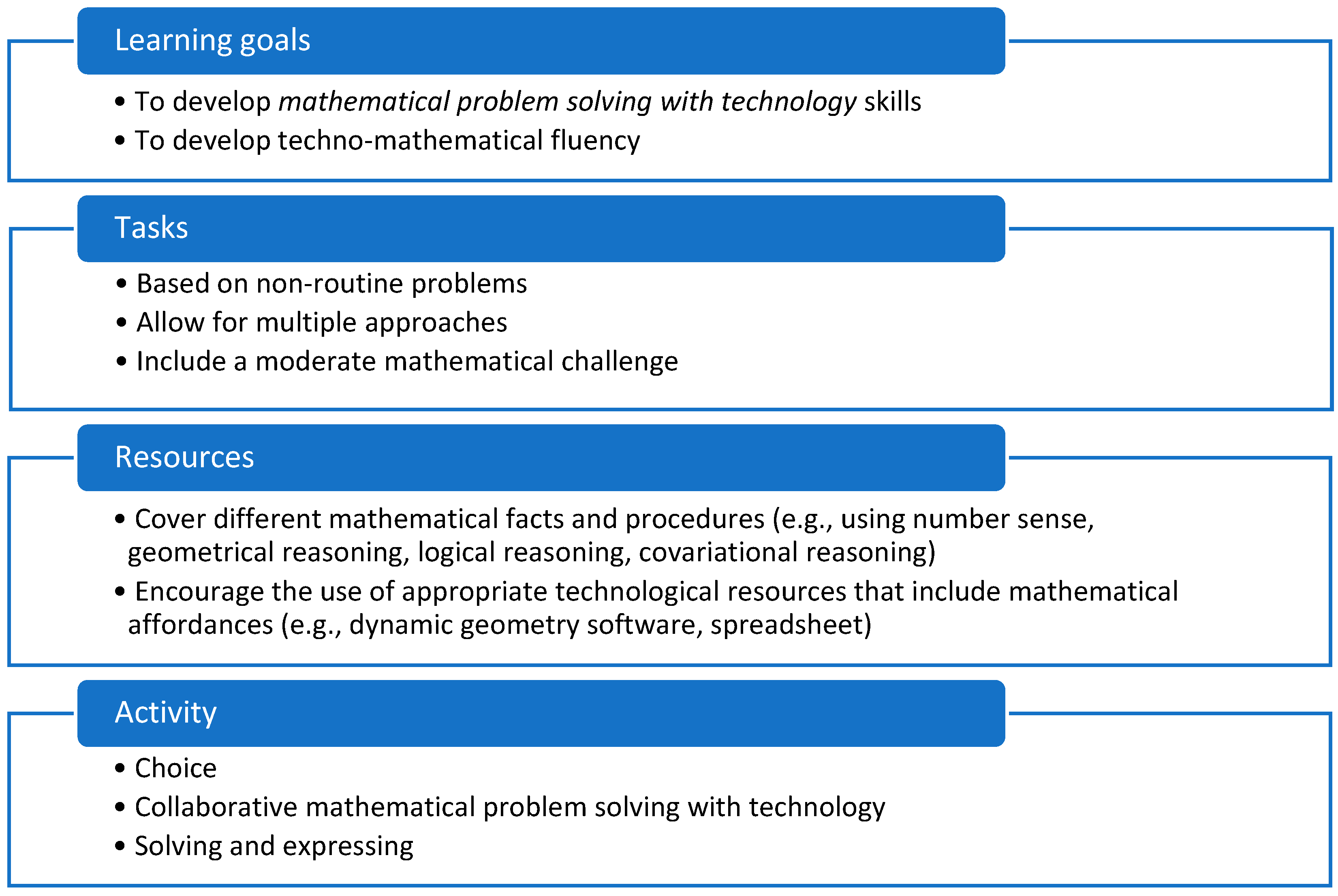
4.1. The Design and Implementation of the Tecn@Mat Club
4.1.1. How Tecn@Mat Works
The Tecn@Mat Club aims to be a special forum for students who are enthusiastic about mathematical challenges and enjoy using digital technologies, regardless of their achievement level in Mathematics. The students will have the opportunity to engage in an enjoyable, challenging, and exciting mathematical activity, in a relaxed yet learning atmosphere.[translation of excerpt from the advertisement leaflet]
4.1.2. The Tecn@Mat Curriculum: Problems, Mathematical and Technological Resources
4.1.3. A Typical Session at the Club
4.2. The Voices and Experiences of Participants in the Tecn@Mat Club
4.2.1. On the Mathematics Problems
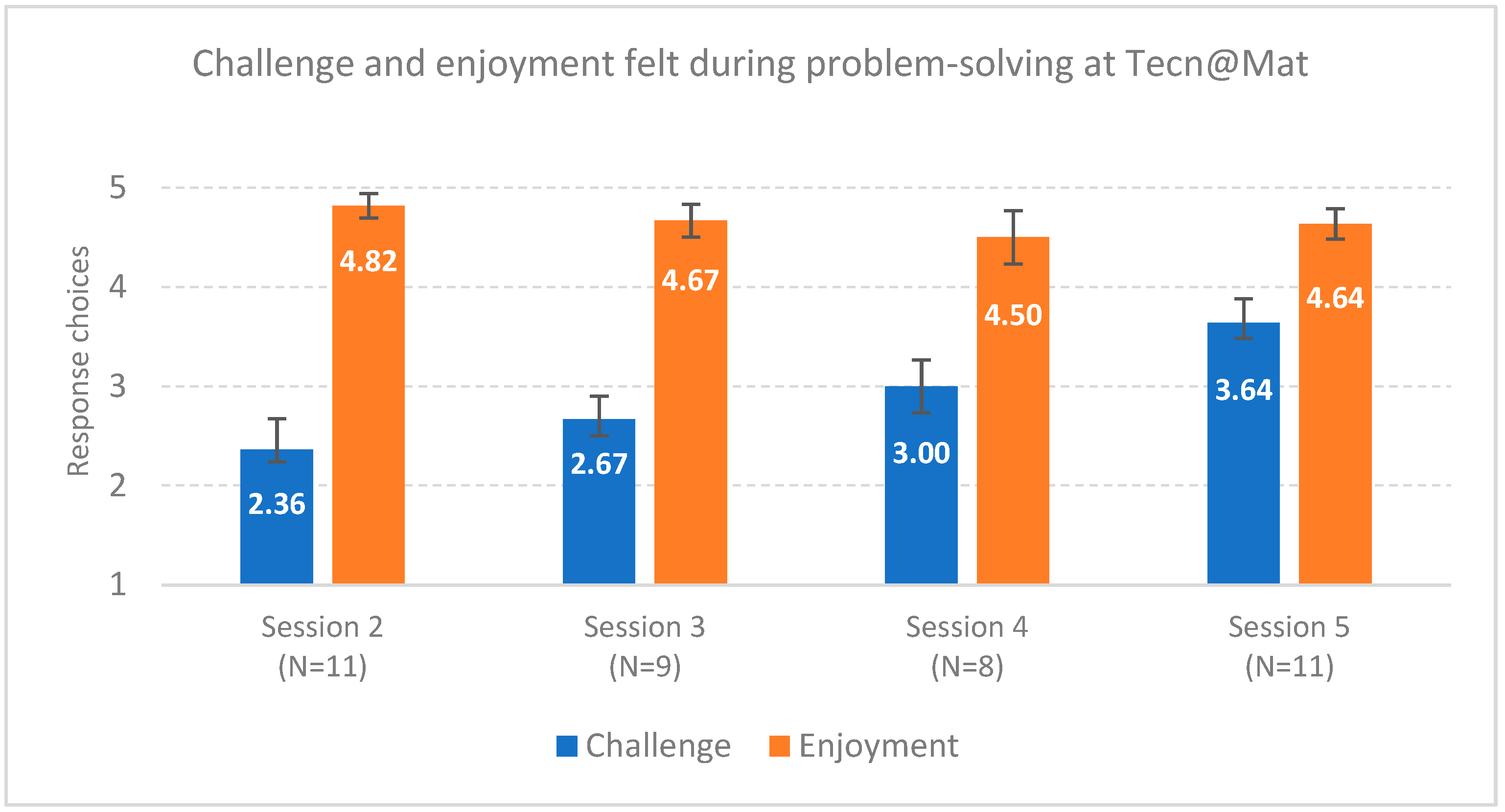
They weren’t very difficult, but they weren’t easy either, it’s right there in the middle.[FN, interview]
For example, the one with the tables, as I was saying, in the restaurant, it wasn’t very easy but it wasn’t very difficult either…the pizza one, I even thought it was easy.[MP, interview]
4.2.2. On the Use of Technologies to Solve-and-Express Mathematical Problems
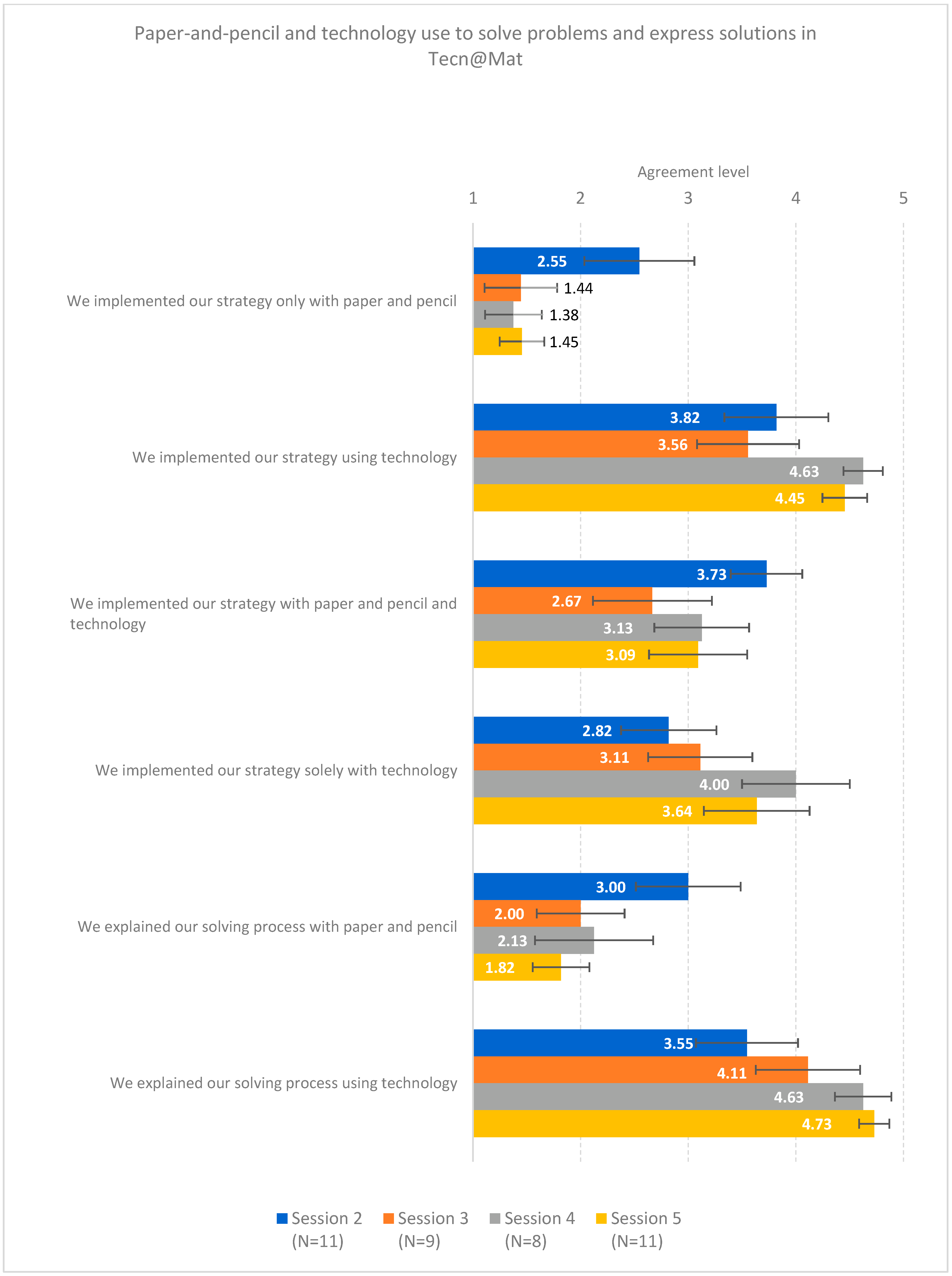
I think it was only on the first time we used paper and pencil. Yup. I think it was to visualize the problem more easily because I still I wasn’t sure how to solve it with technology, but later realized it would be simpler with technology.[CC, interview]
In my case, after solving it… and after the explanation of how it worked, I found it more convenient to do it on a computer, but before I preferred solving the problem on paper.[LC, interview]
[to explain,] paper and pencil may be easier because we are not so used to express our ideas easily… with technology I think it is easier to find the solution to the problem, but yes… I didn’t use paper and pencil because I realized that I could find my way with technology but sometimes it is useful to make diagrams faster.[CC, interview]
That includes every step… it has to be well explained. As my older sister says: “Explain it as if you were explaining it to a 5-year-old kid”. State the [final] answer. I think it has to be complete. Also, showing a sequence, we can’t present loose calculations.[LA, interview]
First [put] the topics that the problem deals with …then explain our thinking process, then see if everything is ok and I think that’s it.[LC, interview]
I think it’s always better this way because we end up meeting students from schools from north to south of the country and not just from the school where I go to. Even though I’m not much friendly and not very good at working in a group, I think it was good. I liked the feeling that I’m not alone.[LA, interview]
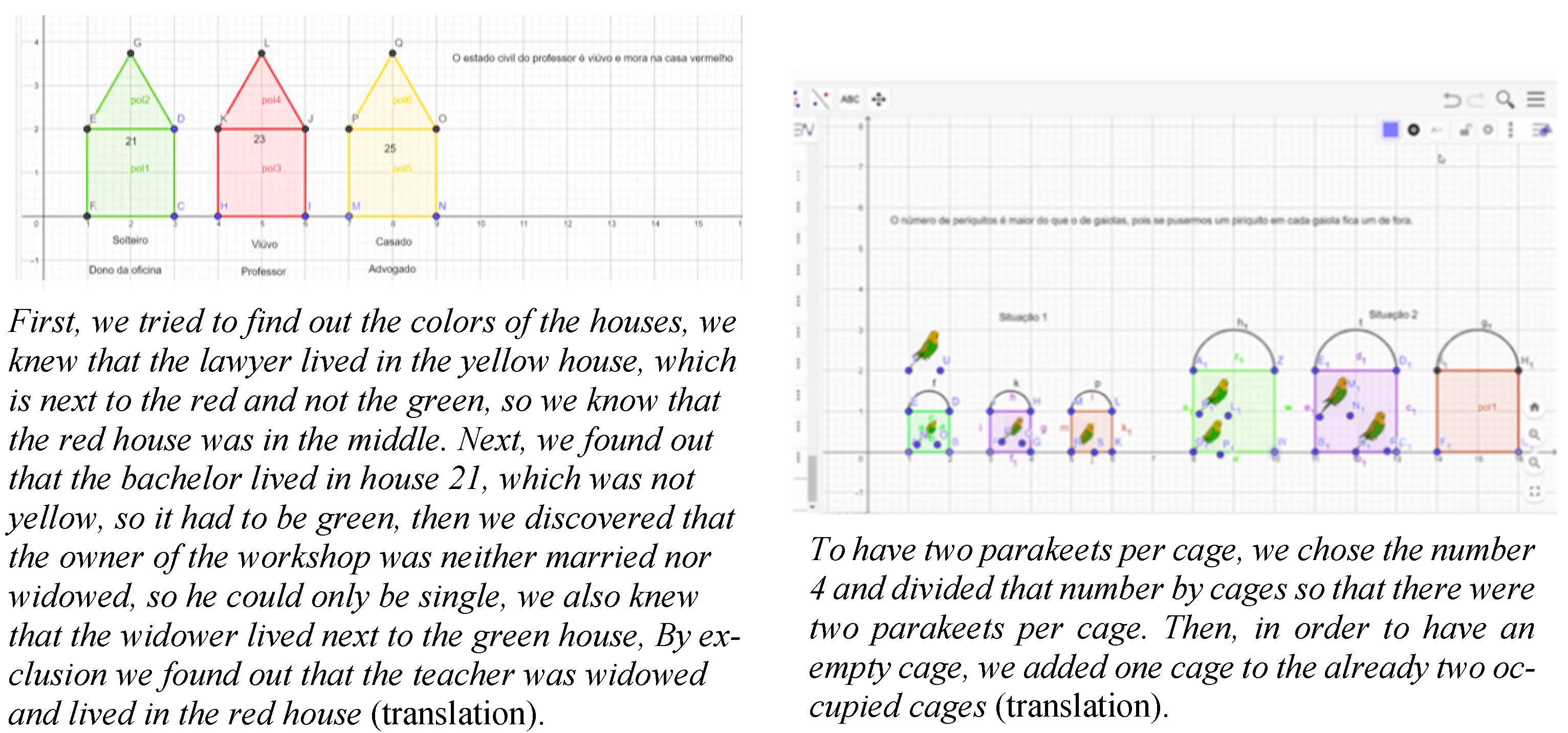
I really enjoyed working on the explanations and including images there and so on.[LC, interview]
I thought it was cool to be with colleagues from other parts of the country and… and to get to know new tools that I didn’t know about…[CC, interview]
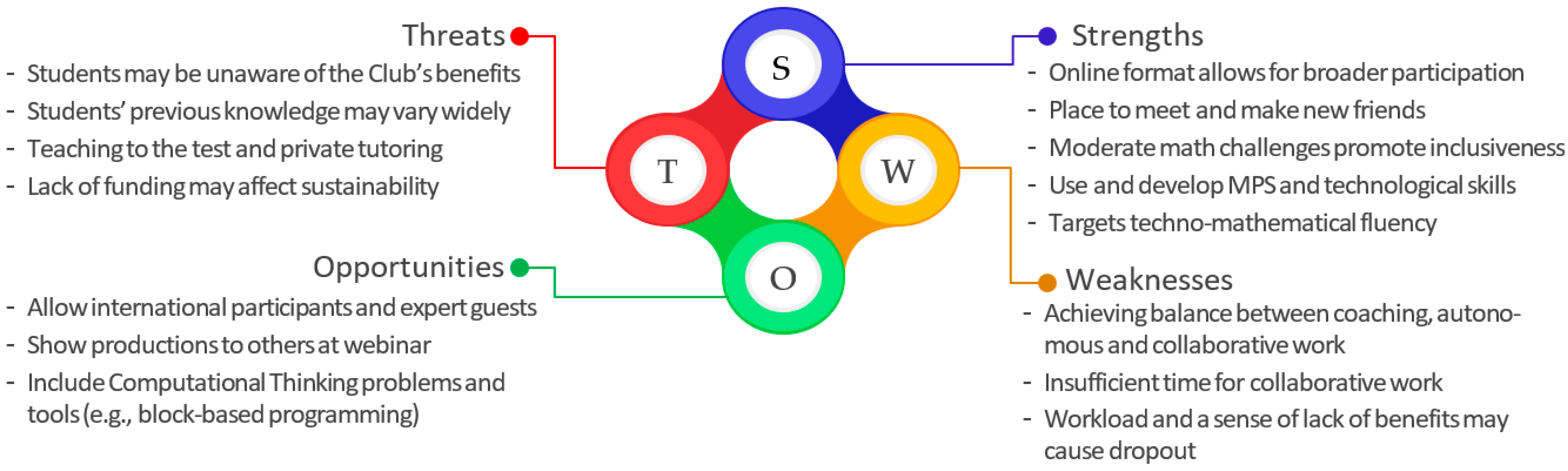
4.3. Strenghts, Weaknesses, Opportunities, and Threats: Inspiring the Future of the Tecn@Mat Club
4.3.1. On the Strengths and Weaknesses of Tecn@Mat
It gives the participants the opportunity to meet and make friends with other fellow mates that share the same interest and enjoyment for mathematical problem solving and technology use.[Maths Ed, interview]
I thought it was fun to be with colleagues from other parts of the country and get to know new tools that I didn’t know[CC, interview]
I would like to explore GeoGebra more at school because I found it useful. I also understand Excel better now, but I didn’t use to understand the mathematical formulas well, I used to use it to draw tables.[CC, interview]
I enjoyed using [Google] Drive.[LC, interview]
Problems are also nicer than the ones at school.[CC, interview]
The possibility of comparing solutions, ideas and strategies is quite important to many students…[they] may profit from new ideas, strategies, methods, and approaches that are not prevalent in the regular mathematics classes, unfortunately.[Maths Ed, interview]
[My recommendation would be] A little more time to solve the problems.[SS, interview]
I can handle two hours! No problem for me.[LC, interview]
4.3.2. On the Opportunities of and Threats to Tecn@Mat
5. Discussion and Conclusions
5.1. Design Features of Tecn@Mat: Structure, Content, and Organization
5.2. Participants’ Perspectives on Problem Solving with Digital Tools at Tecn@Mat
5.3. Tecn@Mat’s Strengths, Weaknesses, Opportunities, and Threats
5.4. Final Considerations
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Aldon, G.; Cusi, A.; Schacht, F.; Swidan, O. Teaching mathematics in a context of lockdown: A study focused on teachers’ praxeologies. Educ. Sci. 2021, 11, 38. [Google Scholar] [CrossRef]
- Drijvers, P.; Thurm, D.; Vandervieren, E.; Klinger, M.; Moons, F.; van der Ree, H.; Mol, A.; Barzel, B.; Doorman, M. Distance mathematics teaching in Flanders, Germany, and The Netherlands during COVID-19 lockdown. Educ. Stud. Math. 2021, 108, 35–64. [Google Scholar] [CrossRef] [PubMed]
- Kalogeropoulos, P.; Roche, A.; Russo, J.; Vats, S.; Russo, T. Learning mathematics from home during COVID-19: Insights from two inquiry-focussed primary schools. Eurasia J. Math. Sci. Technol. Educ. 2021, 17, em1957. [Google Scholar] [CrossRef]
- Foster, C.; Burkhardt, H.; Schoenfeld, A. Crisis-ready educational design: The case of mathematics. Curric. J. 2022, 33, 519–535. [Google Scholar] [CrossRef]
- Papanastasiou, E.C.; Bottiger, L. Math clubs and their potentials: Making mathematics fun and exciting. A case study of a math club. Int. J. Math. Educ. Sci. Technol. 2004, 35, 159–171. [Google Scholar] [CrossRef]
- Elizondo, A.M.; Bruun, F.; Pletcher, B.C. Perceptions of student’s, parent’s, and instructor’s experience in a summer math camp. Sch. Sci. Math. 2021, 121, 201–210. [Google Scholar] [CrossRef]
- Kennedy, E.; Smolinsky, L. Math circles: A tool for promoting engagement among middle school minority males. Eurasia J. Math. Sci. Technol. Educ. 2016, 12, 717–732. [Google Scholar] [CrossRef]
- Carreira, S.; Jones, K.; Amado, N.; Jacinto, H.; Nobre, S. Youngsters Solving Mathematics Problems with Technology; Springer: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Stahl, G. Studying Virtual Math Teams; Springer: New York, NY, USA, 2009. [Google Scholar]
- Freiman, V.; Manuel, D. Relating Students’ Perceptions of Interest and Difficulty to the Richness of Mathematical Problems Posted on the CAMI Website. Quadrante 2015, 24, 61–84. [Google Scholar] [CrossRef]
- Durbin, J.M. An Examination of Effects of Student Math Extracurricular Participation on Math Self-Efficacy and Proficiency. J. High. Educ. Theory Pract. 2020, 20, 121–126. [Google Scholar] [CrossRef]
- Mueller, M.; Maher, C. Learning to reason in an informal math after-school program. Math. Educ. Res. J. 2009, 21, 7–35. [Google Scholar] [CrossRef]
- Stott, D.; Baart, N.; Graven, M. Partnering with districts to expand an after-school maths club programme. Afr. Educ. Rev. 2019, 16, 183–200. [Google Scholar] [CrossRef]
- Koichu, B. Mathematical Problem Solving in Choice-Affluent Environments. In Invited Lectures from the 13th International Congress on Mathematical Education, ICME-13 Monographs; Kaiser, G., Forgasz, H., Graven, M., Kuzniak, A., Simmt, E., Xu, B., Eds.; Springer: Cham, Switzerland, 2018; pp. 307–324. [Google Scholar] [CrossRef]
- Jacinto, H.; Carreira, S. Mathematical problem solving with technology: The techno-mathematical fluency of a student-with-GeoGebra. Int. J. Sci. Math. Educ. 2017, 15, 1115–1136. [Google Scholar] [CrossRef]
- Jacinto, H.; Carreira, S. Digital Tools and Paper-and-Pencil in Solving-and-Expressing: How Technology Expands a Student’s Conceptual Model of a Covariation Problem. J. Math. Educ. 2021, 12, 113–132. [Google Scholar] [CrossRef]
- Geiger, V. Master, servant, partner and extension of self: A finer grained view of this taxonomy. In Building Connections: Theory, Research and Practice; Clarkson, P., Downton, A., Gronn, D., Horne, M., McDonough, A., Pierce, R., Roche, A., Eds.; MERGA: Sydney, Australia, 2005; pp. 369–376. [Google Scholar]
- Borba, M.; Villarreal, M. Humans-with-Media and the Reorganization of Mathematical Thinking; Springer: New York, NY, USA, 2005. [Google Scholar]
- Sinclair, N. On Teaching and Learning Mathematics–Technologies. In STEM Teachers and Teaching in the Digital Era; Kolikant, Y., Martinovic, D., Milner-Bolotin, M., Eds.; Springer: New York, NY, USA, 2020; pp. 91–107. [Google Scholar]
- Saadati, F.; Felmer, P. Assessing impact of a teacher professional development program on student problem-solving performance. ZDM Math. Educ. 2021, 53, 799–816. [Google Scholar] [CrossRef]
- Schoenfeld, A. Mathematical Problem Solving; Academic Press: New York, NY, USA, 1985. [Google Scholar]
- Lesh, R.; Zawojewski, J. Problem solving and modeling. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F., Ed.; Information Age Publishing and NCTM: Charlotte, NC, USA, 2007; pp. 763–804. [Google Scholar]
- Lesh, R.; Harel, G. Problem solving, modeling, and local conceptual development. Math. Think. Learn. 2003, 5, 157–189. [Google Scholar] [CrossRef]
- Carreira, S.; Amado, N.; Ferreira, R.; Jacinto, H.; Nobre, S.; Amaral, N. O Projeto Problem@Web: Perspetivas de investigação em resolução de problemas. In Atas do XXIV Seminário de Investigação em Educação Matemática. Fernandes, J.A., Martinho, M.H., Tinoco, J., Viseu, F., Eds.; APM e CIEd da Universidade do Minho: Braga, Portugal, 2013; pp. 51–71. [Google Scholar]
- Lesh, R.; Doerr, H. Foundations of a models and modeling perspective on mathematics teaching, learning, and problem solving. In Beyond Constructivism: Models and Modeling Perspectives on Mathematics Problem Solving, Learning, and Teaching; Lesh, R., Doerr, H., Eds.; Erlbaum Associates: Mahwah, NJ, USA, 2003; pp. 3–33. [Google Scholar]
- Turner, J.; Meyer, D. A classroom perspective on the principle of moderate challenge in mathematics. J. Educ. Res. 2004, 97, 311–318. [Google Scholar] [CrossRef]
- Schweinle, A.; Berg, P.J.; Sorenson, A.R. Preadolescent perceptions of challenging and difficult course activities and their motivational distinctions. Educ. Psychol. 2013, 33, 797–816. [Google Scholar] [CrossRef]
- Hoyles, C.; Noss, R.; Kent, P.; Bakker, A. Improving Mathematics at Work: The Need for Techno-Mathematical Literacies; Routledge: London, UK, 2010. [Google Scholar]
- Papert, S.; Resnick, M. Technological Fluency and the Representation of Knowledge; Proposal to the National Science Foundation; MIT Media Laboratory: Cambridge, MA, USA, 1995. [Google Scholar]
- Jacinto, H.; Carreira, S. Different ways of using GeoGebra in Mathematical Problem-Solving beyond the Classroom: Evidences of Techno-Mathematical Fluency. Bolema 2017, 31, 266–288. [Google Scholar] [CrossRef]
- Barron, B.; Martin, C.; Roberts, E. Sparking self-sustained learning: Report on a design experiment to build technological fluency and bridge divides. Int. J. Technol. Des. Educ. 2007, 17, 75–105. [Google Scholar] [CrossRef]
- Yao, X.; Manouchehri, A. Middle school students’ generalizations about properties of geometric transformations in a dynamic geometry environment. J. Math. Behav. 2019, 55, 100703. [Google Scholar] [CrossRef]
- Stake, R.E. The Art of Case Study Research; Sage: Thousand Oaks, CA, USA, 1995. [Google Scholar]
- Creswell, J.W.; Plano Clark, V.L. Designing and Conducting Mixed Methods Research, 3rd ed.; Sage Publications: Thousand Oaks, CA, USA, 2017. [Google Scholar]
- Rutherford, C. Planning to change: Strategic planning and comprehensive school reform. Educ. Plan. 2009, 18, 1–10. [Google Scholar]
- Oliveras, M.L.; Cardeñoso, J.M.; Molina, M.; Servín, C.Y. Use of Integrated Projects in a Mathematics Education Course for Prospective Kindergarten Teachers. Int. J. Interdiscip. Soc. Sci. 2008, 2, 165–174. [Google Scholar] [CrossRef]
- Hazzan, O.; Heyd-Metzuyanim, E.; Even-Zahav, A.; Tal, T.; Dori, Y.J. Application of Management Theories for STEM Education: The Case of SWOT Analysis; Springer: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Cabello, V.M.; Martínez, M.L.; Armijo, S.; Maldonado, L. Promoting STEAM learning in the early years: “Pequeños Científicos” Program. LUMAT Int. J. Math Sci. Technol. Educ. 2021, 9, 33–62. [Google Scholar] [CrossRef]
- Jacinto, H.; Carreira, S.; Mariotti, M.A. Mathematical problem solving with technology beyond the classroom: The use of unconventional tools and methods. In 40th Conference of the International Group for the Psychology of Mathematics Education; Csikos, C., Rausch, A., Szitanyi, J., Eds.; International Group for the Psychology of Mathematics Education: Szeged, Hungary, 2016; Volume 3, pp. 27–34. [Google Scholar]
- Carreira, S.; Amado, N.; Jacinto, H. Venues for Analytical Reasoning Problems: How Children Produce Deductive Reasoning. Educ. Sci. 2020, 10, 169. [Google Scholar] [CrossRef]
- Schoenfeld, A. Reflections on doing and teaching mathematics. In Mathematical Thinking and Problem Solving; Schoenfeld, A., Ed.; Lawrence Erlbaum Associates: Hove, UK, 1994; pp. 53–70. [Google Scholar]
- Pina Stranger, A.; Varas, G.; Mobuchon, G. Students’ Perceptions of Gained and Lost Value: A Case Study of a Summer School That Had to Suddenly Move Online. Educ. Sci. 2022, 12, 364. [Google Scholar] [CrossRef]
- Weinhandl, R.; Lavicza, Z.; Houghton, T.; Hohenwarter, M. A look over students’ shoulders when learning mathematics in home-schooling. Int. J. Math. Educ. Sci. Technol. 2022, 53, 2879–2899. [Google Scholar] [CrossRef]
- Engelbrecht, J.; Borba, M.C.; Kaiser, G. Will we ever teach mathematics again in the way we used to before the pandemic? ZDM Math. Educ. 2023, 55, 1–16. [Google Scholar] [CrossRef]
- UNESCO. COVID-19 Education Response. 2020. Available online: https://en.unesco.org/covid19/educationresponse/globalcoalition (accessed on 7 December 2022).
- Sullivan, P.; Bobis, J.; Downton, A.; Feng, M.; Hughes, S.; Livy, S.; McCormick, M.; Russo, J. Threats and opportunities in remote learning of mathematics: Implication for the return to the classroom. Math. Educ. Res. J. 2020, 32, 551–559. [Google Scholar] [CrossRef]
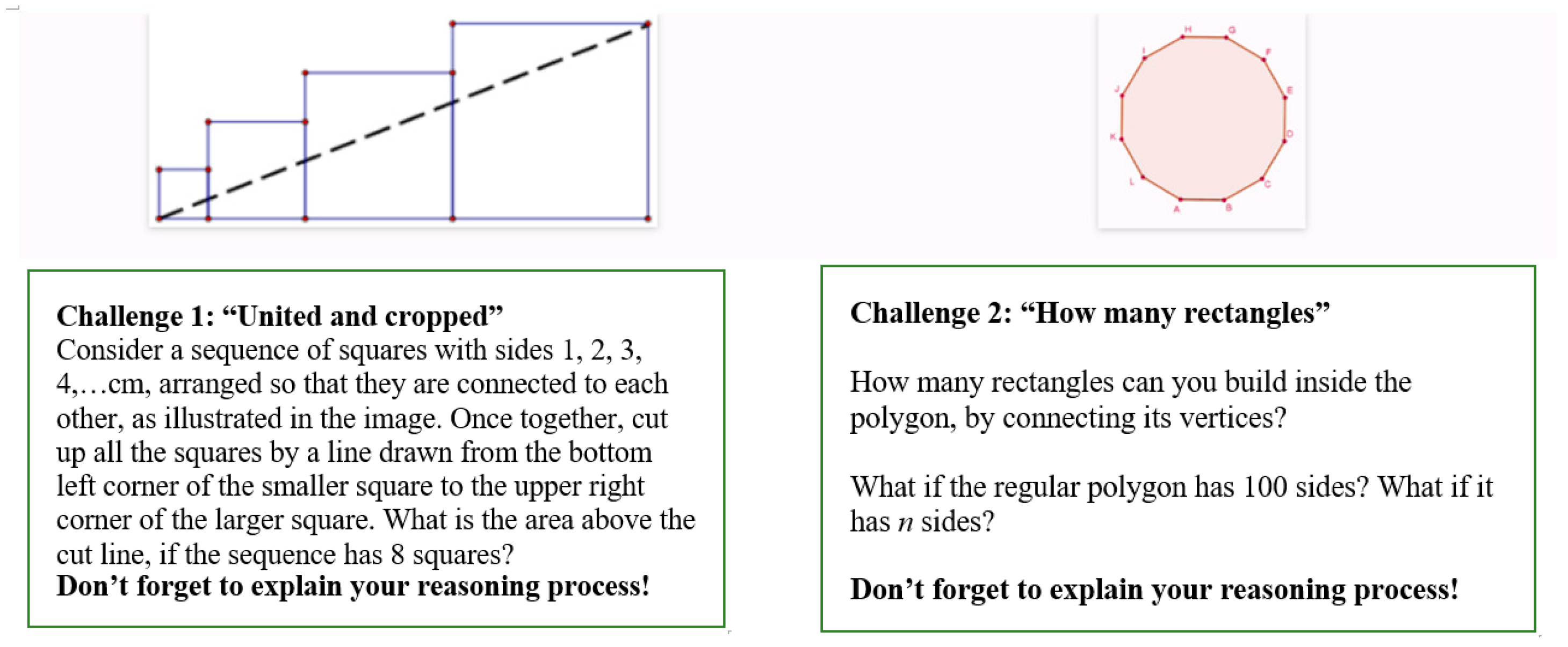
| Session | Challenge | Mathematical Concepts | Technological Tools |
|---|---|---|---|
| 1 | United and cropped | Areas of polygons | GeoGebra (constructing robust figures; computing areas; spreadsheet) |
| How many rectangles? | Quadrilaterals. Sum of the first n positive integers. | GeoGebra (constructing figures; spreadsheet). | |
| 2 | Snap rings | Circle area. Ratio. | GeoGebra (constructing figures; computing areas; spreadsheet). |
| The three houses | Logical reasoning. | Text and presentation editors (tabular representation). | |
| 3 | Cages and parakeets | Numerical and algebraic relations, involving the concept of variable (system of two equations with two unknowns). | Spreadsheet (writing, cell formatting, simple formulas, autocomplete cells). |
| The opening of the “Sombrero Style” | Numerical and algebraic relations, involving the concept of fraction, multiple, and variable. | Spreadsheet (writing, cell formatting, formulas, autocomplete). | |
| 4 | A costumed pizza | Combinatorics. | Text, presentation, and video editors. |
| Friends’ reunion | Co-variational reasoning. | Spreadsheet (writing, cell formatting, formulas, autocomplete). | |
| 5 | Cubes on the floor | Numerical and algebraic relations, involving the concept of perfect square. | Spreadsheet (writing, cell formatting, formulas, autocomplete). |
| Keys and lockers | Combinatorics. | Text, presentation, and video editors. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jacinto, H. Engaging Students in Mathematical Problem Solving with Technology during a Pandemic: The Case of the Tecn@Mat Club. Educ. Sci. 2023, 13, 271. https://doi.org/10.3390/educsci13030271
Jacinto H. Engaging Students in Mathematical Problem Solving with Technology during a Pandemic: The Case of the Tecn@Mat Club. Education Sciences. 2023; 13(3):271. https://doi.org/10.3390/educsci13030271
Chicago/Turabian StyleJacinto, Hélia. 2023. "Engaging Students in Mathematical Problem Solving with Technology during a Pandemic: The Case of the Tecn@Mat Club" Education Sciences 13, no. 3: 271. https://doi.org/10.3390/educsci13030271
APA StyleJacinto, H. (2023). Engaging Students in Mathematical Problem Solving with Technology during a Pandemic: The Case of the Tecn@Mat Club. Education Sciences, 13(3), 271. https://doi.org/10.3390/educsci13030271






