E-Learning at-Risk Group Prediction Considering the Semester and Realistic Factors
Abstract
:1. Introduction
2. Theoretical Background
2.1. At-Risk Prediction in E-Learning Using a Single Algorithm
2.2. eXplainable AI (XAI)
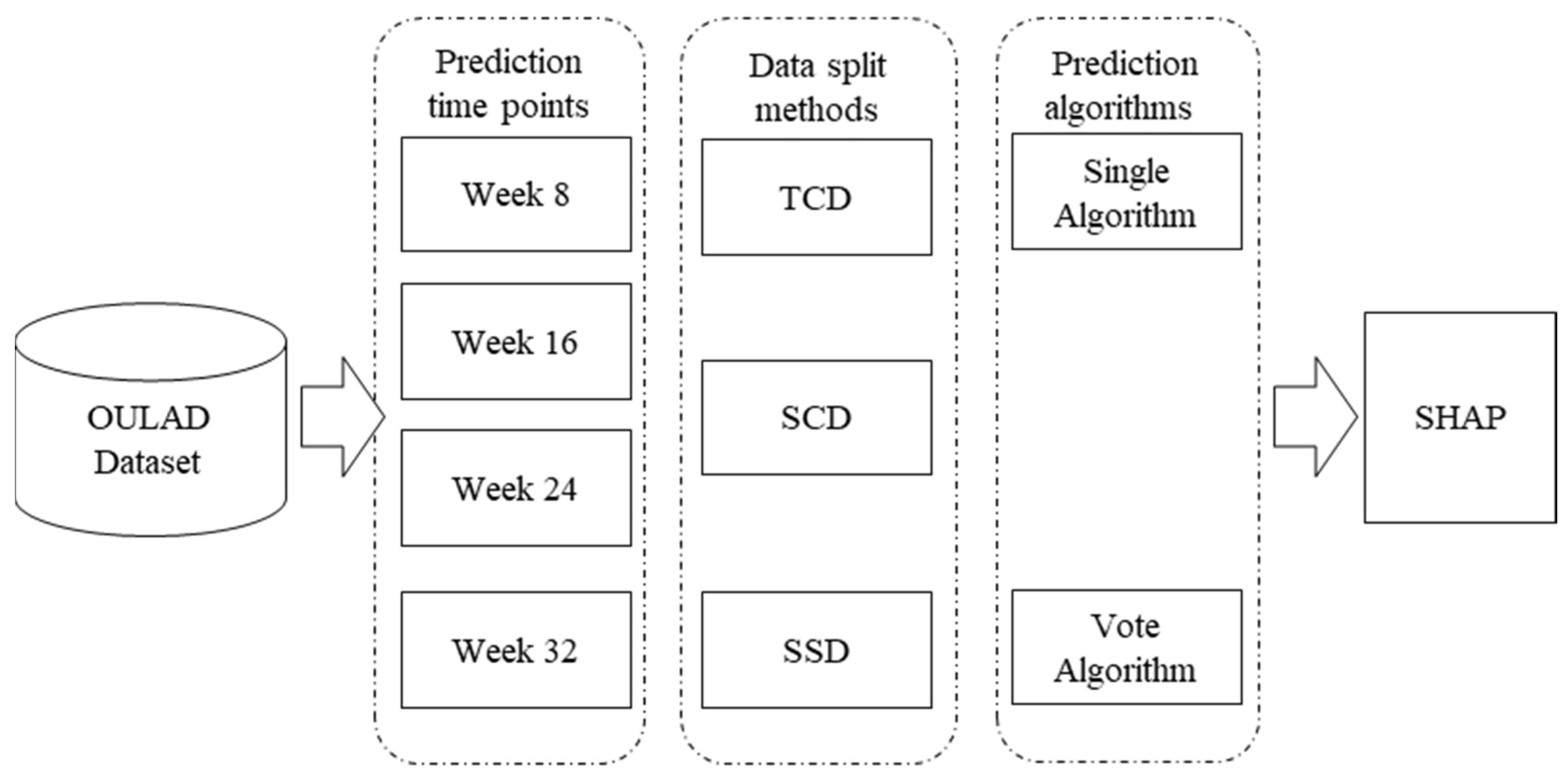
3. Research Model
3.1. Dataset
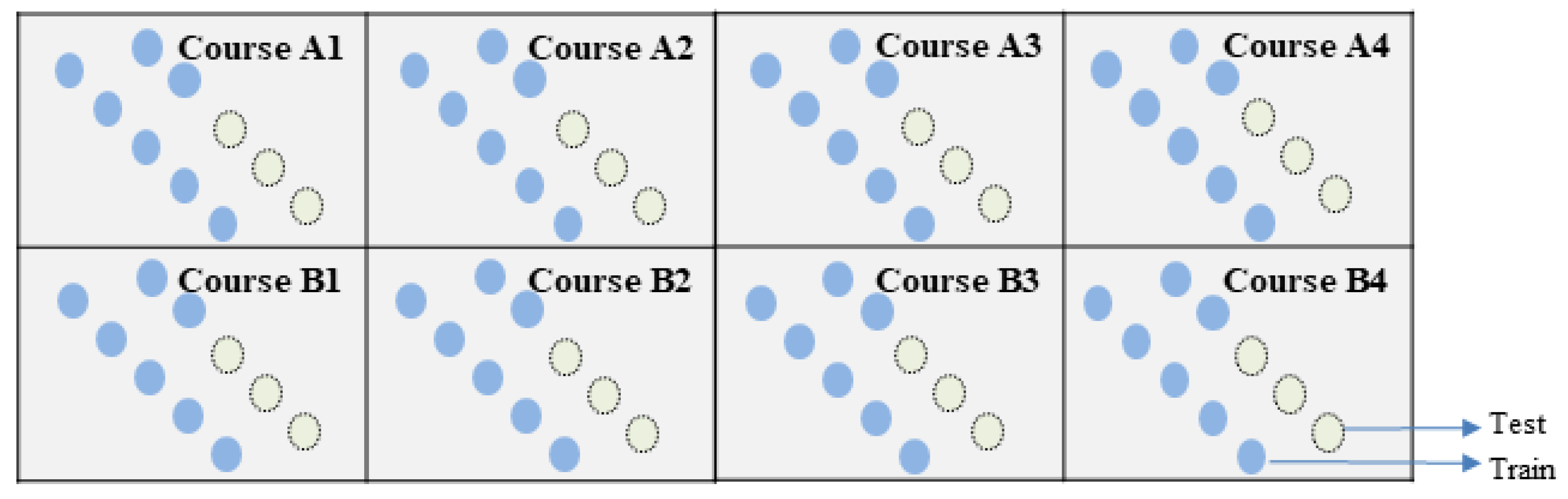
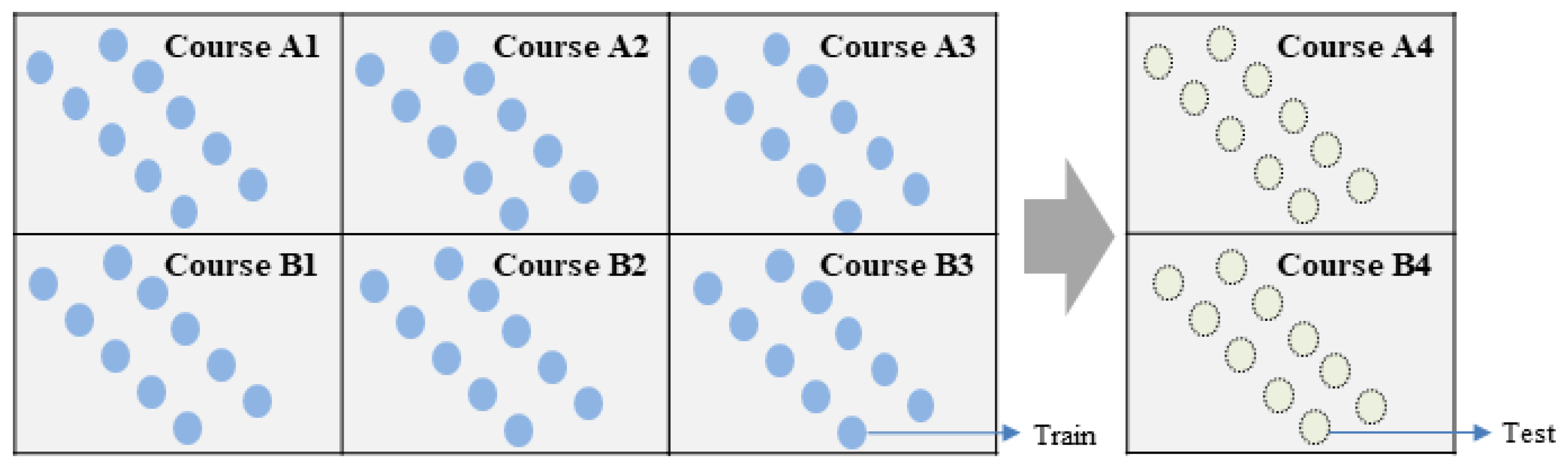
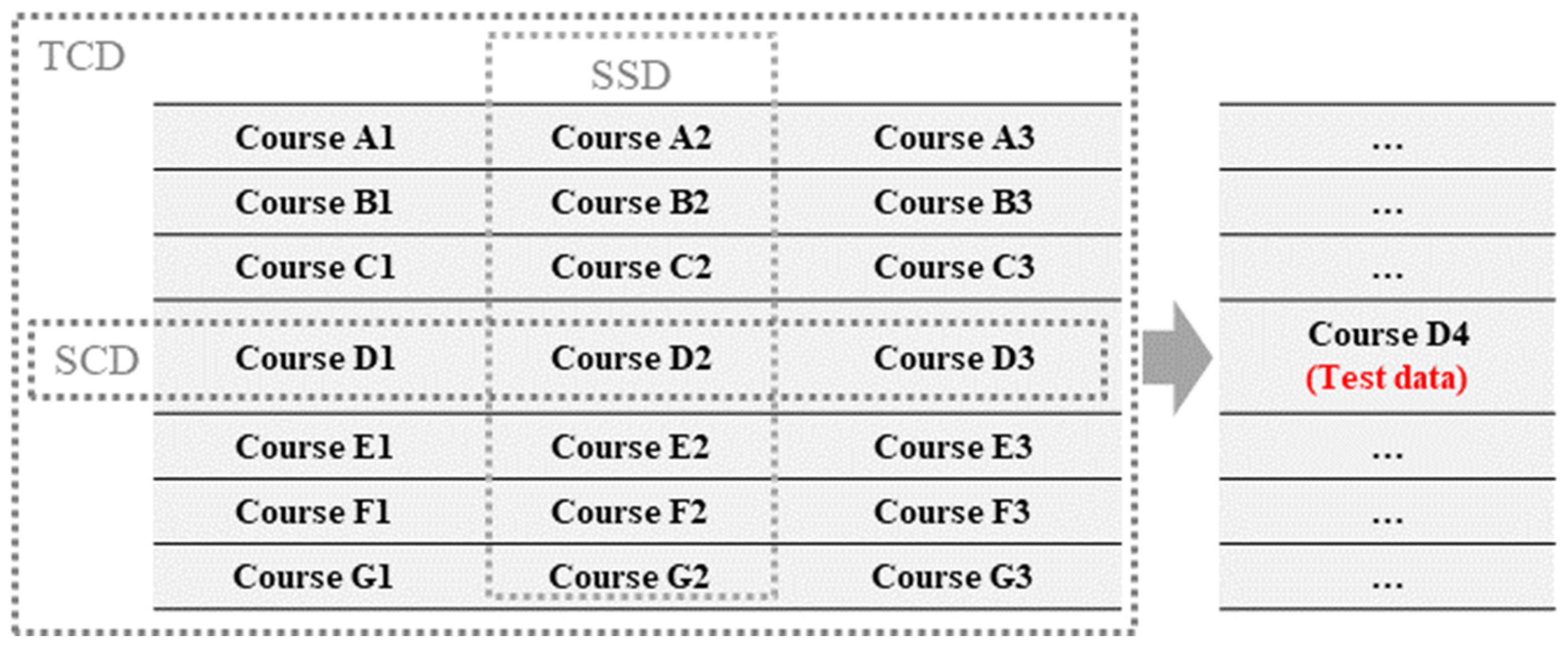
3.2. Data Split Method
3.3. Time Points for the Prediction
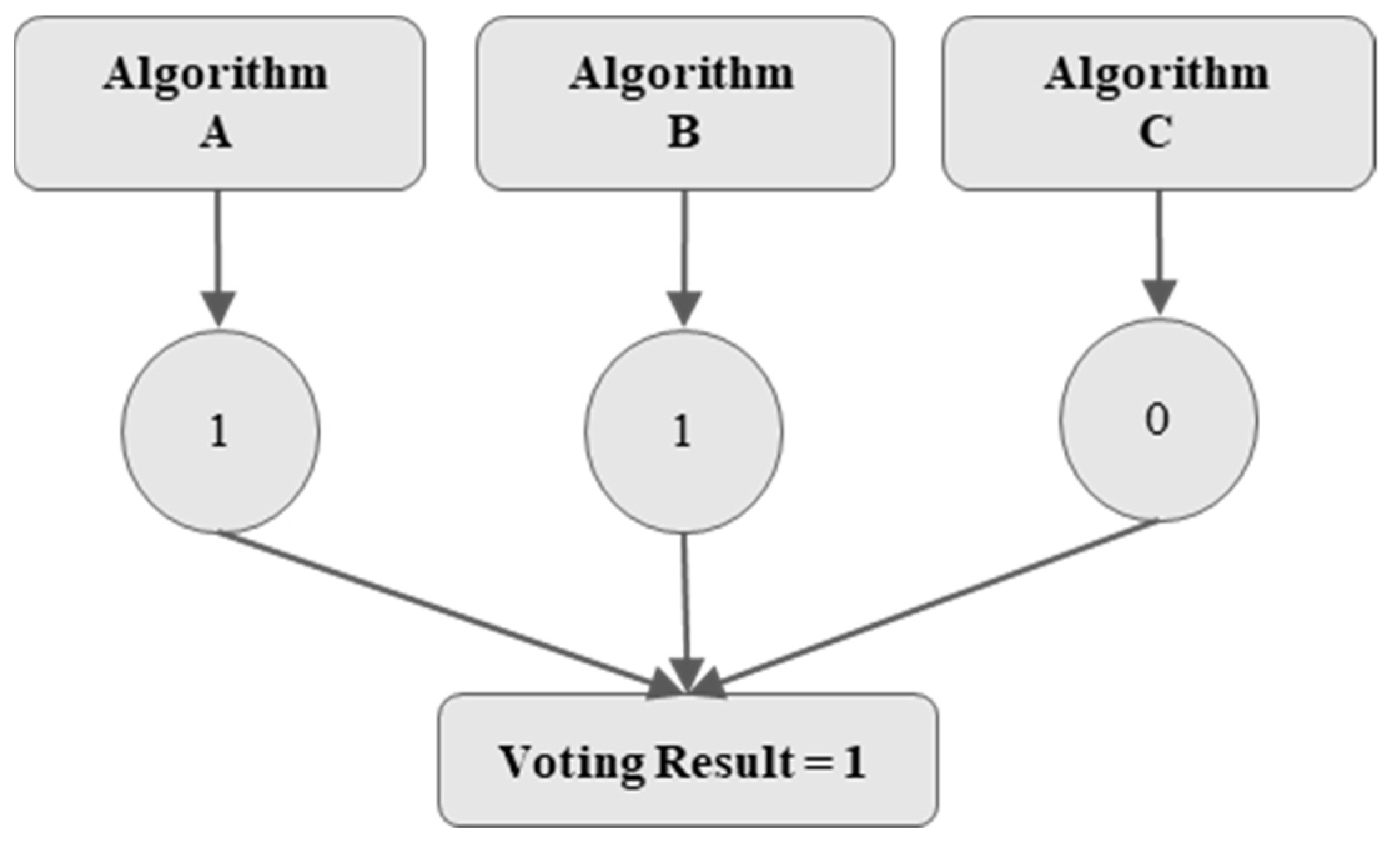
3.4. Algorithms
3.5. Variables
3.6. Evaluation
- ▪
- True Negative (TN): The number of instances that were actually negative and were correctly predicted as negative.
- ▪
- False Positive (FP): The number of instances that were actually negative but were incorrectly predicted as positive.
- ▪
- False Negative (FN): The number of instances that were actually positive but were incorrectly predicted as negative.
- ▪
- True Positive (TP): The number of instances that were actually positive and were correctly predicted as positive.
3.7. Explanation with SHAP
4. Experiment
4.1. Prediction Results
- (1)
- The prediction accuracy gradually increased as the number of weeks increased. As more weekly data were used, the closer the training data was to the final exam, and the better it reflected student learning. So, the prediction accuracy was highest for week 32.
- (2)
- The algorithm with the highest prediction accuracy across the weekly time points was GB in week 8 (0.759); GB was the same as Vote-5 and Vote-8 in week 16 (0.788); and the best prediction was from Vote-5 in week 24 (0.812) and week 32 (0.84).
- (3)
- With the average value calculated in the last line among the three data split methods, the prediction accuracy of SSD was the highest at each time point. As seen in Table 7, the best-performing algorithms at each time point was SSD.
4.2. Interpretation Using XAI
5. Conclusion and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuzilek, J.; Hlosta, M.; Zdrahal, Z. Open university learning analytics dataset. Sci. Data 2017, 4, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Feng, W.; Tang, J.; Liu, T.X. Understanding dropouts in MOOCs. Proc. AAAI Conf. Artif. Intell. 2019, 33, 517–524. [Google Scholar] [CrossRef]
- Kuzilek, J.; Hlosta, M.; Herrmannova, D.; Zdrahal, Z.; Vaclavek, J.; Wolff, A. OU Analyse: Analysing at-risk students at The Open University. Learn. Anal. Rev. 2015, LAK15-1, 1–6. [Google Scholar]
- Alshabandar, R.; Hussain, A.; Keight, R.; Laws, A.; Baker, T. The application of Gaussian mixture models for the identification of at-risk learners in massive open online courses. In Proceedings of the 2018 IEEE Congress on Evolutionary Computation (CEC), Rio de Janeiro, Brazil, 8–13 July 2018; pp. 1–8. [Google Scholar]
- Hlosta, M.; Zdrahal, Z.; Zendulka, J. Ouroboros: Early identification of at-risk students without models based on legacy data. In Proceedings of the Seventh International Learning Analytics & Knowledge Conference, Vancouver, BC, Canada, 13–17 March 2017; pp. 6–15. [Google Scholar]
- Lykourentzou, I.; Giannoukos, I.; Nikolopoulos, V.; Mpardis, G.; Loumos, V. Dropout prediction in e-learning courses through the combination of machine learning techniques. Comput. Educ. 2009, 53, 950–965. [Google Scholar] [CrossRef]
- Chaplot, D.S.; Rhim, E.; Kim, J. Predicting student attrition in MOOCs using sentiment analysis and neural networks. In Proceedings of the Workshop at the 17th International Conference on Artificial Intelligence in Education (AIED-WS 2015), Madrid, Spain, 22–26 June 2015; pp. 7–12. [Google Scholar]
- Liang, J.; Li, C.; Zheng, L. Machine learning application in MOOCs: Dropout prediction. In Proceedings of the 2016 11th International Conference on Computer Science & Education (ICCSE), Nagoya, Japan, 23–25 August 2016; pp. 52–57. [Google Scholar]
- Cobos, R.; Wilde, A.; Zaluska, E. Predicting attrition from massive open online courses in FutureLearn and edX. In Proceedings of the 7th International Learning Analytics and Knowledge Conference, Vancouver, BC, Canada, 13–17 March 2017. [Google Scholar]
- Yukselturk, E.; Ozekes, S.; Turel, Y.K. Predicting dropout student: An application of data mining methods in an online education program. Eur. J. Open Distance e-Learn. 2014, 17, 118–133. [Google Scholar] [CrossRef]
- Queiroga, E.M.; Lopes, J.L.; Kappel, K.; Aguiar, M.; Araújo, R.M.; Munoz, R.; Villarroel, R.; Cechinel, C. A learning analytics approach to identify students at risk of dropout: A case study with a technical distance education course. Appl. Sci. 2020, 10, 3998. [Google Scholar] [CrossRef]
- Mubarak, A.A.; Cao, H.; Zhang, W. Prediction of students’ early dropout based on their interaction logs in online learning environment. Interact. Learn. Environ. 2022, 30, 1414–1433. [Google Scholar] [CrossRef]
- Haiyang, L.; Wang, Z.; Benachour, P.; Tubman, P. A time series classification method for behaviour-based dropout prediction. In Proceedings of the 2018 IEEE 18th International Conference on Advanced Learning Technologies (ICALT), Mumbai, India, 9–13 July 2018; pp. 191–195. [Google Scholar]
- Zhou, Y.; Zhao, J.; Zhang, J. Prediction of learners’ dropout in E-learning based on the unusual behaviors. Interact. Learn. Environ. 2020, 31, 1–25. [Google Scholar] [CrossRef]
- Abd El-Rady, A. An ontological model to predict dropout students using machine learning techniques. In Proceedings of the 2020 3rd International Conference on Computer Applications & Information Security (ICCAIS), Riyadh, Saudi Arabia, 19–21 March 2020; IEEE: New York, NY, USA; pp. 1–5. [Google Scholar]
- Jha, N.I.; Ghergulescu, I.; Moldovan, A.N. OULAD MOOC dropout and result prediction using ensemble, deep learning and regression techniques. In Proceedings of the 11th International Conference on Computer Supported Education (CSEDU 2019), Crete, Greece, 2–4 May 2019; pp. 154–164. [Google Scholar]
- Tan, M.; Shao, P. Prediction of student dropout in e-Learning program through the use of machine learning method. Int. J. Emerg. Technol. Learn. 2015, 10, 11–17. [Google Scholar] [CrossRef]
- Batool, S.; Rashid, J.; Nisar, M.W.; Kim, J.; Mahmood, T.; Hussain, A. A random forest students’ performance prediction (rfspp) model based on students’ demographic features. In Proceedings of the 2021 Mohammad Ali Jinnah University International Conference on Computing (MAJICC), Karachi, Pakistan, 15–17 July 2021; pp. 1–4. [Google Scholar]
- Kittler, J.; Hatef, M.; Duin, R.P.; Matas, J. On combining classifiers. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 226–239. [Google Scholar] [CrossRef]
- Kizilcec, R.F.; Piech, C.; Schneider, E. Deconstructing disengagement: Analyzing learner subpopulations in massive open online courses. In Proceedings of the Third International Conference on Learning Analytics and Knowledge, Leuven, Belgium, 8–13 April 2013; pp. 170–179. [Google Scholar]
- Aldowah, H.; Al-Samarraie, H.; Alzahrani, A.I.; Alalwan, N. Factors affecting student dropout in MOOCs: A cause and effect decision-making model. J. Comput. High. Educ. 2020, 32, 429–454. [Google Scholar] [CrossRef]
- Coussement, K.; Phan, M.; De Caigny, A.; Benoit, D.F.; Raes, A. Predicting student dropout in subscription-based online learning environments: The beneficial impact of the logit leaf model. Decis. Support Syst. 2020, 135, 113325. [Google Scholar] [CrossRef]
- Dewan MA, A.; Lin, F.; Wen, D. Predicting dropout-prone students in e-learning education system. In Proceedings of the 2015 IEEE 12th International Conference on Ubiquitous Intelligence and Computing and 2015 IEEE 12th International Conference on Autonomic and Trusted Computing and 2015 IEEE 15th International Conference on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom), Beijing, China, 10–14 August 2015; pp. 1735–1740. [Google Scholar]
- da Silva, P.M.; Lima, M.N.; Soares, W.L.; Silva, I.R.; de Fagundes, R.A.; de Souza, F.F. Ensemble regression models applied to dropout in higher education. In Proceedings of the 2019 8th Brazilian Conference on Intelligent Systems (BRACIS), Salvador, Brazil, 15–18 October 2019; pp. 120–125. [Google Scholar]
- Patacsil, F.F. Survival analysis approach for early prediction of student dropout using enrollment student data and ensemble models. Univers. J. Educ. Res. 2020, 8, 4036–4047. [Google Scholar] [CrossRef]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should I trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Lundberg, S.M.; Lee, S.I. Consistent feature attribution for tree ensembles. arXiv 2017, arXiv:1706.06060. [Google Scholar]
- Bach, S.; Binder, A.; Montavon, G.; Klauschen, F.; Müller, K.R.; Samek, W. On pixel-wise explanations for non-linear classifier decisions by layer-wise relevance propagation. PLoS ONE 2015, 10, e0130140. [Google Scholar] [CrossRef] [PubMed]
- Selvaraju, R.R.; Cogswell, M.; Das, A.; Vedantam, R.; Parikh, D.; Batra, D. Grad-cam: Visual explanations from deep networks via gradient-based localization. In Proceedings of the IEEE International Conference on Computer Vision, Venice, Italy, 22–29 October 2017; pp. 618–626. [Google Scholar]
- Alwarthan, S.; Aslam, N.; Khan, I.U. An explainable model for identifying at-risk student at higher education. IEEE Access 2022, 10, 107649–107668. [Google Scholar] [CrossRef]
- Smith, B.I.; Chimedza, C.; Bührmann, J.H. Individualized help for at-risk students using model-agnostic and counterfactual explanations. Educ. Inf. Technol. 2022, 27, 1539–1558. [Google Scholar] [CrossRef]
- Dass, S.; Gary, K.; Cunningham, J. Predicting student dropout in self-paced MOOC course using random forest model. Information 2021, 12, 476. [Google Scholar] [CrossRef]
- Baranyi, M.; Nagy, M.; Molontay, R. Interpretable deep learning for university dropout prediction. In Proceedings of the 21st Annual Conference on Information Technology Education, Virtual Event, USA, 7–9 October 2020; pp. 13–19. [Google Scholar]
- Albreiki, B. Framework for automatically suggesting remedial actions to help students at risk based on explainable ML and rule-based models. Int. J. Educ. Technol. High. Educ. 2022, 19, 1–26. [Google Scholar] [CrossRef]
- Alonso, J.M.; Casalino, G. Explainable artificial intelligence for human-centric data analysis in virtual learning environments. In International Workshop on Higher Education Learning Methodologies and Technologies Online; Springer: Cham, Switzerland, 2019; pp. 125–138. [Google Scholar]
- OULAD Dataset Link. Available online: https://analyse.kmi.open.ac.uk/open_dataset (accessed on 12 November 2023).
- Github Code Link. Available online: https://github.com/githubthank/At-Risk_Prediction (accessed on 12 November 2023).
- Sasaki, Y. The truth of the F-measure. Teach Tutor Mater 2007, 1, 1–5. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Powers, D.M. Evaluation: From precision, recall and F-measure to ROC, informedness, markedness and correlation. J. Mach. Learn. Technol. 2011, 2, 37–63. [Google Scholar]



| Citation | Dataset | Algorithms |
|---|---|---|
| Lykourentzou et al. [6] | The National Technical University of Athens | FFNN, SVM, PESFAM |
| Yukselturk et al. [10] | Government University in the capital city of Turkey | KNN, DT, NB, ANN, |
| Chaplot et al. [7] | Coursera | NN, SA |
| Kuzilek et al. [3] | The Open University (UK) | KNN, CART, NB, Voting |
| Tan and Shao [17] | Open University of China | DT, BN, ANN |
| Cobos et al. [9] | EdX | GBM, KNN, LR, XGB |
| Hlosta et al. [5] | The Open University (UK) | LR, SVM, RF, NB, XGB |
| Haiyang et al. [13] | The Open University (UK) | TSF |
| Alshabandar et al. [4] | The Open University (UK) | EDDA |
| Jha et al. [16] | The Open University (UK) | GB, DRF, DL, GLM |
| Queiroga et al. [11] | Instituto Federal Sul Rio-Grandense (IFSul) in Brazil | GA, AdaBoost, DT, LR, MLP, RF |
| Zhou et al. [14] | E-learning big data technology company in China | Cox proportional hazard model |
| Mubarak et al. [12] | The Open University (UK) | SELOR, IOHMM, LR, SVM, DT, RF |
| Citation | Dataset | Algorithms |
|---|---|---|
| Dewan et al. [23] | Simulation data | Vote (KNN, RBF, SVM) |
| Kuzilek et al. [3] | The Open University (UK) | Vote (KNN, CART, NB) |
| da Silva et al. [24] | National Institute of Educational Studies and Research (INEP) in the year 2013, Brazil | Ensemble (bagging + LR, robust regression, ridge regression), lasso regression, boosting, RF, support vector regression, KNN |
| Patacsil [25] | Pangasinan State University Urdaneta City Campus | DT, forest tree, J-48, ensemble model (bagging + DT, bagging + forest tree, bagging + J-48), AdaBoost + DT, AdaBoost + forest tree, AdaBoost + J-48 |
| Citation | Dataset | Algorithms |
|---|---|---|
| Alonso et al. [35] | The Open University (UK) | J48, RepTree, random tree, FURIA (+ ExpliClas) |
| Baranyi [33] | Budapest University of Technology and Economics | FCNN, TabNet, XGB, RF, bagging (+ SHAP) |
| Dass [32] | Math course College Algebra and Open edX offered by EdPlus at Arizona State University | RF (+ SHAP) |
| Alwarthan et al. [30] | The preparatory year students from the humanities track at Imam Abdulrahman Bin Faisal University (SMOTE) | RF, ANN, SVM (+ LIME, + SHAP) |
| Albreiki [34] | United Arab Emirates University (UAEU) | XGB, LightGBM, SVM, GaussianNB, ExtraTrees, bagging, RF, MLP (+ LIME) |
| Semester 2013-B | Semester 2013-J | Semester 2014-B | Semester 2014-J | |
| Course AAA | (TCD) | (TCD) | (TCD) | (Test data) |
| Course GGG | (TCD) | (TCD) | (TCD) | |
| Semester 2013-B | Semester 2013-J | Semester 2014-B | Semester 2014-J | |
| Course AAA | (SCD) | (SCD) | (SCD) | (Test data) |
| Course GGG | ||||
| Semester 2013-B | Semester 2013-J | Semester 2014-B | Semester 2014-J | |
| Course AAA | (SSD) | (Test data) | ||
| Course GGG | (SSD) | |||
| Algorithm | GB | Bagging | XGB | AdaBoost | RF | LR | SVM | KNN |
| Vote-5 (XGB, RF, bagging, AdaBoost, GB) | Vote-3 (LR, SVM, KNN) | |||||||
| Vote-8 (LR, SVM, KNN, XGB, RF, bagging, AdaBoost, GB) | ||||||||
| Type | Variable |
|---|---|
| Demographic data (independent variables) | Studied_Credits |
| Number_of_Previous_Attempts | |
| Highest_Education | |
| IMD_Band | |
| Age_Band | |
| Gender | |
| Region | |
| Disability | |
| Date_registration | |
| VLE activity data (independent variables) | The number of clicks for each 20 VLE activity variables |
| The number of visits for each 20 VLE activity variables | |
| The number of clicks for all the VLE activity variables | |
| The number of visits for all the VLE activity variables | |
| The number of visit days | |
| Dependent variable | Final_result |
| Algorithm | Week 8 (F1) | Week 16 (F1) | Week 24 (F1) | Week 32 (F1) | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| TCD | SCD | SSD | TCD | SCD | SSD | TCD | SCD | SSD | TCD | SCD | SSD | |
| LR | 0.732 | 0.702 | 0.742 | 0.754 | 0.745 | 0.776 | 0.829 | 0.777 | 0.774 | 0.802 | 0.841 | 0.807 |
| SVM | 0.688 | 0.730 | 0.728 | 0.743 | 0.752 | 0.766 | 0.781 | 0.794 | 0.798 | 0.817 | 0.831 | 0.825 |
| KNN | 0.690 | 0.733 | 0.723 | 0.737 | 0.750 | 0.750 | 0.772 | 0.803 | 0.767 | 0.806 | 0.833 | 0.806 |
| XGB | 0.706 | 0.685 | 0.709 | 0.769 | 0.758 | 0.768 | 0.780 | 0.779 | 0.797 | 0.817 | 0.832 | 0.835 |
| RF | 0.712 | 0.682 | 0.738 | 0.770 | 0.750 | 0.785 | 0.796 | 0.777 | 0.809 | 0.820 | 0.821 | 0.839 |
| Bagging | 0.712 | 0.643 | 0.741 | 0.765 | 0.756 | 0.780 | 0.781 | 0.733 | 0.803 | 0.821 | 0.816 | 0.839 |
| AdaBoost | 0.722 | 0.666 | 0.745 | 0.761 | 0.748 | 0.767 | 0.757 | 0.784 | 0.781 | 0.778 | 0.781 | 0.819 |
| GB | 0.733 | 0.658 | 0.759 | 0.782 | 0.749 | 0.788 | 0.793 | 0.771 | 0.798 | 0.808 | 0.797 | 0.836 |
| Vote-3 | 0.720 | 0.735 | 0.745 | 0.760 | 0.775 | 0.779 | 0.793 | 0.805 | 0.800 | 0.824 | 0.838 | 0.830 |
| Vote-5 | 0.724 | 0.675 | 0.745 | 0.783 | 0.760 | 0.788 | 0.797 | 0.787 | 0.812 | 0.824 | 0.833 | 0.840 |
| Vote-8 | 0.719 | 0.674 | 0.747 | 0.776 | 0.756 | 0.788 | 0.788 | 0.787 | 0.803 | 0.814 | 0.828 | 0.837 |
| Average | 0.714 | 0.689 | 0.738 | 0.764 | 0.754 | 0.776 | 0.788 | 0.782 | 0.795 | 0.812 | 0.823 | 0.828 |
| Course | Gradient Boosting (GB) | Vote-5 | ||||
|---|---|---|---|---|---|---|
| F1 | AUC | ACC | F1 | AUC | ACC | |
| AAA | 0.817 | 0.697 | 0.745 | 0.846 | 0.701 | 0.775 |
| BBB | 0.733 | 0.766 | 0.765 | 0.765 | 0.783 | 0.782 |
| CCC | 0.744 | 0.77 | 0.74 | 0.744 | 0.77 | 0.739 |
| DDD | 0.696 | 0.747 | 0.763 | 0.705 | 0.754 | 0.77 |
| EEE | 0.9 | 0.862 | 0.877 | 0.908 | 0.875 | 0.888 |
| FFF | 0.849 | 0.85 | 0.847 | 0.866 | 0.866 | 0.862 |
| GGG | 0.844 | 0.816 | 0.818 | 0.85 | 0.814 | 0.821 |
| Avg | 0.798 | 0.787 | 0.794 | 0.812 | 0.795 | 0.805 |
| Feature | Course DDD | Course GGG | ||
|---|---|---|---|---|
| XGBoost | GB | XGBoost | GB | |
| homepage_visit | Top 1 | Top 1 | Top 1 | Top 2 |
| external_quiz_click | Top 2 | Top 2 | Top 10 | |
| quiz_visit | Top 7 | Top 3 | Top 6 | |
| sum_visit_date | Top 4 | Top 4 | Top 6 | Top 4 |
| highest_education | Top 6 | Top 5 | Top 3 | Top 3 |
| studied_credits | Top 5 | Top 6 | Top 2 | Top 1 |
| imd_band | Top 9 | Top 7 | Top 5 | Top 5 |
| ouwiki_click | Top 8 | Top 8 | ||
| forumng_click | Top 9 | |||
| resource_visit | Top 10 | Top 8 | ||
| page_visit | Top 9 | |||
| resource_click | Top 7 | |||
| oucontent_click | Top 10 | |||
| date_registration | Top 7 | |||
| homepage_click | Top 3 | Top 4 | ||
| total_activity_click | Top 10 | Top 8 | ||
| Feature | AAA | BBB | CCC | DDD | EEE | FFF | GGG |
|---|---|---|---|---|---|---|---|
| homepage_visit | Top 1 | Top 1 | Top 1 | Top 1 | Top 1 | Top 1 | Top 2 |
| external_quiz_click | Top 10 | Top 2 | Top 10 | Top 10 | |||
| quiz_visit | Top 3 | Top 2 | Top 2 | Top 3 | Top 2 | Top 2 | Top 6 |
| sum_visit_date | Top 2 | Top 4 | Top 5 | Top 4 | Top 5 | Top 3 | Top 4 |
| highest_education | Top 4 | Top 3 | Top 4 | Top 5 | Top 3 | Top 4 | Top 3 |
| studied_credits | Top 6 | Top 5 | Top 3 | Top 6 | Top 4 | Top 5 | Top 1 |
| imd_band | Top 5 | Top 6 | Top 6 | Top 7 | Top 6 | Top 6 | Top 5 |
| ouwiki_click | Top 8 | ||||||
| forumng_click | Top 10 | Top 7 | Top 9 | Top 7 | |||
| resource_visit | Top 8 | Top 9 | Top 10 | Top 7 | Top 8 | ||
| page_visit | Top 9 | Top 9 | Top 8 | Top 9 | Top 8 | Top 9 | |
| resource_click | Top 10 | Top 7 | |||||
| oucontent_click | Top 8 | Top 10 | |||||
| page_click | |||||||
| oucontent_visit | Top 7 | Top 8 | Top 9 | ||||
| quiz_click | Top 7 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, C.; Ahn, H. E-Learning at-Risk Group Prediction Considering the Semester and Realistic Factors. Educ. Sci. 2023, 13, 1130. https://doi.org/10.3390/educsci13111130
Zhang C, Ahn H. E-Learning at-Risk Group Prediction Considering the Semester and Realistic Factors. Education Sciences. 2023; 13(11):1130. https://doi.org/10.3390/educsci13111130
Chicago/Turabian StyleZhang, Chenglong, and Hyunchul Ahn. 2023. "E-Learning at-Risk Group Prediction Considering the Semester and Realistic Factors" Education Sciences 13, no. 11: 1130. https://doi.org/10.3390/educsci13111130
APA StyleZhang, C., & Ahn, H. (2023). E-Learning at-Risk Group Prediction Considering the Semester and Realistic Factors. Education Sciences, 13(11), 1130. https://doi.org/10.3390/educsci13111130








