Abstract
This paper examines how 17 secondary mathematics teacher candidates (TCs) in four university teacher preparation programs implemented technology in their classrooms to teach for conceptual understanding in online, hybrid, and face to face classes during COVID-19. Using the Professional Development: Research, Implementation, and Evaluation (PrimeD) framework, TCs, classroom mentor teachers, field experience supervisors, and university faculty formed a Networked Improvement Community (NIC) to discuss a commonly agreed upon problem of practice and a change idea to implement in the classroom. Through Plan-Do-Study-Act cycles, participants documented their improvement efforts and refinements to the change idea and then reported back to the NIC at the subsequent monthly meeting. The Technology Pedagogical Content Knowledge framework (TPACK) and the TPACK levels rubric were used to examine how teacher candidates implemented technology for Mathematics conceptual understanding. The Mathematics Classroom Observation Protocol for Practices (MCOP2) was used to further examine how effective mathematics teaching practices (e.g., student engagement) were implemented by TCs. MCOP2 results indicated that TCs increased their use of effective mathematics teaching practices. However, growth in TPACK was not significant. A relationship between TPACK and MCOP2 was not evident, indicating a potential need for explicit focus on using technology for mathematics conceptual understanding.
1. Introduction
Teaching with technology to support conceptual development has been a focus in mathematics education for decades (National Council of Teachers of Mathematics (NCTM) [1,2,3]). Employing multiple technologies in the teaching of mathematics is much more challenging than using technology in everyday life. Teachers need extensive preparation and support to be able to unleash the benefits of technology in the mathematics classroom [4,5,6,7].
The knowledge needed to use technology to teach mathematics for conceptual understanding is technology pedagogical content knowledge, or TPACK [8,9]. The present study measured TPACK by scoring teacher candidate lessons on the TPACK levels rubric [10]. The teacher candidates (TCs) who participated in the study were in preparation programs that used the Professional Development: Research, Implementation, and Evaluation framework (PrimeD [11,12]) as a program improvement structure. As part of the PrimeD framework, the preparation programs emphasized the use of the NCTM effective mathematics teaching practices [13] (e.g., student engagement). TC growth in the NCTM effective mathematics teaching practices was measured with the Mathematics Classroom Observation Protocol for Practices (MCOP2) [14]. The study took place during the 2020–2021 academic year, in which student teaching placements at the participating institutions were online due to COVID-19. Throughout the year, some schools moved to hybrid models of teaching. Because TCs were using technology so extensively to teach, growth in the NCTM effective teaching practices, as measured by MCOP2, was hypothesized to correlate to growth in TPACK as measured by the TPACK levels rubric.
The two research questions were:
- In what ways did secondary mathematics teacher candidates show evidence of growth in TPACK and the use of effective mathematics teaching practices during the student teaching year?
- To what degree did TPACK correlate with the use of effective mathematics teaching practices?
Importance
The use of digital technology in mathematics education (e.g., online applications, calculators) has long been promoted as a fundamental teaching practice (e.g., [1,2,3,13,15]) and is integrated into the latest standards for secondary mathematics teacher preparation [13]. The use of validated measures to assess TC use of technology in teaching mathematics provides a strong foundation for entry into the profession. The present study uses two validated instruments to investigate the research questions, TPACK levels [10] and the MCOP2 [14]. The PrimeD framework provided opportunities for participants (e.g., TCs, along with their classroom mentor teachers and field supervisors) to engage in collaborative improvement cycles focused on a mutually agreed upon problem of practice. These problems of practice did not focus directly on technology use. Technology was integrated within the problems of practice and was a necessary component of instruction during COVID-19 for communication, mathematics conceptual development, and a blend of communication and conceptual development. The present study, therefore, provides a window into TCs’ growth in technology through integrated approaches, rather than focused initiatives or coursework.
2. Background Literature
The theoretical foundations for this study are based on the Mathematics Knowledge for Teaching (e.g., [4]), TPACK (e.g., [11]), and PrimeD frameworks (e.g., [8,9]). These three frameworks provide a unique lens for blending mathematics pedagogical content knowledge and technology in teacher preparation programs.
2.1. Mathematics Knowledge for Teaching and the Use of Technology
Mathematics Knowledge for Teaching (MKT) indicates the extent to which teachers understand the mathematics content and how well they can explain and model concepts, guide students, and expand thinking [4]. When TCs complete their preparation programs, they need comprehensive knowledge beyond the mathematics they will be teaching and an understanding of students’ conceptual development and misconceptions [16]. MKT enables teachers to choose appropriate pedagogical tools to effectively teach mathematical concepts [4,16,17,18,19,20,21].
Despite the wide acceptance of technology as an effective teaching tool, many teacher preparation programs focus on technology skills rather than blending technology into pedagogy for a whole new approach to student learning [22]. While TCs are often comfortable and adept with using technology, they need more support to develop the knowledge and skills to effectively integrate it into their teaching [9,23].
Technology applications frequently focus on mathematics procedural fluency rather than conceptual understanding [24]. For example, graphing calculators are often used to solve algebraic expressions in ways that exclude conceptual understanding [25]. When procedural fluency is the main focus of a lesson, learning is usually limited to finding answers rather than developing mathematical understanding [24,26,27]. In addition, the COVID-19 crisis and the move to virtual learning has highlighted the need for more teacher preparation in using technology [28]. Emerging research has found that, during the pandemic and the transition to virtual teaching, teachers needed more support in using technology for conceptual understanding [28,29].
2.2. The TPACK Framework
TPACK is a framework (Figure 1) that guides teacher use of digital technology to develop student understanding [30]. TPACK combines pedagogical content knowledge (PCK) [31] with knowledge of technology for learning [8,9,32]. TPACK also addresses the relationship between teachers’ pedagogical decisions and contextual factors, such as class size, environment, resources, and culture [8].
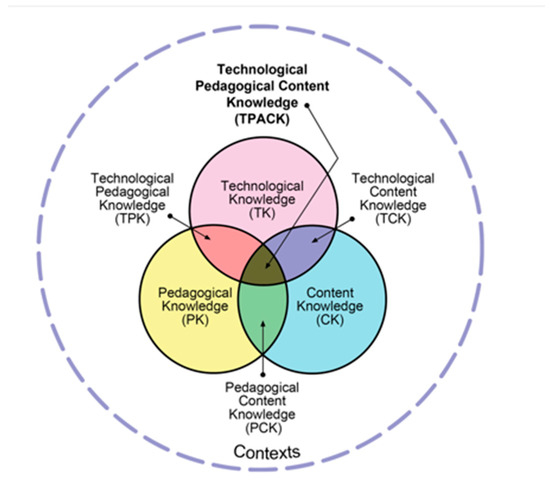
Figure 1.
The TPACK Framework (reproduced by permission of the publisher, © 2012 by tpack.org).
Niess et al. [33] created a developmental model to describe the degree to which teachers integrate technology into their mathematics instruction. The model describes five levels of TPACK: Recognizing (Level 1), Accepting (2), Adapting (3), Exploring (4), and Advancing (5). Increasing TPACK levels is not a linear process but requires teachers to re-examine content and pedagogy. As new technologies emerge, teachers must consider how those technologies can be used to teach mathematics. These levels should be considered benchmarks along a spectrum, rather than discrete jumps in proficiency (Figure 2). As teachers learn to use different technologies to teach mathematics, they may repeat earlier levels that they had already moved through for other technologies; that is, teachers may be at different levels for different technologies. Furthermore, as their pedagogical content knowledge matures, their understanding of the role of technology in teaching may require them to confront misconceptions and revisit earlier levels before moving toward a fully integrated TPACK.

Figure 2.
Model of teacher levels as TPACK components become more robust and interconnected [33] (reproduced by permission of the author).
Each level includes two indicators to describe the integration of technology into (1) teaching and learning and (2) assessment. At Level 1, teachers’ knowledge of technology is distinct from their pedagogical content knowledge. Teachers at Level 1 acknowledge the usefulness of technology for making sense of various topics but resist the use of technology in assessments. For example, they may believe that the use of technology obstructs a teacher’s ability to determine students’ level of understanding about a topic [33]. At Level 2, teachers desire to integrate technology but may struggle to find ways to connect it to a topic. They may also acknowledge the limited usefulness of technology in assessment. At Level 3, teachers begin to make noticeable adjustments in their pedagogy to test the use of technology in their classrooms. They also recognize that the use of technology in assessment requires different types of questions and prompts to evaluate students’ conceptual understanding. At Level 4, teachers begin seeking more ways to integrate technology throughout the curriculum as another learning tool. At this level, teachers also incorporate technology as simply another platform for mathematics assessment; that is, student use of technology can improve teachers’ ability to assess conceptual understanding. At Level 5, teachers incorporate technology as an essential and regular part of teaching and learning to deepen student understanding. Assessments require the full use of technology to demonstrate learning and inform teaching.
2.3. The PrimeD Framework
The PrimeD framework provides organization for teacher professional development (PD). Teacher preparation is often thought of as teachers’ first professional development (PD) experience (e.g., [34,35]). PrimeD has been applied to a wide variety of PD settings, including teacher preparation [36,37]. The PrimeD framework emerged from a systematic review of literature [38] and the evaluation of two state funded PD programs [11,39]. PrimeD was developed using principles of improvement science [40,41,42,43], and lessons learned from research on other PD frameworks (e.g., [44,45]).
Organized into four phases (I Design and Development, II Implementation, III Evaluation, and IV Research) and developed following early field trials, PrimeD (Figure 3) provides structured flexibility while also addressing both universal and unique challenges [37].

Figure 3.
Summary model of the PrimeD framework. Full model available at primedframework.com.
Phase I establishes a challenge space for the program, which describes the vision, goals, contexts, strategies, assessments, and outcomes. The challenge space guides implementation, evaluation, and research in the program. Networked improvement communities (NICs) provide an overarching structure that interweaves practice, research, and evaluation and informs the challenge space. The challenge space evolves as results are understood. Within the challenge space, TPACK may be a desired outcome as well as an individual context. For example, the technology available to the teacher might be a context, while the PD focuses on enhancing a teacher’s ability to use the available technology.
Phase II carries out the challenge space and is divided into two elements: whole group engagement and classroom implementation [11]. NIC and plan–do–study–act (PDSA) cycles provide a means to connect PD activities to classroom practice [42]. NICs provide a supportive place where robust, social discourse is used to focus on common goals, develop a deep understanding of an agreed upon problem of practice and develop a change idea. Once change ideas are developed as potential approaches, participants try out and refine the change idea in their classrooms through multiple PDSA cycles. They return to subsequent NIC meetings to share the results of their PDSA cycles, and the group refines the change idea as needed. These PDSA cycles empower participants to connect theory to classroom practice. By engaging as leaders in the PD, participants also carry out evaluation and research as a normal part of their practice [46,47]. A NIC may focus its change idea on improving teachers’ use of available technology, and PDSA cycles provide a structured process for teachers to apply technology in the classroom at increasing levels of proficiency. We note that a single PDSA cycle may be about the use of technology for particular content, but refinements of the technology change idea for subsequent PDSA cycles will necessarily be applied to subsequent topics in the curriculum. For example, a teacher might begin a PDSA cycle on using Desmos to teach mathematics. For the initial cycle, students in an algebra class might be studying different methods of solving linear equations. In subsequent PDSA cycles, the students might be studying other topics, such as systems of linear equations or polynomial function, while the teacher moves from hunches and theories about how to use Desmos to teach mathematics effectively, to more effective practices to measurable improvement. Phase III evaluation is carried out through information cycles related to the challenge space and implementation. These cycles are intended to be both formative and summative in nature. The evaluation categories (Design, Context, Cycles and Activities, Measures and Assessments, and Outcomes) were developed to align with the five Joint Committee on Standards for Educational Evaluation (JCSEE) program evaluation standard recommendation categories [48]. Formative feedback is intended to be a continuous process throughout the program, to inform the evolution of the challenge space. Participants drive the process by collecting data and analyzing and interpreting results in the NICs to determine whether the change idea worked [41,43]. The TPACK levels assessment informs the evaluation with respect to the use of technology to teach mathematics in the challenge space, implementation, and PDSA cycles.
Participants are also involved in Phase IV Research: determining how, why, and under what conditions a change idea did or did not work. Research is an everyday activity for participants, although it is often seen as distinct from professional practice. Engaging participants in research as a seamless component of PD situates them as leaders in the profession. During Phase II Implementation, participants develop research questions as part of the PDSA cycles. Findings from various classrooms are generalized in Phase IV by sharing results in the whole group meetings of the NICs, so that they are tested in different classrooms and contexts to eventually inform the field. For example, participants in a NIC may agree upon and share practices they tested for framing technology to best develop conceptual understanding of mathematics concepts.
3. Methods
The present study examined lesson videos at the beginning and end of full-time student teaching (hereafter “pre” and “post” videos) from TCs (the unit of analysis) in four university teacher preparation programs. The research questions examined TC growth in TPACK and effective mathematics teaching practices (Research Question 1) as well as the correlation between TPACK and effective mathematics teaching practices (Research Question 2). The mixed methods study followed a single group pre–post correlational design [49] with focus groups as an explanatory supporting component to the quantitative analyses.
3.1. Sample
Four universities in three U.S. states participated in the study. TCs from three of the universities had completed a pre and post video at the end of Year 1 (the fourth university follows a different student teaching schedule—spring to fall rather than fall to spring). Due to COVID-19, student teaching placements at all four universities began fully online. School districts limited the number of observers and one university disallowed video recording. Approximately 42.5% of TCs had complete pre and post videos for full analysis (Table 1).

Table 1.
Sample of TCs by University.
Due to COVID-19 constraints, several schools and districts limited the observation and video recording of lessons. As a result, the TC sample for the present study was reduced, as shown in Table 1. A total of 17 TCs submitted a pre and post student teaching lesson video (n = 34 videos).
3.2. Measures
Two observation protocols were used to analyze TC videos before and after student teaching, the TPACK levels rubric [12] and the Mathematics Classroom Observation Protocol for Practices (MCOP2) [13,50]. The TPACK levels rubric measured four components of technology integration, which served as variables for the study: Overarching Concept, Knowledge of Curriculum, Knowledge of Students, and Instructional Strategies. Each variable was scored from 0 to 5, corresponding with the TPACK levels from Niess et al. [33]. Scores for each variable were either integers or half integers (0.5, 1.5, 2.5, 3.5, or 4.5), as recommended by Lyublinskaya and Tournaki [12]. The performance descriptors for each level of the components included an indicator for assessment and one for teaching/learning. To be scored at a TPACK level, the lesson needed to meet both descriptions for that level. For example, a lesson that met Level 2 for teaching and learning but Level 1 for assessment would be scored a 1.5. The rubric was validated for use with preservice teacher lessons [51]. The rubric authors reported moderate inter-rater agreement, ranging from r = 0.613 to 0.679 (p < 0.01).
Two videos were coded on the TPACK levels rubric by the full group to facilitate consistent scoring, leaving 32 videos to code. For the two videos coded by the full group, initial scores indicated a moderate inter-rater reliability, ICC = 0.510. Next, 16 of the 32 lesson videos were double coded. Coders scored the lessons independently, then met to determine a final set of scores based on consensus agreement. Initial scores showed very good inter-rater agreement, with 85% of the double scores having a difference of 0 or 0.5 (i.e., exact or adjacent).
MCOP2 [14] measures effective mathematics teaching practices and has demonstrated strong inter-rater reliability, even with little to no training (intraclass correlations in the “good” range, >0.616) [50]. Its two subscales, Teacher Facilitation and Student Engagement, served as variables of effective mathematics teaching practices. These two variables were validated through an exploratory factor analysis [50] and measure teacher and student practices with high internal consistency (α > 0.85). Content validity was assessed by two rounds of expert panel review. The Teacher Facilitation variable provided information about how the teacher structures a lesson, guides the problem-solving process, and leads classroom discourse [13,50]. The Student Engagement variable measured the degree to which the role of the student has shifted to active engagement, leadership, and collaboration from the traditional passive role.
In the present study, a three step process was used to ensure that the meaning of the constructs was commonly understood and agreed upon by all coders and that scores across coders were well aligned. In Step 1, all coders watched a video of a one hour lesson together, coded each MCOP2 indicator independently, and then discussed ratings and rationale as a group. Step 2 repeated Step 1 with a different lesson video. By the end of Step 2, the group discussions indicated a great deal of qualitative agreement in how coders were interpreting the performance descriptors for each indicator. The process, therefore, moved to Step 3, which consisted of all coders independently coding another lesson video and submitting their scores for analysis. The intraclass correlation was 0.814, which is considered good reliability based on Koo and Li’s [52] criteria. Coding assignments were then distributed for Year 1 lessons, all of which were online. Approximately 28% of the Year 1 lessons were double coded (16/56) to provide additional reliability information for use in Year 2 training.
3.3. Procedures
This analysis was conducted as part of a larger longitudinal study. The present study focuses on Year 1 results. TCs, classroom mentor teachers, field experience supervisors, and faculty participated in monthly networked improvement community (NIC) meetings. During these NIC meetings, participants discussed pedagogical strategies and agreed upon a change idea for a problem of practice.
Between the NIC meetings, participants implemented the change idea in their classrooms through plan–do–study–act (PDSA) cycles, collected evidence of how the change idea impacted student outcomes, and refined their strategy based on their evidence. At each subsequent NIC meeting, participants reported their results and refinements. The group then agreed upon which refinements needed to be adopted by the whole group and then returned to their classrooms for another month of PDSA cycles.
At the beginning of the year, PDSA cycles were broad and incomplete (e.g., focused on general pedagogy such as engagement, no formal measures collected). As the cycles progressed through the academic year, the focus tightened to more specific pedagogical content connections such as inquiry practices in mathematics and student learning behaviors (e.g., using multiple representations, communicating mathematical ideas in multiple formats, critiquing competing ideas).
3.4. Analytic Methods
To examine the amount of growth in TPACK and mathematical practices (MCOP2) from pre to post student teaching (Research Question 1), two tailed paired t-tests were conducted. Pearson correlations were then analyzed between TPACK and mathematical practices (Research Question 2) for post student teaching scores and pre–post gain scores. All variable analyses were reported, regardless of whether they reached statistical significance, as recommended by Makel et al. [53]. Values of p < 0.05 were accepted as statistically significant.
Power analysis for the paired t-tests indicated statistical power of 0.80 to detect an effect size of 0.71 for n = 17 at the 0.05 level. For the correlations, n = 17 yielded a statistical power of 0.80 to detect a correlation of 0.62 at the 0.05 level.
Paired t-test and correlation analyses share three statistical assumptions: independence, no extreme outliers, and normality. As each observation was from a unique TC, independence was assumed. No variables contained any values more than 3 standard deviations from the mean, so the assumption of no extreme outliers was satisfied. For normality, Shapiro–Wilk tests revealed that approximately 30% of the variables were statistically significant; however, Q–Q plots were examined and revealed no major deviations from the normal distribution (see supplemental file). Correlations also assume a linear relationship between the variables. As the MCOP2 and TPACK levels rubrics both assign higher scores to instruction focused on conceptual understanding and active learning, they were assumed to have a linear relationship.
Focus groups were conducted at the end of the fall and spring semesters by an evaluator at each institution and a lead evaluator. The evaluators were external to the teacher preparation program, and the lead evaluator was external to all four institutions, adding a layer of objectivity to the analyses. The results were analyzed as a qualitative cross case synthesis [54] of the four institutions. The goal of the synthesis was to identify common and unique patterns within and across institutions that may have contributed to effects on the TPACK levels and MCOP2 rubrics. The focus groups were semi-structured by six overarching questions with subquestions:
- How has participation in this project changed your relationship with your (apprentice/mentor/cooperating teacher/student teacher)?
- In what ways has the PrimeD project influenced your beliefs/thinking about teaching mathematics?
- 2a.
- Would you recommend that other mathematics teachers get involved in a project such as this one?
- How has participation in this project changed your approach to teaching mathematics?
- 3a.
- To what degree has this project changed how you teaching mathematics?
- 3b.
- Please share an example of one mathematics concept and/or teaching practice that changed in your teaching as a result of PrimeD.
- In what ways did participation in this project lead to better mathematics learning for your students?
- 4a.
- Describe any changes in student achievement on mathematics quizzes and tests.
- 4b.
- Describe any changes in your students’ persistence in problem solving activities.
- 4c.
- Describe any changes in your students’ engagement in class activities. (make sure this is addressed)
- How has the COVID-19 pandemic impacted this project—thinking about your teaching, student learning, your participation in this project?
- In what ways has this project changed this teacher preparation program? (If you feel this has not already been addressed).
The qualitative responses to the focus group questions were tabulated and analyzed using a consensual coding process [55]. Responses were first created and grouped into categories. Categories were established from the participants’ responses. “Core ideas” ([55], p. 200) were established to justify the category groupings. Finally, the evaluators cross analyzed the data and created themes. The process was completed through researcher triangulation to reconcile any differences. Overall, 98% interrater reliability was established. Consensus was then established through discussion.
4. Results
TPACK and MCOP2 scores were measured at the beginning and end of the fulltime student teaching semester. Table 2 provides the descriptive statistics for each variable.

Table 2.
Descriptive Statistics for TPACK and MCOP2.
The descriptive statistics show that, on average, TC lessons scored between 1 and 2 on a five-point scale for all four TPACK variables and the total mean. No lesson scored a 4 or 5 on the TPACK levels rubric. Coders noted that much of the technology use focused on communication or to verify computations rather than exploration or the development of conceptual understanding.
TC lesson scores averaged between one and two on a three-point scale for both MCOP2 variables and the Total Mean. Some lessons scored as high as 2.6 and 2.7 on a 3-point scale.
4.1. Comparisons between Growth in TPACK and MCOP2
TPACK and MCOP2 scores from before and after fulltime student teaching were compared using paired sample t-tests. The analysis showed significant growth in MCOP2 during student teaching but not in TPACK scores (Table 3).

Table 3.
Paired sample t-tests for pre and post student teaching.
Pearson correlations between TPACK and MCOP2 showed no significant correlations between TPACK and MCOP2 overall and subscale scores (Table 4). Gain scores (post–pre) were computed for both the overall TPACK score and each indicator, overall MCOP2 score, MCOP2 Teacher Facilitation subscale, and MCOP2 Student Engagement subscale. Pearson correlations were computed for each (Table 5).

Table 4.
Pearson correlations of TPACK and MCOP2 post student teaching scores.

Table 5.
Pearson Correlations of TPACK and MCOP2 Gain Scores.
In summary, growth in TPACK was nonsignificant, while growth in MCOP2 scores (representing mathematical practices) were significant at the 0.05 level. None of the correlations between TPACK and MCOP2 indices or gain scores were statistically significant.
4.2. Focus Groups
Focus groups were conducted at each institution at the end of the fall and spring semesters. Responses to focus group questions fell into two themes: improved pedagogy and communication/collaboration for pedagogy. Improved pedagogy included responses about utilizing technology, working through problems of practice and using real world contexts in teaching. For example, one TC noted, “This group has been a blessing for me; it has opened my eyes to some other perspectives and has given me new ideas to try. I always leave the meetings pumped to try something new or work on something,” while an alumni shared, “If it weren’t for this group, I would just be in survivor mode this year, and I wouldn’t take a deep look at a lot of the lessons.”
The second theme from the focus groups was collaboration and communication for pedagogy and included responses related to feedback cycles, relationships, and community. One TC noted, “What covid took away this is giving me back. I love the open discussions these meeting have created both inside the meetings and continued outside of the meetings. It’s great to hear from the aspect of other perspective teachers, like myself, as well as mentor teachers and coordinators. It still amazes me that I am able to have these discussions with such a diverse environment of educators and be able to be heard and also relate to what others are saying and implementing.” Mentor teachers also noted a positive impact from their participation. One mentor noted, “When we discussed some of the issues we are all facing, especially during the pandemic, it made me realize that some of what I used to do maybe isn’t best anymore and I realized what I should be focusing on and not focusing on” while another mentor shared, “I appreciate the NIC because you can come with problems/complaints and we always ask what is the solution?” A TC followed up by sharing, “The discussion we were just having in the meeting about other subjects and their connections to math; it’s important to get out of the math brain sometimes and make more external connections”.
Overall, participants indicated that the inclusion of classroom mentor teachers and supervisors in the NIC meetings may have contributed to TC growth in MCOP2. TCs were able to interact and gain insights from all mentor teachers, not just the one with whom they shared a classroom. Participants across all four institutions consistently pointed to this broader potential for collaboration as a contributing factor to pedagogical improvement. They noted that classroom mentor teachers learned from each other and from supervisors, gained tips for mentoring, and challenged themselves in their own teaching. Participants agreed that there was a stronger sense of community and broader sharing of resources because of the NICs and that they often found solutions for problems in the NICs that might not have been found otherwise.
5. Conclusions
The present study investigated TC growth in TPACK and effective mathematics teaching practices during the fulltime student teaching semester. The results indicated that TCs grew significantly in their ability to use effective mathematics teaching practices as measured by the MCOP2, but TPACK growth was not significant, nor was there a significant relationship between TPACK and MCOP2. TPACK was not the direct focus of the innovation but was considered an important inquiry because of the national emphasis on the integration of technology in mathematics teaching demonstrated by the literature and national education organizations (e.g., [13]). The NIC meetings and PDSA cycles focused directly on effective teaching practices. An indirect focus was not sufficient for teacher candidates, even though they were teaching in online environments due to COVID-19 and relied heavily on technology.
6. Limitations
Due to COVID-19 shutdowns and the move to online teaching, many partner schools and districts disallowed the recording of lessons. Those lessons were, therefore, observed live during synchronous instruction and were unable to be included in the TPACK analyses for the present study. TCs who were in the study but unable to be included may have possibly demonstrated stronger relationships between TPACK and MCOP2 and/or stronger growth in TPACK. Statistical power was generally too low to detect small effects. In general, the small sample size warrants caution when interpreting the findings.
7. Discussion
The NIC and PDSA cycles provided a unique forum for TCs to explore effective mathematics pedagogy during their student teaching year. TCs and mentors noted that the NIC discussions made pedagogical discussions during the month easier: they felt that they were on the same page, with none of the typical differences between the expectations of university faculty, supervisors, and mentors (as described by Gainsburg [56]).
Participants in the focus groups were not able to pinpoint specific changes in their pedagogy, but MCOP2 scores demonstrated that they had made significant albeit small improvement. The Student Engagement variable represented lesson characteristics such as students engaging in exploration, using multiple means of representation, critically assessing strategies, and communicating their ideas to others [14]. The Teacher Facilitation variable represented characteristics such as teacher questioning opening up the conceptual space, using student questions to open the conceptual space, promoting a climate of respect for ideas and encouraging students to engage in and share their thinking [13]. These two variables together measured characteristics that are consistent with the best practices described by Beesley and Apthorp [57].
The focus of the NICs on effective mathematics pedagogy was not sufficient to help TCs grow in TPACK. With teaching being online during COVID, TCs largely used technology for communication rather than to develop mathematics conceptual understanding. Dick and Hollebrands [58] referred to such uses of technology as “conveyance technologies” and are most effective when invisible but can still improve student learning if they are used to increase opportunities for mathematical reasoning and sense making [59]. The more effective uses of technology are mathematics action technologies, which have mathematically defined functionality and are specifically for the learning and performing of mathematics [58]. When mathematics was the focus of technology in the sample lessons, the technology was often used to develop procedural skills and compute answers. Instead, a more productive use of technology is to focus on questions that can be motivated by the technology rather than answers [58]. The focus groups indicated that participants felt more supported, and they were willing to take more risks in the classroom by using an expanded repertoire of strategies. Although the NICs enhanced communication and offered a means of support during the unprecedented teaching environments surrounding COVID-19, participant comments implied enhanced knowledge (e.g., being able to try new strategies). In contrast, they did not indicate that they felt more knowledgeable, and the TPACK scores indicate that their ability to use technology for conceptual understanding did not grow.
Another contributing factor for a TC not illustrating stronger growth in TPACK may be a concurrent synthesis of several important simultaneous factors. During their internship, TCs are learning how to teach, still learning about mathematical/pedagogical technology as a tool, growing in the implementation of effective teaching strategies, and when/how to teach mathematical concepts with purposeful technology integration, all concurrently. Not only does this professional/pedagogical synthesis take time, but TCs were often asked to balance teaching with technology (at times) in a hybrid environment, with some students in person and others attending remotely. As such, measuring growth in TPACK may have included several layers for the TC as learners of instructional technology. Gaining experience in teaching in a new hybrid format may have led to more complexity in attaining and illustrating stronger growth in TPACK.
This study examined the first year of the PrimeD innovation, and the limited duration of the PD may explain some of the lack of growth in TPACK. The lack of correlation between TPACK and MCOP2 was somewhat surprising, given that both rubrics emphasize student engagement and inquiry-based practices [10,14]. We suspect that the lack of correlation is not an artifact of low statistical power but rather confirmation that the “T” in TPACK is an important and unique type of knowledge that is not automatically developed along with PCK, consistent with descriptions by Niess [9]. Putting the “T” back into PCK will require explicit emphasis in the PD experience with the technology purposefully integrated with the pedagogy, as recommended by Roschelle et al. [60].
The use of a framework such as PrimeD provides guidance for the integration of NICs and PDSA cycles in teacher preparation. These structures are a critical tool to ensure the exploration of effective mathematics pedagogy. PrimeD establishes professional communication and collaborative leadership as the norm at the outset of new teacher careers. Preparing teachers in this way will serve the participants well in their careers, which will then have a positive effect on the profession.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/educsci12020133/s1, File S1: Normality Tests.
Author Contributions
Conceptualization and Methodology, C.R.R. and R.N.R.; Project Administration, C.R.R.; Supervision, C.R.R., M.L.S., R.N.R., S.B.B., M.H.F., F.S., J.B.A., J.S., L.A., M.J.M.-S. and J.V.; Formal Analysis, C.R.R., M.L.S., R.N.R., S.B.B., M.H.F., F.S., S.D., A.S., J.B.A., J.S., L.A., M.J.M.-S. and J.V.; Writing-Original Draft, C.R.R., M.L.S. and R.N.R.; Writing-Review and Editing, S.B.B., M.H.F., F.S., S.D., A.S., J.B.A., J.S., L.A., M.J.M.-S. and J.V. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by the National Science Foundation, grant numbers 2013250, 2013397, 2013266, 2013256.
Institutional Review Board Statement
The study was conducted in accordance with the Declaration of Helsinki, and approved by the Institutional Review Board of University of Maryland Baltimore County (protocol code Y17CR24115, approved on 7/2/2020).
Informed Consent Statement
Informed consent was obtained from all subjects involved in the study.
Data Availability Statement
Data supporting the reported results can be found at DOI:10.17632/f6757wv8bw.1.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
References
- National Council of Teachers of Mathematics. Curriculum and Evaluation Standards for School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 1989. [Google Scholar]
- National Council of Teachers of Mathematics. Principles and Standards of School Mathematics; National Council of Teachers of Mathematics: Reston, VA, USA, 2000. [Google Scholar]
- National Council of Teachers of Mathematics. Principles to Actions: Ensuring Mathematical Success for All; National Council of Teachers of Mathematics: Reston, VA, USA, 2014. [Google Scholar]
- Hill, H.C.; Rowan, B.; Ball, D.L. Effects of Teachers’ Mathematical Knowledge for Teaching on Student Achievement. Am. Educ. Res. J. 2005, 42, 371–406. [Google Scholar] [CrossRef] [Green Version]
- National Academy of Sciences; National Academy of Engineering; National Academies, Institute of Medicine. Rising above the Gathering Storm, Revisited: Rapidly Approaching Category 5; National Academies Press: Washington, DC, USA, 2010; Available online: http://www.nap.edu/catalog.php?record_id=12999 (accessed on 10 November 2021).
- National Research Council. Rising above the Gathering Storm: Energizing and Employing America for a Brighter Economic Future; National Academies Press: Washington, DC, USA, 2007. [Google Scholar]
- National Research Council. Preparing Teachers: Building Evidence for Sound Policy; National Academies Press: Washington, DC, USA, 2010. [Google Scholar]
- Mishra, P.; Koehler, M.J. Technological Pedagogical Content Knowledge: A Framework for Teacher Knowledge. Teach. Coll. Rec. 2006, 108, 1017–1054. [Google Scholar] [CrossRef]
- Niess, M.L. Preparing teachers to teach science and mathematics with technology: Developing a technology pedagogical content knowledge. Teach. Teach. Educ. An. Int. J. Res. Stud. 2005, 21, 509–523. [Google Scholar] [CrossRef]
- Lyublinskaya, I.; Tournaki, N. The Effects of Teacher Content Authoring on TPACK and on Student Achievement inAlgebra: Research on Instruction with the TI-Nspire™ Handheld. In Educational Technology, Teacher Knowledge, and Classroom Impact: A Research Handbook on Frameworks and Approaches; Ronau, R.N., Rakes, C.R., Niess, M.L., Eds.; IGI Global: Hershey, PA, USA, 2011; pp. 295–322. [Google Scholar]
- Saderholm, J.; Ronau, R.N.; Rakes, C.R.; Bush, S.B.; Mohr-Schroeder, M. The critical role of a well-articulated, coherent design in professional development: An evaluation of a state-wide two-week program for mathematics and science teachers. Prof. Dev. Educ. 2017, 43, 789–818. [Google Scholar] [CrossRef]
- Rakes, C.R.; Bush, S.B.; Mohr-Schroeder, M.J.; Ronau, R.N.; Saderholm, J. Making teacher PD effective using the PrimeD framework. N. Engl. Math. J. 2017, 50, 52–63. [Google Scholar]
- National Council of Teachers of Mathematics. Catalyzing Change in Middle School Mathematics: Initiating Critical Conversations; National Council of Teachers of Mathematics: Reston, VA, USA, 2020. [Google Scholar]
- Gleason, J.; Livers, S.D.; Zelkowski, J. Mathematics Classroom Observation Protocol for Practices: Descriptors Manual. Tuscaloosa, AL, USA, 2015. Available online: http://jgleason.people.ua.edu/uploads/3/8/3/4/38349129/mcop2_descriptors.pdf (accessed on 10 November 2021).
- National Council of Teachers of Mathematics. Catalyzing Change in High School Mathematics: Initiating Critical Conversations; National Council of Teachers of Mathematics: Reston, VA, USA, 2018. [Google Scholar]
- Eli, J.A.; Mohr-Schroeder, M.J.; Lee, C.W. Mathematical Connections and Their Relationship to Mathematics Knowledge for Teaching Geometry. Sch. Sci. Math. 2013, 113, 120–134. [Google Scholar] [CrossRef]
- Conference Board of Mathematical Sciences (CBMS). The Mathematical Education of Teachers; ERIC No. ED457030; Conference Board of Mathematical Sciences (CBMS): Washington, DC, USA, 2001. [Google Scholar]
- Fennema, E.; Franke, M.L. Teachers’ knowledge and its impact. In Handbook of Research on Mathematics Teaching and Learning: A Project of the National Council of Teachers of Mathematics; Macmillan: Reston, VA, USA, 1992; pp. 147–164. [Google Scholar]
- Ma, L. Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States; Lawrence Erlbaum Associates: Mahwah, NJ, USA, 1999. [Google Scholar]
- Niess, M.L.; Roschelle, J. Transforming Teachers’ Knowledge for Teaching Mathematics with Technologies through Online Knowledge-Building Communities. In Proceedings of the 40th Annual Meeting of the North American Chapter of the International Group for the Psychology of Mathematics Education, Greenville, SC, USA; 2018. Available online: https://files.eric.ed.gov/fulltext/ED606569.pdf (accessed on 10 November 2021).
- Roshelle, J.; Leinwand, S. Improving student achievement by systematically integrating effective technology. NCSM J. Math. Educ. Leadersh. 2011, 13, 3–9. [Google Scholar]
- Hsu, P.-S.; Sharma, P. A Systemic Plan of Technology Integration. J. Educ. Technol. Soc. 2006, 9, 173–184. [Google Scholar]
- Graham, C.R.; Burgoyne, N.; Cantrell, P.P.; Smith, L.M.; Clair, L.S.; Harris, R. TPACK Development in Science Teaching: Measuring the TPACK Confidence of Inservice Science Teachers. TechTrends 2009, 53, 70–79. [Google Scholar]
- Chiu, T.K.F.; Churchill, D. Exploring the characteristics of an optimal design of digital materials for concept learning in mathematics. Comput. Educ. 2015, 82, 280–291. [Google Scholar] [CrossRef] [Green Version]
- Rakes, C.R.; Valentine, J.; McGatha, M.C.; Ronau, R.N. Methods of instructional improvement in algebra: A systematic review and meta-analysis. Rev. Educ. Res. 2010, 80, 372–400. [Google Scholar] [CrossRef]
- Rakes, C.R.; Ronau, R.N.; Bush, S.B.; Driskell, S.O.; Niess, M.L.; Pugalee, D.K. Mathematics achievement and orientation: A systematic review and meta-analysis of education technology. Educ. Res. Rev. 2020, 31, 100337. [Google Scholar] [CrossRef]
- Skemp, R.R. Relational understanding and instrumental understanding. Math. Teach. Middle Sch. 2006, 12, 88–95. [Google Scholar] [CrossRef]
- Sonnenschein, S.; Stites, M. Preschool teachers’ views on distance learning during COVID-19. In Contemporary Perspectives in Early Childhood Education; Saracho, O., Ed.; Information Age Publishing: Scottsdale, AZ, USA, in press.
- Arcueno, G.; Arga, H.; Manalili, T.A.; Garcia, J.A. TPACK and ERT: Understanding teacher decisions and challenges with integrating technology in planning lessons and instruction. In DLSU Research Congress 2021; De La Salle University: Manila, Philippines, 2021. [Google Scholar]
- Niess, M.L. Teacher Knowledge for Teaching with Technology: A TPACK Lens. In Educational Technology, Teacher Knowledge, and Classroom Impact: A Research Handbook on Frameworks and Approaches; Ronau, R.N., Rakes, C.R., Niess, M.L., Eds.; IGI Global: Hershey, PA, USA, 2011; pp. 1–15. [Google Scholar]
- Shulman, L.S. Those who understand: Knowledge growth in teaching. Educ. Res. 1986, 15, 4–14. [Google Scholar] [CrossRef]
- Koehler, M.J.; Mishra, P. What is technological pedagogical content knowledge? Contemp. Issues Technol. Teach. Educ. 2009, 9, 60–70. [Google Scholar] [CrossRef] [Green Version]
- Niess, M.L.; Ronau, R.N.; Shafer, K.G.; Driskell, S.O.; Harper, S.R.; Johnston, C.J.; Browning, C.; Özgün-Koca, S.A.; Kersaint, G. Mathematics Teacher TPACK Standards and Development Model. Contemp. Issues Technol. Teach. Educ. 2009, 9, 4–24. [Google Scholar]
- Darling-Hammond, L. Teaching as a Profession: Lessons in Teacher Preparation and Professional Development. Phi. Delta Kappan 2005, 87, 237–240. [Google Scholar] [CrossRef]
- Pollock, M.; Bocala, C.; Deckman, S.L.; Dickstein-Staub, S. Caricature and Hyperbole in Preservice Teacher Professional Development for Diversity. Urban. Educ. 2016, 51, 629–658. [Google Scholar] [CrossRef]
- Bush, S.B.; Cook, K.L.; Ronau, R.N.; Mohr-Schroeder, M.J.; Rakes, C.R.; Saderholm, J. Structuring Integrated STEM Education Professional Development: Challenges Revealed and Insights Gained from a Cross-Case Synthesis. J. Res. Sci. Math. Educ. 2020, 24, 26–55. Available online: https://files.eric.ed.gov/fulltext/EJ1255599.pdf (accessed on 10 November 2021).
- Rakes, C.R.; Saderholm, J.; Bush, S.B.; Mohr-Schroeder, M.J.; Ronau, R.N.; Stites, M. Structuring secondary mathematics teacher preparation through a professional development framework. Under Review.
- Driskell, S.O.; Bush, S.B.; Ronau, R.N.; Niess, M.L.; Rakes, C.R.; Pugalee, D.K. Mathematics Education Technology Professional Development: Changes over Several Decades. In Handbook of Research on Transforming Mathematics Teacher Education in the Digital Age; Niess, M.L., Driskell, S.O., Hollebrands, K., Eds.; IGI Global: Hershey, PA, USA, 2016. [Google Scholar]
- Bush, S.B.; Cook, K.L.; Ronau, R.N.; Rakes, C.R.; Mohr-Schroeder, M.J.; Saderholm, J. A highly structured collaborative STEAM program: Enacting a professional development framework. J. Res. STEM Educ. 2018, 2, 106–125. [Google Scholar] [CrossRef]
- Bryk, A.S.; Gomez, L.M.; Grunow, A. Getting Ideas into Action: Building Networked Improvement Communities in Education. Carnegie Perspectives; Carnegie Foundation for the Advancement of Teaching: Stanford, CA, USA, 2011. [Google Scholar]
- Bryk, A.S.; Gomez, L.M.; Grunow, A.; LeMahieu, P.G. Learning to Improve: How America’s Schools Can Get Better at Getting Better; Harvard Education Press: Cambridge, MA, USA, 2015. [Google Scholar]
- Martin, W.G.; Gobstein, H. Generating a Networked Improvement Community to Improve Secondary Mathematics Teacher Preparation: Network Leadership, Organization, and Operation. J. Teach. Educ. 2015, 66, 482–493. [Google Scholar] [CrossRef]
- Yeager, D.; Bryk, A.S.; Muhich, J.; Hausman, H.; Morales, L. Practical Measurement; Carnegie Foundation for the Advancement of Teaching: Stanford, CA, USA, 2013; Available online: https://www.carnegiefoundation.org/wp-content/uploads/2013/12/Practical_Measurement.pdf (accessed on 10 November 2021).
- Desimone, L.M. Improving Impact Studies of Teachers’ Professional Development: Toward Better Conceptualizations and Measures. Educ. Res. 2009, 38, 181–199. [Google Scholar] [CrossRef] [Green Version]
- Loucks-Horsley, S.; Hewson, P.W.; Love, N.; Stiles, K.E. Designing Professional Development for Teachers of Science and Mathematics; Corwin Press: Thousand Oaks, CA, USA, 2010. [Google Scholar]
- Shulman, L.S. Theory, Practice, and the Education of Professionals. Elem. Sch. J. 1998, 98, 511–526. [Google Scholar] [CrossRef] [Green Version]
- Shulman, L.S.; Wilson, S.M. The Wisdom of Practice: Essays on Teaching, Learning, and Learning to Teach; Jossey-Bass: Hoboken, NJ, USA, 2004. [Google Scholar]
- Yarbrough, D.B.; Shulha, L.M.; Hopson, R.K.; Caruthers, F.A. The Program Evaluation Standards: A Guide for Evaluators and Evaluation Users, 3rd ed.; Sage: Thousand Oaks, CA, USA, 2010. [Google Scholar]
- Shadish, W.R.; Cook, T.D.; Campbell, D.T. Experimental and Quasi-Experimental Designs for Generalized Causal Inference; Houghton Mifflin: Elkridge, MD, USA, 2002. [Google Scholar]
- Gleason, J.; Livers, S.; Zelkowski, J. Mathematics Classroom Observation Protocol for Practices (MCOP2): A validation study. Investig. Math. Learn. 2017, 9, 111–129. [Google Scholar] [CrossRef]
- Kaplon-Schilis, A.; Lyublinskaya, I. Analysis of differences in the levels of TPACK: Unpacking performance indicators in the TPACK Levels Rubric. In American Educational Research Association; Virtual: Washington, DC, USA, 2021. [Google Scholar]
- Koo, T.K.; Li, M.Y. A Guideline of Selecting and Reporting Intraclass Correlation Coefficients for Reliability Research. J. Chiropr. Med. 2016, 15, 155–163. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Makel, M.C.; Hodges, J.; Cook, B.G.; Plucker, J.A. Both Questionable and Open Research Practices are Prevalent in Education Research. Educ. Res. 2021, 50, 493–504. [Google Scholar] [CrossRef]
- Yin, R.K. Case Study Research and Applications: Design and Methods; Sage: Thousand Oaks, CA, USA, 2018. [Google Scholar]
- Hill, C.E.; Thompson, B.J.; Hess, S.A.; Knox, S.; Williams, E.N.; Ladany, N. Consensual Qualitative Research: An Update. J. Couns. Psychol. 2005, 52, 196–205. [Google Scholar] [CrossRef] [Green Version]
- Gainsburg, J. Why new mathematics teachers do or don’t use practices emphasized in their credential program. J. Math. Teach. Educ. 2012, 15, 359–379. [Google Scholar] [CrossRef]
- Beesley, A.; Apthorp, H. (Eds.) Classroom Instruction that Works. Research Report, 2nd ed.; MCREL International: Denver, CO, USA; Available online: https://www.mcrel.org/wp-content/uploads/2016/03/McREL-research-report_Nov2010_Classroom-Instruction-that-Works_Second-Edition.pdf (accessed on 10 November 2021).
- Dick, T.P.; Hollebrands, K.F. Focus in High School Mathematics: Technology to Support Reasoning and Sense Making; National Council of Teachers of Mathematics: Reston, VA, USA, 2011. [Google Scholar]
- Cohen, J.; Hollebrands, K.F. Technology tools to support mathematics teaching. In Focus in High. School Mathematics: Technology to Support Reasoning and Sense Making; Dick, T.P., Hollebrands, K.F., Eds.; National Council of Teachers of Mathematics: Reston, VA, USA, 2011; pp. 105–122. [Google Scholar]
- Roschelle, J.; Shechtman, N.; Tatar, D.; Hegedus, S.; Hopkins, B.; Empson, S.; Knudsen, J.; Gallagher, L.P. Integration of technology, curriculum, and professional development for advancing middle school mathematics: Three large-scale studies. Am. Educ. Res. J. 2011, 47, 833–878. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).