The Lawson’s Test for Scientific Reasoning as a Predictor for University Formative Success: A Prospective Study
Abstract
1. Introduction
2. Materials and Methods
2.1. Dimensions of Intelligence and Predictors of Educational Success
2.2. Lawson’s Test for Aptitude for Scientific Reasoning
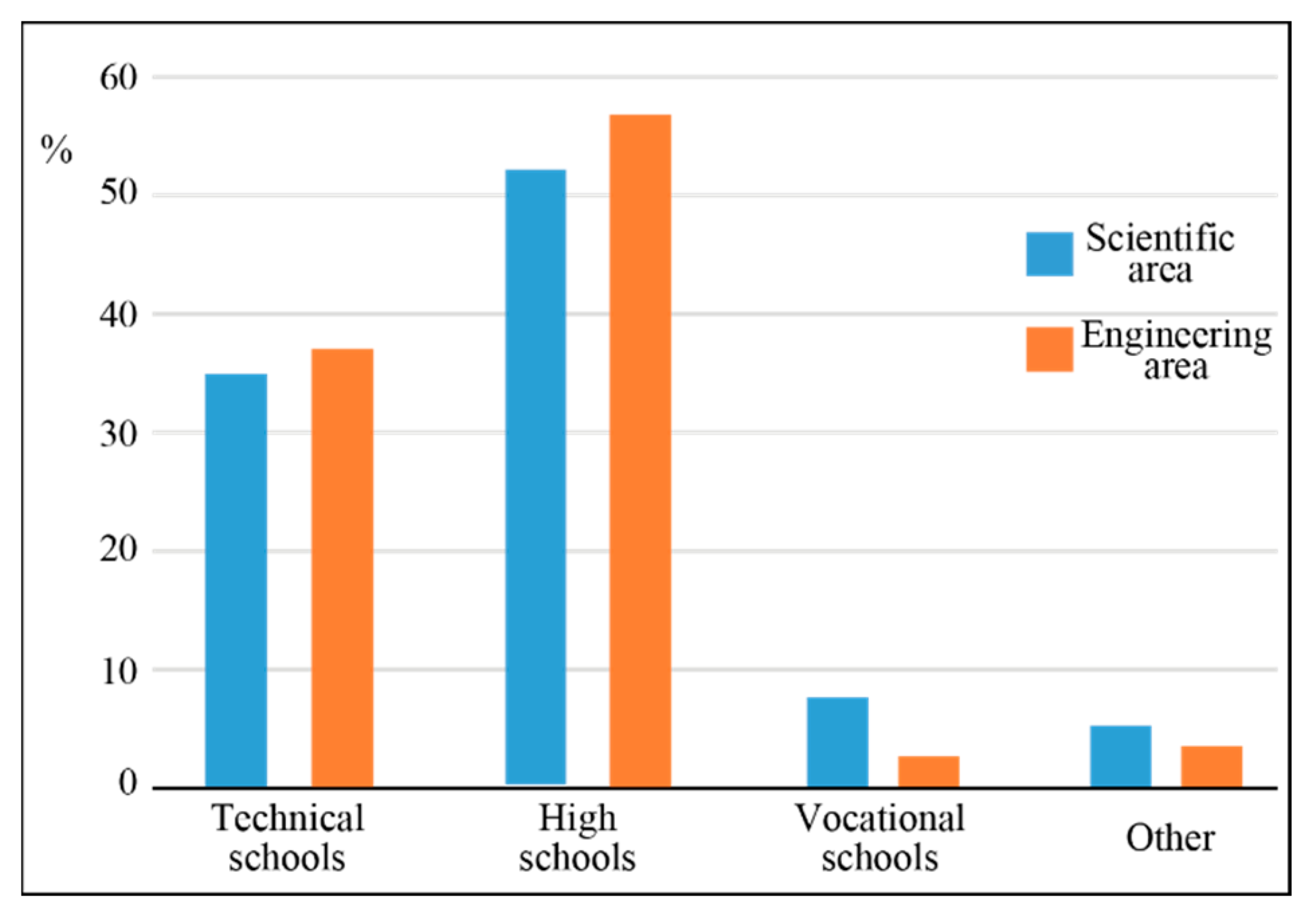
2.3. Context
2.4. Methods
2.4.1. Methods of Administration of Lawson’s Test and Acquisition of Careers Data
2.4.2. Criteria and Methods of Data Analysis
- (i)
- They chose more answers to one or more questions;
- (ii)
- They wrote unsolicited and inappropriate comments;
- (iii)
- They did not write the identification number.
3. Results
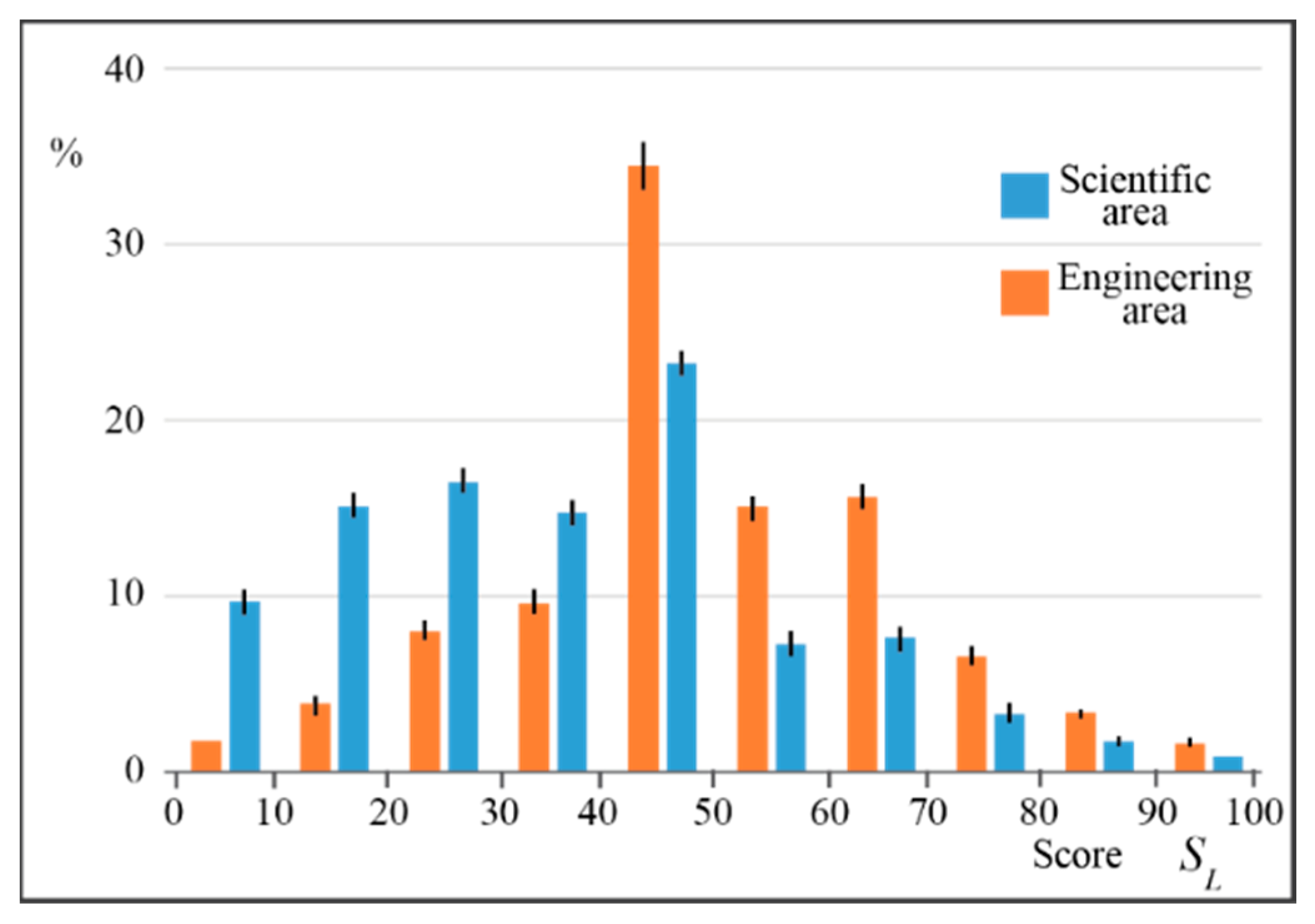
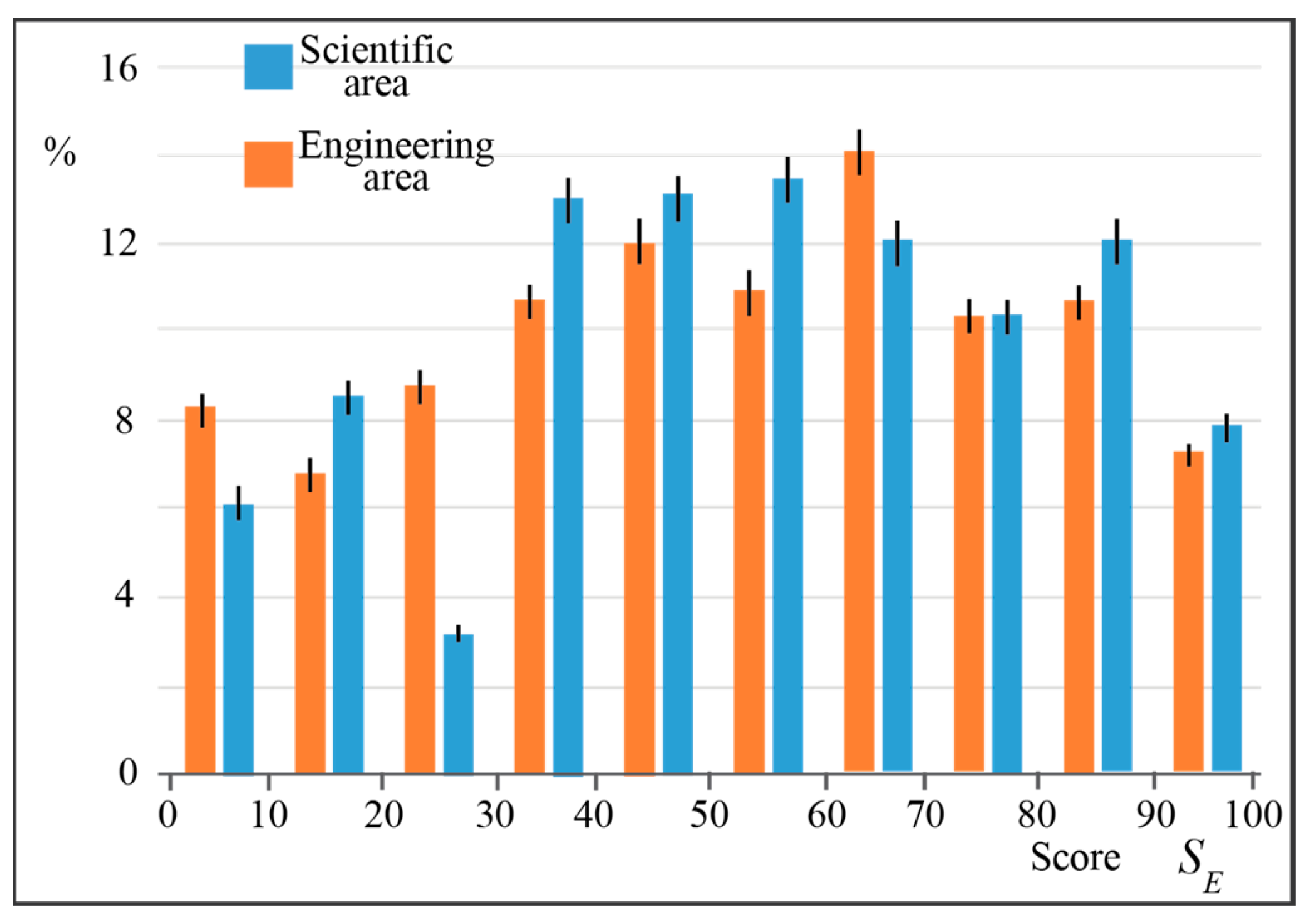
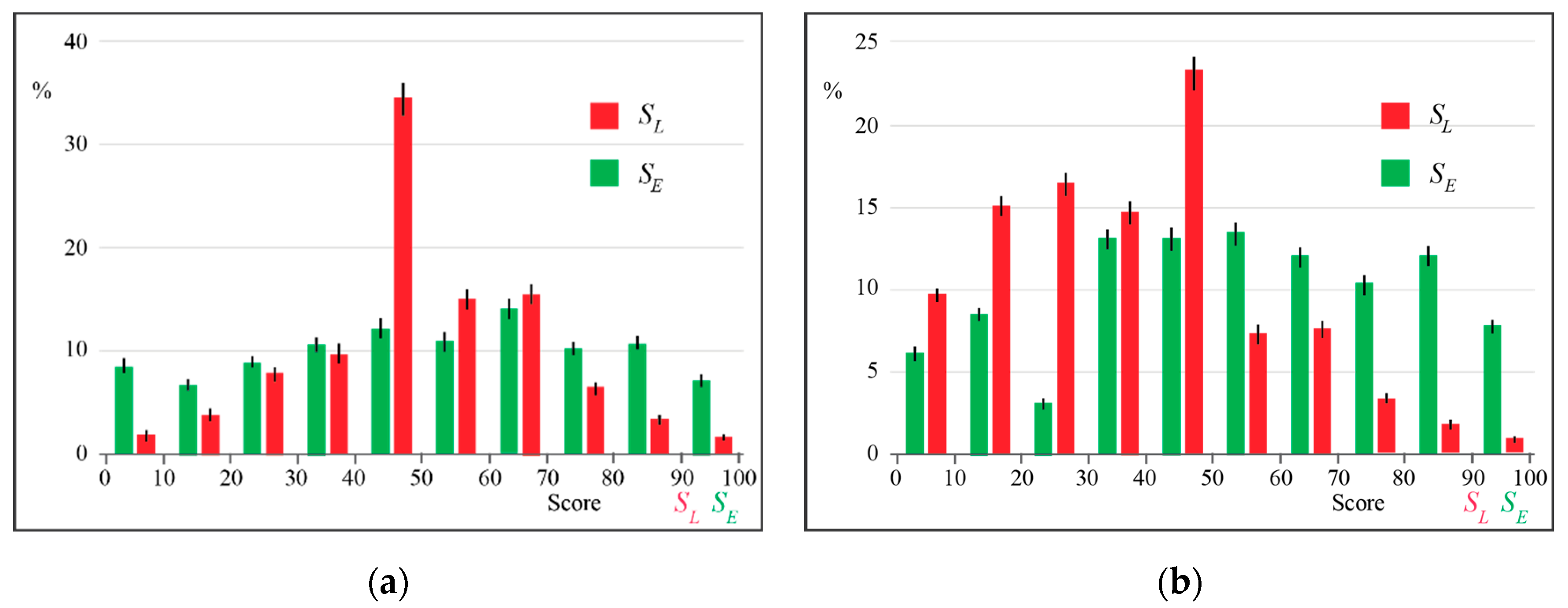
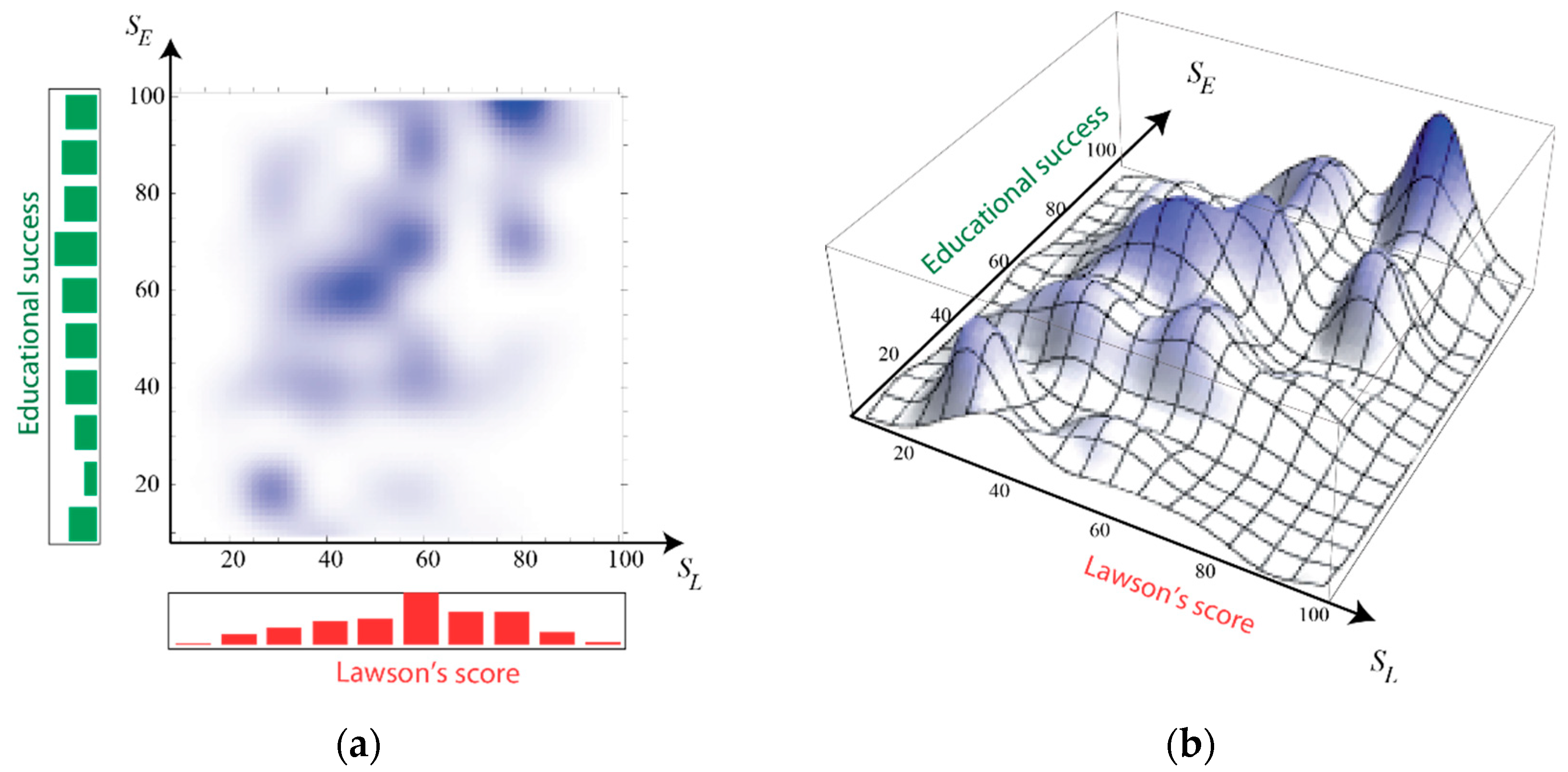
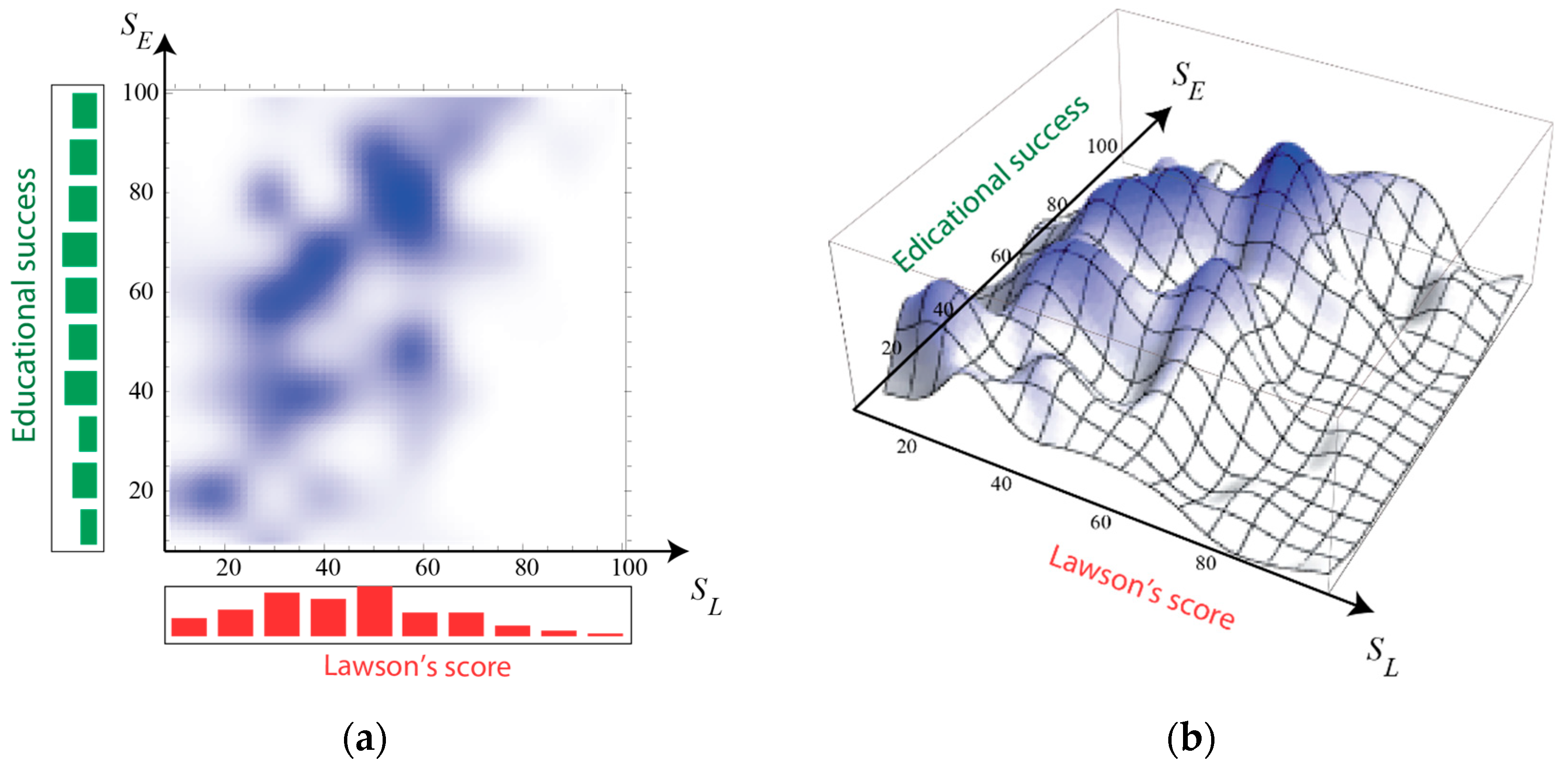
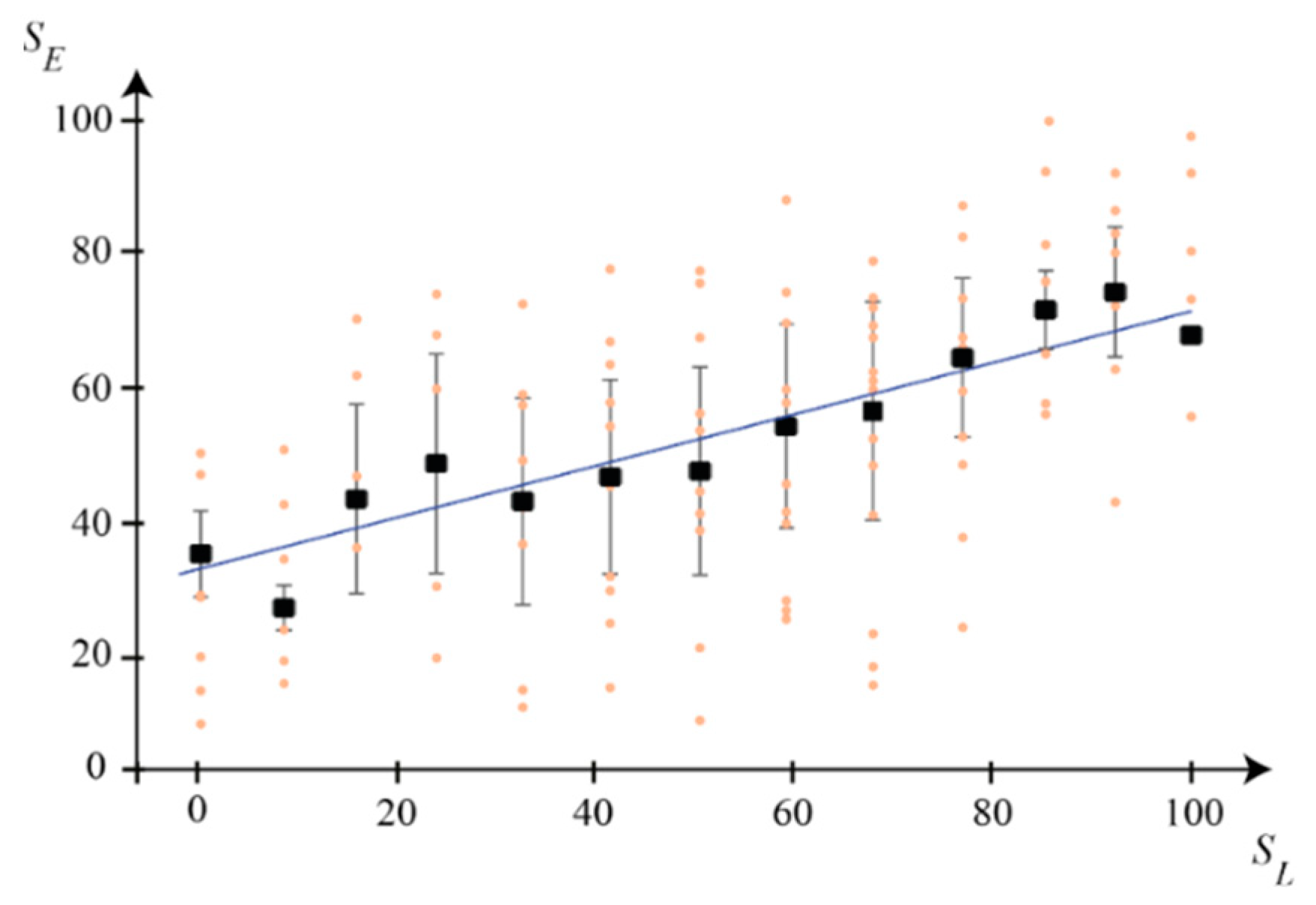
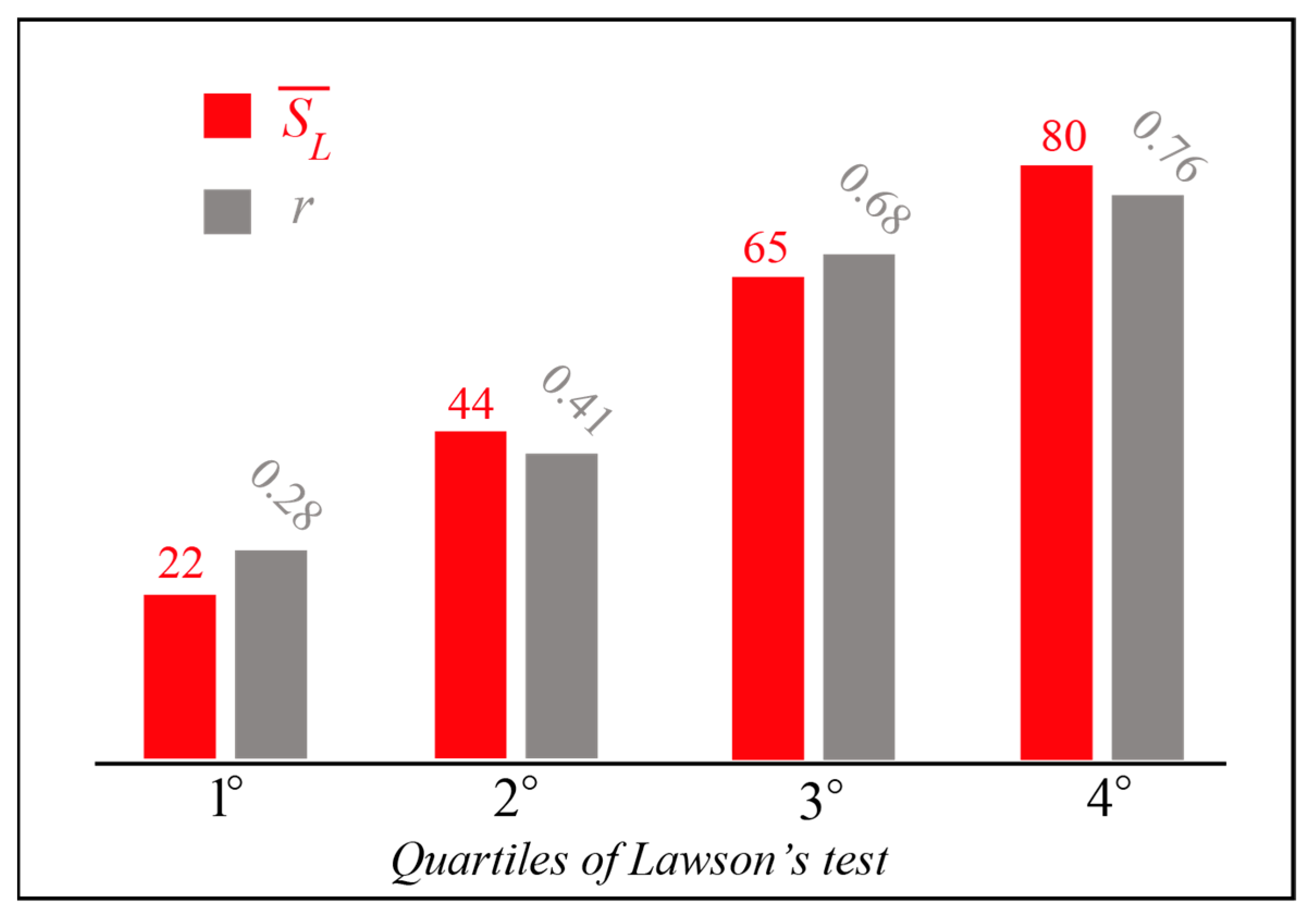
3.1. Correlation with Global Performance
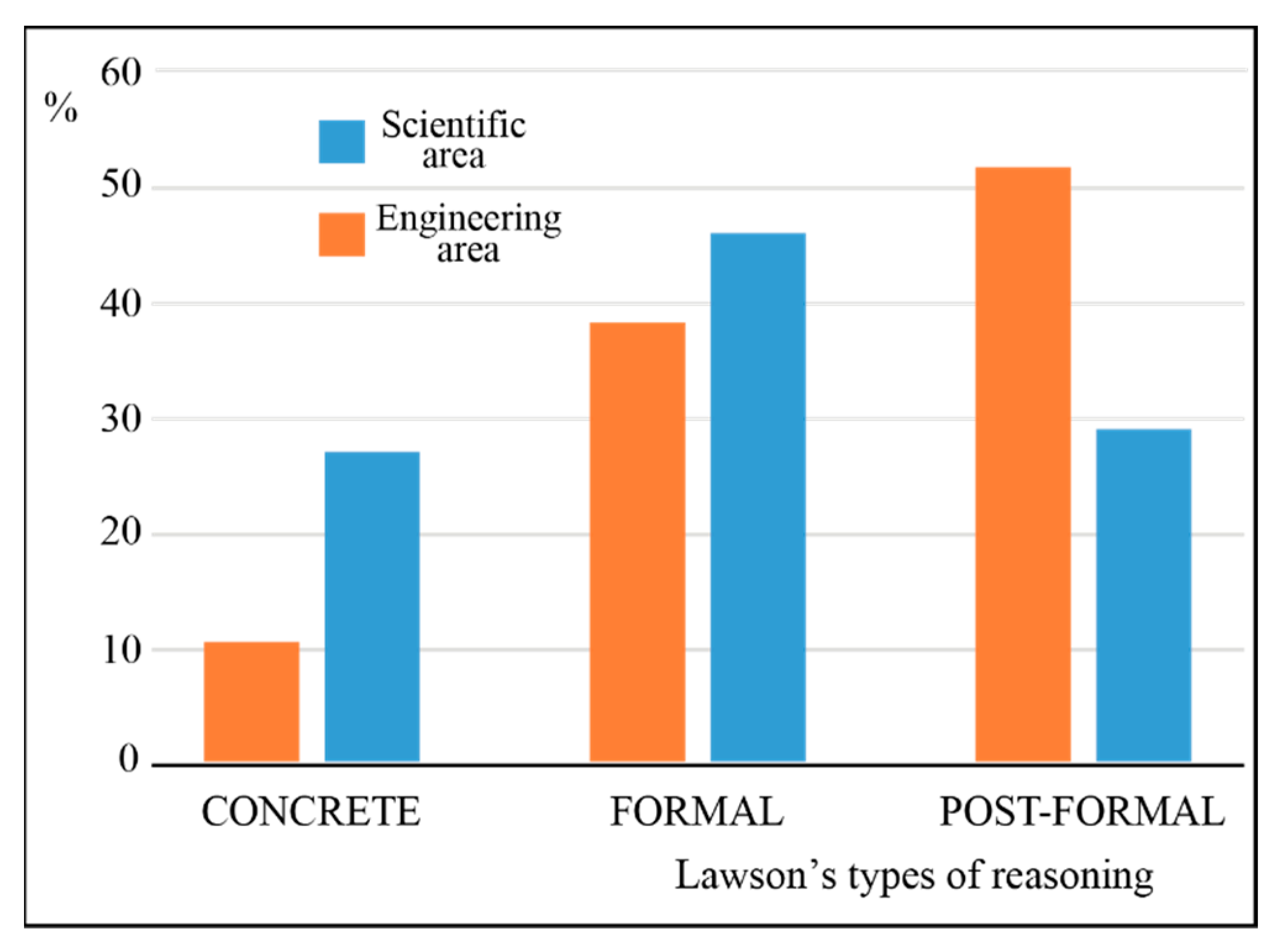
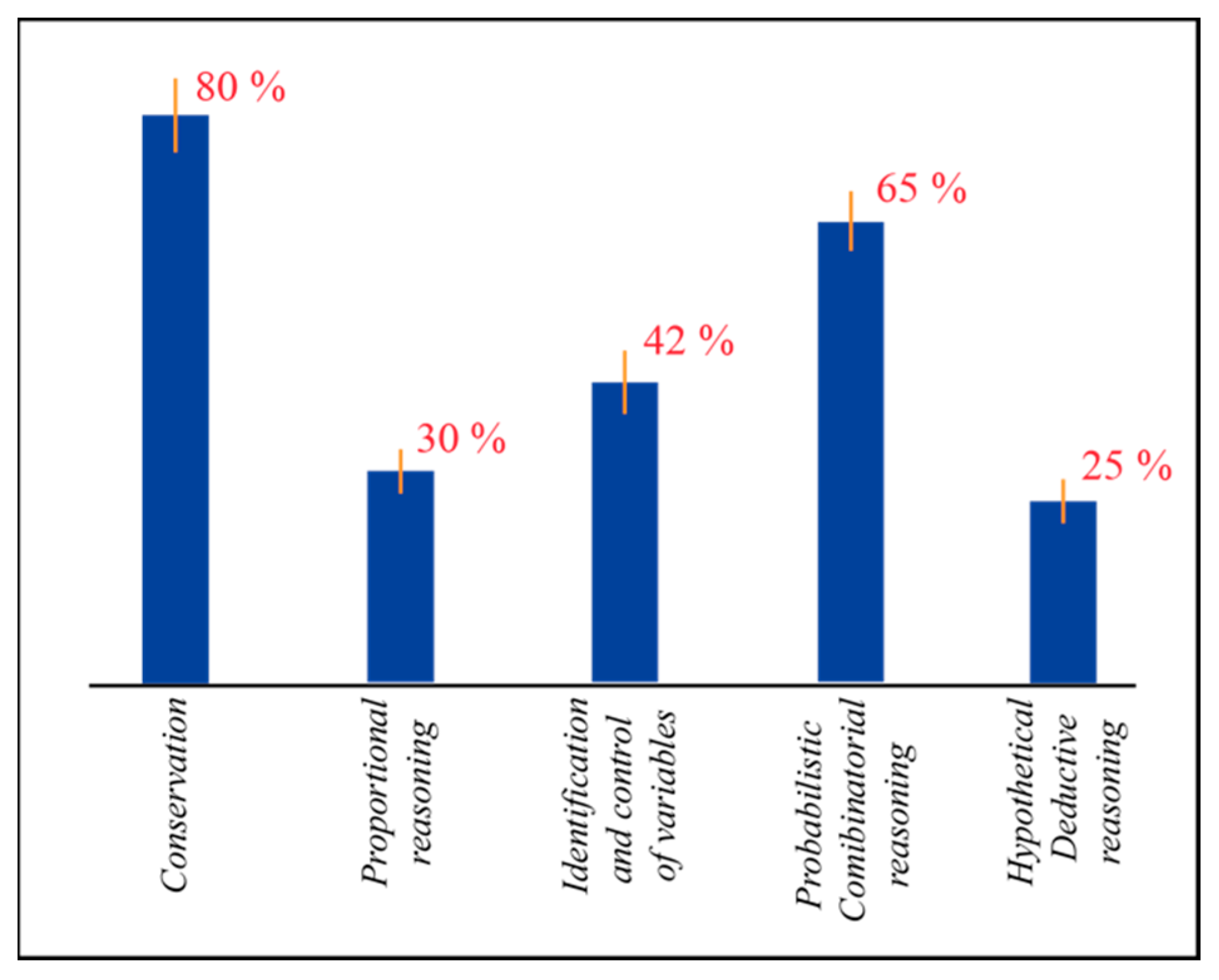
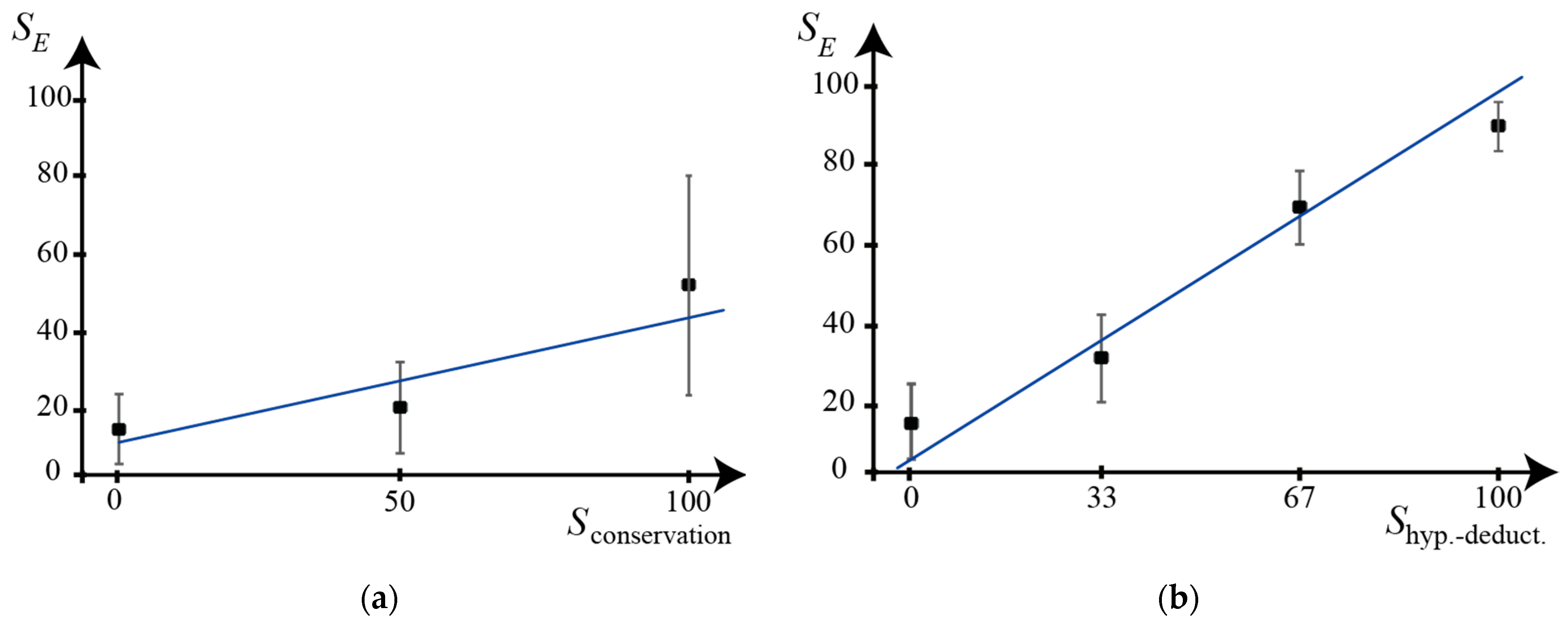
3.2. Correlation Analysis with the Individual Dimensions of the Lawson’s Test
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- EPC. Educational Policies Commission: The Central Purpose of American Education; National Education Association: Washington, DC, USA, 1961. [Google Scholar]
- Lawson, A.E. The nature and development of scientific reasoning: A synthetic view. Int. J. Sci. Math. Educ. 2004, 2, 307–338. [Google Scholar] [CrossRef]
- EPC. Educational Policies Commission: Education and the Spirit of Science; National Education Association: Washington, DC, USA, 1966. [Google Scholar]
- EURYDICE. Mathematics Education in Europe: Common Challenges and National Policies; Education, Audiovisual and Culture Executive Agency: Brussels, Belgium, 2011. [Google Scholar]
- EURYDICE. Science Education in Europe: National Policies, Practices and Research; Education, Audiovisual and Culture Executive Agency: Brussels, Belgium, 2011. [Google Scholar]
- Laugksch, R.C. Scientific Literacy: A Conceptual Overview. Sci. Educ. 2000, 84, 71–94. [Google Scholar] [CrossRef]
- Durant, J. What is scientific literacy? Eur. Rev. 1994, 2, 83–89. [Google Scholar] [CrossRef]
- Roth, W.M.; Désautels, J. Educatingfor citizenship: Reappraising the role of science education. Can. J. Sci. Math. Technol. Educ. 2004, 4, 149–168. [Google Scholar] [CrossRef]
- Pinch, T. The sociology of the scientific community. In Companion to the History of Modern Science; Olby, R.C., Cantor, G.N., Christie, J.R.R., Hodge, M.J.S., Eds.; Routledge: London, UK, 1990; pp. 87–99. [Google Scholar] [CrossRef]
- Lenoir, T. The discipline of nature and the nature of disciplines. In Knowledges: Historical and Critical Studies in Disciplinarity; Messer-Davidov, E., Shumway, D.R., Sylvan, D.J., Eds.; University Press of Virginia: Charlottesville, VA, USA, 1993; pp. 70–102. [Google Scholar]
- Turrini, T.; Dörler, D.; Richter, A.; Heigl, F.; Bonn, A. The threefold potential of environmental citizen science—Generating knowledge, creating learning opportunities and enabling civic participation. Biol. Conserv. 2018, 225, 176–186. [Google Scholar] [CrossRef]
- Forrester, T.D.; Baker, M.; Costello, R.; Kays, R.; Parsons, A.W.; McShea, W.J. Creating advocates for mammal conservation through citizen science. Biol. Conserv. 2017, 208, 98–105. [Google Scholar] [CrossRef]
- Sapia, P. Educazione civica e alfabetizzazione scientifica. L’Eco della Scuola Nuova 2019, LXXIV, 12–14. [Google Scholar]
- Kolstø, S.D. Consensus projects: Teaching science for citizenship. Int. J. Sci. Educ. 2000, 22, 645–664. [Google Scholar] [CrossRef]
- Harlen, W. ASE Guide to Primary Science Education; Association for Science Education: Hatfield, UK, 2006. [Google Scholar]
- Lin, S.S. Science and non-science undergraduate students’ critical thinking and argumentation performance in reading a science news report. Int. J. Sci. Math. Educ. 2014, 12, 1023–1046. [Google Scholar] [CrossRef]
- Yacoubian, H.A. Scientific literacy for democratic decision-making. Int. J. Sci. Educ. 2018, 40, 308–327. [Google Scholar] [CrossRef]
- Hofstein, A.; Eilks, I.; Bybee, R. Societal issues and their importance for contemporary science education—A pedagogical justification and the state-of-the-art in Israel, Germany, and the USA. Int. J. Sci. Math. Educ. 2011, 9, 1459–1483. [Google Scholar] [CrossRef]
- Ministerial Conference of Bologna. 1999. Available online: http://www.ehea.info/page-ministerial-conference-bologna-1999 (accessed on 1 October 2022).
- Lawson, A.E. The development and validation of a classroom test of formal reasoning. J. Res. Sci. Teach. 1978, 15, 11–24. [Google Scholar] [CrossRef]
- Popper, K.R. Conjectures and refutations. The Growth of Scientific Knowledge; Routledge: London, UK, 1962. [Google Scholar]
- Kuhn, T.S. The Structure of Scientific Revolutions, 2nd ed.; The University of Chicago Press: Chicago, IL, USA, 1970. [Google Scholar]
- Reckase, M.D.; Ackerman, T.A.; Carlson, J.E. Building a Unidimensional Test Using Multidimensional Items. J. Educ. Meas. 1998, 25, 193–203. [Google Scholar] [CrossRef]
- Inhelder, B.; Piaget, J. The Growth of Logical Thinking: From Childhood to Adolescence; Routledge: London, UK, 1958. [Google Scholar] [CrossRef]
- Tidman, P.; Kahane, H. Logic and Philosophy: A Modern Introduction; Thomson/Wadsworth: Belmont, CA, USA, 2003. [Google Scholar]
- Krumm, S.; Ziegler, M.; Buehner, M. Reasoning and working memory as predictors of school grades. Learn. Individ. Differ. 2008, 18, 248–257. [Google Scholar] [CrossRef]
- Strand, S. Comparing the predictive validity of reasoning tests and national end of Key Stage 2 tests: Which tests are the ‘best’? Br. Educ. Res. J. 2006, 32, 209–225. [Google Scholar] [CrossRef]
- Titcombe, R. Cognitive ability and school improvement. Pract. Res. Educ. 2006, 36, 27–34. [Google Scholar] [CrossRef]
- Schagen, I. Comments on “Cognitive ability and school improvement”. Pract. Res. Educ. 2007, 35, 83–92. Available online: https://eraexperts.wordpress.com/2013/10/29/ian-schagen-cv/ (accessed on 1 October 2022).
- Oberauer, K.; Süß, H.-M.; Wilhelm, O.; Wittman, W.W. The multiple faces of working memory: Storage, processing, supervision, and coordination. Intelligence 2003, 31, 167–193. [Google Scholar] [CrossRef]
- Kosslyn, S.M.; Koenig, O. Wet Mind. The New Cognitive Neuroscience; The Free Press: New York, NY, USA, 1995. [Google Scholar]
- St Clair-Thompson, H.L.; Gathercole, S.E. Executive functions and achievements in school: Shifting, updating, inhibition, and working memory. Q. J. Exp. Psychol. 2006, 59, 745–759. [Google Scholar] [CrossRef]
- Luo, D.; Thompson, L.A.; Detterman, D.K. The criterion validity of tasks of basic cognitive processes. Intelligence 2006, 34, 79–120. [Google Scholar] [CrossRef]
- Kuhn, D.; Franklin, S. The Second Decade: What Develops (and How). In Handbook of Child Psychology, Volume 2: Cognition, Perception and Language, 6th ed.; Kuhn, D., Siegler, R.S., Eds.; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Zimmerman, C. The development of scientific thinking skills in elementary and middle school. Dev. Rev. 2007, 27, 172–223. [Google Scholar] [CrossRef]
- Wilkening, F.; Sodian, B. Scientific, reasoning in young children: Introduction. Swiss J. Psychol. 2005, 64, 137–139. [Google Scholar] [CrossRef]
- Rohde, T.E.; Thompson, L.A. Predicting academic achievement with cognitive ability. Intelligence 2007, 35, 83–92. [Google Scholar] [CrossRef]
- Lawson, A.E.; Clark, B.; Cramer-Meldrum, E.; Falconer, K.A.; Sequist, J.M.; Kwon, Y.-J. Development of Scientific Reasoning in College Biology: Do Two Levels of General Hypothesis-Testing Skills Exist? J. Res. Sci. Teach. 2000, 37, 81–101. [Google Scholar] [CrossRef]
- Lawson, A.E. What do tests of ‘formal’ reasoning actually measure? J. Res. Sci. Teach. 1992, 29, 965–983. [Google Scholar] [CrossRef]
- Lawson, A.E.; Oehrtman, M.; Jensen, J. Connecting science and mathematics: The nature of scientific and statistical hypotheses testing. Int. J. Sci. Math. Educ. 2008, 6, 405–416. [Google Scholar] [CrossRef]
- Moore, J.C.; Rubbo, L.J. Scientific reasoning abilities of nonscience majors in physics-based courses. Phys. Rev. ST Phys. Educ Res. 2012, 8, 010106. [Google Scholar] [CrossRef]
- Lawson, A.E.; Banks, D.L.; Logvin, M. Self-efficacy, reasoning ability, and achievement in college biology. J. Res. Sci. Teach. 2007, 44, 706–724. [Google Scholar] [CrossRef]
- Horst, S.J.; Finney, S.J.; Barron, K.E. Moving beyond academic achievement goal measures: A study of social achievement goals. Contemp. Educ. Psychol. 2007, 32, 667–698. [Google Scholar] [CrossRef]
- Deary, I.J.; Strand, S.; Smith, P.; Fernandes, C. Intelligence and educational achievement. Intelligence 2007, 35, 13–21. [Google Scholar] [CrossRef]
- Hong, E. Homework style, homework environment and academic achievement. Learn. Environ. Res. 2001, 4, 7–23. [Google Scholar] [CrossRef]
- McKillup, S. Statistics Explained: An Introductory Guide for Life Sciences; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
- Stephens, A.L.; Clement, J.J. Documenting the use of expert scientific reasoning processes by high school physics students. Phys. Rev. ST Phys. Educ Res. 2010, 6, 020122. [Google Scholar] [CrossRef]
- Spinath, B.; Spinath, F.M.; Harlaar, N.; Plomin, R. Predicting school achievement from general cognitive ability, self-perceived ability, and intrinsic value. Intelligence 2006, 34, 363–374. [Google Scholar] [CrossRef]
- Valanides, N. Formal reasoning abilities and school achievement. Stud. Educ. Eval. 1997, 23, 169–185. [Google Scholar] [CrossRef]
- Steinberg, R.; Cormier, S. Understanding and affecting science teacher candidates’ scientific reasoning in introductory astrophysics. Phys. Rev. ST Phys. Educ Res. 2013, 9, 020111. [Google Scholar] [CrossRef]
- Ates, S.; Cataloglu, E. The effects of students’ reasoning abilities on conceptual understandings and problem-solving skills in introductory mechanics. Eur. J. Phys. 2007, 28, 1161–1171. [Google Scholar] [CrossRef]
- Coletta, V.P.; Phillips, J.A. Interpreting FCI scores: Normalized gain, preinstruction scores, and scientific reasoning ability. Am. J. Phys. 2005, 73, 1172–1182. [Google Scholar] [CrossRef]
- Furnham, A.; Chamorro-Premuzic, T. Personality and intelligence as predictors of statistics examination grades. Pers. Individ. Dif. 2004, 37, 943–955. [Google Scholar] [CrossRef]

| Investigated Dimension | Pairs of Items |
|---|---|
| Conservation (mass and volume) | (1,2)–(3,4) |
| Proportional reasoning | (5,6)–(7,8) |
| Identification and control of variables | (9,10)–(11,12)–(13,14) |
| Probabilistic and combinatorial reasoning | (15,16)–(17,18) |
| Hypothetical-deductive reasoning (in particular, aimed at testing the existence of not-observable entities) | (19,20)–(21,22)–(23,24) |
| Score Range | Type of Reasoning |
|---|---|
| <25 | CONCRETE: subjects unable to test hypotheses involving observable causal agents. |
| 26 ÷ 58 | FORMAL: subjects able to test hypotheses involving observable causal agents, but in an incoherent way. |
| >58 | POST-FORMAL: subjects able to coherently test hypotheses involving observable causal agents, or even hypotheses involving unobservable causal agents. |
| Area | Female | Male | Total |
|---|---|---|---|
| Science | 275 | 217 | 492 |
| Engineering | 143 | 380 | 523 |
| Total | 418 | 597 | 1015 |
| Type of Data | Description |
|---|---|
| Personal data | School of origin. |
| Gender. | |
| Career data | Degree course. |
| Exams passed at the end of the three-year period, with the grade, number of credits and date for each exam. | |
| Exams included in the study plan. |
| Area | Starting Number of Students | Among which | Number of Valid Questionnaires | Among which | Valid Career Data |
| Science | 577 | 564 | 492 | ||
| Engineering | 563 | 540 | 523 | ||
| Total | 1140 | 1104 | 1015 |
| Group | r Correlation Coefficient | m Angular Coefficient of the Best-Fit Line | p Significance Index |
|---|---|---|---|
| Science subset | 0.38 | 1.15 | 0.08 |
| Engineering subset | 0.68 | 0.59 | 0.002 |
| Whole sample | 0.52 | 0.43 | 0.008 |
| Dimension Investigated | r Correlation Coefficient | m Angular Coefficient of the Best-Fit Line | p Significance Index |
|---|---|---|---|
| Conservation (mass and volume) | 0.15 | 0.35 | 0.004 |
| Proportional reasoning | 0.59 | 0.64 | 0.002 |
| Identification and control of variables | 0.58 | 0.65 | 0.004 |
| Probabilistic and combinatorial reasoning | 0.50 | 0.45 | 0.002 |
| Hypothetical-deductive reasoning (to test the existence of not-observable entities) | 0.73 | 0.95 | 0.0008 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sapia, P.; Napoli, F.; Bozzo, G. The Lawson’s Test for Scientific Reasoning as a Predictor for University Formative Success: A Prospective Study. Educ. Sci. 2022, 12, 814. https://doi.org/10.3390/educsci12110814
Sapia P, Napoli F, Bozzo G. The Lawson’s Test for Scientific Reasoning as a Predictor for University Formative Success: A Prospective Study. Education Sciences. 2022; 12(11):814. https://doi.org/10.3390/educsci12110814
Chicago/Turabian StyleSapia, Peppino, Federica Napoli, and Giacomo Bozzo. 2022. "The Lawson’s Test for Scientific Reasoning as a Predictor for University Formative Success: A Prospective Study" Education Sciences 12, no. 11: 814. https://doi.org/10.3390/educsci12110814
APA StyleSapia, P., Napoli, F., & Bozzo, G. (2022). The Lawson’s Test for Scientific Reasoning as a Predictor for University Formative Success: A Prospective Study. Education Sciences, 12(11), 814. https://doi.org/10.3390/educsci12110814






