Evaluating Differences in Mathematical Competencies in Middle School Students during Pandemic Conditions through Preparatec Platform
Abstract
1. Introduction
1.1. Mathematics Teaching-Learning Process
1.2. PISA Test to Assess Mathematical Competencies
1.3. Flipped Learning
- Define the tasks to be performed by the student and encourage self-learning by introducing students to the pedagogical strategy;
- Accompany the student in determining the educational resources’ actual content;
- Check that students have seen the resources by asking interesting questions to help them understand the topic;
- In the classroom, prepare the space to encourage collaboration and the development of activities;
- Encourage the student to organize his or her time;
- Encourage collaboration working in teams;
- Use instruments of formative evaluation;
2. Materials and Methods
2.1. Innovation Description
2.2. Instrument
2.3. Analysis of Results
3. Results
3.1. Sociodemographic Characteristics of Students
3.2. Differences between Pre-Test and Post-Test
3.3. Comparison of Total Groups with Other Countries
4. Discussion
5. Conclusions
Limitations
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Contini, D.; Di Tommaso, M.L.; Muratori, C.; Piazzalunga, D.; Schiavon, L. Who lost the most? Mathematics achievement during the COVID-19 pandemic. BE J. Econ. Anal. Policy 2022, 22, 399–408. [Google Scholar] [CrossRef]
- García, L. COVID-19 y educación a distancia digital: Preconfinamiento, confinamiento y posconfinamiento. RIED 2021, 24, 9–32. [Google Scholar] [CrossRef]
- Government of Mexico. Available online: https://coronavirus.gob.mx/medidas-de-seguridad-sanitaria/ (accessed on 20 March 2022).
- Statista. Available online: https://es.statista.com/estadisticas/1196749/estudiantes-afectados-cierre-escuelas-covid-mexico-nivel-educativo/ (accessed on 15 March 2022).
- Gonzalez, T.; de la Rubia, M.; Hincz, K.; Comas-Lopez, M.; Subirats, L.; Fort, S.; Sacha, G. Influence of COVID-19 confinement on students’ performance in higher education. PLoS ONE 2020, 15, e0239490. [Google Scholar] [CrossRef] [PubMed]
- Pirrone, C.; Di Corrado, D.; Privitera, A.; Castellano, S.; Varrasi, S. Students’ mathematics anxiety at distance and in-person learning conditions during COVID-19 pandemic: Are there any differences? An Exploratory Study. Educ. Sci. 2022, 12, 379. [Google Scholar] [CrossRef]
- Rincón-Flores, E.; Mena, J.; López-Camacho, E. Gamification as a teaching method to improve performance and motivation in tertiary education during COVID-19: A research study from Mexico. Educ. Sci. 2022, 12, 49. [Google Scholar] [CrossRef]
- Martínez, F.; Jacinto, E.; Montiel, H. The use of online learning environments in higher education as a response to the confinement caused by COVID-19. J. E-Learn. Knowl. Soc. 2021, 17, 10–17. [Google Scholar] [CrossRef]
- Condor, H. Educating in times of COVID-19. CienciAmérica 2020, 9, 1–7. [Google Scholar] [CrossRef]
- Zhao, Y. COVID-19 as a catalyst for educational change. Prospects 2020, 49, 29–33. [Google Scholar] [CrossRef]
- Espinosa, M.P.P.; Cartagena, F.C. Advanced technologies to face the challenge of educational innovation. RIED 2021, 24, 35–53. [Google Scholar] [CrossRef]
- Palomares-Ruiz, A.; Cebrián, A.; López-Parra, E.; García-Toledano, E. Influence of ICTs on math teaching–learning processes and their connection to the digital gender gap. Sustainability 2020, 12, 6692. [Google Scholar] [CrossRef]
- Dziuban, C.; Graham, C.R.; Moskal, P.D.; Norberg, A.; Sicilia, N. Blended learning: The new normal and emerging technologies. Int. J. Educ. Technol. High Educ. 2018, 15, 38. [Google Scholar] [CrossRef]
- Dúo-Terrón, P.; Moreno-Guerrero, A.-J.; Marín-Marín, J.A. ICT motivation in sixth-grade students in pandemic times-the influence of gender and age. Educ. Sci. 2022, 12, 183. [Google Scholar] [CrossRef]
- Brunetto, D.; Bernardi, G.; Abdrá, C.; Liljedahl, P. Teaching as a system: COVID-19 as a lens into teacher change. Educ. Stud. Math. 2022, 110, 65–81. [Google Scholar] [CrossRef] [PubMed]
- Martínez-Sierra, G.; García-García, J.; Dolores Flores, C. Mathematics should be applied: The mathematical beliefs of secondary school mathematics teachers. Math. Educ. 2019, 31, 92–120. [Google Scholar] [CrossRef]
- Lavidas, K.; Apostolou, Z.; Papadakis, S. Challenges and opportunities of mathematics in digital times: Preschool teachers’ views. Educ. Sci. 2022, 12, 459. [Google Scholar] [CrossRef]
- Pérez Rojas, F.J. El razonamiento lógico en la enseñanza de las matemáticas. Nextia 2018, 5, 26–28. [Google Scholar]
- PISA 2022 Mathematics Framework. Available online: https://pisa2022-maths.oecd.org/ (accessed on 15 April 2022).
- Yusupova, N.G.; Skudareva, G.N. Quality Accordingly PISA: From Math Teachers’ Continuing Education to Students’ Mathematical Literacy. In Proceedings of the VI International Forum on Teacher Education (IFTE-2020), Kazan, Russia, 25 November 2020. [Google Scholar] [CrossRef]
- Žnidaršič, A.; Brezavšček, A.; Rus, G.; Jerebic, J. Has the COVID-19 pandemic affected mathematics achievement? A case study of university students in social sciences. Mathematics 2022, 10, 2314. [Google Scholar] [CrossRef]
- Segbenya, M.; Bervell, B.; Minadzi, V.M.; Asante Somuah, B. Modelling the perspectives of distance education students towards online learning during COVID-19 pandemic. Smart Learn. Environ. 2022, 9, 13. [Google Scholar] [CrossRef]
- Sampedro Requena, B.E.; Maldonado Berea, G.A. Valoraciones de los estudiantes mexicanos y españoles sobre el uso de las TIC como recurso para trabajar la educación inclusiva. Bordón 2017, 69, 89–106. [Google Scholar] [CrossRef]
- Huang, H.K. Implementing a theory-driven gamification model in higher education flipped courses: Effects on out-of-class activity completion and quality of artifacts. Comput. Educ. Int. J. 2018, 125, 255–257. [Google Scholar] [CrossRef]
- Mahfuzah, M.S. Gamification approaching education to increase learning engagement. Int. J. Humanit. Soc. Sci. 2018, 4, 22–32. [Google Scholar] [CrossRef]
- OECD. PISA 2012 Results: What Students Know and Can Do—Student Performance in Mathematics, Reading and Science (Volume I, Revised edition, February 2014); OECD Publishing: Paris, France, 2014. [Google Scholar] [CrossRef]
- OECD. PISA 2012 Results in Focus. What Students Know at Age 15 and What They Can Do with What They Know. Available online: https://www.oecd.org/pisa/keyfindings/PISA2012_Overview_ESP-FINAL.pdf (accessed on 30 July 2022).
- Hernández-Fernández, J. Admission and academic selection in upper secondary education. Arch. Analíticos Políticas Educ. 2021, 29, 1–29. [Google Scholar] [CrossRef]
- Skipp, C.S.; Dommett, E.J. Understanding and addressing the deficiencies in UK mathematics education: Taking an international perspective. Educ. Sci. 2021, 11, 141. [Google Scholar] [CrossRef]
- Mora, C.D. Strategies for learning and teaching mathematics. J. Pedagogy 2003, 24, 181–272. [Google Scholar]
- Ramírez-Montoya, M.S.; Loaiza-Aguirre, M.I.; Zúñiga-Ojeda, A.; Portuguez-Castro, M. Characterization of the teaching profile within the framework of education 4.0. Future Internet 2021, 13, 91. [Google Scholar] [CrossRef]
- Gamal, C.E.; Casas, J.A.; Pérez, C.; Ortega-Ruíz, R. Teaching and learning Mathematics: The need for a multidisciplinary analysis. Psychol. Soc. Educ. 2017, 9, 1–10. [Google Scholar] [CrossRef][Green Version]
- Pekrun, R. The control-value theory of achievement emotions: Assumptions, corollaries, and implications for educational research and practice. Educ. Psychol. Rev. 2006, 18, 315–341. [Google Scholar] [CrossRef]
- Robertson, S.L. Provincializing the OECD-PISA global competences project. Glob. Soc. Educ. 2021, 19, 167–182. [Google Scholar] [CrossRef]
- Osuna, C.; Díaz, K. Mathematics learning achievement in PISA, ENLACE and PLANEA in Mexican adolescents. A retrospective analysis. Arch. Analíticos Políticas Educ. 2019, 28, 3. [Google Scholar] [CrossRef]
- PISA 2013, Prueba de Matemáticas y Solución de Problemas. Available online: https://drive.google.com/file/d/16fYvZGzBUVRgje5pB_8Lr-ZKGwE4LjvM/view (accessed on 26 June 2022).
- OECD’s PISA Program. Available online: https://www.oecd.org/pisa/39730818.pdf (accessed on 10 March 2022).
- Programa para la Evaluación Internacional de Alumno. Informe PISA 2003, Aprender Para el Mundo del Mañana. Available online: https://www.oecd.org/pisa/39732493.pdf (accessed on 26 June 2022).
- Green, A.; Pensiero, N. The effects of upper-secondary education and training systems on skills inequality. A quasi-cohort analysis using PISA 2000 and the OECD survey of adult skills. Br. Educ. Res. J. 2016, 42, 756–779. [Google Scholar] [CrossRef]
- Sortkær, B.; Reimer, D. Classroom disciplinary climate of schools and gender—Evidence from the Nordic countries. Sch. Eff. Sch. Improv. 2018, 29, 511–528. [Google Scholar] [CrossRef]
- Boman, B. PISA Achievement in Sweden from the perspective of both individual data and aggregated cross-country data. Front. Educ. 2022, 6, 753347. [Google Scholar] [CrossRef]
- Basarkod, G.; Marsh, H.W.; Parker, P.D.; Dicke, T.; Guo, J. The immigrant paradox and math self-concept: An SES-of-origin-country hypothesis. Learn. Instr. 2022, 77, 101539. [Google Scholar] [CrossRef]
- Beneito, P.; Vicente-Chirivella, Ó. Banning mobile phones in schools: Evidence from regional-level policies in Spain. Appl. Econ. 2022; Ahead of print. [Google Scholar] [CrossRef]
- Divjak, B.; Rienties, B.; Iniesto, F.; Vondra, P.; Zĭzăk, M. Flipped classrooms in higher education during the COVID-19 pandemic: Findings and future research recommendations. Int. J. Educ. Technol. High Educ. 2022, 19, 9. [Google Scholar] [CrossRef]
- Ospina Espinal, Y.A.; Galvis López, J. The paradigm of traditional education towards a virtual curricular approach. Virtualmente 2016, 3, 4–29. [Google Scholar]
- Nederveld, A.B. Flipped learning in the workplace. J. Workplace Learn. 2015, 27, 162–172. [Google Scholar] [CrossRef]
- Prieto, M.A. Flipped Learning: Aplicar el Modelo de Aprendizaje Inverso; Narcea: Madrid, Spain, 2017. [Google Scholar]
- Ramírez-Montoya, M.S.; Andrade-Vargas, L.; Rivera-Rogel, D.; Portuguez-Castro, M. Trends for the future of education programs for professional development. Sustainability 2021, 13, 7244. [Google Scholar] [CrossRef]
- Strelan, P.; Osborn, A.; Palmer, E. The flipped classroom: A meta-analysis of effects on student performance across disciplines and education levels. Educ. Res. Rev. 2020, 30, 100314. [Google Scholar] [CrossRef]
- Van Alten, D.C.D.; Phielix, C.; Janssen, J.; Kester, L. Effects of flipping the classroom on learning outcomes and satisfaction: A meta-analysis. Educ. Res. Rev. 2019, 28, 100281. [Google Scholar] [CrossRef]
- Zainuddin, Z.; Haruna, H.; Li, X.; Zhang, Y.; Chu, S.K.W. A systematic review of flipped classroom empirical evidence from different fields: What are the gaps and future trends? Horizon 2019, 27, 72–86. [Google Scholar] [CrossRef]
- Yang, Q.F.; Lin, C.J.; Hwang, G.J. Research focuses and findings of flipping mathematics classes: A review of journal publications based on the technology-enhanced learning model. Interact. Learn. Environ. 2021, 29, 905–938. [Google Scholar] [CrossRef]
- Fornons, J.V.; Palau, M.R. Flipped classroom in mathematics education: A systematic review. Educ. Knowl. Soc. (EKS) 2021, 22, 1–11. [Google Scholar] [CrossRef]
- Bergmann, J.S.; Sams, A. Flip Your Classroom: Reach Every Student in Every Classroom Every Day, 1st ed.; International Society for Technology in Education: Eugene, OR, USA, 2012. [Google Scholar]
- Portuguez Castro, M. El aula invertida como estrategia didáctica en educación superior. In Educación y Aprendizaje Significativo Durante la Pandemia de COVID 19; Venteño Jaramillo, G., Bethzabe, R.T., Eds.; UNAM: Oaxaca, Mexico, 2021; pp. 89–94. [Google Scholar]
- Inee, PISA Stimuli Released. Available online: http://recursostic.educacion.es/inee/pisa/ (accessed on 26 June 2022).
- Retnawati, H.; Wulandari, N.F. The development of students’ mathematical literacy proficiency. Probl. Educ. 21st Century 2019, 77, 502–514. [Google Scholar] [CrossRef]

| Area | Topics | Learning Objectives | Learning and Assessment Resource for all topics |
|---|---|---|---|
| Arithmetic and Algebra | Basic operations, fractions, real numbers, decimals, successions, equations, percentages, hierarchy of operations | Reproducing representations, definitions and facts. |
|
| Functions and Graphs | Linear functions, table analysis | Interpretation of problem situations and mathematical statements, using multiple well-defined methods. | |
| Geometry | Areas, perimeters and volume | Engaging in simple mathematical Reasoning. | |
| Descriptive statistics | Histograms, mean, median and mode | Reflecting on, and gaining insight into, mathematics and constructing original mathematical approaches. | |
| Combinations and Probability | Combinations, estimation of quantities |
| Item Name | Number of Questions | Level of Competence | Proficiency Level | Area |
|---|---|---|---|---|
| Walking | 2 | Level 1 (Reproduction), level 2 (Connections) | level 5 (611), level 6 (723), level 5 (666) | Arithmetic and Algebra |
| Cubes | 1 | Level 1 (Reproduction | level 2 (478) | Arithmetic and Algebra |
| Coloured Candies | 1 | Level 1 (Reproduction | level 4 (549) | Combinations and Probability |
| Science Tests | 1 | Level 1 (Reproduction | level 4 (556) | Descriptive statistics |
| Growing Up | 3 | Level 1 (Reproduction), level 2 (Connections) | level 2 (477), level 4 (574), level 3 (525), level 1 (420) | Functions and Graphs |
| Exchange Rate | 3 | Level 1 (Reproduction), level 2 (Connections), Level 3 (Reflection) | level 1 (406), level 2 (439), leve 4 (586) | Arithmetic and Algebra |
| Skateboard | 3 | Level 1 (Reproduction), level 2 (Connections) | Level 3 (496), level 2 (464), level 4 (570), level 4 (554) | Combinations and Probability |
| Table Tennis Tournament | 1 | Level 1 (Reproduction | Pilot test | Combinations and Probability |
| Shoes for Kids | 1 | Level 1 (Reproduction | Pilot test | Arithmetic and Algebra |
| Robberies | 1 | Level 2 (Connections) | Level 6 (694), level 4 (577) | Functions and Graphs |
| Carpenter | 1 | Level 2 (Connections) | level 6 (687) | Functions and Graphs |
| Chat | 2 | Level 2 (Connections), Level 3 (Reflection) | Level 3 (533), level 5 (636) | Arithmetic and Algebra |
| Shelving | 1 | Level 2 (Connections) | level 3 (499) | Arithmetic and Algebra |
| Fair | 1 | Level 2 (Connections) | Pilot Test | Combinations and Probability |
| Earthquake | 1 | Level 3 (Reflection) | level 4 (557) | Combinations and Probability |
| Proficiency Level | Example of a PISA Item | What Is Assessed at Each Level |
|---|---|---|
| Level 6 more than 668 points | Walking Question 2 scoring 3 (723) | Conceptualise, generalise, and utilise information; are capable of advanced mathematical thinking and reasoning; have a mastery of symbolic and formal mathematical operations and relationships; formulate and precisely communicate their findings, interpretations, and arguments. Example: Bernard knows his pacelength is 0.80 metres. The formula applies to Bernard’s walking. Calculate Bernard’s walking speed in metres per minute and in kilometres per hour. Show your working out. |
| Level 5 607 to 668 points | Walking Question 1 scoring 2 (666) | Develop and work with models for complex situations; select, compare, and evaluate appropriate problem-solving strategies for dealing with complex problems; work strategically using broad, well-developed thinking and reasoning skills; reflect on their actions and formulate and communicate their interpretations and reasoning. Example: ¿If the formula applies to Heiko’s walking and Heiko takes 70 steps per minute, what is Heiko’s pacelength? Show your work. |
| Level 4 545 to 606 points | Coloured Candies Question 1 Scoring 3 (549) | Work effectively with explicit models for complex concrete situations; select and integrate different representations, including symbolic ones; utilise well-developed skills and reason flexibly; construct and communicate explanations and arguments. Example: Robert’s mother lets him pick one candy from a bag. He can’t see the candies. The number of candies of each colour in the bag is shown in the following graph. |
| Level 3 483 to 544 points | Skateboard Question 1 Scoring 3 (496) | Execute clearly described procedures, including those that require sequential decisions; select and apply simple problem-solving strategies; interpret and use representations; develop short communications reporting these. Example: Eric is a great skateboard fan. He visits a shop named SKATERS to check some prices. At this shop you can buy a complete board. Or you can buy a deck, a set of 4 wheels, a set of 2 trucks and a set of hardware and assemble your own board. Eric wants to assemble his own skateboard. What is the minimum price and the maximum price in this shop for self-assembled skateboards? |
| Level 2 421 to 482 points | Exchange Rate Question 2 Scoring 3 (439) | Interpret and recognise situations in contexts that require no more than direct inference; extract relevant information from a single source and make use of a single representational mode; employ basic procedures; make literal interpretations of the results. Example: On returning to Singapore after 3 months, Mei-Ling had 3 900 ZAR left. She changed this back to Singapore dollars, noting that the exchange rate had changed to: 1 SGD = 4.0 ZAR How much money in Singapore dollars did Mei-Ling get? |
| Level 1 358 to 420 points | Growing Up Question 3 Scoring 2 (420) | Answer questions involving familiar contexts where all relevant information is present, and the questions are clearly defined; identify information and carry out routine procedures according to direct instructions in explicit situations; perform actions that are obvious and follow immediately from the given stimuli. Example: Explain how the graph shows that on average the growth rate for girls slows down after 12 years of age. |
| Below Level 1 | less than 358 points | Not demonstrate even the most basic types of mathematical literacy that PISA measures. These students are likely to be seriously disadvantaged in their lives beyond school. |
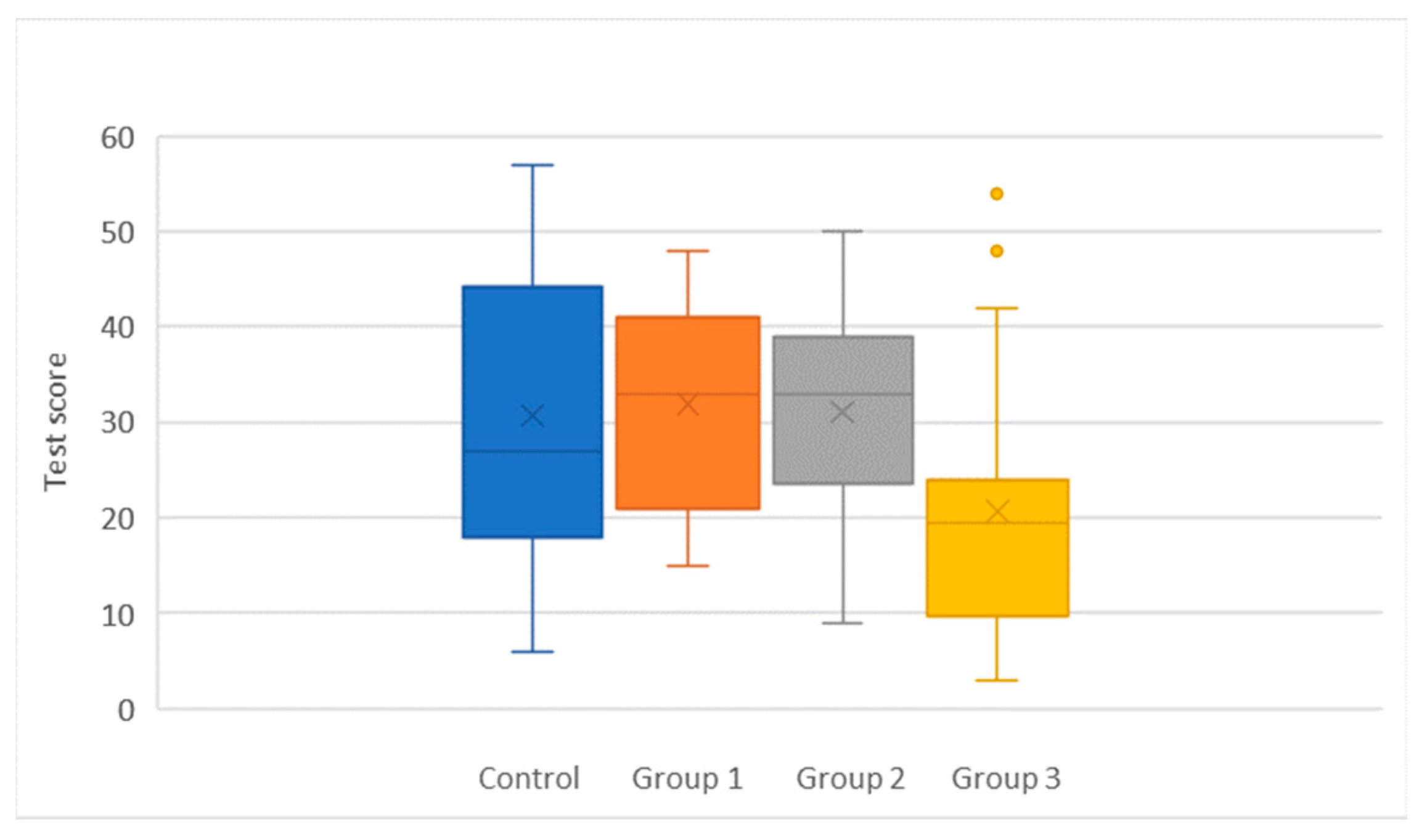
| Pre-Test Data Analysis | Control Group | Group 1 | Group 2 | Group 3 | |
|---|---|---|---|---|---|
| median | 27 | 33 | 33 | 19.5 | |
| rank sum | 905 | 928.5 | 1181 | 555.5 | |
| count | 20 | 19 | 25 | 20 | 84 |
| r2/n | 40,951.25 | 45,374.3289 | 55,790.44 | 15,429.0125 | 157,545.031 |
| H-stat | 9.78156546 | ||||
| H-ties | 9.80628719 | ||||
| df | 3 | ||||
| p-value | 0.02028661 | ||||
| α | 0.05 | ||||
| sig | yes |
| Group A | Group B | R Mean | Std Err | Q-Stat | p-Value | R-Crit |
|---|---|---|---|---|---|---|
| Control Group | Group 1 | 3.61842105 | 5.52565786 | 0.65483987 | 0.96703761 | 20.1465485 |
| Control Group | Group 2 | 1.99 | 5.17445649 | 0.38458145 | 0.99296408 | 18.8660684 |
| Control Group | Group 3 | 17.475 | 5.45435606 | 3.20386125 | 0.1076538 | 19.8865822 |
| Group 1 | Group 2 | 1.62842105 | 5.24956139 | 0.31020135 | 0.99627179 | 19.1399008 |
| Group 1 | Group 3 | 21.0934211 | 5.52565786 | 3.81735924 | 0.03608361 | 20.1465485 |
| Group 2 | Group 3 | 19.465 | 5.17445649 | 3.76174774 | 0.04018029 | 18.8660684 |
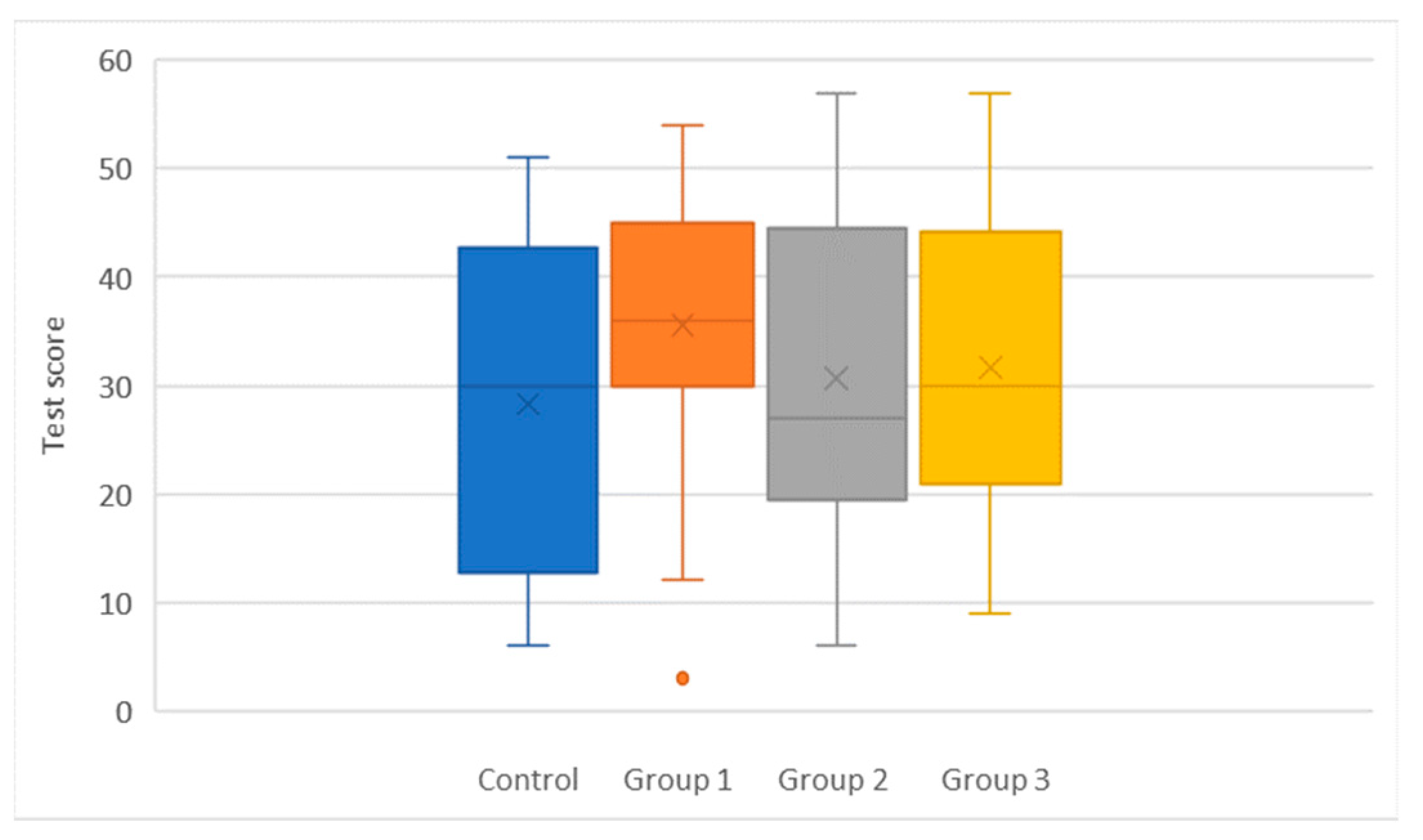
| Post-Test Data Analysis | Control Group | Group 1 | Group 2 | Group 3 | |
|---|---|---|---|---|---|
| median | 30 | 36 | 27 | 30 | |
| rank sum | 754 | 951 | 1020 | 845 | |
| count | 20 | 19 | 25 | 20 | 84 |
| r2/n | 28,425.8 | 47,600.0526 | 41,616 | 35,701.25 | 153,343.103 |
| H-stat | 2.71950022 | ||||
| H-ties | 2.72371941 | ||||
| df | 3 | ||||
| p-value | 0.43621147 | ||||
| α | 0.05 | ||||
| sig | no |
| Group 1 | Group 2 | R Mean | Std Err | Q-Stat | p-Value | R-Crit |
|---|---|---|---|---|---|---|
| Control Group | Group 1 | 12.3526316 | 5.52565786 | 2.23550424 | 0.39059675 | 20.1465485 |
| Control Group | Group 2 | 3.1 | 5.17445649 | 0.59909674 | 0.97442956 | 18.8660684 |
| Control Group | Group 3 | 4.55 | 5.45435606 | 0.83419563 | 0.93513002 | 19.8865822 |
| Group 1 | Group 2 | 9.25263158 | 5.24956139 | 1.76255327 | 0.59765036 | 19.1399008 |
| Group 1 | Group 3 | 7.80263158 | 5.52565786 | 1.41207288 | 0.75033384 | 20.1465485 |
| Group 2 | Group 3 | 1.45 | 5.17445649 | 0.28022267 | 0.99724245 | 18.8660684 |
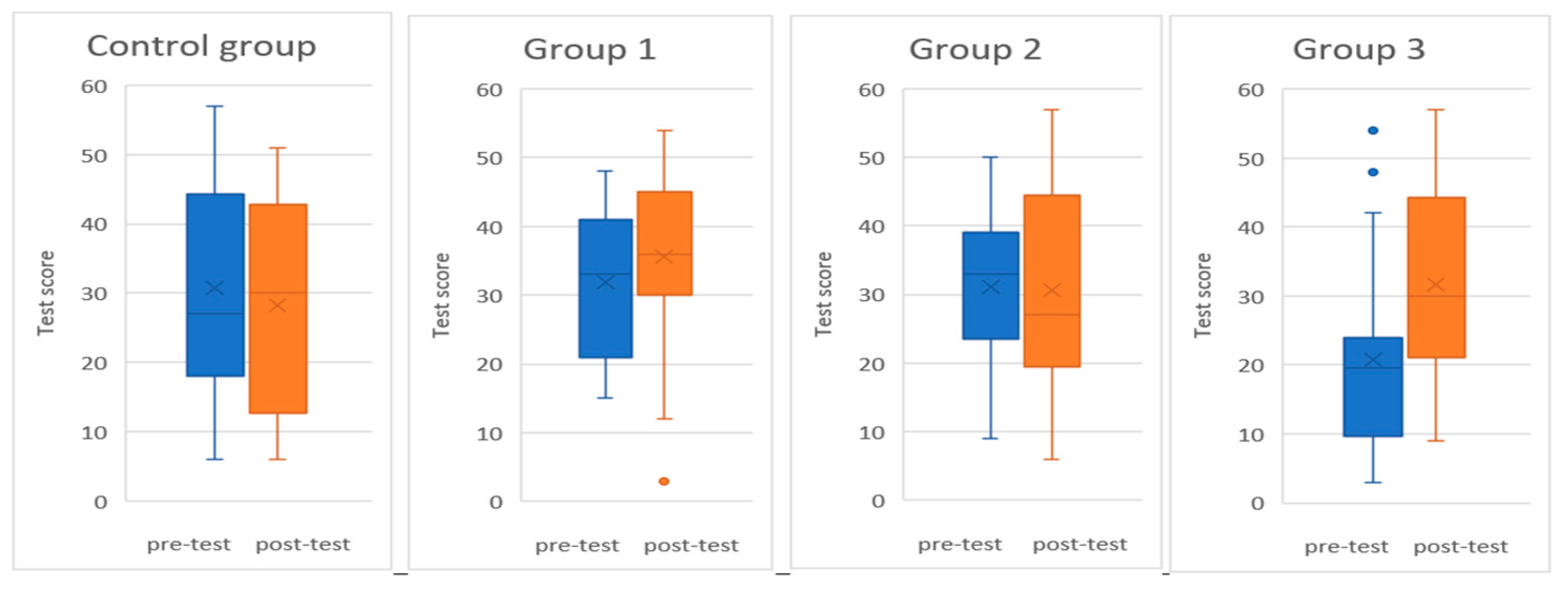
| Data Analysis | Control Grupo Pre-test | Control Group Post-test | Group 1 Pre-Test | Group 1 Post-Test | Group 2 Pre-Test | Group 2 Post-Test | Group 3 Pre-Test | Group 3 Post-Test |
|---|---|---|---|---|---|---|---|---|
| count | 20 | 20 | 19 | 19 | 25 | 25 | 20 | 20 |
| median | 27 | 30 | 33 | 36 | 33 | 27 | 19.5 | 30 |
| rank sum | 430.5 | 389.5 | 327.5 | 413.5 | 652.5 | 622.5 | 317.5 | 502.5 |
| U | 179.5 | 220.5 | 223.5 | 137.5 | 297.5 | 327.5 | 292.5 | 107.5 |
| one tail | two tails | one tail | two tails | one tail | two tails | one tail | two tails | |
| U | 179.5 | 137.5 | 297.5 | 107.5 | ||||
| mean | 200 | 180.5 | 312.5 | 200 | ||||
| std dev | 36.879916 | ties | 34.1795735 | ties | 51.5016841 | ties | 36.8068416 | ties |
| z-score | 0.54230058 | yates | 1.24343272 | yates | 0.28154419 | yates | 2.4995353 | yates |
| effect r | 0.08574525 | 0.20171142 | 0.03981636 | 0.39521123 | ||||
| p-norm | 0.29380573 | 0.58761145 | 0.10685421 | 0.21370842 | 0.38914652 | 0.77829304 | 0.00621782 | 0.01243563 |
| p-exact | 0.29155711 | 0.58311423 | 0.10600238 | 0.21200475 | 0.38649309 | 0.77298618 | 0.00560338 | 0.01120677 |
| Item Name | Scoring | Levels of Performance | % Correct OECD | % Correct Spain | % Correct Pre-Test | % Correct Post-Test |
|---|---|---|---|---|---|---|
| Cubes | 3 | level 2 (478) | 69.0% | 72.5% | 76.56% | 82.81% |
| (Q1) Growing Up | 3 | level 2 (477) | 67.0% | 66.5% | 81.25% | 70.31% |
| Shoes for Kids | 3 | Pilot Test | Pilot Test | Pilot Test | 51.56% | 68.75% |
| Coloured Candies | 3 | level 4 (549) | 50.2% | 42.1% | 50.00% | 64.06% |
| (Q3) Growing Up | 3 | level 3 (525) | 54.7% | 62.4% | 70.31% | 62.50% |
| Science Tests | 3 | level 4 (556) | 46.8% | 30.4% | 29.69% | 40.63% |
| Table Tennis Tournament | 3 | Pilot Test | Pilot Test | Pilot Test | 32.81% | 40.63% |
| (Q1) Skateboard | 2 | level 2 (464) | 10.6% | 10.1% | 7.81% | 14.06% |
| (Q1) Walking | 3 | level 5 (611) | 36.3% | 38.4% | 18.75% | 12.50% |
| (Q3) Growing Up | 2 | level 1 (420) | 28.1% | 19.2% | 0.00% | 0.00% |
| (Q1) Skateboard | 3 | level 3 (496) | 66.7% | 66.6% | 23.44% | 29.69% |
| (Q2) Skateboard | 3 | level 4 (570) | 45.5% | 43.0% | 15.63% | 35.94% |
| (Q1) Exchange Rate | 2 | level 1 (406) | 79.7% | 79.0% | 64.06% | 56.25% |
| (Q2) Exchange Rate | 3 | level 2 (439) | 73.9% | 72.0% | 51.56% | 46.88% |
| Item Name | Scoring | Levels of Performance | % Correct OECD | % Correct Spain | % Correct Pre-Test | % Correct Post-Test |
|---|---|---|---|---|---|---|
| (Q2) Walking | 2 | level 5 (666) | 9.00% | 8.30% | 7.81% | 15.63 |
| Shelving | 3 | level 3 (499) | 60.90% | 57.00% | 42.19% | 60.94% |
| (Q1) Chat | 3 | level 3 (533) | 53.70% | 46.00% | 50.00% | 48.40% |
| (Q2) Growing Up | 3 | level 4 (574) | 44.80% | 36.50% | 29.69% | 43.75% |
| Robberies | 3 | level 6 (694) | 15.40% | 9.90% | 31.25% | 35.94% |
| Carpenter | 3 | level 6 (687) | 20.00% | 12.90% | 9.38% | 14.06% |
| Fair | 3 | Pilot Test | Pilot Test | Pilot Test | 40.63% | 73.44% |
| (Q3) Skateboard | 3 | level 4 (554) | 49.80% | 46.00% | 17.19% | 34.38% |
| (Q2) Walking | 1 | level 4 (605) | 19.90% | 23.70% | 0% | 6.25% |
| Robberies | 2 | level 4 (577) | 28.10% | 31.30% | 1.56% | 6.24% |
| (Q2) Walking | 3 | level 6 (723) | 8.00% | 7.50% | 9.38% | 0% |
| Item Name | Scoring | Levels of Performance | % Correct OECD | % Correct Spain | % Correct Pre-Test | % Correct Post-Test |
|---|---|---|---|---|---|---|
| (Q2) Chat | 3 | level 5 (636) | 28.80% | 21.60% | 40.63% | 28.13% |
| (Q3) Exchange Rate | 3 | level 4 (586) | 40.30% | 30.30% | 45.31% | 39.06% |
| Earthquake | 3 | level 4 (557) | 46.50% | 38.80% | 34.38% | 43.75% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Maldonado-García, B.E.; Ocampo-Díaz, A.; Portuguez-Castro, M. Evaluating Differences in Mathematical Competencies in Middle School Students during Pandemic Conditions through Preparatec Platform. Educ. Sci. 2022, 12, 546. https://doi.org/10.3390/educsci12080546
Maldonado-García BE, Ocampo-Díaz A, Portuguez-Castro M. Evaluating Differences in Mathematical Competencies in Middle School Students during Pandemic Conditions through Preparatec Platform. Education Sciences. 2022; 12(8):546. https://doi.org/10.3390/educsci12080546
Chicago/Turabian StyleMaldonado-García, Blanca Estela, Alejandra Ocampo-Díaz, and May Portuguez-Castro. 2022. "Evaluating Differences in Mathematical Competencies in Middle School Students during Pandemic Conditions through Preparatec Platform" Education Sciences 12, no. 8: 546. https://doi.org/10.3390/educsci12080546
APA StyleMaldonado-García, B. E., Ocampo-Díaz, A., & Portuguez-Castro, M. (2022). Evaluating Differences in Mathematical Competencies in Middle School Students during Pandemic Conditions through Preparatec Platform. Education Sciences, 12(8), 546. https://doi.org/10.3390/educsci12080546







