Designing Visualisations for Bayesian Problems According to Multimedia Principles
Abstract
1. Introduction
2. Theoretical Background
2.1. Bayesian Reasoning
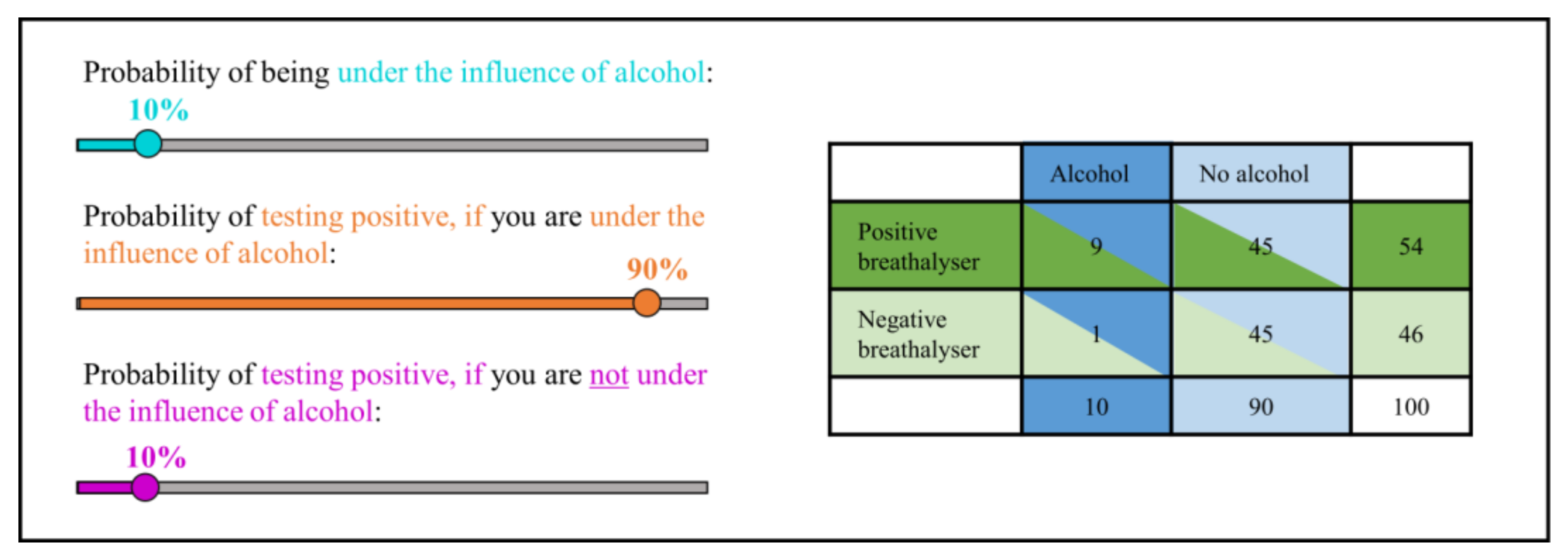
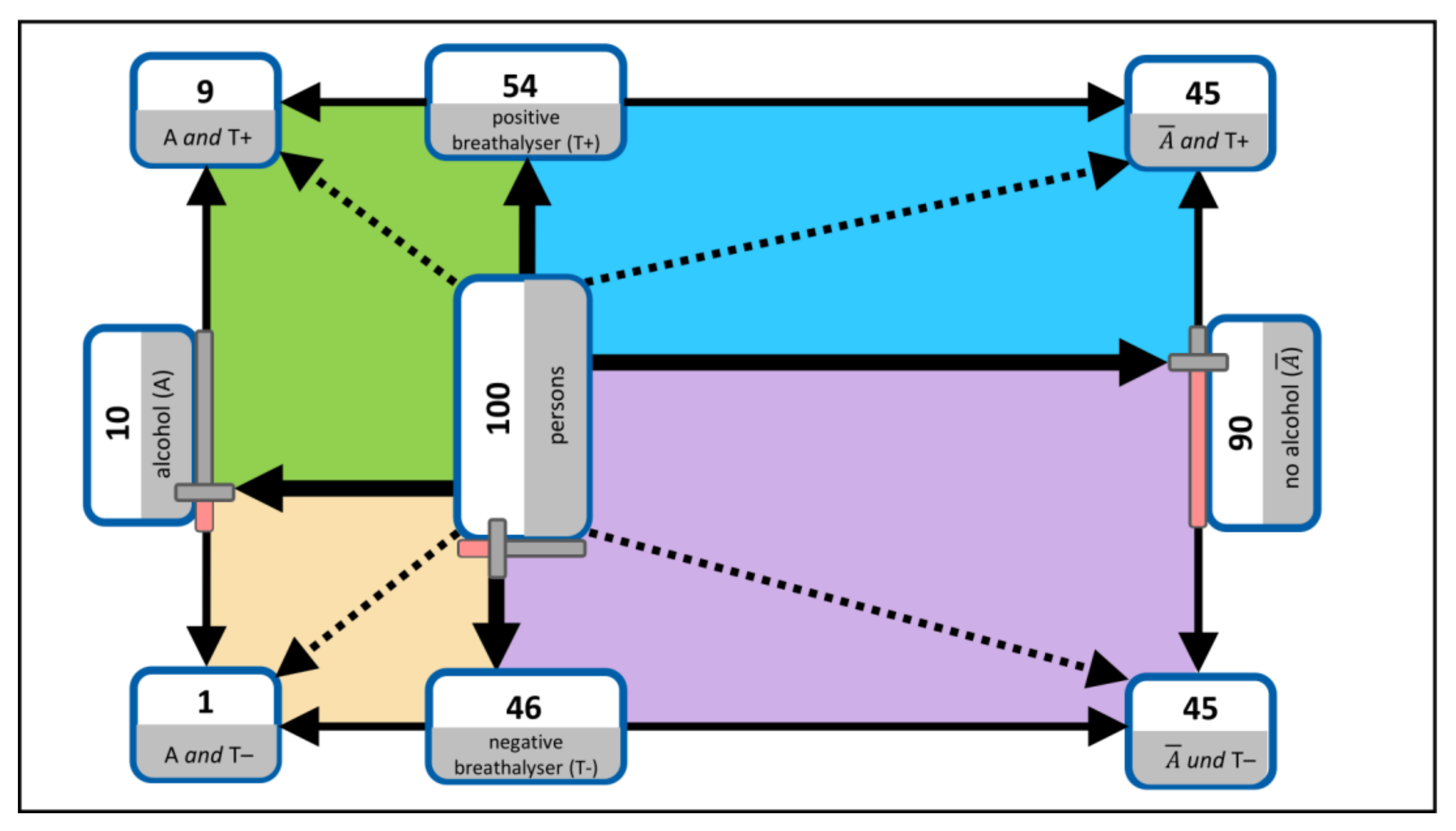
- The so-called base rate: the a priori probability that the hypothesis is true (prior to the presence of an indicator). In the example above, this corresponds to the probability of a person stopped by the police being under the influence of alcohol on a Saturday night, .
- The so-called true-positive rate: the probability that an indicator is present when the hypothesis is true. In the example above, this corresponds to the probability that the result of a person’s breathalyser test is positive, if that person is indeed under the influence of alcohol, .
- The so-called false-positive rate: the probability that an indicator is present even though the hypothesis is false. In the example above, this corresponds to the probability that the result of a person’s breathalyser test is positive even if that person is not under the influence of alcohol, .
- The so-called positive predictive value (PPV): the probability that a hypothesis is actually true, if an indicator is given. In the example above, this corresponds to the probability that a person is actually under the influence of alcohol, if the breathalyser test is positive, .
- The so-called negative predictive value (NPV): the probability that a hypothesis is actually false, if no indicator is given or information is given which suggests that the hypothesis is false. In the example above, this corresponds to the probability that a person is actually not under the influence of alcohol, if the breathalyser test is negative, .
- Static aspect of Bayesian Reasoning: interpreting the formula’s structure in the sense that the given parameters (e.g., base rate, true- and false-positive rate) directly correspond to one result (e.g., PPV), which is calculated. This relates to the aspect of mapping in the concept of functional thinking [26,27] or the action conception of a function [28], because three given parameters, e.g., the base rate , the true-positive rate and the false-positive rate , interpreted as independent variables, are used to calculate the requested dependent variable PPV . Thus, the solution is a function value mapped to the three given variables , , and via the Bayes’ formula. In Bayesian Reasoning, we refer to the ability to map three given parameters to the solution of Bayes’ formula as the aspect of performance (with or without the explicit use of Bayes’ formula).
- Dynamic aspect of Bayesian Reasoning: interpreting the formula’s structure in the sense that changes in the given parameters (e.g., base rate, true- or false-positive-rate) influence the result (e.g., the PPV). This relates to the aspect of covariation of the concept of functional thinking [26,27] or the process conception of a function [28] because a variation in one (or more) of the parameters being interpreted as independent variables (e.g., base rate , true-positive rate or false-positive rate ) alters the dependent variable (e.g., PPV ) when is understood as a function value of the Bayes’ formula, which is seen as a three-dimensional function with the given parameters (e.g., base rate, true- and false-positive rate) as the independent variables. Consequently, we refer to the ability to evaluate the influence of changes to the given parameters on the result of Bayes’ formula as the aspect of covariation.
2.2. Visualisations and Bayesian Reasoning
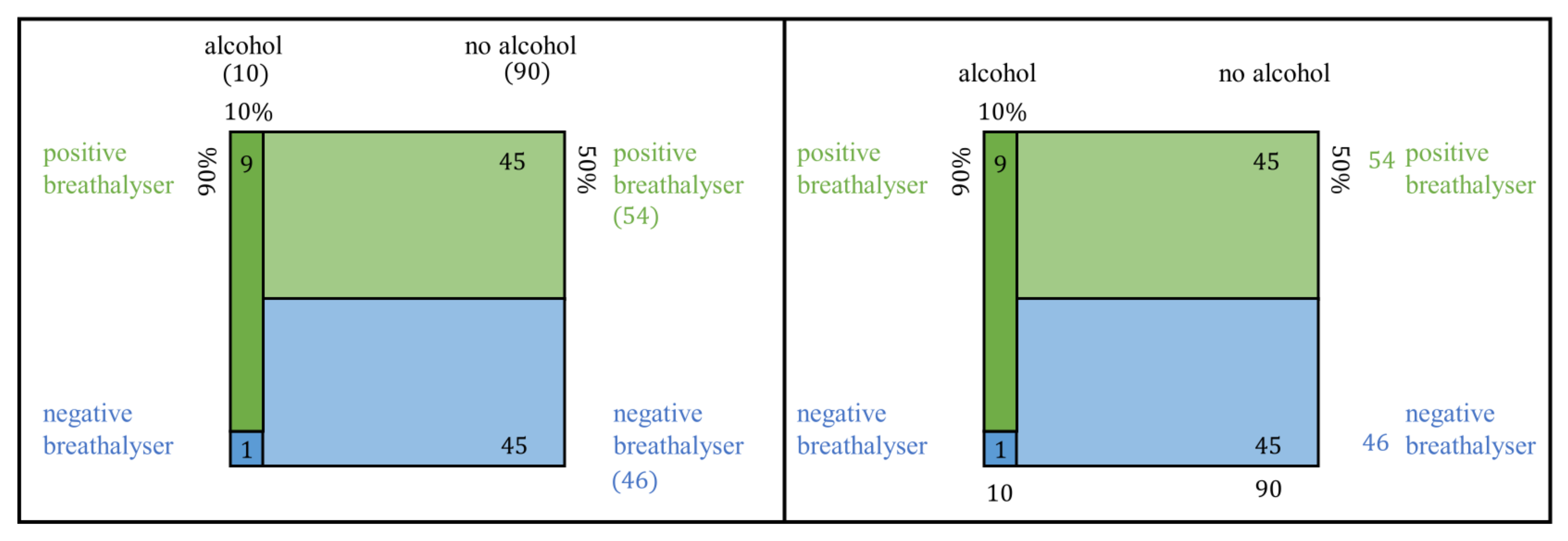
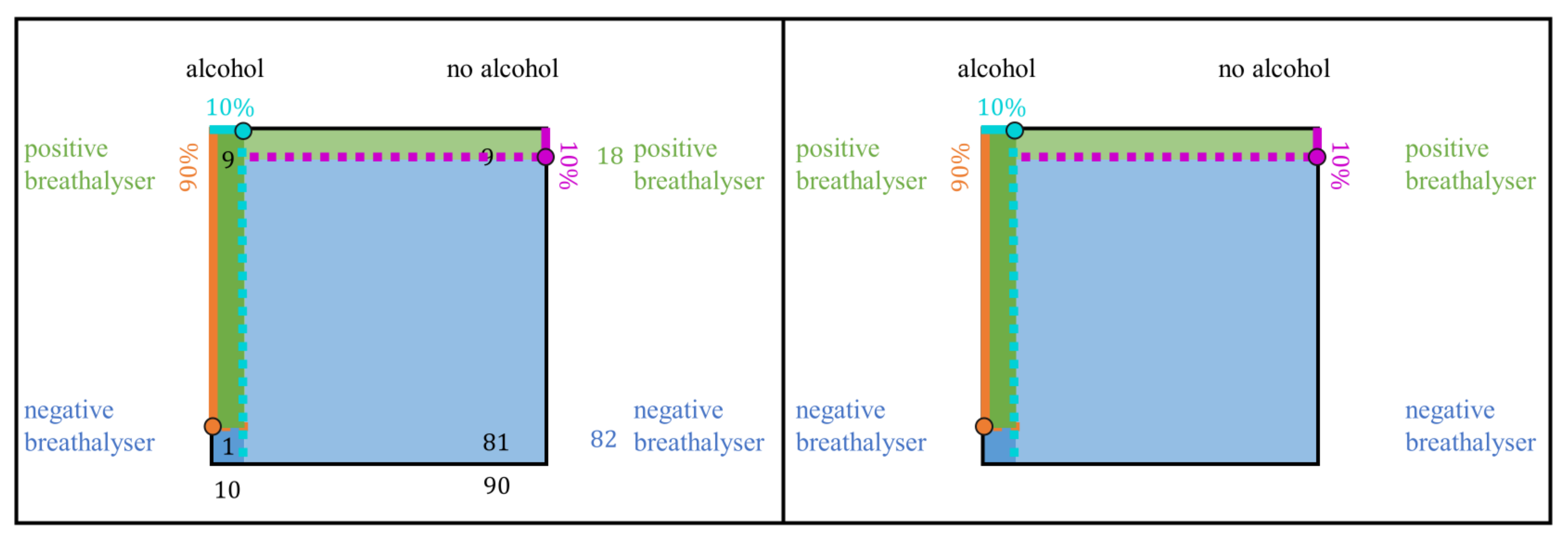
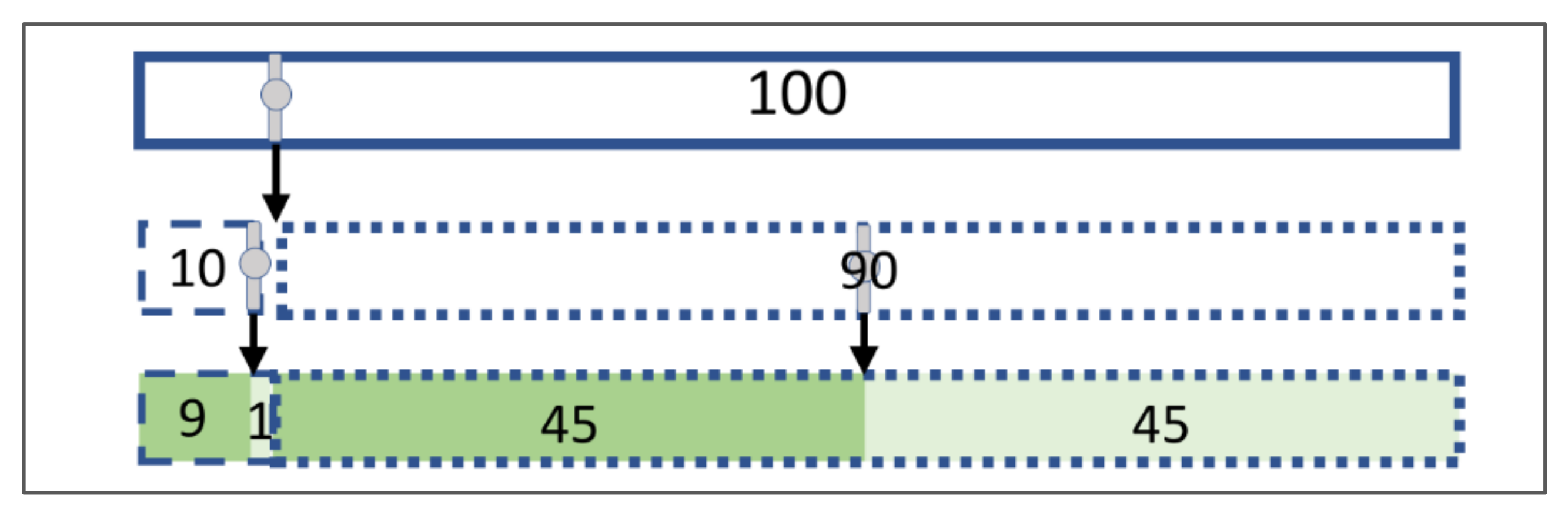
- Static tasks: Static tasks address the static aspect of Bayesian Reasoning. Therefore, in static tasks, the three given parameters are used to calculate the PPV (for example with Bayes’ formula). Bayes’ formula for two dichotomous events can be simplified to two conceptually simpler ratios: .Both transformations have a simpler structure than the original Bayes’ formula. As a consequence, we argue that a visualisation that represents the equivalence of these algebraic transformations can more easily lead to simpler (and correct) calculation of the result (even if the formula is not explicitly used in the teaching process). In order to do so, two equivalences should be observable in the visualisation: first, the equivalence of the product of the simple and conditional probability to the joint probability (first equal sign), and second, the equivalence of the sum of the two intersects (the true- and false-positives) to their shared superset (all positives; second equal sign). Consequently, in order to be supportive for static tasks, we argue (from a subject-didactical perspective) that it is important that the visualisation (in addition to the three pieces of information given in the task itself) shows these two intersections (or associated joint probabilities), and also makes it transparent that they both belong to the same superset. In doing so, the solution to static tasks of Bayesian Reasoning should become easier from a theoretical point of view.
- Dynamic tasks: Dynamic tasks address the dynamic aspect of Bayesian Reasoning. The question here is how modifications in the given parameters affect the result (PPV, NPV). Therefore, from a subject-didactical perspective, we regard it as important that the three pieces of information, which are given in the task itself, can be represented at all, and that the structure of the visualisation can visually represent how a change in these parameters affects the result (or the relevant intersections/joint probabilities).
2.3. Aspects of Multimedia Learning
2.3.1. Processing Multimedia Material
2.3.2. Cognitive Load
2.3.3. Design Principles
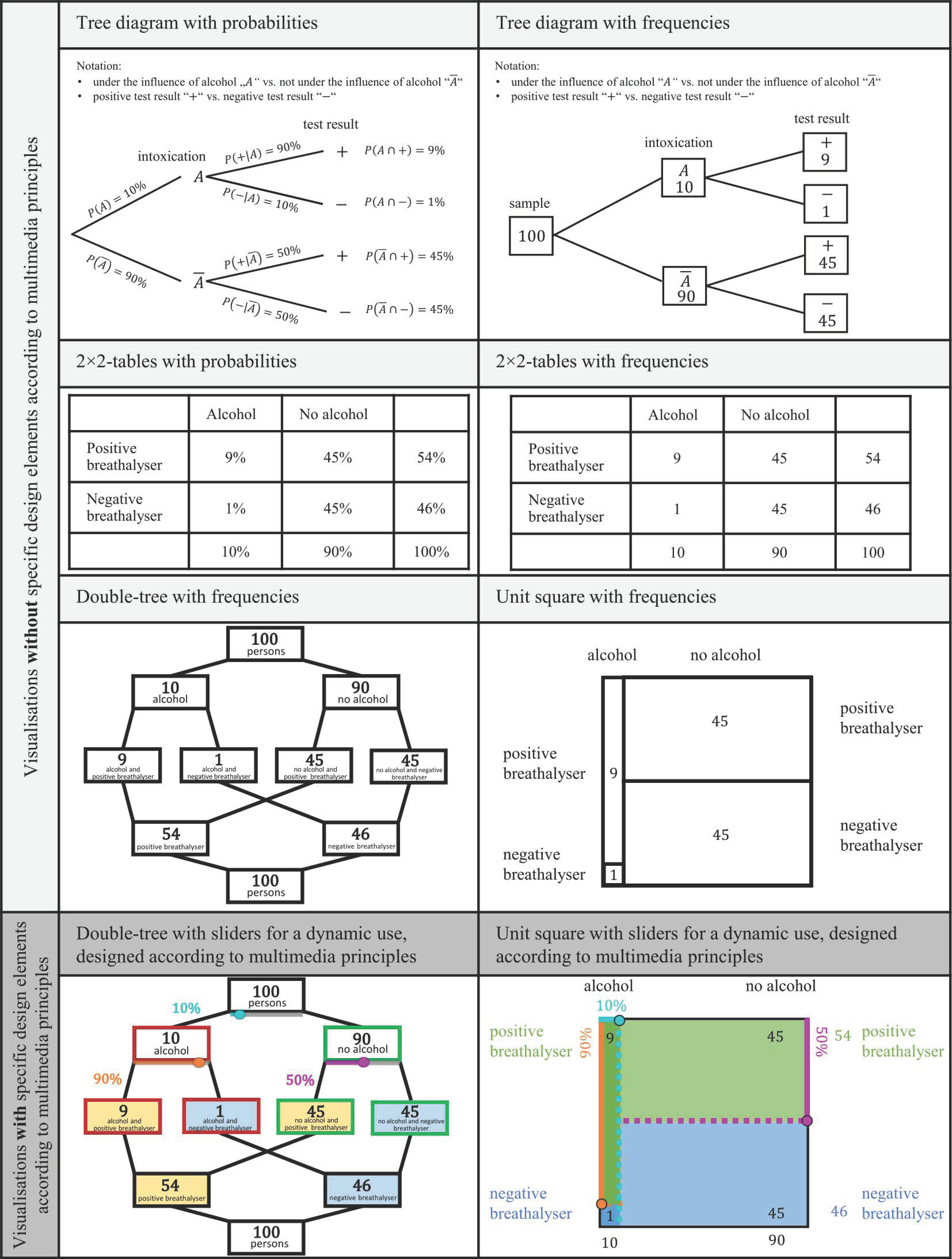
3. Designing the Double-Tree and Unit Square
3.1. Static Visualisations
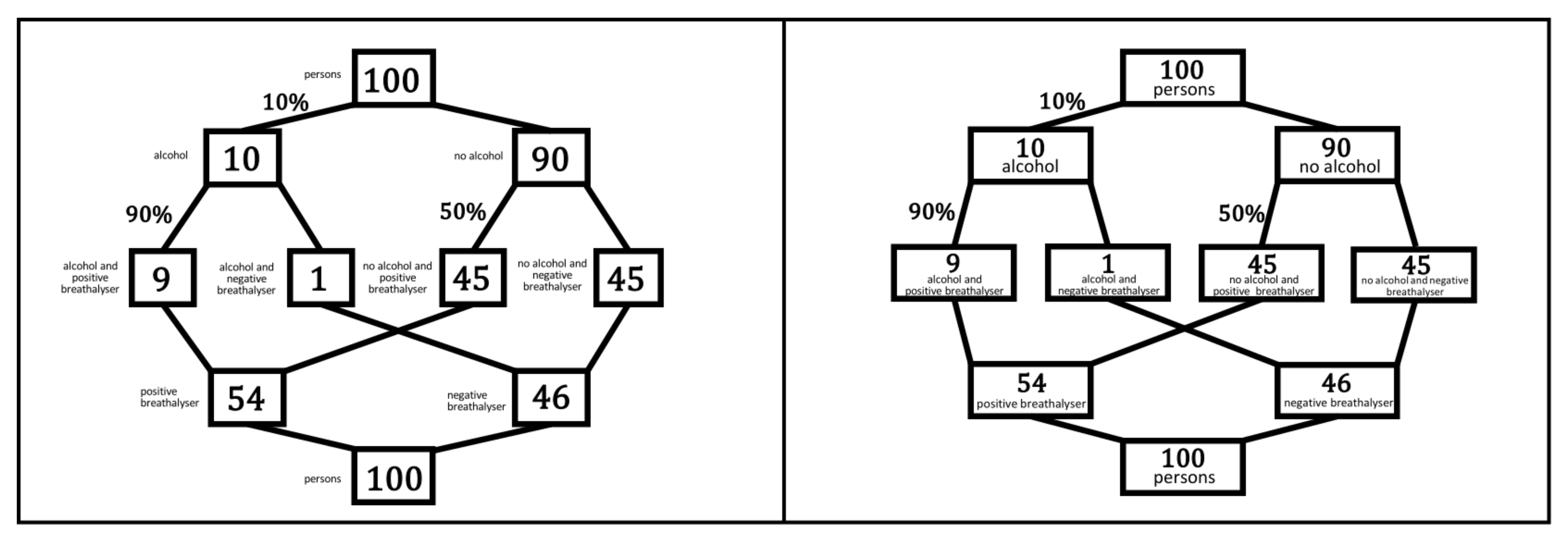
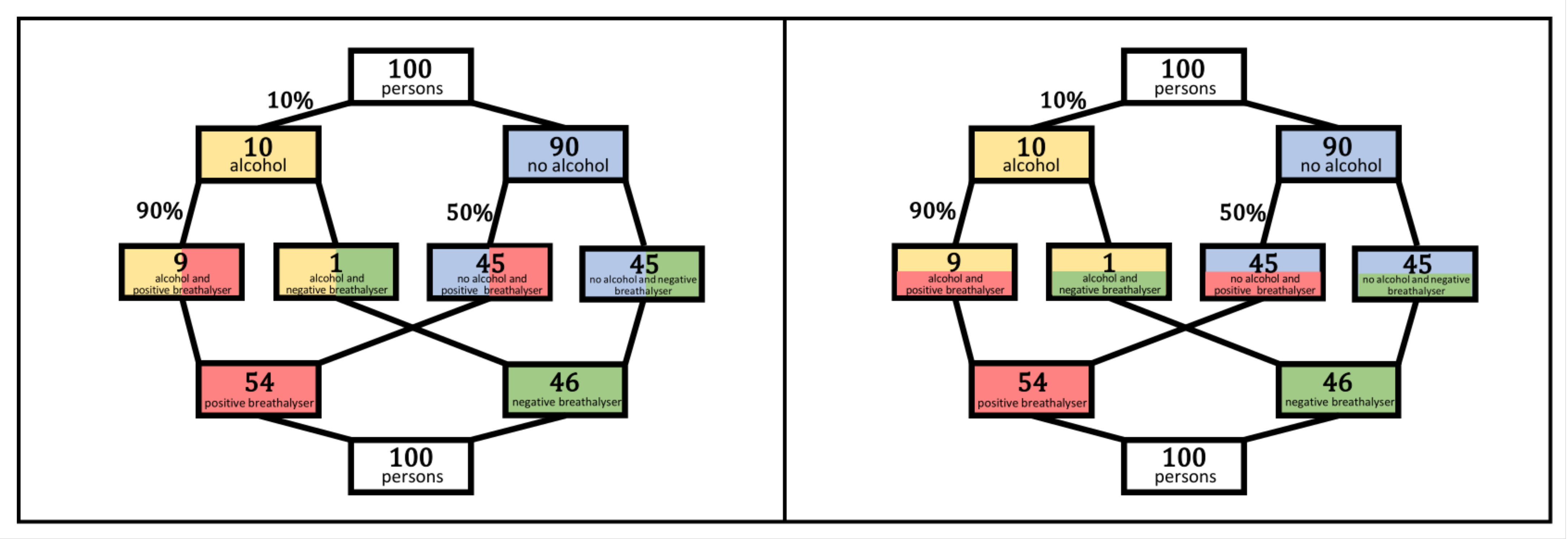
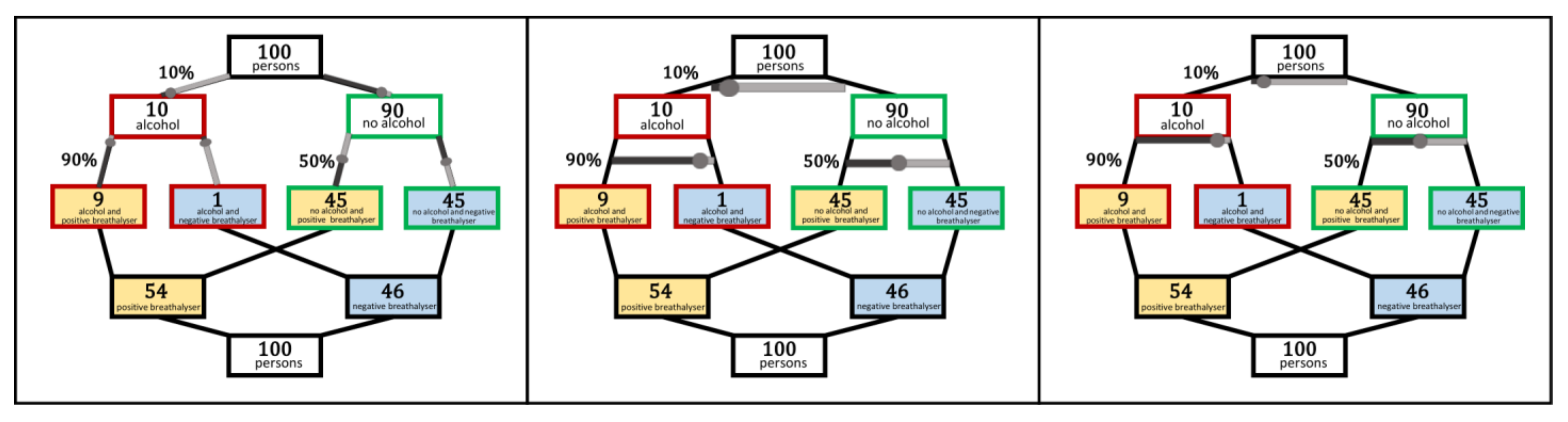
3.1.1. Static Double-Trees
3.1.2. Static Unit Squares
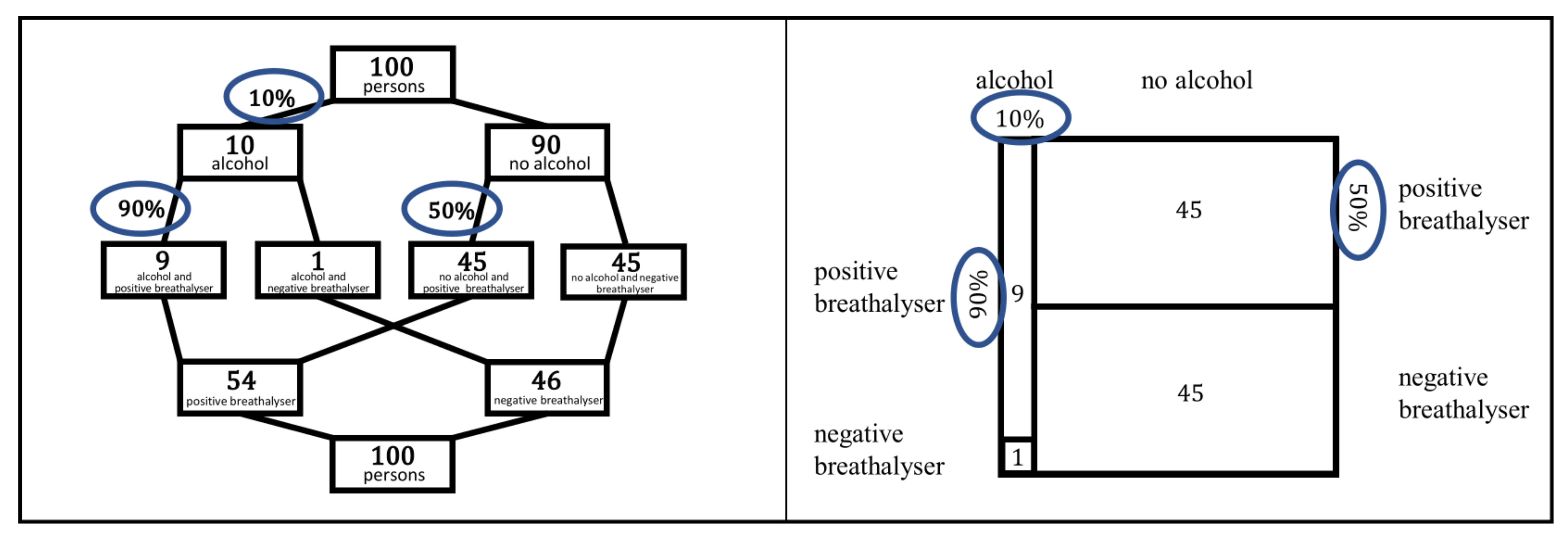
3.2. Dynamic Visualisations
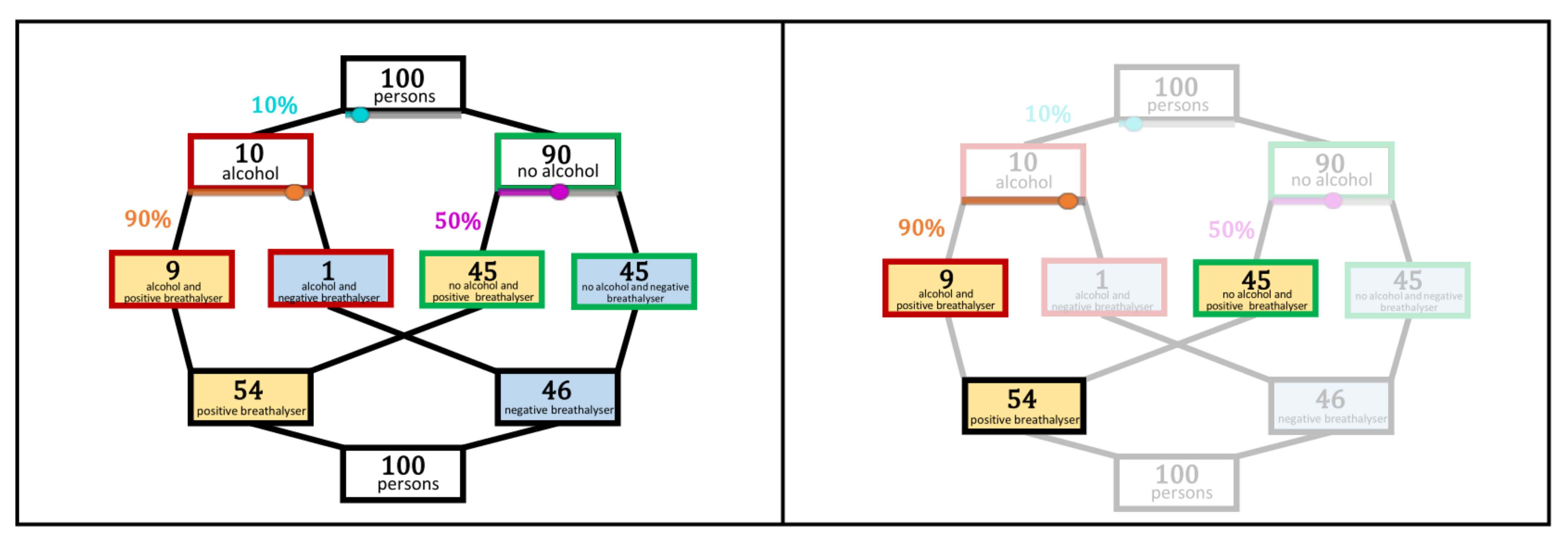
3.2.1. Dynamic Double-Tree
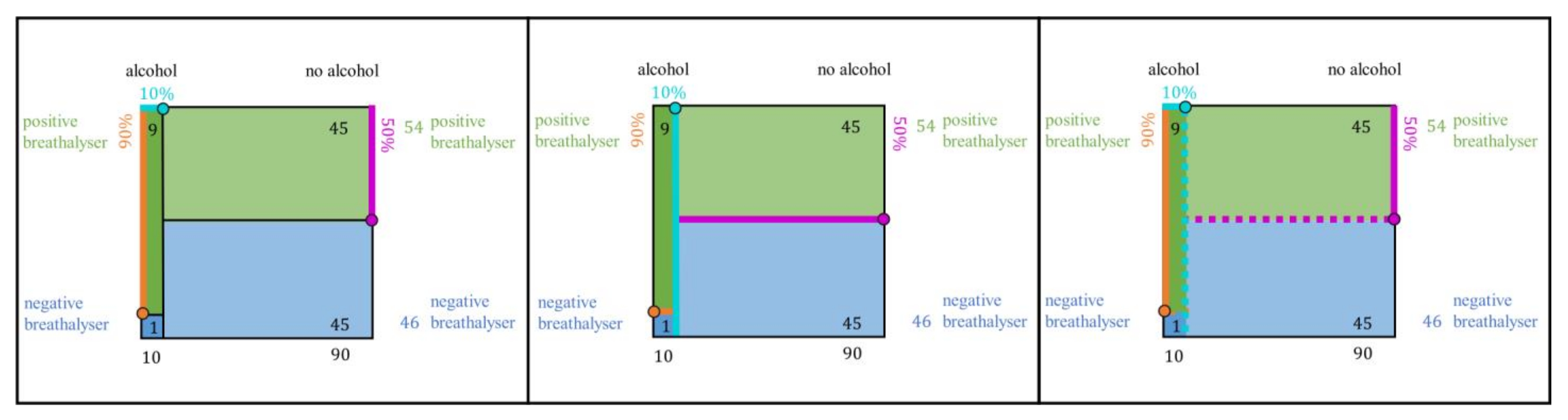
3.2.2. Dynamic Unit Square
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- O’Halloran, K.L.; Beezer, R.A.; Farmer, D.W. A new generation of mathematics textbook research and development. ZDM Math. Educ. 2018, 50, 863–879. [Google Scholar] [CrossRef]
- Phillips, L.M.; Norris, S.P.; Macnab, J.S. Visualizations and Mathematics. In Visualization in Mathematics, Reading and Science Education; Phillips, L.M., Norris, S.P., Macnab, J.S., Eds.; Springer: Dordrecht, The Netherlands, 2010; pp. 45–50. ISBN 978-90-481-8815-4. [Google Scholar]
- Gilbert, J.K.; Reiner, M.; Nakhleh, M. Visualization: Theory and Practice in Science Education; Springer: Dordrecht, The Netherlands, 2008; ISBN 9781402052675. [Google Scholar]
- Mayer, R. Instruction Based on Visualization. In Handbook of Research on Learning and Instruction, 2nd ed.; Mayer, R.E., Alexander, P.A., Eds.; Routledge: New York, NY, USA; London, UK, 2017; pp. 483–501. ISBN 9781138831759. [Google Scholar]
- Zhu, L.; Gigerenzer, G. Children can solve Bayesian problems: The role of representation in mental computation. Cognition 2006, 98, 287–308. [Google Scholar] [CrossRef]
- McDowell, M.; Jacobs, P. Meta-analysis of the effect of natural frequencies on Bayesian reasoning. Psychol. Bull. 2017, 143, 1273–1312. [Google Scholar] [CrossRef] [PubMed]
- Spiegelhalter, D.; Pearson, M.; Short, I. Visualizing uncertainty about the future. Science 2011, 333, 1393–1400. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Breslav, S.; Hornbæk, K. Interactive Instruction in Bayesian Inference. Hum.-Comput. Interact. 2018, 33, 207–233. [Google Scholar] [CrossRef]
- Binder, K.; Krauss, S.; Bruckmaier, G.; Marienhagen, J. Visualizing the Bayesian 2-test case: The effect of tree diagrams on medical decision making. PLoS ONE 2018, 13, e0195029. [Google Scholar] [CrossRef]
- Wu, C.M.; Meder, B.; Filimon, F.; Nelson, J.D. Asking better questions: How presentation formats influence information search. J. Exp. Psychol. Learn. Mem. Cogn. 2017, 43, 1274–1297. [Google Scholar] [CrossRef]
- Clinton, V.; Morsanyi, K.; Alibali, M.W.; Nathan, M. Learning about Probability from Text and Tables: Do Color Coding and Labeling through an Interactive-user Interface Help? Cogn. Psychol. 2016, 30, 440–453. [Google Scholar] [CrossRef]
- Mayer, R.E.; Fiorella, L. Principles for Reducing Extraneous Processing in Multimedia Learning: Coherence, Signaling, Redundancy, Spatial Contiguity, and Temporal Contiguity Principles. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 279–315. ISBN 9781139547369. [Google Scholar]
- Budgett, S.; Pfannkuch, M. Visualizing Chance: Tackling Conditional Probability Misconceptions. In Topics and Trends in Current Statistics Education Research; Springer: Cham, Switzerland, 2019; pp. 3–25. [Google Scholar]
- Martignon, L.; Kuntze, S. Good Models and Good Representations are a Support for Learners’ Risk Assessment. Math. Enthus. 2015, 12, 157–167. [Google Scholar] [CrossRef]
- Khan, A.; Breslav, S.; Glueck, M.; Hornbæk, K. Benefits of visualization in the Mammography Problem. Int. J. Hum.-Comput. Stud. 2015, 83, 94–113. [Google Scholar] [CrossRef]
- Ottley, A.; Kaszowska, A.; Crouser, R.J.; Peck, E.M. The Curious Case of Combining Text and Visualization. EUROVIS 2019, 121–125. [Google Scholar] [CrossRef]
- Shen, H.; Jin, H.; Cabrera, Á.A.; Perer, A.; Zhu, H.; Hong, J.I. Designing Alternative Representations of Confusion Matrices to Support Non-Expert Public Understanding of Algorithm Performance. Proc. ACM Hum.-Comput. Interact. 2020, 4, 1–22. [Google Scholar] [CrossRef]
- Mosca, A.; Ottley, A.; Chang, R. Does Interaction Improve Bayesian Reasoning with Visualization? In Proceedings of the CHI’21: CHI Conference on Human Factors in Computing Systems, Yokohama, Japan, 8–13 May 2021; Kitamura, Y., Ed.; Association for Computing Machinery: New York, NY, USA, 2021; pp. 1–14, ISBN 9781450380966. [Google Scholar]
- Tsai, J.; Miller, S.; Kirlik, A. Interactive Visualizations to Improve Bayesian Reasoning. Proc. Hum. Factors Ergon. Soc. Annu. Meet. 2011, 55, 385–389. [Google Scholar] [CrossRef]
- Garcia-Retamero, R.; Cokely, E.T. Designing Visual Aids That Promote Risk Literacy: A Systematic Review of Health Research and Evidence-Based Design Heuristics. Hum. Factors 2017, 59, 582–627. [Google Scholar] [CrossRef]
- Kellen, V.J. The Effects of Diagrams and Relational Complexity on User Performance in Conditional Probability Problems in a Non-Learning Context. Ph.D. Thesis, DePaul University, Chicago, IL, USA, 2012. [Google Scholar]
- Ottley, A.; Peck, E.M.; Harrison, L.T.; Afergan, D.; Ziemkiewicz, C.; Taylor, H.A.; Han, P.K.J.; Chang, R. Improving Bayesian Reasoning: The Effects of Phrasing, Visualization, and Spatial Ability. IEEE Trans. Vis. Comput. Graph. 2016, 22, 529–538. [Google Scholar] [CrossRef]
- Navarrete, G.; Correia, R.; Sirota, M.; Juanchich, M.; Huepe, D. Doctor, what does my positive test mean? From Bayesian textbook tasks to personalized risk communication. Front. Psychol. 2015, 6, 1327. [Google Scholar] [CrossRef]
- Sokolowski, A. Are Physics Formulas Aiding Covariational Reasoning? Students’ Perspective. In Understanding Physics Using Mathematical Reasoning: A Modeling Approach for Practitioners and Researchers; Sokolowski, A., Ed.; Springer: Cham, Switzerland, 2021; pp. 177–186. ISBN 978-3-030-80205-9. [Google Scholar]
- Borovcnik, M. Multiple Perspectives on the Concept of Conditional Probability. Av. Investig. Educ. Matemática 2012, 1, 5–27. [Google Scholar] [CrossRef]
- Lichti, M.; Roth, J. Functional Thinking—A Three-Dimensional Construct? J. Math. Didakt. 2019, 40, 169–195. [Google Scholar] [CrossRef]
- Wittmann, G. Elementare Funktionen und Ihre Anwendungen; Springer Spektrum: Berlin/Heidelberg, Germany, 2019; ISBN 978-3-662-58059-2. [Google Scholar]
- Oerthmann, M.; Carlson, M.; Thompson, P.W. Foundational Reasoning Abilities that Promote Coherence in Student’s Function Understanding. In Making the Connection: Research and Teaching in Undergraduate Mathematics Education; Carlson, M.P., Rasmussen, C., Eds.; Mathematical Association of America: Washington, DC, USA, 2008; pp. 27–42. ISBN 9780883851838. [Google Scholar]
- Binder, K.; Krauss, S.; Bruckmaier, G. Effects of visualizing statistical information—An empirical study on tree diagrams and 2 × 2 tables. Front. Psychol. 2015, 6, 1186. [Google Scholar] [CrossRef]
- Hoffrage, U.; Hafenbrädl, S.; Bouquet, C. Natural frequencies facilitate diagnostic inferences of managers. Front. Psychol. 2015, 6, 642. [Google Scholar] [CrossRef]
- Siegrist, M.; Keller, C. Natural frequencies and Bayesian reasoning: The impact of formal education and problem context. J. Risk Res. 2011, 14, 1039–1055. [Google Scholar] [CrossRef]
- Chapman, G.B.; Liu, J. Numeracy, frequency, and Bayesian reasoning. Judgm. Decis. Mak. 2009, 4, 34–40. [Google Scholar]
- Gigerenzer, G.; Hoffrage, U. How to improve Bayesian reasoning without instruction: Frequency formats. Psychol. Rev. 1995, 102, 684–704. [Google Scholar] [CrossRef]
- Binder, K.; Krauss, S.; Wiesner, P. A New Visualization for Probabilistic Situations Containing Two Binary Events: The Frequency Net. Front. Psychol. 2020, 11, 750. [Google Scholar] [CrossRef]
- Eichler, A.; Böcherer-Linder, K.; Vogel, M. Different Visualizations Cause Different Strategies When Dealing With Bayesian Situations. Front. Psychol. 2020, 11, 1897. [Google Scholar] [CrossRef]
- Brase, G.L. Pictorial representations in statistical reasoning. Appl. Cogn. Psychol. 2008, 23, 369–381. [Google Scholar] [CrossRef]
- Cosmides, L.; Tooby, J. Are humans good intuitive statisticians after all? Rethinking some conclusions from the literature on judgment under uncertainty. Cognition 1996, 58, 1–73. [Google Scholar] [CrossRef]
- Böcherer-Linder, K.; Eichler, A.; Vogel, M. The impact of visualization on flexible Bayesian reasoning. AIEM 2017, 25–46. [Google Scholar] [CrossRef]
- Yamagishi, K. Faciliating Normative Judgments of Conditional Probability: Frequency or Nested Sets. Exp. Psychol. 2003, 50, 97–106. [Google Scholar] [CrossRef]
- Sedlmeier, P.; Gigerenzer, G. Teaching Bayesian reasoning in less than two hours. J. Exp. Psychol. Gen. 2001, 130, 380–400. [Google Scholar] [CrossRef]
- Wassner, C. Förderung Bayesianischen Denkens: Kognitionspsychologische Grundlagen und Didaktische Analysen. Ph.D. Thesis, Universität Kassel; Franzbecker, Hildesheim, Germany, 2004. [Google Scholar]
- Oldford, R.W.; Cherry, W.H. Picturing probability: The poverty of Venn diagrams, the richness of Eikosograms. 2003. Available online: http://www.math.uwaterloo.ca/~rwoldfor/papers/venn/eikosograms/paper.pdf (accessed on 5 May 2020).
- Pfannkuch, M.; Budgett, S. Reasoning from an Eikosogram: An Exploratory Study. Int. J. Res. Undergrad. Math. Ed. 2017, 3, 283–310. [Google Scholar] [CrossRef]
- Talboy, A.N.; Schneider, S.L. Improving Accuracy on Bayesian Inference Problems Using a Brief Tutorial. J. Behav. Dec. Mak. 2017, 30, 373–388. [Google Scholar] [CrossRef]
- Steckelberg, A.; Balgenorth, A.; Berger, J.; Mühlhauser, I. Explaining computation of predictive values: 2 × 2 table versus frequency tree. A randomized controlled trial ISRCTN74278823. BMC Med. Educ. 2004, 4, 13. [Google Scholar] [CrossRef]
- Zikmund-Fisher, B.J.; Witteman, H.O.; Dickson, M.; Fuhrel-Forbis, A.; Kahn, V.C.; Exe, N.L.; Valerio, M.; Holtzman, L.G.; Scherer, L.D.; Fagerlin, A. Blocks, ovals, or people? Icon type affects risk perceptions and recall of pictographs. Med. Decis. Mak. 2014, 34, 443–453. [Google Scholar] [CrossRef]
- Reani, M.; Davies, A.; Peek, N.; Jay, C. How do people use information presentation to make decisions in Bayesian reasoning tasks? Int. J. Hum. -Comput. Stud. 2018, 111, 62–77. [Google Scholar] [CrossRef]
- Binder, K.; Steib, N.; Krauss, S. Von Baumdiagrammen über Doppelbäume zu Häufigkeitsnetzen—kognitive Überlastung oder didaktische Unterstützung? in press.
- Micallef, L.; Dragicevic, P.; Fekete, J.-D. Assessing the Effect of Visualizations on Bayesian Reasoning through Crowdsourcing. IEEE Trans. Vis. Comput. Graph. 2012, 18, 2536–2545. [Google Scholar] [CrossRef]
- Böcherer-Linder, K.; Eichler, A. How to Improve Performance in Bayesian Inference Tasks: A Comparison of Five Visualizations. Front. Psychol. 2019, 10, 267. [Google Scholar] [CrossRef]
- Büchter, T.; Eichler, A.; Steib, N.; Binder, K.; Böcherer-Linder, K.; Krauss, S.; Vogel, M. How to Train Novices in Bayesian Reasoning. Mathematics 2022, 10, 1558. [Google Scholar] [CrossRef]
- Ainsworth, S. DeFT: A conceptual framework for considering learning with multiple representations. Learn. Instr. 2006, 16, 183–198. [Google Scholar] [CrossRef]
- Ainsworth, S.; Wood, D.; O’Malley, C. There is more than one way to solve a problem: Evaluating a learning environment that supports the development of children’s multiplication skills. Learn. Instr. 1998, 8, 141–157. [Google Scholar] [CrossRef]
- Schnotz, W. Integrated Model of Text and Picture Comprehension. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 72–103. ISBN 9781139547369. [Google Scholar]
- Mayer, R.E. Cognitive Theory of Multimedia Learning. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 43–71. ISBN 9781139547369. [Google Scholar]
- Schweppe, J.; Eitel, A.; Rummer, R. The multimedia effect and its stability over time. Learn. Instr. 2015, 38, 24–33. [Google Scholar] [CrossRef]
- Paas, F.; Sweller, J. Implications of Cognitive Load Theory for Multimedia Learning. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 27–42. ISBN 9781139547369. [Google Scholar]
- Sweller, J.; van Merriënboer, J.J.G.; Paas, F. Cognitive Architecture and Instructional Design: 20 Years Later. Educ. Psychol. Rev. 2019, 31, 261–292. [Google Scholar] [CrossRef]
- Ayres, P. Using subjective measures to detect variations of intrinsic cognitive load within problems. Learn. Instr. 2006, 16, 389–400. [Google Scholar] [CrossRef]
- Sweller, J.; Ayres, P.; Kalyuga, S. (Eds.) Cognitive Load Theory; Springer: New York, NY, USA, 2011; ISBN 978-1-4419-8125-7. [Google Scholar]
- Sweller, J.; Ayres, P.; Kalyuga, S. The Split-Attention Effect. In Cognitive Load Theory; Sweller, J., Ayres, P., Kalyuga, S., Eds.; Springer: New York, NY, USA, 2011; pp. 111–128. ISBN 978-1-4419-8125-7. [Google Scholar]
- Ayres, P.; Sweller, J. The Split-Attention Principle in Multimedia Learning. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 206–226. ISBN 9781139547369. [Google Scholar]
- Sweller, J.; van Merrienboer, J.J.G.; Paas Fred, G.W.C. Cognitive Architecture and Instructional Design. Educ. Psychol. Rev. 1998, 10, 251–296. [Google Scholar] [CrossRef]
- Sweller, J.; Ayres, P.; Kalyuga, S. The Redundancy Effect. In Cognitive Load Theory; Sweller, J., Ayres, P., Kalyuga, S., Eds.; Springer: New York, NY, USA, 2011; pp. 141–154. ISBN 978-1-4419-8125-7. [Google Scholar]
- Mayer, R.E.; Heiser, J.; Lonn, S. Cognitive constraints on multimedia learning: When presenting more material results in less understanding. J. Educ. Psychol. 2001, 93, 187–198. [Google Scholar] [CrossRef]
- Seufert, T. Kohärenzbildung beim Wissenserwerb mit multiplen Repräsentationen. In Was ist Bildkompetenz?: Studien zur Bildwissenschaft; Sachs-Hombach, K., Ed.; Dt. Univ.-Verl.: Wiesbaden, Germany, 2003; pp. 117–129. ISBN 978-3-8244-4498-4. [Google Scholar]
- Mayer, R.E. Multimedia Learning, 2nd ed.; Cambridge University Press: Cambridge, UK, 2009; ISBN 9780511811678. [Google Scholar]
- Van Gog, T. The Signaling (or Cueing) Principle in Multimedia Learning. In The Cambridge Handbook of Multimedia Learning, 2nd ed.; Mayer, R.E., Ed.; Cambridge University Press: Cambridge, UK, 2014; pp. 263–278. ISBN 9781139547369. [Google Scholar]
- Tabbers, H.K.; Martens, R.L.; van Merriënboer, J.J.G. Multimedia instructions and cognitive load theory: Effects of modality and cueing. Br. J. Educ. Psychol. 2004, 74, 71–81. [Google Scholar] [CrossRef]
- Jamet, E.; Gavota, M.; Quaireau, C. Attention guiding in multimedia learning. Learn. Instr. 2008, 18, 135–145. [Google Scholar] [CrossRef]
- Mautone, P.D.; Mayer, R.E. Signaling as a cognitive guide in multimedia learning. J. Educ. Psychol. 2001, 93, 377–389. [Google Scholar] [CrossRef]
- Moreno, R.; Abercrombie, S. Promoting Awareness of Learner Diversity in Prospective Teachers: Signaling Individual and Group Differences within Virtual Classroom Cases. J. Technol. Teach. Educ. 2010, 18, 111–130. [Google Scholar]
- Kalyuga, S.; Chandler, P.; Sweller, J. Managing split-attention and redundancy in multimedia instruction. Appl Cogn. Psychol 1999, 13, 351–371. [Google Scholar] [CrossRef]
- Folker, S.; Ritter, H.; Sichelschmidt, L. Processing and integrating multimodal material—The influence of color-coding. Proc. Annu. Meet. Cogn. Sci. Soc. 2005, 27. Available online: https://escholarship.org/content/qt5ch098t2/qt5ch098t2.pdf (accessed on 5 May 2020).
- Wang, L.; Giesen, J.; McDonnell, K.T.; Zolliker, P.; Mueller, K. Color design for illustrative visualization. IEEE Trans. Vis. Comput. Graph. 2008, 14, 1739–1746. [Google Scholar] [CrossRef] [PubMed]
- Kertil, M. Covariational Reasoning of Prospective Mathematics Teachers: How Do Dynamic Animations Affect? Turk. J. Comput. Math. Educ. (TURCOMAT) 2020, 11, 312–342. [Google Scholar] [CrossRef]
- Günster, S.M.; Weigand, H.-G. Designing digital technology tasks for the development of functional thinking. ZDM Math. Educ. 2020, 52, 1259–1274. [Google Scholar] [CrossRef]
- Padberg, F.; Wartha, S. Didaktik der Bruchrechnung; Springer: Berlin/Heidelberg, Germany, 2017; ISBN 9783662529690. [Google Scholar]
- Mayer, R.E. (Ed.) The Cambridge Handbook of Multimedia Learning, 2nd ed.; Cambridge University Press: Cambridge, UK, 2014; ISBN 9781139547369. [Google Scholar]
- Brock, T. How to Explain Screening Test Outcomes. Available online: https://www.significancemagazine.com/science/547-a-visual-guide-to-screening-test-results (accessed on 5 May 2020).
- Hafenbrädl, S.; Hoffrage, U. Toward an ecological analysis of Bayesian inferences: How task characteristics influence responses. Front. Psychol. 2015, 6, 939. [Google Scholar] [CrossRef]

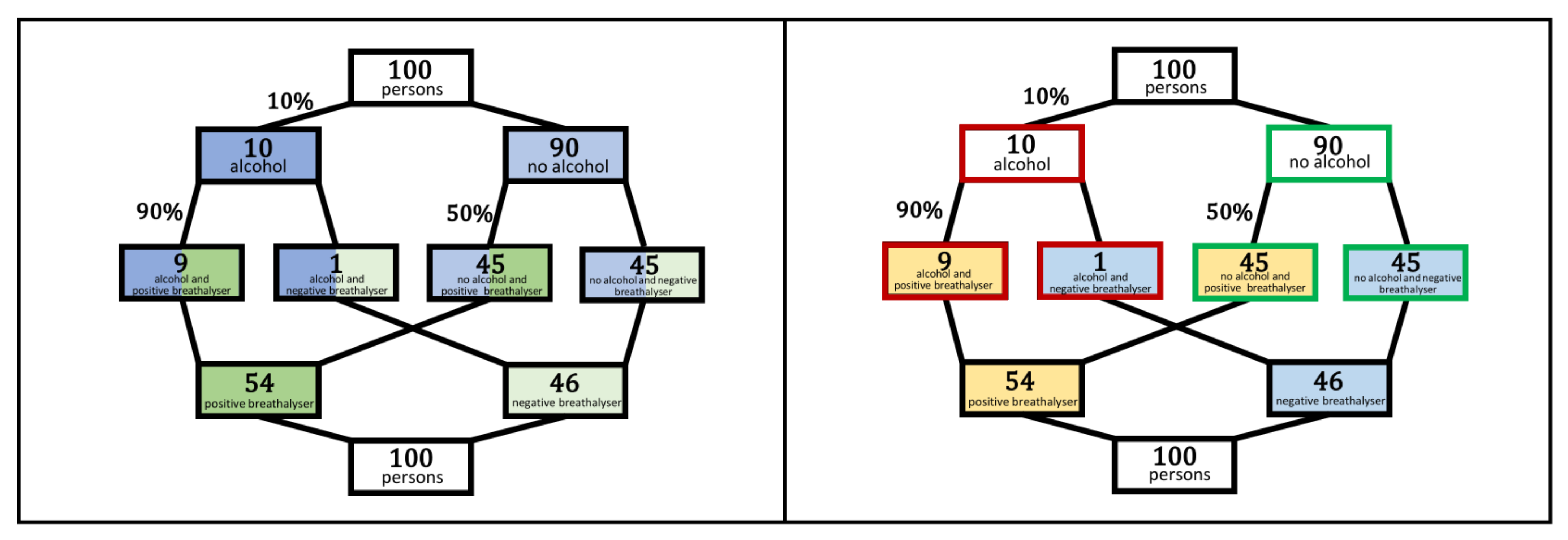
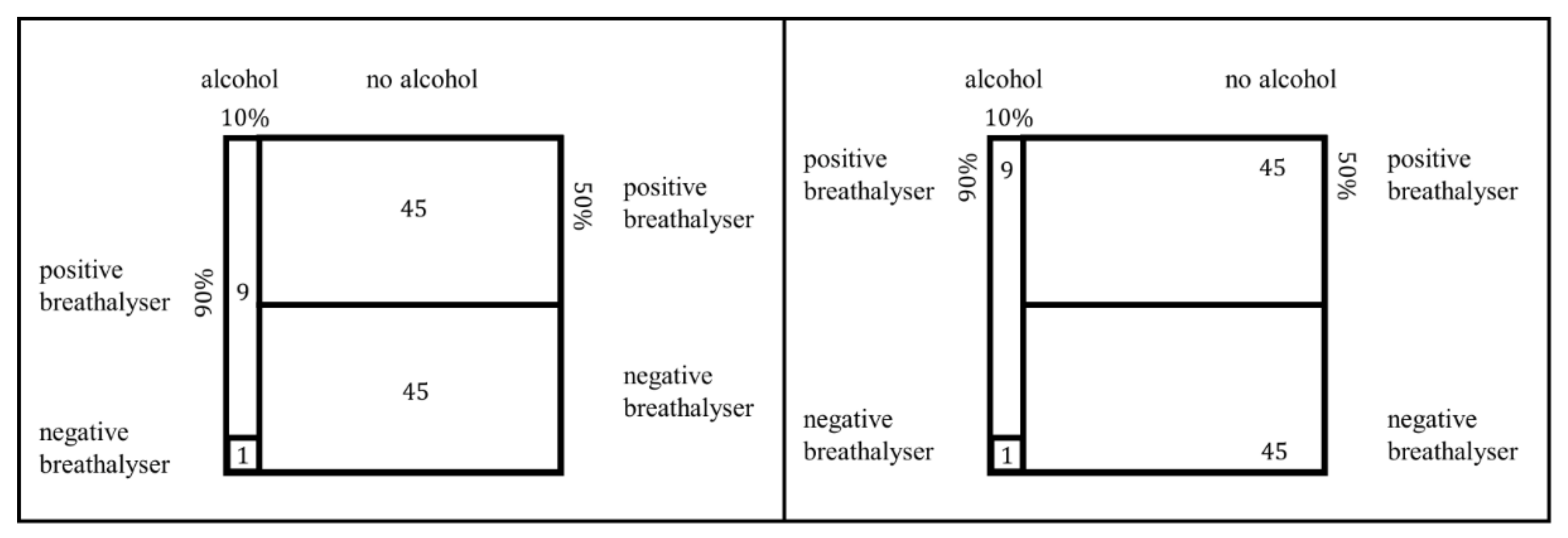
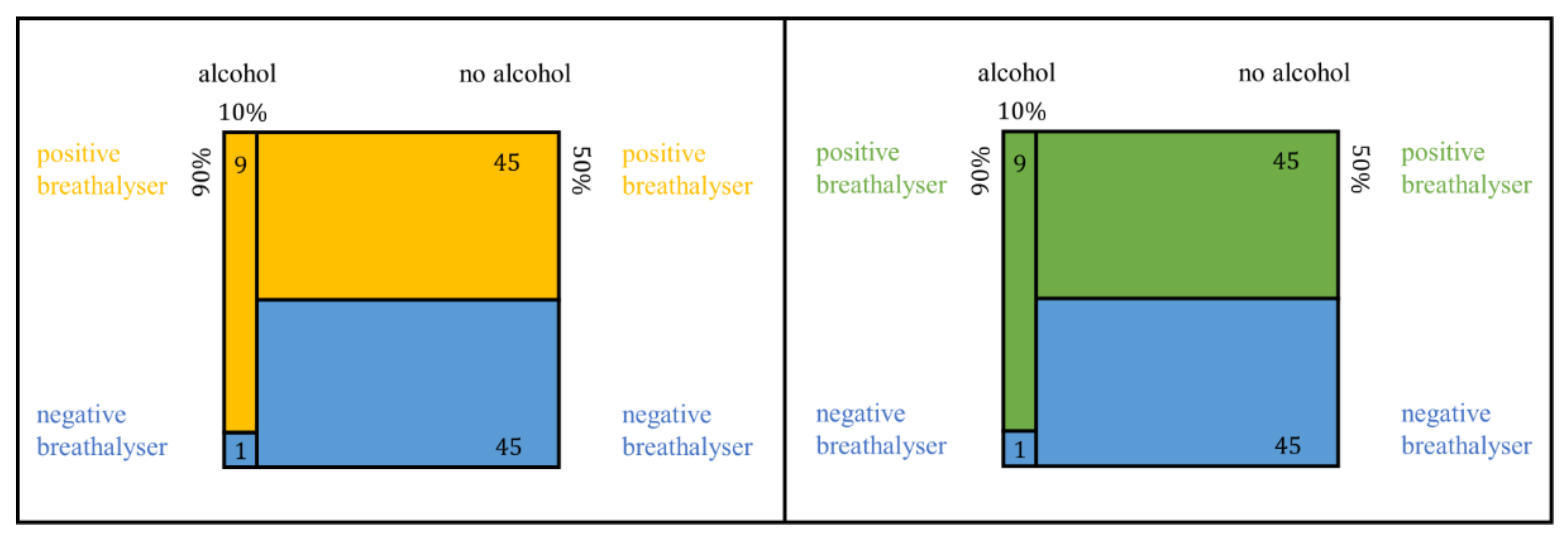
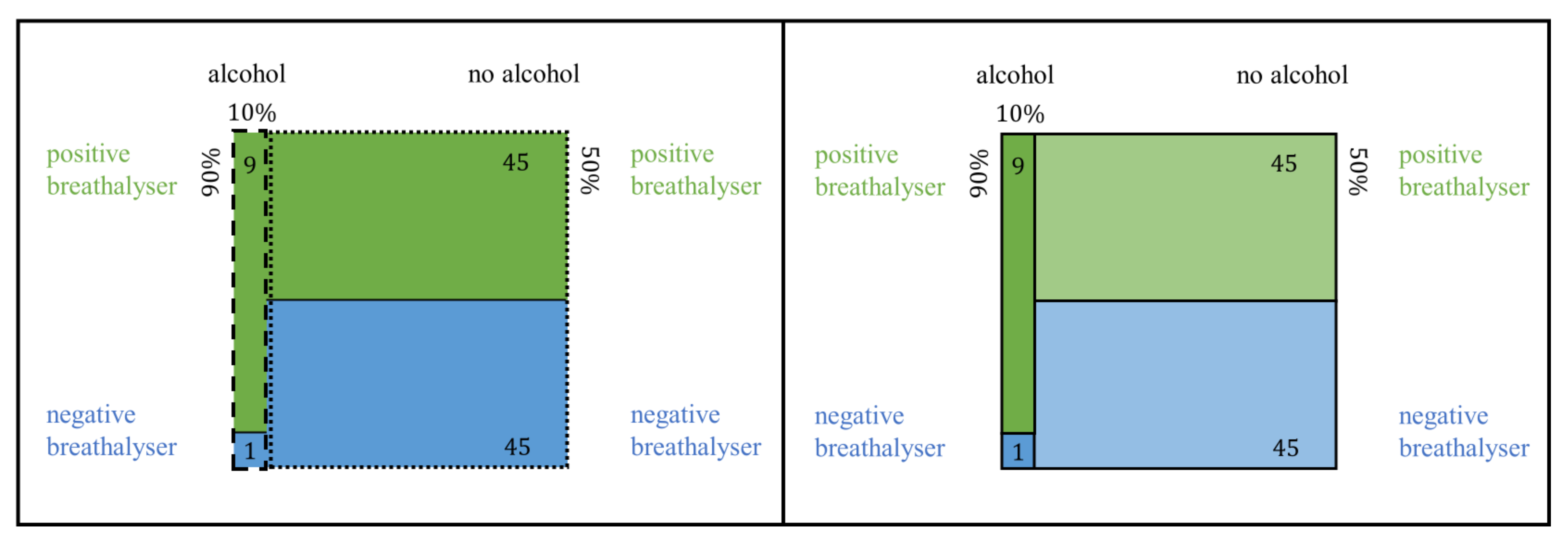





| Probabilities | Natural Frequencies | |
|---|---|---|
| base rate | The probability is 10% that a person stopped by the police is under the influence of alcohol on a Saturday night. | 10 out of 100 people are under the influence of alcohol when stopped by the police on a Saturday night. |
| true-positive rate | If a person who is under the influence of alcohol is tested, the probability is 90% that the breathalyser test is actually positive. | In 9 out of 10 people who are under the influence of alcohol, the breathalyser test is actually positive. |
| false-positive rate | If a person who is not under the influence of alcohol is tested, the probability is 50% that the breathalyser test is positive nevertheless. | In 45 out of 90 people who are not under the influence of alcohol, the breathalyser test is nevertheless positive. |
| Tree Diagram | Double-Tree | 2 × 2 Table | Unit Square | |
|---|---|---|---|---|
| Static tasks | ||||
| Given probabilities | Represented on the branches | Represented on the branches | Not directly represented | Represented as the ratio of the division of the sides |
| Representation of the two relevant intersections (joint probabilities) | Joint probabilities can stand at the end of one path (probability tree) or intersections as frequencies in the nodes at the end of one path (frequency tree) | Intersections given in in the nodes of the middle level as frequencies | Intersections given in the inner fields as frequencies (2 × 2 table with frequencies) or joint probabilities given as probabilities (2 × 2 table with probabilities) | Intersections given as frequencies inside the inner areas and as the size of the inner areas |
| Belonging of the intersection (joint probability) to the superset | Expressed through the connection of the intersection to the superset by a branch; only given for one superset (node above the intersection) | Expressed through the connection of the intersection to the superset by a branch; given for both supersets (node above and below intersections) | Expressed through the adjoining positions of the inner fields: next to each other (as a row) or underneath each other (as a column) | Expressed through the adjoining positions of the areas (as in the 2 × 2 table) |
| Dynamic tasks | ||||
| Dependence of the intersection (joint probability) on the given information | Connectedness of the nodes with the branches reveals the influence of the parameters on the associated absolute frequencies | Connectedness of the nodes with the branches reveals the influence of the parameters on the associated absolute frequencies | Cannot be visualised, as given probabilities are not directly represented | Size of the inner areas (i.e., intersections) depends on its length and width, which correspond to the ratios of the divisions on the sides (i.e., the given probabilities) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Büchter, T.; Steib, N.; Böcherer-Linder, K.; Eichler, A.; Krauss, S.; Binder, K.; Vogel, M. Designing Visualisations for Bayesian Problems According to Multimedia Principles. Educ. Sci. 2022, 12, 739. https://doi.org/10.3390/educsci12110739
Büchter T, Steib N, Böcherer-Linder K, Eichler A, Krauss S, Binder K, Vogel M. Designing Visualisations for Bayesian Problems According to Multimedia Principles. Education Sciences. 2022; 12(11):739. https://doi.org/10.3390/educsci12110739
Chicago/Turabian StyleBüchter, Theresa, Nicole Steib, Katharina Böcherer-Linder, Andreas Eichler, Stefan Krauss, Karin Binder, and Markus Vogel. 2022. "Designing Visualisations for Bayesian Problems According to Multimedia Principles" Education Sciences 12, no. 11: 739. https://doi.org/10.3390/educsci12110739
APA StyleBüchter, T., Steib, N., Böcherer-Linder, K., Eichler, A., Krauss, S., Binder, K., & Vogel, M. (2022). Designing Visualisations for Bayesian Problems According to Multimedia Principles. Education Sciences, 12(11), 739. https://doi.org/10.3390/educsci12110739








