A First Ever Look into Greece’s Vast Educational Data: Interesting Findings and Policy Implications

Abstract

Intro: In this survey the academic performance of primary and secondary school students in Greece, for three consecutive school years, was examined. The data concerned all Greek students of the last two grades of elementary school and the three grades of junior high school. Method: Unsupervised learning methods such as an X-means algorithm in combination with descriptive and inductive statistical methods were used, in order to examine students’ performance levels. The longitudinal stability of academic performance levels and the influence of demographic characteristics such as the region, gender and guardians’ profession were also examined. Results: The existence of four levels of academic performance and longitudinal stability of frequencies per performance level was confirmed. There was also statistically significant differentiation based on the profession of guardian, gender, and area of residence. Discussion: The results demonstrated specific challenges that the educational policy of the country has to address. The stability of the percentages of students in the four groups of academic performance that emerged over time, shows corresponding stability in the factors that affect academic performance. A gradual reduction in the performance of students in high School was found, as the level of difficulty of the courses increases from class to class. Some demographic characteristics of students are not independent of their performance. However, due to the compliance with the general regulation of personal data, there was no access to additional features that may be related to performance, such as nationality and exact place of residence.

1. Introduction

Students’ academic performance is an issue of interdisciplinary interest. A huge volume of literature has been published and many determinants have been suggested. A wide range of non-cognitive factors has been proposed. These factors can be categorized into internal: such as learning motivation [1,2], learning style [3] students’ attitudes [4], self-efficacy [5], self-concept [6], self-regulation [7], self-esteem [8,9], goal orientation [10], and external factors: such as educational leadership [11], school culture [12], school climate [13], teachers’ expectations [14], parent involvement [15] and socioeconomic status proposed by Coleman [16].

In an extensive meta-analysis in a total of 2138 surveys, it was found that the socio-economic status had a high impact on performance, also school climate, school culture, self-efficacy, student attitudes, school leadership, and expectations of teachers have a moderate effect, while anxiety, motivation, goal orientation, and family support have a lesser effect [17].

A method for identifying standards and draw conclusions from educational data is the use of education data mining techniques. The field of educational data mining has grown rapidly over the last fifteen years. The number of publications increases year to year and a significant number of bibliographic reviews have been published [17,18,19,20]. Two different approaches have been developed [18]:

• EDM, that aims to provide answers to important educational questions through the application of data mining techniques (DM) and
• Learning analytics, aiming at understanding and improving the learning process.

According to literature reviews many data mining techniques and a wide variety of algorithms are widely used [18,21,22,23]. Articles published in this scientific field have greatly increased in recent years. It is a common finding in the literature that assessing students’ academic performance is often an objective of studies.

Another finding is that supervised learning techniques such as classification and regression are most often used, with quite good results. However, a common feature of research is the frequent use of limited data in quantity, which come mainly from higher education. Unsupervised or semi-supervised learning techniques have been used on a much smaller scale [18,20].

Using unsupervised learning, it is possible to draw conclusions from the educational data, without requiring prior judgment by researchers. Using clustering algorithms, it is possible to identify the levels of academic performance of students. Most of the published research in this field using unsupervised learning that has been conducted, concerns higher education [24]. The main focus of the research was on identifying the levels of academic performance and predicting the performance of students in combination with other algorithms [25,26,27,28,29]. Clustering is also used for the initial separation of performance levels, which are used as features for further analysis.

In this work, the use of unsupervised techniques for characterizing student performance was preferred. Clustering algorithms can rank students in specific clusters of performance levels without the intervention of researchers. The main research objectives were to separate student performance at different levels, examining the longitudinal dimension of this separation and the impact of certain demographic factors in performance. In particular, three research questions (RQ) were examined:

RQ1: Identifying the number of student performance levels and frequency of occurrence.

RQ2: Examining the students’ performance over time.

RQ3: Examining the effects of demographic characteristics.

2. Data and Methods

2.1. The Dataset

The Greek educational system is structured in three levels, six-year primary education (elementary school), six-year secondary education (three-year high school and three-year lyceum) and higher education. In academic year 2015–2016 Greece’s Ministry of Education reverted to a new information management system named “«My_School»”. This MIS collects all information regarding students in all 12 grades of primary and secondary education.

Data entry is the responsibility of school principals across the country. Recorded data include a variety of information including:

• Demographic characteristics such as gender, profession of guardians, nationality, religion
• Academic characteristics such as grades per course, absences, behavior
• Information about the teaching staff such as contact details, the class(es) they teach, the years of service, the hours they teach, the qualifications they hold, etc.
• Information about the school units such as contact details, what the infrastructure they have, their equipment, the needs for teaching staff, etc.

«My_School» is currently the only tool that can support the export of statistical results about all students in the Greek educational system, while the information it collects is ever increasing in order to provide for further possibilities.

Still, to this day, access to this data is limited to staff in different administrative levels of education, each one able to access different aspects of the data based on their role and only via the interfaces and pre-determined views provided by «My_School».

For this work we have been allowed direct access to a subset of the data stored by «My_School», for research purposes. For obvious reasons the data have been heavily redacted and anonymized, but still it is far more than what has ever been provided to the research community in the past. In fact, to the best of our knowledge, this is the first time that any data originating from «My_School» have been provided to researchers outside of the ministry.

2.1.1. Structure of the Dataset

The dataset includes a portion of the demographic data that is stored in «My_School». We have been provided with only an instance of the demographic data. In other words, we do not know whether any of that information has changed over the period of three years that we examine in this work, we only have their values at one specific point in time at the end of the three years.

The demographic attributes that are available to this study are summarized in

Table 1. Demographic information in the dataset.

Element	Type	Description
Student_Id	Character	Fake Student ID
Region	Text	50 counties + (6 regions of Attika and 2 regions for Thessaloniki)
Gender	Boolean	Male/Female
Guardian Occupation	Text	Free text (As completed from school, in Greek language)

. The Student_Id field deserves a special mention for clarification: this is not a value that is found anywhere in «My_School» or that can be in any way linked to a specific student. As the data has been anonymized, a fake ID has been inserted upon export by the ministry so that using it we can track the same student over the course of the three years. Other attributes include the student’s gender, the region (of the school) and the occupation of the parents (or whoever is the legal guardian).

Then, for each grade that a student follows we have additional information as summarized in

Table 2. Grade information in the dataset.

Element	Type	Description
Class	Character	E, ST (Elementary) and A, B, C (High School)
GPA	Numeric	Average score (according to Greek law), with an accuracy of two decimals
Number of absences	Numeric	One per day (Elementary) and Seven per day (High School), without decimal digits

. The information includes the GPA, computed in the way the Greek law specifies for each grade, and the number of absences the student has had over the year. The information of how these absences are distributed over the course of the year is not available.

Finally, detailed information about the grades the students have achieve in each course subject are also provide as shown in

Table 3. Course grades.

Element	Type	Description
Lesson	Text	Elementary and High School Courses, selected from list (see Table 4 and Table 5),
Lesson_Score	Numeric	Numerical scoring, 1–10 (Elementary) and 0–20 (High School) without decimal digits

.

The list of courses is of course different for each grade.

Table 4. List of courses in Elementary school.

Elementary School Cources
5th and 6th grade
Greek Language
Geography
Social and Political Education
Religious Education
History
Mathematics
Physics
English Language
Second Foreign Language
Computer Science

summarizes the courses offered in the 5th and 6th grades of elementary school and

Table 5. List of courses in High School.

High School Courses
1st Class	2nd Class	3nd Class
Ancient Greek Language	Ancient Greek Language	Ancient Greek Language
Greek Literature	Greek Literature	Greek Literature
Greek Language	Greek Language	Greek Language
English Language	English Language	English Language
Religious Education	Religious Education	Religious Education
History	History	History
Mathematics	Mathematics	Mathematics
Home economics	Computer Science	Social and Political Education
Computer Science	Technology	Computer Science
Technology	Physics	Technology
Physics	Chemistry	Physics
Biology	Biology	Chemistry
Geography	Geography	Biology

the courses offered in the three grades of high school.

2.1.2. Range of Data

As has already been mentioned, data has been provided for three consecutive years. In fact, two different portions of the data have been provided for the years from 2016–2017 to 2018–2019. The data includes information from all general schools, and also all music schools and all art schools. Comparisons between them are possible because at the considered grades the same courses are taught in these three types of schools.

The first subset of the dataset includes the students that started the 5th grade of elementary school in year 2015 and follows them to the 1st grade of high school.

The second subset of the data set includes the students that started the 1st grade of high school in year 2015 and follows them to the 3rd grade of high school.

Of course, when examining a whole country, it is expected that not every student will follow exactly the same path. Some students drop out of school. Others come from abroad and enter the educational system at a grade based on their age. Of course, there are also those that repeat a class, either because they did not have sufficient attendance (for example if they missed a large portion of the year for medical reasons) or because they did not succeed academically.

2.2. Method

Datasets of this scale are of course rarely perfect. Ours is no exception to that. Frist of all, there are some missing grades. In some instances, this is because some students don’t follow all courses (religious education is an example of a course that a number of students sits out) and in other instances due to data entry mistakes. In the cases that a single grade was missing, its value was extrapolated using the average grade from other courses. In the cases that more than one grades were missing, the whole record was deleted.

In addition to missing grades, there are also cases with illogical data (for example impossible grades) that are due to mistakes upon data entry. And there are also cases with incomplete data (for example missing demographic data). Records with illogical data or multiple missing attributes were removed.

Finally, since we aim to examine students’ progress from one grade to the next, we also removed records of students that do not appear in all three years of the corresponding data set.

This left us with records of 85680 (80.83%) distinct students in the first subset (

Table 6. Records of the first dataset before and after data cleaning.

Class	Initial Records	Final Records
5th Elementary School	101,644	85,680
6th Elementary School	104,559
1st High School	111,785

) of the dataset and records of 85344 (86.28%) distinct students in the second subset (

Table 7. Records of the second dataset before and after data cleaning.

Grade	Initial Records	Final Records
1st High School	96,359	85,344
2nd High School	99,431
3rd High School	100,943

) of the data set. This is the largest dataset to have ever been examined for primary/secondary education in Greece and perhaps one of the largest internationally for these age groups.

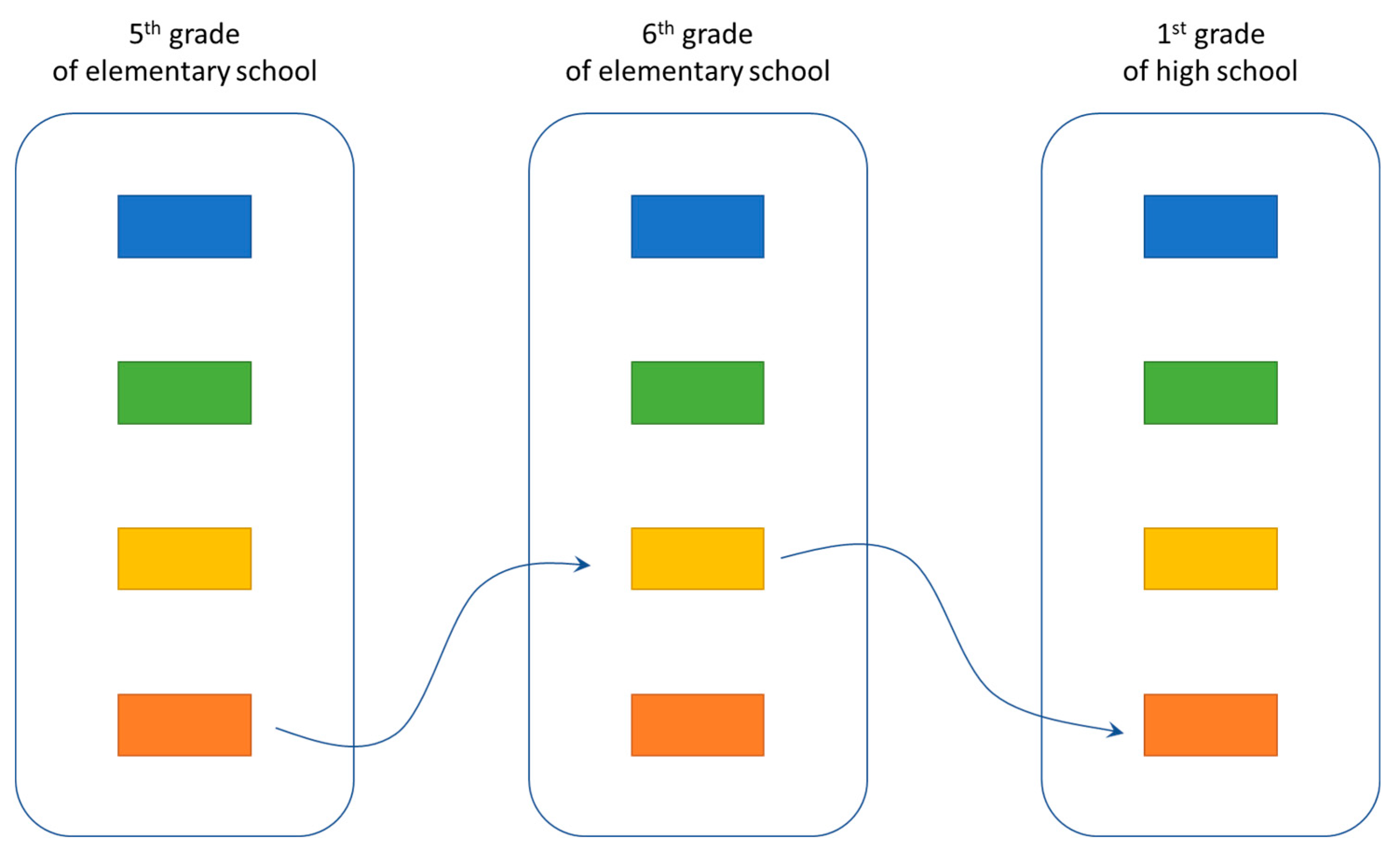
After data cleaning, two datasets were created. The first dataset included grades from the last two classes of primary.

School and the first class of high school and covers the transition from primary to high school. The second included grades from all three classes of high school. X-means algorithm was executed for each class separately and student performance clusters for each student in each class were exported. Each class performance cluster was added to the dataset as a new variable. In this way, it was possible to use statistical techniques to respond to research questions. In particular, there were examined: (a) the relative frequency of each performance level, (b) the longitudinal stability of performance clusters frequencies, (c) the differentiation of the average score (GPA) per cluster and its statistical significance (using non-parametric tests (Kruskal Wallis) due to the lack of homogeneity in variables), (d) the effect of some demographic features in student performance, the features were the profession of guardian, the gender and student residence area. For these tests, the “x²” statistic test was used.

Initially, we used a data clustering algorithm to divide students’ grades into performance levels, but without specifying the number of levels. We used the X-means algorithm, which requires the determination of only the minimum and maximum number of possible clusters, while the selection of the optimal number of clusters is done using BIC criterion. The data used were related to the students’ grades in each lesson for the fifth and sixth class of elementary school as well as the three classes of high school. After characterizing the level of students’ performance, we mainly used descriptive statistics tools in order to answer the following research questions.

• Research Question 1: Number of academic performance levels and frequencies.

We tried to identify the number of levels of academic performance as well as the average and standard deviation of the overall grade (GPA) per level of academic performance. The average frequency of each level per class should also have been estimated.

• Research Question 2: Students’ performance over time.

The aim of the second research question was to highlight the change in the frequencies of the levels of academic performance over time. The transition from primary to secondary education and the variation of students’ performance at high school were studied.

• Research Question 3: Effects of demographic characteristics.

Finally, we studied the effect of some demographic characteristics such as (a) the profession of guardian, (b) the gender of the students and (c) the area of the student’s residence. We identified differences between the observed percentages per level of performance and the theoretically expected percentage, based on the distribution of demographic characteristics in the population. A representation of the method we followed in this study is presented at Figure 1.

3. Results

3.1. First Research Question

Our first aim was to examine whether/how students’ academic performance can be grouped into generic academic performance levels. Intuitively we know that teachers know who the good students are in their classes, who are the mediocre students and who are the very weak or non-participating ones; but rather than follow teachers’ intuition we opted to follow the data.

Therefore, we clustered the data using the grades of the lessons mentioned in Table 4 and Table 5. In order to avoid the bias of looking for a specific number of clusters (for example the 3 groups that teachers tell us exist in most classes) we used x-means [30,31,32], an extension to k-means that also estimates the value of k.

After applying the clustering algorithm, four levels of students’ academic performance emerged. These specific levels are the same in both elementary school and high school.

Table 8. Grades averages and standard deviations per class and cluster.

Cluster	GPA 5th Elementary School	GPA 6th Elementary School	GPA 1st High School	GPA 2nd High School	GPA 3rd High School
A	9.988/0.002	9.979/0.023	19.070/0.038	19.100/0.088	19.076/0.014
B	9.727/0.029	9.680/0.264	17.144/0.071	16.934/0.170	16.826/0.062
C	9.008/0.018	8.912/0.081	15.205/0.118	14.811/0.120	14.696/0.183
D	8.180/0.066	8.263/0.574	13.073/0.256	12.845/0.346	12.962/0.471

presents the averages GPA (centroids) and standard deviations of the grades per class for the three years. All students of Greece were included in the dataset and

Table 9. BIC values per class and year.

Class	School Year	No of Clusters	BIC–Value
5th Elementary School	16–17	4	770,325.77
	17–18	4	924,904.65
	18–19	4	938,884.65
6th Elementary School	16–17	4	886,493.46
	17–18	4	917,255.56
	18–19	4	742,378.62
1st High School	16–17	4	467,536.44
	17–18	4	485,932.55
	18–19	4	494,685.45
2nd High School	16–17	4	401,889.33
	17–18	4	404,857.79
	18–19	4	566,802.06
3rd High School	16–17	4	475,555.07
	17–18	4	378,631.03
	18–19	4	416,664.98

shows the BIC values per sub dataset (class).

A first observation is that we did not find three but instead four distinct groups of academic performance. This strengthens the data driven approach of avoiding biases and letting the data “speak”.

A much more important observation, though, is that all five runs of the x-means algorithm produced the same number of clusters. Therefore, we can conclude that this is not a random result or an outlier; the different levels of academic performance in primary and secondary school, or at least from 5th grade of elementary school until the end of high school, are four. In the remaining of this paper, we will refer to these levels as Very strong, Strong, Weak and Very weak.

We also observe that the clusters are quite distinct, as the standard deviation is very low in almost all cases. An exception to this is the lowest (Very Weak) group, which is expected as the group includes the whole range of grades down to almost zero.

We can also notice that the four levels of academic performance are quite close in elementary school and the distance is greater (in terms of GPA) in high school. This is mainly due to the fact that whereas in high school almost the whole range of grades from 1 to 20 can be used, in elementary school most grades are in the 7–10 region and grades lower than that are rarely, if ever, used. Therefore, this does not necessarily depict a difference in academic performance but rather a difference in grading. In the above we have focused on the center and radius of each cluster, but we have not examined the size of clusters. 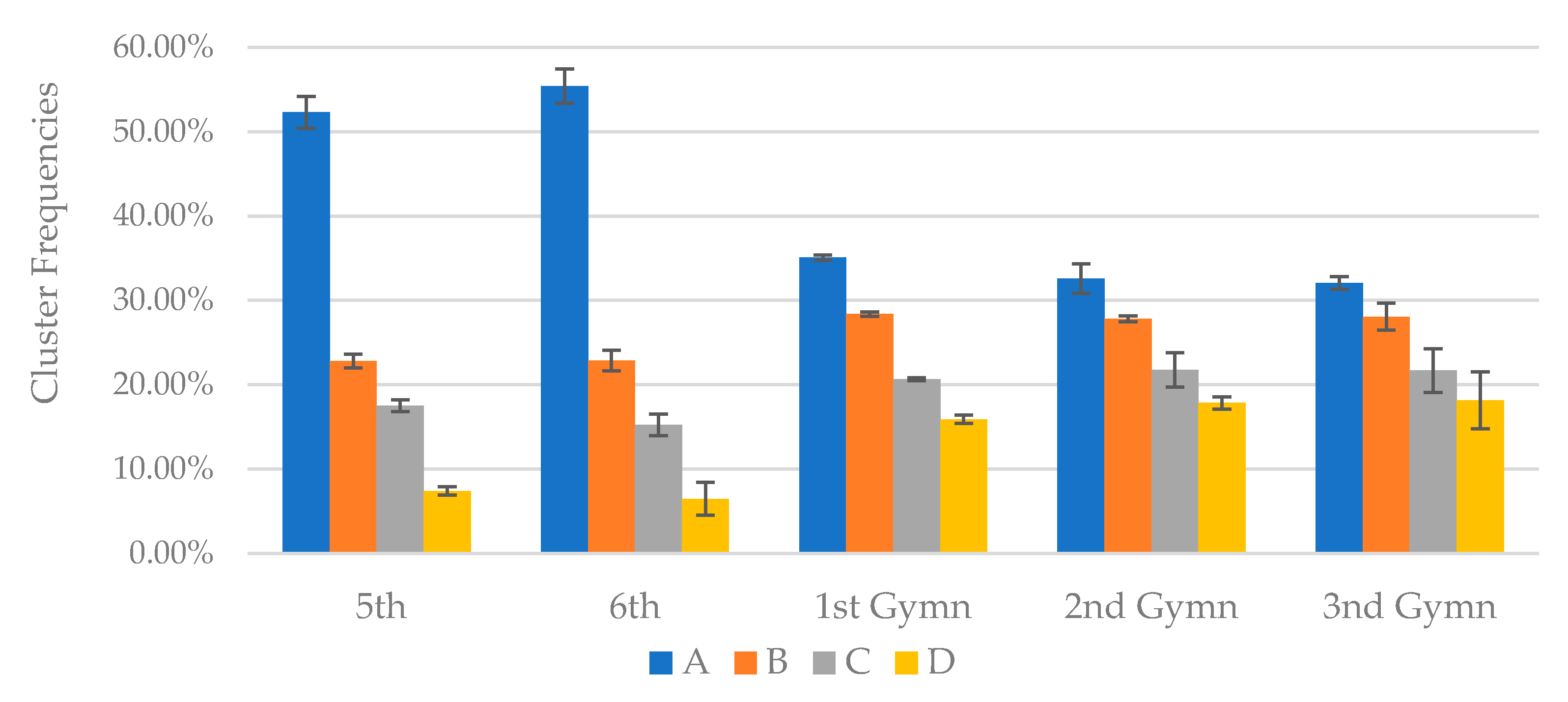Figure 2 presents the relative size of each cluster.

We can observe a clear separation between elementary and high school. In elementary school the majority of students belong in the group with the very strong academic performance, while in high school very strong academic performance is attributed to about one third of the students and weaker performances become relatively more common. In junior high school, on the other hand, the differences between the averages per level become greater. This is an indication of a greater dispersion of the distribution of grades received by students in high school. Over time, there is a slight downward trend in junior high school averages in all performance categories, except excellent students. In addition to the stability of the level of performance in each category, there is also a stability of the frequency of occurrence of the specific levels as shown in

Table 10. Frequencies per cluster and class.

Cluster	5th Elementary School	6th Elementary School	1st High School	2nd High School	3rd High School	Mean/St. Dev Elementary	Mean/St. Dev High School
A	52.30%/1.90%	55.40%/2.03%	35.08%/0.32%	32.57%/1.75%	32.07%/0.78%	53.8%/1.97%	33.24%/0.95%
B	22.80%/0.80%	22.87%/1.22%	28.38%/0.27%	27.81%/0.37%	28.07%/1.59%	22.84%/1.01%	28.09%/0.74%
C	17.50%/0.70%	15.25%/1.29%	20.64%/0.17%	21.78%/2.04%	21.69%/2.59%	16.37%/0.99%	21.37%/1.60%
D	7.40%/0.50%	6.48%/1.98%	15.91%/0.50%	17.84%/0.74%	18.17%/3.38%	6.94%/1.24%	17.31%/1.54%

.

In junior high school, on the other hand, the frequencies for each level of performance are distributed differently. One-third of the students are now graded with excellent, while the percentage of students belonging to the lower performance category more than doubles. This highlights a difference in the level of difficulty of the lessons in high school and in the adaptation of the students to the new school, as well as the non-competitive character of assessment in primary schools, which refers not only to the performance but also to other features, such as the effort, the initiatives, the creativity, and the cooperation with classmates etc. Finally, we can observe that the group of students with very weak academic performance grows steadily as we move from one grade to the next. This shows, unfortunately, that as the years go by more and more students are left behind.

3.2. Second Research Question

3.2.1. First Dataset

With the second research question we examined the variation of student performance over three school years. The transition of students from elementary to junior high school was covered, using data from the fifth and sixth grade of elementary School as well as the first grade of high school. The variation of student performance in the three classes of junior high school over time was also studied. A stability of performance levels in primary school is presented in

Table 11. Cluster Frequencies over time First Dataset.

Cluster	Class	5th Class Elementary School Level
		A	B	C	D
A	6th Class ES 1	90.10%	9.20%	0.70%	0.00%
	1st Class HS 2	62.30%	30.00%	7.10%	0.60%
B	6th Class ES	34.80%	50.50%	13.70%	1.00%
	1st Class HS	14.20%	42.60%	35.50%	7.70%
C	6th Class ES	4.50%	29.50%	53.90%	12.10%
	1st Class HS	1.50%	17.10%	47.90%	33.50%
D	6th Class ES	0.50%	5.60%	36.50%	57.40%
	1st Class HS	0.20%	4.00%	28.20%	67.60%

¹ Elementary School. ² High School.

. Of those who were characterized as excellent in the fifth class, 93.1% are still characterized as excellent in the sixth grade. Furthermore, 62.2% of them are characterized as excellent in elementary school and are still characterized as excellent in the first class of secondary education.

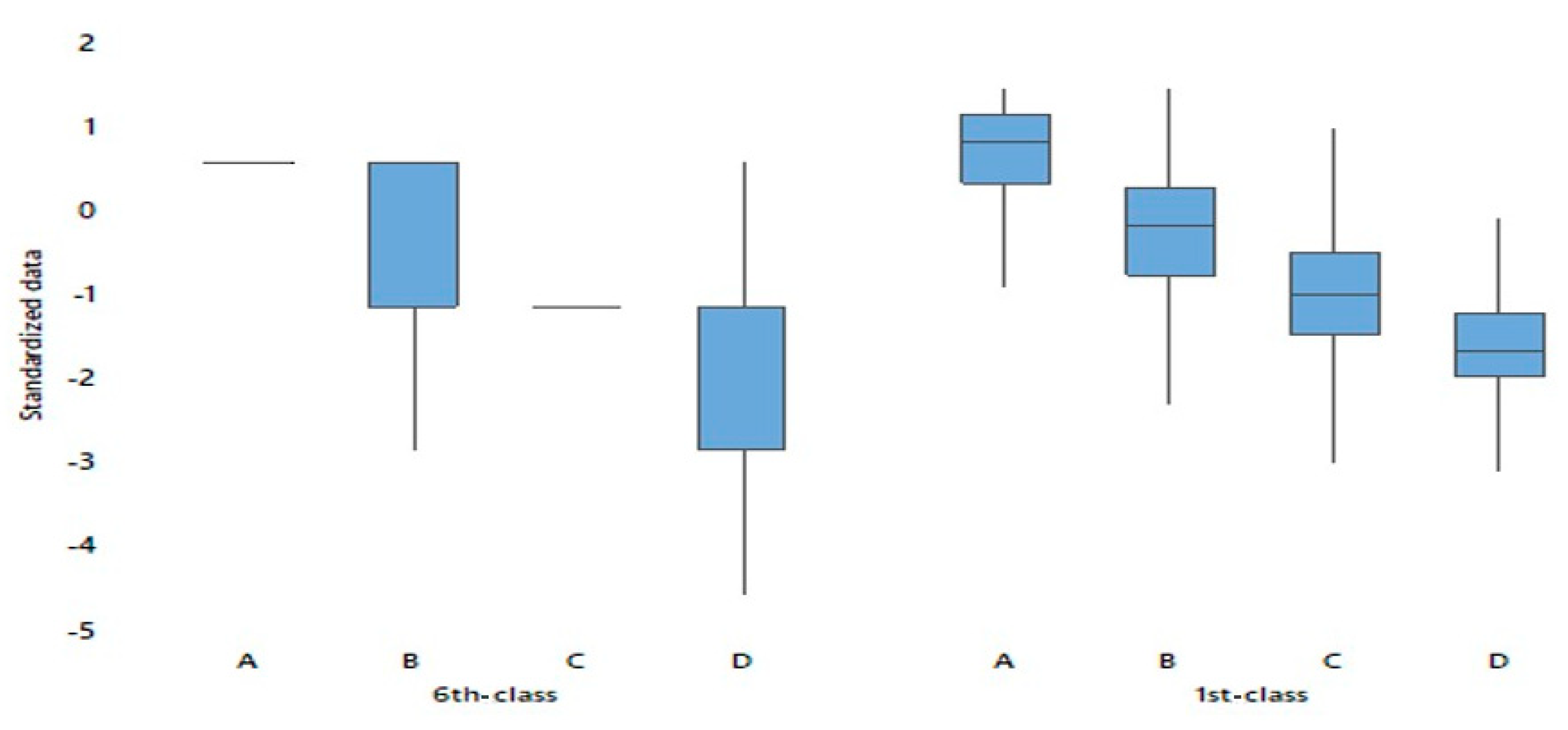
The categories of students with average performance (B and C) show increased variability between classes. Of those who were classified in category B in the fifth grade of elementary school, 45.1% are characterized as excellent in the sixth grade of elementary school, but only 12.9% manage to maintain this performance in high school. On the contrary, the average student in high school seems to be moving at a lower level. A percent of 38.60% from the students who were classified in category C in the fifth grade fall in the lowest D category in the first class of junior high school and a 34.8% of those classified as B fall to C category, confirming the increasing difficulty that students face when attending high school. Those who have been grouped in the lowest performance category in the fifth grade of elementary school, in a large percentage also remain in the same category in the first grade of high school, while very few manage to excel.

Figure 2 shows a clearly different distribution of performance in high school based on the initial characterization of students’ performance in fifth grade. Although in the normalized data there are different variations, the performance in the sixth grade of elementary school and in the first year of high school seems to depend on the initial characterization of the students’ performance (Figure 3).

Table 12. Descriptive statistics of GPA, based on the initial classification.

Variable	5th Class Level	Mean	SE Mean	St. Dev	Median
6th Class ES 1 GPA	A	9.9784	0.00073	0.146	10.0
	B	9.7059	0.00344	0.467	10.0
	C	9.1154	0.00441	0.515	9.0
	D	8.4096	0.00992	0.671	8.0
1st Class HS 2 GPA	A	18.247	0.0068	1.348	18.6
	B	16.227	0.0117	1.581	16.4
	C	14.658	0.0133	1.558	14.6
	D	13.286	0.0215	1.455	13.1

¹ Elementary School. ² High School.

presents in more detail the basic descriptive statistics of GPA, based on the initial classification into categories in the fifth grade of primary school.

We also examined the statistical significance of GPA differentiation based on the initial classification of students using the non-parametric Kruskal-Wallis Test. Statistically significant differences in GPA were observed between the different initial classifications of the students (

Table 13. Independent-Samples Kruskal-Wallis Test of GPA, based on the initial classification (1st dataset).

Class	Statistic	p-Value
5th Elementary School	57,365.28	0.0000
6th Elementary School	44,992.44	0.0000
1st High School	41,402.00	0.0000

Asymptotic significances are displayed. The significance level is 0.05.

).

3.2.2. Second Dataset

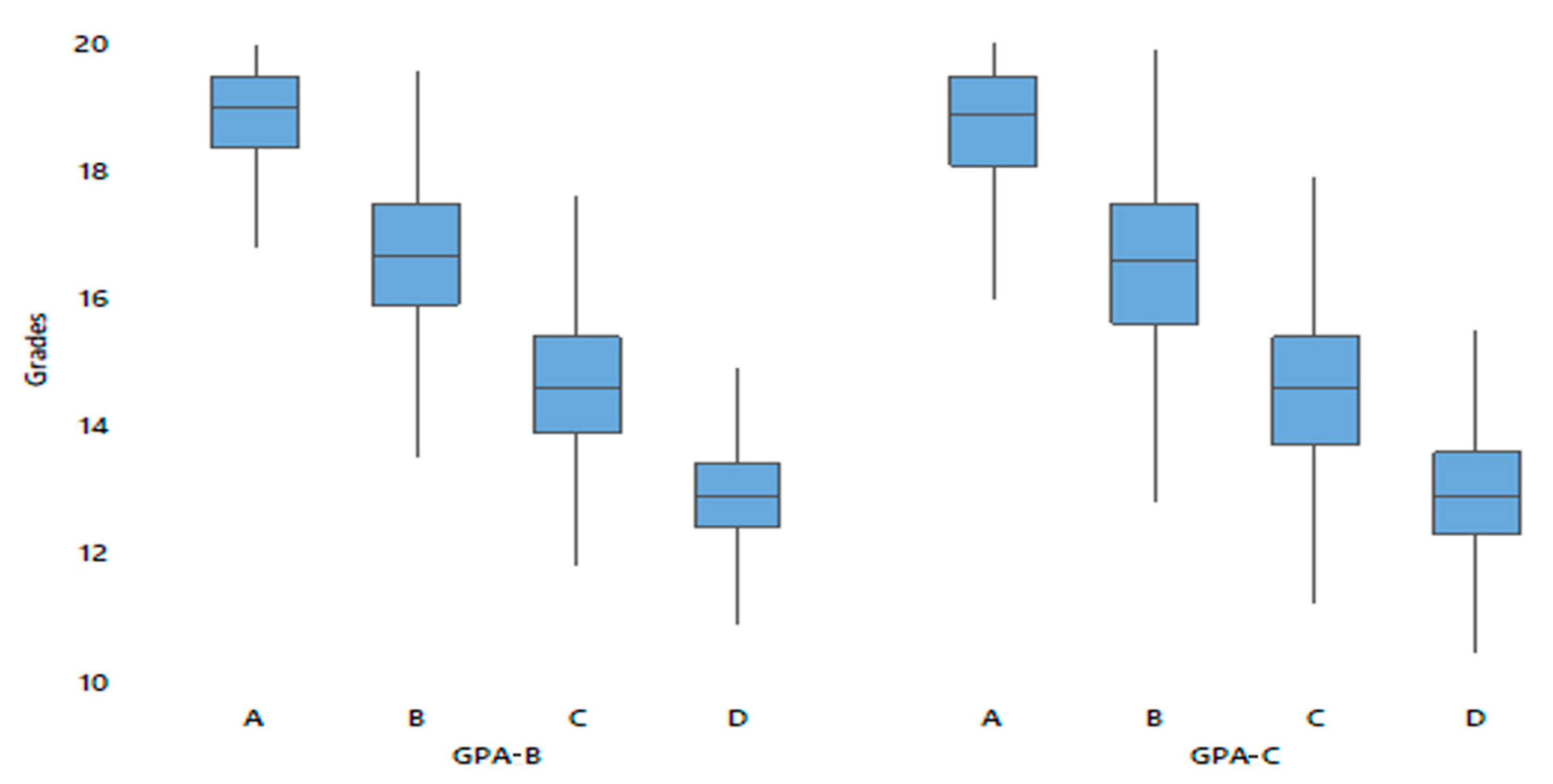
Following the same approach to the performance data of the high school students, we observe that 78.3% of the excellent first graders are still excellent in the third class of high school (

Table 14. Cluster Frequencies over time—Second Dataset.

Cluster	Class	1st_High School Cluster
		A	B	C	D
A	2nd class	83.70%	11.00%	0.10%	0.00%
	3rd class	78.30%	15.50%	0.60%	0.00%
B	2nd class	15.90%	65.70%	13.20%	0.40%
	3rd class	20.20%	60.50%	22.90%	1.40%
C	2nd class	0.40%	22.30%	60.90%	12.00%
	3rd class	1.40%	22.50%	61.00%	34.20%
D	2nd class	0.00%	0.90%	25.70%	87.60%
	3rd class	0.10%	1.50%	15.60%	64.40%

). Furthermore, a total of 21.60% of the excellent first graders reduce their performance in third class and a 16.30% in the second class. While only a few students with the best performance in the first class fell into the lowest performance category.

The trend of students classified in the low performance category is the reverse in the first high school class. Nearly two-thirds of these students are still in the same performance in the third year of high school. They improve to a small extent without being able to be classified in a category higher than B.

There are mixed trends in students who are characterized of average performance (B, C), but the largest percentage still remains at the same level of performance. From class to class, it is observed that the percentage of students who fall to lower levels of performance increases, while the percentage that manages to improve its performance decreases (Figure 4).

There is a similarity in the distribution of GPAs’ in the second and third class of high school, when they are grouped based on the performance in the first class (

Table 15. High School GPA, based on initial characterization.

Variable	A Class Cluster	Mean	SE Mean	St. Dev	Median
B class HS 1 GPA	A	18.846	0.00522	0.855	19.0
	B	16.674	0.00742	1.095	16.7
	C	14.650	0.00873	1.075	14.6
	D	12.939	0.00900	0.876	12.9
C class HS 2 GPA	A	18.716	0.00635	1.040	18.9
	B	16.525	0.00910	1.341	16.6
	C	14.610	0.01000	1.234	14.6
	D	12.996	0.00996	0.969	12.9

¹ Elementary School. ² High School.

). The averages are almost equal, while the lowest standard deviation is shown by the excellent students, as their score reaches the maximum value of the scale 0–20.

Correspondingly to the first dataset, the statistical significance of GPA differentiation was examined, based on the initial classification of students in the first class of high school, using the non-parametric Kruskal-Wallis Test. Statistically significant differences in GPA were observed between different initial classifications. of pupils (

Table 16. Independent-Samples Kruskal-Wallis Test of GPA, based on the initial classification (2nd dataset).

Class	Statistic	p-Value
1st High School	77,827.42	0.0000
2nd High School	69,654.86	0.0000
3rd High School	63,991.20	0.0000

Asymptotic significances are displayed. The significance level is 0.05.

).

3.3. Third Research Question

We like to think, as a society, that the educational system is a great equalizer that gives all children equal opportunities to excel and pursue their dreams. Should that really be the case, then demographic data that are related to the students themselves could be expected to have a correlation with academic performance, but other demographic data should ideally be uncorrelated.

In order to examine this hypothesis, for each parents’ occupation we have examined the frequency of students in each of the four levels of academic performance based and compared it to the frequencies shown in Figure 2. As the occupations in the dataset are free text, they were first manually categorized based on the International Standard Classification of Occupations (ISCO) ranking [33].

Due to the limitations of the General Data Protection Regulation (GDPR), a limited number of demographic variables have been provided, related to the socio-economic profile of the students. The differences in the profession of guardian, the gender and area where students live are examined.

3.3.1. Guardians’ Occupation

A x² statistical test was performed to identify significant differences in performance levels between the different occupations of the guardians. Differences were identified between the observed and the expected percentage, based on the frequency of each profession (x² = 603495.000, p-value < 0.0001). The professions were categorized based on the International Standard Classification of Occupations (ISCO) ranking.

Table 17. Differences between observed and expected performance of A: Very strong, D: Very weak Students (based on ISCO categorization).

ISCO	Academic Performance Level
Category	A Average/ St. Deviation	D Average/ St. Deviation
Professionals	20.72%/14.70%	−8.28%/5.12%
Armed forces occupations	13.69%/1.99%	−7.56%/2.43%
Clerical support workers	10.30%/11.62%	−5.01%/4.18%
Managers	7.23%/8.63%	−6.97%/3.42%
Technicians and associate professionals	6.26%/12.37%	−4.75%/5.46%
Service and sales workers	6.00%/13.74%	−3.45%/6.06%
Skilled agricultural. forestry and fishery workers	−4.61%/11.56%	1.97%/5.91%
Plant and machine operators and assemblers	−5.42%/5.07%	0.63%/3.14%
Craft and related trades workers	−6.03%/8.62%	0.63%/4.85%
Elementary occupations	−14.64%/5.77%	5.98%/4.27%

shows the percentage differences between observed and expected performance for the low and high-performance categories.

In Table 17 we summarize the results for the two ends of the spectrum (the very strong and the very weak academic performances).

There seems to be a divergence; higher than expected scores are received by students whose guardians are self-employed, they are teachers of all levels, officers of the armed forces, private and civil servants. On the contrary, the low level of academic performance is dominated by students whose guardians declare themselves unskilled workers, manual workers, farmers, and stockbreeders.

It is immediately obvious that our idealistic hypothesis does not hold. There are some professions whose children are more often very strong students and more rarely very weak students while for professions the exact opposite is true.

This is particularly true when it comes to the case of very strong academic performance, where the children of self-employed professionals have a much greater chance of performing well. It is this type of performance that a few years down the road will allow them to enter one of the most coveted schools and by building on it continue a path in the higher classes of society.

On the other end, children whose parents are employed in elementary occupations have a much smaller chance to follow such a path and are thus more likely to remain at the same classes.

In other words, the data shows that the Greek educational system is not in fact the great equalizer that it is claimed to be.

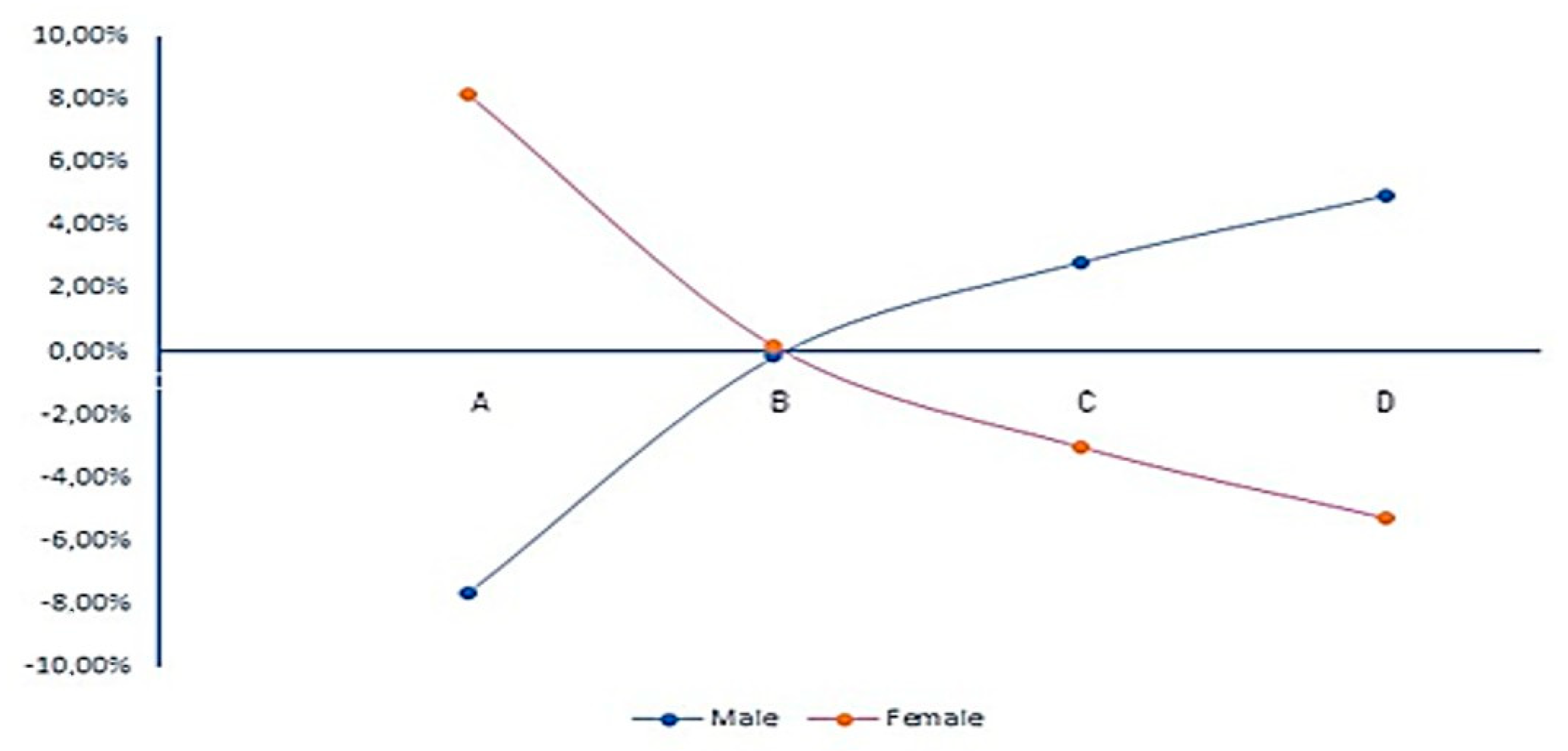
3.3.2. Gender

Using a corresponding methodology, the percentage differences between the observed and the expected frequencies of the four clusters in terms of the gender of the students were calculated. (x² = 17,514.29, p-value < 0.0001). Figure 5 shows that females have a higher frequency of high performance (8.15%) and a lower-than-expected frequency of low performance. In contrast, males show lower frequency than expected in high performance and higher in low academic performance.

3.3.3. District

The test was repeated based on the district where the students live for elementary and junior high school (x² = 6612,839, p-value < 0.0001). After calculating the percentage difference in performance, the largest and smallest differences in the high and low performance clusters were identified.

Table 18. Cluster frequencies per region.

Region	A	B	C	D
Kastoria (Pr 1.)	18.40%	−3.88%	−7.57%	−6.95%
Arta (Pr.)	16.17%	−6.20%	−6.22%	−3.75%
Rodopi (Pr.)	16.02%	−4.00%	−6.19%	−5.83%
Trikala (Pr.)	14.69%	−5.03%	−6.94%	−2.72%
Karditsa (Pr.)	13.75%	−6.85%	−10.33%	3.43%
Karditsa (Sec 2.)	11.82%	−5.08%	−2.72%	−4.02%
Chios (Pr.)	11.47%	−1.58%	−4.87%	−5.02%
Larisa (Sec.)	11.00%	−2.22%	−2.68%	−6.10%
Chios (Sec.)	10.93%	−1.01%	−5.28%	−4.65%
Kastoria (Sec.)	10.45%	0.57%	−2.49%	−8.53%
Ioannina (Pr.)	10.39%	−1.72%	−4.44%	−4.24%
Thessaloniki (Pr.)	10.13%	0.25%	−5.28%	−5.10%
Lefkada (Pr.)	−12.50%	6.95%	0.27%	5.29%
Corfu (Pr.)	−10.87%	1.69%	3.67%	5.51%
Religious Directorate	−14.17%	1.19%	6.46%	6.52%
Lasithi (Pr.)	−10.52%	−2.90%	6.42%	7.00%
Rethymnon (Sec.)	−10.31%	−1.10%	3.79%	7.62%
West Attica (Pr.)	−13.04%	−1.61%	6.02%	8.63%

¹ Primary Education. ² Secondary Education.

demonstrates the areas that show the strongest divergence in relation to high and low academic performance.

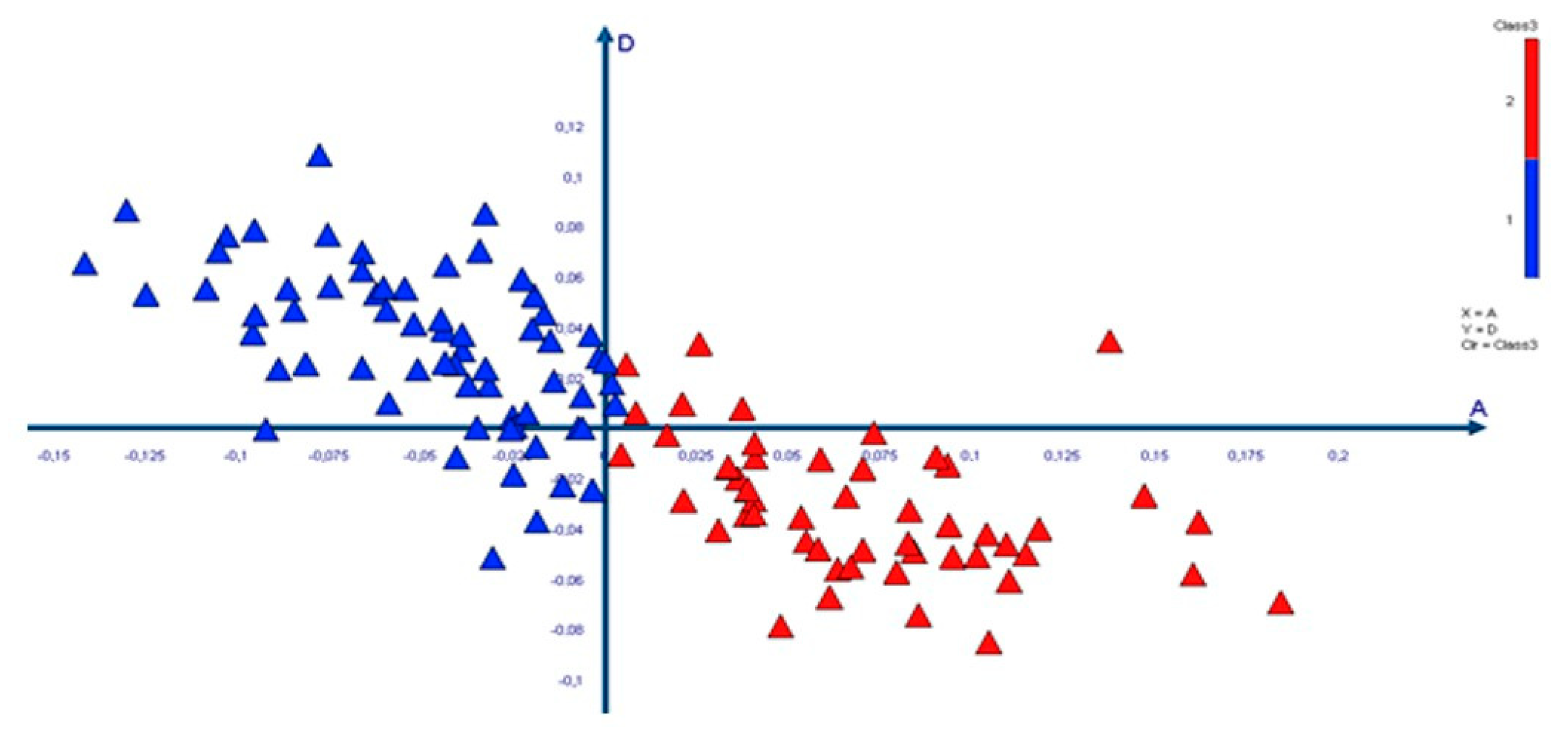
The last line in Table 18 is referred to Western Attica, an area that is degraded and in which a large number of minorities reside, such as Roma. Moreover, in high performance areas there is also a reduced percentage of low performance students and vice versa. In areas with a high rate of low D performance, the percentage of students classified as A is lower. Thus, Figure 6 includes observations mainly in the second and fourth quadrants.

4. Discussion

4.1. Educational Policy for Low-Achieving Students

The policies regarding low-achieving students in Greece refer to the provision of remedial teaching to primary school students who need “additional teaching assistance, preferably in grades A′ and B′ or have not acquired the basic reading, writing and numerical calculation mechanisms. Respectively in high school it covers subjects such as the modern Greek language, the ancient Greek language, mathematics, natural sciences, and the English language.

At the same time, actions have been developed to support students with special needs, who can attend special schools (elementary, high schools) or general education schools with corresponding support. The data of this research concerned students who attend general education schools. The educational activities for the support of students with special needs who study in general education are (1) the study in special integration departments and (2) the study in a regular class with the support of an additional teacher.

Integrating classrooms serve the theoretical framework of students’ integration values with the aim of respecting human rights, providing equal opportunities, assisting in the participation in social structures, enabling them to become as important and autonomous members of society [34]. The integration process is related to the increase of participation and equal opportunities for students, while providing appropriate support to schools in order to respond most effectively to the diversity, interests and skills of children with special educational needs or/and disability [35]. The integration departments are attended by students who, in their majority, have a medical report from an interdisciplinary team, in which it is proposed that they study in such a department [36].

In-class support is provided to students who can with appropriate individual support attend the classroom curriculum or to students with more serious educational needs when there is no other special education structure in their area or when this support becomes necessary based on the opinion of special diagnostic centers operating in the country.

Research on the results of these policies has been conducted in the past. The practical benefit of the Integrating Classrooms has been recorded in the past through the improvement of performance [37,38,39], while it was found that they also contribute to the reduction of student dropout whose main cause is school failure.

Corresponding findings are presented regarding in-class support. According to research, there has been an improvement in children’s learning skills since the presence of a second teacher in the classroom reduces the teacher-student ratio by providing a more individualized and collaborative teaching [40].

Despite the positive elements that emerged, the main argument of criticism they received is that for students that move away from their classrooms, their separation and stigma is strengthened [41]. It is also reported that there is no organized and planned process of locating students [42], while there are shortcomings in the timely treatment of educational needs resulting in many students remaining undiagnosed and the benefit of early intervention is lost.

In relation to in-class support within the regular classroom by a second teacher, ambiguities of legislation leading to misunderstandings have been reported. Furthermore, a lack of adaptations of the programs, teaching methods and practices that will aim to develop the basic skills of these children as well as organizational issues have been recorded [43].

4.2. Data for Low-Achieving Students

Due to the very wide application of the policies, we expect to see its impact in the datasets that we are examining. Remedial teaching is available to the weakest students in elementary school. Therefore, it is applied for students in the weakest group of the first dataset but not applied for students in the second dataset that only includes high school. This allows us to use the two datasets for comparisons.

Focusing on the very weak students in 5th grade, we see that a huge 36.5% of them move up to being weak (and not very weak anymore) for the next year. For comparison, the corresponding percentage for very weak students of 1st high school grade that move up to weak in the other data set is a mere 13.4%, almost one third. The difference is huge, and it is only natural to assume that this is the effect of remedial education. Perhaps it is data like this that makes the ministry assess this as a very successful measure (Figure 7).

Upon more careful consideration, we have a different opinion. Following the progress of the students for one more year we see that the majority of them (67.6%) return to being very weak students at the 1st grade of high school.

This is the only case in the two datasets where a majority changes academic level rather than remains at the same one. The only reasonable explanation we can see is that remedial education does not have a long-lasting impact on the students. It may help them get better grades in the short run, but it fails to give them the tools they need in order to successfully continue on the academic path on their own; since that was the very goal of the measure of remedial teaching, our data suggest that the measure is actually not successful.

4.3. Why This Is Important

First of all, in a country where many classes have 30 students and the average is more than 20 students per class, having an additional teacher devoted to a single student is understandably a huge financial investment. Clearly, being able to accurately assess the success of a huge investment is important. The examination of the educational data included in MIS can provide an excellent opportunity for such an evaluation.

An even better evaluation could be done using the full data of MIS, to which we have not been granted access, as these would also include the IDs of the specific students that received remedial teaching each year.

Another reason to base such an evaluation on data, is that a subjective bias is removed. Assigning the lowest grade to a student that receives remedial teaching can be thought of as an indirect help of the remedial teacher. Therefore, it is possible that more positive grades are assigned that do not necessarily correspond to reality.

More importantly, we based our reasoning on observing the differences in academic performance between the 6th grade of elementary school and the 1st grade of high school. These grades are in different schools, operating in different buildings and having different teachers. There is no exchange of information between the two schools and therefore it would be impossible for any teacher at either school to assess how remedial teaching works in the long run; they would know either only the student’s performance in elementary school or only the student’s performance in high school.

5. Conclusions

In this work we studied two educational datasets from the «My_School» MIS of the Greek Ministry of Education. The data covers consecutive years and includes records for ALL students in the examined grades in general schools, music schools and art schools. In total we have examined the progress of more than 170,000 students over a period of three years. To the best of our knowledge, it is the first time any part of this data has been made available to research; our intention with this work is to demonstrate that meaningful and useful conclusions can be drown by having data scientists work on the data.

We have presented the structure and content of the dataset, as well as the pre-processing steps taken in order to prepare it for analysis. We then started with the more conventional “static” examination of the data, which produced results in accordance with what one might expect based on the domain’s literature. Thus, we have shown that the dataset is sane. The most important result of this static analysis is the observation that there are four distinct levels of academic performance in elementary and high school. It is worth mentioning that our results also indicate that the school does not succeed in serving it social mobility role to the advertised degree, as children of the more wealthy (as estimated based on the occupation) are much more likely to do better in school.

We then proceeded to examine the same students and their academic progress over a period of time, something that we rarely see in the literature (and never with a dataset of this size). The main observation here is that students tend to remain at the same level of academic performance; good students remain good students, weak students remain weak students. We observed that many students who start as very weak in elementary school go on to become better, only to return to being very weak once they reach high school.

The stability of the percentages of students in the four groups of academic performance that emerged over time, shows corresponding stability in the factors that affect academic performance. These factors are related to internal characteristics of students which are not expected to change in the study horizon, but also to external characteristics of the educational system, such as school climate and school culture, school leadership and more. These factors have not changed [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16].

The inability to improve performance may be due to factors related to students’ internal characteristics (cognitive ability, learning motivation and many others). However, the lack of upward mobility of the category of low-performing students, combined with the lower socio-economic profile of these students, which results from the manual profession of the guardian or the specific area of residence (West Attica) shows a general weakness of this educational policy. This area is home to a significant number of minorities such as Roma. For the social integration of these minorities, education policy is an important tool, and many actions are implemented.

This research has shown that there is room for improvement in these policies. The stability of low structural performance in some areas also shows that the problem of low performance is a consistent characteristic, which needs to be investigated in-depth in order to be addressed. Our intention is to demonstrate that there is value in looking at the data and we hope that we have produced an argument strong enough to convince the ministry to include data science in its decision-making tools in the future. For our future work we intend to further examine the data that is already available to us and to try to acquire access to a richer dataset of «My_School», so that a deeper analysis is possible.

We also found that some demographic characteristics of students are not independent of their performance. However, due to the compliance with the general regulation of personal data, there was no access to additional features that may be related to performance, such as nationality and exact place of residence

In our research, the professional profile of the guardians was an important variable. There was a significant difference between students whose guardians practiced manual professions and those who practiced more spiritual (non-manual) occupations. The underperformance of students whose parents engage in manual and often low-paying occupations is, in our view, the main challenge. After all, the improvement of social mobility is a key role of education over time, which does not seem to be achieved, based on the specific data.

We believe that the issue of the possible correlation of students’ socio-economic profile with their academic performance should be the subject of a study on the effectiveness of educational policies. This effectiveness is often referred to in the function of education as a tool to reduce social inequalities.