Predictors of College Enrollment across the Life Course: Heterogeneity by Age and Gender
Abstract
1. Introduction
2. Theory and Prior Research
2.1. Accounts of Non-Traditional Enrollment
2.2. Heterogeneity by Age
2.3. Gender, Age, and Enrollment
3. Data and Methods
3.1. Data
3.2. Variables
3.3. Event History Models
4. Findings
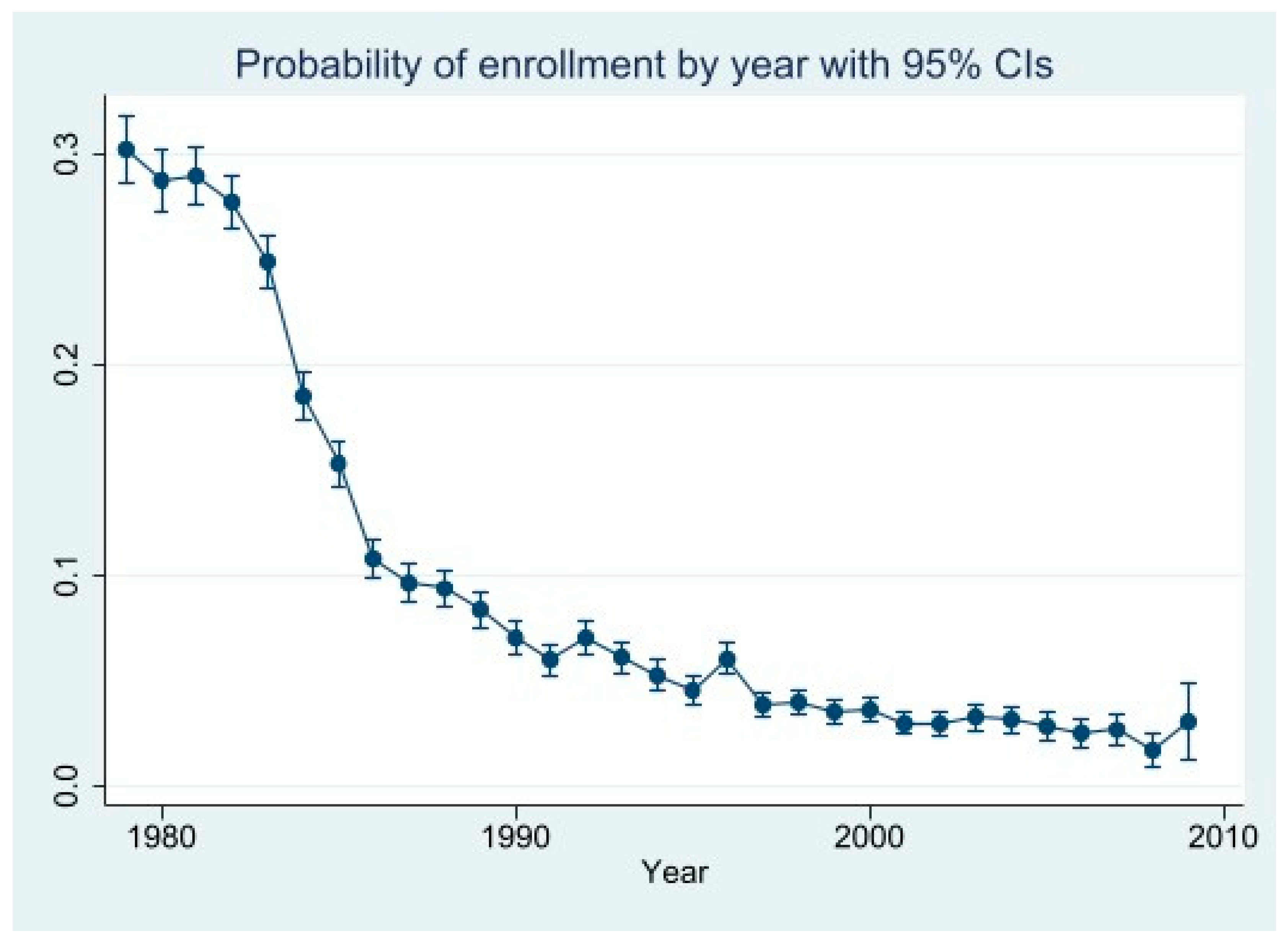
4.1. Descriptive Findings
4.2. Heterogeneity by Age Group
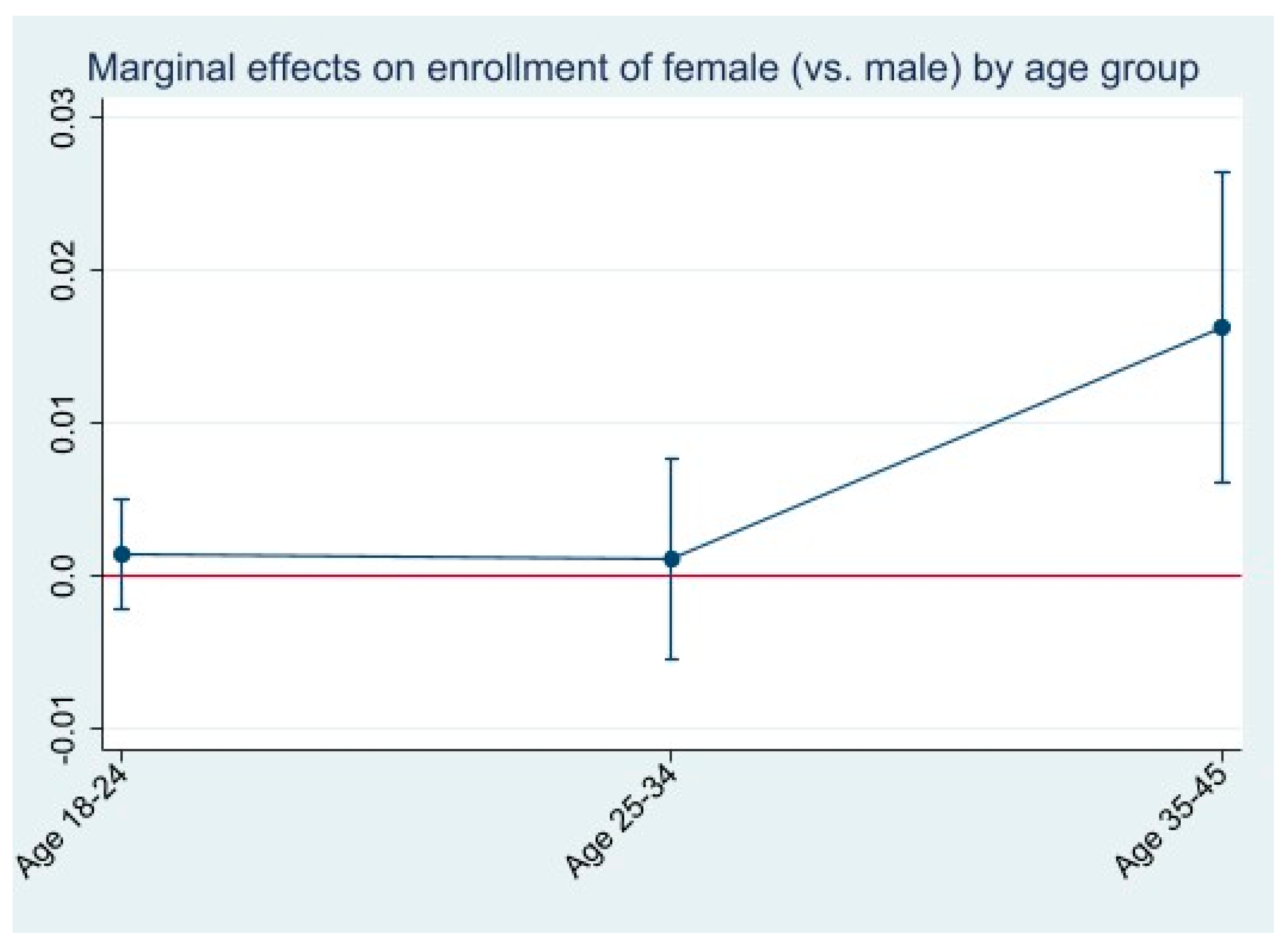
4.3. Heterogeneity by Age and Gender
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- National Center for Education Statistics Datalab. Available online: https://nces.ed.gov/datalab/index.aspx (accessed on 21 January 2020).
- Deil-Amen, R. The “traditional” college student: A smaller and smaller minority and its implications for diversity and access institutions. In Remaking College: The Changing Ecology of Higher Education; Kirst, M.W., Stevens, M.L., Eds.; Stanford University Press: Stanford, CA, USA, 2015; pp. 134–168. [Google Scholar]
- Donaldson, J.F.; Townsend, B.K. Higher education journals’ discourse about adult undergraduate students. J. Higiher Ed. 2007, 78, 27–50. [Google Scholar] [CrossRef]
- Arum, R.; Roksa, J. Academically Adrift: Limited Learning on College Campuses; University of Chicago Press: Chicago, IL, USA, 2011. [Google Scholar]
- Armstrong, E.A.; Hamilton, L.T. Paying for the Party: How College Maintains Inequality; Harvard University Press: Cambridge, MA, USA, 2013. [Google Scholar]
- Calcagno, J.C.; Crosta, P.; Bailey, T.; Jenkins, D. Does age of entrance affect community college completion probabilities? Evidence from a discrete-time hazard model. Ed. Eval. Pol. Anal. 2007, 29, 218–235. [Google Scholar] [CrossRef]
- Baum, S.; Bailey, T.; Bettinger, E.; Dynarski, S.; Hauptman, A.; Holzer, H.; Jacobs, J.; Little, K.; Long, B.T.; McPherson, M.; et al. Rethinking Pell Grants; College Board: New York, NY, USA, 2013. [Google Scholar]
- Manski, C.F. Adolescent econometricians: How do youth infer the returns to schooling. In Studies of Supply and Demand in Higher Education; Clotfelter, C., Rothschild, M., Eds.; University of Chicago Press: Chicago, IL, USA, 1993; pp. 43–60. [Google Scholar]
- Becker, G.S. Human Capital: A Theoretical and Empirical Analysis, with Special Reference to Education; University of Chicago Press: Chicago, IL, USA, 1964. [Google Scholar]
- Bourdieu, P.; Passeron, J.C. Reproduction in Education, Society and Culture; Sage: Beverly Hills, CA, USA, 1977. [Google Scholar]
- Elman, C.; Weiss, F. Adult educational participation and implications for employment in the US context. In Adult Learning in Modern Societies: An International Comparison from a Life-Course Perspective; Blossfeld, H., Kilpi-Jakonen, E., de Vilhena, D.V., Buchholz, S., Eds.; Edward Elgar: Northampton, MA, USA, 2014; pp. 79–97. [Google Scholar]
- Jepsen, C.; Montgomery, M. Back to school: An application of human capital theory for mature workers. Econ. Educ. Rev. 2012, 31, 168–178. [Google Scholar] [CrossRef]
- Monks, J. The impact of college timing on earnings. Econ. Educ. Rev. 1997, 16, 419–423. [Google Scholar] [CrossRef]
- Taniguchi, H. The influence of age at degree completion on college wage premiums. Res. Higher Educ. 2005, 46, 861–881. [Google Scholar] [CrossRef]
- Light, A. Hazard model estimates of the decision to reenroll in school. Labour Econ. 1995, 2, 381–406. [Google Scholar] [CrossRef]
- Kerckhoff, A.C.; Glennie, E. The Matthew effect in American education. Res. Soc. Educ. Social. 1999, 12, 35–66. [Google Scholar]
- Elman, C.; O’Rand, A.M. The effects of social origins, life events, and institutional sorting on adults’ school transitions. Soc. Sci. Res. 2007, 36, 1276–1299. [Google Scholar] [CrossRef]
- Bradburn, E.M.; Moen, P.; Dempster-McClain, D. Women’s return to school following the transition to motherhood. Soc. Forces 1995, 73, 1517–1551. [Google Scholar] [CrossRef]
- Astone, N.M.; Schoen, R.; Ensminger, M.; Rothert, K. School reentry in early adulthood: The case of inner-city African Americans. Soc. Educ. 2000, 73, 133–154. [Google Scholar] [CrossRef]
- Elman, C.; O’Rand, A.M. The race is to the swift: Socioeconomic origins, adult education, and wage attainment. Am. J. Soc. 2004, 110, 123–160. [Google Scholar] [CrossRef]
- Taniguchi, H.; Kaufman, G. Belated entry: Gender differences and similarities in the pattern of nontraditional college enrollment. Soc. Sci. Res. 2007, 36, 550–568. [Google Scholar] [CrossRef]
- Jacob, M.; Weiss, F. Class origin and young adults’ re-enrollment. Res. Soc. Strat. Mob. 2011, 29, 415–426. [Google Scholar] [CrossRef]
- Bean, J.P.; Metzner, B.S. A conceptual model of nontraditional undergraduate student attrition. Rev. Educ. Res. 1985, 55, 485–540. [Google Scholar] [CrossRef]
- Hostetler, A.J.; Sweet, S.; Moen, P. Gendered career paths: A life course perspective on returning to school. Sex Roles 2007, 56, 85–103. [Google Scholar] [CrossRef]
- Elder, G.H. Age differentiation and the life course. Annu. Rev. Soc. 1975, 1, 165–190. [Google Scholar] [CrossRef]
- Settersten, R.A.; Mayer, K.U. The measurement of age, age structuring, and the life course. Annu. Rev. Soc. 1997, 23, 233–261. [Google Scholar] [CrossRef]
- Neugarten, B.L.; Moore, J.W.; Lowe, J.C. Age norms, age constraints, and adult socialization. Am. J. Soc. 1965, 70, 710–717. [Google Scholar]
- Macmillan, R. ‘Constructing adulthood’: Agency and subjectivity in the transition to adulthood. Adv. Life Course Res. 2006, 11, 3–29. [Google Scholar] [CrossRef]
- Hogan, D.P. The variable order of events in the life course. Am. Soc. Rev. 1978, 43, 573–586. [Google Scholar] [CrossRef]
- Settersten, R.A. Age structuring and the rhythm of the life course. Handb. Life Course 2003, 1, 81–98. [Google Scholar]
- Erikson, E.H. Identity and the life cycle. Psychol Issue 1959, 1, 1–171. [Google Scholar]
- Reay, D.; Ball, S.; David, M. ‘It’s taking me a long time but I’ll get there in the end’: Mature students on access courses and higher education choice. Br. Educ. Res. J. 2002, 28, 5–19. [Google Scholar] [CrossRef]
- Wilsey, S.A. Comparisons of adult and traditional college-age student mothers: Reasons for college enrollment and views of how enrollment affects children. J. Coll. Stud. Dev. 2013, 54, 209–214. [Google Scholar] [CrossRef]
- McCune, V.; Hounsell, J.; Christie, H.; Cree, V.E.; Tett, L. Mature and younger students’ reasons for making the transition from further education into higher education. Teach. High. Educ. 2010, 15, 691–702. [Google Scholar] [CrossRef][Green Version]
- Bye, D.; Pushkar, D.; Conway, M. Motivation, interest, and positive affect in traditional and nontraditional undergraduate students. Adult Educ. Q. 2007, 57, 141–158. [Google Scholar] [CrossRef]
- Johnson, M.L.; Taasoobshirazi, G.; Clark, L.; Howell, L.; Breen, M. Motivations of traditional and nontraditional college students: From self-determination and attributions, to expectancy and values. J. Contin. High. Educ. 2016, 64, 3–15. [Google Scholar] [CrossRef]
- Buchmann, C.; DiPrete, T.A. The growing female advantage in college completion: The role of family background and academic achievement. Am. Soc. Rev. 2006, 71, 515–541. [Google Scholar] [CrossRef]
- Goldin, C.; Katz, L.F.; Kuziemko, I. The homecoming of American college women: The reversal of the college gender gap. J. Econ. Perspect. 2006, 20, 133–156. [Google Scholar] [CrossRef]
- DiPrete, T.A.; Buchmann, C. Gender-specific trends in the value of education and the emerging gender gap in college completion. Demography 2006, 43, 1–24. [Google Scholar] [CrossRef]
- Jacob, B.A. Where the boys aren’t: Non-cognitive skills, returns to school and the gender gap in higher education. Econ. Educ. Rev. 2002, 21, 589–598. [Google Scholar] [CrossRef]
- Owens, J. Early childhood behavior problems and the gender gap in educational attainment in the United States. Soc. Educ. 2016, 89, 236–258. [Google Scholar] [CrossRef] [PubMed]
- Goldin, C. A grand gender convergence: Its last chapter. Am. Econ. Rev. 2014, 104, 1091–1119. [Google Scholar] [CrossRef]
- Barone, C. Some things never change: Gender segregation in higher education across eight nations and three decades. Soc. Educ. 2011, 84, 157–176. [Google Scholar] [CrossRef]
- Quadlin, N. From Major Preferences to Major Choices: Gender and Logics of Major Choice. Soc. Educ. 2020, 93, 91–109. [Google Scholar] [CrossRef]
- Morris, E.W. “Rednecks,”“Rutters,” and Rithmetic: Social Class, Masculinity, and Schooling in a Rural Context. Gend. Soc. 2008, 22, 728–751. [Google Scholar] [CrossRef]
- Heyder, A.; Kessels, U. Is school feminine? Implicit gender stereotyping of school as a predictor of academic achievement. Sex Roles 2013, 69, 605–617. [Google Scholar] [CrossRef]
- Wells, R.S.; Bills, D.B.; Devlin, M.E. The work-to-college transition: Postsecondary expectations and enrolment for young men and women in the US labour force. J. Vocat. Educ. Train. 2014, 66, 113–134. [Google Scholar] [CrossRef]
- Monaghan, D.B. Surviving the Gauntlet: Adult Undergraduates in American Higher Education. Doctoral Dissertation, CUNY Graduate Center, New York, NY, USA, 2015. [Google Scholar]
- Denice, P. Back to school: Racial and gender differences in adults’ participation in formal schooling, 1978–2013. Demography 2017, 54, 1147–1173. [Google Scholar] [CrossRef]
- Marks, A.; Turner, E.; Osborne, M. ‘Not for the likes of me’: The overlapping effect of social class and gender factors in the decision made by adults not to participate in higher education. J. Furth. High. Educ. 2003, 27, 347–364. [Google Scholar] [CrossRef]
- Wainwright, E.; Marandet, E. Parents in higher education: Impacts of university learning on the self and the family. Educ. Rev. 2010, 62, 449–465. [Google Scholar] [CrossRef]
- Ciocca Eller, C.; DiPrete, T.A. The paradox of persistence: Explaining the Black-White gap in bachelor’s degree completion. Am. Soc. Rev. 2018, 83, 1171–1214. [Google Scholar] [CrossRef]
- Citro, C.; Michaels, R. Measuring Poverty: A New Approach; National Academies Press: Washington, DC, USA, 1995. [Google Scholar]
- Sacerdote, B. Peer effects in education: How might they work, how big are they and how much do we know thus far? Handb. Econ. Educ. 2011, 3, 249–277. [Google Scholar]
- Elman, C.; O’Rand, A.M. Perceived job insecurity and entry into work-related education and training among adult workers. Soc. Sci. Res. 2002, 31, 49–76. [Google Scholar] [CrossRef]
- Box-Steffensmeier, J.M.; Zorn, C. Duration models for repeated events. J. Pol. 2002, 64, 1069–1094. [Google Scholar] [CrossRef]
- Box-Steffensmeier, J.M.; Jones, B.S. Event History Modeling: A Guide for Social Scientists; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Bennett, P.R.; Lutz, A. How African American is the net black advantage? Differences in college attendance among immigrant blacks, native blacks, and whites. Soc. Educ. 2009, 82, 70–100. [Google Scholar] [CrossRef]
- Royster, D. Race and the Invisible Hand: How White Networks Exclude Black Men from Blue-Collar Jobs; University of California Press: Berkeley, CA, USA, 2003. [Google Scholar]
- Alexander, K.; Entwisle, D.; Olson, L. The Long Shadow: Family Background, Disadvantaged Urban Youth, and the Transition to Adulthood; Russell Sage: New York, NY, USA, 2014. [Google Scholar]
| Age | Frequency | Age | Frequency |
|---|---|---|---|
| 18 | 4746 | 32 | 7148 |
| 19 | 5980 | 33 | 7118 |
| 20 | 7036 | 34 | 7077 |
| 21 | 7985 | 35 | 7053 |
| 22 | 8817 | 36 | 6963 |
| 23 | 8206 | 37 | 6865 |
| 24 | 7804 | 38 | 6775 |
| 25 | 7591 | 39 | 6674 |
| 26 | 7468 | 40 | 6588 |
| 27 | 7382 | 41 | 6490 |
| 28 | 7332 | 42 | 6379 |
| 29 | 7273 | 43 | 6275 |
| 30 | 7235 | 44 | 6184 |
| 31 | 7183 | 45 | 6049 |
| Mean | SD | Min | Max | |
|---|---|---|---|---|
| Ever enrolled | 0.58 | 0 | 1 | |
| Earned bachelor’s | 0.30 | 0 | 1 | |
| Female | 0.46 | 0 | 1 | |
| White | 0.80 | 0 | 1 | |
| Latinx | 0.05 | 0 | 1 | |
| Black | 0.13 | 0 | 1 | |
| Parental education = Less than HS | 0.25 | 0 | 1 | |
| Parental education = HS gradute | 0.41 | 0 | 1 | |
| Parental education = Some college | 0.12 | 0 | 1 | |
| Parental education = bachelor’s/higher | 0.20 | 0 | 1 | |
| 1979 Family income (proportion of median) | 0.92 | 0.85 | 0 | 35.38 |
| Dropped out HS | 0.17 | 0 | 1 | |
| Average HS grades | 3.47 | 0.92 | 1 | 7 |
| School disadvantage | −0.15 | 0.72 | −2.69 | 9.22 |
| AFQT score | 49.29 | 28.99 | −35.38 | 112.82 |
| Discipline problem in HS | 0.21 | 0 | 1 | |
| Traditional gender values (1979) | 2.32 | 0.82 | 0.22 | 5 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Female | 0.998 | 0.959 | 1.005 |
| (0.026) | (0.027) | (0.029) | |
| Latinx | 1.143 *** | 1.383 *** | 1.353 *** |
| (0.041) | (0.057) | (0.057) | |
| Black | 0.991 | 1.405 *** | 1.306 *** |
| (Ref = White/other) | (0.029) | (0.057) | (0.055) |
| Parental education = HS | 1.580 *** | 1.276 *** | 1.292 *** |
| (0.076) | (0.061) | (0.064) | |
| Parental education = Some college | 1.842 *** | 1.443 *** | 1.429 *** |
| (0.100) | (0.078) | (0.080) | |
| Parental education = Bachelor’s/more | 2.341 *** | 1.625 *** | 1.566 *** |
| (Ref = Less than HS) | (0.125) | (0.087) | (0.087) |
| Family income 1979 | 1.152 *** | 1.068 ** | 1.057 * |
| (0.024) | (0.023) | (0.023) | |
| Ever dropped out HS | 0.382 *** | 0.393 *** | |
| (0.037) | (0.039) | ||
| HS grades | 1.142 *** | 1.130 *** | |
| (0.026) | (0.025) | ||
| Disadvantaged HS peers | 0.960 | 0.964 | |
| (0.022) | (0.022) | ||
| AFQT | 1.011 *** | 1.011 *** | |
| (0.001) | (0.001) | ||
| Discipline problem in HS | 0.815 *** | 0.824 *** | |
| (0.038) | (0.037) | ||
| Traditional gender beliefs | 0.927 *** | 0.937 ** | |
| (0.019) | (0.019) | ||
| Cumulative experience (years) | 0.872 *** | ||
| (0.012) | |||
| Involuntary unemployment (lag) | 1.059 * | ||
| (0.030) | |||
| Never married | 1.489 *** | ||
| (0.068) | |||
| Formerly married | 1.683 *** | ||
| (Ref = currently married) | (0.19) | ||
| Youngest child 0–5 years | 0.726 *** | ||
| (0.042) | |||
| Youngest child 6–12 years | 1.107 | ||
| (0.232) | |||
| GDP growth (lag) | 0.984 ** | ||
| (0.005) | |||
| Age | 0.172 *** | 0.159 *** | 0.140 *** |
| (0.0342) | (0.034) | (0.031) | |
| Age squared | 1.038 *** | 1.040 *** | 1.045 *** |
| (0.004) | (0.005) | (0.005) | |
| Years since school | 0.844 * | 0.887 | 0.934 |
| (0.058) | (0.060) | (0.067) | |
| Years since school squared | 0.983 | 0.961 | 0.962 |
| (0.034) | (0.026) | (0.030) | |
| Years since school cubed | 1.000 | 1.005 | 1.004 |
| (0.004) | (0.003) | (0.003) | |
| Prior enrollments | 1.344 *** | 1.267 *** | 1.260 *** |
| (0.023) | (0.024) | (0.024) | |
| Enrolled prior year | 4.017 *** | 3.536 *** | 3.496 *** |
| (0.209) | (0.194) | (0.195) | |
| Year | 0.971 *** | 0.973 *** | 0.994 |
| (0.007) | (0.007) | (0.007) | |
| Observations | 50,574 | 50,574 | 50,574 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Female | 1.052 | 1.036 | 1.021 |
| (0.043) | (0.047) | (0.046) | |
| Latinx | 0.948 | 1.076 | 1.081 |
| (0.049) | (0.062) | (0.063) | |
| Black | 0.864 ** | 1.041 | 0.990 |
| (Ref = White/other) | (0.038) | (0.060) | (0.060) |
| Parental education = HS | 1.024 | 0.954 | 0.971 |
| (0.060) | (0.057) | (0.058) | |
| Parental education = Some college | 1.078 | 0.994 | 1.001 |
| (0.074) | (0.073) | (0.074) | |
| Parental education = Bachelor’s/more | 1.196 * | 1.055 | 1.048 |
| (Ref = Less than HS) | (0.086) | (0.075) | (0.074) |
| Family income 1979 | 0.984 | 0.946 | 0.955 |
| (0.033) | (0.033) | (0.033) | |
| Ever dropped out HS | 0.934 | 0.879 | |
| (0.072) | (0.066) | ||
| HS grades | 1.088 * | 1.088 * | |
| (0.037) | (0.037) | ||
| Disadvantaged HS peers | 0.929 * | 0.926 * | |
| (0.029) | (0.029) | ||
| AFQT | 1.005 *** | 1.006 *** | |
| (0.001) | (0.001) | ||
| Discipline problem in HS | 0.999 | 0.992 | |
| (0.059) | (0.060) | ||
| Traditional gender beliefs | 0.928 ** | 0.935 * | |
| (0.026) | (0.026) | ||
| Cumulative experience (years) | 0.972 *** | ||
| (0.0060) | |||
| Involuntary unemployment (lag) | 1.114 | ||
| (0.062) | |||
| Never married | 1.097 | ||
| (0.060) | |||
| Formerly married | 1.125 | ||
| (Ref = currently married) | (0.071) | ||
| Youngest child 0–5 years | 0.831 *** | ||
| (0.041) | |||
| Youngest child 6–12 years | 1.102 | ||
| (0.079) | |||
| GDP growth (lag) | 0.967 ** | ||
| (0.010) | |||
| Age | 0.916 | 0.934 | 1.013 |
| (0.145) | (0.147) | (0.161) | |
| Age Squared | 1.001 | 1.000 | 0.999 |
| (0.002) | (0.003) | (0.002) | |
| Years since school | 0.617 *** | 0.625 *** | 0.644 *** |
| (0.040) | (0.041) | (0.042) | |
| Years since school squared | 1.029 ** | 1.029 ** | 1.026 * |
| (0.011) | (0.011) | (0.010) | |
| Years since school cubed | 0.999 | 0.999 | 0.999 |
| (0.001) | (0.001) | (0.001) | |
| Prior enrollments | 1.128 *** | 1.115 *** | 1.115 *** |
| (0.012) | (0.013) | (0.013) | |
| Enrolled prior year | 2.232 *** | 2.269 *** | 2.322 *** |
| (0.239) | (0.245) | (0.251) | |
| Year | 1.025 ** | 1.029 ** | 1.040 *** |
| (0.009) | (0.009) | (0.009) | |
| Observations | 72,807 | 72,807 | 72,807 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Female | 1.361 *** | 1.393 *** | 1.349 *** |
| (0.095) | (0.101) | (0.097) | |
| Latinx | 1.092 | 1.189 * | 1.202 * |
| (0.072) | (0.089) | (0.089) | |
| Black | 1.047 | 1.183 * | 1.201 * |
| (Ref = White/other) | (0.062) | (0.095) | (0.097) |
| Parental education = HS | 1.094 | 1.061 | 1.067 |
| (0.075) | (0.073) | (0.073) | |
| Parental education = Some college | 1.152 | 1.102 | 1.106 |
| (0.111) | (0.115) | (0.116) | |
| Parental education = Bachelor’s/more | 1.310 ** | 1.214 | 1.225 |
| (Ref = Less than HS) | (0.135) | (0.132) | (0.135) |
| Family income 1979 | 0.947 | 0.926 | 0.922 |
| (0.046) | (0.043) | (0.044) | |
| Ever dropped out HS | 0.993 | 0.970 | |
| (0.103) | (0.098) | ||
| HS grades | 1.025 | 1.025 | |
| (0.041) | (0.041) | ||
| Disadvantaged HS peers | 0.965 | 0.959 | |
| (0.042) | (0.041) | ||
| AFQT | 1.004 * | 1.004 * | |
| (0.001) | (0.001) | ||
| Discipline problem in HS | 1.032 | 1.032 | |
| (0.090) | (0.089) | ||
| Traditional gender beliefs | 1.018 | 1.009 | |
| (0.038) | (0.039) | ||
| Cumulative experience (years) | 0.996 | ||
| (0.005) | |||
| Involuntary unemployment (lag) | 1.277 ** | ||
| (0.117) | |||
| Never married | 0.834 * | ||
| (0.067) | |||
| Formerly married | 0.952 | ||
| (Ref = currently married) | (0.065) | ||
| Youngest child 0–5 years | 0.809 * | ||
| (0.072) | |||
| Youngest child 6–12 years | 1.067 | ||
| (0.072) | |||
| GDP growth (lag) | 0.955 * | ||
| (0.021) | |||
| Age | 0.665 | 0.640 * | 0.687 |
| (0.150) | (0.145) | (0.157) | |
| Age squared | 1.005 | 1.006 * | 1.005 |
| (0.002) | (0.002) | (0.003) | |
| Years since school | 0.704 *** | 0.698 *** | 0.702 *** |
| (0.035) | (0.035) | (0.035) | |
| Years since school squared | 1.015 ** | 1.016 ** | 1.016 ** |
| (0.005) | (0.005) | (0.005) | |
| Years since school cubed | 1.000 * | 1.000 * | 1.000 * |
| (0.001) | (0.0001) | (0.0001) | |
| Prior enrollments | 1.062 *** | 1.057 *** | 1.063 *** |
| (0.012) | (0.013) | (0.013) | |
| Enrolled prior year | 2.976 *** | 2.950 *** | 2.925 *** |
| (0.396) | (0.393) | (0.390) | |
| Year | 0.997 | 0.996 | 1.000 |
| (0.012) | (0.012) | (0.012) | |
| Observations | 72,295 | 72,295 | 72,295 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Ages 18–24 | Ages 25–34 | Ages 35–45 | |
| Latinx | 1.375 *** | 1.116 | 1.204 * |
| (0.078) | (0.084) | (0.107) | |
| Black | 1.281 *** | 1.049 | 1.178 |
| (Ref = White/other) | (0.073) | (0.077) | (0.109) |
| Parental education = HS | 1.279 *** | 0.849 * | 0.996 |
| (0.088) | (0.064) | (0.078) | |
| Parental education = Some college | 1.459 *** | 0.793 * | 0.983 |
| (0.113) | (0.071) | (0.104) | |
| Parental education = Bachelor’s/more | 1.674 *** | 0.826 * | 0.848 |
| (Ref = Less than HS) | (0.130) | (0.077) | (0.098) |
| Family income 1979 | 1.023 | 1.049 | 0.988 |
| (0.031) | (0.041) | (0.051) | |
| Ever dropped out HS | 0.483 *** | 0.881 | 0.971 |
| (0.064) | (0.096) | (0.115) | |
| HS grades | 1.124 *** | 1.098 * | 1.000 |
| (0.035) | (0.050) | (0.045) | |
| Disadvantaged HS peers | 0.968 | 0.913 * | 0.942 |
| (0.028) | (0.036) | (0.054) | |
| AFQT | 1.009 *** | 1.004 ** | 1.003 |
| (0.001) | (0.001) | (0.002) | |
| Discipline problem in HS | 0.870 * | 1.013 | 0.994 |
| (0.056) | (0.081) | (0.096) | |
| Traditional gender beliefs | 0.898 *** | 0.954 | 0.973 |
| (0.025) | (0.034) | (0.046) | |
| Cumulative experience (years) | 0.914 *** | 0.984 | 1.003 |
| (0.020) | (0.009) | (0.006) | |
| Involuntary unemployment (lag) | 1.040 | 1.201 * | 1.265 * |
| (0.040) | (0.094) | (0.131) | |
| Never married | 1.651 *** | 1.139 | 0.784 * |
| (0.094) | (0.078) | (0.078) | |
| Formerly married | 1.814 *** | 1.357 *** | 1.006 |
| (Re f= currently married) | (0.256) | (0.101) | (0.078) |
| Youngest child 0–5 years | 0.674 *** | 0.824 ** | 0.817 |
| (0.051) | (0.055) | (0.091) | |
| Youngest child 6–12 years | 1.001 | 1.120 | 1.175 * |
| (0.246) | (0.085) | (0.089) | |
| GDP growth (lag) | 0.992 | 0.971 * | 0.928 ** |
| (0.007) | (0.013) | (0.023) | |
| Age | 0.154 *** | 1.330 | 0.499 * |
| (0.045) | (0.273) | (0.137) | |
| Age squared | 1.043 *** | 0.995 | 1.009 * |
| (0.007) | (0.003) | (0.003) | |
| Years since school | 0.918 | 0.657 *** | 0.706 *** |
| (0.087) | (0.055) | (0.042) | |
| Years since school squared | 0.955 | 1.025 | 1.015 * |
| (0.040) | (0.013) | (0.005) | |
| Years since school cubed | 1.005 | 0.999 | 1.000 |
| (0.005) | (0.0005) | (0.0001) | |
| Prior enrollments | 1.259 *** | 1.120 *** | 1.067 *** |
| (0.033) | (0.017) | (0.014) | |
| Enrolled prior year | 3.192 *** | 2.199 *** | 2.596 *** |
| (0.234) | (0.302) | (0.400) | |
| Year | 0.988 | 1.023* | 0.991 |
| (0.010) | (0.012) | (0.015) | |
| Observations | 25,157 | 36,429 | 35,984 |
| (1) | (2) | (3) | |
|---|---|---|---|
| Variables | Ages 18–24 | Ages 25–35 | Ages 35–45 |
| Latinx | 1.318 *** | 1.118 | 1.173 |
| (0.0814) | (0.0961) | (0.148) | |
| Black | 1.320 *** | 0.968 | 1.230 |
| (Ref = White/other) | (0.0812) | (0.0885) | (0.193) |
| Parental education = HS | 1.291 *** | 1.191 * | 1.298 |
| (0.0914) | (0.102) | (0.191) | |
| Parental education = Some college | 1.397 *** | 1.336 ** | 1.489 |
| (0.115) | (0.146) | (0.338) | |
| Parental education = Bachelor’s/more | 1.483 *** | 1.381 ** | 1.943 ** |
| (Ref = Less than HS) | (0.118) | (0.136) | (0.399) |
| Family income 1979 | 1.081 * | 0.862 ** | 0.889 |
| (0.0332) | (0.0485) | (0.0802) | |
| Ever dropped out HS | 0.319 *** | 0.952 | 1.055 |
| (0.0456) | (0.0964) | (0.183) | |
| HS grades | 1.138 *** | 1.075 | 1.059 |
| (0.0358) | (0.0519) | (0.0732) | |
| Disadvantaged HS peers | 0.958 | 0.934 | 1.015 |
| (0.0319) | (0.0481) | (0.0821) | |
| AFQT | 1.012 *** | 1.007 *** | 1.005 |
| (0.00117) | (0.00175) | (0.00352) | |
| Discipline problem in HS | 0.808 *** | 1.000 | 1.132 |
| (0.0495) | (0.0824) | (0.167) | |
| Traditional gender beliefs | 0.977 | 0.907 * | 1.069 |
| (0.0288) | (0.0384) | (0.0715) | |
| Cumulative experience (years) | 0.839 *** | 0.974 ** | 0.986 |
| (0.0154) | (0.00808) | (0.00752) | |
| Involuntary unemployment (lag) | 1.073 | 1.063 | 1.350 |
| (0.0438) | (0.0837) | (0.243) | |
| Never married | 1.301 *** | 1.051 | 0.906 |
| (0.0959) | (0.0901) | (0.115) | |
| Formerly married | 1.453 * | 0.776 * | 0.820 |
| (Ref = currently married) | (0.274) | (0.0858) | (0.113) |
| Youngest child 0–5 years | 0.824 * | 0.837 * | 0.759 |
| (0.0732) | (0.0606) | (0.109) | |
| Youngest child 6–12 years | 1.478 | 0.981 | 0.903 |
| (0.611) | (0.139) | (0.110) | |
| GDP growth (lag) | 0.977 ** | 0.963 * | 1.032 |
| (0.00812) | (0.0155) | (0.0413) | |
| Age | 0.137 *** | 0.779 | 1.388 |
| (0.0438) | (0.192) | (0.557) | |
| Age squared | 1.046 *** | 1.003 | 0.996 |
| (0.00782) | (0.00423) | (0.00502) | |
| Years since school | 0.947 | 0.629 *** | 0.698 *** |
| (0.102) | (0.0653) | (0.0679) | |
| Years since school squared | 0.969 | 1.029 | 1.019 |
| (0.0451) | (0.0171) | (0.0103) | |
| Years since school cubed | 1.003 | 0.999 | 1.000 |
| (0.00593) | (0.000742) | (0.000291) | |
| Prior enrollments | 1.268 *** | 1.115 *** | 1.061 * |
| (0.0353) | (0.0202) | (0.0274) | |
| Enrolled prior year | 3.721 *** | 2.386 *** | 3.706 *** |
| (0.306) | (0.403) | (1.009) | |
| Year | 0.999 | 1.058 *** | 1.012 |
| (0.0113) | (0.0150) | (0.0223) | |
| Observations | 25,417 | 36,378 | 36,311 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monaghan, D.B. Predictors of College Enrollment across the Life Course: Heterogeneity by Age and Gender. Educ. Sci. 2021, 11, 344. https://doi.org/10.3390/educsci11070344
Monaghan DB. Predictors of College Enrollment across the Life Course: Heterogeneity by Age and Gender. Education Sciences. 2021; 11(7):344. https://doi.org/10.3390/educsci11070344
Chicago/Turabian StyleMonaghan, David B. 2021. "Predictors of College Enrollment across the Life Course: Heterogeneity by Age and Gender" Education Sciences 11, no. 7: 344. https://doi.org/10.3390/educsci11070344
APA StyleMonaghan, D. B. (2021). Predictors of College Enrollment across the Life Course: Heterogeneity by Age and Gender. Education Sciences, 11(7), 344. https://doi.org/10.3390/educsci11070344





