The Effects of a Multicomponent Motivational System Intervention Using Peer-Tutoring for Implementation on the Automation of Single-Digit Addition Tasks of Four Struggling Elementary Students
Abstract
1. Introduction
1.1. The Importance of Addition Fact Fluency
1.2. Ways to Foster Math Fact Fluency
1.3. Peer Tutoring as a Means to Implement Effective Interventions under Real-Life Conditions
1.4. Research Question
2. Method
2.1. Participants and Setting
2.2. Experimental Design
2.3. Dependent Variable and Measurement
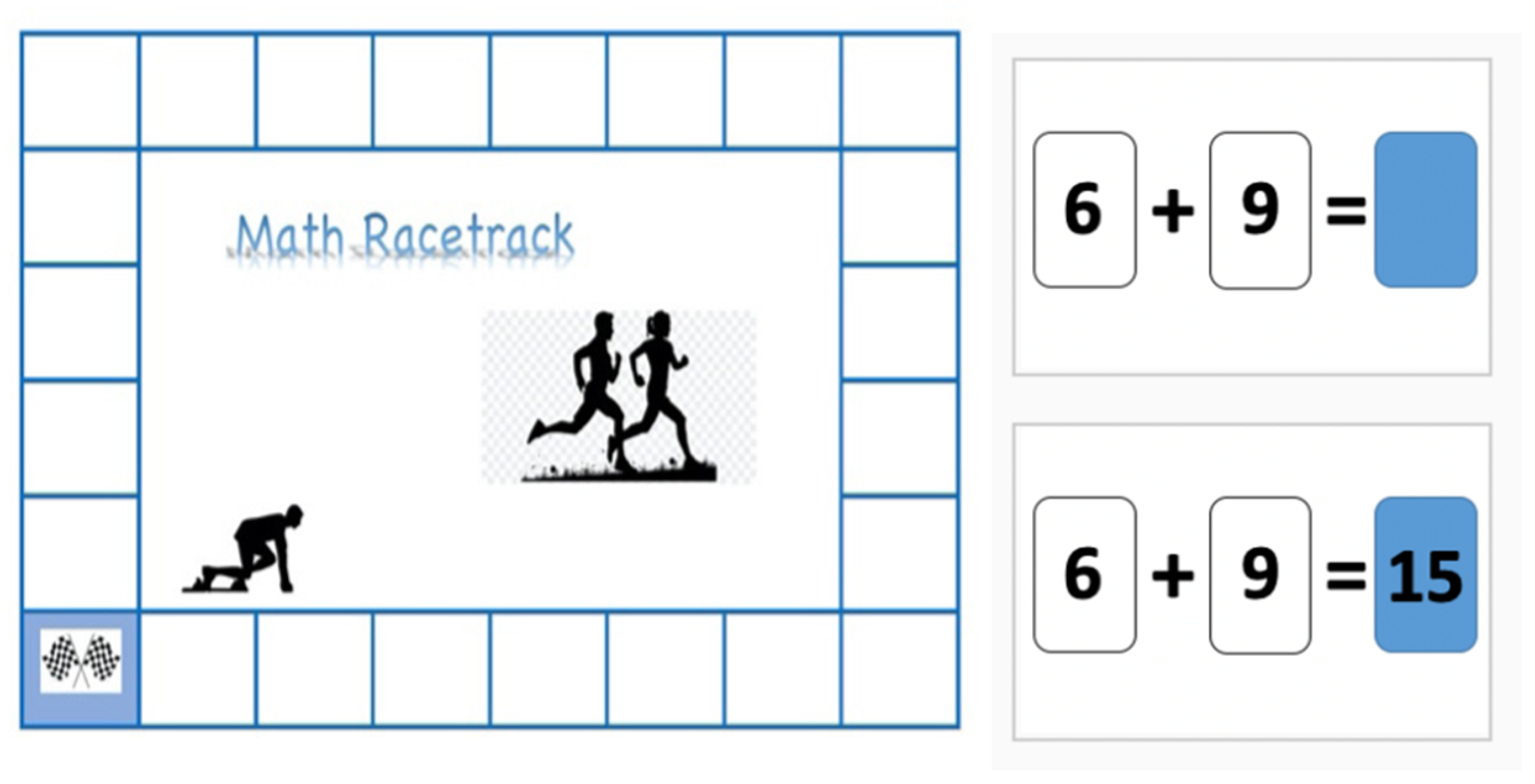
2.4. Materials and Procedures
2.5. Treatment Fidelity and Social Validity
3. Results
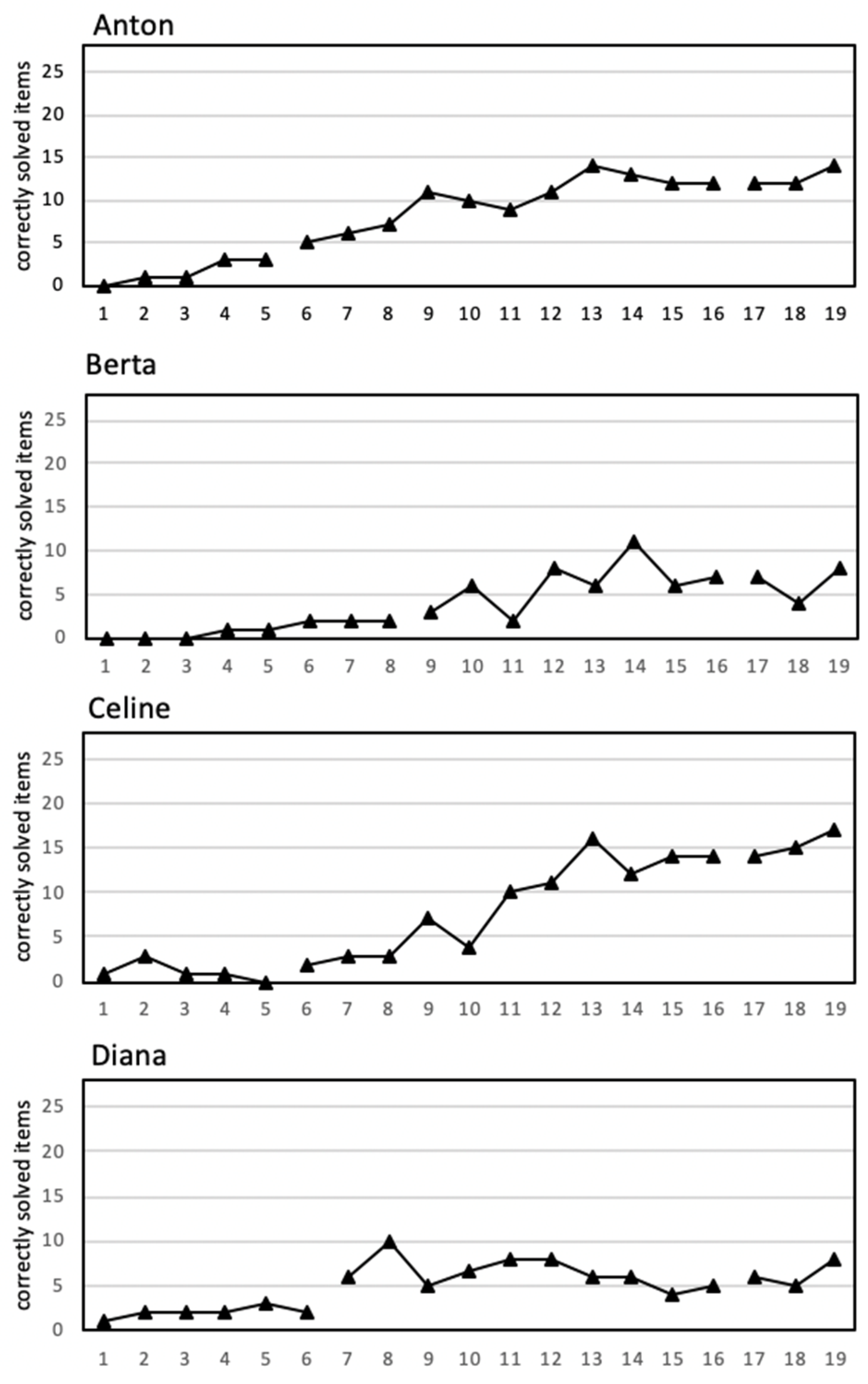
3.1. Visual Analysis
3.2. Quantitative Analysis
4. Discussion
4.1. Main Findings
4.2. Limitations
4.3. Practical Implications and Future Research
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ketterlin-Geller, L.R.; Chard, D.J. Algebra readiness for students with learning difficulties in grades 4–8: Support through the study of number. Aust. J. Learn. Difficulties 2011, 16, 65–78. [Google Scholar] [CrossRef]
- Watts, T.W.; Duncan, G.J.; Siegler, R.S.; Davis-Kean, P.E. What’s Past Is Prologue: Relations between early mathematics knowledge and high school achievement. Educ. Res. 2014, 43, 352–360. [Google Scholar] [CrossRef]
- Bowman, J.A.; McDonnell, J.; Ryan, J.H.; Fudge-Coleman, O. Effective Mathematics Instruction for Students with Moderate and Severe Disabilities: A Review of the Literature. Focus Autism Other Dev. Disabil. 2019, 34, 195–204. [Google Scholar] [CrossRef]
- Jitendra, A.K.; Alghamdi, A.; Edmunds, R.; McKevett, N.; Mouanoutoua, J.; Roesslein, R. The Effects of Tier 2 Mathematics Interventions for Students with Mathematics Difficulties: A Meta-Analysis. Except. Child. 2020, 87, 307–325. [Google Scholar] [CrossRef]
- Cumming, J.J.; Elkins, J. Lack of Automaticity in the Basic Addition Facts as a Characteristic of Arithmetic Learning Problems and Instructional Needs. Math. Cogn. 1999, 5, 149–180. [Google Scholar] [CrossRef]
- Fuchs, L.S.; Compton, D.L.; Fuchs, D.; Paulsen, K.; Bryant, J.D.; Hamlett, C.L. The Prevention, Identification, and Cognitive Determinants of Math Difficulty. J. Educ. Psychol. 2005, 97, 493–513. [Google Scholar] [CrossRef]
- National Center for Education Statistics. Nation’s Report Card. National Assessment of Educational Progress; U.S. Department of Education, Institute of Education Sciences: Washington, DC, USA, 2019.
- Hopkins, S.; Russo, J.; Siegler, R. Is counting hindering learning? An investigation into children’s proficiency with simple addition and their flexibility with mental computation strategies. Math. Think. Learn. 2020, 1–18. [Google Scholar] [CrossRef]
- Hopkins, S.; Bayliss, D. The Prevalence and Disadvantage of Min-Counting in Seventh Grade: Problems with Confidence As Well As Accuracy? Math. Think. Learn. 2017, 19, 19–32. [Google Scholar] [CrossRef]
- Aud, S.; Hussar, W.; Kena, G.; Bianco, K.; Frohlich, L.; Kemp, J.; Tahan, K. The Condition of Education 2011 (NCES 2011-033); U.S. Government Printing Office: Washington, DC, USA, 2011.
- National Mathematics Advisory Panel (NMAP). Foundations for Success: The Final Report of the National Mathematics Advisory Panel; U.S. Department of Education: Washington, DC, USA, 2008.
- Geary, D.C. Cognitive predictors of achievement growth in mathematics: A 5-year longitudinal study. Dev. Psychol. 2011, 47, 1539–1552. [Google Scholar] [CrossRef] [PubMed]
- Nelson, P.M.; Parker, D.C.; Zaslofsky, A.F. The Relative Value of Growth in Math Fact Skills across Late Elementary and Middle School. Assess. Eff. Interv. 2016, 41, 184–192. [Google Scholar] [CrossRef]
- Musti-Rao, S.; Plati, E. Comparing Two Classwide Interventions: Implications of Using Technology for Increasing Multiplication Fact Fluency. J. Behav. Educ. 2015, 24, 418–437. [Google Scholar] [CrossRef]
- Steel, S.; Funnell, E. Learning Multiplication Facts: A Study of Children Taught by Discovery Methods in England. J. Exp. Child Psychol. 2001, 79, 37–55. [Google Scholar] [CrossRef]
- Alloway, T.P. Working Memory, but Not IQ, Predicts Subsequent Learning in Children with Learning Difficulties. Eur. J. Psychol. Assess. 2009, 25, 92–98. [Google Scholar] [CrossRef]
- Geary, D.C. Development of Mathematical Understanding. In Handbook of Child Psychology; Wiley: Hoboken, NJ, USA, 2007; pp. 777–810. Available online: https://onlinelibrary.wiley.com/doi/full/10.1002/9780470147658.chpsy0218 (accessed on 7 May 2021).
- Passolunghi, M.C.; Siegel, L.S. Working memory and access to numerical information in children with disability in mathematics. J. Exp. Child Psychol. 2004, 88, 348–367. [Google Scholar] [CrossRef]
- Tournaki, N. The Differential Effects of Teaching Addition through Strategy Instruction Versus Drill and Practice to Students With and Without Learning Disabilities. J. Learn. Disabil. 2003, 36, 449–458. [Google Scholar] [CrossRef]
- Cozard, L.E.; Riccomini, P.J. Effects of digital-based math fluency interventions on learners with math difficulties: A review of the literature. J. Spec. Educ. Apprenticesh. 2016, 5, Available. Available online: https://scholarworks.lib.csusb.edu/josea/vol5/iss2/2 (accessed on 26 May 2021).
- Bouck, E.C.; Park, J. A Systematic Review of the Literature on Mathematics Manipulatives to Support Students with Disabilities. Educ. Treat. Child. 2018, 41, 65–106. [Google Scholar] [CrossRef]
- Jitendra, A.K.; Lein, A.E.; Soo-Hyun, I.; Alghamdi, A.A.; Hefte, S.H.; Mouanoutoua, J. Mathematical interventions for secondary students with lerning disabilities and mathematics difficulties: A meta-analysis. Educ. Psychol. 2018, 84, 177–196. [Google Scholar] [CrossRef]
- Lämsä, J.; Hämäläinen, R.; Aro, M.; Koskimaa, R.; Äyrämö, S.-M. Games for enhancing basic reading and maths skills: A systematic review of educational game design in supporting learning by people with learning disabilities. Br. J. Educ. Technol. 2018, 49, 596–607. [Google Scholar] [CrossRef]
- Stocker, J.D.; Kubina, R.M. Impact of Cover, Copy, and Compare on fluency outcomes for students with disabilities and math deficits: A review of the literature. Prev. Sch. Fail. Altern. Educ. Child. Youth 2017, 61, 56–68. [Google Scholar] [CrossRef]
- Morano, S.; Markelz, A.M.; Randolph, K.M.; Myers, A.M.; Church, N. Motivation Matters: Three Strategies to Support Motivation and Engagement in Mathematics. Interv. Sch. Clin. 2021, 1–8. [Google Scholar] [CrossRef]
- Hawkins, R.O.; Collins, T.; Hernan, C.; Flowers, E. Using Computer-Assisted Instruction to Build Math Fact Fluency. Interv. Sch. Clin. 2017, 52, 141–147. [Google Scholar] [CrossRef]
- Fuchs, L.S.; Seethaler, P.M.; Powell, S.R.; Fuchs, D.; Hamlett, C.L.; Fletcher, J.M. Effects of Preventative Tutoring on the Mathematical Problem Solving of Third-Grade Students with Math and Reading Difficulties. Except. Child. 2008, 74, 155–173. [Google Scholar] [CrossRef] [PubMed]
- Grays, S.D.; Rhymer, K.N.; Swartzmiller, M.D. Moderating Effects of Mathematics Anxiety on the Effectiveness of Explicit Timing. J. Behav. Educ. 2017, 26, 188–200. [Google Scholar] [CrossRef]
- Duhon, G.J.; House, S.; Hastings, K.; Poncy, B.; Solomon, B. Adding Immediate Feedback to Explicit Timing: An Option for Enhancing Treatment Intensity to Improve Mathematics Fluency. J. Behav. Educ. 2015, 24, 74–87. [Google Scholar] [CrossRef]
- Wells, J.C.; Sheehey, P.H.; Sheehey, M. Using Self-Monitoring of Performance With Self-Graphing to Increase Academic Productivity in Math. Beyond Behav. 2017, 26, 57–65. [Google Scholar] [CrossRef]
- Weiner, B. Attribution Theory, Achievement Motivation, and the Educational Process. Rev. Educ. Res. 1972, 42, 203–215. [Google Scholar] [CrossRef]
- Chinn, S.J. Addressing the Unproductive Classroom Behaviors of Students with Special Needs; Kingsley: London, UK, 2010. [Google Scholar]
- Tan, A.; Nicholson, T. Flashcards revisited: Training poor readers to read words faster improves their comprehension of text. J. Educ. Psychol. 1997, 89, 276–288. [Google Scholar] [CrossRef]
- Skarr, A.; Zielinski, K.; Ruwe, K.; Sharp, H.; Williams, R.L.; McLaughlin, T.F. The Effects of Direct Instruction Flashcard and Math Racetrack Procedures on Mastery of Basic Multiplication Facts by Three Elementary School Students. Educ. Treat. Child. 2014, 37, 77–93. [Google Scholar] [CrossRef]
- Irvin, J.L.; Meltzer, J.; Dukes, M. Student motivation, engagement, and achievement. In Taking Action on Adolescent Literacy: An Implementation Guide for School Leaders; Irvin, J.L., Meltzer, J., Dukes, M., Eds.; ASCD: Alexandria, VA, USA, 2007; pp. 27–50. [Google Scholar]
- Christenson, S.L.; Reschly, A.L.; Wylie, C. Handbook of Research on Student Engagement; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar] [CrossRef]
- Burns, M.K.; Ysseldyke, J.; Nelson, P.M.; Kanive, R. Number of repetitions required to retain single-digit multiplication math facts for elementary students. Sch. Psychol. Q. 2015, 30, 398–405. [Google Scholar] [CrossRef]
- Utley, C.A.; Mortweet, S.L.; Greenwood, C.R. Peer-Mediated Instruction and Interventions. Focus Except. Child. 1997, 29, 1–23. [Google Scholar] [CrossRef]
- Mitchell, D. What Really Works in Special and Inclusive Education. Using Evidence-Based Teaching Strategies; Routledge: New York, NY, USA, 2014. [Google Scholar]
- Fuchs, D.; Fuchs, L.S.; Mathes, P.G.; Simmons, D.C. Peer-Assisted Learning Strategies: Making Classrooms More Responsive to Diversity. Am. Educ. Res. J. 1997, 34, 174–206. [Google Scholar] [CrossRef]
- Delquardi, J.; Greenwood, C.R.; Whorton, D.; Carta, J.J.; Hall, R.V. Classwide Peer Tutoring. Except. Child. 1986, 52, 535–542. [Google Scholar] [CrossRef]
- Lo, Y.-Y.; Cartledge, G. Total class peer tutoring and interdependent group oriented contingency: Improving the academic and task related behaviours of fourth-grade urban students. Educ. Treat. Child. 2004, 27, 235–262. [Google Scholar]
- Greenwood, C.R.; Terry, B.; Utley, C.A.; Montagna, D.; Walker, D. Achievement, Placement, and Services: Middle School Benefits of Classwide Peer Tutoring used at the Elementary School. Sch. Psychol. Rev. 1993, 22, 497–516. [Google Scholar] [CrossRef]
- Dufrene, B.A.; Reisener, C.D.; Olmi, D.J.; Zoder-Martell, K.; McNutt, M.R.; Horn, D.R. Peer Tutoring for Reading Fluency as a Feasible and Effective Alternative in Response to Intervention Systems. J. Behav. Educ. 2010, 19, 239–256. [Google Scholar] [CrossRef]
- Alegre, F.; Moliner, L.; Maroto, A.; Lorenzo-Valentin, G. Peer tutoring and mathematics in secondary education: Literature review, effect sizes, moderators, and implications for practice. Heliyon 2019, 5, e02491. [Google Scholar] [CrossRef]
- Bowman-Perrott, L.; Davis, H.; Vannest, K.J.; Williams, L.; Greenwood, C.R.; Parker, R. Academic Benefits of Peer Tutoring: A Meta-Analytic Review of Single-Case Research. Sch. Psychol. Rev. 2013, 42, 39–55. [Google Scholar] [CrossRef]
- Dennis, L.M.; Canas, M.; Ortega, M.M. Effects of Team Competition Versus Team Cooperation in Classwide Peer Tutoring. J. Educ. Res. 2007, 100, 155–160. [Google Scholar] [CrossRef]
- Ginsburg-Block, M.D.; Rohrbeck, C.A.; Fantuzzo, J.W. A meta-analytic review of social, self-concept, and behavioral outcomes of peer-assisted learning. J. Educ. Psychol. 2006, 98, 732–749. [Google Scholar] [CrossRef]
- Hayes, J.R.; Berninger, V.W. Relationships between idea generation and transcription: How the act of writing shapes what children write. In Traditions of Writing Research; Bravermen, R.K., Lunsford, K., McLeod, S., Null, S., Rogers, A.S.P., Eds.; Taylor and Frances/Routledge: New York, NY, USA, 2009; pp. 166–180. [Google Scholar]
- Haffner, J.; Baro, K.; Parzer, P.; Resch, F. Heidelberger Rechentest (HRT 1–4); Hogrefe: Göttingen, Germany, 2005. [Google Scholar]
- Thomas, G.; Dowker, A. Mathematics Anxiety and Related Factors in Young Children. In Proceedings of the 2000 British Psychological Society Developmental Section Conference, Online, 30 June–1 July 2020; British Psychological Society: Bristol, UK, 2000. [Google Scholar]
- Gast, D.L.; Lloyd, B.P.; Ledford, J.R. Multiple baseline and multiple probe designs. In Single Case Research Methodology; Ledford, J.R., Gast, D.L., Eds.; Routledge: New York, NY, USA, 2018; pp. 239–282. [Google Scholar] [CrossRef]
- Gast, D.L.; Hammond, D. Withdrawal and reversal designs. In Single Subject Research Methodology in Behavioral Sciences; Gast, D.L., Ed.; Routledge: New York, NY, USA, 2009; pp. 234–275. [Google Scholar] [CrossRef]
- Tate, R.L.; Perdices, M.; Rosenkoetter, U.; McDonald, S.; Togher, L.; Vohra, S. The Single-Case Reporting Guideline in behavioural Interventions (SCRIBE) 2016: Explanation and elaboration. Arch. Sci. Psychol. 2016, 4, 10–31. [Google Scholar] [CrossRef]
- Wilbert, J. Package “Scan”. 2020. Available online: https://www.uni-potsdam.de/fileadmin01/projects/inklusion/scan/scan.pdf (accessed on 26 May 2021).
- O’Brien, S.; Repp, A.C. Reinforcement-Based Reductive Procedures: A Review of 20 Years of their Use with Persons with Severe or Profound Retardation. J. Assoc. Pers. Sev. Handicap. 1990, 15, 148–159. [Google Scholar] [CrossRef]
- Parker, R.I.; Vannest, K.J.; Davis, J.L.; Sauber, S.B. Combining Nonoverlap and Trend for Single-Case Research: Tau-U. Behav. Ther. 2011, 42, 284–299. [Google Scholar] [CrossRef] [PubMed]
- Karnes, J.; Grünke, M.; Barwasser, A. The effects of a math racetracks intervention on the single-digit multiplication facts fluency of four struggling elementary students. Insights Learn. Disabil. 2021, 18, 1–25. [Google Scholar]
- Erbey, R.; McLaughlin, T.F.; Derby, K.M.; Everson, M. The effects of using flashcards with reading racetrack to teach letter sounds, sight words, and math facts to elementary students with learning disabilities. Int. Electron. J. Elem. Educ. 2011, 3, 213–226. Available online: http://www.iejee.com/index.html (accessed on 26 May 2021).
- Hopkins, S.; Russo, J. Does (problem-based) practice always make proficient? In 40 Years on: We Are Still Learning! Proceedings of the 40th Annual Conference of the Mathematics Education Research Group of Australasia, Victoria, Melbourne, 2–6 July 2017; Downton, A., Livy, S., Hall, J., Eds.; Merga: Melbourne, Australia, 2017; pp. 317–324. [Google Scholar] [CrossRef]
| n (A) | n (B) | n (E) | M (A) SD | M (B) SD | M (E) SD | |
|---|---|---|---|---|---|---|
| Anton | 5 | 11 | 3 | 1.60 (1.30) | 10 (2.93) | 12.67 (1.15) |
| Berta | 8 | 8 | 3 | 1 (0.93) | 6.13 (2.80) | 6.33 (2.08) |
| Celina | 5 | 11 | 3 | 1.20 (1.09) | 8.78 (5.12) | 15.33 (1.53) |
| Diana | 6 | 10 | 3 | 2 (0.63) | 6.45 (1.77) | 6.33 (0.58) |
| Tau-Ucorrected | p | NAP | p | MBD | |
|---|---|---|---|---|---|
| Anton | 0.63 | 0.001 ** | 100 | 0.001 *** | 525.0% |
| Berta | 0.43 | 0.019 * | 97.66 | 0.000 *** | 512.5% |
| Celina | 0.84 | 0.000 ** | 96.36 | 0.002 ** | 627.5% |
| Diana | 0.27 | 0.144 | 100 | 0.001 *** | 222.5% |
| B | SE | t | p | |
|---|---|---|---|---|
| Intercept | 2.18 | 2.10 | 1.04 | 0.30 |
| Trend | 0.15 | 0.38 | 0.40 | 0.69 |
| Level Phase B | 1.44 | 1.54 | 0.94 | 0.53 |
| Level Phase E | 13.39 | 5.03 | 2.66 | 0.01 |
| Slope B | 1.01 | 0.42 | 2.58 | 0.01 |
| Slope E | −0.25 | 1.11 | −0.23 | 0.82 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Karnes, J.; Grünke, M. The Effects of a Multicomponent Motivational System Intervention Using Peer-Tutoring for Implementation on the Automation of Single-Digit Addition Tasks of Four Struggling Elementary Students. Educ. Sci. 2021, 11, 265. https://doi.org/10.3390/educsci11060265
Karnes J, Grünke M. The Effects of a Multicomponent Motivational System Intervention Using Peer-Tutoring for Implementation on the Automation of Single-Digit Addition Tasks of Four Struggling Elementary Students. Education Sciences. 2021; 11(6):265. https://doi.org/10.3390/educsci11060265
Chicago/Turabian StyleKarnes, Jennifer, and Matthias Grünke. 2021. "The Effects of a Multicomponent Motivational System Intervention Using Peer-Tutoring for Implementation on the Automation of Single-Digit Addition Tasks of Four Struggling Elementary Students" Education Sciences 11, no. 6: 265. https://doi.org/10.3390/educsci11060265
APA StyleKarnes, J., & Grünke, M. (2021). The Effects of a Multicomponent Motivational System Intervention Using Peer-Tutoring for Implementation on the Automation of Single-Digit Addition Tasks of Four Struggling Elementary Students. Education Sciences, 11(6), 265. https://doi.org/10.3390/educsci11060265






