A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra
Abstract
1. Introduction
2. Materials and Methods
2.1. Theoretical Framework
2.2. Historical Notes on the Writing of Abū Kāmil
3. Results
From the Editing of Abū Kāmil to the General Formulation of A Proposition
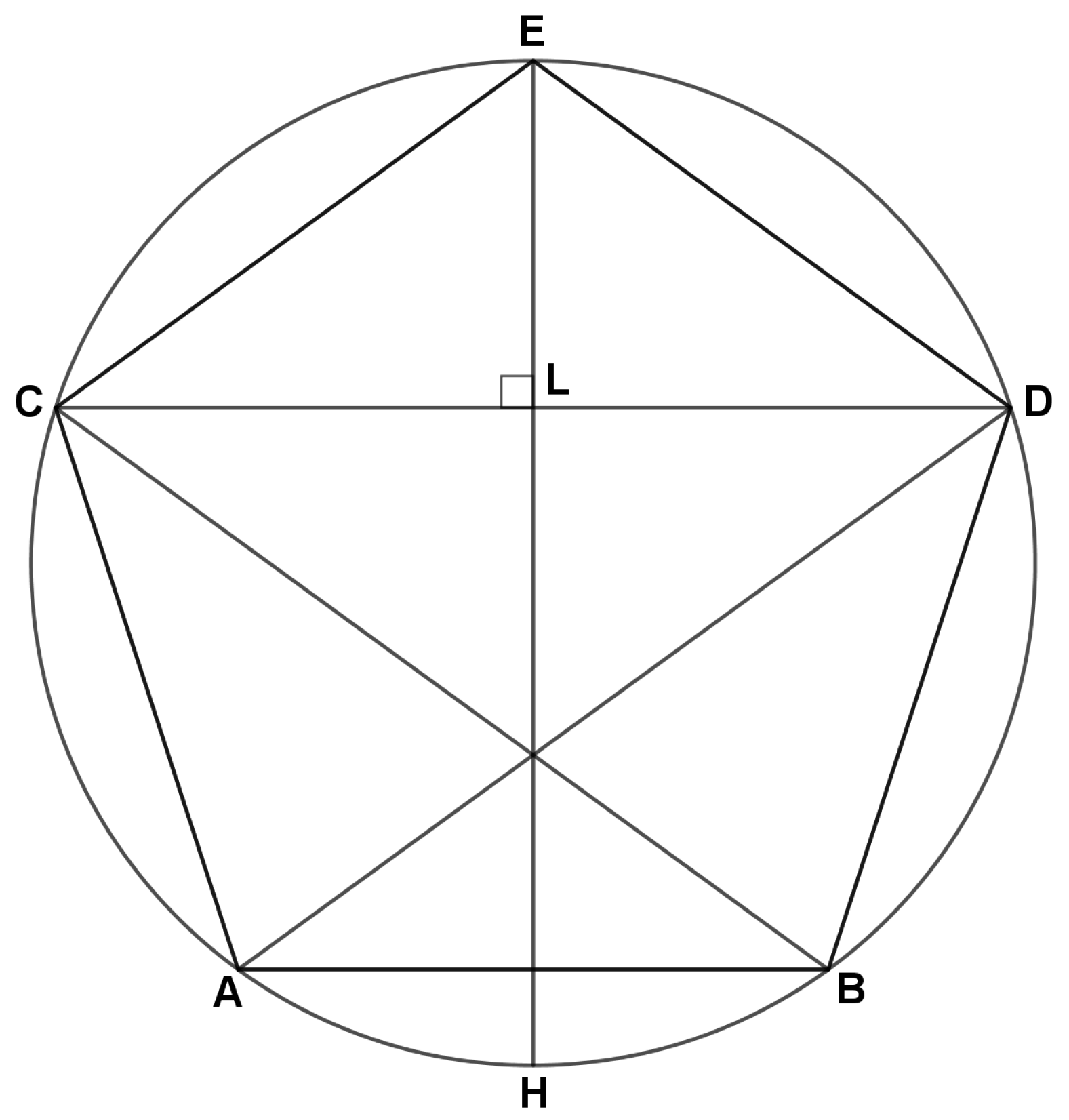
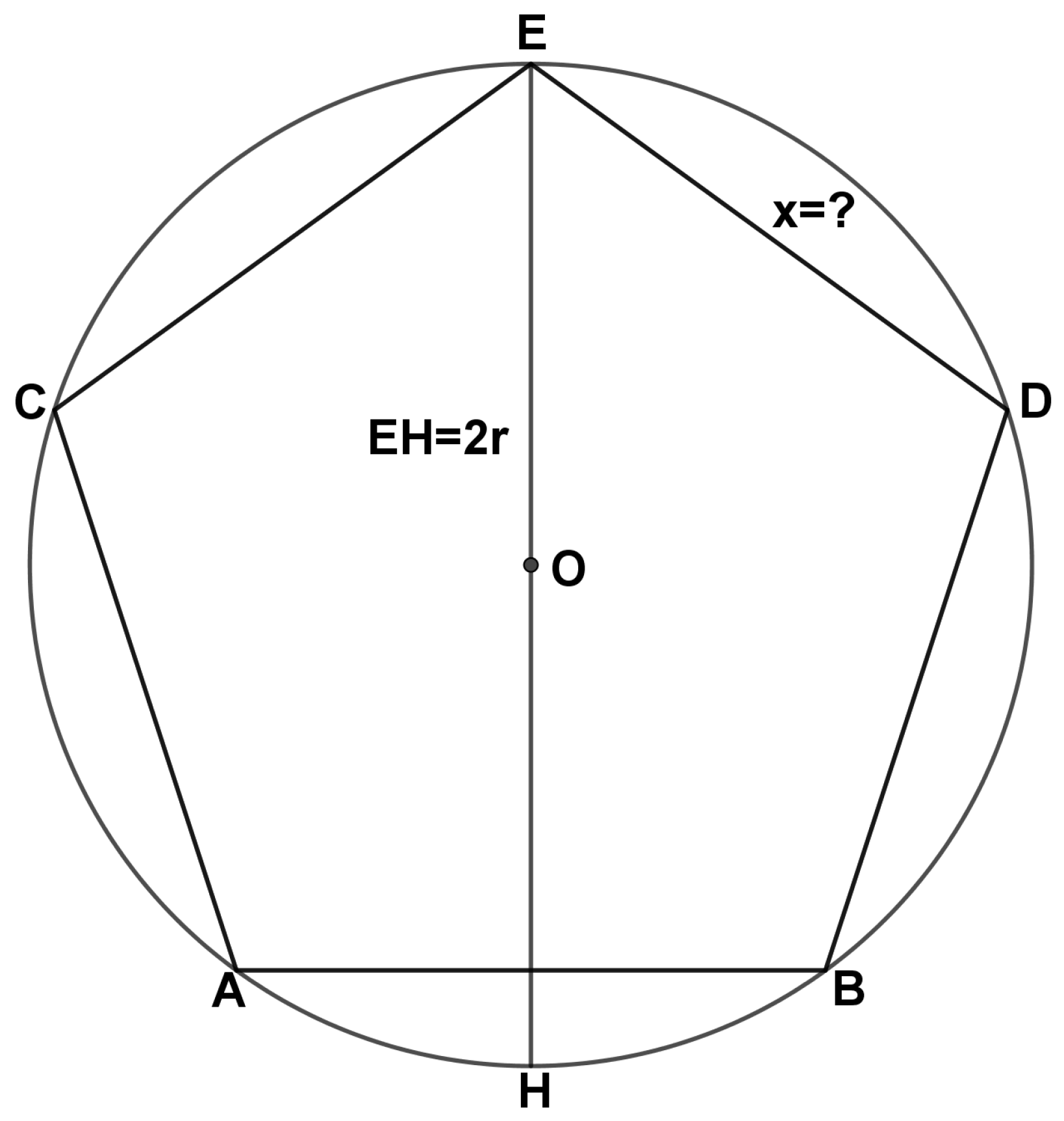
Assume the known circle in which the diameter is ten in number, it is the straight line , and in which a regular pentagon is inscribed; it is the pentagon . If we want to know what is the size of each of the sides of this pentagon, we draw the straight line that is the chord of two-fifths of the circle, and we assume the straight line a thing. We know that the straight line is a tenth of a māl (Here, the authors used the transliteration of the original Arabic word. Literally, this word means a quantity of money (among other things). In modern mathematical translations, it is usually translated as “square”, as in Reference [1]. I preferred here to maintain the original word used by Abū Kāmil. I have referred to translations into a number of languages [1,46,47,49,50]), since the product of by itself is equal to the product of by ; the straight line is the root of māl minus one-tenth of one-tenth of māl-māl and straight line is equal to the straight line ; the straight line is therefore the root of four māl minus two-fifths of one-tenth of māl-māl. But we know that the sum of the product of and plus by itself is equal to the product of by itself, because the product of and plus by is equal to the product of by ; or by is equal to by itself, by is equal to by itself, and by itself is four māl minus two-fifths of one-tenth of māl-māl. Eliminate from this the product of by itself, that is a māl; thus remain three māl minus two-fifths of one-tenth of māl-māl, equal to the product of by . We then divide three māl minus two-fifths of one-tenth of māl-māl by the straight line , which is a thing; we get the straight line , three things minus two-fifths of one-tenth of a cube. But we have shown that the straight line is the root of four māl minus two-fifths of one-tenth of māl-māl. We multiply three things minus two-fifths of one-tenth of a cube by themselves; we get nine māl and one part of six hundred-twenty-five parts of cube-cube minus six parts of twenty-five parts of māl-māl equal to four māl minus two-fifths of one-tenth of māl-māl. Reducing from this, we have a fifth of māl-māl equal to five māl and a part of six hundred twenty-five parts of a cube-cube. Dividing all that you have by a māl, you get five “dirhams” and one part of six hundred twenty-five parts of māl-māl equal to one-fifth of māl. Make whole māl-māl for which you have a māl-māl, and so multiply it by six hundred twenty-five, so all that you have by six hundred and twenty-five; we have a māl-māl plus three thousand one hundred twenty-five “dirhams” equal to one hundred twenty-five māl. Divide the māl into two halves, get sixty-two and a half; multiply them by themselves, you get three thousand nine hundred six and a quarter; subtract three thousand one hundred twenty-five, it remains seven hundred eighty-one and a quarter. We remove the root of this one from sixty-two and a half, we take the root of what remains, we have the straight line which is one of the sides of the pentagon.
Find the side of the regular pentagon inscribed within a circle of diameter .
4. Discussion
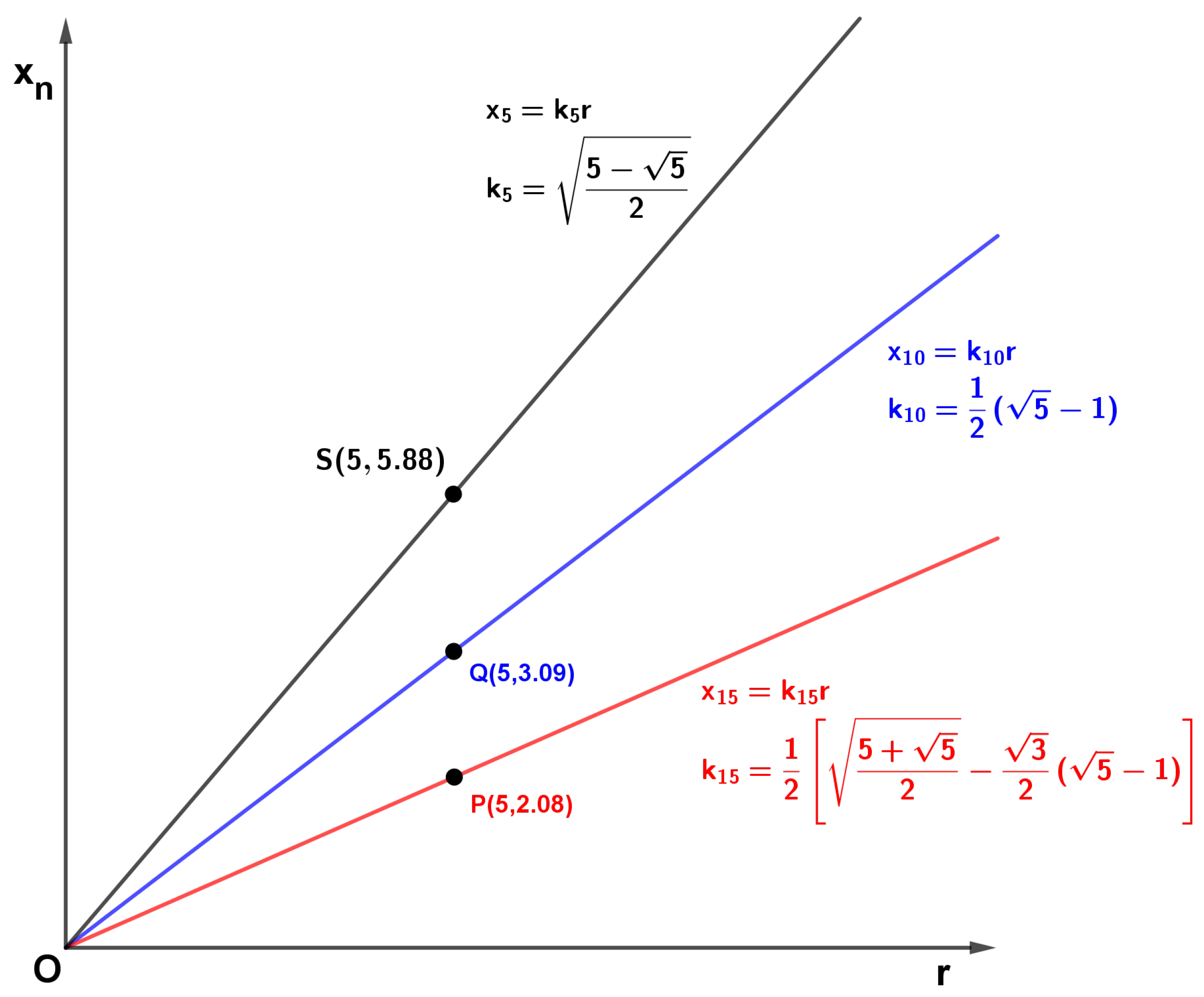
5. Conclusions
6. Patents
Author Contributions
Funding
Conflicts of Interest
References
- Rashed, R. Abū Kāmil: Algèbre et Analyse Diophantienne; Walter de Gruyter GmbK & C.: Berlin, Germany, 2012; ISBN 311029561X. [Google Scholar]
- Jankvist, U.T.; Clark, K.M.; Mosvold, R. Developing mathematical knowledge for teaching teachers: Potentials of history of mathematics in teacher educator training. J. Math. Teach. Educ. 2020, 23, 311–332. [Google Scholar] [CrossRef]
- Takeko Gobara, S.; Radford, L. Teoria da Objetivação: Fundamentos e Aplicações para o Ensino e Aprendizagem de Ciências e Matemática; Livraria da Fìsica: São Paulo, Brasil, 2020; ISBN 9788578616380. [Google Scholar]
- Mosvold, R.; Jakobsen, A.; Jankvist, U.T. How mathematical knowledge for teaching may profit from the study of history of mathematics. Sci. Educ. 2014, 23, 47–60. [Google Scholar] [CrossRef]
- Ball, D.; Thames, M.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Furinghetti, F. Teacher education through the history of mathematics. Educ. Stud. Math. 2007, 66, 131–143. [Google Scholar] [CrossRef]
- Bagni, G.T. History of Mathematics and Didactics: Reflections on teachers education. In ICME–10, Discussion Group 6, Proceedings of the 10th International Congress on Mathematical Education, Roskilde, Denmark, 4–11 July 2004; Niss, M., Ed.; IMFUFA: Roskilde, Denmark, 2004. [Google Scholar]
- Bagni, G.T. Linguaggio, Storia e Didattica Della Matematica; Pitagora: Bologna, Italy, 2006; ISBN 8837116276. [Google Scholar]
- D’Enfert, R.; Djebbar, A.; Radford, L. Dimensions historique et culturelle dans l’enseignement des mathématiques. In Compte-Rendu du Groupe de Travail No. 4, Proceedings of EMF2012-GT4 Espace Mathématique Francophone, Geneva, Switzerland, February 2012; Dorier, J.-L., Coutat, S., Eds.; EMF: Geneva, Switzerland, 2012; pp. 523–528. [Google Scholar]
- Kobiela, M.; Zanazanian, P. Crossing Disciplinary Borders in Pre-service Teacher Education: Historical Consciousness as a Tool to Develop Awareness of Mathematical Positionality to Achieve Epistemic. In Borders in Mathematics Pre-Service Teacher Education; Radakovic, N., Jao, L., Eds.; Springer: Cham, Switzerland, 2020; pp. 47–73. ISBN 978–3-030-44292-7. [Google Scholar]
- Boero, P.; Guala, E. Development of mathematical knowledge and beliefs of teachers: The role of cultural analysis of the content to be taught. In The International Handbook of Mathematics Teacher Education; Sullivan, P., Wood, T., Eds.; Sense: Rotterdam, The Netherlands, 2008; Volume 1, pp. 223–244. ISBN 978-90-8790-542-2. [Google Scholar]
- Radford, L. On Psychology, Historical Epistemology and the Teaching of Mathematics: Towards a Socio-Cultural History of Mathematics. Learn. Math. 1997, 17, 26–33. [Google Scholar]
- D’Amore, B.; Fandiño Pinilla, M.I. Storia ed epistemologia della matematica, basi etiche. La Matematica e la Sua Didattica 2005, 19, 503–515. [Google Scholar]
- Radford, L. The ethics of being and knowing: Towards a cultural theory of learning. In Semiotics in Mathematics Education: Epistemology, History, Classroom, and Culture; Radford, L., Schubring, G., Seeger, F., Eds.; Sense: Rotterdam, The Netherlands, 2008; pp. 215–234. ISBN 978-90-8790-596-5. [Google Scholar]
- Roth, W.M.; Radford, L. A Cultural Historical Perspective on Teaching and Learning; Sense: Rotterdam, The Netherlands, 2011; ISBN 9460915620. [Google Scholar]
- D’Amore, B.; Radford, L. Enseñanza y Aprendizaje de Lasmatemáticas: Problemas Semióticos, Epistemológicos y Prácticos; Universidad Distrital Francisco José de Caldas: Bogotá, Columbia, 2017; ISBN 978-958-5434-48-6. [Google Scholar]
- Fauvel, J. Using history in mathematics education. Learn. Math. 1991, 11, 3–6. [Google Scholar]
- Bartolini Bussi, M.G.; Sierpinska, A. The relevance of historical studies in designing and analysing classroom activities. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluwer: Dortrecht, The Netherlands, 2000; pp. 154–160. ISBN 978-0-306-47220-6. [Google Scholar]
- Furinghetti, F.; Radford, L.; Katz, V. The history of mathematics in mathematics education: Theory and practice. Educ. Stud. Math. 2007, 66, 107–271. [Google Scholar] [CrossRef]
- D’Amore, B.; Speranza, F. La Matematica e la Sua Storia. Alcuni Esempi per Spunti Didattici; Angeli: Milano, Italy, 1995; ISBN 8820493543. [Google Scholar]
- Jahnke, H.N.; Arcavi, A.; Barbin, E.; Bekken, O.; Furinghetti, F.; Elidrissi, A.; Silva da Silva, C.M.; Weeks, C. The use of original sources in the mathematics classroom. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluver: Dordrecht, The Netherlands, 2000; pp. 291–328. ISBN 978-0-306-47220-6. [Google Scholar]
- Radford, L.; Bussi, M.G.B.; Bekken, O.; Boero, P.; Dorier, J.L.; Katz, V.; Rogers, L.; Sierpinski, A.; Vasco, C. Historical formation and student understanding of mathematics. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluver: Dordrecht, The Netherlands, 2000; ISBN 978-0-306-47220-6. [Google Scholar]
- Clark, K.M.; Kjeldsen, T.H.; Schorcht, S.; Tzanakis, C. History of Mathematics in Mathematics Education— An Overview. Math. Didact. 2019, 42, 1–26. [Google Scholar]
- Carreira, S.; Barquero, B.; Kaiser, G.; Cooper, J. Introducing CERME’s Thematic Working Group 6— Applications and Modelling. Newsl. Eur. Math. Soc. Math. Educ. ERME Column 2019, 111, 48–49. [Google Scholar]
- Stillman, G.A.; Blum, W.; Salett Biembengut, M. Mathematical Modelling in Education Research and Practice Cultural, Social and Cognitive Influences, International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer International Publishing: Cham, Switzerland, 2015; ISBN 9783319182711. [Google Scholar]
- Barbin, É. Les Constructions Mathématiques avec des Instruments et des Gestes; Ellipses: Paris, France, 2015; ISBN 2340002060. [Google Scholar]
- Radford, L.; Boero, P.; Vasco, C. Epistemological assumptions framing interpretations of students understanding of mathematics. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluver: Dordrecht, The Netherlands, 2000; pp. 162–167. ISBN 978-0-306-47220-6. [Google Scholar]
- Furinghetti, F. Rethinking history and epistemology in mathematics education. Int. J. Math. Educ. Sci. Technol. 2020, 51, 967–994. [Google Scholar] [CrossRef]
- Duval, R. Understanding the Mathematical Way of Thinking: The Registers of Semiotic Representations; Springer International: Cham, Switzerland, 2018; ISBN 3319569090. [Google Scholar]
- Bartolini Bussi, M.; Mariotti, M.A. Semiotic mediation in the mathematics classroom: Artefacts and signs after a Vygotskian perspective. In Handbook of International Research in Mathematics Education, 2nd ed.; English, L., Ed.; Routledge, Taylor and Francis: New York, NY, USA, 2008; pp. 746–783. ISBN 9780415832045. [Google Scholar]
- Sáenz Ludlow, A.; Kadunz, G. Semiotic as a Tool for Learning Mathematics; Sense: Rotterdam, The Netherlands, 2016; ISBN 9463003363. [Google Scholar]
- Radford, L.; Schubring, G.; Seeger, F. Semiotics in Mathematics Education: Epistemology, History, Classroom, and Culture; Sense: Rotterdam, The Netherlands, 2008; ISBN 978-90-8790-596-5. [Google Scholar]
- Presmeg, N.; Radford, L.; Roth, M.; Kadunz, G. Signs of Signification. Semiotics in Mathematics Education Research; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-70286-5. [Google Scholar]
- Florio, E.; Maierù, L.; Fenaroli, G. The construction of regular polygons between geometry and algebra: A didactic-historical example. Learn. Math. 2020, 40, 23–24. [Google Scholar]
- Radford, L. De la teoría de la objetivación. Rev. Latinoam. Etnomatem. 2014, 7, 132–150. [Google Scholar]
- D’Amore, B. Oggetti matematici e senso. Le trasformazioni semiotiche cambiano il senso degli oggetti matematici. La Matematica e la Sua Didattica 2006, 4, 557–583. [Google Scholar]
- D’Amore, B.; Fandiño Pinilla, M.I.; Iori, M. Primeiros Elementos de Semiótica. Sua Presença e Sua Importância no Processo de Ensino-Aprendizagem da Matemática; Livraria da Física: Sao Paolo, Brazil, 2015; ISBN 9788578613525. [Google Scholar]
- Blum, W.; Leiss, D. How do students and teachers deal with mathematical modelling problems? The example “Filling up”. In Mathematical Modelling (ICTMA 12): Education, Engineering and Economics; Haines, C., Galbraith, P., Blum, W., Khan, S., Eds.; Woodhead Publishing: Cambridge, UK, 2007; pp. 222–231. ISBN 1904275206. [Google Scholar]
- Kaiser, G. Mathematical modelling and applications in education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; ISBN 978-94-007-4978-8. [Google Scholar]
- Schukajlow, S.; Kaiser, G.; Stillman, G. Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. ZDM Math. Educ. 2018, 50, 5–18. [Google Scholar] [CrossRef]
- Stillman, G.A.; Kaiser, G.; Blum, W.; Brow, J.P. Teaching Mathematical Modelling: Connecting to Research and Practice, International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer Science + Business Media: Dordrecht, The Netherlands, 2013; ISBN 9789400765399. [Google Scholar]
- Rashed, R. Al-Khwārizmī. Le commencement de l’algèbre; Librairie Scientifique et Technique A. Blanchard: Paris, France, 2007; ISBN 2853672417. [Google Scholar]
- Karpinski, L.C. The algebra of Abu Kamil. Am. Math. Mon. 1914, 21, 37–48. [Google Scholar] [CrossRef]
- Maierù, L.; Florio, E. Le Costruzioni Geometriche: Un Percorso Storico-Didattico tra i Matematici Arabi Dei Secc. IX-XIII: Parte Prima; Aracne: Roma, Italy, 2018; ISBN 882551235X. [Google Scholar]
- Florio, E.; Maierù, L. The scientific knowledge of book XVI De subtilitate by G. Cardano used in the Trattato sulla divinatione naturale cosmologica by P. A. Foscarini. Open J. Humanit. 2019, 1, 385–422. [Google Scholar]
- Sacerdote, G. Il trattato del pentagono e del decagono di Abu Kámil Shogia ben Aslam ben Muhammed. In Festschrift zum Achtzigsten Geburtstage Moritz Steinschneiders; Otto Harrassowitz: Leipzig, Germany, 1896; pp. 169–194. [Google Scholar]
- Lorch, R. Abu Kamil on the pentagon and decagon. In Vestigia Mathematica. Studies in Medieval and Early Modern Mathematics in Honour of H. L. L. Busard; Folkerts, M., Hogendijk, J.P., Eds.; Rodopi: Amsterdam, The Netherlands, 1993; pp. 215–252. ISBN 9051835361. [Google Scholar]
- Pisano, L. Practica Geometriae. In Scritti di Leonardo Pisano Matematico del Secolo Decimo Terzo; Boncompagni, B., Ed.; Tipografia delle Scienze Matematiche e Fisiche: Roma, Italy, 1862; Volume 2. [Google Scholar]
- Levey, M. The Algebra of Abu Kamil, Kitāb fī al-jābr wa’l-muqābala in a Commentary by Mordecai Finzi: Hebrew Text, Translation, and Commentary with Special Reference to the Arabic Text; The University of Wisconsin: Madison, WI, USA, 1966; ISBN 0299038009. [Google Scholar]
- Chalhoub, S. Die Algebra: Kitab al-Gabr wal-Muqabala des Abu Kamil Soga ibn Aslam; Institute for the History of Arabic Science: Aleppo, Syria, 2004. [Google Scholar]
- Florio, E.; Galuzzi, M.; Maierù, L.; Santoro, N. La “nuova algebra” da François Viète a Leonhard Euler; Aracne: Roma, Italy, 2015; ISBN 978-88-548-8866-1. [Google Scholar]
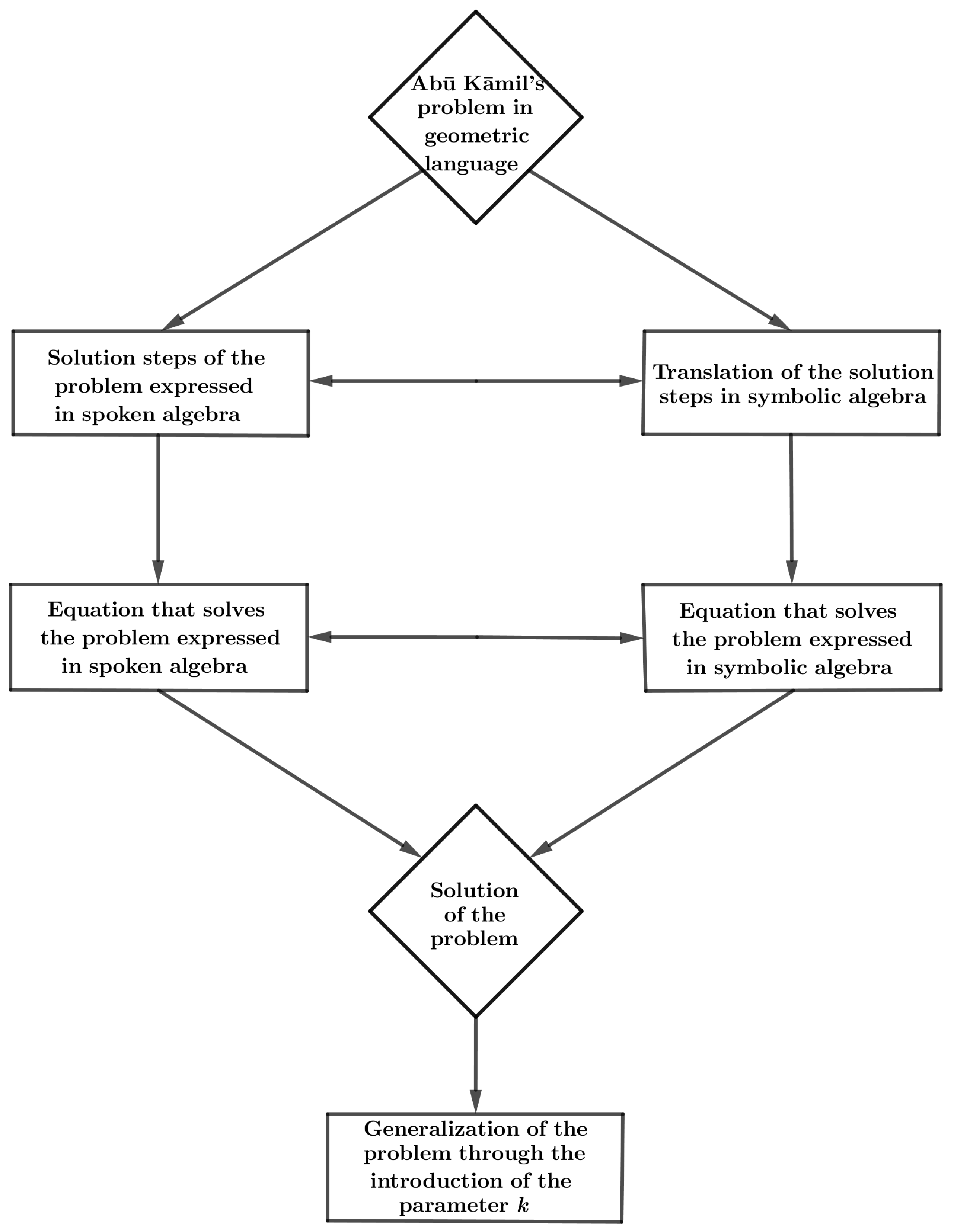
| Step | Statement and Solution Steps of the Problem Expressed in Spoken Algebra | Translation of the Statement and of the Solution Steps in Symbolic Algebra |
|---|---|---|
| 1 | Determine the length of a chord of a fifth of a known circle starting from its diameter. | Find the side of the regular pentagon inscribed in a given circle. |
| 2 | Assume the known circle in which the diameter is ten in number, it is the straight line , and in which a regular pentagon is inscribed, it is the pentagon . | Let be the known circle of diameter and let be the regular pentagon inscribed within it. |
| 3 | Draw the straight line that is the chord of two-fifths of the circle. | Draw the chord that subtends of the circumference. |
| 4 | Assume the straight line is a thing. | Assume . |
| 5 | We know that the straight line is a tenth of a māl, since the product of by itself is equal to the product of by ; | We know that since ; |
| 6 | the straight line is the root of māl minus one-tenth of one-tenth of māl-māl and straight line is equal to the straight line ; | and ; |
| 7 | the straight line is therefore the root of four māl minus two-fifths of one-tenth of māl-māl. | therefore, . |
| 8 | But we know that the sum of the product of and plus by itself is equal to the product of by itself, because the product of and plus by is equal to the product of by ; | We know that because ; |
| 9 | or by is equal to by itself, by is equal to by itself, and by itself is four māl minus two-fifths of one-tenth of māl-māl. | or , , and . |
| 10 | Eliminate from this the product of by itself, that is a māl, thus remaining three māl minus two-fifths of one-tenth of māl-māl, equal to the product of by . | Subtract from this , thus remaining with . |
| 11 | We then divide three māl minus two-fifths of one-tenth of māl-māl by the straight line , which is a thing; we get the straight line , three things minus two-fifths of one-tenth of a cube. | Divide by , and we obtain . |
| 12 | But we have shown that the straight line is the root of four māl minus two-fifths of one-tenth of māl-māl. | We have shown that . |
| 13 | Multiply three things minus two-fifths of one-tenth of a cube by themselves; we get nine māl and one part of six hundred-twenty-five parts of cube-cube minus six parts of twenty-five parts of māl-māl equal to four māl minus two-fifths of one-tenth of māl-māl. | Multiply by itself, and we obtain:
|
| 14 | Reducing from this, we have a fifth of māl-māl equal to five māl and a part of six hundred twenty-five parts of a cube-cube. | Reduce this and we get . |
| 15 | Dividing all that you have by a māl, you get five “dirhams” and one part of six hundred twenty-five parts of māl-māl equal to one-fifth of māl. | Divide all by , and we obtain . |
| 16 | Make whole māl-māl for which you have a māl-māl, and so multiply it by six hundred twenty-five, so all that you have by six hundred and twenty-five; we have a māl-māl plus three thousand one hundred twenty-five “dirhams” equal to one hundred twenty-five māl. | Multiply all by 625, and we have . |
| 17 | Divide the māl into two halves, get sixty-two and a half; | Divide by half, and we have ; |
| 18 | multiply them by themselves, you get three thousand nine hundred six and a quarter; | multiply by itself, and we obtain ; |
| 19 | subtract three thousand one hundred twenty-five, it remains seven hundred eighty-one and a quarter. | subtract 3125 and we are left with . |
| 20 | We remove the root of this one from sixty-two and a half, we take the root of what remains, we have the straight line which is one of the sides of the pentagon. | Take away the root of from and we get the root of the remainder; thus, we have the line that is one of the sides of the pentagon
|
| # | Expressions in Spoken Algebra | Expressions in Symbolic Algebra |
|---|---|---|
| 1 | a fifth (or one-fifth) | |
| 2 | two-fifths | |
| 3 | a tenth (or one-tenth) | |
| 4 | one-tenth of one-tenth | |
| 5 | two-fifths of one-tenth | |
| 6 | one-part of six hundred-twenty-five parts | |
| 7 | six parts of twenty-five parts | |
| 8 | sixty-two and a half | |
| 9 | a thing (or one-thing) | x |
| 10 | a māl (or one-māl) | |
| 11 | a cube (or one-cube) | |
| 12 | māl-māl | |
| 13 | cube-cube | |
| 14 | five dirhams | 5 |
| 15 | three thousand one hundred twenty five dirhams | 3125 |
| 16 | three thousand nine hundred and a quarter | |
| 17 | seven hundred eighty one and a quarter |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Florio, E. A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra. Educ. Sci. 2020, 10, 243. https://doi.org/10.3390/educsci10090243
Florio E. A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra. Education Sciences. 2020; 10(9):243. https://doi.org/10.3390/educsci10090243
Chicago/Turabian StyleFlorio, Emilia. 2020. "A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra" Education Sciences 10, no. 9: 243. https://doi.org/10.3390/educsci10090243
APA StyleFlorio, E. (2020). A Synergy between History of Mathematics and Mathematics Education: A Possible Path from Geometry to Symbolic Algebra. Education Sciences, 10(9), 243. https://doi.org/10.3390/educsci10090243





