Abstract
This paper proposes an experimental path aimed at guiding upper secondary school students to overcome that discontinuity, often perceived by them, between learning geometry and learning algebra. This path contributes to making students aware of how the algebraic language, formalized in the most powerful form by Descartes, grafts itself onto the geometric language. This is realized by introducing a problem included in a text written by Abū Kāmil before the year 870. This awareness acquired by the students, when accompanied by some semiotic considerations, allows the translation of the problem from “spoken” algebra to “symbolic” algebra, and it represents the background for a possible use of the same problem within the framework of analytic geometry. This proposition manifests a didactic and popular efficacy that supports and favors the recognition of the object it is talking about in different contexts, helping to create a unitary vision of mathematics.
1. Introduction
This work proposes a didactic path, designed for an upper secondary school class, aimed at showing a connection between geometric knowledge and algebraic knowledge starting from the use of the first problem of the chapter on the regular pentagon and decagon of the Kitāb fī al-jabr wa al-muqābala (Book on algebra and science of reduction and cancellation) of Abū Kāmil [1].
The choice of a proposition taken from the history of mathematics is encouraged by the fact that knowledge of the latter and its use in teaching constitute a significant part of the cultural background of future mathematics teachers [2]. The knowledge of how a mathematical concept was born and evolved can contribute to a better understanding of that concept itself [3], and the study of historical sources contains a potential suitable to increase awareness of possible misconceptions, obstacles, and impediments related to various mathematical concepts and ideas [4].
Useful feedback on the training of teachers are found in Reference [5] with the practice-based theory of mathematical knowledge for teaching, in Reference [6,7,8] where the authors specify the positive elements of the teacher education through the history of mathematics, in Reference [9] where the importance of the historical and cultural dimensions in mathematics education is underlined, in Reference [10], concerning the support of history in changing individual’s epistemic beliefs about the nature of mathematical knowledge, and in Reference [11] for the implementation of teachers’ skills in the cultural analysis of content.
The same choice of Abū Kāmil’s proposition is also motivated by the fact that the teaching and learning of mathematics are favorably affected by a programming that takes into account the social context in which they develop [12,13]. A further motivation is given from the cultural elements [14,15,16] that can suggest suitable communicative means of the mathematical concepts and can address towards adequate choices of specific contents [17,18,19]. Other authors [20,21,22] evidenced that history of mathematics certainly takes on a relevant role among the possible cultural elements to consider. Moreover, important considerations on the fact that the history of mathematics provides significant material for teaching in the classroom are included in the wide review [23].
Why does the problem of Abū Kāmil contains aspects of novelty for educational use among the available historical material?
With regard to the learning of mathematical language, it constitutes a particularly simple environment to effectively explore the potential of some forms and registers with which mathematics expresses itself, to ascertain how the changes between these registers can occur in a reliable and effective way and to evaluate the types of responses that these changes can produce in a problem solving.
The Abū Kāmil’s problem constitutes an experiential environment of rare transparency to start students of secondary school to develop the ability to compose the mathematical structure that allows them to solve and then to generalize the problem, thus making a significant part of the path towards modeling in mathematics, that has for years been the subject of a constructively critical and argumentative discussion among researchers in mathematics education [24,25].
In the initial part of this path, starting from the problem posed by Abū Kāmil, students are invited to become aware that in the geometric field the figure performs the task of visualizing the object which the problem is centered on and which you can reflect on to understand and demonstrate their specific properties.
Subsequently, still following the path of Abū Kāmil, they can enter into the heart of the question constituted by the search for the measure of an element of the pentagon, its side in the specific case, as a function of the radius of the circumscribed circle. The question is, in fact, to establish numerical relationships that require a linguistic and narrative change with respect to the Euclidean one and contain the need for a new model that, as history shows, if realized, will have unpredictable consequences.
More specifically, the chosen problem is particularly suitable for showing the passages in which some properties, enumerated in Euclid’s Elements in geometric language, are translated into the rhetorical language of Arabic algebra, in order to write the resolutive equation of the problem; subsequently those passages that realize a translation of the same properties from the language of spoken algebra in the language of symbolic algebra and, finally, those that lead to the generalization of the problem through the use of a parameter. These passages are sketched in the flowchart shown in Figure 1.
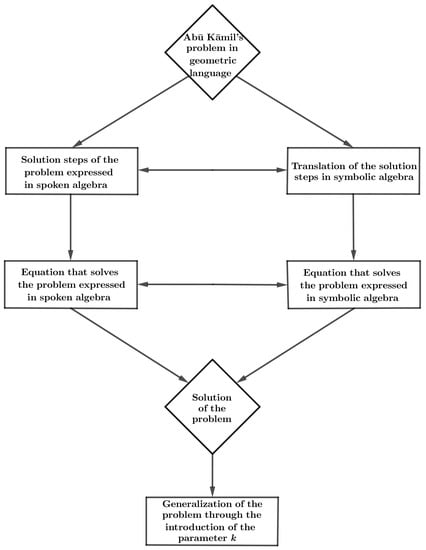
Figure 1.
Flowchart showing the logical steps in the proposed path from geometry to algebra.
This problem is grafted on the geometric construction of regular polygons inscribed or circumscribed in a circle, the importance of which is evident in learning mathematics [26]. By reflecting on it, one can help to clarify the formative role of geometry and algebra, before going on to the real contents of analysis, as well as to the understanding of the significance of “demonstration/solution” within the study of algebra, considered much more than a mere tool for calculation.
Under a more general point of view, this kind of process of translating by the spoken algebra to symbolic algebra helps the students to understand better the “natural” historical evolution of mathematics through the progressive elimination of verbal components in the expression of algebraic procedures by realizing a more practical, fluid and effective language. Such an advantageous language, that represents a general tool for studying mathematical problems given in the past, and still remains, a strong impulse to science allowing the possibility to generalize both the problems and their solution through parameterization. All this is of utmost importance in the algorithmic expression of the mathematical problems and, therefore, in their numerical solution, as well as in the possibility to use computer science tools for a didactic aim.
The organization of the paper is the following. In next section, it is explained as the problem proposed by Abū Kāmil allows the students to “see” and “tell” a mathematical object with different languages and signs. Moreover, essential information about Abū Kāmil and his main work are given. In the third section, the passage from the formulation of the proposition given by Abū Kāmil to a more general one, is described. Finally, a brief discussion and some conclusions are drawn.
2. Materials and Methods
2.1. Theoretical Framework
The path proposed in this paper aspires to take into account the significant relationships between the construction of mathematical knowledge by students and the historical construction of mathematical knowledge highlighted in literature [27,28]. Moreover, the historical material presented in this article can take on a particular value of support for the teaching of mathematics within specific semiotic and epistemological considerations [16,29,30,31,32,33].
Abū Kāmil’s chapter appears indeed as one of the first “written recordings” of a crucial moment of the semiotic evolution of the language of mathematics and of its expressive potential. It shows a didactic and informative efficacy that justifies its particular diffusion in a separate form from the rest of the work. The text by Abū Kāmil presents and solves some “simple” problems using the “signs of spoken algebra”, not yet “signs of literal algebra”, which for this reason naturally begin to ferry from the universe of the consolidated Euclidean narrative to that of the future Cartesian narrative [34].
As an element to graft the semiotic “metamorphosis”, the geometric constructions that, in the context of Abū Kāmil’s writing and, even now, in class work with the students, manifest their potential as a suitable element to support and encourage the recognition of the object one is talking about, take on a key role. This recognition [35] is fundamental for the realization of learning through a diversification of the way in which this object is “seen” and then “told” through a new sign [36,37]. In the text of Abū Kāmil, resonances and differences can be glimpsed between the “knowledge” underlying the use of the Euclidean language and that underlying the algebraic language, considering the knowledge as potential that emerges from human activity in a process of becoming to “materialize” into knowing (see Reference [16], p. 100). The first language (Euclidean) is strongly rooted in its spatial development, as the reading of any Euclid’s passage reveals, the second (algebraic) is projected to develop in successive states linked to temporally distinct “moments” [36], a prelude to the powerful mathematical tools indispensable to the expression of Newtonian physics and mathematics of the 18th century.
In this perspective, the proposed path develops. The change of register, introduced to the students “at the suggestion” of Abū Kāmil in order to speak of the pentagon with “new” signs in respect to those of Euclid, contains some prodromes to the modeling process which are crucial for the development of the skills of problem solving [38,39,40,41].
2.2. Historical Notes on the Writing of Abū Kāmil
The name Abū Kāmil Shuja ibn Aslam ibn Muhammad ibn Shuja (850–930), also known as a-Hasib al-Misri, or as the Egyptian “calculator”, frequently occurs in the first Western algebraic tradition, when reference is made to the transmission of algebra. The name slowly disappears in the later Latin algebraic tradition, until finally lost without trace. Abū Kāmil is especially remembered by later generations as the first commentator on Kitāb al-jabr wa al-muqābala (Book of algebra and science of reduction and cancellation) by Muhammad ibn Mūsā al-Khwārizmī, written between 813 and 830 [42]. Commentary by Abū Kāmil is the Kitāb fī al-jabr wa al-muqābala (Book on algebra and science of reduction and cancellation), written before 870 (see Reference [43] for a historical collocation of Abū Kāmil’s work on algebra among Arab mathematicians). In this treatise, the author devoted a chapter to problems on the regular pentagon and decagon inscribed in or circumscribing a circle in which the Latin translation by Gerard (from the 12th century) can be found at the Bibliotèque Nationale de Paris (Ms. lat. 7377A).
From the analysis of the historical literature available, it is possible to hypothesize an autonomous diffusion of this chapter with respect to the rest of the treatise, if we assume it was directed at readers already familiar with algebra and equations. It is possible to hypothesize that this could have happened during the period most favorable to the spread of algebra. Bearing in mind the considerable interest in the discipline following publication of the work of al-Khwārizmī and Abū Kāmil, the relevant period could lie between the years 950 and 1200 in the case of the Arab world, as seems most likely, or alternatively the years after 1100 in Europe, with the establishment of a Latin tradition in algebra and the birth of cultural centres on this subject in Europe, both among Jewish and Latin scholars. As to why this should have happened, it is possible to put forward the hypothesis that the contents of the chapter are easily placed in relation to certain propositions in books IV and XIII of the Elements by Euclid, that deal with the construction of regular polygons with a ruler and compass, and to the tradition built around this work.
Since the issue of the construction of polygons inscribed within or circumscribed by a circle is a fundamental part of basic mathematical training [44,45], as attested by numerous Arab mathematicians, one can believe that Abū Kāmil chose the construction of the pentagon and decagon as examples of the beauty and value of algebra in finding solutions to problems. Indeed, in the introduction to the second part of the treatise, after having displayed the indispensable elements for an understanding of algebra, Abū Kāmil turns his attention to that which “important” and “skilful” geometers have read in Euclid’s book and other works, explaining and commenting on it in his writing, starting from consideration of the measurement of the side of a pentagon and a decagon, inscribed within or circumscribed by a circle, and the measurement of the diameter of the circle in the two cases [1,46,47].
Al-Qūhī (second half of the X century) was inspired by this short chapter of Abū Kāmil when he wrote On the construction of an equilateral pentagon in a given square. This highlights the fact that Arab mathematicians recognized the importance of the chapter vis-à-vis the treatise on algebra.
The same chapter was a certain point of reference for Leonardo Pisano when writing his book Practica Geometriae [48].
3. Results
From the Editing of Abū Kāmil to the General Formulation of A Proposition
The propositions of the chapter of Abū Kāmil’s treatise contain problems regarding regular pentagons and decagons inscribed in or circumscribing a circle (1–11), the triangles and squares in which figures are inscribed (12–15) and regular pentagons and decagons and how to determine the length of their sides when the area is known (16–20).
As mentioned above, to show students an example of connection between geometric knowledge and algebraic knowledge the first proposition is presented below in a didactic fashion. Figure 2 represents the original picture realized by Abū Kāmil (see Reference [1], pp. 524–525) to introduce the problem of finding the length of the side of the regular pentagon inscribed into a circle of diameter equal to 10.
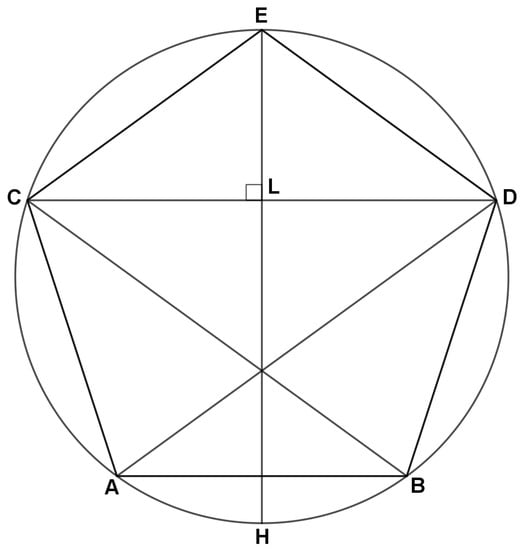
Figure 2.
Abū Kāmil’s construction to obtain the length of the side of the regular pentagon (see Reference [1], pp. 524–525).
Here, below, the English translation of the first of the twenty geometric problems that Abū Kāmil solves in the chapter concerning the regular pentagon and decagon of Kitāb fī al-jabr wa al-muqābala, is reported (see Reference [1], pp. 522–527, for a French translation of the original Arabic text):
Assume the known circle in which the diameter is ten in number, it is the straight line , and in which a regular pentagon is inscribed; it is the pentagon . If we want to know what is the size of each of the sides of this pentagon, we draw the straight line that is the chord of two-fifths of the circle, and we assume the straight line a thing. We know that the straight line is a tenth of a māl (Here, the authors used the transliteration of the original Arabic word. Literally, this word means a quantity of money (among other things). In modern mathematical translations, it is usually translated as “square”, as in Reference [1]. I preferred here to maintain the original word used by Abū Kāmil. I have referred to translations into a number of languages [1,46,47,49,50]), since the product of by itself is equal to the product of by ; the straight line is the root of māl minus one-tenth of one-tenth of māl-māl and straight line is equal to the straight line ; the straight line is therefore the root of four māl minus two-fifths of one-tenth of māl-māl. But we know that the sum of the product of and plus by itself is equal to the product of by itself, because the product of and plus by is equal to the product of by ; or by is equal to by itself, by is equal to by itself, and by itself is four māl minus two-fifths of one-tenth of māl-māl. Eliminate from this the product of by itself, that is a māl; thus remain three māl minus two-fifths of one-tenth of māl-māl, equal to the product of by . We then divide three māl minus two-fifths of one-tenth of māl-māl by the straight line , which is a thing; we get the straight line , three things minus two-fifths of one-tenth of a cube. But we have shown that the straight line is the root of four māl minus two-fifths of one-tenth of māl-māl. We multiply three things minus two-fifths of one-tenth of a cube by themselves; we get nine māl and one part of six hundred-twenty-five parts of cube-cube minus six parts of twenty-five parts of māl-māl equal to four māl minus two-fifths of one-tenth of māl-māl. Reducing from this, we have a fifth of māl-māl equal to five māl and a part of six hundred twenty-five parts of a cube-cube. Dividing all that you have by a māl, you get five “dirhams” and one part of six hundred twenty-five parts of māl-māl equal to one-fifth of māl. Make whole māl-māl for which you have a māl-māl, and so multiply it by six hundred twenty-five, so all that you have by six hundred and twenty-five; we have a māl-māl plus three thousand one hundred twenty-five “dirhams” equal to one hundred twenty-five māl. Divide the māl into two halves, get sixty-two and a half; multiply them by themselves, you get three thousand nine hundred six and a quarter; subtract three thousand one hundred twenty-five, it remains seven hundred eighty-one and a quarter. We remove the root of this one from sixty-two and a half, we take the root of what remains, we have the straight line which is one of the sides of the pentagon.
All this can be equally and more synthetically expressed in the modern algebraic language as (see Reference [1], pp. 115–117):
Let be the known circle of diameter and let be the regular pentagon inscribed within it. Draw the chord that subtends of the circumference (because each side of the pentagon subtends of the circle). Assume (that is the side of the pentagon we want to find). We know that since (for Euclid’s first theorem applied to the right triangle , in which is a cathetus, and is the projection of on the hypotenuse ).
For Pythagoras’ theorem applied to the right triangle , we have: ; moreover ; therefore, .
We know that because, for Ptolemy’s theorem applied to the quadrilateral , , or , , and . Let us subtract from this ; thus, we remain with . Let us divide the last relation by , and we obtain .
Let us multiply by itself, and we obtain:
Since we have shown that , by equating the two expressions for we have just found, we get . If we divide this relation by , we obtain: .
By multiplying the last relation by 625, we get: . This is a biquadratic equation, in which the acceptable solution (for our problem) is:
Table 1 contains the steps of the solution of the problem under consideration, given through a one-by-one correspondence between Abū Kāmil’s solution expressed in “spoken” algebra and a “translation” in symbolic algebra. The left part of the table shows how, drawing on the knowledge contained in Euclid’s Elements on the pentagon and expressed in the Euclidean geometric register, the problem proposed by Abū Kāmil takes expression and form in the register of rhetorical algebra and how the solution is found through its rules. In other words, a first expression of modeling of the problem and its solution is realized. The right part of the table contains a further expressive passage, the “translation” of the solution in the register in which today’s mathematical culture requires students to learn to express themselves, the one to which Descartes invited us in his Géométrie, that of formal algebra.

Table 1.
The first of the twenty geometric problems that Abū Kāmil solves in the pentagon and decagon chapter. The left part contains the problem expressed in rhetorical algebra. The right part contains a translation in the register of symbolic algebra.
In this way, students can be stimulated to observe how Arabic algebra, as a numerical problem solving technique, uses the properties of the figure considered, expressed by Euclid in the geometric language of the Elements, in order to write the equation that solves the proposed problem and then to express themselves with the signs of our current mathematical culture.
In order to facilitate understanding of the learners, in Table 2 a translation of the symbols from spoken algebra to symbolic algebra used in Table 1, is shown.

Table 2.
Table useful to convert from rhetorical algebra into symbolic algebra for the fundamental operations.
Students of secondary school can be pointed out that Abū Kāmil starts from Euclid’s result (Elements IV, 11), which allows him to think of the given figure as “built”. This gives meaning to the search for the length of its side. This measure constitutes new knowing, produced by diversification through semiotic change. The “dual” and crucial role of Euclidean constructions becomes evident. Euclid teaches to build and attributes the dignity of existence to objects that become “realizable” and therefore “measurable” with the new creative role in the signs of algebra [34].
Both the drawn figure and the beginning of Abū Kāmil’s speech are in the Euclidean register for the terms introduced, for the use of capital letters to indicate points and segments, and for the proposal to “build” the straight line . When Abū Kāmil assumes equal to “a thing”, the register changes: in fact, he passes from the geometric register to the algebraic register.
At this stage, students can observe and learn, on an elementary example, how the change of register instantly generates the beginning of the process that will then be named mathematical modeling by the teacher.
While Abū Kāmil indicates with the term “draw” the movement made in Euclid’s “space”, in which the construction takes place, with the term “assume” he introduces the reader to the algebraic “narrative” and, therefore, to the possibility of taking a measurement. It is in this passage that one can see the beginning of those semiotic transformations described in Reference [29,36,37].
Abū Kāmil continues to transform the “objects” from the Euclidean to the algebraic register, justifying each passage with appropriate Euclidean propositions, up to obtaining for the square of two expressions in which the “thing” appears. By matching the two expressions, he obtains the equation that allows him to solve the problem. Abū Kāmil so completes the operation that, several centuries later, will be taken up by Descartes in his Géométrie (1637). That is, he writes the equation that solves the problem by equating the two different “narratives” that “tell” the same object multiplied by itself. At this point, he resolves the equation in the algebraic register with the passages he learned from the work of al-Khwārizmī.
Having acquired the foregoing, students can now move towards a general formulation of the statement and the solution of the same proposition, introducing the concept of parameter and reflecting on the articulated relationship between parameter and unknown. Introducing the concept of parameter and reflecting on the relationship between parameter and variable leads one to imagine dynamic transformations of the figure. In the transition from the particular case to the generalized case, students can be guided to consciously complete the linguistic transformation, to comment on its effects and descriptive effectiveness, gradually acquiring familiarity with forms of increasing complexity and flexibility in interpreting, reflecting, and analyzing.
In the example, if one indicates the diameter of the circle with the parameter (), one can rewrite the proposition in the following way:
Find the side of the regular pentagon inscribed within a circle of diameter .
With the aim to facilitate the understanding of the students, in Figure 3, a pictorial representation of this problem is given.
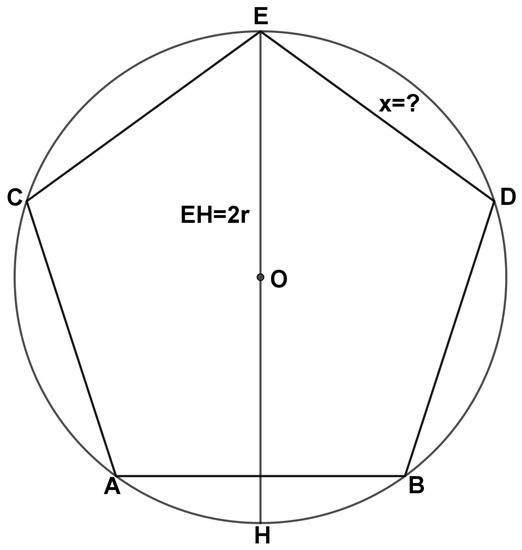
Figure 3.
Pictorial representation of the problem proposed to students in its general form.
By going over the steps contained in the right part of Table 1, one can determine the acceptable solution for the problem: .
The new formulation allows us to observe that the relationship between the side x of a regular pentagon and the radius r of the circle circumscribing it is constant and independent of the pentagon considered: .
In the given semiotic and epistemic reading, this generalization, with the introduction of parameters, has the characteristics of a new core of “knowledge” produced by the “determination” constituted by the moment of the particular solution produced in numerical terms. In this sense, it is configured as an example similar to those described in Reference [3,16].
When a proposition (statement and solution) is formulated in a more general language, a reflection naturally takes on what character the geometric construction offered in the Elements assumes with the parameterization.
Considering a “parameter”, that is a “variable” measure among the positive values that can be assumed, gives the construction a more universal reading, that is, a reading that includes all possible cases. Thus, that particular figure, which expresses a specific case, is not considered, if not exceptionally, in its specificity, but rather in the context of the general formulation of the problem: that figure contains in itself all possible cases. Consequently, to look at “that” figure implies a rational and intellectual vision, for which the physical “looking” is only the starting point of observation.
On the sidelines to the solution of Abū Kāmil’s problem, it is also possible to reflect on a possible extension of its use within the teaching of plane analytic geometry. This immediately leads to the realization that “treating” the equations does not automatically imply being in the context of the “analytical method”. The equation treated in this path has its own consistency, and it helps to understand what it means to operate in algebra. But, if the teacher wants to lead students to give a meaning to this specific equation in the context of analytic geometry, he should “re-read” inside it its geometric texture.
In this regard, students can be noted that the ontological character of the solution of the problem is a length (that of the side of the pentagon). This solution expresses the length of the side of the pentagon in units of the radius of the circumscribed circle; that is, the side of the pentagon, which has the dimensions of a length, is proportional, through the dimensionless constant , to the radius of the circumference, which also has the dimensions of a length. There is therefore a linear relationship between the side of the pentagon and the radius of the circle. Being the latter positive, the equation that describes the dependence between the x side and the radius r will be represented, in the Cartesian plane , as a half-line coming out of the origin.
Then, wanting to interpret the problem proposed in the context of analytic geometry, it can be observed that the length of the side of the pentagon depends, “is a function” of the radius of the circumscribed circle. One can express this by writing (k constant, and ), which represents the half-lines of the first quadrant, each point of which is a solution of the problem. Thus, one is faced with infinite solutions (infinite are the points of a half-line), and the half-line is the “locus” of the solutions of the problem.
In the same chapter of the book Kitāb fī al-jabr wa al-muqābala, Abū Kāmil further calculated the length of the sides of the regular decagon (see Reference [1], pp. 526–529) and of the regular polygon with 15 sides (see Reference [1], pp. 546–551) both inscribed in a circle of radius 10. Therefore, the linear relation , already found for the regular pentagon inscribed in a circle, can be generalized in the form: in the case of a polygon with n sides. Here, below, the values for the cases , and are given:
Such a situation is given a representation in terms of analytic geometry in Figure 4, in which some solutions of the generalized problem, , for the three values of corresponding to , and , are shown in the first quadrant of the Cartesian plane. The black half-line, in particular, represents the solution for the side of the regular pentagon inscribed in the circle of radius r and the point S is the solution found by Abū Kāmil, obtained in the case . Analogously, the blue and red half-lines represent the solutions for the regular decagon and polygon with 15 sides, respectively, and the points Q and P are the solutions found by Abū Kāmil.
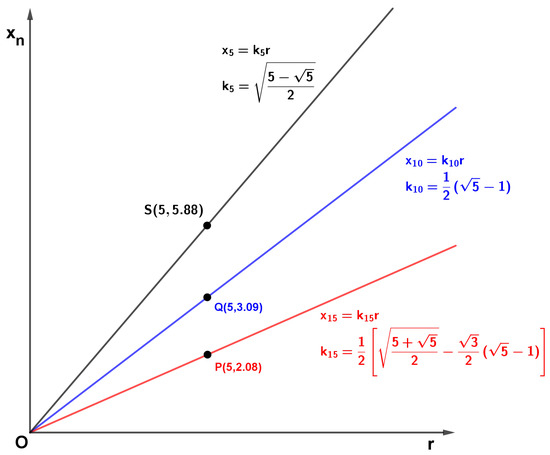
Figure 4.
Diagram showing the solution of the generalized problem in the first quadrant of the cartesian plane for three different values of n: , black half-line; , blue half-line; , red half-line. The points S, Q, and P lying on the three half-lines represent the solutions found by Abū Kāmil in the case , for the three cited values of n, respectively.
One therefore arrive, naturally, at modeling the locus of solutions of the generalized problem.
4. Discussion
The didactic proposal presented in this article allows to concretely follow: the realization of a metamorphosis of objects, described in the Euclidean register, into the same objects, told in the algebraic-rhetorical register; the translation of the same objects in terms of symbolic algebra; the transition from the particular formulation of a problem to its general formulation, hinting at its possible use within analytic geometry. All this helps to recognize, in different contexts, results obtained in a specific context, making possible an intellectual experience of a continuum of meaning instead of a discontinuity, which is often found in mathematics teaching, between learning geometry and learning algebra.
The reference to results present in the Elements, as well as to the theorem of Ptolemy and that of Pythagoras, within the proof of the proposition, contributes to creating a unitary vision of mathematics and an awareness of the strength inherent in a new semiotic transformation.
The use of history of mathematics to improve learning abilities of the students has been largely discussed in several works. The proposed path could even be used in the framework of the Mathematical Knowledge for Teaching. In particular, comparing the approach of the present work with Reference [2], some similarities with their case study n. 1 emerge, although they used a different (and more modern) geometrical example excerpted from Viète’s theory of equations. For instance, the model they show in Figure 1, that provides an analysis of meta-discursive rules in the excerpt from Viète versus modern day meta-discursive rules, can be compared to Table 1 of the present work. This shows how examples of this kind could be of fundamental importance not only for the learning process of students but for the training of teachers, as well. This kind of approach could be the starting point for further developments that will be given in future works.
5. Conclusions
In this work, a possible didactic path has been presented, that could be followed in a secondary school class, in which it is shown a relationship between geometric knowledge and algebraic knowledge. The starting point for this didactic path was the first proposition of a chapter of the book Kitāb fī al-jabr wa al-muqābala written by the Arab mathematician Abū Kāmil before the year 870. Starting from Abū Kāmil’s proof, based on Euclidean geometric properties and expressed in the language of spoken algebra, and afterwards in the language of symbolic algebra, the learners can apprehend to “translate” from a mathematical language to another. This is a paradigmatic example to experiment with the changes in registers with which mathematics is expressed and to assess how such a procedure can be received by the students. This kind of approach can help the learners to be trained with the process of generalizing a problem and constitutes a starting point in mathematical modeling. This is the basis for modern science, as well as also a fundamental component for the application of computer science to the solution of scientific problems.
This didactic path has the further advantage of making the students aware of the huge power of symbolic algebra with respect to spoken algebra. Not only the language of symbolic algebra is more compact and versatile, when compared to spoken algebra, since it can treat similar situations with the same formalism, but also the use of symbolic algebra is a necessary prerequisite for mathematical modeling. Last but not least, the use of symbolic algebra makes the communication of scientific results almost independent on the language spoken by the persons, resulting in a more “universal” approach to scientific advancements.
Reflecting on the link between the formulation of a problem and its geometric construction [44,45], understanding how the “feasibility” of the geometric construction supports the possibility of “narrating” the objects of the image in algebraic language up to identify an equation that models the problem, understanding the character of the root that solves an equation [51], identifying one of the first historical sources of the long path that will lead to express similar problems in the context of the analytical method, etc., all opens culturally broader horizons in which successive mathematical theories will develop and opens the students’ mind towards new situations that stimulate their creative potential.
6. Patents
There is no patent resulting from the work reported in this manuscript.
Author Contributions
All the work contained in this manuscript has been done by E.F. The author has read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The author declares no conflict of interest.
References
- Rashed, R. Abū Kāmil: Algèbre et Analyse Diophantienne; Walter de Gruyter GmbK & C.: Berlin, Germany, 2012; ISBN 311029561X. [Google Scholar]
- Jankvist, U.T.; Clark, K.M.; Mosvold, R. Developing mathematical knowledge for teaching teachers: Potentials of history of mathematics in teacher educator training. J. Math. Teach. Educ. 2020, 23, 311–332. [Google Scholar] [CrossRef]
- Takeko Gobara, S.; Radford, L. Teoria da Objetivação: Fundamentos e Aplicações para o Ensino e Aprendizagem de Ciências e Matemática; Livraria da Fìsica: São Paulo, Brasil, 2020; ISBN 9788578616380. [Google Scholar]
- Mosvold, R.; Jakobsen, A.; Jankvist, U.T. How mathematical knowledge for teaching may profit from the study of history of mathematics. Sci. Educ. 2014, 23, 47–60. [Google Scholar] [CrossRef]
- Ball, D.; Thames, M.; Phelps, G. Content knowledge for teaching: What makes it special? J. Teach. Educ. 2008, 59, 389–407. [Google Scholar] [CrossRef]
- Furinghetti, F. Teacher education through the history of mathematics. Educ. Stud. Math. 2007, 66, 131–143. [Google Scholar] [CrossRef]
- Bagni, G.T. History of Mathematics and Didactics: Reflections on teachers education. In ICME–10, Discussion Group 6, Proceedings of the 10th International Congress on Mathematical Education, Roskilde, Denmark, 4–11 July 2004; Niss, M., Ed.; IMFUFA: Roskilde, Denmark, 2004. [Google Scholar]
- Bagni, G.T. Linguaggio, Storia e Didattica Della Matematica; Pitagora: Bologna, Italy, 2006; ISBN 8837116276. [Google Scholar]
- D’Enfert, R.; Djebbar, A.; Radford, L. Dimensions historique et culturelle dans l’enseignement des mathématiques. In Compte-Rendu du Groupe de Travail No. 4, Proceedings of EMF2012-GT4 Espace Mathématique Francophone, Geneva, Switzerland, February 2012; Dorier, J.-L., Coutat, S., Eds.; EMF: Geneva, Switzerland, 2012; pp. 523–528. [Google Scholar]
- Kobiela, M.; Zanazanian, P. Crossing Disciplinary Borders in Pre-service Teacher Education: Historical Consciousness as a Tool to Develop Awareness of Mathematical Positionality to Achieve Epistemic. In Borders in Mathematics Pre-Service Teacher Education; Radakovic, N., Jao, L., Eds.; Springer: Cham, Switzerland, 2020; pp. 47–73. ISBN 978–3-030-44292-7. [Google Scholar]
- Boero, P.; Guala, E. Development of mathematical knowledge and beliefs of teachers: The role of cultural analysis of the content to be taught. In The International Handbook of Mathematics Teacher Education; Sullivan, P., Wood, T., Eds.; Sense: Rotterdam, The Netherlands, 2008; Volume 1, pp. 223–244. ISBN 978-90-8790-542-2. [Google Scholar]
- Radford, L. On Psychology, Historical Epistemology and the Teaching of Mathematics: Towards a Socio-Cultural History of Mathematics. Learn. Math. 1997, 17, 26–33. [Google Scholar]
- D’Amore, B.; Fandiño Pinilla, M.I. Storia ed epistemologia della matematica, basi etiche. La Matematica e la Sua Didattica 2005, 19, 503–515. [Google Scholar]
- Radford, L. The ethics of being and knowing: Towards a cultural theory of learning. In Semiotics in Mathematics Education: Epistemology, History, Classroom, and Culture; Radford, L., Schubring, G., Seeger, F., Eds.; Sense: Rotterdam, The Netherlands, 2008; pp. 215–234. ISBN 978-90-8790-596-5. [Google Scholar]
- Roth, W.M.; Radford, L. A Cultural Historical Perspective on Teaching and Learning; Sense: Rotterdam, The Netherlands, 2011; ISBN 9460915620. [Google Scholar]
- D’Amore, B.; Radford, L. Enseñanza y Aprendizaje de Lasmatemáticas: Problemas Semióticos, Epistemológicos y Prácticos; Universidad Distrital Francisco José de Caldas: Bogotá, Columbia, 2017; ISBN 978-958-5434-48-6. [Google Scholar]
- Fauvel, J. Using history in mathematics education. Learn. Math. 1991, 11, 3–6. [Google Scholar]
- Bartolini Bussi, M.G.; Sierpinska, A. The relevance of historical studies in designing and analysing classroom activities. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluwer: Dortrecht, The Netherlands, 2000; pp. 154–160. ISBN 978-0-306-47220-6. [Google Scholar]
- Furinghetti, F.; Radford, L.; Katz, V. The history of mathematics in mathematics education: Theory and practice. Educ. Stud. Math. 2007, 66, 107–271. [Google Scholar] [CrossRef]
- D’Amore, B.; Speranza, F. La Matematica e la Sua Storia. Alcuni Esempi per Spunti Didattici; Angeli: Milano, Italy, 1995; ISBN 8820493543. [Google Scholar]
- Jahnke, H.N.; Arcavi, A.; Barbin, E.; Bekken, O.; Furinghetti, F.; Elidrissi, A.; Silva da Silva, C.M.; Weeks, C. The use of original sources in the mathematics classroom. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluver: Dordrecht, The Netherlands, 2000; pp. 291–328. ISBN 978-0-306-47220-6. [Google Scholar]
- Radford, L.; Bussi, M.G.B.; Bekken, O.; Boero, P.; Dorier, J.L.; Katz, V.; Rogers, L.; Sierpinski, A.; Vasco, C. Historical formation and student understanding of mathematics. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluver: Dordrecht, The Netherlands, 2000; ISBN 978-0-306-47220-6. [Google Scholar]
- Clark, K.M.; Kjeldsen, T.H.; Schorcht, S.; Tzanakis, C. History of Mathematics in Mathematics Education— An Overview. Math. Didact. 2019, 42, 1–26. [Google Scholar]
- Carreira, S.; Barquero, B.; Kaiser, G.; Cooper, J. Introducing CERME’s Thematic Working Group 6— Applications and Modelling. Newsl. Eur. Math. Soc. Math. Educ. ERME Column 2019, 111, 48–49. [Google Scholar]
- Stillman, G.A.; Blum, W.; Salett Biembengut, M. Mathematical Modelling in Education Research and Practice Cultural, Social and Cognitive Influences, International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer International Publishing: Cham, Switzerland, 2015; ISBN 9783319182711. [Google Scholar]
- Barbin, É. Les Constructions Mathématiques avec des Instruments et des Gestes; Ellipses: Paris, France, 2015; ISBN 2340002060. [Google Scholar]
- Radford, L.; Boero, P.; Vasco, C. Epistemological assumptions framing interpretations of students understanding of mathematics. In History in Mathematics Education. The ICMI Study; Fauvel, J., Van Maanen, J., Eds.; Kluver: Dordrecht, The Netherlands, 2000; pp. 162–167. ISBN 978-0-306-47220-6. [Google Scholar]
- Furinghetti, F. Rethinking history and epistemology in mathematics education. Int. J. Math. Educ. Sci. Technol. 2020, 51, 967–994. [Google Scholar] [CrossRef]
- Duval, R. Understanding the Mathematical Way of Thinking: The Registers of Semiotic Representations; Springer International: Cham, Switzerland, 2018; ISBN 3319569090. [Google Scholar]
- Bartolini Bussi, M.; Mariotti, M.A. Semiotic mediation in the mathematics classroom: Artefacts and signs after a Vygotskian perspective. In Handbook of International Research in Mathematics Education, 2nd ed.; English, L., Ed.; Routledge, Taylor and Francis: New York, NY, USA, 2008; pp. 746–783. ISBN 9780415832045. [Google Scholar]
- Sáenz Ludlow, A.; Kadunz, G. Semiotic as a Tool for Learning Mathematics; Sense: Rotterdam, The Netherlands, 2016; ISBN 9463003363. [Google Scholar]
- Radford, L.; Schubring, G.; Seeger, F. Semiotics in Mathematics Education: Epistemology, History, Classroom, and Culture; Sense: Rotterdam, The Netherlands, 2008; ISBN 978-90-8790-596-5. [Google Scholar]
- Presmeg, N.; Radford, L.; Roth, M.; Kadunz, G. Signs of Signification. Semiotics in Mathematics Education Research; Springer: Cham, Switzerland, 2018; ISBN 978-3-319-70286-5. [Google Scholar]
- Florio, E.; Maierù, L.; Fenaroli, G. The construction of regular polygons between geometry and algebra: A didactic-historical example. Learn. Math. 2020, 40, 23–24. [Google Scholar]
- Radford, L. De la teoría de la objetivación. Rev. Latinoam. Etnomatem. 2014, 7, 132–150. [Google Scholar]
- D’Amore, B. Oggetti matematici e senso. Le trasformazioni semiotiche cambiano il senso degli oggetti matematici. La Matematica e la Sua Didattica 2006, 4, 557–583. [Google Scholar]
- D’Amore, B.; Fandiño Pinilla, M.I.; Iori, M. Primeiros Elementos de Semiótica. Sua Presença e Sua Importância no Processo de Ensino-Aprendizagem da Matemática; Livraria da Física: Sao Paolo, Brazil, 2015; ISBN 9788578613525. [Google Scholar]
- Blum, W.; Leiss, D. How do students and teachers deal with mathematical modelling problems? The example “Filling up”. In Mathematical Modelling (ICTMA 12): Education, Engineering and Economics; Haines, C., Galbraith, P., Blum, W., Khan, S., Eds.; Woodhead Publishing: Cambridge, UK, 2007; pp. 222–231. ISBN 1904275206. [Google Scholar]
- Kaiser, G. Mathematical modelling and applications in education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; ISBN 978-94-007-4978-8. [Google Scholar]
- Schukajlow, S.; Kaiser, G.; Stillman, G. Empirical research on teaching and learning of mathematical modelling: A survey on the current state-of-the-art. ZDM Math. Educ. 2018, 50, 5–18. [Google Scholar] [CrossRef]
- Stillman, G.A.; Kaiser, G.; Blum, W.; Brow, J.P. Teaching Mathematical Modelling: Connecting to Research and Practice, International Perspectives on the Teaching and Learning of Mathematical Modelling; Springer Science + Business Media: Dordrecht, The Netherlands, 2013; ISBN 9789400765399. [Google Scholar]
- Rashed, R. Al-Khwārizmī. Le commencement de l’algèbre; Librairie Scientifique et Technique A. Blanchard: Paris, France, 2007; ISBN 2853672417. [Google Scholar]
- Karpinski, L.C. The algebra of Abu Kamil. Am. Math. Mon. 1914, 21, 37–48. [Google Scholar] [CrossRef]
- Maierù, L.; Florio, E. Le Costruzioni Geometriche: Un Percorso Storico-Didattico tra i Matematici Arabi Dei Secc. IX-XIII: Parte Prima; Aracne: Roma, Italy, 2018; ISBN 882551235X. [Google Scholar]
- Florio, E.; Maierù, L. The scientific knowledge of book XVI De subtilitate by G. Cardano used in the Trattato sulla divinatione naturale cosmologica by P. A. Foscarini. Open J. Humanit. 2019, 1, 385–422. [Google Scholar]
- Sacerdote, G. Il trattato del pentagono e del decagono di Abu Kámil Shogia ben Aslam ben Muhammed. In Festschrift zum Achtzigsten Geburtstage Moritz Steinschneiders; Otto Harrassowitz: Leipzig, Germany, 1896; pp. 169–194. [Google Scholar]
- Lorch, R. Abu Kamil on the pentagon and decagon. In Vestigia Mathematica. Studies in Medieval and Early Modern Mathematics in Honour of H. L. L. Busard; Folkerts, M., Hogendijk, J.P., Eds.; Rodopi: Amsterdam, The Netherlands, 1993; pp. 215–252. ISBN 9051835361. [Google Scholar]
- Pisano, L. Practica Geometriae. In Scritti di Leonardo Pisano Matematico del Secolo Decimo Terzo; Boncompagni, B., Ed.; Tipografia delle Scienze Matematiche e Fisiche: Roma, Italy, 1862; Volume 2. [Google Scholar]
- Levey, M. The Algebra of Abu Kamil, Kitāb fī al-jābr wa’l-muqābala in a Commentary by Mordecai Finzi: Hebrew Text, Translation, and Commentary with Special Reference to the Arabic Text; The University of Wisconsin: Madison, WI, USA, 1966; ISBN 0299038009. [Google Scholar]
- Chalhoub, S. Die Algebra: Kitab al-Gabr wal-Muqabala des Abu Kamil Soga ibn Aslam; Institute for the History of Arabic Science: Aleppo, Syria, 2004. [Google Scholar]
- Florio, E.; Galuzzi, M.; Maierù, L.; Santoro, N. La “nuova algebra” da François Viète a Leonhard Euler; Aracne: Roma, Italy, 2015; ISBN 978-88-548-8866-1. [Google Scholar]
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).