Understanding of Inverse Proportional Reasoning in Pre-Service Teachers

Abstract

From an early age, understanding proportional reasoning is a fundamental pillar in mathematics education, and therefore, teachers should have a thorough knowledge of it. Despite its significance, there are few studies that analyse the difficulties that student teachers have in understanding proportionality, and even less so inverse proportionality. We emphasised inverse missing-value problems by analysing them according to the type of unknown and the representation used. We checked which strategies they use to solve them and related them to other generic problems of proportional reasoning. For such purposes, we used a combined quantitative and qualitative empirical study applied to how pre-service teachers solve fifteen problems. The results show that the representations used in the statements aid their understanding and help solve the problems. Similarly, it is shown here that certain problem-solving strategies complicate proportional reasoning in pre-service teachers.

1. Introduction

“The cornerstone of higher mathematics and the capstone of elementary concepts” is how Lesh et al. [1] (p. 98) defined proportional reasoning. This same definition was paraphrased by Ben-Chaim et al. [2] (p. 49), who stated that, at the elementary school level, it “is the peak of the basic tenets of mathematics”. Furthermore, the National Council of Teachers of Mathematics (NCTM) points out in its Curriculum and Evaluation Standards report [3] (p. 82) that “ the ability to reason proportionally develops in students through grades 5–8. It is of such great importance that it merits whatever time and effort must be expended to assure its careful development”.

Much of the mathematical community agrees that knowledge of proportional reasoning is essential to support algebraic thinking, so their research is crucial for simply understanding where we stand [4]. Despite its fundamental role in learning-teaching, Arican [5] and Lamon [6] indicated that research on proportional reasoning was very limited, especially with regard to teachers’ command of this knowledge.

Some studies (e.g., [2,4,7,8,9,10,11,12]) suggest that teachers, like their pupils, have difficulties with proportional reasoning. Cramer et al. [13] and Lim [14] found that future primary and secondary school teachers in the United States had problems when applying proportionality strategies to problems of constant difference, as they used inappropriate strategies. Similarly, Orrill et al. [11] showed that middle school teachers had difficulty identifying which situations required the use of a proportionality approach and they also confused inversely proportional problems with directly proportional ones.

As Arican [5] asserts, there are even fewer research studies on the proportional reasoning of teachers that explore inverse proportionality, some of which include: [2,4,5,7,14,15,16].

Fisher [16] (p. 160) analysed how 20 secondary school mathematics teachers solved different proportionality problems. For example, in the following problem of inverse proportionality

If it takes nine workers 5 h to mow a certain lawn, how long would it take six workers to mow the same lawn? (Assume that the workers are all performing at the same rate and all working for the entire time).

Fisher [16] found that only 8 of the 20 teachers solved the problem correctly, and among the 12 who were wrong, 9 of them considered that the relationship between the variables was directly proportional.

Lobato et al. [17] indicated that an understanding of ratios and proportions and proportional reasoning, in addition to being an essential part of pupils’ learning, is difficult for teachers to teach. Sowder et al. [18] argued that many teachers (both in pre- and in-service) lack the pedagogical knowledge to teach proportionality.

According to Izsák and Jacobson [7], one of the main problems when teaching proportional relationships is the emphasis on memorising rules to solve problems. Reinforcing that theory, Stemn [19] noted that however valid one of these memorised strategies may be for solving problems of proportionality, such as the cross-multiplication algorithm, it means the pupils do not understand the multiplicative relationship.

When a teacher presents the different proportional magnitudes, it is also common for them to use standardised phrases, such as, “As one magnitude increases, the other also increases, and if one decreases, the other also decreases”; or in the case of inverse proportionality, “When one increases, the other decreases” [20], as seen in [21], which could encourage the use of additive strategies [21]. The same author also points out that the typology of the magnitudes has a relative value because it can vary according to the context and the global relationship with all the magnitudes. Frequently these considerations are not worked on “because teaching is more concerned with simplifying the formulation of the concept of directly or inversely proportional magnitudes than with explaining the true dimensions of the concept” [21].

According to Initiative [22], in order to be able to reason proportionally, pupils must be competent at deciding whether two quantities are proportional. Beckmann [23] indicated that there are two types of proportionality relationships between quantities: a (directly) proportional relationship and an inversely proportional relationship. The word “directly” is written in brackets because the concept of a proportional relationship is usually identified with the directly proportional one. Based on NCTM [24] (p. 19), 7th grade students should “distinguish proportional relationships…from other relationships, including inverse proportionality”.

According to Lamon [25] one of the best ways to understand mathematics requires the transformation of quantities or equations in such a way that some underlying structure remains unchanged. Within the conceptual field of multiplicative structures proposed by Vergnaud [26,27], the product of measures would be the one that would correspond to the inversely proportional relationship, because the product of two quantities would be constant. Within this theory, Beckmann and Izsák [28] (p. 19) observed that the models of multiplication, division and proportional relationship problems could be unified under the equation:

$$M\times N=P$$

where M, N and P are known constants (M = number of groups, N = number of units in each group and P is the total number of units in M groups). If x and y are unknown variables or two covariant values, then the inversely proportional relationships would correspond to the “collection of pairs of x and y values” that satisfy the equation $x\times y=P$. Therefore the product of the values of the inversely proportional quantities remains constant. P would represent the constant of proportionality, and for Lamon [6] this plays a key role in understanding proportionality. “She describes the constant of proportionality as a slippery character, since its role depends on the situation where it is used. For example, she explains that in a graph it is the slope, in symbols it is a constant, in rate situations it is the constant rate, in reading maps it is the scale, in similar figures it is the scale factor, and it may mean the percentage if we think about sales tax.” [15].

As indicated by Riley [4], it is imperative that prospective teachers have an extensive, in-depth knowledge of proportional reasoning that goes far beyond the application of a cross-multiplication strategy in order to consolidate, through proportional reasoning, the mathematical foundations that students will need in the future for other content, such as algebra.

2. Objective

The main objective of our research was to explore, in pre-service teachers, the understanding of proportional reasoning by focusing on inverse proportionality, identifying representations that help with its understanding and offering a plausible model that explains the emergence of errors, especially confusion with direct proportionality.

Carrying on from the research carried out by Arican [29] and Riley [4], we intended to characterise the proportionality comprehension by studying what kind of problem-solving strategy pre-service teachers use, in this case, almost exclusively, for inverse proportionality problems. We further investigated the influence of the type of unknown (whether intensive quantity (IQ) or extensive quantity (EQ)) and also the variety of representation systems used to provide information in the statement. As in Cabero and Epifanio [30], it is important to discern the needs of learners in order to more accurately implement and focus the support we give them.

In this article, specifically, we will:

i

Study the proportional reasoning skills of pre-service teachers, using a range of problems (missing-value, comparison, additive thinking and mean value).

ii

Determine whether there are differences in the types of answers to problems of inverse proportionality, with unknowns in intensive and extensive amounts, depending on whether or not different representations are included in the statements.

iii

Describe the difficulties and the types of incorrect answers that prospective teachers give in this type of task.

iv

Identify which method they use to solve the different types of inverse proportionality problems.

3. Problems Features

A set of 15 problems has been used to collect the data. As we were interested in studying inverse proportionality, twelve of them were inverse missing-value problems. Regarding the remaining three, as indicated by Lobato et al. [17] (p. 78), it was necessary to contrast the problem-solving capacity for a specific problem model with other types of problems in order to really discern the degree of proportional reasoning that our population had. We therefore chose a mean value problem proposed by Lobato et al. [17] (p. 79), one of inverse proportionality, which also involves additive thinking, as proposed by Sinn and Spence [31] and obtained in Riley [4] (p. 1058), and another comparison problem of inversely proportional magnitudes. All three suggest a semantic relationship with inverse proportionality, even though they are solved differently from inverse missing-value problems. From now on, we will refer to these three problems as “generic proportional reasoning problems” (GPRP).

We also added the support of the most commonly used systems of representation (graphs and tables) to some problem statements in order to investigate their impacts on how the problems are solved and on the types of strategy used. More specifically, out of the fifteen problems considered, the three problems that referred to a more generic reasoning (GPRP), which did not focus exclusively on inverse proportionality, did not have any additional representations for the statement. The remaining twelve problems are divided into two sets, where the unknown of six of them refers to an intensive quantity and the other six to an extensive quantity. In both groups, the six problems are represented as follows:

• Word problem where the data and the unknown use a double-half relationship.
• Word problem + graphic representation needed to obtain the data.
• Word problem + table needed to obtain the data.
• Difficult word problem + graphic representation (not essential to solve the problem).
• Word problem.
• Gear word problem + visual representation of the gear ratio or wheels.

It was expected that the latter representation would generate a verification mechanism that could possibly help students to understand the implicit inverse relationship in gears and how it is solved.

Table 1. List of the basic features of the problems.

Problem Number	Context	Type of Problem	Type of Unknown	Feature
I	Cake	Inverse missing-value	IQ	Double/half
II	Helmet	Inverse missing-value	IQ	Required use of the graph
III	Gears	Inverse missing-value	IQ	Visual representation
IV	Water	Inverse missing-value	EQ	Graphs help
V	Bread	Inverse missing-value	EQ	Chart help
VI	Balloons	Inverse with additive thinking
VII	Teams	Comparison
VIII	Compare	Mean value
IX	Guitar	Inverse missing-value	EQ
X	Pie	Inverse missing-value	IQ	Chart help
XI	Puzzles	Inverse missing-value	EQ	Double/half
XII	Transport	Inverse missing-value	IQ	Graphs help
XIII	Bicycle	Inverse missing-value	EQ	Visual representation
XIV	Decoration	Inverse missing-value	EQ	Required use of the graph
XV	Bricklayers	Inverse missing-value	IQ

shows the basic features of the problems in the same order in which they were solved by the students. Note that GPRP problems differ from missing-value problems and are not involved in the analysis of the types of unknown and the representations used.

The original problems are:

I

Cake: George is making cakes and he has a bag of blackberries. Right now, he can make about 12 cakes with 7 blackberries per cake. With the same number of blackberries, how many blackberries per cake should he put in, if he is going to make 24 cakes?

II

Helmet: George’s friends want to give him a bicycle helmet as a present. The following chart shows the amount in € that each friend would have to pay according to the number of friends involved. How much money do each of them have to pay if they are 6 friends?

III

Gears: The green gear has 18 teeth and has made 14 turns in a specific period; how many teeth will the red gear have to have to make 36 turns in that period?

IV

Water: We are filling a water tank from a tap. If the flow of the tap was 6 L/min, it would take 8 min to fill it. How many minutes will it take if the flow increases by 2 L/min?

V

Bread: Olivia and Charlie are making sandwiches that will be sold at a charity fair. If they make 3 sandwiches from each stick of bread, they have enough with 14 sticks of breads. How many sticks of bread will they need if they make 2 sandwiches from each stick of bread?

VI

Balloons: Hannah and Adele are decorating the gym with helium-filled balloons for the graduation. Hannah can inflate and tie off 7 balloons every 6 min. Adele takes 3 min to finish 4 balloons. Working together, how long will it take for them to have 25 balloons ready?

VII

Teams: Two teams of workers have built a wall, with the same dimensions on each side of a road. One team had 7 workers and it took 2 days to build it while the other, with only 5 workers, took 3 days. Which team was more efficient?

VIII

Compare: Gear A has 48 teeth, and gear C has 12 teeth. How many teeth should gear B have so that the ratio of revolutions of gear A to gear B is the same as the ratio of revolutions from gear B to gear C?

IX

Guitar: In a guitar workshop, working at a rate of 6 guitars/day, it takes 10 days to complete an order. How many days will it take to complete the same order if they work at a rate of 4 guitars/day?

X

Pie: We are cutting birthday cakes into pieces. If we divide each cake into 8 pieces we have enough with three cakes. For the same birthday party, if we had four cakes, how many pieces would we have to cut per cake?

XI

Puzzles: Some teachers have a lot of wooden pieces to make puzzles for students. They want to use all the pieces. If they make 8 puzzles they could use 64 pieces in each one. If they used 32 pieces in each puzzle, how many puzzles could they make?

XII

Transport: A lorry driver must plan the route. If he drives at 100 km/h, he knows that it will take 35 h in total. How fast should he go to make the journey take 15 h longer?

XIII

Bicycle: A bicycle has unevenly sized wheels. The circumference of the rear wheel is 80 cm. In the same distance, the rear wheel has turned 50 times and the front wheel 40 times. What is the circumference of the front wheel?

XIV

Decoration: Every class in a school is in charge of decorating the same space in the garden with pots. The following graph shows the number of flowerpots that each student has to look after according to the number of students in class. How many students will a class in which each student has to look after 7 flowerpots have?

XV

Bricklayers: Some bricklayers are building a wall. A team of 8 bricklayers takes about 18 h to finish it. How many bricklayers will have to work to finish it in 16 h?

Classification of the Different Problem-Solving Strategies

To be able to answer the questions posed in the objectives, we need to classify the pre-service teachers’ answers according to the different reasoning strategies employed.

Although a lot of research has been carried out using different scenarios when classifying proportionality problems for students (e.g., [2,10,32,33,34]), we will use the classification described by Arican [5], Fisher [16], Karplus [35] and Lamon [36], since they used it to classify problems of direct and inverse proportionality solved by in-service or pre-service teachers.

The first five strategies are listed as incorrect and the other four as correct [16] (pp. 161–162):

I1.

No answer.

I2.

Intuitive: a guess or illogical computation (a correct guess is possible).

I3.

Additive: an incorrect focus on the difference between the given quantities.

I4.

Proportion attempt: the subject realises that proportion is involved but does not correctly express the relationship.

I5.

Incorrect other: an incorrect solution that cannot be placed in another category;

C1.

Proportion formula: a correct strategy that utilises an equation expressing the equality of two products accompanied by an explicit statement recognising the inverse elationship.

C2.

Proportional reasoning: a correct proportion strategy other than the use of the proportion formula.

C3.

Algebra: a correct strategy utilising an algebraic equation other than the proportion formula.

C4.

Correct other: a correct solution that cannot be placed in another category.

Similarly, we have also considered it relevant to study the two types of quantity, described by researchers, intensive quantity and extensive quantity, based on the definitions shown in [15]:

Schwartz [37] (p. 42) indicated that an intensive quantity is “a type of quantity that is ordinarily not either counted or measured directly”, which can be recognised by the fact that its unit measures contain the word per. For Kaput and West [38] (p. 239), the intensive quantity is used as “a blanket term to cover all the types of quantities typically described in our culture as rates, …unit conversion factors, …scale conversion factors, …”. On the other hand, Thompson [39] (p. 6) defines extensive quantity as “a quantity that may be measured directly or is a combination of directly measurable quantities”.

By considering these two types of quantity, we aim to discern whether the fact that the unknown is an intensive or extensive quantity influences the difficulty of understanding and solving a problem of inverse proportionality.

4. Participants and General Methodology

The set of 15 problems was given to 71 students who were finishing their third year of a teaching degree in primary education at a public university in Spain. Therefore, similarly to Riley [4] and Arican [29], they had already received, besides some didactics, the mathematical training that is given in the degree, including inverse proportionality.

According to Weiland et al. [40] the following requirements in

Table 2. Framework for a robust understanding of proportional reasoning [40].

Robust Understanding	Description
Appropriateness	Not all situations are proportional; therefore, it is important to identify if a situation is appropriate or not for using proportional reasoning based on the mathematical structure of the situation
Reasoning	Proportional relationships can be reasoned about (see earlier definition from Lamon [41] (pp. 637–638))
Structure	There are mathematical structures in proportional situations, and they are important to make use of in sense making and problem solving
Comparison of Quantities	A ratio is a comparison of two quantities
Abstractable Quantity	There is a constant relationship between the two quantities in a ratio that leads to the emergence of a third quantity that can stand on its own (e.g., speed or tartness)
Multiplicative	A proportion represents two quantities whose measures are in a fixed relationship in which one is a multiple of the other, that is, a proportion represents a multiplicative comparison
Variable Parts	Proportional situations can be reasoned about as a fixed number of parts that are variable in size (see  Beckmann and Izsák [28])
Fraction/Ratio Relationship	Ratios and fractions have some distinct differences as well as similarities making it important to realise each and know how to translate from one to the other when appropriate
Multiple Representation	There are multiple representations drawn (e.g., double number lines, ratio tables, strip diagram, etc.) and symbolic (e.g., fraction, decimal, percent) that can support reasoning proportionally
Connections	Proportional reasoning is meaningfully connected to other topics in mathematics, for example: similarity, scale factor, probability, instantaneous rate of change

should be achieved in order to have a robust understanding of proportional reasoning for teaching.

Focusing on mathematical training, which we assessed, and discarding didactic-mathematical knowledge, content on proportionality that our students received included:

• Ratios between two quantities.
• Related figures.
• Magnitudes that are directly proportional: condition of regularity, ratio and inverse ratio.
• Inversely proportional magnitudes: condition of regularity and ratios.
• Comparison problems with directly proportional magnitudes and with inversely proportional magnitudes.
• Missing value problems with directly proportional magnitudes and with inversely proportional magnitudes.
• Compound proportionality.
• Directly and inversely proportional distributions.

Burgos et al. [42] noted that teachers’ training must take into account the development of mathematical and didactic knowledge and skills in relation to each section of the curriculum, including proportionality, through specific training interventions. The pre-service teachers tested had worked on the content, described above, taking into account:

• The types of tasks that have been worked on with the students for simple direct proportionality are those defined by Cramer et al. [13] (pp. 404–407) which were generalised for any type of relationship by Martínez Juste et al. [43]. These are divided into two groups:

  I

  Tasks according to the type of proportional relationship: direct proportionality, inverse proportionality and compound proportionality.

  II

  Proportional reasoning tasks of comparison (qualitative and quantitative) and missing value.

• All these tasks were worked on using different types of magnitudes according to López and Guzmán [44], so examples were presented with extensive (additive magnitudes, such as weight, cardinality or surface) and intensive (non-additive reasons, such as speed, unit price, density or temperature) magnitudes. Examples with discrete continuous magnitudes were presented, as well as fundamental and derived magnitudes.
• The contexts used were: personal, educational or work, public and scientific.
• Representation systems used were those presented by Valverde et al. [45]: symbolic, verbal, algebraic, Cartesian, graphic, tabular and with icons and diagrams.

Likewise, the aforementioned publications [4,29] used students of the same educational level as ours, which opened the door for our research and provides a reference point for analysing the data obtained. In any case, our approach is different, since we focus on the reasoning of inverse proportionality and use a large set of problems that will allow us to investigate more detailed aspects such as the type of variable and the representations used in the statement.

As described by Kelle and Buchholtz [46], we have combined a quantitative empirical study with a subsequent qualitative case study in order to enhance the virtues of both methods within the analysis carried out.

The empirical results, which are obviously descriptive, were obtained from a non-random convenience sample. The problem solving was not voluntary and all the students in both groups participated in the study. It should be noted that there was no reward or punishment for correctly or incorrectly solving problems.

Instruments

In this research we used a combination of two telematic tools (a GeoGebra book and a form https://www.geogebra.org/m/gnh4xpr9#material/pbwu6esc) that allowed us to record open answers to the 15 proposed problems. The use of GeoGebra also provided a more attractive environment in which to display charts, interactive graphs and gear representations that were either necessary to obtain data or facilitated the emergence of the underlying inverse relationship.

In addition, when carrying out the qualitative study, semi-structured personal interviews with students were used with the aim of extending and enriching the reasoning used to solve the problems.

The R [47] code and data for reproducing the results are freely available at https://drive.google.com/file/d/1W-rRJcKINkYhL4qO-wIVScexi7WzTpCX/view?usp=sharing.

5. Results

The following

Table 3. Answers to problems according to strategy.

	I Cake	II Helmet	X Pie	XII Transport	XV Bricklayers	III Gears
I1. No answer.	0	0	0	0	0	0
I2. Intuitive	0	0	0	0	0	0
I3. Additive	2	0	1	0	2	3
I4. Proportion attempt	12	0	4	7	10	22
I5. Incorrect other	4	11	0	6	5	14
C1. Proportion formula	4	4	15	19	34	15
C2. Proportional reasoning	46	16	49	29	15	14
C3. Algebra	0	0	0	0	0	0
C4. Correct other	3	40	2	10	5	3
% Correct answers	74.6	84.5	93.0	81.7	76.1	45.1
	XI Puzzles	XIV Decoration	V Bread	IV Water	IX Guitar	XIII Bicycle
I1. No answer.	0	0	0	0	0	0
I2. Intuitive	0	0	0	0	0	0
I3. Additive	0	0	0	0	1	0
I4. Proportion attempt	9	6	3	14	9	30
I5. Incorrect other	3	8	6	11	0	6
C1. Proportion formula	12	3	9	15	24	15
C2. Proportional reasoning	46	10	44	20	36	17
C3. Algebra	0	0	0	0	0	0
C4. Correct other	1	44	9	11	1	3
% Correct answers	83.1	80.3	87.3	64.8	85.9	49.3

shows the type of answer for each of the questions in the test. In the first row are the questions with unknown IQ, and in the second row, in the same order, analogous questions with unknown EQ. The percentage of correct answers for each of the questions is also displayed.

Upon comparing the results of the problem “VI Balloons” with those obtained in the article [4] (from which the problem was taken), it can be seen that the percentages of correct answers are very similar—39% in Riley’s case and 42% in ours.

The types of answers between parallel problems where the only difference is the type of unknown, IQ or EQ, are similar and there is no significant difference (in most problems the most used strategies coincide) that makes us believe any type of unknown is more difficult to understand. In fact, the total numbers of correct answers with unknown IQ and EQ were 323 and 320, respectively.

The different representations in the problems do encourage the use of a different type of problem-solving strategy, so we have observed the following:

• If the statement clearly showed a double-half relationship with no more representation than the written statement (problems I Cake and XI Puzzles), a large majority of the students who answered correctly used proportional reasoning (82%) and did not use a proportional formula (14%). We understand that this double-half relationship simplifies the understanding of the problem and is the reason why students have been able to use proportional reasoning to a greater extent, which can be exemplified in: “If we have twice as many cakes, we will have to use half as many blackberries in each cake”; and “With half of the pieces in each puzzle, we can make twice as many puzzles”. Even so, there were considerable numbers of students, 16.9% and 12.6% respectively, who mixed up the type of proportionality and applied direct proportionality.
• When the statement had no data and it was necessary to consult the graph (problems II Helmet and XIV Decoration), most students used only the graph to discover the solution (56.3% and 61.9% respectively). In many cases proportional reasoning was also used (looking for the total of euros or the total of flowerpots), and to a lesser extent a formula was used to check the result, based on a more perceptible point of the graph that does not lead any doubt.
• The problems in which tabular representation was a help (problems V Bread and X Pie) had the highest percentages of correct answers, 87.3% and 93.0%, respectively. Mostly, a proportional reasoning strategy was used (looking for the total number of sandwiches or the total number of pieces) to solve it, so we deduce that the table, as well as presenting the ordered data, manages to facilitate an understanding of the problem.
• When there was no other representation apart from the statement, a simple word problem (problems IX Guitar and XV Bricklayers), an increase in the use of the proportional formula was observed in detriment to proportional reasoning, which benefits from representations other than a statement. Not applying proportional reasoning also promotes the wrong choice of proportionality and the use of a direct cross-multiplication strategy.
• The gears or wheel problems (III Gears and XIII Bicycle) were the most complicated. On the one hand, they did not have any tabular or graphic representation. On the other hand, the possible relationship with physical formulas (radius with the circumference and the number of teeth on each gear) made it hard to understand the inversely proportional relationship that was proposed, and the fact that problems can be solved by the multiplicative relationship (if $R_N$ = number of revolutions of the gear N).

  $$R_A\times Num.teet{h}_A=R_B\times Num.teet{h}_B$$
  The percentages of correct answers were 45.1% and 49.3% respectively, the lowest of all the inverse missing-value problems.
• Problems in which a graph was added as a supporting element (problems IV Water and XII Transport) had added difficulty; they had more complicated statements by indirectly hiding the final unknown (11 and 6 students, respectively, answered wrongly because of the statement). This is the reason why the effect of a graphic representation has not been reflected and why this is the pair of problems with the least similarity.

Differences between Inverse Missing-Value Problems and GPRP Answers

The proportion of correctly solved problems is shown separately in two sequential charts in Figure 1—in the upper one the rate of correct answers for the three more general proportionality problems (GPRP), and in the lower one for the twelve inverse missing-value problems (EQ + IQ), expressed as per-unit.

Although there is a certain similarity for the trends of the results of both sets of problems, that is not conclusive (if we apply a linear regression model, we obtain a multiple R-squared: 0.249, and therefore the linear relationship is not confirmed).

However, we have indeed found a relationship between the strategy used to solve the inverse missing-value problems and the number of well-solved GPRPs

Table 4. Comparison between the strategy used to solve the inverse missing-value problems and the number of well-solved GPRPs.

	Total %	High GPRP %	Low GPRP %
I1. No answer.	0	0	0
I2. Intuitive	0	0	0
I3. Additive	1.1	1.4	0.7
I4. Proportion attempt	14.8	7.2	22.0
I5. Incorrect other	8.7	5.0	12.3
C1. Proportion formula	19.8	18.8	20.8
C2. Proportional reasoning	40.1	51.4	29.2
C3. Algebra	0.0	0.0	0.0
C4. Correct other	15.5	15.9	15.0

. If we compare the percentage of the strategy type (in the inverse missing-value problems) of those who have two or three correct answers in the generic proportional reasoning problems (high GPRP), with those who have only one or no correct answers (low GPRP), we notice a large difference in the use of algebraic reasoning (from 51.4% to 29.2% respectively) and in the number of errors caused by confusion regarding the type of proportionality (7.2% and 22%, respectively). We think that these dissimilarities reflect the difference in proportional reasoning capacity, which is shown in a different use of algebraic reasoning and a higher rate of error when discerning the type of proportionality to be used.

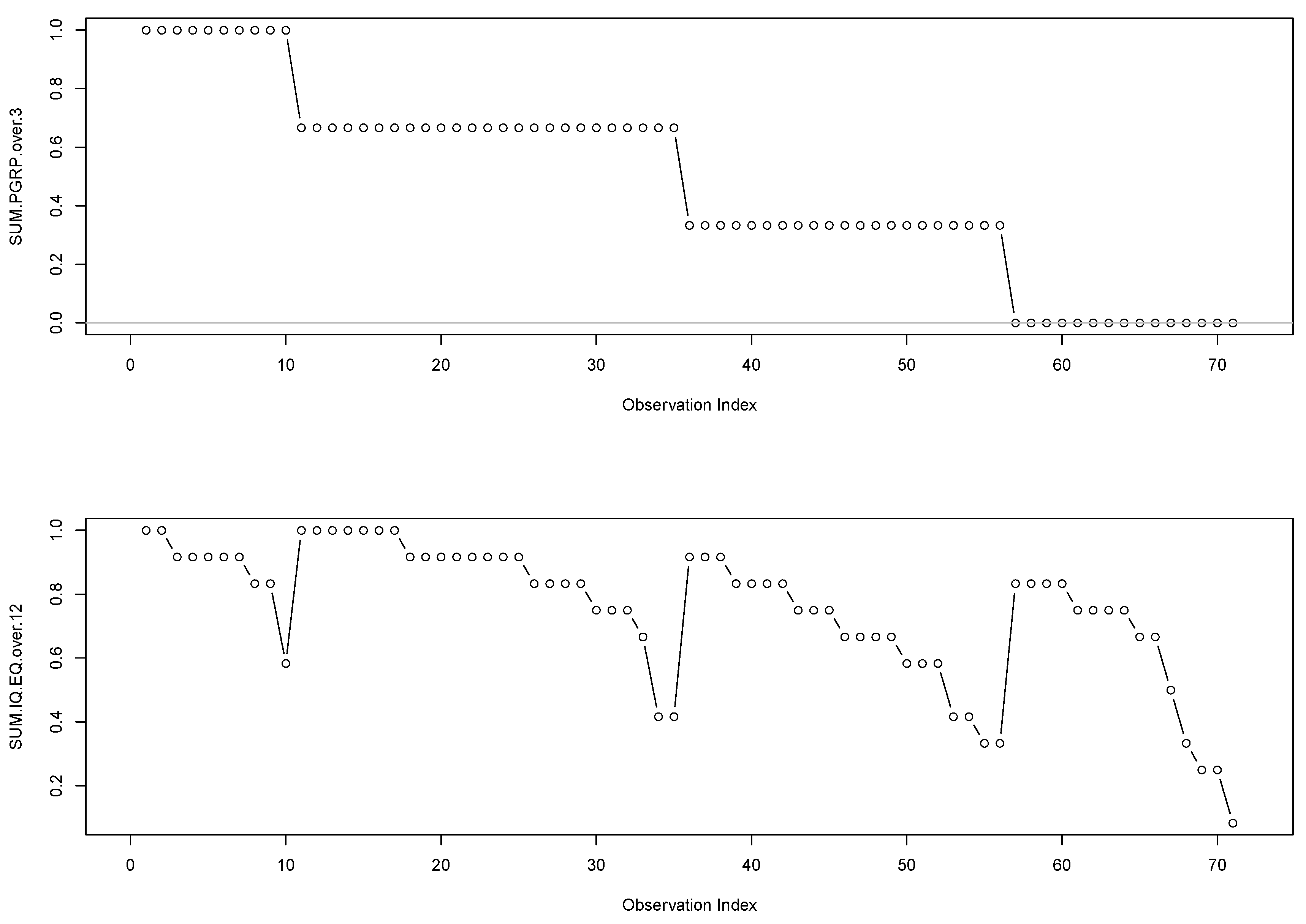
6. Cases Studies

In this research, we consider it very enriching to use a case study for an in-depth examination of pre-service teachers’ understanding of proportionality relationships, especially inverse proportionality. Studying cases where important errors are made that may provide clues on how to help students in the future.

Five students were selected; three of them occupied extreme positions within graph Figure 1 (high score in GPRP and low in inverse missing-value problems; low score in GPRP and high in inverse missing-value problems; and finally, the one with the lowest score in both types of problems). We also included two students with large differences between IQ and EQ problems.

In other words, we examined a different student for each of the following categories:

• A high number of correct answers in GPRP problems and low numbers of correct answers in IQ and EQ problems.
• High numbers of correct answers in IQ and EQ problems and a low number of correct answers in GPRP.
• A high degree of confusion about the type of proportionality.
• A high number of correct answers in EQ and a low number of correct answers in IQ.
• A high number of correct answers in IQ and a low number of correct answers in EQ.

The data in this qualitative study came from the pre-service teachers’ written responses to the fifteen open problems and short semi-structured video interviews.

The explanations given by the students for their answers appear in inverted commas.

6.1. Student 1

This student was chosen due to the difference between correct EQ (3) and correct IQ (1) answers and for the casuistry of errors or misinterpretations, which is rich in nuances.

• Helmet In the first problem we show that, although she understood the question, it seems that she did not quite understand the graph and confused the value on the x-axis, because she thought that the graph showed what each of the friends paid, which would be numbered from one.
  “The first 24, the second 16, another 14, another 9, another 7 and another 6. I guessed the answer”.

In the remaining answers, she understood that there was a relationship of proportionality and the direction of it (if the result is to be greater or less than a certain quantity), but as she did not know how to calculate it, she used additive strategies:

• Teams The student compares the magnitudes of the two variables equally. “Faster with 7 workers, but more efficient with 5. That’s two few members less and it only took one more day”.
• Compare In this problem she knows that the answer has to be between the two numbers. However, since she does not know how to solve it, she comes up with a solution as if there were an additive relationship. “36. Gear B has to be smaller than gear A but larger than gear C. In order to find out how many teeth gear B should have, I subtracted 12 from 48”.
• Cake “4 pieces. The table gives us the information that, with two cakes, they cut 12 pieces, and with three cakes, 8 pieces. I solved it by looking for the difference between 12 and 8, which is four”.
• Bricklayers In this problem the student translates the statement into an algebraic form, using the “word order matching process” [48], which does not correspond to the truly proportional relationship it has. “10 bricklayers. First I tried the cross-multiplication strategy, but I got fewer bricklayers in a shorter time and it didn’t fit, so I used an equation (to try it out) that was 8 + 18 = x + 16, which gave me ten. I saw that it made sense, since the difference between 16 h and 18 h is 2 h, and the difference between 8 and 10 is 2 men as well”.

Although Karplus et al. [49] and Rupley [50] in Fisher [16] indicated that experience and age mitigated the use of the additive strategy, this student has used it repeatedly; our result does not fit with the other authors’ result probably due to the lack of previous experience with inverse proportionality, as explained by Fisher [16] (p. 166): it is more common than it should be. Additive strategy seems to be an escape route when the results of the proportionality formula are not as expected.

The fact that she scores well in the PGRP leads us to assume that it has assimilated direct proportionality, but obviously not so with inverse proportionality, which applies additive strategies. Such learners could be faced with simple inverse proportionality situations (such as double-halves that are easier to understand) and find that additive strategies do not work.

6.2. Student 2

The next student correctly performed five of the IQ problems but only one EQ. He confused the type of proportionality (especially in the EQ problems) and solved them using a direct cross-multiplication strategy.

• Guitar: “6.7. I have used a cross-multiplication strategy. If it takes 10 days to complete an order of 6 guitars per day, with 4 guitars per day it will take x days”.
• Transport: “142.8. I have used a cross-multiplication strategy. If it takes 25 h at 100 km/h, to take 50 h it will have to go at x km/h”.
• Bicycle: “64 cm. Cross-multiplication strategy. If it makes 50 turns with 80 cm, with x cm it makes 40 turns”.

It seems that he has identified that these are proportionality problems, but he has not identified the type of proportionality; furthermore, he has not considered whether the solution was meaningful. This student makes us wonder whether the confusion with direct proportionality is more prevalent in problems with unknown EQ than in problems with unknown IQ

Table 5. Comparison of the different strategies used (as a percentage) according to the type of question.

	Total %	Unknown IQ	Unknown EQ
I1. No answer.	0	0	0
I2. Intuitive	0	0	0
I3. Additive	1.1	1.9	0.2
I4. Proportion attempt	14.8	12.9	16.7
I5. Incorrect other	8.7	9.4	8
C1. Proportion formula	19.8	21.4	18.3
C2. Proportional reasoning	40.1	39.7	40.6
C3. Algebra	0	0	0
C4. Correct other	15.5	14.8	16.2

. Indeed, that gap does exist, but it is very small, from 12.9% in IQ to 16.7% in EQ.

However, this student solved the other problems correctly using proportional reasoning. For example:

• Puzzles: “16 puzzles. I have multiplied $64\times 8=512$ which is the total number of pieces and then I have divided those 512 by 32 pieces that are in each puzzle”.

In this case we have achieved direct proportionality, but inverse proportionality was in the process, because although the IQ problems have been solved correctly, the same was not true of the EQ problems where the wrong type of proportionality was being used. We do not have conclusive results between the differences in IQ and EQ; they could have deeper involvement in this type of student beyond what has been studied. In future research that should be investigated.

6.3. Student 3

This student solved 83% of the problems of the IQ or EQ, but none of the GPRP problems. The answers to the three most generic proportionality problems were:

• Balloons: “20. I have used another cross-multiplication strategy. If you inflate 11 balloons in 9 min, then 25 will be x. The more balloons they have to inflate, the longer they will be”.
• Teams: “The one of five workers; it’s a guess”.
• Compare: “20. I have added up the number of teeth of the two gears and I have divided it by the three gears”.

It seems that she has not understood them and it is surprising that she correctly solved most of the inverse missing-value problems. Strategically, when she could, she has used the graph and in the other problems a proportional formula (reverse cross-multiplication strategy). One explanation, which is plausible for the strategies she has correctly used in the problems, is that the use of a cross-multiplication strategy (in this case inverse) has simplified the problem solving process but not improved understanding.

Solving only IQ and EQ problems does not involve a thorough knowledge of proportionality; rather, it shows skill in a learned mechanism or method of resolution that helps them solve inverse missing-value problems. The PGRP problems have allowed us to discern the difficulty in understanding proportionality in general, at least certain deficiencies, and so we agree with Lobato et al. [17] about the importance of diversifying the types of problems to be used in teacher training.

6.4. Student 4

The next student correctly completed two of the GPRP exercises (Balloons and Compare), but solved seven of the inverse missing-value problems incorrectly. As shown in Figure 1, there are only two students who correctly solved the GPRP problems but were not able to solve the majority of the inverse missing-value problems. It is logical that there are only a few such exceptions, as good proportional reasoning makes it easier to solve inverse missing-value problems. In this case, besides confusing it with direct proportionality (Cake, Water, Puzzles and Bicycle problems), she also used additive strategies in some problems (Gears, Guitars and Bricklayers problems).

• Cake: “After a cross-multiplication strategy, the result is 14 blackberries”.
• Water: “At a flow rate of 8 L/min, it takes 10.67 min to fill the tank. The procedure I have followed is to use a cross-multiplication strategy”.
• Gears: “There is a difference between the green gear and the red gear, i.e. a difference of 8 teeth. So let’s subtract 8 from 14 and find the turns of the red gear. Then we use a cross-multiplication strategy and the result is that the red gear will need 60 teeth to make 36 turns”.
• Guitar: “The difference between 6 guitars and 4 guitars is 2 guitars, so we add 2 days that it would take you to make the remaining 2 guitars to the 10 days. It will take 12 days to finish the total order”.
• Puzzles: “They used 64 pieces at the beginning, now they use 32 (which is half of 64). Therefore, they also need half of the puzzles, in this case 4 puzzles”.
• Bicycle: “The circumference of the front wheel is 80 cm and it turns 50 times, so we have to calculate using a cross-multiplication strategy. As the rear wheel turn 40 times, we can determine that the circumference of the rear wheel is 64 cm”.
• Bricklayers: “8 bricklayers take 18 h and x bricklayers take 16 h. The difference in hours between the case of employing 8 bricklayers or x is 2 h, for this reason two more must be added to the 8 bricklayers. Therefore, 10 bricklayers will have to work to finish it in 16 h”.

Although a generic understanding implies a good resolution of inverse missing-value problems, in this case the two types of errors that existed in subjects 1 and 2, additive strategy errors and proportionality errors, have been brought together. To these types of students we should apply situations in which the additive strategy clearly does not work, and also make explicit, in different ways (manipulative, contextualization to situations they can recognise, error analysis, deeper analysis of the tasks, etc.), the inverse proportional relationships.

6.5. Student 5

This student is a paradigmatic example of those who confuse the type of proportionality to be used, which is the most common error. The reason why we include it is that, as indicated by Izsák and Jacobson [7], one of the usual problems when teaching proportional relationships is the emphasis on the use of rote rules and repetitive learning of algorithms. That is why the most used strategy in textbooks to solve missing-value problems is the cross-multiplication strategy [16], which requires a proportion and also needs to multiply its values. However, Izsák and Jacobson [7] already warned that the acquisition of proportional reasoning involves much more than the use of a simple rule. Riley [4] pointed out that teachers could be overly dependent on its use.

In this case, as we mentioned above, most of the errors correspond to the use of direct rather than inverse proportionality, even if this gives a meaningless result. In some problems we must also add other errors, such as additive reasoning, lack of knowledge of the problem-solving method (when more than three data appear) and misinterpretation of the graph.

• Cake: “Here I would perform a cross-multiplication strategy. If 7 blackberries equal 12 cakes, x blackberries equal 24. Therefore, $7\times 24$ and the result divided by 12. The result would be 14 blackberries for 24 cakes”. Obviously the answer is meaningless once you have read in the statement that the number of blackberries available is the same as at the beginning. We will see in the following problems how this scheme is reiterated, in which the student does not consider a critical analysis of the answer and simply identifies a proportional situation and applies the algorithm that she knows.
• Gears: “If we subtract green gear turns from red gear turns we have $36-14=22$. Therefore the red gear must have $18+22=40$ teeth”.
• Water: “Another cross-multiplication rule. If 6 litres take 8 min, 2 take x. Therefore $8\times 2$ divided by 6 = would take 2.66 period, which in minutes is equivalent to 3 min”.
• Bread: In the following problem, she has needed to use all the data in what she has termed a “compound cross-multiplication strategy”.
  “We carry out a compound cross-multiplication strategy. 2/x $=14/3\times 7/6$ which is equal to 2/x $=18/70=140/18=7.7$ sticks of bread”.
• Balloons: “compound cross-multiplication strategy. 25/x $=7/6\times 3/4$ is equal to 25/x $=21/24$ min”.
• Teams: she has not been able to compare the two proportions.

  “7 workers in 2 days = 5 workers in 3 days”.
• Compare: she has not solved the problem, she has simply tried to write what was asked of him.

  “A = 48, B = x, C = 12. For A = B and B = C”.
• Guitar: “I would implement a cross-multiplication rule, in which at a rate of 6 guitars/day it takes 10 days, at 4 guitars/day it would take x days. Therefore, $4\times 10$ divided by 6 = 40/6 = 6.6 days”.
• Pie: “I would apply a compound cross-multiplication rule where 2 is 12, 3 is 8 and 4 is x. So I would multiply $12\times 8\times 4$ and divide it by $2\times 3$. The result would be 64 slices of pie”.
• Puzzles: “I would perform a cross-multiplication rule in which if 8 puzzles use 64 pieces, x with 32 pieces. Therefore, I would multiply $32\times 8$ and divide by 64 = 4 puzzles”.
• Transport: “I would carry out a cross-multiplication rule. If 100 km/h is equal to 35 h, calculating that x is equal to 35 h + 15 h more that are added, if we multiply $50\times 100/35=$ it should run at 142 km/h”.
• Bicycle: “The same as in the previous ones, I would use a cross-multiplication strategy in which 80 cm makes 50 turns, and x makes 40 turns. $80\times 40/50=64$ cm”.
• Decoration: “When looking at the axes of the graph, we see that on the vertical axis it indicates the number of flowerpots per student, and on the horizontal axis the number of students, we have to follow the line of 7 on the vertical axis until we find the point, which in this case is at number 26, therefore there is a class of 26 students in which each student has to look after 7 flowerpots. The result is 26 students”. In this case the explanation looks correct but does not correspond to the real number on the graph.
• Bricklayers: “A cross-multiplication strategy in which 8 workers take 18 h and therefore x workers take 16 h. We multiply $16\times 8$ and divide by 18. The answer is that 7 bricklayers will be needed to do the job in 16 h”.

This is the prototypical example of a student who has the cross-multiplication strategy so integrated that she applies it to all situations of proportionality regardless the resource you give her ( table, graph, etc.) and without analysing the result. In this case she depends excessively on the cross-multiplication strategy and avoids making any statement analysis; if there is a proportional relationship she has an anchorage to a resolution using the cross-multiplication strategy.

This type of student should be provided with different proportionality problem-solving strategies (proportional reasoning, algebra, manipulative strategies, etc.) and faced with proportionality problems, to avoid the use of the rule of three, in order to have better of resolution emerge.

A study of the cases shows that once you have acquired direct proportionality but not inverse proportionality, additive strategies become a common strategy to solve problems where one does not recognise problematic situations as proportionality. We have also found understanding of direct proportionality and the beginnings of the recognition of inverse proportionality, and that is why direct resolution strategies appear. Furthermore, we have found cases in which the inverse proportionality has been acquired but they have not been able to solve the PGRP correctly. We attribute this to a (senseless) application of a valid inverse strategy without a deep and real understanding of proportionality, and we affirm, as [17], that PGRP-type problems have value as detectors of these cases. Finally, and relating these results to the representations, we opted for the use of tables as a complement to the information contained in the problem. We can affirm that to help future teachers we should:

• Provide a progression of varied proportionality problems (direct, inverse, generic proportionality, etc.)
• Use different representations.
• Use familiar, close contexts, with testable results.
• Encourage the construction of tables that facilitate the visualisation of the proportionality type.

7. Discussion

The main purpose of this paper was to analyse the acquisition of inverse proportionality by pre-service teachers by relating it to the more generic proportional reasoning, and the influences of different kinds of representation and different kinds of quantities on the unknown when solving inverse missing-value problems. As indicated by Fisher [16] (p. 167) we have to be aware that the lack of understanding of inverse proportionality by teachers undermines the use of proportional strategies in problem solving. This tendency is reflected in our case, as it was to Ben-Chaim et al. [2] and Riley [4]; the results show difficulties in pre-service teachers’ understanding of inverse proportionality and general proportional reasoning. These difficulties increase problem solving through proportional formulas (cross-multiplication strategy) that can be used without correctly interpreting either the wording or the answers to the problems. Consequently, pupils should work on and develop their understanding of the different strategies of proportional reasoning before they are taught the algorithm of the cross-multiplication strategy (both direct and inverse).

It has been shown that students who were able to solve GPRP problems (therefore with a higher degree of proportional reasoning) faced inverse missing-value problems using more reflexive and less mechanical strategies. That result fits well with the Buforn et al. [51] suggestion that the use of different methods in the proportionality problems’ resolution is essential, since it increases the understanding of proportional reasoning. Furthermore, in order to provide students with a deeper understanding in different proportionate situations, Burgos and Godino [52] indicated that teachers should be able to use different methods beyond the rule of three. Based on Arican [5], teachers’ trainers have to encourage students to use other strategies than ones they generally employed, because pre-service teachers usually persisted in using a strategy if they observed that the strategy yielded the correct result.

In addition, it has been revealed that the use of different representations or statements (tables, graphs, double/half) that facilitated understanding of the problem, showed a greater number of responses that are analytically driven and non-automatic. Therefore, the use of proportional reasoning goes hand in hand with a thorough understanding of the problem. Otherwise, the use of an algorithm such as the cross-multiplication strategy leads to confusion with direct proportionality and this lack of acquisition of proportional reasoning. Furthermore, in many cases, those who used a repetitive algorithm accepted very unreasonable solutions, which is why we assert that their understanding of the statement was weaker.

Similarly, Son [53] noted that when teachers solving their students’ difficulties, focus on rules and procedures due to a poor understanding of proportionality. If we are to avoid this, it is essential to broaden the understanding of future teachers in inverse proportionality and to strengthen their learning, among other aspects, by promoting the use of different representations and statements, which in turn will encourage the use of different resolution techniques. As shown, the use of different solving techniques supports the proportional understanding, but also, following Sztajn et al. [54]’s suggestion, it will allow prospective teachers to better understand their pupils’ ways of thinking by facilitating the two dimensions to developing the knowledge of a mathematical task, the cognitive demand of the task and pupils’ developmental paths to a mathematical concept involved in solving the task.

Regarding to other research question, Beckmann and Izsák [28] indicated that it is difficult for students and teachers to understand ratios as measures of intensive quantities, such as slope, taste or speed, but our results indicate that there are not a substancial difference with extensive quantities. In fact, in inverse missing-value problems with unknown EQ, we found a larger number of cases of confusion with problems of direct proportionality, but the difference with unknown IQ is minimal and we do not consider that there is a dissimilarity in the understanding of the problems of both types of quantities.

Our results show that there is still some way to go to ensure that future teachers have a full understanding of proportionality, and more specifically, of inverse proportionality. There are pre-service teachers who have difficulties differentiating the type of proportionality in the problem, as discussed in Orrill et al. [11], and obviously, this deficit will soon be reflected in the teaching-learning process that they will supervise. It is necessary to improve and strengthen the teaching of proportionality in education, and for in-service teachers, to require retraining that will allow educators to obtain a robust conceptual understanding to support their pupils.

Summarising, we consider that prospective teachers must be frequently exposed to problem solving in order to develop the skills to solve and teach them appropriately. These problems should be as varied as possible in order to avoid learning misunderstandings through rules by rote. Strengthen the use of various representations in problem solving; in addition, the generalisation of all kinds of resolutions is required. It is crucial to include, in the course of mathematics teaching methodology, the analysis of cognitive barriers and how to overcome them.

As we mentioned in the introduction, the acquisition of proportional reasoning is so significant that algebra depends on it. In-service teachers must continue to study and learn, because as Weiland et al. [55]’s results show, the issues found in students and pre-service teachers also seem to be prevalent with in-service teachers. More research will be needed to explore teachers’ requirements and how their acquisition of proportional reasoning could be improved.