Abstract
Nowadays, Augmented Reality (AR) is one of the emerging technologies with a greater impact in the Education field. Research has proved that AR-based activities improve the teaching and learning processes. Also, the use of this type of technology in classroom facilitates the understanding of contents from different areas as Arts, Mathematics or Science. In this work we propose an AR-based instruction in order to explore the benefits in a 6th-grade Primary course related to 3D-geometry shapes. This first experiment, designed from an exploratory approach, will shed light on new study variables to perform new implementations whose conclusions become more consistent. The results obtained allow us to envisage that AR-based proposals slightly improve the classical didactic methods.
1. Introduction
In the last decade the use of the technological tools linked to the Information and Communication Technologies (ICT) has acquired a big importance, both as a didactic tool and as well as a provider of new environments for promoting the learning. Different authors are reporting the learning effects of a significant use of technological environments in the classroom, specially those regarding to the Augmented Reality (AR) [1,2,3]. Although, AR has been defined from different perspectives [4], we understand an AR environment as a system that allows for combining real world objects with virtual objects or superimposed information. As a result virtual objects seem to coexist in the same space with the real world [5].
These AR-based learning environments reinforce the significant learning through new possibilities and motivational practices [6,7]. The AR has been considered as a technological tool capable to permeate on the teaching and learning mechanisms providing significant impact on both processes. Due to the affordability and the ease of use, AR has been reported as a mid-term technological adoption (2–3 years) for K-12 levels and High Education levels [8,9]. Possibilities for AR applications in research are also promising. Different studies had demonstrated the AR usefulness for increasing the student motivation, as well as for enhancing a wide variety of learning domains [3,7,10,11,12,13,14,15,16]. In particular, the meta-analysis provided by [4] among JCR publications on the state of AR applications in the Education field, concludes that there is a increasing trend, specially during the last 4 years, on the Science and Humanities & Arts areas.
The AR has been applied with different goals to medicine, engineering, psychological treatments, etc. [17]. Concerning the educational approach, the benefits of AR applications had been told to strengthen the comprehension of complex concepts, supporting the contextualisation [11]. In this line, the use of the AR-based technologies allows an individual learning for each student and the manipulation of both tangible and virtual objects in an enhanced and motivational scenery. In spite of the generalised though that AR is an expensive resource, the integration of AR devices in the classroom does not imply a high cost because of the mobile devices. Different educational studies are providing clues to implement AR-based proposals at different ages [10,18,19].
As we will describe in the next section, the use of AR can support the learning of specific domains regarding to geometric and spatial abilities. The key point is that AR enhances the students’ visual perception. An AR-based activity allows us to manipulate virtual objects as well as to physical objects in the real world [14]. Thus, students can move around a 3D-virtual figure and view it from any vantage point, just like a real object. Different researchers have delved into the geometric and spatial abilities developed by students when using AR-based activities from Primary to High Education levels [14,20,21,22]. In particular, the 3D-activities based on AR in which the students have to represent and manipulate spatial and virtual objects are depicting promising results for extending the resources used in the Mathematics classroom [23].
Although nowadays AR has been incorporated to many educational practices [11], different aspects have to be explored in order to complete the implementation of AR-based activities in real class situations. In particular, this work pretends to explore the applicability of AR-based activities for the learning of 3D-geometric contents in a 6-grade Primary classroom.
2. AR for Geometric and Spatial Learning
Geometry comprises those branches of mathematics that exploit visual intuition (the most dominant of our senses) to remember theorems, understand proofs, inspire conjectures, perceive realities, and give global insight.(Zeeman, quoted in [24], p. 12)
Historically, spatial abilities have been addressed from a psychological standpoint [25]. Nowadays, the recent research on teaching and learning of Geometry covers geometric and spatial thinking among other content domains, as the geometric measurement or the teacher development [26]. In one hand, the spatial reasoning, underlying the most geometric thought, is defined as a vital capacity for human action and thought, not always supported in school curricula ([27], p. 3). On the other hand, the geometric reasoning consists on the inventions and the use of formal conceptual systems that allows us to investigate the space and the shape in a mathematical way ([28], p. 843).
The learning of Geometry at Primary levels can be exciting and fun for those pupils who are engaged with Mathematics, but the same cannot be told for those pupils showing less interest in Mathematics [29]. Usually, the geometric ideas in the curriculum are reduced to the identification of 2D- and 3D-geometric shapes, related to area and volume measurements, not taking to much time on developing spatial reasoning and visualisation contents [26]. This approach does not fit the international guidelines, that claim the use of visualisation, spatial reasoning, and geometric modelling to solve problems [30]. In this line, Duval in 1998 stood up for a teaching of Geometry beyond the arithmetic operations, in which three cognitive processes are involved: visualisation, construction and reasoning [31]. This position has strong implications on the teaching of Geometry, in the sense of involving spatial reasoning tasks on the Geometry teaching proposals. Moreover, has been stated that the interaction with technological environments improves the visualisation and spatial reasoning on the students [30,32].
The use of manipulatives in the Mathematics classroom is not new. In the longstanding history different kinds of physical materials have been used in order to explore, acquire, or investigate mathematical concepts or processes and to perform problem-solving activities drawing on perceptual (visual, tactile, or, more generally, sensory) evidence [33]. Nowadays, the technological progress is providing a big amount of virtual materials that, combined with the physical ones, offer a wide variety of possibilities to explore teaching activities in new and motivational manners. In particular, the AR-based learning experiences produce as physical benefits as virtual benefits [23].
Concerning the AR-based educational implementations related to Mathematics, these can be a powerful tool to strengthen the spatial visualisation. From a Mathematical Education approach, the spatial visualisation is determined as a set of mental skills that allow individuals to act in the context of mathematical graphical representations, taking this context in a broad sense that includes the usual representations in the different mathematical fields such as Geometry, Algebra, Arithmetic or Statistics [34]. In this line, the manipulation of AR 3D-geometric shapes enhances the spatial visualisation ability, in the terms described by Gutiérrez [35], by means of the use of visual or spatial elements, developed to solve problems or demonstrate properties.
The learning of geometric contents through AR implementations is still a recent field [23,36,37]. Modern dynamic geometric software (DGS) has stimulated research on students’ assessment regarding geometric content [38], through software like GeoGebra [39] or 3D computer-aided design (CAD) software [36]. However, the incorporation of AR into teaching situations still requires the exploration of several principles, such the design of the technological environment, the viability of the implementation, the curricular contents capable to address with the AR-based activities, the limitations posed by the context, the digital competences of the teachers and/or students, etc. [11]. Along these lines, this work tries to explore different variables related to the application of AR implementations on a real class context.
3. Aim
With this research we aim to explore the potential of the AR-based activities through a short classroom intervention in a 6th-grade Primary class. Moreover, this experiment aims to test if AR-based activities enhances the acquisition of 3D-geometric contents, in particular those related with spatial abilities.
4. Materials and Methods
This quasi-experimental study consists of an AR-based intervention of 5 sessions in a 6th-grade Primary classroom related to 3D-geometric contents. Although we have considered experimental and control groups to test our hypothesis, this is an exploratory study since we have not established an standard pre-post comparison. However, to determine the level of the students in geometric concepts, an initial test was developed. It was divided in five basic questions displayed in Table 1. The results presented in this manuscript have to be considered as a case study of an specific group from an specific school.

Table 1.
Questions of the initial test.
4.1. The Intervention Design
In order to test if AR-based activities enhances the geometric reasoning acquisition we have designed an intervention to be conducted in a Primary school. The intervention was intentionally designed to have a short duration (3.75 h), consisting in 5 sessions (described in Table 2). We opted for designing a 5-session duration intervention in order to be realistic according to the time usually devoted to technological activities (AR-based in our case) in real class situations. The participating students were separated into an experimental group and a control group. During the intervention, both groups carried out the same 3D-geometric activities, but the experimental group uses AR-based materials and the control group worked with traditional manipulative materials. The schematic path of the experimental design of our research is provided in Figure 1 and will be described in detail later in the text.

Table 2.
Distribution of sessions and contents addressed in each of the designed sessions.
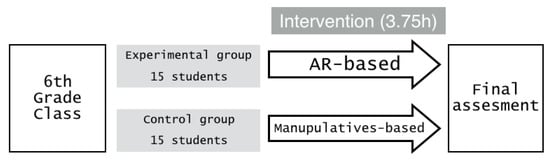
Figure 1.
Scheme of the experimental design followed in this work.
4.2. Participants
As mentioned above, the participants of this exploratory research were 30 students (56% male) of 6th Primary course (age 11 to 12 year-old) from an Spanish school. The sample was ethnically and socio-economically diverse. The intervention was conducted during the last semester of the academic year 2018–2019. The students were equally distributed into experimental group and control group, consisting each one of 15 students. Those groups were randomly selected. All participants were informed that we were carrying a research study and warned that the results obtained in the different assessment tests would not be considered in their grades. In addition, the parents were informed about this intervention with an ordinary communication.
4.3. Procedure and Materials
The schematic procedure for this exploratory experiment is depicted in Figure 1. Once the class was separated in two groups both receive an intervention for the learning of 3D-geometric content according to their grade level. The academic content related to the intervention has not been presented prior in the academic course. Participants, in both the control and the experimental group, had to complete the same set of tasks during the intervention phase. The only difference was that the experimental group uses AR-based technological devices and the control group uses standard manipulative materials. It is important to mention that all students had been introduced to AR-based devices during the previous academic course. Specifically, they had been working with AR-devices on Science subject. Therefore, no instrumental factors due to the ability on the use of the AR-devices interfere in our experiment.
The intervention took 5 sessions, 45 min each one, related to different aspects of 3D-geometric content, as shown in Table 2. Participants, divided into experimental and control group were encouraged to complete the tasks in each session. The control group made use of manipulative materials (Figure 2, right panel) while the experimental group worked with AR-based applications (Figure 2, left panel), in particular they work with the apps Geometry and Quiver. The manipulative materials of the control group were those typically present on an standard Primary classroom, i.e., 3D solids and developed nets.

Figure 2.
(Left panel): AR-based task. (Right panel): standar manipulative task.
4.4. Instrument
In order to measure the learning achieved by the students an instrument was specifically developed taking into account the contents that the students deal with during the intervention phase. The instrument (no validated) consisted of six items (showed in Table 3). All items were related to the 3D-geometric contents from the 6th Primary grade curriculum. Each item in the test was coded with a score between 0 (totally incorrect) and 10 (totally correct). The test was completed by the students two days after the intervention in a paper-and-pencil format.

Table 3.
Items selected to be completed by each student as final assessment.
5. Results and Discussion
As a pre-test was not administered previously to the intervention, in the present study we use the results provided by the instrument to focus, exclusively, on the benefits of implementing AR-based activities from an exploratory approach. In the following, we describe the results obtained by group in the initial test. These results prove that the group is homogeneous and that the students do not know the 3D-geometric concepts previous to the intervention abovementioned.
5.1. Mean Scores on the Initial Test
In this section we show the results of the answers given by the complete group, i.e., 30 students. In the first question (Table 1), only 4 students define correctly a polyhedron (13.33%). In terms of the typos of polyhedrons more than half of the students confuse the 3D-shapes with the 2D-shapes (53.33%). Only two are capable to explain the different typos of polyhedrons. Respect to the notable elements, any scholar made a satisfactory identification on the parts of a polyhedron. It is interesting to note that only 26.66% of the students distinguish between 1 and 4 notable elements. The best results are provided in the 4th question, due to 42% of the pupils mark successfully 2 phrases. However, in this question a noise is introduced in the result because the multiple choice answer. Finally, 13% of the students are not capable to draw neither the development of a cone nor the development of a prism, 17% of the students answer correctly to this question and the rest of the students only draw one development. In conclusion, the results obtained allow us to divide the class in the two groups (experimental and control) using any probabilistic method.
5.2. Mean Scores on the Final Assessment Test
Firstly, we address to the assessment of the items posed on the final test. Figure 3 shows the mean results obtained for each item, the mean score taking into account all students was a 8.38. It is important to point out that in the question 4 the mean score is bigger than 9. It indicates that the students are capable to distinguish between prisms and revolution solids. Therefore, using AR-based activities as well as using manipulative elements, the scholars improve their capacity to understand the principal properties of the solids. Also, in question 6, the mean achieves 9.23, therefore, the pupils draw correctly the development of the 3D solids. It is specially relevant in AR-based activities because of the apps used to teach it. In questions 1 and 2, the mean is between 8.5 and 8.9. The mistakes presented in the answers are due to little confusions in similar polyhedron and special notable elements as the radius. We can considerate that the concepts are satisfactory acquired. In the items 3 and 5 the mean is minor than the rest of items. Probably, the principal reason which explains these scores is that items are related with memorising abilities. In any case, the results evidence the improvement showed by the students in comparison with the initial prove. On the other hand, the exploratory study points out that teaching 3D-geometric solids with AR produces a more motivating learning. Also, the performance showed by the students points along these lines. But more rigorous experiments are necessary to obtain clearer conclusions.
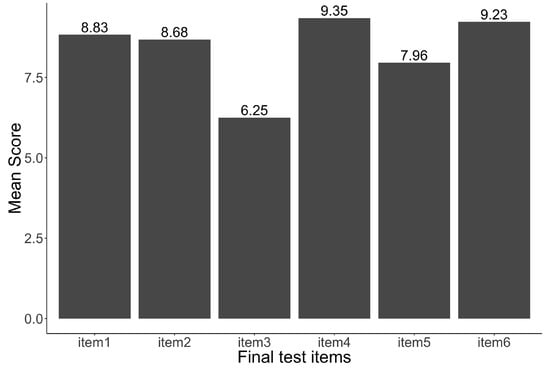
Figure 3.
Mean score obtained for each item of the final test.
5.3. Comparison between Control and Experimental Groups
By the initial test, we suppose that the students of control and experimental groups obtain similar qualifications before the instruction (see Section 5.1). However, the mean score obtained for the experimental group, 8.7, is slightly higher than the score obtained for the control group, 8.1. It is important to remark that the manipulative didactic elements are an excellent way to introduce 3D-geometric solids and their characteristics. Thus, this explains that the differences between the results of the two methods (manipulative vs. AR-based) are minor. Despite of this, with the AR-based activities presented in this paper the mean score is improved. Also, the students present a high degree of satisfaction when learn with this new instruction based on AR.
6. Final Remarks
The present study provides results on the effectiveness of AR-based instruction for the development of 3D-geometric contents in a 6th-grade Primary students. This study has underlined the potential of AR-based activities in promoting students’ acquisition of geometric and spatial abilities, according to previous works [11,15]. However, our results are weak due to the absence of an evaluation of the students’ knowledge previously to the intervention phase. This experimental approach has shown hints for future intervention designs, as the study of 3D-geometric development learning with AR-based technology. Moreover, it will be interesting to introduce new and more difficult 3D shapes, as the semiregular polyhedrons, oblique cylinders or oblique cones, that are not habitual to find as manipulative materials. Also, we plan to measure emotional factors in further interventions using AR-based activities. The goal will be to check the influence of these technological environments on the students’ motivation. Therefore, future studies are necessary in order to delve into the causes of the academic gains showed on this research.
Author Contributions
Data curation, R.V.-T. and D.F.Y.; Investigation, R.V.-T. and P.D.D.; Methodology, M.F.-B.; Project administration, P.D.D.; Supervision, P.D.D. and D.F.Y.; Writing—original draft, M.F.-B.; Writing—review & editing, P.D.D., R.V.-T. and D.F.Y. All authors have read and agreed to the published version of the manuscript.
Funding
This research was funded by Conselleria d’Innovació, Universitats, Ciència i Societat Digital de la Generalitat Valenciana, grant number GV/2019/146.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Fernández, B. Adopción de la realidad aumentada por estudiantes del grado de educación primaria. In Tecnología, innovación e investigación en los procesos de enseñanza-aprendizaje; Roig-Vila, R., Ed.; Octaedro: Barcelona, Spain, 2016; pp. 432–439. [Google Scholar]
- Sarracino, F. ¿Mejora la realidad aumentada el aprendizaje de los alumnos? Una propuesta de experiencia de museo aumentado. Profesorado. Revista de Currículum y formación del profesurrículum y formación del profesorado 2014, 3, 1–18. [Google Scholar]
- Duh, H.B.; Klopfer, E. Augmented reality learning: New learning paradigm in co-space. Comput. Educ. 2013, 68, 534–535. [Google Scholar] [CrossRef]
- Bacca, J.; Baldiris, S.; Fabregat, R.; Graf, S.; Kinshuk, G. Augmented Reality Trends in Education: A Systematic Review of Research and Applications. Educ. Technol. Soc. 2014, 17, 133–149. [Google Scholar]
- Azuma, R.; Billinghurst, M.; Klinker, G. Special section on mobile augmented reality. Comput. Graph. 2011, 35. [Google Scholar] [CrossRef]
- Cuendet, S.; Bonnard, Q.; Do-Lenh, S.; Dillenbourg, P. Designing augmented reality for the classroom. Comput. Educ. 2013, 68, 557–569. [Google Scholar] [CrossRef]
- Iftene, A.; Trandabat, D. Enhancing the Attractiveness of Learning through Augmented Reality. Procedia Comput. Sci. 2018, 126, 166–175. [Google Scholar] [CrossRef]
- Freeman, A.; Adams Becker, S.; Cummins, M.; Davis, A.; Hall Giesinger, C. NMC/CoSN Horizon Report: 2017 K–12 Edition; The New Media Consortium: Austin, TX, USA, 2017. [Google Scholar]
- Adams Becker, S.; Brown, M.; Dahlstrom, E.; Davis, A.; DePaul, K.; Diaz, V.; Pomerantz, J. NMC Horizon Report: 2018 Higher Education Edition; EDUCAUSE: Louisville, CO, USA, 2018. [Google Scholar]
- Cózar, R.; Sáez, J.M. Realidad aumentada, proyectos en el aula de primaria: Experiencias y casos en Ciencias Sociales. EDMETIC 2016, 6, 165–180. [Google Scholar] [CrossRef]
- Cabero, J.; Barroso, J. The educational possibilities of Augmented Reality. J. New Approaches Educ. Res. 2016, 5, 44–50. [Google Scholar]
- Leiva, J.J.; Moreno, N.M. Tecnologías de geolocalización y realidad aumentada en contextos educativos: Experiencias y herramientas didácticas. Rev. DIM 2015, 31, 1–18. [Google Scholar]
- Cubillo, J.; Martín, S.; Castro, M.; Colmenar, A. Recursos Digitales Autónomos Mediante Realidad Aumentada. Rev. Iberoam. Educac. Distancia 2014, 17, 241–274. [Google Scholar]
- Kesim, M.; Ozarslan, Y. Augmented Reality in Education: Current Technologies and the Potential for Education. Procedia Soc. Behav. Sci. 2012, 47, 297–302. [Google Scholar] [CrossRef]
- Wu, H.K.; Wen-Yu, S.; Chang, H.Y.; Liang, J.C. Current status, opportunities and challenges of augmented reality in education. Comput. Educ. 2013, 62, 41–49. [Google Scholar] [CrossRef]
- Orcos, L.; Jordán, C.; Magreñán, A. 3D visualization through the hologram for the learning of area and volume concepts. Mathematics 2019, 7, 247. [Google Scholar] [CrossRef]
- Jamali, S.S.; Shiratuddin, M.F.; Wong, K.W.; Oskam, C.L. Utilising Mobile-Augmented Reality for Learning Human Anatomy. Procedia Soc. Behav. Sci. 2015, 197, 659–668. [Google Scholar] [CrossRef]
- Luna, Ú.; Ibáñez-Etxeberria, A.; Rivero, P. El patrimonio aumentado. 8 apps de Realidad Aumentada para la enseñanza-aprendizaje del patrimonio. Rev. Interuniv. Formación del Profesor. 2019, 94, 43–62. [Google Scholar]
- Piqueras, E.M.; Cózar, R.; González-Calero, J.A. Incidencia de la realidad aumentada en la enseñanza de la historia. Una experiencia en tercer curso de educación primaria. Enseñan. Teach. Rev. Interuniv. Didáct. 2018, 36, 23–39. [Google Scholar]
- Prendes, C. Realidad aumentada y educación: Análisis de experiencias prácticas. Píxel-Bit. Rev. de Medios y Educ. 2015, 46, 187–203. [Google Scholar]
- Fonseca, D.; Redondo, E.; Valls, F. Motivación y mejora académica utilizando realidad aumentada para el estudio de modelos tridimensionales arquitectónicos. Educ. Knowl. Soc. 2016, 17, 45. [Google Scholar] [CrossRef]
- Escrivà, M.T.; Jaime, A.; Gutiérrez, Á. Educación Matemática en la Infancia. Edma 0-6 Educ. Mat. Infanc. 2018, 7, 42–62. [Google Scholar]
- Bujak, K.R.; Radu, I.; Catrambone, R.; MacIntyre, B.; Zheng, R.; Golubski, G. A psychological perspective on augmented reality in the mathematics classroom. Comput. Educ. 2013, 68, 536–544. [Google Scholar] [CrossRef]
- Royal Society. Teaching and Learning Geometry; Royal Society: London, UK, 2001; pp. 11–19. [Google Scholar]
- Bishop, A.J. Spatial abilities and mathematics achievement—A review. Educ. Stud. Math. 1980, 11, 257–269. [Google Scholar] [CrossRef]
- Jones, K.; Tzekaki, M. Research on the teaching and learning of geometry. In The Second Handbook of Research on the Psychology of Mathematics Education: The Journey Continues; Gutiérrez, Á., Leder, G.C., Boero, P., Eds.; Sense Publishers: Rotterdam, The Netherlands, 2016; pp. 109–149. [Google Scholar]
- Whiteley, W.; Sinclair, N.; Davis, B. What is spatial reasoning? In Spatial Reasoning in the Early Years; Davis, B., The Spatial Reasoning Study Group, Eds.; Routledge: New York, NY, USA, 2015; pp. 3–14. [Google Scholar]
- Battista, M.T. The development of geometric and spatial thinking. In Second Handbook of Research on Mathematics Teaching and Learning; Lester, F.K., Ed.; National Council of Teachers of Mathematics: Charlotte, NC, USA, 2007; pp. 843–908. [Google Scholar]
- Dowker, A.; Cheriton, O.; Horton, R.; Mark, W. Relationships between attitudes and performance in young children’s mathematics. Educ. Stud. Math. 2019, 100, 211. [Google Scholar] [CrossRef]
- National Council of Teachers of Mathematics. Principles and Standards for School Mathematics; NCTM: Reston, VA, USA, 2000. [Google Scholar]
- Duval, R. Geometry from a cognitive point of view. In Perspectives on the Teaching of the Geometry for the 21st Century; Mammana, C., Villani, V., Eds.; Kluwer Academic Publishers: Dordrecht, The Netherlands, 1998; pp. 37–51. [Google Scholar]
- Clements, D.H.; Battista, M.T.; Sarama, J.; Swaminathan, S. Development of Students’ Spatial Thinking in a Unit on Geometric Motions and Area. Elem. Sch. J. 1997, 98, 171–186. [Google Scholar] [CrossRef]
- Bartolini, M.G.; Martignone, F. Manipulatives in mathematics education. In Encyclopedia of Mathematics Education; Lerman, S., Ed.; Springer: Dordrecht, The Netherlands, 2014; pp. 365–372. [Google Scholar]
- Guillén, G.; Gutiérrez, Á.; Jaime, A.; Cáceres, M. La enseñanza de la geometría de sólidos en la E.G.B.; Technical Report; Universitat de València: Valencia, Spain, 1992. [Google Scholar]
- Gutiérrez, Á. Visualization in 3-dimensional geometry: In search of a framework. In Proceedings of the 20th PME Conference, Valencia, Spain, 8–12 July 1996; Volume 1, pp. 3–19. [Google Scholar]
- Kaufmann, H.; Schmalstieg, D. Mathematics and geometry education with collaborative augmented reality. Comput. Graph. 2003, 27, 339–345. [Google Scholar] [CrossRef]
- Kaufmann, H. Geometry Education with Augmented Reality; Technical Report; Technischen Universität Wien: Wien, Austria, 2004. [Google Scholar]
- Marrades, R.; Gutiérrez, Á. Proofs produced by secondary school students learning geometry in a dynamic computer environment. Educ. Stud. Math. 2000, 44, 87–125. [Google Scholar] [CrossRef]
- Saha, R.A.; Ayub, A.F.M.; Tarmizi, R.A. The effects of GeoGebra on mathematics achievement: Enlightening Coordinate Geometry learning. Procedia Soc. Behav. Sci. 2010, 8, 686–693. [Google Scholar] [CrossRef]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).