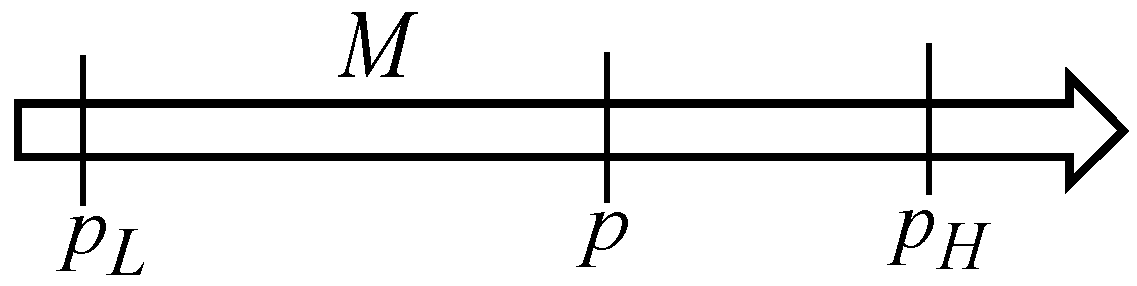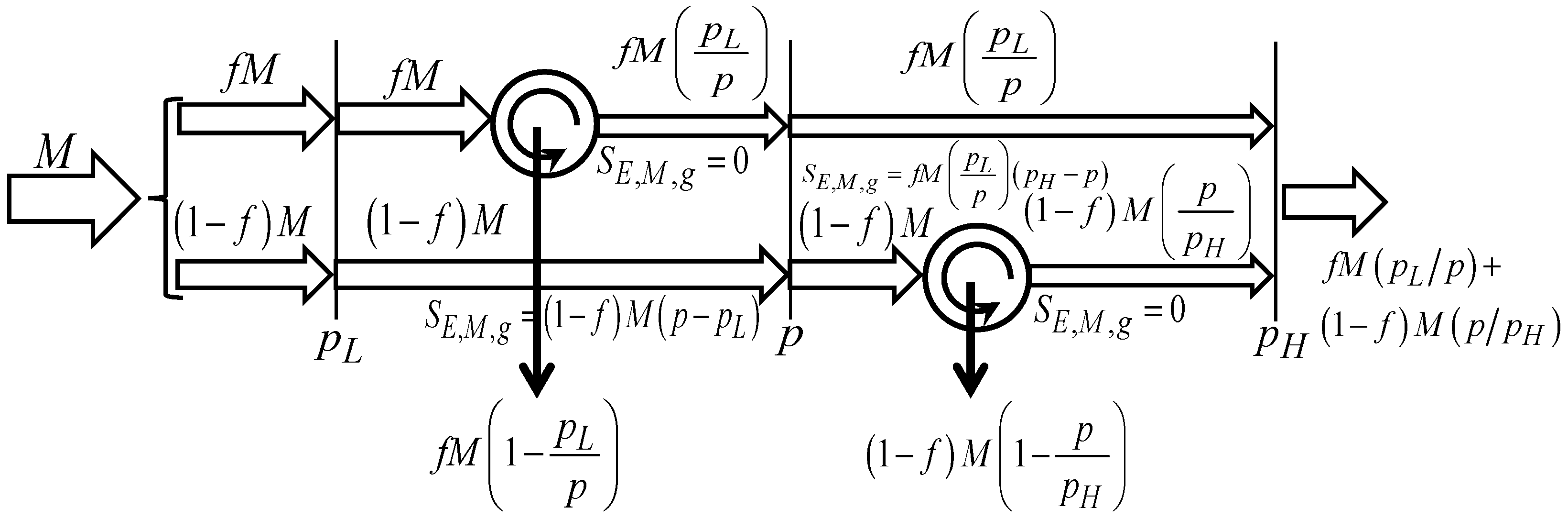Additional Contributions of Thermodynamics to Economics

Abstract

The contributions of Thermodynamics to Economics have been masterfully pioneered by P. A. Samuelson in his Foundations of Economic Analysis, adapting the Le Châtelier Principle to relate changes in economic variables. Recent contributions have been given, including the economic counterparts of energy, temperature, reversibility, and irreversibility, the Carnot engine, entropy, entropy generation, and the four Laws of Thermodynamics. Starting from them, toward a more efficient (more perfect) economy, the present work aims at (i) showing the contribution of negotiation to a more perfect economy; (ii) proposing endoreversible economic processes, and evaluating their efficiency at maximum merchandise wealth delivery; (iii) proposing the dynamic economic processes’ analysis based on the Economics analogue of specific heat, closely related to the demand elasticity coefficient; (iv) exploring ways to maximize merchandise wealth delivery instead of maximizing merchandise economic entropy generation (financial value generation) in dynamic processes; and (v) defining and evaluating the Economics analogue of exergy, the maximum potential of economic systems to deliver merchandise wealth.

1. Introduction

Everyone makes their own economic decisions, and differences exist between the decisions of different economic players. However, considering a large set of economic players and conducting statistical analysis, clear patterns emerge, which can be taken as those of the common economic player. Those patterns are usually translated into the form of laws or equations. Similarly, in Physics, each particle has its own behaviour. However, if a large set of particles is considered, statistical treatment of their individual behaviours leads to patterns. Such a large set of particles can be taken as a whole, described by macroscopic variables like temperature (a measure of the average kinetic energy of the vibrating particles), pressure (a measure of the average boxing action of the vibrating particles on a surface with unit area), and volume (a measure of the average space occupied by the particles’ set). Equations relating those macroscopic variables (Sears & Salinger, 1975) in the form of state equations or behaviour laws can be established. This is the essence of Macroscopic Thermodynamics.

This observation of the particles’ behaviour and setting of Thermodynamics occurred before a similar treatment had been made in Economics, to translate and quantify the observed economic patterns in the form of laws and equations. The pioneering work in this direction was conducted by P. A. Samuelson, as reported in his seminal book Foundations of Economic Analysis (Samuelson, 1947), based on similarities, and adapting to Economics what had been made in Thermodynamics. Quoting Backhouse (2015), ‘this was an argument for the use of mathematics in Economics at a time when most economic theory was conducted using verbal reasoning.’ The contributions of Thermodynamics to Economics are not new. This work aims to provide new and useful contributions of Thermodynamics to Economics, with mutual benefits for both fields.

Samuelson (1947) conducted his work to ‘mathematize Economics’, taking the common nature of consumer behaviour as the key to economic theory, looking essentially at what had been made before in Thermodynamics. The front page of Samuelson’s book (Samuelson, 1947) quotes the motto of J. Willard Gibbs (one of the great Thermodynamicists), saying that ‘Mathematics is a Language’.

The book of Samuelson (Samuelson, 1947) begins with the statement “‘The existence of analogies between central features of various theories implies the existence of a general theory which underlies the particular theories and unifies them with respect to those central features.’ This fundamental principle of generalization by abstraction was enunciated by the eminent American mathematician E. H. Moore more than thirty years ago. It is the purpose of the pages that follow to work out its implications for theoretical and applied economics.” The words ‘analogy’ and ‘analogous’ were used by Samuelson (1947) 12 and 5 times, respectively.

The Le Châtelier’s Principle appeared in the context of Thermodynamics (Thomsen, 2000), and, in general terms, it can be stated as ‘If the equilibrium of a system is disturbed by a change in one or more of the determining factors (as temperature, pressure, or concentration) the system tends to adjust itself to a new equilibrium by counteracting as far as possible the effect of the change.’ In (Samuelson, 1947, p. 38), when explaining the ‘generalized Le Châtelier Principle’, which is one of the bases of his work, he wrote, ‘This is a purely mathematical theorem. It corresponds to some of the phenomena which fall under the heading of the celebrated principle of Le Chatelier. Because of the almost metaphysical vagueness of its formulation, the latter’s meaning is often in doubt, and it is used at one and the same time to cover diverse phenomena. The above formulation explains why the change in volume with respect to a given change in pressure is greater when temperature is constant than when entropy is held constant and temperature is permitted to vary in accordance with the conditions of equilibrium.’ In (Thomsen, 2000) are pointed some areas of knowledge in which the Le Châtelier’s Principle is used, once adapted from its original Thermodynamics-oriented formulation. In the specific case of Economics, it is said that ‘The “Law of Supply and Demand” has been called Le Châtelier’s principle applied to Economics. And indeed, when we examine a statement of this law, the analogy becomes apparent.’ In (Samuelson, 1947, p. 21), he wrote that ‘… It may be pointed out that this is essentially the method of thermodynamics, which can be regarded as a purely deductive science based upon certain postulates (notably the First and Second Laws of Thermodynamics).’, and in (Samuelson, 1947, p. 36), that ‘How is the equilibrium displaced when there are no auxiliary constraints as compared to the case when constraints are imposed? How does the demand for a factor vary with its price when other factors cannot be optimally adjusted because of time lags, etc.? This type of question is important in thermodynamics as well as in economic systems.’

Previous quotes clearly show that Samuelson’s work (Samuelson, 1947) was based on the methods of Thermodynamics, resulting in the remarkable contribution of Thermodynamics to Economics. Based on that pioneering work, much of the economic descriptions became expressed in the form of mathematical expressions involving the relevant variables. It helped clarity, conciseness, and rigour; among others, it also allowed evaluation of how the change in a variable or parameter affects other variables and parameters, thus allowing the dynamic character of Economics to be described. This, in a way, was similar to that previously set for Thermodynamics, relating variables and parameters through well-established expressions, some of constitutive (particular) character and others of balance (general) character.

A different way of exploring analogies between Thermodynamics and Economics was followed by Georgescu-Roengten, focusing on economic scarcity and long-term sustainability (impossibility of full recycling, due to the material entropy increase). His work (Georgescu-Roegen, 1976) compiles some of his publications, trying to set analogies between Mechanics, Thermodynamics, production, and Economics. Special emphasis is put on the Entropy Law and its connections with economic activity and sustainable evolution. These are theoretical considerations, without proposing or setting parallel structures for Economics and Thermodynamics, or quantification tools for that. His work (Georgescu-Roegen, 1979) is also a theoretical treatise, discussing evolution, entropy, order, probability, cause, purpose, evolution, value, and development. In (Georgescu-Roegen, 2020), he theoretically explores connections between energy, entropy, Economics, evolution, ecology, and ethics, looking at the one-way direction set by the Second Law of Thermodynamics. The work of Georgescu-Roegen is still the seed for studies trying to relate Economics and Thermodynamics, as condensed in (Ferrari, 2023).

Burley and Foster (1994) edited a set of works trying to set analogies between the First and Second Laws of Thermodynamics and their Economics’ counterparts. However, there were no conclusive results or usable relations for practical application. Schulz (2003) presents a work of a statistical nature, exploring similarities and parallelisms between Thermodynamics and Economics. Chen (2005) and Kummel (2011) explore the analogies between Thermodynamics and Economics from a theoretical point of view; however, they did this without setting usable relations for practical application.

Ayres and Nair (1984) theoretically explore analogies between Thermodynamics and Economics, the main statement being that ‘The Laws of the conservation of energy and of the increase of entropy constrain the processes by which raw materials are transformed into consumable goods, and therefore have implications for the way economists model these processes.’ In another paper (Ayres, 1998), Ayres followed a theoretical approach with a strong emphasis on the Second Law’s one-way character, highlighting concerns on resource scarcity and sustainability, processes utilizing low-entropy raw materials and discarding high-entropy wastes. Saslow (1999) proposes analogous variables and concepts in Economics and Thermodynamics. However, without considering the dynamic character of the economic processes and the one-way character of the Second Law or usable balance equations. It is a thermostatic and not a thermodynamic work (from which time and inequalities are absent). Belables (2019) theoretically dissertates on the main lessons taught by Thermodynamics to economists and energy engineers.

A different way of setting and exploring analogies between Thermodynamics and Economics has recently been proposed (Costa, 2024a, 2024b, 2024c), based on the two main ideas:

-

The number of units (with intrinsic value, and thus of economic interest) of an economic system composed of goods, services, and monetary units is a property of the system (the economic analogue of energy). The number of units and their accounting is the basis of the Economics counterpart of the First Law balance equations.

-

Merchandise (goods and services) are traded in an increasing unit price direction. Traded merchandise is transferred, driven by an economic temperature difference, or, in other words, driven by a unit price difference, generating economic entropy in that transfer process. Similarly, heat is transferred, driven by a temperature difference, generating entropy in that transfer process. The one-way character of merchandise transfer in trading operations, from smaller to higher unit prices, and the profit generation in trading operations, is the Economics counterpart of the Second Law. Financial value generation is the Economics counterpart of entropy generation in Thermodynamics. Economic entropy (the financial value) accounting is the basis of the Economics counterpart of the Second Law balance equations.

From these main ideas, developments can be made, leading to the Economics counterparts (inside brackets) of (Costa, 2024c): temperature and thermal equilibrium (economic temperature and economic equilibrium), heat reservoir (merchandise reservoir), energy and energy transfer interactions (units and units transfer interactions), the First Law and the energy balance equation (the Economics First Law and the units balance equations), heat transfer through (driven by) a temperature difference (traded merchandise transfer through (driven by) an economic temperature difference), reversibility, irreversibility and spontaneity (economic reversibility, irreversibility and spontaneity), entropy and entropy generation (economic entropy and economic entropy generation), the Second Law and the entropy balance equation (the Economics Second Law and the economic entropy balance equation), friction and irreversibility (economic friction and economic irreversibility).

Additionally, a Four-Laws structure similar to both Thermodynamics and Economics has been proposed (Costa, 2024a), which includes economic thermal equilibrium, economic temperature, Economic Zeroth Law, traded merchandise, merchandise transfer interactions, merchandise wealth, merchandise units generation, merchandise reservoir, monetary transfer interactions, monetary wealth, monetary units generation, monetary exchanges in trading operations, units balance equations, Economics First Law, Economics Second Law, Economics Kelvin–Planck Second Law statement, Economics Clausius Second Law statement, Economics Carnot cycle, economic reversibility and irreversibility, absolute economic temperature scale and absolute unit price scale, Economic Bucher diagram, Economics Clausius inequality, economic merchandise entropy definition through a differential equation, economic entropy generation, economic entropy transfer interactions, economic entropy balance equations, merchandise economic entropy generation in merchandise transfer through an economic temperature difference, Economics Third Law, and the absolute value of the merchandise economic entropy.

This work proposes and explores ways toward a more perfect economy, searching for more perfect (less irreversible) economic operations, and presents additional contributions of Thermodynamics to Economics. It mainly includes

-

Negotiation as contributing to a more efficient economy (as contributing to smaller merchandise economic entropy generation).

-

Endoreversible economic processes’ analysis. Similarly, as in Thermodynamics (Bejan, 2016), endoreversible economic processes include a series of both irreversible traded merchandise transfer through an economic temperature difference, and (reversible) operation of an economic Carnot engine operating when in contact with two economic temperatures (Costa, 2024b, 2024c). It analyzes the endoreversible economic engine and evaluates its intermediate unit price and efficiency for maximum merchandise wealth delivery.

-

For the first time, the relationship between the change in the number of merchandise units of an economic system and the change in the economic temperature (in the unit price) of those merchandise units is set, introducing the economic analogue of the specific heat usual in Thermodynamics (Bejan, 2016; Moran et al., 2018), in the form of a constitutive (particular) law. How the so-introduced merchandise economic specific heat is related to the demand elasticity coefficient (Samuelson & Nordhaus, 2010) can be seen. After that, analysis comprises dynamic economic processes analogous to usually explored dynamic thermodynamic processes (Bejan, 2016; Moran et al., 2018).

-

Definition and evaluation of the Economics analogue of exergy (Bejan, 2016; Moran et al., 2018), as the economic availability, the maximum merchandise wealth that can be obtained when the economic system is allowed to evolve, reversibly, when in contact with the economic merchandise environment, up to reach the equilibrium with that environment.

The very recent work (Chater & MacKay, 2025) revealed by one of the Reviewers proposes an axiomatic approach to derive an Economics analogy of Thermodynamics, including the Economics analogue of entropy. The first major difference is that the present approach is based on the two main ideas (Costa, 2024b, 2024c): (i) the number of units of an economic system is a property of the system (the economic analogue of energy); the number of units accounting being the basis of the Economics counterpart of the First Law balance equations, and (ii) merchandise is transferred (traded) in an decreasing economic temperature direction, driven by an economic temperature difference; similarly, heat is transferred in a decreasing temperature direction, driven by a temperature difference. Financial value generation, a measure of economic irreversibility, is the Economics counterpart of entropy generation. The economic entropy (financial value) accounting serves as the basis for the Economics counterpart of the Second Law balance equations. Additionally, the present approach states the Economics Second Law from its Kelvin–Planck and Clausius statements, the economic entropy being defined through a differential equation obtained from the Economics Clausius’ inequality (Costa, 2024b, 2024c), similarly, as in Thermodynamics (Bejan, 2016), and not following an axiomatic approach. Only one short reference is made in (Chater & MacKay, 2025) to the entropy production in Economics, a measure of irreversibility/imperfection of economic processes, without highlighting its relevance and significance, and without specifying how it is evaluated. The present approach emphasizes the (general) balance equations (Costa, 2024b, 2024c); this is not the case of the work (Chater & MacKay, 2025), which is focused on exploring relations between the economic variables in a similar way as made in Thermodynamics. Work (Chater & MacKay, 2025) defines the economic temperature as ‘inversely proportional to the marginal aggregate utility of money’, which ‘provides a view of the value of money’, the economic temperature determining how ‘money will flow from the economy with the higher temperature to that with the lower temperature’. From the definition of economic temperature comes the definition of economic equilibrium. The proposed approach is different, setting the merchandise economic temperature as the inverse of the merchandise unit price, as suggested by the expression giving the merchandise economic entropy generation (the profit generation) in merchandise transfer across a finite economic temperature difference (in merchandise trading) (Costa, 2024c). Analogously, the economic equilibrium corresponds to the same merchandise economic temperature, the situation for which the traded merchandise transfer (trading) ceases. Chater and MacKay (2025) sets that ‘money transfer for goods at market prices should qualify as work and any other money transfer as heat’. That is substantially different from the proposed approach, which sets that traded merchandise transfer (trading) is the economic analogue of heat transfer, and that merchandise wealth transfer (merchandise transfer at null unit price, or at an infinite economic temperature) is the economic analogue of mechanical work transfer (Costa, 2024b, 2024c). Another relevant difference is that in (Chater & MacKay, 2025), the objective of the economic Carnot cycle is obtaining money by taking advantage of the economic temperature difference, whereas in the proposed approach, the objective of the economic Carnot cycle is obtaining the maximum allowable merchandise wealth by taking advantage of the economic temperature difference (Costa, 2024b, 2024c) without generating financial value. Additionally, the work (Chater & MacKay, 2025) is especially focused on ‘Making money out of price differences’, or in ‘Making money out of temperature differences’, when the present work is especially focused on delivering the maximum merchandise wealth out of merchandise economic temperature differences (out of merchandise unit price differences) (Costa, 2024b, 2024c), in a similar way as when dealing with thermal engines, the focus being on their reversible operation when in contact with two heat reservoirs (at different temperatures) to deliver the maximum work transfer (Bejan, 2016). Even thus, even if with remarkable differences, the work in (Chater & MacKay, 2025) may be useful for further developments of the present approach, and the reciprocal also seems true.

Entropy generation is the measure of the imperfection of thermodynamic processes. Similarly, economic entropy generation (financial value generation) can be considered a measure of the imperfection of economic processes. This work, looking at Economics through the eyes of Thermodynamics, searches for more perfect (less irreversible) economic processes and for opportunities to deliver more merchandise wealth, taken as the major objective of the economic processes, instead of the maximization of economic entropy generation (instead of the maximization of financial value generation). The proposed developments and approaches challenge the ways of thinking, the reading and interpreting of the messages they contain, and how they are related to the real-world economy, the concepts, the paradigms, and the ways of thinking and acting toward a more efficient economy. This way of looking at Economics gives new insights and opens up new ways toward a more perfect and more efficient economy, and for Economics thinking, teaching, and research.

2. Main Results from Previous Work

This section summarizes the main concepts, developments, and results of previous works by Costa (Costa 2024a, 2024b, 2024c), which serve as the basis for the proposed and presented additional developments.

2.1. Similar Variables and Terms

Table 1. Main Thermodynamics and Economics analogies from the previous works by Costa (2024b, 2024c).

Thermodynamics		Economics
m [kg]	Mass in the system
E [J]	Energy in the system
		$N_M$ [U]	Number of merchandise units in the system
		$N_m$ [U]	Number of monetary units in the system
U [J]	Internal energy in the system	$N$ [U]	Number of (merchandise and monetary) units in the system
T [K]	Temperature	$T_E$ [U/€]	Economic temperature
		$p$ [€/U]	Merchandise unit price
$Q$ [J]	Heat transfer interaction	$M$ [U]	Traded merchandise transfer interaction
$\dot{Q}$ [J/s]	Heat transfer flow rate	$\dot{M}$ [U/s]	Traded merchandise transfer flow rate
$W$ [J]	Work transfer interaction	$W_M$ [U/s]	Merchandise wealth transfer interaction
$\dot{W}$ [J/s]	Work transfer flow rate	${\dot{W}}_M$ [U/s]	Merchandise wealth transfer flow rate
		$W_m$ [U/s]	Monetary wealth transfer interaction
		${\dot{W}}_m$ [U/s]	Monetary wealth transfer flow rate
		$N_{M,g}$ [U]	Merchandise units’ generation in the system
		${\dot{N}}_{M,g}$ [U/s]	Merchandise units’ generation rate in the system
		$N_{m,g}$ [U]	Monetary units’ generation in the system
		${\dot{N}}_{m,g}$ [U/s]	Monetary units’ generation rate in the system
${\displaystyle \oint \frac{\delta Q}{T}}\le 0$ [J/K]	Clausius inequality	${\displaystyle \oint \frac{\delta M}{T_E}}\le 0$ [€]	Merchandise economic Clausius inequality
$dS\equiv {\left({\displaystyle \frac{\delta Q}{T}}\right)}_{\begin{array}{l}\mathrm{int}\\ \mathrm{rev}\end{array}}$ [J/K]	Differential equation defining entropy	$d{S}_{E,M}\equiv {\left({\displaystyle \frac{\delta M}{T_E}}\right)}_{\begin{array}{l}\mathrm{int}\\ \mathrm{rev}\end{array}}$ [€]	Differential equation defining merchandise economic entropy
S [J/(kg·K)]	Entropy	$S_E$ [€]	Economic entropy
		$S_{E,M}$ [€]	Merchandise economic entropy
		$S_{E,m}$ [€]	Monetary economic entropy
$S_g$ [J/K]	Entropy generation in the system	$S_{E,g}$ [€]	Economic entropy generation in the system
		$S_{E,M,g}$ [€]	Merchandise economic entropy generation in the system
		$S_{E,m,g}$ [€]	Monetary economic entropy generation in the system
${\dot{S}}_g$ [U/s]	Entropy generation rate in the system	${\dot{S}}_{E,g}$ [€/s]	Economic entropy generation rate in the system
		${\dot{S}}_{E,M,g}$ [€/s]	Merchandise economic entropy generation rate in the system
		${\dot{S}}_{E,m,g}$ [€/s]	Monetary economic entropy generation rate in the system
$W_{friction}$ [J]	Mechanical work lost (converted into heat) due to friction in the system, and lost	$W_{M,friction}$ [U]	Merchandise wealth lost (converted into traded merchandise) due to economic friction (services) in the system, and lost.
${\eta }_C=1-{\displaystyle \frac{T_2}{T_1}}$ [-]	Efficiency of the (reversible) Carnot engine	${\eta }_{E,C}=1-{\displaystyle \frac{T_{E,2}}{T_{E,1}}}$ [-]	Efficiency of the (reversible) economic Carnot engine

summarizes the analogy between Thermodynamics and Economics as proposed by Costa (2024b, 2024c).

Only one merchandise species is considered; if more than one merchandise species is involved, additive contributions of all the merchandise species need to be considered. As new ideas, concepts, variables, and relations/equations are proposed, introduced, and developed, units are indicated inside square brackets for all variables, equations, and inequations for increased clarity, accuracy, and easier reading and understanding. Euro (€) is used as the monetary unit; however, other monetary units can be equally considered (Costa, 2024c).

Of special relevance is the concept of merchandise wealth as merchandise that is not in the market, and that has thus an infinite economic temperature (a null unit price), as the analogue of mechanical work in Thermodynamics, which can be seen as heat at an infinite temperature.

2.2. Merchandise Units Balance Equation

As made for the energy balance equation, a similar equation can be written, setting the balance of the number of merchandise units in an economic system. This is written in the same form as usual in Engineering Thermodynamics (Moran et al., 2018), on a time rate basis, such that the equation sets that (Costa, 2024c)

$$\begin{array}{l}\underset{\mathrm{in} \mathrm{the} \mathrm{system}}{\underbrace{\left(\begin{array}{l}\mathrm{time} \mathrm{rate} \mathrm{of} \mathrm{change}\\ \mathrm{of} \mathrm{the} \mathrm{number} \mathrm{of}\\ \mathrm{merchandise} \mathrm{units}\\ \mathrm{in} \mathrm{the} \mathrm{system}\end{array}\right)}}=\\ \underset{\mathrm{through} \mathrm{the} \text{system’s} \mathrm{boundary}}{\underbrace{\left(\begin{array}{l}\mathrm{net} \mathrm{flow} \mathrm{rate} \mathrm{of}\\ \mathrm{traded} \mathrm{merchandise}\\ \mathrm{units} \mathrm{entering} \mathrm{the}\\ \mathrm{system}\end{array}\right)-\left(\begin{array}{l}\mathrm{net} \mathrm{flow} \mathrm{rate} \mathrm{of}\\ \mathrm{wealth} \left(\mathrm{non}\text{-}\mathrm{traded}\right)\\ \mathrm{merchandise} \mathrm{units}\\ \mathrm{leaving} \mathrm{the} \mathrm{system}\end{array}\right)}}+\hspace{0.17em}\underset{\mathrm{in} \mathrm{the} \mathrm{system}}{\underbrace{\left(\begin{array}{l}\mathrm{net} \mathrm{generation}\\ \mathrm{rate} \mathrm{of} \mathrm{merchandise}\\ \mathrm{units} \mathrm{in} \mathrm{the} \mathrm{system}\end{array}\right)}}\end{array} [\mathrm{U}/\mathrm{s}]$$

Such an equation can be written in more detail as (Costa, 2024c)

$${\displaystyle \frac{d{N}_M}{dt}}={\displaystyle \sum _{j=1}^{N_{Mj}}{\dot{M}}_j}-{\dot{W}}_M+{\dot{N}}_{M,g} [\mathrm{U}/\mathrm{s}]$$

(1)

The traded merchandise transfer interactions ${\dot{M}}_j$ [U/s] are positive when entering the economic system and negative when leaving it. A merchandise reservoir means an economic system whose economic temperature remains unchanged independently of the number of traded merchandise units it receives or releases. By its own turn, the merchandise wealth transfer interactions are taken as positive when released by the economic system, assuming that the positive effect of the economic engine is the delivered merchandise wealth, similarly, as made in Thermodynamics where the delivered mechanical work is the positive effect of the thermal engine (Moran et al., 2018).

Multiplying Equation (1) by dt leads to the differential merchandise units balance equation.

$$d{N}_M={\displaystyle \sum _{j=1}^{N_{Mj}}\delta M}-\delta W_M+\delta N_{M,g} [\mathrm{U}]$$

(2)

It is noted that symbol $d$ is used for the differential of an exact differential (a property of the system), ${\displaystyle {\int }_1^{2}d\left(\cdot \right)}={\left(\cdot \right)}_2-{\left(\cdot \right)}_1$, ${\displaystyle \oint d\left(\cdot \right)}=0$ and ${\left(\cdot \right)}_1$ and ${\left(\cdot \right)}_2$ have physical meanings, while symbol $\delta$ is used for the differential of an inexact differential (a non-property of the system), ${\displaystyle {\int }_1^2\delta \left(\cdot \right)}\ne {\left(\cdot \right)}_2-{\left(\cdot \right)}_1$, ${\displaystyle \oint \delta \left(\cdot \right)}\ne 0$, and ${\left(\cdot \right)}_1$ and ${\left(\cdot \right)}_2$ have no physical meanings (Sears & Salinger, 1975; Moran et al., 2018).

Each ${\dot{M}}_j$ [U/s] in Equation (1) is the sum of negative (released) and positive (received) traded merchandise rates exchanged by the economic system through its boundary with the merchandise reservoir at the temperature $T_{E,j}$ [U/€]. By its own turn, ${\dot{W}}_M$ [U/s] is the sum of negative (received) and positive (released) merchandise wealth rates exchanged by the economic system through its boundary.

Contrary to what happens with energy, which is conserved, units of merchandise can be generated or destroyed in the economic system. For example, new ideas, new knowledge, or new combinations of goods or services give rise to new (additional) numbers of merchandise units in the system without forcefully implying destruction of other merchandise units, cases for which ${\dot{N}}_{M,g}\ge 0$ [U/s]. Situations can exist for which units of merchandise are destroyed in the economic system; these are cases in which ${\dot{N}}_{M,g}\le 0$ [U/s].

2.3. Monetary Units Balance Equation

The monetary units balance equation can be written as (Costa, 2024c)

$${\displaystyle \frac{d{N}_m}{dt}}=-{\dot{W}}_m+{\displaystyle \sum _{in}\dot{m}}\hspace{0.17em}-{\displaystyle \sum _{out}\dot{m}}+{\dot{N}}_{m,g} [\mathrm{U}/\mathrm{s}]$$

(3)

As monetary units generation is restricted to the central banks, ${\dot{N}}_{m,g}=0$ [U/s] in common trading operations. The way traded merchandise units and monetary units are related in common trading operations will be seen further in this section.

Multiplying Equation (3) by dt leads to the differential monetary units balance equation.

$$d{N}_m=-\delta W_m+\delta m\hspace{0.17em}+\delta N_{m,g} [\mathrm{U}]$$

(4)

2.4. Economic Temperature

The economic temperature of a merchandise species, and thus that merchandise species economic temperature, is defined as the inverse of its unit price, that is

$$T_E\equiv {\displaystyle \frac{1}{p}} [\mathrm{U}/€]$$

(5)

The reason for this definition is explained in (Costa, 2024b, 2024c). As a note on the so-defined economic temperature, its sense is contrary to the usually assumed/referred one in common Economics language, saying that the economy is hotter when unit prices of traded merchandise are higher (on the contrary, the economy tends to freeze when unit prices of merchandise are higher).

Temperature is an intensive property of a thermodynamic system, which is intimately related to its other thermodynamic properties. Additionally, different chemical species in the same thermodynamic system share the same temperature value. By its own turn, the proposed economic temperature is not a property of the economic system but a property of a merchandise species. Different merchandise species have different unit prices, thus having different economic temperatures, even if they are in the same economic system (Costa, 2024c).

2.5. Merchandise Economic Entropy

The merchandise economic entropy $S_{E,M}$ [€] of an economic system, which is a property of the system, is defined by the differential equation (Costa, 2024b, 2024c)

$$d{S}_{E,M}\equiv {\left({\displaystyle \frac{\delta M}{T_E}}\right)}_{\mathrm{int}\mathrm{rev}}={\left({\displaystyle \frac{d{N}_M}{T_E}}\right)}_{\mathrm{int}\mathrm{rev}} [€]$$

(6)

as $\delta M=d{N}_M$ [U], subscript ‘int rev’ meaning an internally reversible economic process.

In the general case, the merchandise economic entropy $S_{E,M}$ [€] of an economic system is different from the financial value $N_M/T_E=N_M\cdot p$ [€] of its $N_M$ [U] merchandise units, as it is $d\left(N_M/T_E\right)=d{N}_M/T_E-\left(N_M/T_E^2\right)d{T}_E\ne d{N}_M/T_E$ [€]. Section 5.3 includes more developments concerning the merchandise economic entropy and evaluation of its change.

It is noted that ${\left(\delta M\right)}_{\mathrm{int}\mathrm{rev}}$ [U] is not an exact differential, but that ${\left(\delta M/T_E\right)}_{\mathrm{int}\mathrm{rev}}$ [€] is, as obtained from the merchandise economic Clausius inequality and expressed by Equation (6), which makes it a Pfaffian.

2.6. Merchandise Economic Entropy Balance Equation

Written in the same form as usual in Engineering Thermodynamics (Moran et al., 2018), the merchandise economic entropy balance equation sets that (Costa, 2024c)

$$\underset{\mathrm{in} \mathrm{the} \mathrm{system}}{\underbrace{\left(\begin{array}{l}\mathrm{time} \mathrm{rate} \mathrm{of} \mathrm{change}\\ \mathrm{of} \mathrm{the} \mathrm{merchandise}\\ \mathrm{economic} \mathrm{entropy}\\ \mathrm{in} \mathrm{the} \mathrm{system}\end{array}\right)}}=\underset{\mathrm{through} \mathrm{the} \text{system’s} \mathrm{boundary}}{\underbrace{\left(\begin{array}{l}\mathrm{net} \mathrm{flow} \mathrm{rate} \mathrm{of} \mathrm{traded}\\ \mathrm{merchandise} \mathrm{economic}\\ \mathrm{entropy} \mathrm{entering} \mathrm{the}\\ \mathrm{system}\end{array}\right)}}+\underset{\mathrm{in} \mathrm{the} \mathrm{system}}{\underbrace{\left(\begin{array}{l}\mathrm{net} \mathrm{merchandise}\\ \mathrm{economic} \mathrm{entropy}\\ \mathrm{generation} \mathrm{rate}\\ \mathrm{in} \mathrm{the} \mathrm{system}\end{array}\right)}} [€/\mathrm{s}]$$

The merchandise economic entropy balance equation can be written in more detail as (Costa, 2024c)

$${\displaystyle \frac{d{S}_{E,M}}{dt}}={\displaystyle \sum _{j=1}^{N_{Mj}}\frac{{\dot{M}}_j}{T_{E,j}}}+{\dot{S}}_{E,M,g} [€/\mathrm{s}]$$

(7)

In Thermodynamics, the heat flow rate $\dot{Q}$ [J/s] that crosses the system’s boundary at temperature $T$ [K] corresponds to the entropy flow rate $\dot{Q}/T$ [J/(s·K)], and the work flow rate $\dot{W}$ [J/s] that crosses the system’s boundary corresponds to a null entropy flow rate. This is why the work transfer terms are absent from the entropy balance equation (Bejan, 2016; Moran et al., 2018; Costa, 2024c). Thus, the work flow rate $\dot{W}$ [J/s] can be seen as a heat flow rate crossing the system’s boundary at an infinite temperature. From the energy transfer viewpoint, it continues to be the work flow rate transfer interaction $\dot{W}$ [J/s], and from the entropy viewpoint, it corresponds to the entropy transfer interaction flow rate ${\left(\dot{W}/T\right)}_{T\to \infty }=0$ [J/(s·K)].

In a similar way, the traded merchandise flow rate $\dot{M}$ [U/s] that crosses the economic system’s boundary at the economic temperature $T_E=1/p$ [U/€] corresponds to the merchandise economic entropy flow rate $\dot{M}/T_E=\dot{M}\cdot p$ [€/s], and the merchandise wealth flow rate ${\dot{W}}_M$ [U/s] that crosses the economic system’s boundary corresponds to a null merchandise economic entropy flow rate (Costa, 2024c). This is why the merchandise wealth transfer terms are absent from the merchandise economic entropy balance Equation (7). Thus, the merchandise wealth flow rate ${\dot{W}}_M$ [U/s] can be seen as a traded merchandise flow rate crossing the economic system’s boundary at an infinite economic temperature. From the merchandise transfer viewpoint, it continues to be the merchandise wealth flow rate transfer interaction ${\dot{W}}_M$ [U/s], and from the merchandise economic entropy viewpoint, it corresponds to the merchandise economic entropy flow rate ${\left(\dot{W}/T_E\right)}_{T_E\to \infty }=0$ [€/s] or, given the economic temperature definition in Equation (5), the merchandise wealth crosses the system’s boundary at a null unit price.

Units of energy from the sun, from the waves, or from the wind are available at null unit prices, and they are thus available as merchandise wealth. If these units of energy are harvested and placed in the market, giving them non-zero unit prices, merchandise wealth is converted into traded merchandise. In principle, it will no longer be converted back into merchandise wealth (into units of energy available at null unit prices). Imagination, ideas, time, previously acquired knowledge, and writing skills are available for free, at null unit prices; they are thus available as merchandise wealth.

In common language, it is usual to say that the (true) wealth corresponds to things that are not in the market, and/or that are not to be purchased or sold, and that they have no price, or that, in the present context, that they have a null unit price, which is the same as saying that they have an infinite economic temperature.

Multiplying Equation (7) by dt leads to the differential merchandise economic entropy balance equation.

$$d{S}_{E,M}={\displaystyle \sum _{j=1}^{N_{Mj}}\frac{\delta M_j}{T_{E,j}}}+\delta S_{E,M,g} [€]$$

(8)

When comparing with what happens with the Second Law of Thermodynamics (Bejan, 2016; Moran et al., 2018), for which irreversibility and entropy generation are associated with imperfection of the thermodynamic systems’ operation, the developed and proposed economic Second Law says that the economic irreversibility, or economic imperfection, of the economic systems’ operation is associated with the economic entropy generation (financial value generation) (Costa, 2024c).

It is also worth mentioning that friction in Thermodynamics has its analogue in Economics, which are the non-reproductive services. For example, electricity used for lighting cannot be retrieved as electricity; that is, this is a process that cannot be reversed (and it is thus an irreversible process). The same happens with cleaning services, communication services, etc.

2.7. Monetary Economic Entropy Balance Equation

The monetary economic entropy balance equation can be written as (Costa, 2024c)

$${\displaystyle \frac{d{S}_{E,m}}{dt}}={\displaystyle \sum _{in}\dot{m}\times 1}-{\displaystyle \sum _{out}\dot{m}\times 1}+{\dot{S}}_{E,m,g} [€/\mathrm{s}]$$

(9)

where multiplications by 1 are retained to highlight the difference between the monetary flow rate $\dot{m}$ [U/s] and its corresponding monetary economic entropy flow rate $\dot{m}\times 1$ [(U/s) × (€/U)] = [€/s].

Multiplying Equation (9) by dt leads to the differential monetary economic entropy balance equation

$$d{S}_{E,m}=dm\times 1+\delta S_{E,m,g} [€]$$

(10)

2.8. Trading Operations

In common trading operations, the merchandise economic entropy flow rates are balanced by the exchanged monetary economic entropy flow rates, such that (Costa, 2024c)

$${\displaystyle \sum _{j=1}^{N_{Mj}}\frac{{\dot{M}}_j}{T_{E,j}}}+\left({\dot{m}}_{in}\times 1-{\dot{m}}_{out}\times 1\right)=0 [€/\mathrm{s}]$$

(11)

For those cases, the addition of both the merchandise and monetary economic entropy balance equations, Equations (7) and (9), respectively, gives

$${\displaystyle \frac{d{S}_{E,M}}{dt}}+{\displaystyle \frac{d{S}_{E,m}}{dt}}={\dot{S}}_{E,M,g}+{\dot{S}}_{E,m,g} [€/\mathrm{s}]$$

(12)

Equation (12) sets a relation between the terms of the merchandise and monetary economic entropy balance equations, Equations (7) and (9), respectively, leading to a simplified version of the joint original merchandise and monetary economic entropy balance equations that applies to trading operations. Due to that, in any subsequent developments based on Equation (12), terms involving the traded merchandise can no longer be separated from terms involving the exchanged monetary units. In common trading operations, ${\dot{S}}_{E,m,g}=0$ [€/s], and as $d{S}_{E,m}/dt=\left(d{N}_m/dt\right)\times 1$ [€/s], Equation (12) can be rewritten as

$${\displaystyle \frac{d{N}_m}{dt}}\times 1={\dot{S}}_{E,M,g}-{\displaystyle \frac{d{S}_{E,M}}{dt}} [€/\mathrm{s}]$$

(13)

which can be read as follows: the monetary financial value accumulation rate is equal to the merchandise economic entropy generation rate minus the merchandise economic entropy accumulation rate, all of them in the economic system.

3. How Negotiation Contributes to a More Efficient Economy

Consider the situation illustrated in Figure 1, where a seller has $M$ [U] merchandise units which he/she plans to sell at the unit price $p_H$ [€/U], and the buyer wants to buy those merchandise units at the unit price $p_L$ [€/U]. It is assumed that the seller obtained the $M$ [U] merchandise units at the unit price $p_L$ [€/U], and it makes no sense to consider trading those merchandise units at a unit price smaller than $p_L$ [€/U].

If the trading operation would go ahead under those conditions, the merchandise economic entropy generation is

$$S_{E,M,g,0}=M\left(p_H-p_L\right) [€]$$

(14)

However, through the negotiation process, the seller and the buyer agree to sell, and purchase, respectively, those $M$ [U] merchandise units at the unit price

$$p=f_p{p}_H+\left(1-f_p\right)p_L [€/\mathrm{U}]$$

(15)

The dimensionless factor $f_p$ [-] ∈ [0, 1] [-] is defined as

$$f_p={\displaystyle \frac{p-p_L}{p_H-p_L}} [\text{-}]$$

(16)

Trading of those $M$ [U] merchandise units at the agreed/negotiated unit price $p\hspace{0.17em}\in \left[p_L,p_H\right]$ [€/U] leads to the merchandise economic entropy generation.

$$S_{E,M,g}=M\left(p-p_L\right)=f_p{S}_{E,M,g,0} [€]$$

(17)

It is thus concluded that negotiation is a way to decrease the trading merchandise unit price $p$ $\in \left[p_L,p_H\right]$ [€/U], starting from the expectations of the seller, leading to a reduction in the economic entropy generation in the trading process. In numerical terms, it is concluded that if the negotiated unit price is given by Equation (15), it leads to a reduction factor $f_p$ [-] in the merchandise economic entropy generation in the trading operation, as given by Equation (17).

The proposed approach states that merchandise economic entropy generation exists in a trading operation if profit generation (economic entropy generation, or financial value generation) exists in the trading operation. In this sense, the equilibrium situation does not correspond to that of the market equilibrium as referring to an agreed unit price for the trading operation, but to the trading operation as a whole with no profit generation (no economic entropy generation, or no financial value generation). This is similar to what happens in a heat transfer process across a temperature difference, which always generates entropy (unless there is no temperature difference or no heat transfer (unless no finite temperature difference exists)).

If an economy is as perfect as its economic entropy generation is smaller, it is thus concluded that the negotiation process in merchandise trading contributes toward a more perfect economy.

4. Endoreversible Economic Processes

Consider the situation illustrated in Figure 2, where $M$ [U] merchandise units are available at the unit price $p_L$ [€/U], and that they are split into two parts. One part, $fM$ [U], enters an economic Carnot engine (Costa, 2024b, 2024c) at the unit price $p_L$ [€/U], from which fraction $fM\left(p_L/p\right)$ [U] leaves at the unit price $p$ [€/U], after which that fraction is transferred through the unit price difference $\left(p_H-p\right)$ [€/U], and leaves the economic system at the unit price $p_H$ [€/U]. The other part, $\left(1-f\right)M$ [U], is transferred through the unit price difference $\left(p-p_L\right)$ [€/U], leaving at the unit price $p$ [€/U] to enter an economic Carnot engine at that unit price $p$ [€/U], from which fraction $\left(1-f\right)M\left(p/p_H\right)$ [U] leaves at the unit price $p_H$ [€/U], and leaves the economic system.

The economic process is said to be endoreversible as it consists of a series of reversible processes (the economic Carnot engines) and irreversible processes (the traded merchandise transfers through unit price differences) (Bejan, 2016).

The merchandise wealth obtained from the process is

$$W_M=M\left[f\left(1-{\displaystyle \frac{p_L}{p}}\right)+\left(1-f\right)\left(1-{\displaystyle \frac{p}{p_H}}\right)\right] [\mathrm{U}]$$

(18)

and the merchandise economic entropy generation in the process is

$$S_{E,M,g}=M\left[f\left({\displaystyle \frac{p_L}{p}}\right)\left(p_H-p\right)+\left(1-f\right)\left(p-p_L\right)\right] [€]$$

(19)

Once the limiting unit prices $p_L$ [€/U] and $p_H$ [€/U] are set, the (floating) unit price $p_{opt}$ [€/U] leading to the maximum delivered merchandise wealth, $W_{M,\max }$ [U], can be evaluated from Equation (19) as

$$p_{opt}={\left(p_L{p}_H\right)}^{1/2}{\left({\displaystyle \frac{f}{1-f}}\right)}^{1/2} [€/\mathrm{U}]$$

(20)

Similarly, it can be found from Equation (19) that this same unit price $p_{opt}$ [€/U] leads to the minimum merchandise economic entropy generation, $S_{E,M,g,\min }$ [€]. This is an expected result, as the maximum merchandise wealth is obtained from the less imperfect economic process, to which the minimum merchandise economic entropy generation corresponds.

From Equation (20), it can be obtained that

$${\displaystyle \frac{\partial p_{opt}}{\partial f}}={\displaystyle \frac{1}{2}}{\left(p_L{p}_H\right)}^{1/2}{\left[f{\left(1-f\right)}^3\right]}^{-1/2}>0 [€/\mathrm{U}]$$

(21)

that is, the unit price $p_{opt}$ [€/U] leading to maximum $W_M$ [U] and minimum $S_{E,M,g}$ [€] is an increasing function of the dimensionless splitting factor f.

Substituting $p_{opt}$ [€/U] in Equations (18) and (19) leads to

$$W_{M,\max }=M\left\{1-2{\left({\displaystyle \frac{p_L}{p_H}}\right)}^{1/2}{\left[f\left(1-f\right)\right]}^{1/2}\right\} [\mathrm{U}]$$

(22)

$$S_{E,M,g,\min }=M{\left(p_L{p}_H\right)}^{1/2}\left\{2{\left[f\left(1-f\right)\right]}^{1/2}-{\left({\displaystyle \frac{p_L}{p_H}}\right)}^{1/2}\right\} [€]$$

(23)

From Equation (22), it can be found that $\partial W_{M,\max }/\partial f=0$ [U] for $f=1/2$ [-], and from Equation (23), that $\partial S_{E,M,g,\min }/\partial f=0$ [€] for $f=1/2$ [-], and that $W_{M,\max }$ [U] is minimum and $S_{E,g,\min }$ [€] is maximum for $f=1/2$ [-], and it is thus

$$W_{M,\max ,\min }=M\left[1-{\left({\displaystyle \frac{p_L}{p_H}}\right)}^{1/2}\right] [\mathrm{U}]$$

(24)

$$S_{E,M,g,\min ,\max }=M{\left(p_L{p}_H\right)}^{1/2}\left[1-{\left({\displaystyle \frac{p_L}{p_H}}\right)}^{1/2}\right] [€]$$

(25)

Figure 3 schematically shows how $W_{M,\max }$ [U] and $S_{E,M,g,\min }$ [€] change with the dimensionless splitting factor $f$ [-].

At this point, it is interesting to look at the similarity between these expressions and the Curzon–Ahlborn (Curzon & Ahlborn, 1975; Bejan, 2016) expressions obtained for the endoreversible thermal engines, and especially the dimensionless term $\left[1-{\left(p_L/p_H\right)}^{1/2}\right]$ [-] in Equation (24), which can be interpreted as

$${\left(\eta \right)}_{W_{M,\max ,f=1/2}}=W_{M,\max ,f=1/2}/M=1-{\left(p_L/p_H\right)}^{1/2} [\text{-}]$$

(26)

This equation describes the efficiency of the endoreversible economic engine operating at the maximum merchandise wealth delivery, for the equipartition situation $\left(f=1/2\right)$ [€/U]. However, it is noted that simple ‘merchandise conductances’ crossed by traded merchandise units are not possible in this case, as there is no constitutive transfer law relating the transferred (traded) merchandise units $fM\left(p_L/p\right)$ [U] and the economic temperature difference $\left(p_H-p\right)$ [€/U] as $fM\left(p_L/p\right)=K_1\left(p_H-p\right)$ [U], and relating the transferred (traded) merchandise units $\left(1-f\right)M$ [U] and the economic temperature difference $\left(p-p_L\right)$ [€/U] as $\left(1-f\right)M=K_2\left(p-p_L\right)$ [U], as made with heat transfer in Thermodynamics, where such a constitutive transfer law exists (Curzon & Ahlborn, 1975; Bejan, 2016).

It is to be noted, however, that the unit price $p_{opt}$ [€/U] needs to be in the range $p_L\le p_{opt}\le p_H$ [€/U], from which it is obtained that the dimensionless splitting factor $f$ [-] needs to be in the range

$${\displaystyle \frac{\left(p_L/p_H\right)}{1+\left(p_L/p_H\right)}}\le f\le {\displaystyle \frac{1}{1+\left(p_L/p_H\right)}} [\text{-}]$$

(27)

5. Dynamic Economic Processes’ Analysis

In this work, as well as in previous works (Costa, 2024a, 2024b, 2024c), only general balance equations have been considered, but not any constitutive law/equation. Up to this point, no way was available to relate the change in the number of merchandise units $d{N}_M$ [U] in an economic system with the change in their economic temperature, $d{T}_E$ [U/€] (and the change in their unit price, $dp$ [€/U]), what is made in what follows for the first time. This section uses the economic temperature $T_E=1/p$ [U/€] instead of the unit price $p$ [€/U], for a greater similarity with what happens in Thermodynamics, whose ‘main’ variable is temperature.

5.1. Economic Merchandise Specific Heat

The specific heat of a system is defined as the heat received (or released) by its unit mass to increase (or decrease) its temperature by 1 K, that is

$$c\equiv {\displaystyle \frac{1}{m}}\left({\displaystyle \frac{\delta Q}{dT}}\right) [\mathrm{J}/(\mathrm{kg}·\mathrm{K})]$$

(28)

If what changes in the system when it receives or releases heat $\delta Q$ [J] is its internal energy $dU$ [J] (Bejan, 2016; Moran et al., 2018), it is

$$\delta Q=dU [\mathrm{J}]$$

(29)

and it is thus

$$dU=mcdT [\mathrm{J}]$$

(30)

If the temperature increases, $dT>0$ [K] (decreases $dT<0$ [K]) the internal energy also increases, $dU>0$ [J] (decreases $dU<0$ [J]), and as mass $m$ [kg] is a positive value, the specific heat $c$ [J/(kg·K)] is also a positive value.

Looking at the equation defining entropy (Bejan, 2016),

$$dS\equiv {\left({\displaystyle \frac{\delta Q}{T}}\right)}_{\mathrm{int}\hspace{0.17em}\mathrm{rev}} [\mathrm{J}/\mathrm{K}]$$

(31)

for a reversible process, it can be written that

$$dS={\displaystyle \frac{\delta Q}{T}}=mc{\displaystyle \frac{dT}{T}} [\mathrm{J}/\mathrm{K}]$$

(32)

In a similar way, the economic merchandise specific heat $c_E$ [€/U], an empirical (in the general case variable, and depending on the economic temperature) coefficient, can be defined as

$$c_E\equiv {\displaystyle \frac{1}{N_M}}\left({\displaystyle \frac{\delta M}{d{T}_E}}\right) [€/\mathrm{U}]$$

(33)

and as $\delta M=d{N}_M$ [U], from this defining Equation (33), it can be written that

$$d{N}_M=N_M{c}_{E}d{T}_E [\mathrm{U}]$$

(34)

which is the economic analogue of Equation (30).

If the economic temperature increases, $d{T}_E>0$ [U/€] (decreases $d{T}_E<0$ [U/€]) the number of merchandise units in the economic system also increases, $d{N}_M>0$ [U] (decreases, $d{N}_M<0$ [U]), and as the number of merchandise units $N_M$ [U] is a positive value, the merchandise economic specific heat $c_E$ [€/U)] is also a positive value. Equation (34) can be rewritten using the unit price $p=1/T_E$ [€/U] instead of the economic temperature $T_E$ [U/€] as

$$d{N}_M=-N_M{c}_E{\displaystyle \frac{dp}{p^2}} [\mathrm{U}]$$

(35)

By its own turn, considering Equation (6) defining the merchandise economic entropy of the economic system, for an economic reversible process, using Equation (34), it is thus

$$d{S}_E=N_M{c}_E{\displaystyle \frac{d{T}_E}{T_E}} [€]$$

(36)

which is the economic analogue of Equation (32).

From Equation (34) it can be obtained that

$${\displaystyle \frac{N_M}{N_{M,0}}}=\exp \left({\displaystyle \underset{T_{E,0}}{\overset{T_E}{\int }}{c}_{E}d{T}_E}\right) [\text{-}]$$

(37)

expression containing the exponential–character relationship between $N_M$ [U] and $T_E$ [U/€].

In what concerns the merchandise economic entropy of the economic system, integration of Equation (36), considering Equation (37), gives

$$S_{E,M}=S_{E,M,0}+{\displaystyle \underset{T_{E,0}}{\overset{T_E}{\int }}\left[N_{M,0}\exp \left({\displaystyle \underset{T_{E,0}}{\overset{T_E}{\int }}{c}_{E}d{T}_E}\right)\right]c_E\frac{d{T}_E}{T_E}} [€]$$

(38)

From this equation, it is concluded that, in a reversible process, if the economic temperature increases, $T_E>T_{E,0}$ [U/€] (if the unit price decreases, $p<p_0$ [€/U]) the inner integral in Equation (38) is positive, and $S_{E,M}>S_{E,M,0}$ [€]. This means that in such a process, the increase in the economic temperature is accompanied by an increase in the number of merchandise units in the economic system (through traded merchandise units entering into the economic system), such that it is $T_E>T_{E,0}$ [U/€] and $N_M>N_{M,0}$ [U]. As the economic process is reversible, at each economic temperature $T_E$ [U/€] the economic system exchanges (receives or releases) traded merchandise units with at least another economic system at that same economic temperature $T_E$ [U/€].

Using the fact that $T_E=1/p$ [U/€], Equation (35) can be written as

$${\displaystyle \frac{d{N}_M/N_M}{dp/p}}=-{\displaystyle \frac{c_E}{p}} [\text{-}]$$

(39)

It is recognized that

$$\epsilon ={\displaystyle \frac{d{N}_M/N_M}{dp/p}} [\text{-}]$$

(40)

is the well-known (in Economics) demand elasticity coefficient, Figure 4 (Samuelson & Nordhaus, 2010), and from Equation (39) it is thus

$$c_E=-\epsilon \cdot p=-{\displaystyle \frac{\epsilon }{T_E}} [€/\mathrm{U}]$$

(41)

It is highlighted here that $N_M$ [U] refers to the number of merchandise units in the economic system, relevant for the present purposes being its change in trading operations; thus, the most important in this context is $\delta M=d{N}_M$ [U], which expresses the traded (transferred) merchandise units.

It is opportune to recall (Thomsen, 2000) where it is referred to that ‘The “Law of Supply and Demand” has been called Le Châtelier’s principle applied to Economics. And indeed, when we examine a statement of this law, the analogy becomes apparent.’, to reinforce that once known the economic merchandise specific heat, which is the same as saying that once known the demand elasticity coefficient, Equations (34) and (36) are thus like constitutive equations describing the economic system’s behaviour in economically reversible processes.

5.2. Expressions for the Economic Merchandise Specific Heat

The expression

$$c_E\left(T_E\right)={\displaystyle \frac{a}{1+b{T}_E}}={\displaystyle \frac{a}{1+B\left(T_E/T_{E,0}\right)}} [€/\mathrm{U}]$$

(42)

can be used to approximate the economic merchandise specific heat $c_E$ [€/U], defining the dimensionless parameter

$$B=b{T}_{E,0} [\text{-}]$$

(43)

and this equation is used in what follows. Any specific case can be studied based on this expression, assuming that over the range of economic temperature of interest, a good approximation can be obtained for the economic merchandise specific heat by tuning the numerical values of coefficients a and b. It is noted that coefficients a and b both have units of [€/U].

Defining the dimensionless economic temperature

$${\tau }_E={\displaystyle \frac{T_E}{T_{E,0}}} [\text{-}]$$

(44)

integration of Equation (34) leads to

$${\displaystyle \frac{N_M}{N_{M,0}}}={\left({\displaystyle \frac{1+B{\tau }_E}{1+B}}\right)}^{a/b} [\text{-}]$$

(45)

Combination of Equations (36) and (42) leads to

$$d{S}_{E,M}=N_{M,0}a{\left(1+B\right)}^{-a/b}{\left(1+B{\tau }_E\right)}^{a/b-1}{\displaystyle \frac{d{\tau }_E}{{\tau }_E}} [€]$$

(46)

Obtaining analytical expressions for $S_{E,M}$ [€] from Equation (46) requires that some conditions must be observed concerning coefficients a and b. For simplicity of the involved analytical expressions, and given the present purposes, in what follows, it is considered the case for which $-b/\left(a-b\right)=-1$ [-], that is, for which $a=2b$ [€/U] and $\left(a-b\right)/b=1$ [-]. Real cases may require the use of other (analytical or numerical) expressions as the best fits for the economic merchandise specific heat, once the demand elasticity coefficient is known, and using Equation (41) to relate them.

From Equation (45),

$${\displaystyle \frac{N_M}{N_{M,0}}}={\left({\displaystyle \frac{1+B{\tau }_E}{1+B}}\right)}^2 [\text{-}]$$

(47)

and the integration of Equation (46) gives

$${\displaystyle \frac{S_{E,M}}{S_{E,M,0}}}=1+2B{\left(1+B\right)}^{-2}\left[\ln \left({\tau }_E\right)+B\left({\tau }_E-1\right)\right] [\text{-}]$$

(48)

It is also of major relevance, in the present context, the relation between the number of merchandise units in the economic system and their unit price $p=1/T_E$ [€/U], which can be obtained from Equation (47) as

$${\displaystyle \frac{N_M}{N_{M,0}}}={\left({\displaystyle \frac{1+B{\pi }_E}{1+B}}\right)}^2 [\text{-}]$$

(49)

where $B=b{T}_{E,0}=b/p_0$ [-] and ${\pi }_E=\left(T_E/T_{E,0}\right)={\left(p/p_0\right)}^{-1}$ [-].

Figure 5 is the graphical representation of Equations (47)–(49), noting that Equation (49) (Figure 5, middle) is the dimensionless demand curve.

5.3. Notes on the Merchandise Economic Entropy Change

The merchandise differential economic entropy balance, Equation (8), for an economic system that exchanges traded merchandise with just one merchandise reservoir can be written as

$$d{S}_{E,M}={\displaystyle \frac{\delta M}{T_E}}+\delta S_{E,M,g}={\displaystyle \frac{d{N}_M}{T_E}}+\delta S_{E,M,g} [€]$$

(50)

which applies to any (irreversible or reversible) economic process. As for an internally reversible economic process $\delta S_{E,M,g}=0$ [€], Equation (50) results in Equation (6).

To relate the change in the financial value of the merchandise units in the economic system to the change in the merchandise economic entropy of the economic system, it can be written that

$$d\left({\displaystyle \frac{N_M}{T_E}}\right)={\displaystyle \frac{d{N}_M}{T_E}}-{\displaystyle \frac{N_M}{T_E^2}}d{T}_E [€]$$

(51)

5.3.1. Internally Reversible Processes

Only for internally reversible processes it is $d{S}_{E,M}=d{N}_M/T_E$ [€], and only in that case, it can be written from Equation (51) that

$${\left[d{S}_{E,M}=d\left({\displaystyle \frac{N_M}{T_E}}\right)+{\displaystyle \frac{N_M}{T_E^2}}d{T}_E\right]}_{\mathrm{int} \mathrm{rev}} [€]$$

(52)

Thus, for an internally reversible process, the change in the merchandise economic entropy of the economic system, ${\left(\delta M/T_E\right)}_{\mathrm{int} \mathrm{rev}}={\left(d{N}_M/T_E\right)}_{\mathrm{int} \mathrm{rev}}$ [€], is not only the change in the merchandise financial value $d\left(N_M/T_E\right)$ [€] of the merchandise units in the economic system but it also needs to consider the financial value change expressed by the last term of Equation (52).

In this process, as seen before, if the economic temperature increases, $d{T}_E>0$ [U/€] (decreases, $d{T}_E<0$ [U/€]) the number of merchandise units in the economic system also increases, $d{N}_M>0$ [U] (decreases, $d{N}_M<0$ [U]). This raises the relevant question of knowing if the financial value of the number of merchandise units $N_M\left(T_E\right)$ [€] in the economic system increases or decreases as the economic temperature (the inverse of the unit price) of those merchandise units changes. 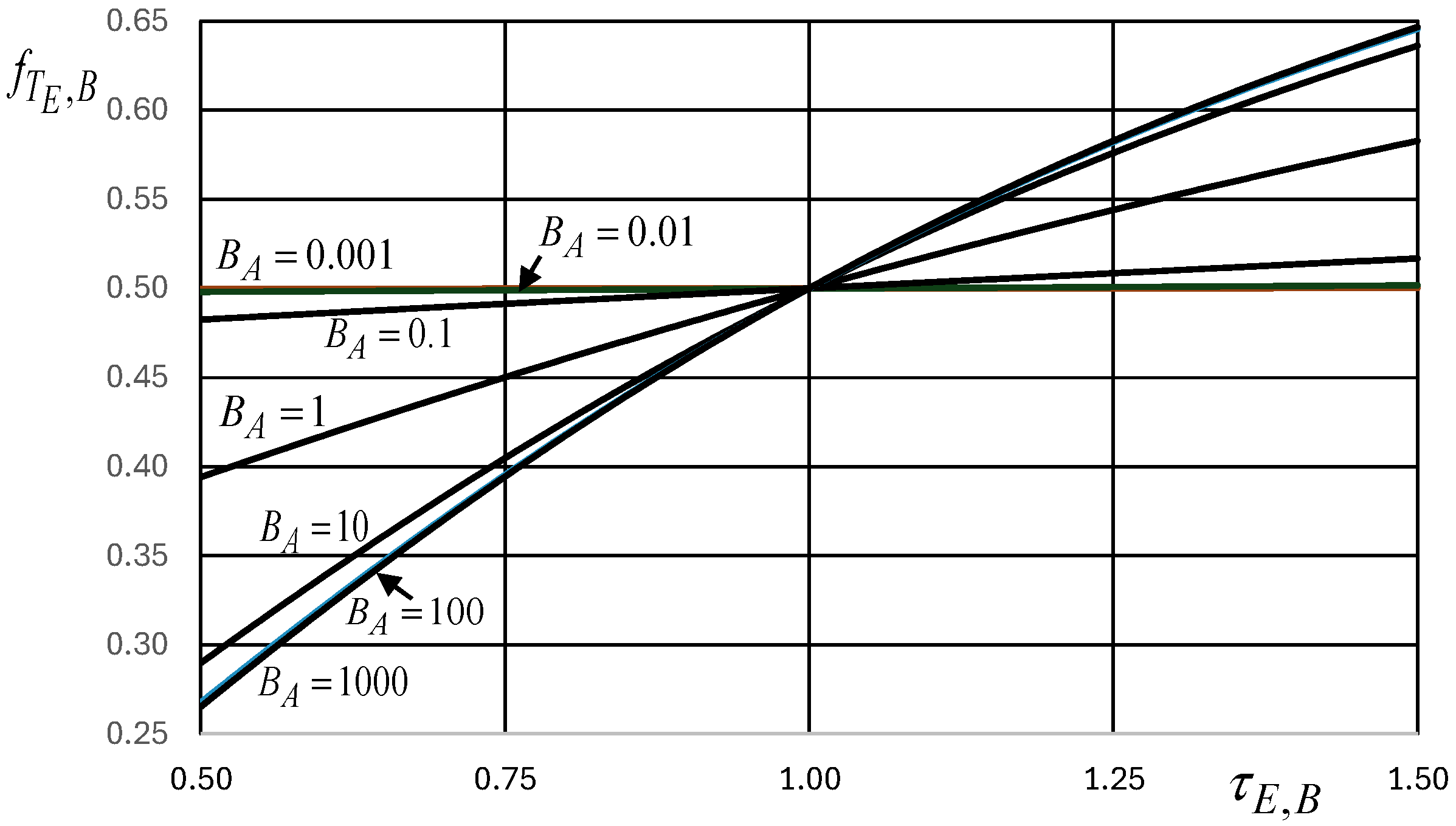Conversely, this is the question of knowing if the change in the number of merchandise units in the economic system is compensated, or not, by the change in the economic temperature (the inverse of the unit price) of the merchandise units in the economic system. For that purpose, it can be found that $d\left(N_M/T_E\right)/d{T}_E=-\left(N_M/T_E^2\right)\left(\epsilon +1\right)$ [€/(U/€)], which is positive if $\epsilon <-1$ [-] and negative if $\epsilon >-1$ [-], thus being strongly dependent on the demand elasticity coefficient $\epsilon$ [-], retaining that it is always $\epsilon <0$ [-] (Figure 4).

Table 2. Summary of what happens with signs of terms of Equation (52).

$d{T}_E$	$dp$	$d{N}_M$	$d{S}_{E,M}$	$\left(N_M/T_E^2\right)d{T}_E$	$d\left(N_M/T_E\right)$
>0	<0	>0	>0	>0	<0 if $\epsilon >-1$ >0 if $\epsilon <-1$
<0	>0	<0	<0	<0	>0 if $\epsilon >-1$ <0 if $\epsilon <-1$

may be constructed to summarize what happens with signs of terms of Equation (52).

For the reversible economic process, integration of Equation (52) leads to

$${\left[\left(S_{E,M,2}-S_{E,M,1}\right)={\left({\displaystyle \frac{N_M}{T_E}}\right)}_2-{\left({\displaystyle \frac{N_M}{T_E}}\right)}_1+{\displaystyle \underset{T_{E,1}}{\overset{T_{E,2}}{\int }}\frac{N_M}{T_E^2}d{T}_E}\right]}_{\mathrm{int} \mathrm{rev}} [€]$$

(53)

Equation (53) must be interpreted as expressing that the change in the financial value of the merchandise units in the economic system in the 1–2 process, ${\left(N_M/T_E\right)}_2-{\left(N_M/T_E\right)}_1$ [€], is equal to the change in the merchandise economic entropy of the economic system associated with the traded merchandise (reversibly) released or received by the economic system in that process, $\left(S_{E,M,2}-S_{E,M,1}\right)={\displaystyle {\int }_1^2\left(\delta M/T_E\right)}={\displaystyle {\int }_1^2\left(d{N}_M/T_E\right)}$ [€], minus the change in the financial value of the merchandise units in the economic system associated with their economic temperature change, $-{\displaystyle {\int }_{T_{E,1}}^{T_{E,2}}\left(N_M/T_E^2\right)d{T}_E}$ [€].

Figure 6 is the graphical representation of Equations (52) and (53).

For the economic process 1–2, along which both the number of merchandise units $N_M$ [U] in the economic system and their economic temperature $T_E$ [U/€] are changed, only for economic reversible processes can these variables be related through constitutive laws like those in Equations (34) and (36). In that case, taking into consideration Equation (53), it can be written that

$${\displaystyle \underset{T_{E,1}}{\overset{T_{E,2}}{\int }}\frac{N_M}{T_E^2}d{T}_E}={\displaystyle \frac{N_{M,1}}{T_{E,1}}}{\left(1+B\right)}^{-2}\left\{B\left[2\ln \left({\tau }_E\right)+B\left({\tau }_E-1\right)\right]-\left({\tau }_E^{-1}-1\right)\right\} [€]$$

(54)

where $B=b{T}_{E,1}$ [-] and ${\tau }_E=\left(T_{E,2}/T_{E,1}\right)$ [-].

For the internally reversible economic process at constant economic temperature $T_E$ [U/€], $d{T}_E=0$ [U/€], and from Equation (52), it is obtained that the change in the merchandise economic entropy ${\left(\delta M/T_E\right)}_{\mathrm{int} \mathrm{rev}}={\left(d{N}_M/T_E\right)}_{\mathrm{int} \mathrm{rev}}$ [€] of the economic system is equal to the change in its merchandise financial value $d\left(N_M/T_E\right)$ [€], and from Equation (53) that

$${\left[\left(S_{E,M,2}-S_{E,M,1}\right)={\left({\displaystyle \frac{N_M}{T_E}}\right)}_2-{\left({\displaystyle \frac{N_M}{T_E}}\right)}_1\right]}_{\mathrm{int} \mathrm{rev},T_E} [€]$$

(55)

5.3.2. Irreversible Processes

In the case of irreversible processes, from Equation (50) it is obtained that

$$\delta S_{E,M,g}=d{S}_{E,M}-{\displaystyle \frac{\delta M}{T_E}} [€]$$

(56)

noting, however, that in this case it is $d{S}_{E,M}\ne \delta M/T_E=d{N}_M/T_E$ [€].

For the limiting situation of the irreversible economic process at a constant number of merchandise units $N_M$ [U] in the economic system, $\delta M=d{N}_M=0$ [U], from Equation (50), it is $\delta S_{E,M,g}=d{S}_{E,M}$ [€], and for irreversible process 1–2, it is

$${\left(S_{E,M,g}\right)}_{1-2}=\left(S_{E,M,2}-S_{E,M,1}\right) [€]$$

(57)

In that case, the merchandise economic entropy of the $N_M$ [U] merchandise units in the economic system can change only by changing their economic temperature, in an irreversible process, as

$${\left(S_{E,M,g}\right)}_{1-2}=\left(S_{E,M,2}-S_{E,M,1}\right)={\displaystyle \frac{N_M}{T_{E,2}}}-{\displaystyle \frac{N_M}{T_{E,1}}}=N_M\left(p_2-p_1\right) [€]$$

(58)

noting that, in this case, the general Equation (50) can be used, but not the relation ${\left(\delta M/T_E\right)}_{\mathrm{int} \mathrm{rev}}={\left(d{N}_M/T_E\right)}_{\mathrm{int} \mathrm{rev}}=d{S}_{E,M}$ [€] as the economic process 1–2 is irreversible. In that case, the change in the merchandise economic entropy is equal to the generated merchandise economic entropy in the economic system; this is equal to the change in the financial value of the merchandise units in the economic system, which changes as a result of the change in the economic temperature of the $N_M$ [U] merchandise units in the economic system from $T_{E,1}$ [U/€] to $T_{E,2}$ [U/€]. Interestingly, also in this case, the change in the merchandise economic entropy $\left(S_{E,M,2}-S_{E,M,1}\right)$ [€] of the economic system is equal to the change in the merchandise financial value $\left(N_M/T_{E,2}-N_M/T_{E,1}\right)$ [€] of the $N_M$ [U] merchandise units in the economic system.

5.4. Dynamic Processes’ Analysis

Consider that two economic subsystems A and B, initially with $N_{M,A,0}=N_{M,B,0}=N_{M,0}$ [U] merchandise units each, at the respective economic temperatures $T_{E,A,0}$ [U/€] and $T_{E,B,0}$ [U/€], are allowed to evolve spontaneously (in the economic sense), exchanging traded merchandise up to reach the equilibrium situation (equal economic temperature $T_{E,f}$ [U/€]), through two different processes: the fully irreversible process, without obtaining any merchandise wealth, and through the reversible process, obtaining the maximum merchandise wealth. Figure 7 schematically represents the economic processes under analysis, where subscripts 0 and f are used for the initial and final states, respectively.

5.4.1. Fully Irreversible Process

Figure 8 schematically represents the fully irreversible process.

From Equation (47), at the end of the fully irreversible process

$$N_{M,A}=N_{M,A,0}{\left({\displaystyle \frac{1+B_A{\tau }_{E,f}}{1+B_A}}\right)}^2 [\mathrm{U}]$$

(59)

where $B_A=b{T}_{E,A,0}$ [-] and ${\tau }_{E,f}=\left(T_{E,f}/T_{E,A,0}\right)$ [-], and

$$N_{M,B}=N_{M,B,0}{\left({\displaystyle \frac{1+B_B{\tau }_{E,f}}{1+B_B}}\right)}^2=N_{M,B,0}{\left({\displaystyle \frac{1+B_A{\tau }_{E,f}}{1+B_A{\tau }_{E,B}}}\right)}^2 [\mathrm{U}]$$

(60)

where $B_B=b{T}_{E,B,0}$ [-] and ${\tau }_{E,B}=\left(T_{E,B,0}/T_{E,A,0}\right)$ [-]. As $B_A=b{T}_{E,A,0}$ [-] and $B_B=b{T}_{E,B,0}$ [-], $B_B=B_A{\tau }_{E,B}$ [-].

At the end of the fully irreversible process, no merchandise units leave or enter the composite (A + B) economic system, and thus

$$N_{M,A}+N_{M,B}=N_{M,A,0}+N_{M,B,0} [\mathrm{U}]$$

(61)

As no merchandise wealth is obtained in the fully irreversible process, $W_M=0$ [U]. Using Equations (59) and (60), it is thus

$${\left({\displaystyle \frac{1+B_A{\tau }_{E,f}}{1+B_A}}\right)}^2+{\left({\displaystyle \frac{1+B_A{\tau }_{E,f}}{1+B_A{\tau }_{E,B}}}\right)}^2=2 [\text{-}]$$

(62)

from which it comes

$${\left(1+B_A{\tau }_{E,f}\right)}^2={\displaystyle \frac{2}{\frac{1}{{\left(1+B_A{\tau }_{E,A}\right)}^2}+\frac{1}{{\left(1+B_A{\tau }_{E,B}\right)}^2}}} [\text{-}]$$

(63)

where ${\tau }_{E,A}=\left(T_{E,A,0}/T_{E,A,0}\right)=1$ [-].

Defining the auxiliary dimensionless term,

$$C={\left[{\left(1+B_A\right)}^{-2}+{\left(1+B_A{\tau }_{E,B}\right)}^{-2}\right]}^{-1/2} [\text{-}]$$

(64)

the final (equilibrium) dimensionless economic temperature can be obtained from Equation (63) as

$${\tau }_{E,f}={\displaystyle \frac{\sqrt{2}C-1}{B_A}} [\text{-}]$$

(65)

noting that this result depends on both $T_{E,A,0}$ [U/€] and $T_{E,B,0}$ [U/€].

Once the initial economic temperatures $T_{E,A,0}$ [U/€] and $T_{E,B,0}$ [U/€] are known, it is of major relevance to know how the final economic temperature $T_{E,f}$ [U/€] depends on those initial economic temperatures, as

$$T_{E,f}=f_{T_E,B}{T}_{E,A,0}+\left(1-f_{T_E,B}\right)T_{E,B,0} [\mathrm{U}/€]$$

(66)

and not as (apparently from Equation (65)) on the initial economic temperature of subsystem A only.

Defining the dimensionless weighting factor $f_{T_E,B}$ [-] as

$$f_{T_E,B}={\displaystyle \frac{T_{E,f}-T_{E,B,0}}{T_{E,A,0}-T_{E,B,0}}} [\text{-}]$$

(67)

it is the ratio of the relative departure of the final economic temperature $T_{E,f}$ [U/€] relative to the initial economic temperature of economic subsystem B, $\left(T_{E,f}-T_{E,B,0}\right)$ [U/€], to the overall (maximum) initial economic temperature difference $\left(T_{E,A,0}-T_{E,B,0}\right)$ [U/€] of economic subsystems A and B. Both the numerator and denominator of Equation (67) can be divided by $T_{E,A,0}$ [U/€] to obtain $f_{T_E,B}$ [-] as

$$f_{T_E,B}={\displaystyle \frac{{\tau }_{E,f}-{\tau }_{E,B}}{1-{\tau }_{E,B}}} [\text{-}]$$

(68)

Figure 9 shows how the dimensionless weighting factor $f_{T_E,B}$ [-] depends on $B_A$ [-] and ${\tau }_{E,B}$ [-].

At this point, it must be noted that if the unit price is being used instead of the economic temperature, from Equation (65), it is $\left(p_f/p_{A,0}\right)=B_A/\left(\sqrt{2}C-1\right)$ [-]. In that case, once the initial unit prices $p_{A,0}$ [€/U] and $p_{B,0}$ [€/U] are known, it is of major relevance to know how the final unit price $p_f$ [€/U] depends on those initial unit prices, as

$$p_f=f_{p,B}{p}_{A,0}+\left(1-f_{p,B}\right)p_{B,0} [€/\mathrm{U}]$$

(69)

Defining the dimensionless weighting factor $f_{p,B}$ [-] as

$$f_{p,B}={\displaystyle \frac{p_{B,0}-p_f}{p_{B,0}-p_{A,0}}} [\text{-}]$$

(70)

it is the ratio of the relative departure of the final unit price $p_f$ [€/U] relative to the initial unit price of subsystem B, $\left(p_{B,0}-p_f\right)$ [€/U], to the overall (maximum) initial unit price difference $\left(p_{B,0}-p_{A,0}\right)$ [€/U] of economic subsystems B and A. Using Equation (65), both the numerator and denominator of Equation (70) can be divided by $p_{A,0}$ [U/€] to obtain $f_{p,B}$ [-] as

$$f_{p,B}={\displaystyle \frac{\left(p_{B,0}/p_{A,0}\right)-\left(p_f/p_{A,0}\right)}{\left(p_{B,0}/p_{A,0}\right)-1}} [\text{-}]$$

(71)

and from Equations (67) and (70) it is $f_{T_E,B}=\left(p_{A,0}/p_f\right)f_{p,B}$ [-].

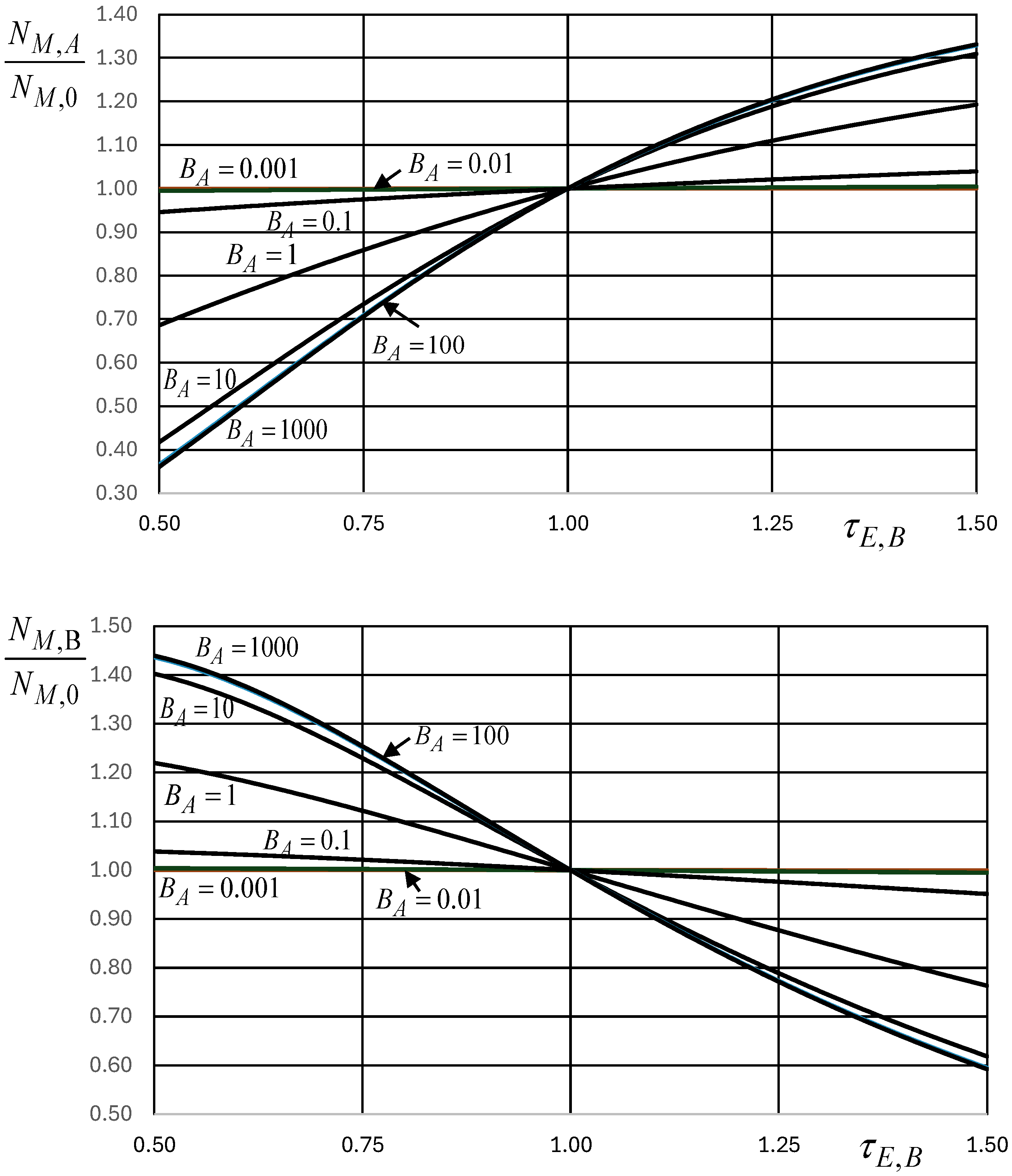
Once the dimensionless economic temperature ratio ${\tau }_{E,f}$ [-] is known, the final numbers of merchandise units in subsystems A and B, $N_{M,A}$ [U] and $N_{M,B}$ [U], can be obtained using Equations (59) and (60), respectively. As $N_{M,A}+N_{M,B}=N_{M,A,0}+N_{M,B,0}=2N_{M,0}$ [U], in dimensionless terms, it is $\left(N_{M,B}/N_{M,0}\right)=2-\left(N_{M,A}/N_{M,0}\right)$ [-]. Figure 10 shows how the dimensionless number of merchandise units in subsystem A at the end of the fully irreversible process, $\left(N_{M,A}/N_{M,0}\right)$ [-], depends on $B_A$ [-] and ${\tau }_{E,B}$ [-].

In what concerns the merchandise economic entropy generation, noting that no merchandise units enter or leave the (A + B) composite economic system, it is, considering Equation (54),

$$\begin{array}{l}{S}_{E,M,g}=S_{E,M,f}-S_{E,M,i}=\\ \left[\left({\displaystyle \frac{N_{M,A}}{T_{E,f}}}\right)+\left({\displaystyle \frac{N_{M,B}}{T_{E,f}}}\right)\right]-\left[\left({\displaystyle \frac{N_{M,A,0}}{T_{E,A,0}}}\right)+\left({\displaystyle \frac{N_{M,B,0}}{T_{E,B,0}}}\right)\right]+\\ {\displaystyle \frac{N_{M,0}}{T_{E,A,0}}}{\left(1+B_A\right)}^{-2}\left\{B_A\left[2\ln \left({\tau }_{E,f}\right)+B_A\left({\tau }_{E,f}-1\right)\right]-\left({\tau }_{E,f}^{-1}-1\right)\right\}+\\ {\displaystyle \frac{N_{M,0}}{T_{E,B,0}}}{\left(1+B_B\right)}^{-2}\left\{\begin{array}{l}{B}_B\left[2\ln \left({\tau }_{E,f}{\tau }_{E,B}^{-1}\right)+B_B\left({\tau }_{E,f}{\tau }_{E,B}^{-1}-1\right)\right]-\\ \left({\tau }_{E,f}^{-1}{\tau }_{E,B}-1\right)\end{array}\right\}\end{array} [€]$$

(72)

and it is thus, in the dimensionless form

$$\begin{array}{l}{\displaystyle \frac{S_{E,M,g}}{\left(N_{M,0}/T_{E,A,0}\right)}}=C^{-2}{\tau }_{E,f}^{-1}{\left(1+B_A{\tau }_{E,f}\right)}^2-\left(1+{\tau }_{E,B}^{-1}\right)+\\ {\left(1+B_A\right)}^{-2}\left\{B_A\left[2\ln \left({\tau }_{E,f}\right)+B_A\left({\tau }_{E,f}-1\right)\right]-\left({\tau }_{E,f}^{-1}-1\right)\right\}+\\ {\tau }_{E,B}^{-1}{\left(1+B_B\right)}^{-2}\left\{\begin{array}{l}{B}_B\left[2\ln \left({\tau }_{E,f}{\tau }_{E,B}^{-1}\right)+B_B\left({\tau }_{E,f}{\tau }_{E,B}^{-1}-1\right)\right]-\\ \left({\tau }_{E,f}^{-1}{\tau }_{E,B}-1\right)\end{array}\right\}\end{array} [\text{-}]$$

(73)

Figure 11 shows how the dimensionless merchandise economic entropy generation, $S_{E,M,g}/\left(N_{M,0}/T_{E,A,0}\right)$ [-], depends on $B_A$ [-] and ${\tau }_{E,B}$ [-].

Beyond numerical values, the main message is that the fully irreversible process makes use of the available economic temperature difference to generate the maximum merchandise economic entropy (to generate the maximum merchandise financial value), and not for any other useful purpose.

5.4.2. Reversible Process

Equations (59) and (60) apply equally to the reversible process, even if it is noted that the final economic temperature $T_{E,f}$ [U/€] is different in this case. Figure 12 is the schematic representation of the reversible process.

From Equations (59) and (60), it is

$$N_{M,A}+N_{M,B}=N_{M,0}{C}^{-2}{\left(1+B_A{\tau }_{E,f}\right)}^2 [\mathrm{U}]$$

(74)

where C [-] is the same as defined by Equation (64).

The merchandise economic entropy generation is null in the reversible process, and it is, considering Equation (54), and defining once again $B_A=b{T}_{E,A,0}$ [-] and $B_B=b{T}_{E,B,0}=B_A{\tau }_{E,B}$ [-],

$$\begin{array}{l}{S}_{E,M,g}=S_{E,M,f}-S_{E,M,i}=0=\\ \left[\left({\displaystyle \frac{N_{M,A}}{T_{E,f}}}\right)+\left({\displaystyle \frac{N_{M,B}}{T_{E,f}}}\right)\right]-\left[\left({\displaystyle \frac{N_{M,A,0}}{T_{E,A,0}}}\right)+\left({\displaystyle \frac{N_{M,B,0}}{T_{E,B,0}}}\right)\right]+\\ {\displaystyle \frac{N_{M,0}}{T_{E,A,0}}}{\left(1+B_A\right)}^{-2}\left\{B_A\left[2\ln \left({\tau }_{E,f}\right)+B_A\left({\tau }_{E,f}-1\right)\right]-\left({\tau }_{E,f}^{-1}-1\right)\right\}+\\ {\displaystyle \frac{N_{M,0}}{T_{E,B,0}}}{\left(1+B_B\right)}^{-2}\left\{\begin{array}{l}{B}_B\left[2\ln \left({\tau }_{E,f}{\tau }_{E,B}^{-1}\right)+B_B\left({\tau }_{E,f}{\tau }_{E,B}^{-1}-1\right)\right]-\\ \left({\tau }_{E,f}^{-1}{\tau }_{E,B}-1\right)\end{array}\right\}\end{array} [€]$$

(75)

and it is thus, in the dimensionless form

$$\begin{array}{l}0=C^{-2}{\tau }_{E,f}^{-1}{\left(1+B_A{\tau }_{E,f}\right)}^2-\left(1+{\tau }_{E,B}^{-1}\right)+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\left(1+B_A\right)}^{-2}\left\{B_A\left[2\ln \left({\tau }_{E,f}\right)+B_A\left({\tau }_{E,f}-1\right)\right]-\left({\tau }_{E,f}^{-1}-1\right)\right\}+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\tau }_{E,B}^{-1}{\left(1+B_B\right)}^{-2}\left\{\begin{array}{l}{B}_B\left[2\ln \left({\tau }_{E,f}{\tau }_{E,B}^{-1}\right)+B_B\left({\tau }_{E,f}{\tau }_{E,B}^{-1}-1\right)\right]-\\ \left({\tau }_{E,f}^{-1}{\tau }_{E,B}-1\right)\end{array}\right\}\end{array} [\text{-}]$$

(76)

This is a transcendental equation, from which the dimensionless economic temperature ratio ${\tau }_{E,f}$ [-] using, for example, the Newton–Raphson method can be obtained. Once the dimensionless economic temperature ratio ${\tau }_{E,f}$ [-] is known, Equation (68) can also be used in this case to find the dimensionless economic temperature weighting factor $f_{T_E,B}=\left({\tau }_{E,f}-{\tau }_{E,B}\right)/\left(1-{\tau }_{E,B}\right)$ [-]; Figure 13 shows how it depends on $B_A$ [-] and ${\tau }_{E,B}$ [-] for the reversible process.

Once the dimensionless economic temperature ratio ${\tau }_{E,f}$ [-] is known, the final numbers of merchandise units in subsystems A and B, $N_{M,A}$ [U] and $N_{M,B}$ [U] are obtained using Equations (59) and (60), respectively. By its own turn, the (maximum) merchandise wealth released by the economic system in the reversible process up to the final equilibrium is given by the difference

$$W_{M,\max }=2N_{M,0}-\left(N_{M,A}+N_{M,B}\right) [\mathrm{U}]$$

(77)

that is, in the dimensionless form

$${\displaystyle \frac{W_{M,\max }}{N_{M,0}}}=2-C^{-2}{\left(1+B_A{\tau }_{E,f}\right)}^2 [\text{-}]$$

(78)

Figure 14 shows how the dimensionless number of merchandise units in subsystems A and B at the end of the fully irreversible process, $\left(N_{M,A}/N_{M,0}\right)$ [-] and $\left(N_{M,B}/N_{M,0}\right)$ [-], respectively, and the dimensionless maximum merchandise wealth released $W_{M,\max }/N_{M,0}$ [-] depend on $B_A$ [-] and ${\tau }_{E,B}$ [-]. It is reinforced, however, that given Equation (77), $\left(N_{M,A}/N_{M,0}\right)$ [-], $\left(N_{M,B}/N_{M,0}\right)$ [-] and $W_{M,\max }/N_{M,0}$ [-] are not independent, their addition being equal to 2.

Beyond the numerical values, the main message is that the reversible process takes advantage of the available economic temperature difference to deliver the (always positive) maximum merchandise wealth.

It is noted that another way of obtaining the (maximum) merchandise wealth released by the economic system in the reversible process consists of considering the (reversible) economic Carnot engine operating between economic temperatures $T_{E,A}$ [U/€] and $T_{E,B}$ [U/€], which change from their initial respective values $T_{E,A,0}$ [U/€] and $T_{E,B,0}$ [U/€] up to the final (equilibrium) economic temperature $T_{E,f}$ [U/€], as schematically represented in Figure 12.

Considering that $T_{E,A,0}>T_{E,B,0}$ [U/€], when the economic temperature $T_{E,A}$ [U/€] changes by $d{T}_{E,A}\hspace{0.17em}\left(<0\right)$ [U/€], the number of merchandise units released by subsystem A at economic temperature $T_{E,A}$ [U/€] is $\left|\delta M_A\right|=N_{M,A}{c}_{E,A}d{T}_{E,A}$ [U], which enters the economic Carnot engine operating between economic temperatures $T_{E,A}$ [U/€] and $T_{E,B}$ [U/€], releasing the merchandise wealth units

$$\delta W_{M,\max }=\left|\delta M_A\right|\left(1-{\displaystyle \frac{T_{E,B}}{T_{E,A}}}\right)=-N_{M,A}{c}_{E,A}d{T}_{E,A}\left(1-{\displaystyle \frac{T_{E,B}}{T_{E,A}}}\right) [\mathrm{U}]$$

(79)

and releasing the traded merchandise units $\left|\delta M_A\right|\left(T_{E,B}/T_{E,A}\right)=-N_{M,A}{c}_{E,A}d{T}_{E,A}\left(T_{E,B}/T_{E,A}\right)$ [U] to subsystem B at the economic temperature $T_{E,B}$ [U/€]. These merchandise units received by subsystem B increase its economic temperature, given that it is $\delta M_B=N_{M,B}{c}_{E,B}d{T}_{E,B}$ [U], with $\delta M_B=\left|\delta M_A\right|\left(T_{E,B}/T_{E,A}\right)$ [U], and the changes in the economic temperatures of subsystems A and B are thus related as

$$-N_{M,A}{c}_{E,A}\left({\displaystyle \frac{T_{E,B}}{T_{E,A}}}\right)d{T}_{E,A}=N_{M,B}{c}_{E,B}d{T}_{E,B} [€]$$

(80)

Equation (80) can be written as

$${\displaystyle \frac{T_{E,B}}{T_{E,A}}}=-{\displaystyle \frac{N_{M,B}{c}_{E,B}}{N_{M,A}{c}_{E,A}}}\left({\displaystyle \frac{d{T}_{E,B}}{d{T}_{E,A}}}\right) [\text{-}]$$

(81)

Introducing this temperature ratio in Equation (79) results in

$$\delta W_{M,\max }=-N_{M,A}{c}_{E,A}d{T}_{E,A}-N_{M,B}{c}_{E,B}d{T}_{E,B} [\mathrm{U}]$$

(82)

and it is thus, in the dimensionless form,

$$\begin{array}{l}{\displaystyle \frac{\delta W_{M,\max }}{N_{M,0}}}=-{\left[{\displaystyle \frac{1+B_A\left(T_{E,A}/T_{E,A,0}\right)}{1+B_A}}\right]}^2{\displaystyle \frac{2b}{1+B_A\left(T_{E,A}/T_{E,A,0}\right)}}d{T}_{E,A}-\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\left[{\displaystyle \frac{1+B_A\left(T_{E,B}/T_{E,A,0}\right)}{1+B_A\left(T_{E,B,0}/T_{E,A,0}\right)}}\right]}^2{\displaystyle \frac{2b}{1+B_A\left(T_{E,B}/T_{E,A,0}\right)}}d{T}_{E,B}\end{array} [\mathrm{U}]$$

(83)

or then,

$${\displaystyle \frac{\delta W_{M,\max }}{N_{M,0}}}=-{\displaystyle \frac{2B_A}{T_{E,A,0}}}\left\{\begin{array}{l}{\displaystyle \frac{1+B_A\left(T_{E,A}/T_{E,A,0}\right)}{{\left(1+B_A\right)}^2}}d{T}_{E,A}+\\ {\displaystyle \frac{1+B_A\left(T_{E,B}/T_{E,A,0}\right)}{{\left[1+B_A\left(T_{E,B,0}/T_{E,A,0}\right)\right]}^2}}d{T}_{E,B}\end{array}\right\} [\mathrm{U}]$$

(84)

This equation can be integrated with the economic temperatures of subsystems A and B changing, respectively, from $T_{E,A,0}$ [U/€] to $T_{E,f}$ [U/€] and from $T_{E,B,0}$ [U/€] to $T_{E,f}$ [U/€], to give

$${\displaystyle \frac{W_{M,\max }}{N_{M,0}}}=-2B_A\left[\begin{array}{l}{\displaystyle \frac{\left({\tau }_{E,f}-1\right)+\frac{B_A}{2}\left({\tau }_{E,f}^2-1\right)}{{\left(1+B_A\right)}^2}}+\\ {\displaystyle \frac{\left({\tau }_{E,f}-{\tau }_{E,B}\right)+\frac{B_A}{2}\left({\tau }_{E,f}^2-{\tau }_{E,B}^2\right)}{{\left(1+B_A{\tau }_{E,B}\right)}^2}}\end{array}\right] [\text{-}]$$

(85)

5.4.3. Comparing Fully Irreversible and Reversible Processes

Comparing the analyzed processes, it is highlighted that the (initial) difference in the economic temperatures of the economic systems can be advantageously used to deliver the maximum merchandise wealth in the reversible process ($W_{M,\max }>0$ [U] if $T_{E,A,0}\ne T_{E,B,0}$ [U/€], and $W_{M,\max }=0$ [U] if $T_{E,A,0}=T_{E,B,0}$ [U/€]), or that the opportunity of delivering that maximum merchandise wealth is lost if the economic systems exchange traded merchandise through a fully irreversible (trading) process ($W_M=0$ [U], no matter if $T_{E,A,0}\ne T_{E,B,0}$ [U/€] or if $T_{E,A,0}=T_{E,B,0}$).

6. Economic Analogue of Availability

Looking at the merchandise units balance Equation (1), it can be written as

$${\displaystyle \frac{d{N}_M}{dt}}={\dot{M}}_{00}+{\displaystyle \sum _{j=1}^{N_{Mj}}{\dot{M}}_j}-{\dot{W}}_M+{\dot{N}}_{M,g} [\mathrm{U}/\mathrm{s}]$$

(86)

and the merchandise economic entropy balance Equation (7) can be written as

$${\displaystyle \frac{d{S}_{E,M}}{dt}}={\displaystyle \frac{{\dot{M}}_{00}}{T_{E,00}}}+{\displaystyle \sum _{j=1}^{N_{Mj}}\frac{{\dot{M}}_j}{T_{E,j}}}+{\dot{S}}_{E,M,g} [€/\mathrm{s}]$$

(87)

In previous equations, the merchandise transfer interaction ${\dot{M}}_{00}$ [U/s] with the merchandise reservoir 00 at economic temperature $T_{E,00}$ [U/€] has been considered separately from the other merchandise transfer interactions, with the other $\left(j=1,2,\dots ,N_{Mj}\right)$ merchandise reservoirs. The merchandise reservoir at economic temperature $T_{E,00}$ [U/€] is considered, in the present context, as the environment merchandise reservoir, understood as the environment to which the economic system is exposed and with which it can exchange traded merchandise.

Multiplying Equation (87) by $T_{E,00}$ [U/€], and subtracting the resulting equation from Equation (86), thus eliminating the merchandise transfer interaction ${\dot{M}}_{00}$ [U/s] from the resulting combined equation leads to

$${\displaystyle \frac{d}{dt}}\left(N_M-T_{E,00}{S}_{E,M}\right)=-{\dot{W}}_M+{\displaystyle \sum _{j=1}^{N_{Mj}}{\dot{M}}_j}\left(1-{\displaystyle \frac{T_{E,00}}{T_{E,j}}}\right)+{\dot{N}}_{M,g}-T_{E,00}{\dot{S}}_{E,M,g} [\mathrm{U}/\mathrm{s}]$$

(88)

which can be rewritten as

$$\begin{array}{l}{\dot{W}}_M=-{\displaystyle \frac{d}{dt}}\left(N_M-T_{E,00}{S}_{E,M}\right)+\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\displaystyle \sum _{j=1}^{N_{Mj}}{\dot{M}}_j}\left(1-{\displaystyle \frac{T_{E,00}}{T_{E,j}}}\right)+{\dot{N}}_{M,g}-T_{E,00}{\dot{S}}_{E,M,g}\end{array} [\mathrm{U}/\mathrm{s}]$$

(89)

The maximum merchandise wealth transfer interaction rate can be obtained from the reversible process, for which ${\dot{S}}_{E,M,g}=0$ [€/s], and Equation (89) can be written for such a reversible situation as

$${\dot{W}}_{M,\max }=-{\displaystyle \frac{d}{dt}}\left(N_M-T_{E,00}{S}_{E,M}\right)+{\displaystyle \sum _{j=1}^{N_{Mj}}{\dot{M}}_j}\left(1-{\displaystyle \frac{T_{E,00}}{T_{E,j}}}\right)+{\dot{N}}_{M,g} [\mathrm{U}/\mathrm{s}]$$

(90)

Considering now the case when the sole merchandise transfer interaction is ${\dot{M}}_{00}$ [U/s], from Equation (90) it is

$${\dot{W}}_{M,\max }=-{\displaystyle \frac{d}{dt}}\left(N_M-T_{E,00}{S}_{E,M}\right)+{\dot{N}}_{M,g} [\mathrm{U}/\mathrm{s}]$$

(91)

equation that can be multiplied by dt to give

$$\delta W_{M,\max }=-d{N}_M\left(1-{\displaystyle \frac{T_{E,00}}{T_E}}\right)=-N_M{c}_E\left(1-{\displaystyle \frac{T_{E,00}}{T_E}}\right)d{T}_E+\delta N_{M,g} [\mathrm{U}/\mathrm{s}]$$

(92)

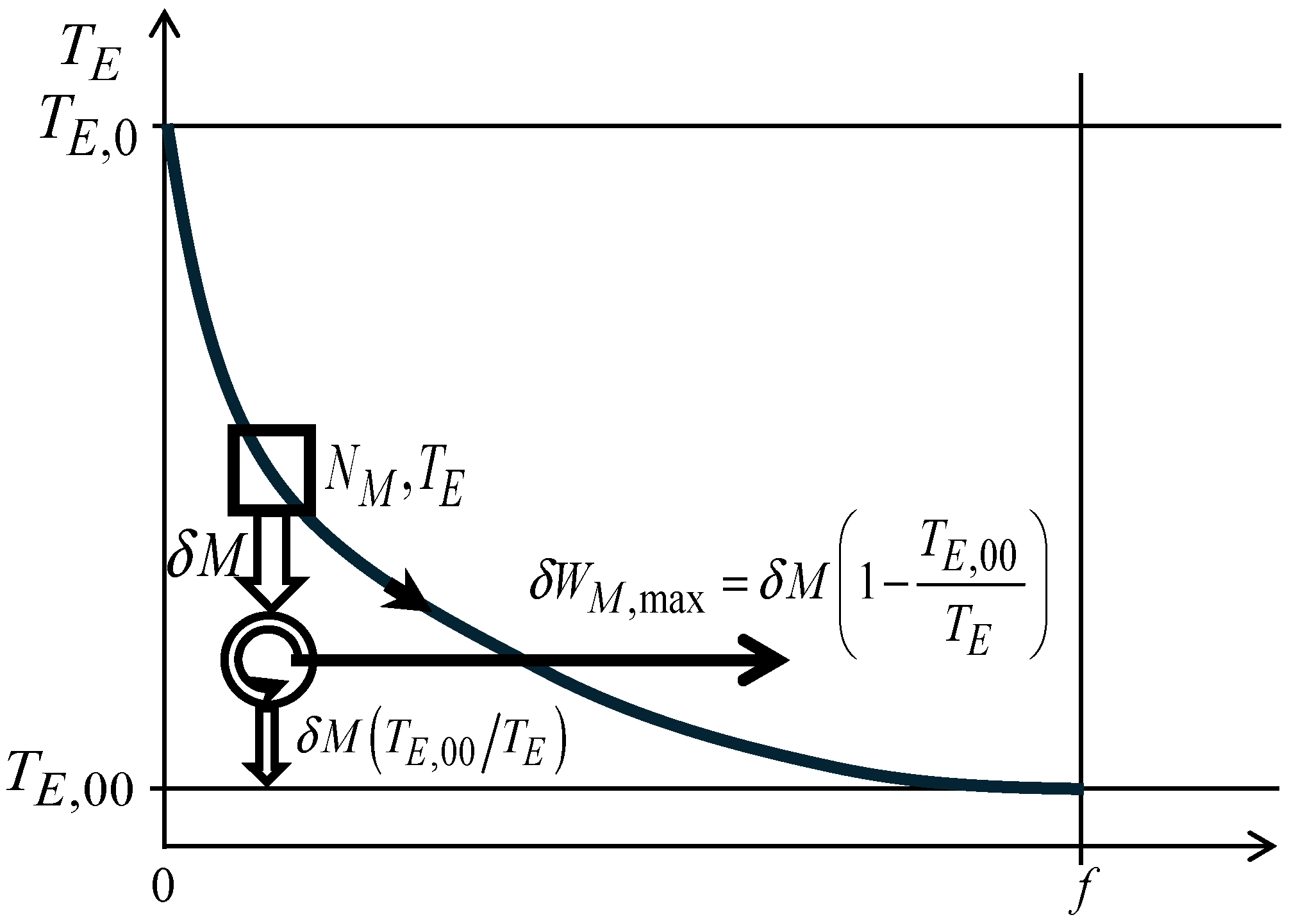
Another way to obtain this same result consists of considering the reversible process schematically illustrated in Figure 15, where the economic system initially at conditions $N_{M,0}$ [U] and $T_{E,0}$ [U/€] evolves reversibly, exchanging merchandise wealth with the merchandise environment at economic temperature $T_{E,00}$ [U/€], having between them an operating economic Carnot engine that receives the traded merchandise $\left|\delta M\right|=-d{N}_M$ [U] from the economic system at economic temperature $T_E$ [U/€], and releases merchandise wealth $\delta W_{M,\max }=\left|\delta M\right|\left(1-T_{E,00}/T_E\right)$ [U] and traded merchandise wealth $\left|\delta M\right|\left(T_{E,00}/T_E\right)$ at the economic temperature $T_{E,00}$ [U/€] to the merchandise environment at the economic temperature $T_{E,00}$ [U/€]. It is thus

$$\begin{array}{l}\delta W_{M,\max }=\left|\delta M\right|\left(1-{\displaystyle \frac{T_{E,00}}{T_E}}\right)=-d{N}_M\left(1-{\displaystyle \frac{T_{E,00}}{T_E}}\right)=\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}-N_M{c}_E\left(1-{\displaystyle \frac{T_{E,00}}{T_E}}\right)d{T}_E+\delta N_{M,g}\end{array} [\mathrm{U}]$$

(93)

which is the same as Equation (92).

In this case, the opportunity of delivering merchandise wealth by taking advantage of the (initial) economic temperature difference $T_{E,0}-T_{E,00}$ [U/€] is used at the maximum, as the maximum merchandise wealth delivered corresponds to the reversible process experienced by the economic system when in economic contact with the merchandise environment at the economic temperature $T_{E,00}$ [U/€], up to reach the final equilibrium with that environment, no matter if $T_{E,0}>T_{E,00}$ [U/€] or if $T_{E,0}<T_{E,00}$ [U/€].

Equations (92) or (93) can be rewritten as

$$\begin{array}{l}\delta W_{M,\max }=\\ -N_{M,0}{\left[{\displaystyle \frac{1+B\left(T_E/T_{E,0}\right)}{1+B}}\right]}^2{\displaystyle \frac{2b}{\left[1+B\left(T_E/T_{E,0}\right)\right]}}\left(1-{\displaystyle \frac{T_{E,00}}{T_E}}\right)d{T}_E+\delta N_{M,g}\end{array} [\mathrm{U}]$$

(94)

where $B=b{T}_{E,0}$ [-]. It is assumed that $\delta N_{M,g}$ [U] does not depend on $T_E$ [U/€], and that it can be considered separately from the remaining terms in Equation (94). If $\delta N_{M,g}$ [U] is absent from Equations (92)–(94), it can be written as $d{W}_{M,\max }$ [U] instead of $\delta W_{M,\max }$ [U], as in that case, $\delta W_{M,\max }=d{W}_{M,\max }$ [U] is an exact differential (Bejan, 2016; Moran et al., 2018).

Defining the dimensionless economic temperature,

$${\tau }_E=\left(T_{E,00}/T_{E,0}\right) [\text{-}]$$

(95)

Equation (94) can be simplified and written in the dimensionless form as

$${\displaystyle \frac{\delta W_{M,\max }}{N_{M,0}}}=-{\displaystyle \frac{2B}{T_{E,0}}}{\left(1+B\right)}^{-2}\left[\left(1-B{\tau }_E\right)-\left({\displaystyle \frac{T_{E,00}}{T_E}}\right)+B\left({\displaystyle \frac{T_E}{T_{E,0}}}\right)\right]d{T}_E+{\displaystyle \frac{\delta N_{M,g}}{N_{M,0}}} [\text{-}]$$

(96)

which can be integrated for $T_E$ [U/€] changing from $T_{E,0}$ [U/€] to $T_{E,00}$ [U/€], and $\delta N_{M,g}$ [U] is (separately) integrated along the evolution of the economic system up to reach the economic thermal equilibrium with the merchandise environment at the economic temperature $T_{E,00}$ [U/€]. Such integration gives

$${\displaystyle \frac{W_{M,\max }}{N_{M,0}}}=2B{\left(1+B\right)}^{-2}\left\{\left[{\displaystyle \frac{B}{2}}\left({\tau }_E-1\right)-1\right]\left({\tau }_E-1\right)+{\tau }_E\ln \left({\tau }_E\right)\right\}+{\displaystyle \frac{N_{M,g}}{N_{M,0}}} [\text{-}]$$

(97)

This is the equation giving the analogue of exergy, or availability in Thermodynamics (Bejan, 2016; Moran et al., 2018), which is the economic availability of the system, originally with $N_{M,0}$ [U] merchandise units at the economic temperature $T_{E,0}$ [U/€], when it is allowed to evolve, in a reversible process, when in economic contact with the merchandise environment at economic temperature $T_{E,00}$ [U/€]. Figure 16 shows how dimensionless economic availability depends on B [-] and ${\tau }_E$ [-].

The number of merchandise units $N_{M,00}$ [-] in the system in the (final) equilibrium situation with the economic environment at the economic temperature $T_{E,00}$ [U/€] is

$$N_{M,00}=N_{M,0}-W_{M,\max }+N_{M,g} [\text{-}]$$

(98)

in which the dimensionless version is

$${\displaystyle \frac{N_{M,00}}{N_{M,0}}}=1-{\displaystyle \frac{W_{M,\max }}{N_{M,0}}}+{\displaystyle \frac{N_{M,g}}{N_{M,0}}} [\text{-}]$$

(99)

7. Finishing and Conclusive Notes

Thermodynamics has given relevant contributions to Economics. That was started masterfully by P. A. Samuelson, relating changes in economic variables and thus describing the economic behaviour. Recent works by the author made additional contributions in that direction, introducing new concepts, variables, equations, and inequations, and their innovative and out-of-the-box messages.

Based on the well-established premise that entropy generation is a measure of the imperfection of thermodynamic processes, it is assumed that, similarly, economic entropy generation (financial value generation) can be considered as a measure of the imperfection (irreversibility) of economic processes. That includes the assumption that the best economic performance corresponds to the maximum merchandise wealth delivery, similarly to what happens in Thermodynamics when searching for the maximum mechanical work delivery. That corresponds to the minimum entropy generation, and in Economics, it corresponds to the minimum economic entropy generation (minimum financial value generation). Once that is set, new developments are made in the direction of more perfect, less irreversible, and more efficient economic processes, and thus toward a more perfect economy.

It is seen how, and in which measure, negotiation in merchandise trading contributes to a decrease in merchandise economic entropy generation (leads to a decrease in merchandise financial value generation), and thus to a more perfect (less irreversible) economy.

Introduction and analysis of endoreversible economic processes, which include a series combination of fully irreversible traded merchandise transfer through economic temperature differences, and (reversible) economic Carnot engines, allows determination of the (floating) intermediate unit price and the efficiency of the endoreversible economic engine operating at the maximum merchandise wealth delivery. Results have strong similarities with those obtained for the endoreversible thermal engines, even if no constitutive laws can be used in Economics to relate the traded merchandise transfers with the driven economic temperature differences, contrary to what happens in Thermodynamics, where constitutive heat transfer laws exist and can be used relating heat transfers with the driven temperature differences.

For the first time, a constitutive law sets how a change in the number of merchandise units of an economic system is related to the change in their economic temperature (in their unit price), which is crucial for the dynamic economic processes analysis. That is made by introducing the economic analogue of specific heat, usual in Thermodynamics, which is intimately related to the demand elasticity coefficient, this usual in Economics. Once that is made, it is detailed and clarified the evaluation of the merchandise economic entropy change in reversible and irreversible processes, and how it is related to the change in the financial value of the merchandise units in the economic system. After that, and similarly, as made in Thermodynamics, some dynamic economic processes are analyzed, considering a particular analytical expression for the economic merchandise specific heat. The analyses show that the difference in the economic temperatures of two economic systems can be advantageously used to deliver the maximum merchandise wealth in a reversible process, or that such an opportunity is lost if those economic systems exchange traded merchandise in a fully irreversible (trading) process.

The economic analogue of exergy, the economic availability, is introduced, and the expression for its quantification is obtained. This is the adaptation to Economics of a concept increasingly used in Thermodynamics to evaluate the availability of an economic system to deliver the maximum merchandise wealth when operating reversibly, when in economic contact with the economic environment (including an economic Carnot engine operating between the economic system and the economic environment characterized by its reference economic temperature).

In addition to the introduced and explored concepts, methodology, analyses, relations, and results, it is expected that the main contribution of this paper is related to its main mindset (maximization of the merchandise wealth delivery and minimization of the merchandise entropy generation, in the search for more reversible and more perfect and efficient economic processes), the out-of-the-box innovative and challenging approach, looking at Economics through the eyes of Thermodynamics, and the motivation and messages contained in, an extracted from, the approach. The premises, approach, conducted analyses and developments, and the obtained results, in the form of expressions and readings from the obtained expressions, are its main contributions. In the end, it is expected that it can be an effective contribution of Thermodynamics to Economics, with relevant mutual scientific and pedagogical contributions to both fields.