Patterns of Intergenerational Educational (Im)Mobility

Abstract

Intergenerational education mobility is a key dimension of social mobility and explores the extent to which educational attainment is transmitted across generations within a society. The implications of low education mobility concern both equity (everyone should have the same opportunities) and efficiency (it would be good for the economy and society if the most gifted and deserving young people were to study and not the children of the already educated). The literature identifies several drivers that can influence the level of social mobility in general and education mobility specifically, including characteristics of educational systems, public spending, degree of urbanisation, informal frictions, and beliefs. This paper seeks to identify ‘patterns of intergenerational education (im)mobility’ through a cluster analysis that takes into account the level of intergenerational mobility in education and a number of variables concerning its possible drivers, considering data on 82 countries (with different levels of development). The advantage of cluster analysis lies in the possibility of identifying regularities, but avoiding reasoning ‘on average’, i.e., safeguarding the possibility that different social patterns may exist. The results also allow us to speculate on possible policies to increase school mobility, highlighting, among other things, the ‘equalising’ role played by public spending on education.

1. Introduction

The study of the intergenerational transmission of socio-economic statuses is interesting and topical in several respects.

On the one hand, it helps us delve into the well-known theme of ‘equality of what?’ (Sen 1980). In fact, it is quite evident that a strong correlation of socio-economic statuses between parents and children is a sign of some lack of equality of opportunity. From this point of view, inequality of outcomes (e.g., income) can be more or less socially acceptable if it is accompanied, or not, by equality of opportunity. Nonetheless, high income inequality can itself be an obstacle to a real equality of opportunity (Corak 2013).

On the other hand, mobility across generations is not only an issue of equality, but also of efficiency, especially when defined in terms of educational mobility (D’Addio 2007). It is important that it is the most able and willing people who study (and gain access to the resulting social roles) and not (only) people from rich families. Otherwise, we would end up with people with inadequate abilities in key roles (indeed, as often seems to be the case), and we would lose the opportunity to socially take advantage of the abilities of gifted people just because they come from ‘disadvantaged’ families or social backgrounds (Glomm and Ravikumar 1992; Lloyd-Ellis 2000; Staffolani and Valentini 2007).

The focus of the research proposed in this paper is precisely on educational mobility, which among other things is considered to be a key element of overall economic mobility across generations (Feinstein et al. 2006; D’Addio 2007; Jerrim and Macmillan 2015; Narayan et al. 2018; Stuhler 2018).

The literature identifies several factors that may influence the level of educational intergenerational mobility (and, through it, intergenerational income mobility).

Public spending in education is a key element. It can not only improve the quality of education in general, but also benefit those who would be at risk of starting off disadvantaged. From a theoretical point of view, Solon (2004) proposes a model according to which intergenerational income elasticity increases as the return on investment in human capital increases, but which decreases with the progressivity of public investment in human capital. The model of Davies et al. (2005) analyses intergenerational earning mobility in a framework where human capital plays a crucial role and concludes that mobility is higher with public than with private education. Herrington (2015) developed an overlapping generations model and calibrated it in order to compare the US and Norway empirically and quantitatively, reaching the conclusion that public education spending plays a key role in intergenerational earning persistence. Lee and Seshadri (2019) present a model of human capital investments that explains the intergenerational persistence of earnings, wealth, and college attainment and conclude that education subsidies can reduce the intergenerational persistence of economic status. Mayer and Lopoo (2008) focused on human capital investment. They used data from the Panel Study of Income Dynamics and the US Census of Governments and found greater intergenerational mobility in high-spending states compared with low-spending states. Neidhöfer et al. (2018) computed several indexes of intergenerational education mobility for 18 Latin American countries, finding significant cross-country differences also associated with public educational expenditures. Balcazar et al. (2015) used data on 48 countries that participated in the Programme for International Student Assessment (PISA) in 2012, finding evidence of a correlation between public spending on schooling and inequality of opportunity in achieving basic proficiency in reading, mathematics, and science. In Narayan et al. (2018), regressions involving data on richer economies showed that higher public spending on education is associated with higher relative intergenerational mobility in education, and the authors concluded that ‘[t]his is consistent with the theory that public spending helps equalise opportunities through investments that compensate for the gap in private investments between children of rich and poor parents’ (Narayan et al. 2018, p. 19).

Moreover, if public spending on education is specifically directed towards individuals from disadvantaged economic backgrounds and is financed through taxes that particularly fall on individuals from wealthy families (e.g., bequests taxation), it can be particularly effective in rebalancing opportunities for access to education itself, fostering equity and efficiency gains (Staffolani and Valentini 2007).

Public intervention in this field can also concern regulation, and the presence and duration (in years) of compulsory education can certainly influence educational mobility, particularly in the most disadvantaged contexts. An uneducated (and therefore more likely to be ‘poor’) parent might decide not to make their child study (or they may study less than they should). If a certain number of years of education is compulsory, this choice is limited. It is important to emphasise that the years of compulsory education in general are somewhat related to the level of public spending on education; however, they represent a slightly different aspect of public intervention directly related to regulation rather than the level of spending.

Socio-economic segregation is another factor that can strongly influence educational mobility. Van der Weide et al. (2021), using data on 153 countries, found that proxies for segregation are negatively correlated with intergenerational education mobility. A specific definition of this concept concerns spatial/residential segregation. Recent research suggests that more residentially segregated areas (i.e., where families with different socio-economic backgrounds and races live in separate neighbourhoods) tend to have lower intergenerational mobility. Chetty et al. (2014) used administrative records of more than 40 million children in the US and, with OLS (Ordinary Least Squares) regressions across 700 areas, found that high-mobility areas have less residential segregation. Connolly et al. (2019) linked microdata from the US and Canada, and their OLS estimates suggest that ‘inequalities between whites and blacks likely play an important role in understanding why the United States has lower rates of intergenerational mobility’ (Connolly et al. 2019, p. 598). In that case, ‘segregation’ is to be understood in terms of ‘social segregation’ (which then often also becomes ‘spatial’ segregation). Corak (2021) used data from 266 Canadian Census Divisions on a cohort of men and women born between 1963 and 1970, finding that low-mobility regions tend to exist outside of urban areas; reading his results, he underlines that Durlauf and Seshadri (2018) explicitly model the influence that inequality has on economic opportunity through its impact on socio-economic segregation. In the present paper, residential segregation is mainly considered in terms of the degree of urbanisation, which seems especially relevant for developing countries; obviously, a lower degree of urbanisation indicates greater spatial segregation and social isolation.

As mentioned earlier, income inequality itself can trigger inequality of opportunity in access to education in a dangerous vicious circle. Corak (2013) hypothesises the existence of this risk with a theoretical approach that also refers to empirical results from the literature. Reardon (2011) carried out a descriptive study on the relationship between academic achievement and family income in the US over the last few decades using data from 12 nationally representative studies that included information on family income and student performance in math or reading. He found that socio-economic status is a predictor of student academic achievement and educational outcomes. Campbell et al. (2005) used microdata from the US census, and their estimates suggest that an increase in family income and wealth inequality leads to a growing dispersion of educational attainments. Kearney and Levine (2016) used US longitudinal microdata, and their regressions confirm that greater income inequality might lead to lower levels of high school completion among individuals from low-income families and, therefore, to lower rates of upward mobility. A study with US data showed that, with respect to income, about 50 percent of intergenerational persistence can be explained by parents’ investments in their children’s education (Restuccia and Urrutia 2004). This mechanism tends to favour access to education for individuals belonging to wealthy families. Duncan and Murnane (2012) found that, in the last few decades, the amount that high-income families spent on their children’s education grew by 150 percent, while the amount spent by low-income families grew by 57 percent.

The relevance of cultural context and ‘family culture’ in influencing intergenerational mobility is often considered in the literature (Becker and Tomes 1979; Mayer 1997; Piketty 2000; see McLanahan 2020 for a very comprehensive review on the subject), but less so in the empirical literature. A factor not studied so far in the empirical literature lies in ‘cultural attitudes’ concerning the importance of children’s independence. If parents consider it important for their children to be independent and self-sufficient, the link between parents’ economic status and children’s opportunities may be weakening. An extreme case that can be used to exemplify this concept is as follows: ‘it is important to me that you are autonomous and independent, I do not pay for your studies, you have to work to pay for them yourself’.

The underlying idea of the analysis in this paper is that the factors listed so far (public spending on education, compulsory education, income inequality, segregation/urbanisation, and importance of children’s independence) may be more or less important in different socio-economic contexts. These differences may especially emerge between advanced economies and developing countries (regarding the trends of intergenerational mobility over time in countries at different stages of development, see also Leone 2019).

Some of the literature suggests that mobility will decline as incomes increase in the absence of public interventions (Becker and Tomes 1979; Becker et al. 2018); therefore, the level of public spending on education could be more effective in fostering educational intergenerational mobility in advanced economies. The effect of income inequality on children’s educational opportunities may be greater in rich countries, since the link may exist through the resources invested by parents in their children’s education; the availability of these resources in addition to those needed to satisfy basic needs is certainly greater in rich economies. Compulsory education may be more important for developing countries because it has a greater influence on low and middle levels of education. The same applies to the degree of urbanisation because the difference between rural and urban environments is the greatest cause of social segregation in developing countries. For example, Reddy and Singh (2021) found that, in India, the intergenerational persistence in educational attainment is much higher in rural areas than in urban areas.

It is conceivable that the cultural emphasis on child autonomy may have greater effects in advanced economies because there are actually more chances to be autonomous and independent (less unemployment, more educational institutions, more public services, more scholarships, etc.).

The average level of education (often related to per capita income) can also influence mobility and can do so differently in countries with different levels of development. ‘In the world’s poorest countries, a large majority of parents have no education. When parents are equally deprived, it matters less what household one is born into, implying a high level of relative mobility. As countries increase their education and income levels, the gaps between poor, middle-class and better-off parents become more pronounced. Without public interventions, children’s education trajectories will eventually start to diverge depending on whether they are born into a poor, middle-class or upper-class family, which is when relative intergenerational mobility will decline’ (Van der Weide et al. 2021, p. 30).

On this basis, this paper proposes a cluster analysis with data from 82 countries in an attempt to verify the existence of different patterns in the relationships between intergenerational mobility in education and the factors discussed above, with particular reference to differences between economies at different stages of development.

Most of the empirical analyses mentioned in this introduction, on the contrary, use individual data and a micro-econometric approach. Therefore, they are also able to deepen the analysis in terms of the causality of the identified relationships. This leads to the biggest limitation of the analysis proposed here: from a technical point of view, it does not allow us to make considerations regarding the causality of the relationships. We shall return to this matter in the subsequent parts of the article as well as in the closing remarks. The approach followed in this article, as already mentioned, uses aggregated data and carries out a more general, cross-country analysis with a cluster methodology.

Nevertheless, the approach followed in the present article has innovative and useful aspects that can improve our understanding of the analysed phenomenon. It allows us to consider together several factors that can influence intergenerational mobility in education, to also include among these factors the cultural aspect (independence of children) that is generally not considered in the empirical literature, and to carry out an analysis on a sample involving a very high number of nations, even at different levels of development, with a methodology that can highlight different relationships between these factors and mobility depending precisely on the level of development.

2. Methodology and Data

As highlighted in the introduction, the idea behind this paper is that the various factors possibly influencing intergenerational mobility in education may have different impacts in economies with different levels of development.

One way, though not the only way, in which this concept can be defined in an empirical analysis in which the units of analysis are national economies is as follows: is it possible to identify patterns (i.e., group countries) according to level of income, mobility in education, public spending on education, compulsory education, income inequality, level of urbanisation, and importance of children’s independence?

Cluster analyses are one of the best ways to search for groups through data (Kaufmann and Rousseeuw 1990). In our case, it seems to be an appropriate way to cluster nations according to level of income and level of intergenerational mobility in education in the first instance and according to the other variables in the second instance. The number (82) of observations available in the dataset constructed for this analysis also suggests the choice of this methodology. If one thinks that the relationships between the variables may be different for groups of countries (e.g., high-, middle-, and low-income economies), the number of available observations would not allow for reliable regressions on subgroups of the available sample.

This paper seeks to identify ‘patterns of intergenerational education (im)mobility’ through a cluster analysis. The advantage of cluster analyses lies in the possibility of identifying regularities but avoiding reasoning ‘on average’, i.e., safeguarding the possibility that different social patterns may exist.

Before exploring the details of the analysis technique, it is useful to describe the variables and data.

Table 1. Dataset description and summary statistics.

Variable	Source	Time	Variable (Shortened)	Mean	Standard Deviation
GDP per capita (Constant 2017 Int. Dollars)	World Bank World Development Indicators	(average value 1980–2015)	GDP	USD 20197	15,392
Educational attainment (% of the population 25+ who at least completed upper secondary school)	World Bank World Development Indicators	(average value 1980–2015)	EDU	53.8%	24.0
Urban population (% of tot. population)	World Bank World Development Indicators	(average value 1980–2015)	URB	61.9%	18.1
Gini Index	World Bank World Development Indicators	(average value 1980–2015)	GINI	0.369	0.083
Government expenditure on education (% GDP)	World Bank World Development Indicators	(average value 1980–2015)	GOV_EDU	4.39%	1.36
Compulsory education (years)	World Bank World Development Indicators	(average value 1980–2015)	COMP_EDU	9.7	1.7
Share of parents indicating ‘Children’s Independence’ as an important quality in children (%)	European Values Study—World Values Study Integrated survey 1981–2021	(average value 1981–2021) 1	CHILD_IND	47.2%	14.3
Expected rank of a child whose parents rank in the bottom half of the education distribution	World Bank Global Database on Intergenerational Mobility 2	1980s cohort (generation born between 1980 and 1989)	MOB_EDU	39.3	3.4

¹ Not all nations are involved in all EVS and WVS waves. Averages were calculated using the data available over the time period 1981–2021. For each available wave, the microdata were processed using the weights suggested by the relevant guidelines. ² (GDIM 2023; Van der Weide et al. 2023).

shows the variables used in the analysis, the databases of origin, and, finally, the mean and standard deviations (for the 82 countries considered). All variables are averaged over a relatively long period of time. This aggregation over time smooths out the changes in and development of a country over 35 years. This may lead to an underestimation of any changes in trends during the period under analysis. On the other hand, it seems to be a good way to approximate the conditions in which people born in the 1980s grew up.

All countries for which data are available are included in the analysis, with the sole exception of those classified by the World Bank (on 1 July 2020) as being in the ‘Low Income’ category in order to avoid data reliability problems (between 1980 and 2015, these nations had few values for some variables, so the values of those variables would not be true ‘period averages’). These are almost exclusively countries from Sub-Saharan Africa (a region that is nevertheless represented in the dataset).

Table A1. Countries included in the analysis, sorted according to the value of MOB_EDU (‘Expected rank of a child whose parents rank in the bottom half of the education distribution’).

Country	MOB_EDU	Country	MOB_EDU	Country	MOB_EDU
Cyprus	49.8	Portugal	40.4	Iran	37.2
Denmark	47.1	Hungary	40.3	Malaysia	37.1
Maldives	46.7	Serbia	40.2	Austria	37.1
Philippines	46.1	Switzerland	40.0	Azerbaijan	37.0
Israel	45.6	Ukraine	39.9	Uruguay	37.0
Russian Fed.	45.5	Kyrgyz Rep.	39.8	Greece	36.9
Zambia	45.1	Egypt	39.8	Iraq	36.8
Iceland	44.9	Korea, Rep.	39.6	Guatemala	36.7
Slovenia	44.4	Sweden	39.6	El Salvador	36.6
Germany	43.8	South Africa	39.1	Kenya	36.6
Slovak Rep.	43.1	Thailand	39.0	China	36.5
Finland	42.8	Belarus	38.9	Brazil	36.3
Belgium	42.8	Italy	38.8	Mexico	36.0
Dominican Rep.	42.5	Poland	38.4	Bangladesh	35.8
Turkey	42.3	Vietnam	38.4	Chile	35.7
Uzbekistan	41.9	Bulgaria	38.4	Ireland	35.6
United Kingdom	41.9	Armenia	38.3	Peru	35.6
Albania	41.9	Moldova	38.3	United States	35.5
France	41.8	Australia	38.2	Romania	35.3
Estonia	41.7	Croatia	38.2	Pakistan	35.0
Japan	41.7	Argentina	38.0	Ecuador	34.9
The Netherlands	41.3	Spain	37.8	Nigeria	34.4
Latvia	41.3	Georgia	37.5	Colombia	34.3
Norway	41.0	Czech Rep.	37.4	Bolivia	34.2
Indonesia	41.0	Kazakhstan	37.4	Lebanon	33.5
Jordan	40.9	Mongolia	37.3	Ghana	32.7
Canada	40.8	Tunisia	37.3
Lithuania	40.8	India	37.3

in Appendix A lists the countries included in the analysis and the values of the variable concerning intergenerational mobility in education. Appendix B details the information required to retrieve data from the databases used to ensure the reproducibility of the analysis.

The variable related to intergenerational mobility in education is listed in the last row of Table 1 and deserves a closer look. It measures ‘the expected rank of an individual in the education distribution whose parents rank in the bottom half of the parent education distribution’ (Van der Weide et al. 2021, p. 8). The education of parents is identified by referring to the parent with the highest level of education, while, for the next generation, the entire population is considered (thus, both sons and daughters). This is a rank-based measure of relative mobility. Relative mobility represents the extent to which an individual’s position in the distribution of educational attainments is independent of the position of his/her parents. If the educational attainment of each individual is independent of the starting conditions (i.e., parental status), the expected rank should be 50 for all individuals (both for those with parents who were in the bottom half of the ranking for their generation and for individuals with parents who were better placed in the same ranking as the previous generation). Hence, the variable represents the degree to which an individual’s educational level is independent of the educational level of parents. A higher value of this variable is associated with greater intergenerational mobility (or, in other words, greater equality of opportunities).

Note that the low standard deviation of the ‘compulsory education’ variable results from 60 of the 82 countries having values between 9 and 12. This does not detract from the fact that there are countries with high values, such as The Netherlands, which has a value of 13 because full-time education is compulsory from the ages of 5 to 16 and at least part-time education is compulsory from the ages of 16 to 18. There are some very low values, such as Bangladesh (5), Malaysia (6), and Iraq (6). Note that these are not the latest values but the average of the values over the period of time considered calculated according to the availability of data, which often does not cover the entire period.

Cluster analyses are affected by the magnitude of the variables. It was therefore necessary to standardise (mean, 0; standard deviation, 1) the variables to make them comparable.

The intention was to group nations according to the values of these (standardised) variables, and this was achieved using a partition cluster analysis method (k-means), in which the observations (countries) are broken up into several nonoverlapping groups (Hastie et al. 2009). Each group brings together nations that share a common pattern in the mean values of the variables considered. The analysis used an iterative algorithm that, starting from k initial cluster centres, minimises the Euclidean distance within each cluster between its mean (k-clustering) and its observations while maximising the distance in terms of means among adjacent clusters. For this, we used the command ‘cluster kmeans’ in Stata, which implements an iterative procedure. It begins with k initial group centres, assigns observations to the group with the closest center, computes the mean of the observations assigned to each of the groups, and then repeats the process. These steps continue until all observations remain in the same group from the previous iteration.

The replicability of results deserves much attention in this type of analysis. Two important choices must be made: the optimal number of groups (k) must be chosen and the number of random starting points (r) must be determined. For both issues, the procedure suggested by (Makles 2012) was followed.

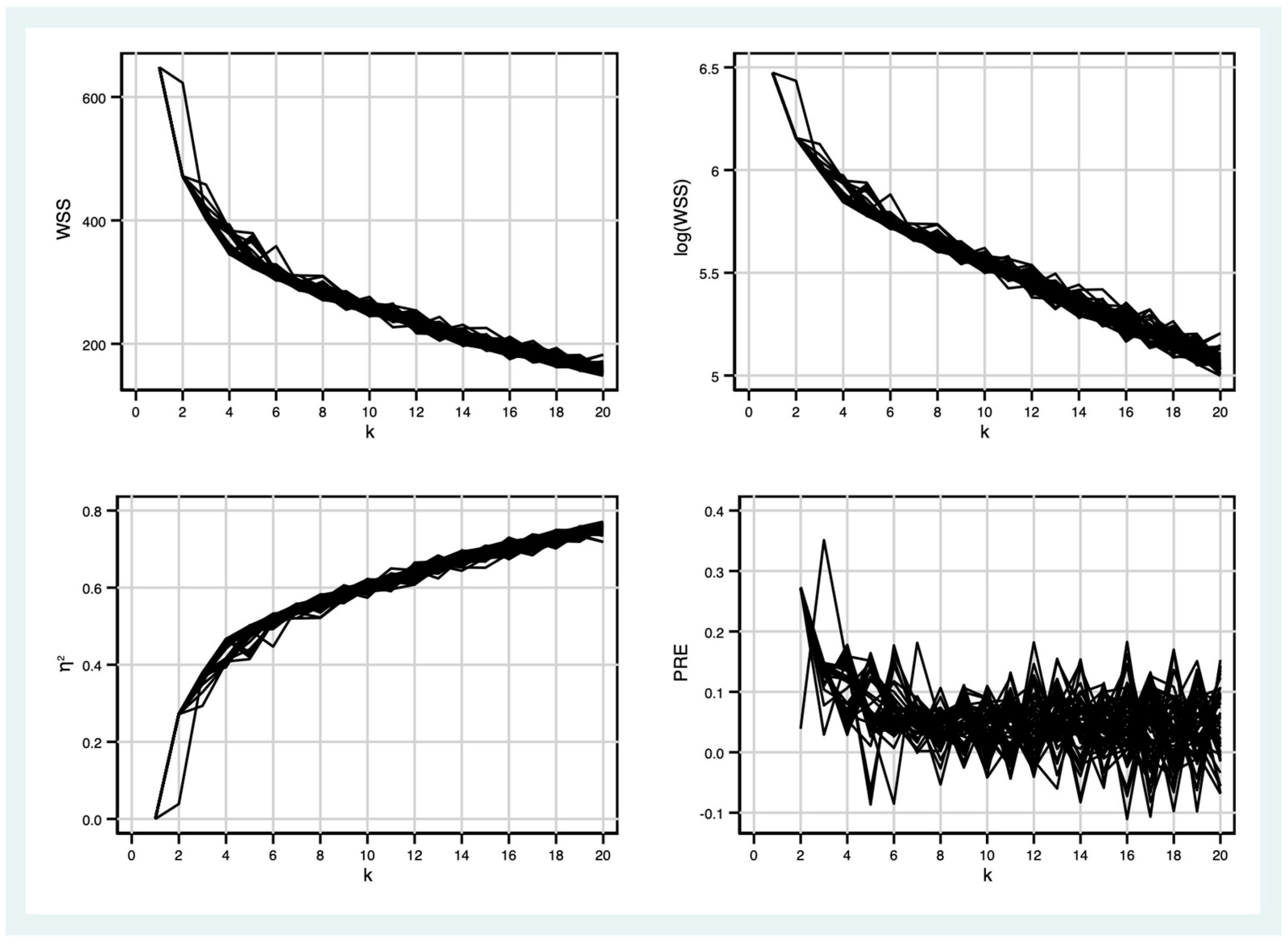
Given a certain number of random starting points, the optimal number of groups can be determined by comparing the values of the within sum of squares (WSS) or its logarithm for each k. In this case, one can stop at the number of groups k beyond which increasing the number of groups does not contribute significantly to the reduction in the WSS (i.e., fragmenting into further groups does not explain the data any better). It is also possible to compare, for each k, the η2 coefficient, which is quite similar to the R2. One should stop at the number of groups k beyond which increasing the number of groups does not significantly increase the η2 coefficient. Finally, the proportional reduction in error (PRE) coefficient can be used. It illustrates ‘the proportional reduction of the WSS for cluster solution k compared with the previous solution with k − 1 clusters’ (Makles 2012, p. 347).

However, even the number of random starting points cannot be chosen arbitrarily. ‘The best way to evaluate the chosen solution is therefore to repeat the clustering several times with different starting points and then compare the different solutions’ (Makles 2012, p. 350).

Figure 1 reports the within sum of squares (WSS), its logarithm, the η² coefficient, and the proportional reduction in error (PRE) as k increases. Each line represents a different repetition of the analysis as the number of random starting points changes (from 100 to 150). Looking at the values of WSS and η², we see that the groups do not add much information when going beyond 4. However, when looking at the PRE, we see that, for up to k = 6, in quite a number of repetitions (i.e., varying the number of random starting points) the addition of another group contributes quite significantly to the reduction in the WSS. So, the most prudent choice seems to be k = 6. Finally, among all the repetitions with k = 6, the repetition selected had the lowest WSS and the greatest η² (in both cases, this occurred with 131 random starting points).

3. Results

The steps illustrated in the previous section suggest grouping the data into six groups with 131 random starting points via a k-means cluster algorithm.

Table 2. Cluster characteristics (mean values of standardised variables).

	Cluster	GDP	MOB_EDU	EDU	URB	GINI	GOV_EDU	COMP_EDU	CHILD_IND	N (Countries 1)
High GDP	A	1.31	0.19	0.58	0.74	−0.50	0.49	0.86	0.11	14
	B	1.23	1.11	0.69	0.77	−0.82	1.03	−0.05	1.33	11
Middle GDP	C	−0.37	−0.04	0.85	−0.07	−0.45	−0.05	−0.22	−0.17	22
	D	−0.54	−0.90	−0.76	0.42	1.77	−0.20	0.83	−0.80	12
Low GDP	E	−0.66	1.50	−1.13	−0.80	1.05	−1.05	−0.52	−1.13	5
	F	−0.77	−0.60	−1.10	−1.01	−0.04	−0.52	−0.77	−0.10	18

¹ Appendix C lists countries that fall under the different clusters. Bold and underlined numbers indicate that the average value for that variable of the cluster is meaningfully higher than that of the cluster in the same category of GDP per capita (High, Middle, and Low).

shows the results of the resulting clusters/groups in terms of average values of the (standardised) variables.

To facilitate a possible reading of the outcomes, the clusters were ordered according to the level of GDP per capita. The idea is to interpret the results by comparing the variables’ values between clusters with similar levels of development (High, Middle, and Low GDP). Cluster A must therefore be compared with cluster B, cluster C must be compared with cluster D, and cluster E must be compared with cluster F. The bold and underlined numbers indicate that the average value for that variable of the cluster is meaningfully higher than that of the cluster it is compared to.

Cluster analyses are often used in the literature to generate hypotheses that should then be tested. In the present analysis, the procedure could be: (a) to group countries into clusters with different links between the variables (e.g., public spending on education is associated with higher intergenerational mobility in rich countries, whereas the relationship seems to be the reverse among poor countries); (b) to test the causality of the relationships (and its direction) in subgroups of countries based on the results of the cluster analysis (e.g., a causality analysis taking only nations from clusters A and B and another causality analysis taking only nations from clusters E and F). This would certainly be interesting, but it goes beyond the scope of this paper. Additionally, a purely technical issue lies in the number of nations in each subgroup, which is too small to carry out any analysis of causality (continuing with the example given above, there would be two groups: one with 25 countries and one with 23 countries). Indeed, this presents a limitation of this study and implies a potential area for future inquiry, which will be discussed in the conclusions.

4. Discussion

Based on the interpretation method described in the previous section, the results can be summarised as follows.

Among both high-GDP and middle-GDP countries, greater intergenerational mobility in education is associated with higher levels of education in general, lower income inequality, higher public spending on education, shorter periods of compulsory education, and a greater emphasis on children’s independence.

The only difference between high-GDP and middle-GDP countries appears to be the degree of urbanisation (irrelevant among the former and negatively associated with intergenerational mobility among the latter). This can be explained by considering that cluster D almost exclusively encompasses Latin American and Caribbean countries (Appendix C) that are highly urbanised (on average, 70% of individuals live in cities, a figure second only to North America (78%)). This degree of urbanisation, however, does not protect against significant socio-economic segregation (‘favelas’ in Brazil and Colombia, ‘villa miseria’ in Argentina, ‘slums’ in Mexico, etc.).

Concerning the importance of public spending on education in high-GDP and middle-GDP countries, further evidence can also be extracted from the results. If one orders the clusters according to the level of mobility (thus, B, A, C, D), the same order also applies to the level of public spending on education.

Among low-GDP countries, greater intergenerational mobility in education is associated with a higher degree of urbanisation, higher income inequality, lower public spending on education, longer periods of compulsory education, and a lower emphasis on children’s independence.

It is not surprising that even relatively poor countries have a high degree of intergenerational mobility in education (cluster E). As mentioned in the introduction, the creators of the database themselves point out that the relationship between intergenerational mobility and income turns out to be non-monotonic (Van der Weide et al. 2021). This may be due to the fact that most parents are not educated in poor nations (in fact, the level of education is low in both clusters E and F) and the family of origin does not matter much when the parents are all equally poor. When the level of education and income begins to increase, the gap in opportunities between the children of poor and wealthy families may begin to widen; however, in wealthy economies, it may narrow when the state invests in public education. All these mechanisms seem to be confirmed by the results of the analysis in this article.

On the other hand, it is interesting to note that greater intergenerational mobility seems to be favoured in poor countries by a higher degree of urbanisation and longer periods of compulsory education (which, on the contrary, does not seem important in rich countries). These results are in line with the considerations stated in the introduction (which illustrates the possible mechanisms in place). Equally, the importance given to children’s independence is more important to improving intergenerational mobility in advanced economies, in which households have additional resources they may devote to private investment in education. The same line of reasoning can be applied to the fact that greater income inequality is associated with lower intergenerational mobility in rich countries (in which household income can have a greater influence on children’s outcomes through private investment), which is not the case in poor countries.

5. Conclusions

In drawing conclusions, it is important to emphasise that the analysis performed in this study allows us to derive an association between the mean values of the variables in the different clusters but does not allow us to make any statements regarding causality. In the case of income inequality, the dilemma is obvious: Does lower intergenerational mobility favour the persistence of income inequality? Or does high income inequality undermine the equality of opportunity? The topic is widely debated, but on balance it does not seem far-fetched to assume that the risk of a vicious circle is present in medium- and high-GDP countries. This vicious circle can, however, be broken by public investment in education as the results of this analysis show. In this case, the causality, although not formally demonstrated, seems clear: it is easier to imagine that a higher level of public spending encourages greater intergenerational mobility rather than the other way around.

The direction of the relationship between intergenerational mobility and the importance given to children’s independence is also ambiguous. Does fostering children’s independence promote mobility (because rich families do not indulge their children too much)? Or do I want my child to be independent because I know he or she has the opportunity?

While bearing in mind the fact that the lack of identification of causal links is a strong limitation, based on the (almost descriptive) evidence obtained it is possible to extract some indications in terms of policies that could help to improve intergenerational mobility. When differentiating between less- and more-developed countries (a distinction that is one of the key elements of this study), the following conclusions can be drawn:

-

For less-developed countries, public policies should limit the effects of physical, social, and economic segregation and increase the number of years of compulsory education. Public spending on education (as a percentage of GDP) does not seem to be directly relevant (in line with some considerations stated in the literature and pointed out in the introduction). However, it becomes relevant again through the above two channels (less segregation and more compulsory education) because both would still require public intervention at their own cost;

-

For more-developed countries, increasing the general level of education and increasing the general level of public spending on education are key elements and, of course, can go hand in hand. Income redistribution policies can also be important (they act through the channel of redistributing income-related opportunities).

The importance given to children’s independence is a cultural trait that seems to play a role in developed countries; however, it does not seem to be an area where direct public intervention is possible or appropriate. Indirectly, policies that increase equality of opportunity could be helpful so that, over time, parents feel able to rely on their children’s independence. It is clear, however, that this discourse opens up considerations of virtuous or vicious circles as pointed out above.

The greatest utility of this analysis lies in the identification of ‘patterns’ by grouping countries according to the level of intergenerational education mobility (or ‘immobility’) and other variables that may be associated with it. This can help us understand the phenomenon of intergenerational mobility in education. The results are in line with those highlighted in the literature and thus support and strengthen them, including by highlighting the non-monotonicity of mechanisms and relationships among countries with different levels of development. This analysis also emphasises the ‘equalising’ role played by public spending on education in middle- and high-income countries. Finally, an element new to the empirical literature was introduced into this analysis: the explicit consideration of the role played by cultural attitudes with respect to children’s independence.

In terms of directions for future research, two aspects can be highlighted. The first is the need to deepen the causal relationships between intergenerational mobility and the factors that may influence it while differentiating between more- and less-developed countries. The second is the need to take cultural aspects into account, both theoretically and empirically.