Drivers of S&P 500’s Profitability: Implications for Investment Strategy and Risk Management

Abstract

The financial markets, shaped by dynamic forces, including macroeconomic trends and technological advancements, are influenced by a multitude of factors impacting the S&P 500 stock index, a pivotal indicator in the US equity markets. This paper highlights the significance of understanding the exogenous variables affecting the index’s profitability for academics, portfolio managers, and investment professionals. Amid the global ramifications of the S&P 500, particularly in combating the eroding purchasing power caused by inflation, investing in stock indexes emerges as a means to safeguard wealth. The study employs various statistical techniques, emphasizing a methodical approach to uncover influential variables, and using static regression and autoregressive models for immediate and time-lagged effects. In conclusion, the findings have broad practical implications beyond investment strategy, extending to portfolio construction and risk management. Acknowledging inherent uncertainties in financial market forecasts, future research endeavors should target long-term trends, specific influences, and the impact of exchange rate fluctuations on index evolution. Collaboration across regulatory bodies, academia, and the financial industry is underscored, holding the potential for effective risk monitoring and bolstering overall economic and financial market stability. This research serves as a foundational step towards enhancing market understanding and facilitating more efficient investment decision-making approaches.

1. Introduction

Financial markets are a highly dynamic and intricate domain that is subject to the influence of numerous factors, including macroeconomic trends, economic and geopolitical developments, the financial performance of individual corporations, and recent technological advancements in artificial intelligence (Hyndman et al. 2008). The Standard & Poor’s 500 Index (S&P 500) is the principal indicator of the overall performance of the US equity markets in this context. Extensive analyses are frequently conducted on its profitability and development, given that the price movement of the asset frequently influences the investment decisions and strategic planning of both retail and professional investors (Petropoulos et al. 2022). Gaining insight into the exogenous variables that impact the S&P 500 index’s formation can furnish academics, portfolio managers, and investment professionals with critical knowledge for enhancing risk management, opportunity identification, and the performance of actual investments (Kaeck 2013).

The S&P 500 holds a prominent position in the realm of the American stock market. While its main function is to ascertain the prevailing economic conditions in the United States, this index also exerts a substantial influence on non-American stock exchanges and investor sentiment on a global scale (Albulescu 2021). As a result of the present high rate of inflation, the real purchasing power of money gradually diminishes, which has a profoundly negative effect on the population’s standard of living. Investing in stock indices is an alternative method for safeguarding the actual purchasing power of money over its course. As a consequence, it is important to determine the variables that influence the profitability of the S&P 500 stock index so as to facilitate judicious investment choices and effectively mitigate the associated risks (Melina et al. 2023). Thus, this study emphasizes that understanding how exogenous factors impact the profitability of the S&P 500 can have significant implications for investment strategies. By uncovering the relevant factors that influence an index’s performance, the research can provide valuable information for investors looking to optimize their portfolios. Nonetheless, when analyzing this index, it is crucial to consider various systematic factors that influence its performance. These factors can be divided into three main categories: economic, market, and systematic risks (Corzo et al. 2020). Macroeconomic indicators (GDP growth, inflation, and unemployment rates, and development of interest rates) have a significant impact on the overall performance of the index (e.g., Chen 2009; Billio et al. 2013 or Wang et al. 2023), and thus they cannot be omitted from the analysis. Market factors, playing a vital role in driving short-term fluctuations, must also be considered, as they can also influence market movements (e.g., Simon and Wiggins 2001; Becker et al. 2009; Stanley and Trainor 2021; etc.), so the volatility index, dollar index, indices of economic activity and industrial production were included. Finally, the stock market performance is also affected by fiscal and monetary policies, and therefore some specific factors—monetary aggregate or trade balance—were considered (e.g., Paule-Vianez et al. 2020 or Shah et al. 2021).

The motivation of the study is to highlight the broader implications of studying exogenous factors on the S&P 500’s profitability for macroeconomic analysis. Utilizing a variety of statistical techniques, this article seeks to identify and assess exogenous factors that impact the growth and profitability of the S&P 500 stock index and thus influence financial markets and decision-making processes over the world. A methodical approach is prioritized in order to identify variables that may exert a substantial influence on the price progression of the S&P 500 index. Furthermore, sophisticated statistical analyses are employed to enhance the comprehension of these variables’ interconnections and repercussions on the stock market (Usmani and Shamsi 2023; Gaspareniene et al. 2021). By employing the static regression model, it will be possible to discern and measure the immediate influence of specific explanatory variables on the S&P 500 index’s profitability. By employing the autoregressive model, the authors will examine the correlation between the time series that represent the S&P 500 index’s value and its delay, or alternatively ascertain whether independent variables with a specified time latency have a statistically significant impact on the index’s value (Ozair 2014). By examining how external factors such as geopolitical events, regulatory changes, or technological advancements influence the index, the research can contribute to a deeper understanding of the interplay between the economy and financial markets. By shedding light on the exogenous factors that drive the S&P 500’s profitability, the research can inform decision-making processes, help stakeholders navigate volatile market conditions more effectively, and emphasize the practical applications of the research findings for market participants, policymakers, and financial analysts.

The paper is divided as follows: the first section of the manuscript summarizes the literature review, focusing on the most relevant and up-to-date studies that highlight the development of the research issue. The Material and Methods section presents information about the data used and describes the statistical methods used for the analysis. The section devoted to the results and discussion portrays the research findings, which are discussed in the context of other relevant studies. The conclusion section focuses on the summary of crucial findings and emphasizes the study contributions.

2. Literature Review

The S&P 500 index stands as a barometer of the U.S. stock market, comprising 500 leading publicly traded companies across various sectors. Understanding the factors and determinants influencing the S&P 500 is imperative for investors, policymakers, and researchers alike. This literature review explores the multifaceted aspects shaping the S&P 500, emphasizing the recent and unprecedented influence of the COVID-19 pandemic. It is often used as a measure of the overall performance of the stock market (Kamalov et al. 2020). Market dynamics play a pivotal role in influencing the S&P 500. According to Fama and French (1992), market risk is a critical determinant of stock returns, and thus it is important to understand broader market trends. Campbell and Shiller (1998) underscore the impact of interest rates and inflation on the S&P 500, highlighting the intricate relationship between macroeconomic factors and index performance. Macroeconomic indicators are integral to comprehending the S&P 500’s movements. Chen et al. (1986) and Fu (2021) delve into the significance of GDP growth, unemployment rates, and consumer confidence. These indicators reflect the broader economic environment, providing insights into the underlying forces influencing the S&P 500. A comprehensive understanding of macroeconomic factors is essential for anticipating market trends. Corporate financial performance, particularly earnings management, is a crucial determinant affecting the S&P 500. Dechow et al. (2010) emphasize the role of corporate earnings in shaping stock prices. The S&P 500 is sensitive to the financial health of its constituent companies, making effective earnings management a focal point for both investors and corporate strategists. The emergence of the COVID-19 pandemic introduced unparalleled challenges to the global financial landscape, significantly impacting the S&P 500. Al-Awadhi et al. (2020) and Baker et al. (2020) shed light on the pandemic’s profound influence on the index. The initial shock led to a rapid decline in stock prices, reflecting heightened market volatility and uncertainty. Government interventions, fiscal policies, and advancements in vaccine development emerged as pivotal factors shaping the S&P 500’s response to the unprecedented crisis (Baker et al. 2020). The role of government interventions during crises becomes evident when examining the S&P 500’s reaction to the COVID-19 pandemic. Baker et al. (2020) also emphasize the impact of fiscal policies and stimulus measures on stabilizing financial markets. The timely implementation of supportive policies played a crucial role in mitigating the economic fallout and restoring investor confidence. Behavioral finance offers valuable insights into the S&P 500’s dynamics, especially during periods of crisis. The works of Shiller (1981) and Kahneman and Tversky (1979) highlight the role of investor sentiment and psychological factors in influencing market movements. Understanding the behavioral aspects of market participants provides a nuanced perspective on the S&P 500’s fluctuations.

Another line of research examines the relationship between the S&P 500 index and other variables. For example, Ersan et al. (2020) investigate the impact of S&P 500 index inclusion on a firm’s cost of capital. They find that firms added to the index exhibit a higher cost of capital over the first year after inclusion compared to non-S&P 500 stocks. Carverhill and Luo (2023) analyze time-varying jump risk in S&P 500 returns and options. They find that simultaneous jumps in returns and volatility help reconcile the time series of returns, volatility, and jump intensities. The COVID-19 pandemic has also had an impact on the S&P 500 index. Uyar and Uyar (2022) examine the volatility levels of S&P 500 sector portfolios’ systematic risks during the pandemic. They use wavelet approaches to analyze the behavior of time series both jointly at the time and frequency spaces. Their findings show that the systematic risks of sectors vary over different investment horizons.

With the development of machine learning and artificial intelligence technologies, the number of studies that use machine learning algorithms to predict the price development of stocks is increasing. However, accurately predicting stock price trends is still an elusive goal, not only because the stock market is affected by the political and market environment, market sentiment, etc., but also as stock price data is inherently complex and non-linear (Biardi et al. 2020). Jiao and Ye (2022) and Wang et al. (2022) discuss the use of a model called Transformer, which applies machine learning to predict the evolution of stock indices. The authors found that the Transformer model demonstrates superior performance compared to other applied investment methods and can generate excessive profits for investors. Similarly, Kamalov et al. (2020) propose the use of machine learning to predict the future price development of the S&P 500 index. Their research shows that neural networks trained with their method outperform neural networks trained on stock index data. He and Kita (2021) report that, before the rise of machine learning, a linear time series forecasting algorithm was widely used to forecast stock prices. Another model for predicting the development of the stock market is applied by Jamous et al. (2021). Their ANN-PSOCoG model uses the so-called hyperparameters to create an optimal neural network, which makes it possible to predict the future development of actions with maximum accuracy. Kim et al. (2023) point to the importance of incorporating news sentiment into stock price forecasts and thus the potential impact of psychological factors on financial markets. Economic and psychological factors influence the collective behavior of investors and issuers, thereby affecting asset prices and market efficiency. The functioning of the financial market depends on the degree of irrationality of its participants, whose behavior is determined by individual psychological characteristics. Bazetska et al. (2021) argue that the economic subject is significantly influenced by psychological factors such as the phase of his/her life, temperament type, psychological type, archetype, and metaprograms. Lin et al. (2018) state that due to the high level of complexity of forecasting trading trends, applying traditional financial analysis and technical analysis indicators to predict short-term market trends is often ineffective. The main reason is that trading behavior is influenced by psychological factors, such as greed and fear, that influence investors during the execution of trading transactions.

Cohen (2023) states that technical analysis helps investors better time the entry and exit of financial asset positions. When predicting the future price trend of a financial asset, this methodology relies exclusively on past information about the price and trading volumes of financial assets. Lento and Gradojevic (2021) point out that trading using technical analysis was profitable even during the COVID-19 pandemic. Schmitt and Westerhoff (2017) argue that if the mass of speculators starts using technical analysis, there will be a sharp increase in volatility and thus extreme fluctuations in the prices of financial assets, which can lead to the creation of investment bubbles in the financial market. According to Chutka and Vagner (2020), technical and fundamental analysis can be considered the two most commonly used methods for analyzing financial markets. The results of fundamental analysis do not always reflect the actual market prices, but the applicability of fundamental analysis is still very broad. Kartasova and Venclauskiene (2014) concluded that, despite all the reasonable arguments against fundamental analysis, its application could be beneficial in the valuation of shares in order to make long-term investment decisions. Menkhoff (2010) states that, compared to other types of analysis, fundamental analysis dominates the implementation of investment decisions by investment fund managers. According to Cohen (2023), experienced investors should combine fundamental analysis and technical analysis to achieve optimal trading results.

The S&P 500’s performance is intricately linked to market dynamics, macroeconomic indicators, and corporate financial health (Grobys 2022; Lee and Kang 2020; Golitsis et al. 2022). The literature on the S&P 500 index covers a wide range of topics, including prediction models, the impact of index inclusion, risk analysis, and the effects of external factors such as the COVID-19 pandemic, inflation or unemployment rates, volatility or dollar indices, indices of economic activity or industrial production, yields of government bonds, gold, and bitcoin. These studies provide valuable insights into the dynamics and implications of the S&P 500 index in the financial market. The unprecedented impact of the COVID-19 pandemic underscored the index’s vulnerability to external shocks. Government interventions, policy measures, and behavioral aspects further shape the S&P 500’s trajectory.

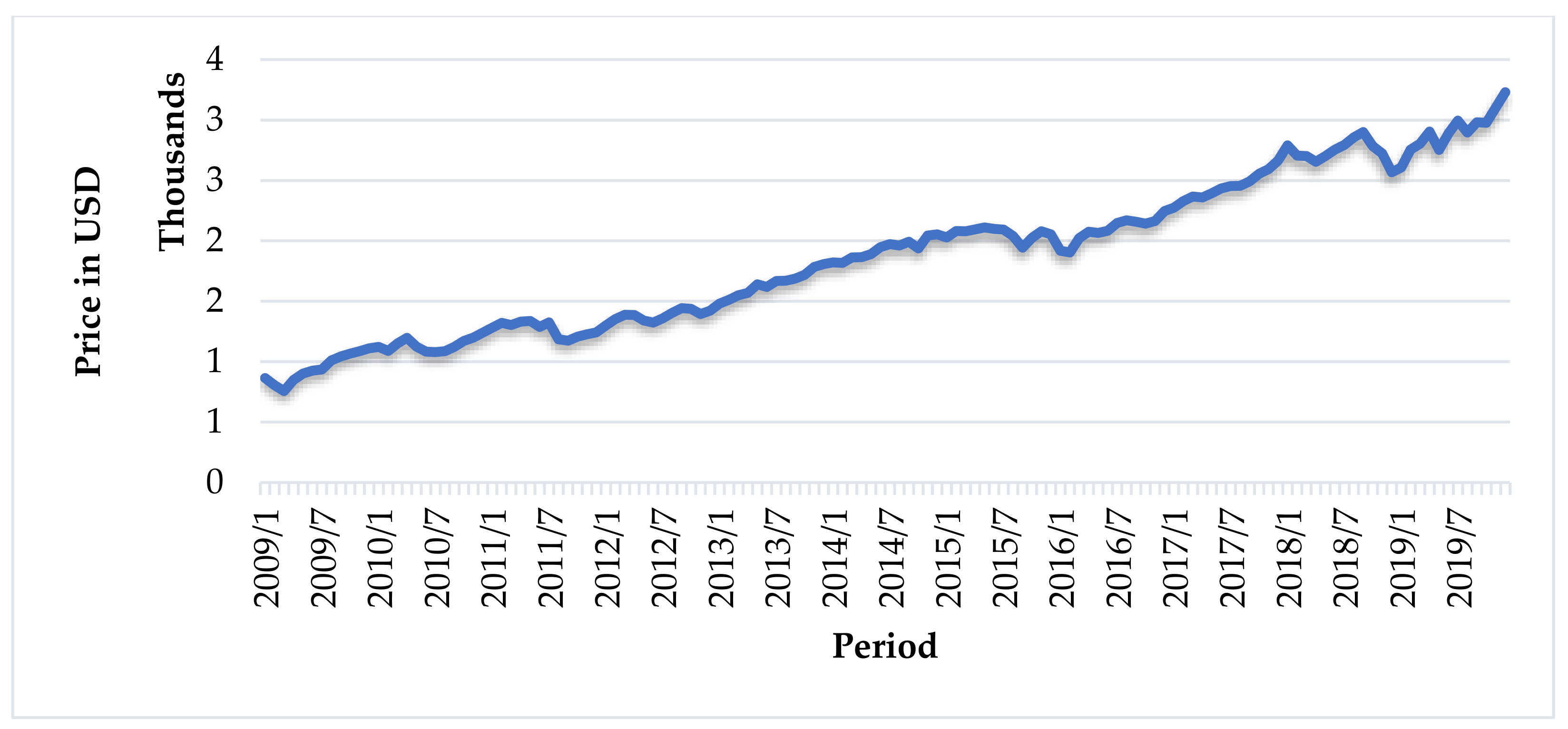
3. Materials and Methods

We focus on the examination of factors that are hypothesized to exert a substantial influence on the performance of the S&P 500 stock index. An exhaustive analysis was conducted to determine the effects of various quantitative variables, including nominal gross domestic product (GDP), unemployment rate, inflation rate, base interest rates, volatility index, dollar index, economic activity index, industrial production index, trade balance, and monetary aggregate M2. Through correlation analysis, the existence of a linear relationship between the monthly returns of the S&P 500 stock index, gold, and bitcoin was analyzed. Among the analyzed qualitative variables, the month and whether there was a presidential election in the USA in a given year (yes, no) were considered. Model specification is the process of determining which independent variables to include and exclude from a regression equation. Often, the variable selection process is a mixture of statistics, theory, and practical knowledge. The standard approaches include information about the adj. R-squared, p-values of independent variables, and automated model selection procedures (Zellner 2001). Frost (2020) also specifies some model selection statistics that can help choose the best regression model, i.e., multicollinearity. The information utilized in the processing of individual analyses was acquired from the following sources:

• Unemployment rate in the USA (UR US 2023),
• Inflation rate in the USA (CPI 2023),
• Nominal amount of GDP in the USA (US GDP 2023),
• Basic interest rates in the USA (FFR 2023),
• Volatility index (CBOE 2023),
• Dollar index (NB US 2023),
• Index of economic activity in the USA (CEAI 2023),
• Index of industrial production in the USA (IP TI 2023),
• Trade balance in the USA (TB 2023),
• Monetary aggregate M2 (M2 2023),
• Return of the S&P 500 stock index (SP 2023; S&P NASDAQ 2023),
• Monthly yield (coupon) of 30-year US government bonds (MY US 2023),
• Gold yield (GSP 2023),
• Bitcoin yield (BHP 2023).

The authors analyzed the evolution of the S&P 500 stock index from 2009 to 2019 using time series data, with partial periods consisting of months, and then selected this time frame due to two significant events: the onset of the global financial crisis in 2008 in the United States, which subsequently hindered the progress of economies worldwide, and the outbreak of the COVID-19 pandemic in 2020. Both global events had an unnaturally negative impact on the price development of the S&P 500 stock index, which would cause inaccuracy in the results of the analysis. Thus, it was determined that the analysis will be centered on the period circumscribed by these two global negative events for the stated reasons. An analysis was conducted on the effects of various quantitative variables, including but not limited to the following: nominal US GDP, US key interest rates, dollar index value, volatility index value, US economic activity index value, US industrial production index value, US trade balance amount, US monetary aggregate M2 amount, yield on 30-year US government bonds, and gold yield. At monthly intervals, all input data for individual explanatory variables were collected. To mitigate the impact of potential seasonal fluctuations on the price trajectory of the S&P 500 stock index, dummy variables were incorporated, representing individual months, into the regression model. January was selected as the period of reference.

The monthly price evolution of the S&P 500 stock index from 2009 to 2019 is depicted in Figure 1. The graphic analysis of the S&P 500 stock index’s price development suggests that there was a consistent upward trend in price without discernible seasonal variations. This suggests that the coefficients of the dummy variables representing the months will not have a significant statistical impact on the model.

The analysis is provided using the static regression model and autoregressive model, which enable the identification and quantification of the immediate impact of individual explanatory variables on profitability of the S&P 500 index. In a static model, the effect of explanatory variables on the dependent variable operates in the same period of time. The autoregressive models include the lagged value of the dependent variable, and they are applied to lag series generated using the original time series. In the case of autoregression models, the output is the future data point, and it can be expressed as a linear combination for past $p$ data points (Kotu and Deshpande 2019). Thus, the autoregressive model can be expressed as:

$$y_t=l+{\alpha }_1{y}_{t-1}+{\alpha }_2{y}_{t-2}+\cdots +{\alpha }_p{y}_{t-p}+\epsilon$$

(1)

where $l$ is the level in the dataset and $\epsilon$ is the noise. α are the coefficients that need to be gained from the data. This can be referred to as an autoregressive model with $p$ lags or an $AR$ model. In an $AR$ model, lag series is a new predictor used to fit the dependent variable, which is still the original series value, $Y_t$.

4. Results and Discussion

The initial analysis centers on hypothesis testing, specifically examining whether the return of the stock index (a quantitative variable) is contingent upon the month in which trading occurs (a qualitative variable). The so-called “Halloween effect” is where the analysis begins. This observation suggests that the winter season (November to April) exhibits a greater degree of profitability compared to the remaining months (Kotu and Deshpande 2019; Yilmazkuday 2023; Lento and Gradojevic 2021). The time period spanned from 1923 to 2022. As the data’s normality could not be confirmed, the non-parametric Kruskal–Wallis test was applied to determine whether the month affected the S&P 500 stock index’s profitability.

Based on the obtained p-value (refer to

Table 1. Kruskal–Wallis test.

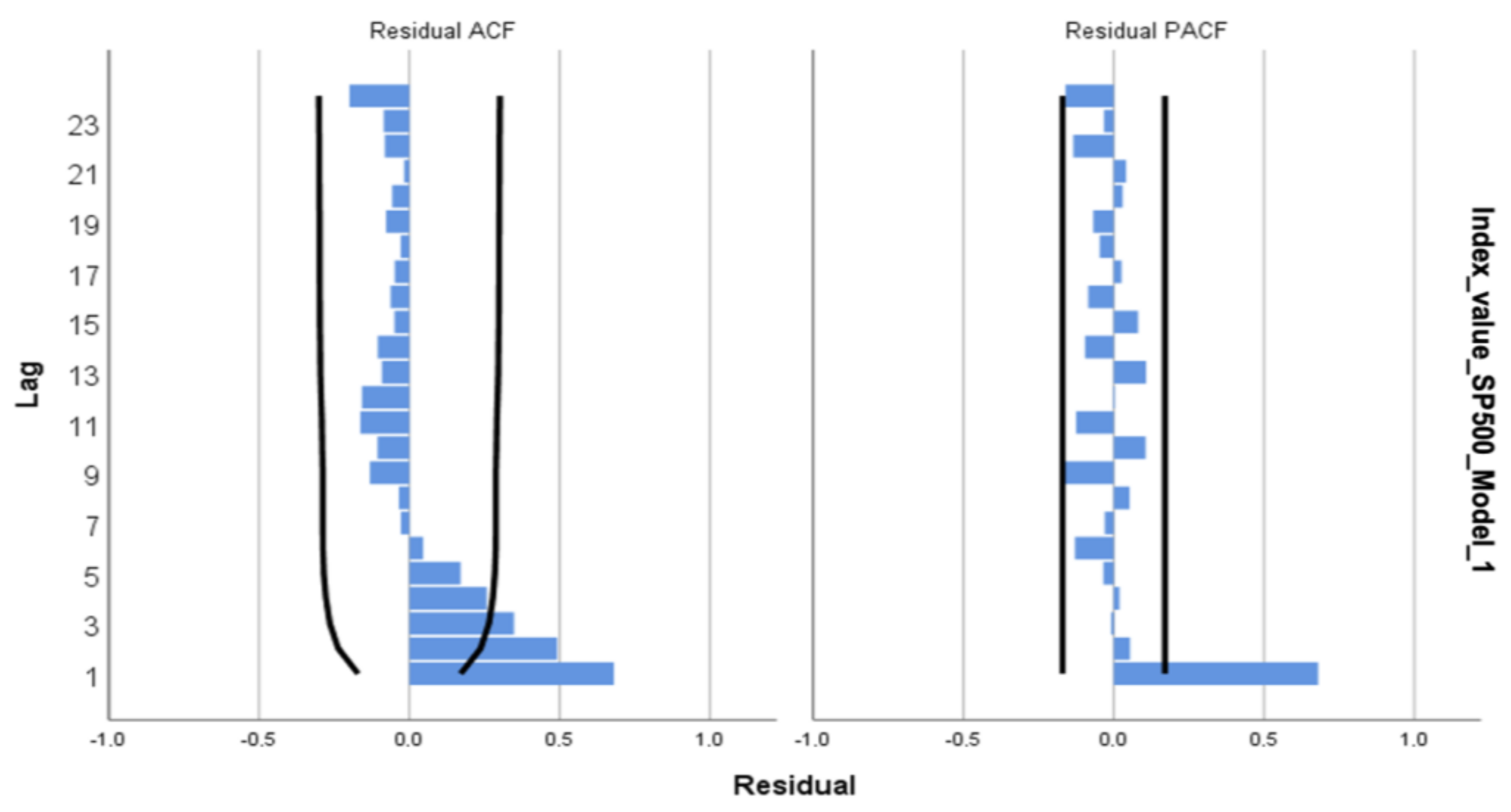
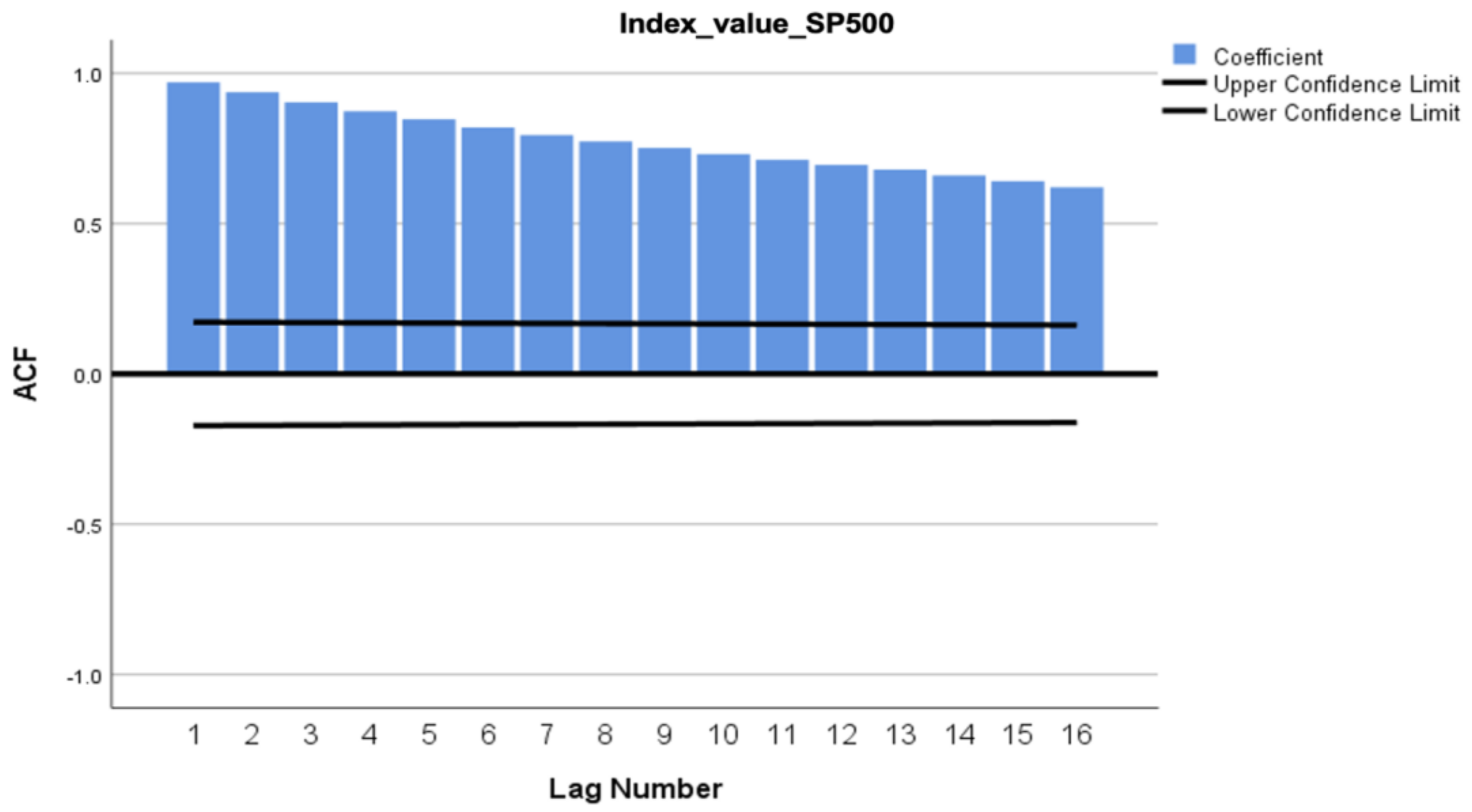
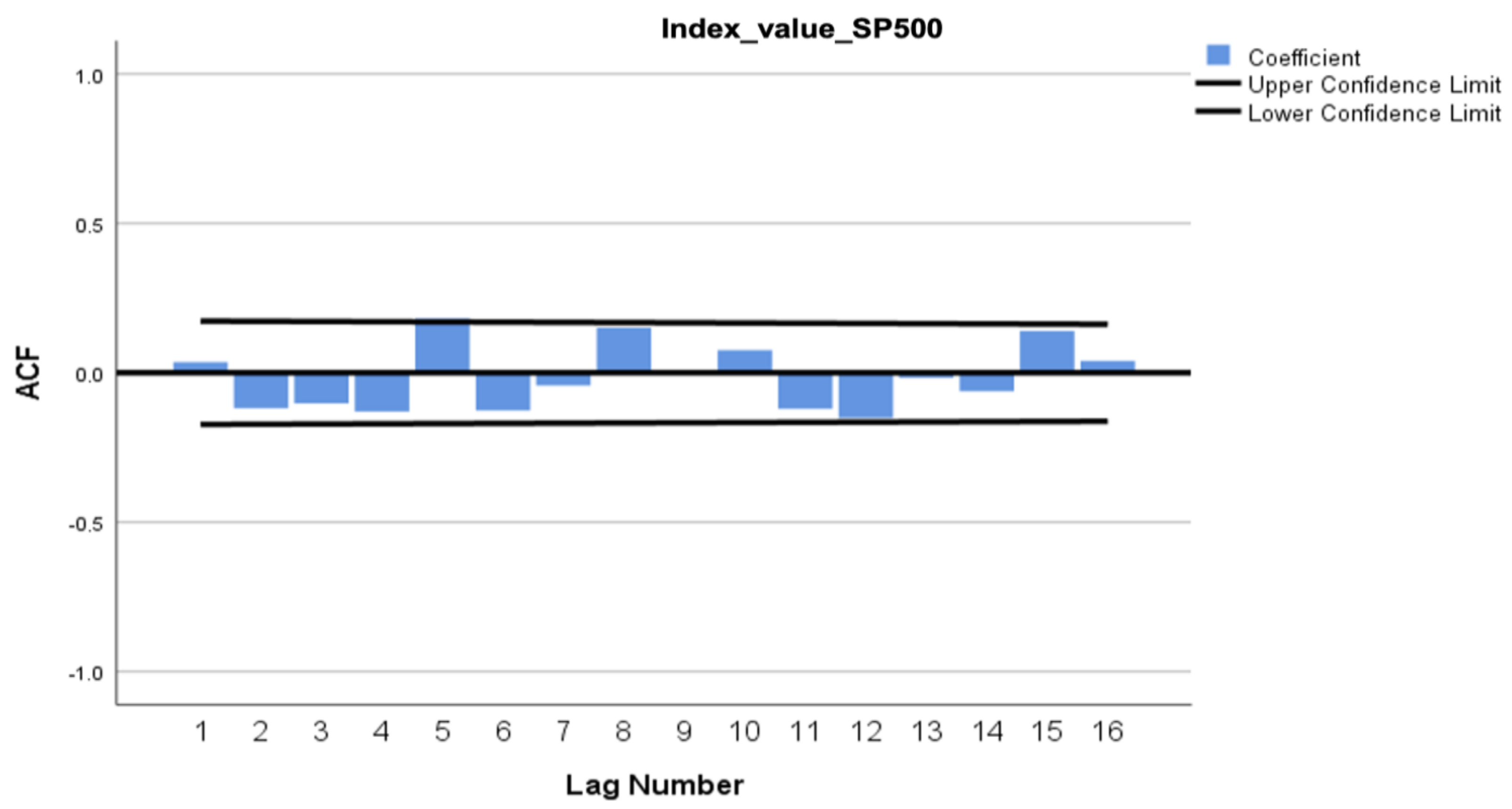
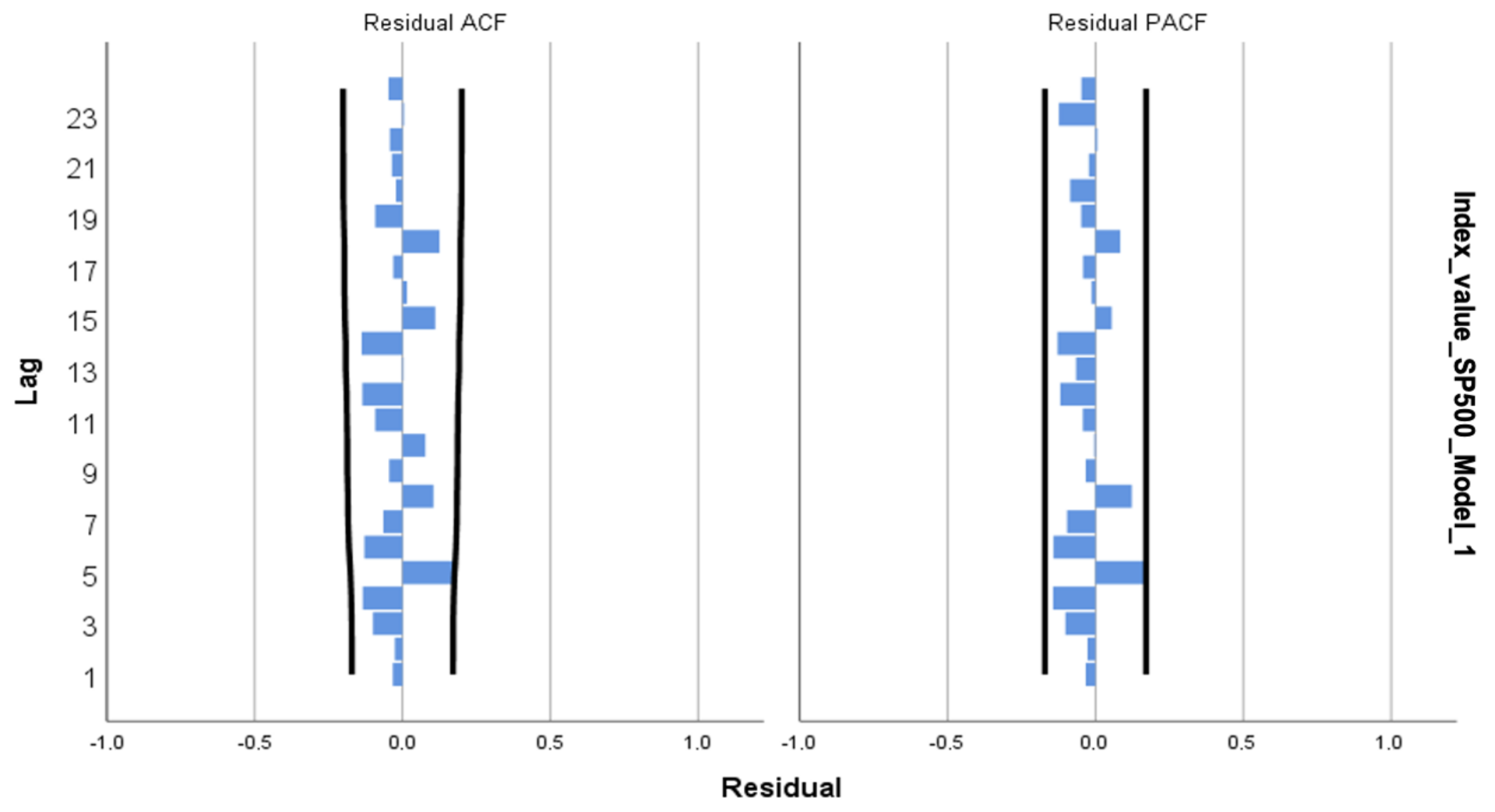
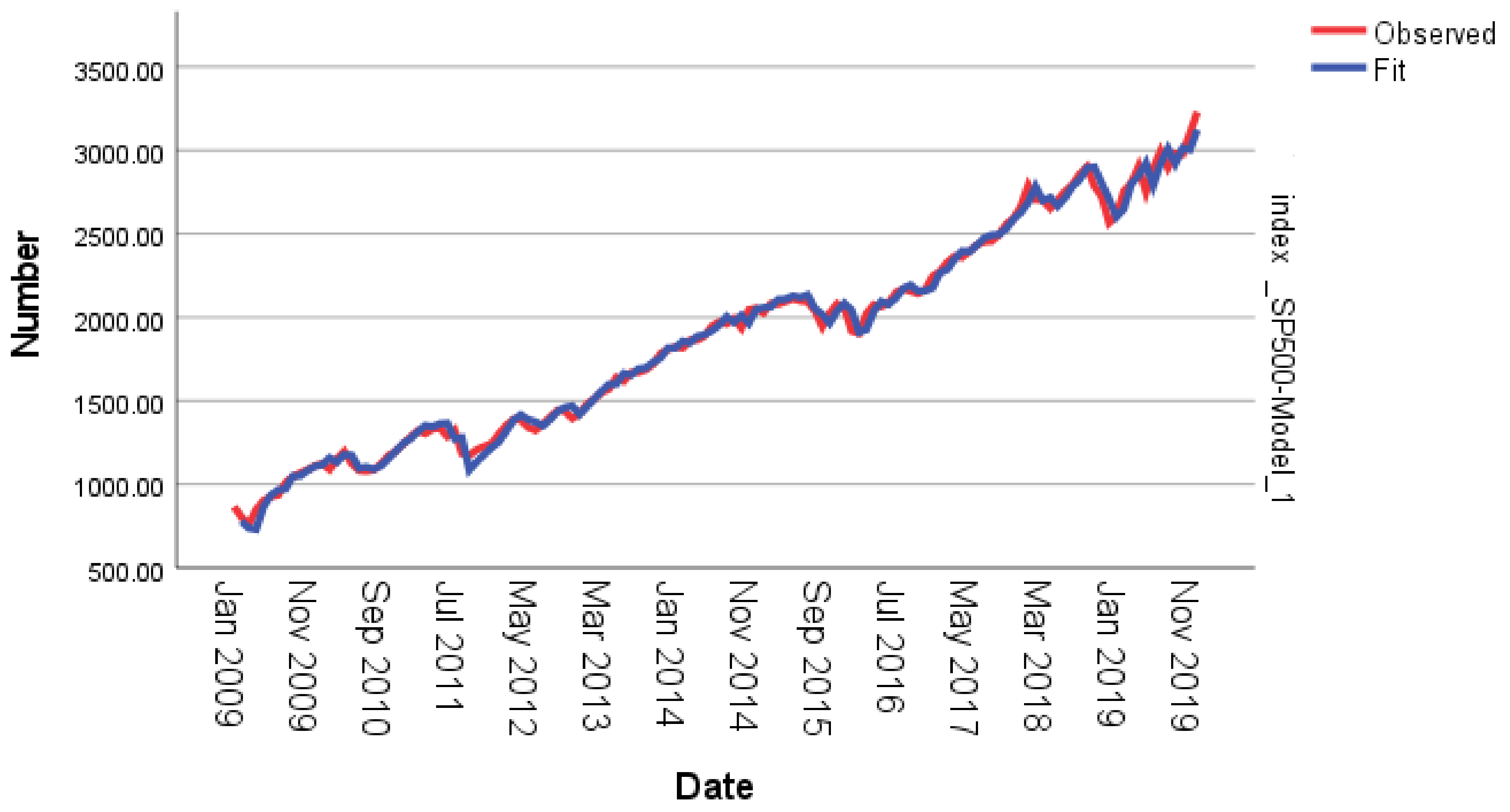
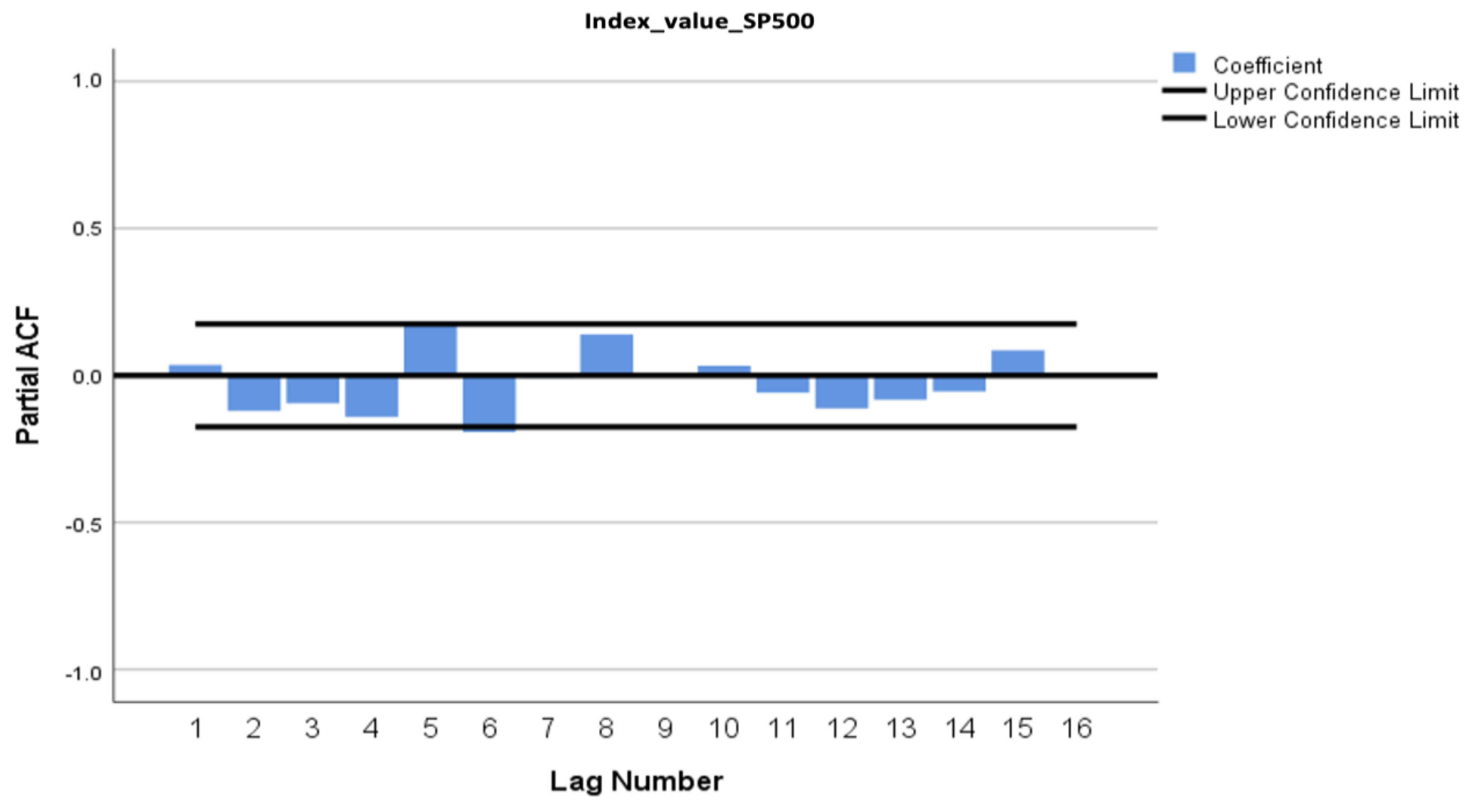
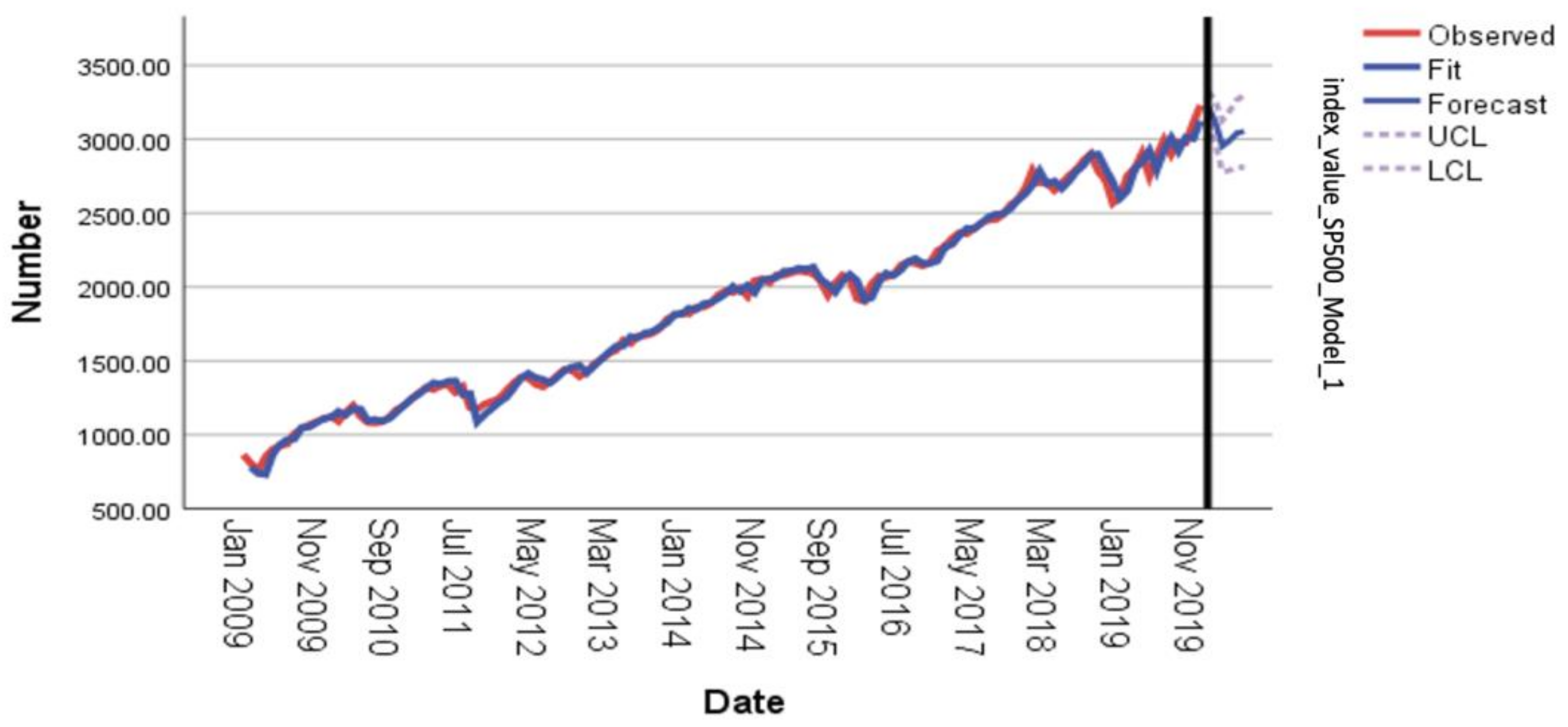
Null Hypothesis	Test	p-Value	Result
The yield distribution is the same within all categories of months.	Kruskal-Wallis	0.067	Rejection of the null hypothesis.

Source: Authors’ compilation.

) surpassing the predetermined significance level (0.05), it can be concluded that the month does not have any influence on the return of the S&P 500 stock index.

The second analysis focuses on examining the hypothesis regarding the presence of a relationship between two categorical variables: the annual change in the value of the S&P 500 index (indicating growth or decline) and the occurrence of the American presidential elections in the specified year (indicating yes or no). It was hypothesized that the American government would implement fiscal policy to stimulate the economy during election years with the intention of regaining its mandate. In order to examine the hypothesis, Pearson’s χ² independence test was utilized. A period spanning from 1923 to 2022 was examined. The data analysis indicates that this circumstance transpired most frequently in years without presidential elections during the analyzed period, coinciding with an annual increase in the value of the S&P 500 index. The scenario in which the S&P 500 index experienced a decline in value year-over-year during a presidential election was depicted in the fewest number of measurements.

On the basis of the summary of the test results in

Table 2. Pearson’s χ² test of independence.

	Value	df	Asymptotic Significance
Pearson’s χ2 test	2.046	1	0.153
Valid measurements	100

Source: Authors’ compilation.

, it is possible to conclude that the course of the American presidential elections has no impact on the S&P 500 index’s development.

An additional area of emphasis is the correlation analysis, which examines the relationship between the returns of Bitcoin, gold, and 30-year US government bonds and the S&P 500 stock index. The rationale behind conducting this analysis was to ascertain whether there is no correlation between returns on stocks, income from shares, or stock indexes and gold returns (Kotu and Deshpande 2019; Yilmazkuday 2023). The authors selected US government bonds with a 30-year maturity because, among bonds issued by the US government, they have the longest maturity. As a result, the risk associated with defaulting on their nominal value is the greatest, bringing their risk level most closely to that of shares. From 1978 to 2022, a correlation analysis was conducted to examine the relationship between the monthly returns of the S&P 500 stock index and the monthly returns (coupons) of 30-year US government bonds. The absence of confirmation regarding the data’s normality resulted in the utilization of a non-parametric Spearman’s rank correlation coefficient (Sig. value 0.537), which failed to establish a statistically significant relationship between the variables.

The objective of the second correlation analysis was to determine whether or not monthly S&P 500 stock index returns and gold returns followed a linear trend. The authors’ objective in conducting the analysis was to corroborate the widely accepted consensus that there is no correlation between gold returns and the performance of the S&P 500 stock index or share returns (Musa et al. 2024; Dvorsky et al. 2023). The analysis encompassed the time span from 1972 to 2022; however, the authors restricted their analysis to the year 1972 due to the gold standard, which remained in effect until 15 August 1971. This change had a substantial influence on the trajectory of gold prices. The aforementioned consequence arose from the fixed exchange rate that existed between one US dollar and one ounce of gold. Similar to the preceding instance, the data set’s normality remained unconfirmed; therefore, Spearman’s rank correlation coefficient was utilized once more to determine the degree and direction of linear dependence among the selected assets’ returns. The results of the tests indicate that there is no statistically significant relationship between the variables (Sig. 0.605).

The authors examined the presence of a linear association between the returns of bitcoin and the S&P 500 stock index using the third correlation analysis. The motivation behind conducting the aforementioned correlation analysis was to validate the hypothesis that the growth of bitcoin returns is equivalent to that of the S&P 500 stock index returns. They conducted an analysis spanning the period from August 2010 to October 2023. In comparison to other investment instruments, the time period chosen for the analysis of this particular instrument was significantly shorter. This is primarily due to the fact that the inaugural platform facilitating the buying and selling of bitcoins was established in this year. Given the unconfirmed normality of the data in this particular sample, Spearman’s rank correlation coefficient was reapplied. Its value of 0.273 (sig value 0.001) indicates that the monthly returns of the S&P 500 stock index and bitcoin exhibit a weak direct relationship; however, this relationship is linearly statistically significant.

Based on the findings of the conducted analyses, it can be deduced that professional and retail investors ought not to place undue emphasis on the month in which they formulate investment decisions concerning the S&P 500 stock index. Furthermore, the profitability of the S&P 500 stock index remains unaffected by the occurrence of American presidential elections in a given year. It can be concluded and suggested that the occurrence of the US presidential elections in a particular year should not exert any influence on investment decisions pertaining to the S&P 500 stock index.

It has not been established that S&P 500 returns and gold returns follow a linear pattern. Furthermore, there was no confirmation of a linear relationship between the returns of 30-year US bonds and the S&P 500 index. Bitcoin emerged as the sole investment instrument that exhibited a direct linear correlation between its monthly returns and those of the S&P 500 stock index. The statistical significance of the quantified direct linear dependence was accompanied by its weakness; consequently, it was determined that the provided factor lacks adequate relevance for investment decision-making. Based on the findings, it can be concluded that the income movement of the investment assets under consideration should not influence the investment decision regarding S&P 500 index investments.

Prior to conducting the time series analysis, it was necessary to validate the multicollinearity assumption, which posits that the explanatory variables operate independently. As an initial criterion, the existence of multicollinearity among explanatory variables was evaluated using variation inflation factors (VIF). Greater VIF values signify increased interdependence among the explanatory variables. VIF values equal to or exceeding 10 indicate that the explanatory variables are highly multicollinear. The individual independent variables’ VIF values from

Table 3. Assessment of multicollinearity—variance inflation factors (all variables).

Variable	Coefficient	Std. Error	t-Statistics	p-Value	Coll. Stat. Tolerance	Coll. Stat. VIF
Constant	−2192.487	2948.861	−0.744	0.459
Unemployment rate	−48.108	52.203	−0.922	0.359	0.003	366.744
Inflation rate	−10.878	8.359	−1.301	0.196	0.414	2.416
Interest rate	−83.985	37.861	−2.218	0.028	0.045	22.418
GDP USA	0.397	0.073	5.425	0.000	0.001	721.017
Trade balance USA	−0.001	0.002	−0.553	0.581	0.354	2.822
Monetary aggregate M2	−0.034	0.090	−0.377	0.707	0.001	1061.71
Dollar index	−6.108	2.602	−2.348	0.021	0.048	20.700
Volatility index	−3.200	1.484	−2.156	0.033	0.306	3.272
Index of US economic activity	−6.806	37.419	−0.182	0.856	0.000	4355.64
US Industrial Production Index	−11.579	6.691	−1.731	0.086	0.032	31.515
Gold yield	−78.890	125.464	−0.629	0.531	0.922	1.085
The yield on 30-year US bonds	10,786.255	1772.370	6.086	0.000	0.263	3.801
R-squared	0.990
Adjusted R-squared	0.989
S. E. of regression	67.476
SS total	52,795,277.94
SS resid	541,809.73
SS model	52,253,468.22
F-stat	956.388
p-value	0.000

Source: Authors’ compilation.

indicate that there is a significant multicollinearity linked to the unemployment rate, interest rate, US GDP, monetary aggregate M2, dollar index, US economic activity index, and US industrial production index.

The remaining characteristics utilized to identify the existence of multicollinearity are detailed in

Table 4. Assessment of multicollinearity—eigenvalue, conditionality index, and variance proportions (all variables).

	Eigenvalue	Condition Index	Constant	Unemployment Rate	Inflation Rate	Interest Rate	GDP USA	US Trade Balance	Monetary Aggregate M2	Dollar index	Volatility Index	Index of US Activity	USIP	Gold Yield	US Bonds
1	10.796	1.000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
2	0.990	3.302	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.91	0.00
3	0.737	3.827	0.00	0.00	0.00	0.03	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0,00
4	0.291	6.090	0.00	0.00	0.39	0.00	0.00	0.00	0.00	0.00	0.01	0.00	0,00	0.00	0.00
5	0.123	9.363	0.00	0.00	0.02	0.03	0.00	0.00	0.00	0.00	0.15	0.00	0.00	0.03	0.00
6	0.045	15.559	0.00	0.00	0.06	0.03	0.00	0.00	0.00	0.00	0.28	0.00	0.00	0.00	0.07
7	0.010	32.412	0.00	0.01	0.11	0.02	0.00	0.12	0.00	0.00	0.06	0.00	0.00	0.00	0.42
8	0.006	42.842	0.00	0.01	0.12	0.02	0.00	0.60	0.00	0.00	0.01	0.00	0.00	0.00	0.16
9	0.001	85.523	0.00	0.00	0.06	0.00	0.00	0.02	0,00	0.21	0.16	0.00	0.01	0.00	0.02
10	0.000	214.53	0.00	0.03	0.20	0.25	0.00	0.19	0.05	0.21	0.25	0.00	0.12	0.01	0.12
11	<0	409.03	0.03	0.07	0.00	0.02	0.05	0.05	0.00	0.42	0.02	0.01	0.14	0.01	0.09
12	<0	544.43	0.00	0.03	0.03	0.18	0.31	0.00	0.25	0.07	0.02	0.00	0.22	0.01	0.06
13	<0	2945.6	0.97	0.86	0.00	0.41	0.63	0.01	0.69	0.09	0.03	0.99	0.50	0.01	0.05

Source: Authors’ compilation.

. The eigenvalue, conditionality index, and variance proportions are examples of these attributes. Confirmation of multicollinearity occurs when each of the subsequent conditions is simultaneously fulfilled:

• The eigenvalue is less than 0.01.
• The conditionality index exceeds 30.
• The variance proportions for at least two explanatory variables are greater than 0.5.

In the absence of at least one of these three conditions, multicollinearity does not present a problem. The explanatory variables, the US economic activity index, unemployment rate, and monetary aggregate M2, met all three conditions. The authors opted to eliminate the explanatory variable representing the US economic activity index from the model on the grounds that they deem other explanatory variables that encounter multicollinearity issues to be more pertinent to this model. An additional factor contributing to the elimination of the specified variable was its simultaneous attainment of the highest value of VIF and variance proportions.

The authors iterated the entire procedure several times until the multicollinearity issue among the independent variables was successfully resolved. In consideration of the outcomes of additional multicollinearity computations, the elimination of a portion of the subsequent explanatory variables from the model was done: the dollar index, US economic activity index, and US industrial production index. The explanatory variables that were mentioned were eliminated due to their violation of the assumption regarding the independence of explanatory variables. The outcomes of the characteristics utilized to identify multicollinearity among the remaining independent variables are presented in

Table 5. Assessment of multicollinearity—variance inflation factors (final model variables).

Variable	Coefficient	Std. Error	t-Statistics	p-Value	Coll. Stat. Tolerance	Coll. Stat. VIF
Constant	3185.349	120.824	26.364	0.000
Unemployment rate	−205.348	10.867	−18.897	0.000	0.171	5.845
Inflation rate	27.273	11.665	2.338	0.021	0.578	1.731
Interest rate	224.424	22.972	9.769	0.000	0.329	3.036
US trade balance	−0.001	0.003	−0.233	0.816	0.472	2.117
Volatility index	−13.684	1.773	−7.720	0.000	0.583	1.717
Gold yield	−51.499	202.308	−0.255	0.799	0.964	1.037
The yield on 30-year US bonds	2254.055	2408.970	0.936	0.351	0.387	2.583
R-square	0.971
Adjusted R-square	0.969
S. E. of regression	111.257
SS total	52,795,277.94
SS resid	1,534,890.53
SS model	51,260,387.41
F-stat	591.600
p-value	0.000

Source: Authors’ compilation.

and

Table 6. Assessment of multicollinearity—eigenvalue, conditionality index, and variance proportions (final model variables).

	Eigenvalue	Condition Index	Constant	Unemployment Rate	Inflation Rate	Interest Rate	US trade Balance	Volatility Index	Gold Yield	Yield of 30-Year Bonds
1	5.910	1.000	0.00	0.00	0.00	0.00	0.00	0.00	0.00	0.00
2	0.983	2.452	0.00	0.00	0.00	0.00	0.00	0.00	0.96	0.00
3	0.722	2.861	0.00	0.00	0.01	0.21	0.00	0.01	0.00	0.00
4	0.275	4.633	0.00	0.00	0.51	0.08	0.00	0.03	0.01	0.00
5	0.068	9.320	0.01	0.00	0.17	0.01	0.01	0.71	0.01	0.02
6	0.029	14.353	0.04	0.15	0.00	0.37	0.07	0.09	0.01	0.11
7	0.009	24.990	0.00	0.83	0.07	0.24	0.03	0.16	0.00	0.72
8	0.004	41.001	0.95	0.02	0.23	0.08	0.90	0.00	0.01	0.14

Source: Authors’ compilation.

. Based on the obtained results, it can be inferred that the multicollinearity problem was successfully resolved, thereby confirming the independence assumption of the explanatory variables.

After ensuring that the independence of the explanatory variables was satisfied, a static regression model was developed. This model includes the following explanatory variables: unemployment rate, inflation rate, interest rate, US trade balance, volatility index, gold yield, and 30-year US bonds. An investigation was conducted into the immediate response of the S&P 500 stock index value (dependent variable) to the explanatory variables (independent variables), which were mentioned earlier, employing a static regression model. In order to incorporate specific months into the model, the authors generated fictitious (dummy) variables with the reference category January. Following the construction of the static regression model, the statistical significance of the explanatory variables was evaluated at the 5% level. Thus, the statistical significance of the individual variables included in the model was evaluated (

Table 7. Statistical significance of variables in a static regression model.

				Estimate	St. dev.	t	Sig.
Value of S&P 500-Model 1	The value of the S&P 500 index	No change	Con.	3127.155	129.115	24.220	0.000
	Unemployment rate	No change	Lag 0	−207.984	11.094	−18.748	0.000
	Inflation rate	No change	Lag 0	27.125	11.832	2.292	0.024
	Interest rate	No change	Lag 0	221.383	23.342	9.484	0.000
	US trade balance	No change	Lag 0	−0.001	0.003	−0.269	0.788
	Volatility index	No change	Lag 0	−13.770	1.812	−7.600	0.000
	Gold yield	No change	Lag 0	−1.952	215.948	−0.009	0.993
	Bond yield	No change	Lag 0	3436.805	2476.101	1.388	0.168
	April	No change	Lag 0	4.867	48.714	0.100	0.921
	August	No change	Lag 0	70.672	48.220	1.466	0.146
	December	No change	Lag 0	67.199	49.139	1.368	0.174
	February	No change	Lag 0	−2.518	48.056	−0.052	0.958
	July	No change	Lag 0	34.706	48.739	0.712	0.478
	June	No change	Lag 0	24.788	48.696	0.509	0.612
	March	No change	Lag 0	−0.849	49.097	−0.017	0.986
	May	No change	Lag 0	20.030	48.881	0.410	0.683
	November	No change	Lag 0	69.700	48.750	1.430	0.156
	October	No change	Lag 0	61.090	48.432	1.261	0.210
	September	No change	Lag 0	80.334	49.186	1.633	0.105

Source: Authors’ compilation.

).

The p-values associated with the following variables: US trade balance, gold yield, 30-year US bond yield, and the months of April, August, December, February, July, June, March, May, November, October, and September, all exceeded the predetermined significance level, so their statistical significance in the model was not confirmed.

Consequently, the provided variables lack statistical significance within the static regression model that was constructed. All statistically insignificant variables were excluded (stepwise) from the model. Following this, a novel static regression model was constructed (

Table 8. Statistical significance of variables in a novel static regression model.

				Estimate	St. dev.	t	Sig.
Value of S&P 500-Model 1	Value of S&P 500	No change	Con.	3239.894	50.653	63.962	0.000
	Unemployment rate	No change	Lag 0	−198.580	7.797	−25.468	0.000
	Inflation rate	No change	Lag 0	28.117	9.598	2.929	0.004
	Interest rate	No change	Lag 0	231.926	20.084	11.548	0.000
	Volatility index	No change	Lag 0	−13.953	1.734	−8.048	0.000

Source: Authors’ compilation.

). Based on the statistical insignificance of the coefficients of the dummy variables representing the months in the model (all months were excluded), it can be deduced that the value of the S&P 500 index does not exhibit seasonality. Following the exclusion of statistically insignificant explanatory variables from the static regression model, the subsequent variables are included in the model: unemployment rate, inflation rate, interest rate, and volatility index.

After removing statistically insignificant variables, a static regression model was developed, and the coefficients of the explanatory variables are listed in Table 8. The equation of the created static regression model has the following formula:

$$\begin{array}{ll}Value of index& \mathrm{S}\&\mathrm{P} 500\\ & =3239.894-198.580·unemployment rate +28.117·inflation rate +231.926\\ & ·interest rate-13.953·volatility index\end{array}$$

(2)

The following describes how the outcomes of the developed static regression model can be interpreted (ceteris paribus). A nominal increase of 1% in the unemployment rate results in an average decrease of USD198.58 in the value of the S&P 500. A 1% rise in the inflation rate results in an average increase of USD 28.12 of the S&P 500. The value of the S&P 500 stock index will increase by an average of USD 231.93, all else being equal, if interest rates rise by 1%. A USD 1 increase in the volatility index results in an average USD 13.95 decline in the value of the S&P 500 stock index. From the foregoing, it can be concluded that the interest rate increase has the greatest impact on the value of the S&P 500 index. The most pronounced effect of the S&P 500 index decline is the expansion of the unemployment rate.

As shown in

Table 9. Assessment of model quality through BIC.

Number of Predictors	Model Verification Statistics		Ljung-Box Q			Number of Outliers
	Stationary R2	Normalized BIC	Statistics	DF	Sig.
4	0.971	9.592	141.949	18	0.000	0

Source: Authors’ compilation.

, the Bayesian Information Criterion (BIC) value for the developed static regression model is 9.592. The authors will use this specified value as one of the criteria to compare the model’s quality to that of other static models that were developed.

Using the autocorrelation function (ACF), which shows the correlation of the time series with its lags, and the partial autocorrelation function (PACF), which shows the dependence between the time series and its lags cleaned from the effects of other lags (Figure 2), the authors assessed the fulfillment of the assumption on the residuals independence. This assumption was not confirmed, as the residuals and their lags are interdependent.

As an additional model assumption, validation of the stationarity of the time series was concluded in the following step. The stationarity was confirmed through the presentation of the autocorrelation function. The time series is not stationary, as shown in Figure 3, as the initial autocorrelation coefficient is close to 1, and the subsequent autocorrelation coefficients diminish to insignificant values only very slowly and gradually. Following this, a specific transformation of the time series was required to satisfy the assumption of stationary.

The autocorrelation function of the S&P 500 stock index time series, as depicted in Figure 4, was subjected to a transformation utilizing the first order differential. This operation computes the difference between two consecutive values within the time series. By transforming the time series with differentiation of the first order, the stationarity assumption of the process generated by the time series was confirmed.

As measured by the BIC value, the quality of the static regression model with the first order differential is greater than that of the previous model due to the reduced BIC value of the newly constructed model (

Table 10. Assessment of model quality through BIC (model with the first order differential).

Number of Predictors	Model Verification Statistics		Ljung-Box Q			Number of Outliers
	Stationary R2	Normalized BIC	Statistics	DF	Sig.
4	0.196	8.046	25.118	18	0.122	0

Source: Authors’ compilation.

).

The assumption of residual independence was satisfied by the first order differential static regression model (Figure 5). Failure of the static regression model without transformation to satisfy the given assumption provided additional support for the superior quality of the new model.

The explanatory variables included in the first order differential static regression model are deemed statistically significant due to the fact that the p-values associated with their coefficients are less than the predetermined significance level of 5%.

Table 11. Statistical significance of variables in the resulting static regression model.

				Estimate	St. dev.	t	Sig.
Value of S&P 500-Model 1	The value of the S&P 500 index	No change	Constant	33.241	23.363	1.423	0.157
			Differentiation	1	-	-	-
	Unemployment rate	No change	Lag 0	11.147	3.652	3.053	0.003
	Inflation rate	No change	Lag 0	−9.141	4.428	−2.065	0.041
	Interest rate	No change	Lag 0	20.207	9.304	2.172	0.032
	Volatility index	No change	Lag 0	−4.641	0.852	−5.449	0.000

Source: Authors’ compilation.

presents the coefficients of the variables utilized in the static regression model. The following formula represents the resultant equation of the static regression model transformed by the first order differential:

$$\begin{array}{ll}The& difference between the value of the S\&P 500 index at time t and at time{ t}_{-1}=\\ & 33.241+11.147·unemployment rate -9.141·inflation rate +20.207·\\ & interest rate-4641·volatility index.\end{array}$$

The interpretation of the static regression model that is obtained is as follows: A marginal increase of 1% in the unemployment rate results in an average monthly change of USD 11.15 in the value of the S&P 500. A 1% increase in the inflation rate results in a USD 9.14 average decrease in the monthly change in the value of the S&P 500 index. The value of the S&P 500 stock index will increase by an average of USD 20.21 per month if the interest rate increases by 1%. A USD 1 increase in the volatility index value, all else being equal, will result in an average monthly decrease of USD 4.64 in the change of value of the S&P 500 stock index. Based on these results, it can be deduced that the interest rate increase has the most significant impact on the monthly value growth of the S&P 500 index. The inflation rate increase has the greatest impact on the monthly decline in the value of the S&P 500 index.

As seen in Figure 6, the developed static regression model shows minimal discrepancies in its predictions of the real values of the S&P 500 index.

Following this, the objective of this paper was to investigate whether the explanatory variables influence the S&P 500 index value with a specified time lag. An autoregressive model was used to proceed further in this analysis. Initially, the order of the autoregressive function was ascertained by employing the partial autocorrelation function illustrated in Figure 7. This function represents the relationship between the time series and its lags after removing the influence of lower order autocorrelation. Based on the partial autocorrelation function, it is possible to conclude that the correlation between the time series representing the S&P 500 index value and its lag is not statistically significant; thus, developing an autoregressive model is illogical.

The p-values necessary to ascertain the statistical significance of specific time series lags are presented in

Table 12. Statistical significance of specific time-series lags.

					Estimate	St. dev.	t	Sig.
Value of S&P 500-Model 1	The value of the S&P 500 index	No change	Constant		173.822	41.662	4.172	0.000
			AR	Lag 1	−0.121	0.096	−1.264	0.209
				Lag 2	−0.236	0.097	−2.419	0.017
				Lag 3	−0.241	0.098	−2.452	0.016
				Lag 4	−0.247	0.100	−2.481	0.015
				Lag 5	0.085	0.099	0.859	0.392
				Lag 6	−0.224	0.102	−2.193	0.031
			Differentiation		1	-	-	-

Source: Authors’ compilation.

. The p-values associated with the lags of 1 and 5 periods are not statistically significant. As a result, the conclusions drawn from the partial autocorrelation function are validated.

Despite developing a fourth order autoregressive model, the issue of statistical insignificance associated with a one-period lag remained unsolved (

Table 13. Statistical significance of lags.

					Estimate	St. dev.	t	Sig.
Value of S&P 500-Model 1	The value of the S&P 500 index	No change	Constant		188.676	44.064	4.282	0.000
			AR	Lag 1	−0.158	0.096	−1.646	0.103
				Lag 2	−0.202	0.096	−2.100	0.038
				Lag 3	−0.214	0.096	−2.225	0.028
				Lag 4	−0.203	0.099	−2.053	0.042
			Differentiation		1	-	-	-

Source: Authors’ compilation.

). It can be concluded that the correlation between the time series and its time lags is statistically insignificant based on the information presented above.

The findings of the statistical analyses hold potential value not only for professional investors but also for stakeholders, investors, and economists, for whom comprehending the interrelationships between macroeconomic development and the evolution of financial markets is of equal significance. The application of modern statistical tools, methods, tests, and models enables the comprehension of the relationship and the influence between exogenous factors and the S&P 500.

The results of the modelling are further used as a forecast for the forthcoming half-year, specifically from January to June 2020. Because the months of February and March 2020 were substantially impacted by the COVID-19 pandemic, which caused unanticipated volatility in the financial markets, the authors opted for a six-month forecast (Kotu and Deshpande 2019; Yilmazkuday 2023; Chebbi et al. 2021). The developed static regression model cannot reflect unpredictable influences, such as the COVID-19 pandemic, in the predicted development external, which led to significant deviations between the prediction and the real development of the S&P 500 stock index, especially in the months of February and March 2020. The impact of the COVID-19 pandemic on stock liquidity in 2020 was proved by several studies (Chan et al. 2021; Lucio and Caiado 2022; Pekar et al. 2022), which enable important stock market participants to identify and predict how stock liquidity may behave during pandemic illness times and which factors (exchange rates, gold returns) may have the most prominent influence on the S&P 500 return in the recovery period (Pekar et al. 2022; Lento and Gradojevic 2021).

The inflation rate, unemployment rate, interest rate, and volatility index were identified by the static regression model as the primary exogenous external factors influencing the profitability of the S&P 500 stock index. The importance of these exogenous factors is also depicted by Hu et al. (2018), who claim that the dollar index, interest rate, unemployment rate, and volatility index have substantial explanatory capacity for predicting the S&P 500 rate of return. Simultaneously, the model validated the outcomes of the initial analysis, which indicated that the profitability of the S&P 500 stock index remains unaffected by the month. According to the static regression model that was developed, the value of the S&P 500 index is most significantly impacted by the increase in interest rates. The most pronounced effect of the S&P 500 index decline is the expansion of the unemployment rate. Nonetheless, investors need to consider the anticipated developments of the unemployment rate (Hu et al. 2018; Jiao and Ye 2022), interest rate (Bhar et al. 2015; Fougue and Saporito 2018), inflation rate (Pineiro-Chousa et al. 2018; Golitsis et al. 2022; Soydemir et al. 2017), and volatility index (Belas and Rahman 2023; Boateng et al. 2022; Biardi et al. 2020), when deciding whether to invest in the S&P 500 stock index as also confirmed by the specified studies. Moreover, investors should also access the historical data, trading volumes, and some other relevant market indicators, e.g., evaluate the risk characteristics of the active strategy compared to the passive index. This could involve analyzing metrics such as volatility, drawdowns, and downside risk. Nonetheless, based on further empirical analysis, which is an important research challenge, it would be possible to draw conclusions about whether the active investor can achieve economically and statistically significant out-of-sample outperformance compared with the passive index.

The predicted price movement of the S&P 500 stock index for the upcoming half-year, specifically from January to June 2020, is illustrated in Figure 8. Lower Control Limit (LCL) and Upper Control Limit (UCL) curves, denoted by dashed lines, depict the upper and lower limits of the confidence interval that specifies the probability that the true values are contained within a particular range. A deviation of the S&P 500 real value from the confidence interval may suggest an atypical or exceptional price movement of the index.

The real and predicted values of the S&P 500 stock index for the period January to June 2020 are presented in

Table 14. Real and predicted values of the S&P 500 stock index.

	January 2020	February 2020	March 2020	April 2020	May 2020	June 2020
Real value	3225.52	2954.22	2584.59	2912.43	3044.31	3100.29
Predicted value	3223.87	3120.87	2954.09	2990.97	3042.85	3052.69
Difference	1.65	−166.65	−369.50	−78.54	1.46	47.60
UCL	3324.59	3263.31	3128.55	3192.41	3268.07	3299.41
LCL	3123.14	2978.43	2779.64	2789.52	2817.63	2805.97

Source: Authors’ compilation.

. The table also includes the lower and upper limits of the confidence interval. March 2020 witnessed the largest discrepancy between the anticipated and real values of the S&P 500 stock index. The difference between the real and predicted values of the S&P 500 stock index was USD −369.50. A possible contributor to the substantial discrepancy between the predicted and real values is the World Health Organization’s (WHO) official declaration that COVID-19 is a pandemic. This statement incited widespread concern about global financial markets, leading to a substantial decline in the price movement of financial instruments, including stock indices (Zhang et al. 2020; Harjoto and Rossi 2021; Orhun 2021; Handoyo et al. 2022). The S&P 500 recorded a real value of USD 2584.59 in March 2020, significantly falling short of the lower limit of the confidence interval of USD 2779.64. This observation suggests that the manner in which the S&P 500 index’s prices evolved during this time period was quite peculiar. However, these outputs are confirmed by several other studies (Dias et al. 2020; John and Li 2021; Rahman et al. 2021) that also claim an inevitable impact of the COVID-19 pandemic on capital markets. The months of January and May in 2020 exhibited the least disparity of USD 1.65 and USD 1.46 between the real and predicted values of the S&P 500 index. The months of February and March 2020 were the most adversely affected by the COVID-19 pandemic on the price development of the S&P 500 index. This is further supported by the fact that the index reached values below the lower limit of the confidence interval during those months. Moreover, the investigation of the effects of the COVID-19 pandemic on the S&P 500 index proved that the negatives were mostly observed in March 2020 (Fiszeder and Malecka 2022; Jackwerth 2021; Choi 2022).

An examination of the discrepancy between the real and predicted values of the S&P 500 stock index revealed that forecasting the price movement of stocks or the index itself is susceptible to a multitude of unforeseeable variables, including the COVID-19 pandemic (or any other crisis), which are not amenable to incorporation into the prediction model (Akhtaruzzaman et al. 2021). One potential strategy for mitigating adverse and unforeseeable external factors that may impact investments is to allocate funds across a variety of investment instrument categories, for instance, to gold, 30-year US bonds, and/or bitcoin cryptocurrency. Kang et al. (2020) revealed a dynamic equicorrelation connection between bitcoin and four important financial assets: S&P 500, US dollars, Treasury bonds, and gold futures. There is an uneven causal relationship between bitcoin and other asset classes, according to their empirical research, which underlines and confirms the outputs of the current analysis. The findings of Doumenis et al. (2021) show that the price volatility of bitcoin and the other three financial assets both before and after COVID-19 have a positive correlation. Therefore, rather than functioning as a reliable store of value, bitcoin is more of a speculative asset; moreover, it has no correlation with the 30-year US debts. The potential influence of these factors on the development of the S&P 500 index is also discussed in other international studies (Aboura 2022; Yao et al. 2023; Kliber 2022). It is evident that there is no evidence to support the existence of a linear relationship between the returns of the S&P 500 stock index and those of gold and 30-year US government bonds (Ghazali et al. 2020). Given the absence of any discernible linear dependence among these alternative investment instruments, it is possible to assert that they constitute viable assets for investors seeking to enhance the diversification of a portfolio that includes the S&P 500 stock index.

5. Conclusions

The S&P 500 index plays a crucial role in global financial markets, serving as a barometer of the US economy’s health and providing investors with a widely recognized benchmark for evaluating investment performance. Given its prominence, movements in the S&P 500 often have ripple effects across global financial markets. Changes in the index can influence investor sentiment and trading activity worldwide. The S&P 500 experienced its significant decline during the financial and economic crisis of 2007–2008, but the worst one happened in 2020 (and partly in 2021) during the COVID-19 pandemic. The S&P 500 showed significant volatility during both crises, which was caused by a complicated interaction of external causes. In the case of the COVID-19 pandemic, strict lockdown protocols and disturbances in international supply networks, instigated by endeavors to impede the virus’s proliferation, resulted in a noteworthy downturn in economic operations, affecting many sectors included in the index. Interest rate reductions and loose monetary policy were hallmarks of central bank interventions intended to bring liquidity and stability to the financial markets. Government fiscal stimulus plans aimed to assist individuals and companies while also reducing economic downturns. An important factor was the mood of investors, as elevated levels of anxiety and uncertainty led to higher market volatility and sudden changes in risk appetite. Therefore, in order to comprehend the differences in predictabilities between these established capital markets, both European and non-European, it is interesting to monitor the evolution of this index, its modifications, and its influence. This complex environment emphasizes how important it is to have a thorough grasp of economic, financial, and public health aspects while evaluating the dynamics of the S&P 500, especially during crises and recessions.

The impact of exogenous factors on the S&P 500 index is not static, but it is subject to constant changes, which require continuous adaptation of statistical methods, input factors, and analytical approaches in order to respond effectively to the changing conditions of the financial environment. Given the constantly changing conditions in financial markets and the complexity of the relationships between individual exogenous factors, it is recommended that institutional and retail investors apply flexible approaches to investments and constantly update their investment strategies and models. Partial statistical analysis shows that a combination of statistical methods and systematic analysis of exogenous factors is essential for a better understanding of market dynamics and the development of the S&P 500 index. In today’s globalized and interconnected economies, it is important to consider not only national but also international influences, such as the COVID-19 pandemic, or other crisis and market deficiencies, which can significantly affect the development of the S&P 500 index. The impact of the COVID-19 pandemic on the price development of the S&P 500 index was demonstrated using a prediction and its subsequent comparison with the real price development of the index. The results of the comparison pointed to the fact that the COVID-19 pandemic most significantly affected the development of the S&P 500 index in the months of February and March 2020. The practical implications of the findings extend beyond investment strategy formulation to encompass portfolio construction and risk management, and confirm that, by considering the impact of exogenous factors on the S&P 500’s profitability, organizations can develop more robust investment strategies, asset allocation plans, and risk management frameworks to navigate changing market conditions effectively. The research findings can also have implications for policymakers and regulators. Understanding how exogenous factors impact S&P 500’s profitability can inform policy decisions related to financial market regulations, economic interventions, and macroeconomic stability. Policymakers can use this information to design policies that support market efficiency and stability. Nevertheless, the degree of limitations and unpredictability that are inherent to forecasts in the realm of financial markets must be given due consideration.

The authors intend to direct their future research efforts towards examining long-term trends, delving into more specific influences, and conducting an analysis of the impact that exchange rate fluctuations have on the price evolution of the index. This research output can be used as a starting point for further studies aimed at deepening our understanding of the functioning of financial markets and contributing to the development of more effective investment decision-making strategies.