Critical Overview of Visual Tracking with Kernel Correlation Filter
Abstract
:1. Introduction
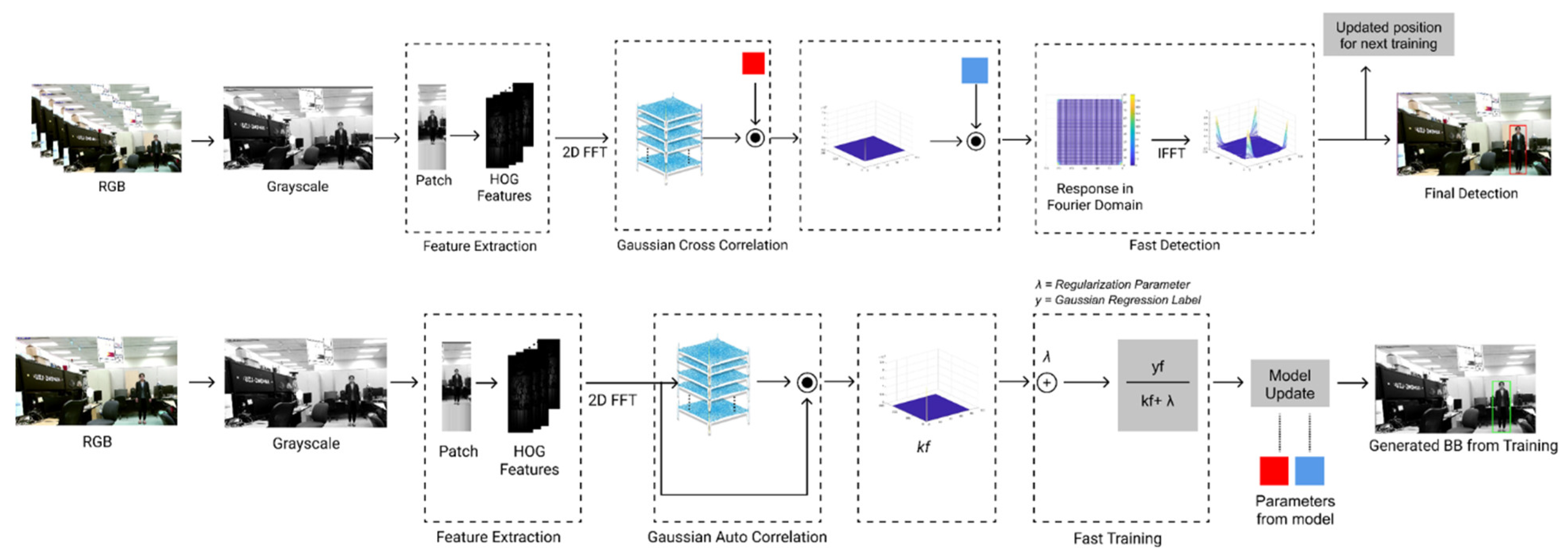
2. An Overview of KCF
3. Mathematical Exposition of KCF
4. KCF Tracker Pipeline and Dataset
5. Results of Performance Analysis Using Experimental Dataset
5.1. Center Error
5.2. Intersection of Union
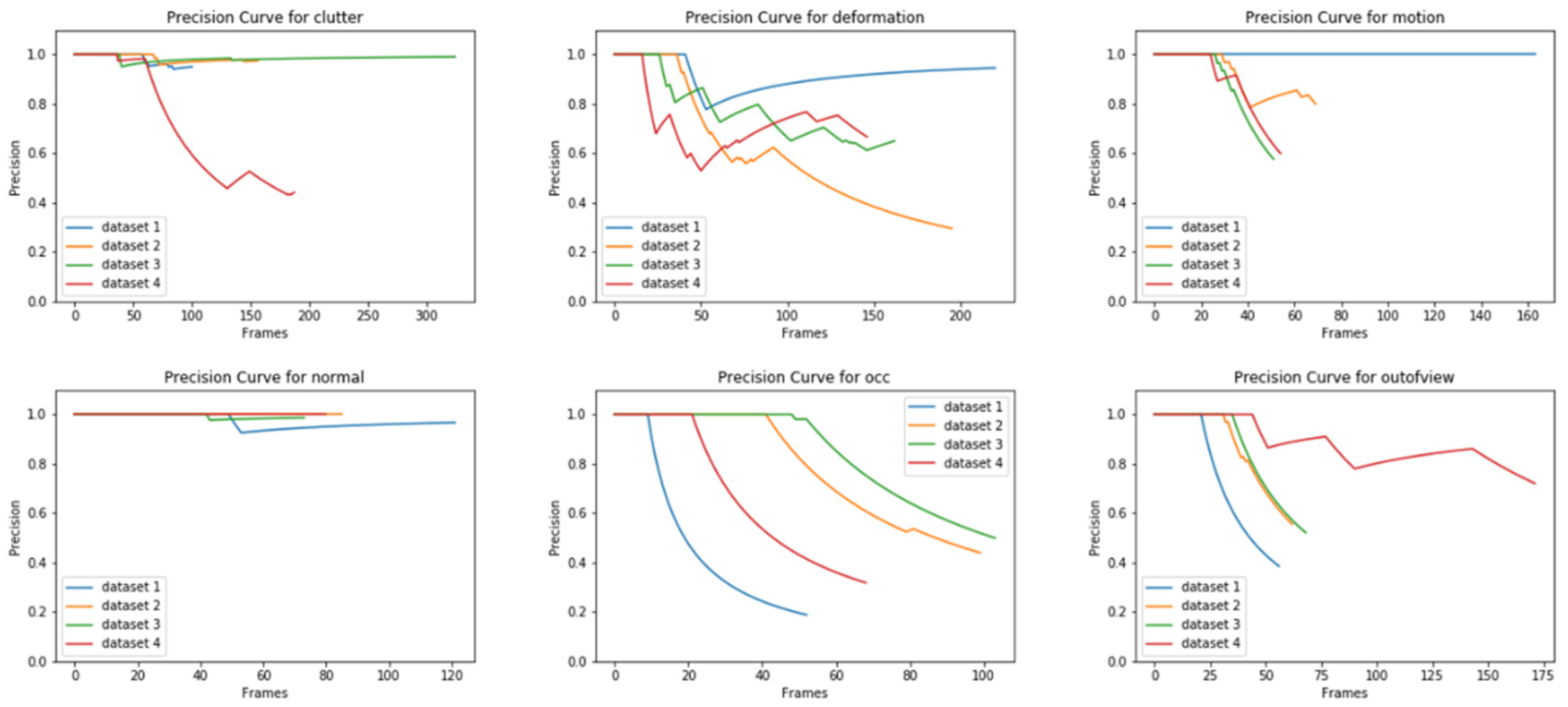
5.3. Precision Curve
6. Results of Performance Analysis Using Public Benchmark
6.1. OTB-50 Benchmark Analysis
6.2. VOT 2015 Performance Analysis
6.3. VOT 2019 Performance Analysis
7. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Consent for Publication
Abbreviations
| ROI | Region of Interest |
| HOG | Histogram of Gradient |
| KCF | Kernelized Correlation Filter |
| CF | Correlation Filter |
| FPS | Frame Per Second |
| CFT | Correlation Filter Tracker |
| BCCM | Block-Circulant Circulant Matrix |
| LRR | Linear Ridge Regression |
| IoU | Intersection of Union |
| TP | True Positive |
| FP | False Positive |
| TN | True Negative |
| FN | False Negative |
| IV | Illumination Variation |
| SV | Scale Variation |
| OCC | Occlusion |
| DEF | Deformation |
| MB | Motion Blur |
| FM | Fast Motion |
| IPR | In-Plane Rotation |
| OPR | Out-of-Plane Rotation |
| OV | Out-of-View |
| BC | Background Clutter |
| LR | Low Resolution |
| SR | Success Rate |
| CNN | Convolution Neural Network |
Appendix A
Dual form of Ridge Regression
References
- Mei, X.; Ling, H. Robust Visual Tracking Using L1 Minimization. In Proceedings of the 2009 IEEE 12th International Conference on Computer Vision, Kyoto, Japan, 29 September–2 October 2009. [Google Scholar]
- Hager, G.D.; Dewan, M.; Stewart, C.V. Multiple Kernel Tracking with SSD. In Proceedings of the 2004 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, (CVPR 2004), Washington, DC, USA, 27 June–2 July 2004. [Google Scholar]
- Parameswaran, V.; Ramesh, V.; Zoghlami, I. Tunable Kernels for Tracking. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR’06), New York, NY, USA, 17–22 June 2006. [Google Scholar]
- Elgammal, A.; Duraiswami, R.; Davis, L.S. Probabilistic Tracking in Joint Feature-Spatial Spaces. In Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, WI, USA, 18–20 June 2003. [Google Scholar]
- Viola, P.; Wells, W.M., III. Alignment by Maximization of Mutual Information PAUL. Int. J. Comput. Vis. 1997, 24, 137–154. [Google Scholar] [CrossRef]
- Bolme, D.S.; Beveridge, J.R.; Draper, B.A.; Lui, Y.M. Visual Object Tracking Using Adaptive Correlation Filters. In Proceedings of the 2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Francisco, CA, USA, 13–18 June 2010. [Google Scholar]
- Chen, Z.; Hong, Z.; Tao, D. An Experimental Survey on Correlation Filter-Based Tracking. arXiv 2015, arXiv:1509.05520. [Google Scholar]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. High-Speed Tracking with Kernelized Correlation Filters. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 37, 583–596. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yang, M.; Jia, Y. Temporal dynamic appearance modeling for online multi-person tracking. Comput. Vis. Image Underst. 2016, 153, 16–28. [Google Scholar] [CrossRef] [Green Version]
- Xiang, Y.; Alahi, A.; Savarese, S. Learning to Track: Online Multi-Object Tracking by Decision Making. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Pirsiavash, H.; Ramanan, D.; Fowlkes, C.C. Globally-Optimal Greedy Algorithms for Tracking a Variable Number of Objects. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Colorado Springs, CO, USA, 20–25 June 2011. [Google Scholar]
- Choi, W. Near-Online Multi-Target Tracking with Aggregated Local Flow Descriptor. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Yadav, S.; Payandeh, S. Understanding Tracking Methodology of Kernelized Correlation Filter. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON 2018), Vancouver, BC, Canada, 1–3 November 2018; pp. 1330–1336. [Google Scholar]
- Yadav, S.; Payandeh, S. Real-Time Experimental Study of Kernelized Correlation Filter Tracker Using RGB Kinect Camera. In Proceedings of the 2018 IEEE 9th Annual Information Technology, Electronics and Mobile Communication Conference (IEMCON 2018), Vancouver, BC, Canada, 1–3 November 2018; pp. 1324–1329. [Google Scholar]
- Smeulders, A.W.M.; Chu, D.M.; Cucchiara, R.; Calderara, S.; Dehghan, A.; Shah, M. Visual Tracking: An Experimental Survey. IEEE Trans. Pattern Anal. Mach. Intell. 2014, 36, 1442–1468. [Google Scholar]
- Liu, S.; Liu, D.; Srivastava, G.; Połap, D.; Woźniak, M. Overview and methods of correlation filter algorithms in object tracking. Complex Intell. Syst. 2020, 1–23. [Google Scholar] [CrossRef]
- Babenko, B.; Yang, M.-H.; Belongie, S. Robust Object Tracking with Online Multiple Instance Learning. IEEE Trans. Pattern Anal. Mach. Intell. 2011, 33, 1619–1632. [Google Scholar] [CrossRef] [Green Version]
- Henriques, J.F.; Caseiro, R.; Martins, P.; Batista, J. Exploiting the Circulant Structure of Tracking-by-Detection with Kernels. In Proceedings of the European Conference on Computer Vision, Florence, Italy, 7–13 October 2012; pp. 702–715. [Google Scholar]
- Cortes, C.; Vapnik, V. Support Vector Network. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Galoogahi, H.K.; Sim, T.; Lucey, S. Multi-Channel Correlation Filters. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Sydney, Australia, 1–8 December 2013. [Google Scholar]
- Cotter, A.; Keshet, J.; Srebro, N. Explicit Approximations of the Gaussian Kernel. arXiv 2011, arXiv:1109.4603. [Google Scholar]
- Cehovin, L.; Leonardis, A.; Kristan, M. Visual object tracking performance measures revisited. IEEE Trans. Image Process. 2016, 25, 1261–1274. [Google Scholar] [CrossRef] [Green Version]
- Wang, D.; Lu, H.; Yang, M.-H. Online Object Tracking with Sparse Prototypes. IEEE Trans. Image Process. 2012, 22, 314–325. [Google Scholar] [CrossRef] [Green Version]
- Yang, F.; Lu, H.; Yang, M.-H. Robust Superpixel Tracking. IEEE Trans. Image Process. 2014, 23, 1639–1651. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Wu, Y.; Lim, J.; Yang, M.-H. Object Tracking Benchmark. IEEE Trans. Pattern Anal. Mach. Intell. 2015, 37, 1834–1848. [Google Scholar] [CrossRef] [Green Version]
- Danelljan, M.; Häger, G.; Khan, F.S.; Felsberg, M. Accurate Scale Estimation for Robust Visual Tracking. In Proceedings of the British Machine Vision Conference 2014 (BMVC 2014), Nottingham, UK, 1–5 September 2014. [Google Scholar]
- Kalal, Z.; Mikolajczyk, K.; Matas, J. Tracking-Learning-Detection. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 34, 1409–1422. [Google Scholar] [CrossRef] [Green Version]
- Hare, S.; Golodetz, S.; Saffari, A.; Vineet, V.; Cheng, M.-M.; Hicks, S.L.; Torr, P.H.S. Struck: Structured Output Tracking with Kernels. IEEE Trans. Pattern Anal. Mach. Intell. 2016, 38, 2096–2109. [Google Scholar] [CrossRef] [Green Version]
- Xu, G.; Zhu, H.; Deng, L.; Han, L.; Li, Y.; Lu, H. Dilated-aware discriminative correlation filter for visual tracking. World Wide Web 2019, 22, 791–805. [Google Scholar] [CrossRef]
- Li, Y.; Zhu, J. A Scale Adaptive Kernel Correlation Filter Tracker with Feature Integration. In Computer Vision—ECCV 2014 Workshops; Lecture Notes in Computer Science (Including Subser. Lect. Notes Artif. Intell. Lect. Notes Bioinformatics); Springer: Cham, Switzerland, 2015; Volume 8926, pp. 254–265. [Google Scholar]
- Qu, L.; Liu, K.; Yao, B.; Tang, J.; Zhang, W. Real-time visual tracking with ELM augmented adaptive correlation filter. Pattern Recognit. Lett. 2018, 127, 138–145. [Google Scholar] [CrossRef]
- Choi, J.; Chang, H.J.; Yun, S.; Fischer, T.; Demiris, Y.; Choi, J.Y. Attentional Correlation Filter Network for Adaptive Visual Tracking. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2017, Las Vegas, NV, USA, 27–30 June 2017; pp. 4828–4837. [Google Scholar]
- Wang, L.; Ouyang, W.; Wang, X.; Lu, H. Visual Tracking with Fully Convolutional Networks. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3119–3127. [Google Scholar]
- Fern, G.; Nebehay, G.; Pflugfelder, R.; Gupta, A.; Bibi, A. The Visual Object Tracking VOT2015 Challenge Results. In Proceedings of the IEEE International Conference on Computer Vision (ICCV) Workshops, Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Danelljan, M.; Hager, G.; Khan, F.S.; Felsberg, M. Learning Spatially Regularized Correlation Filters for Visual Tracking. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 4310–4318. [Google Scholar]
- Danelljan, M.; Hager, G.; Khan, F.S.; Felsberg, M. Convolutional Features for Correlation Filter Based Visual Tracking. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015. [Google Scholar]
- Cehovin, L.; Kristan, M.; Leonardis, A. Robust Visual Tracking Using an Adaptive Coupled-Layer Visual Model. IEEE Trans. Pattern Anal. Mach. Intell. 2012, 35, 941–953. [Google Scholar] [CrossRef] [PubMed]
- Tang, M.; Feng, J. Multi-Kernel Correlation Filter for Visual Tracking. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3038–3064. [Google Scholar]
- Mishra, D.; Matas, J. The Visual Object Tracking VOT2017 Challenge Results. In Proceedings of the IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 1949–1972. [Google Scholar]
- Lukežič, A.; Vojíř, T.; Zajc, L.Č.; Matas, J.; Kristan, M. Discriminative Correlation Filter with Channel and Spatial Reliability. In Proceedings of the 30th IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017. [Google Scholar]
- Danelljan, M.; Bhat, G.; Khan, S.; Felsberg, M.; Khan, F.S.; Felsberg, M. ECO: Efficient Convolution Operators for Tracking. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 6638–6646. [Google Scholar]
- Lukezic, A.; Zajc, L.C.; Kristan, M. Deformable Parts Correlation Filters for Robust Visual Tracking. IEEE Trans. Cybernetics. 2017, 48, 1849–1861. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rasoulidanesh, M.; Yadav, S.; Herath, S.; Vaghei, Y.; Payandeh, S. Deep Attention Models for Human Tracking Using RGBD. Sensors 2019, 19, 750. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Murahari, V.S.; Ploetz, T. On Attention Models for Human Activity Recognition. In Proceedings of the 2018 ACM International Symposium on Wearable Computers, Singapore, 8–12 October 2018. [Google Scholar]
- Ba, J.; Mnih, V.; Kavukcuoglu, K. Multiple Object Recognition with Visual Attention. arXiv 2014, arXiv:1412.7755. [Google Scholar]
- Song, S.; Xiao, J. Deep Sliding Shapes for Amodal 3D Object Detection in RGB-D Images. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 808–816. [Google Scholar]
- Boyd, S.; Boyd, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Schölkopf, B.; Herbrich, R.; Smola, A.J. A Generalized Representer Theorem. In Proceedings of the International Conference on Computational Learning Theory, Amsterdam, The Netherlands, 16–19 July 2001; pp. 416–426. [Google Scholar]
- Horn, R.A.; Johnson, C.R. Matrix Analysis; Cambridge University Press: Cambridge, UK, 2012. [Google Scholar]
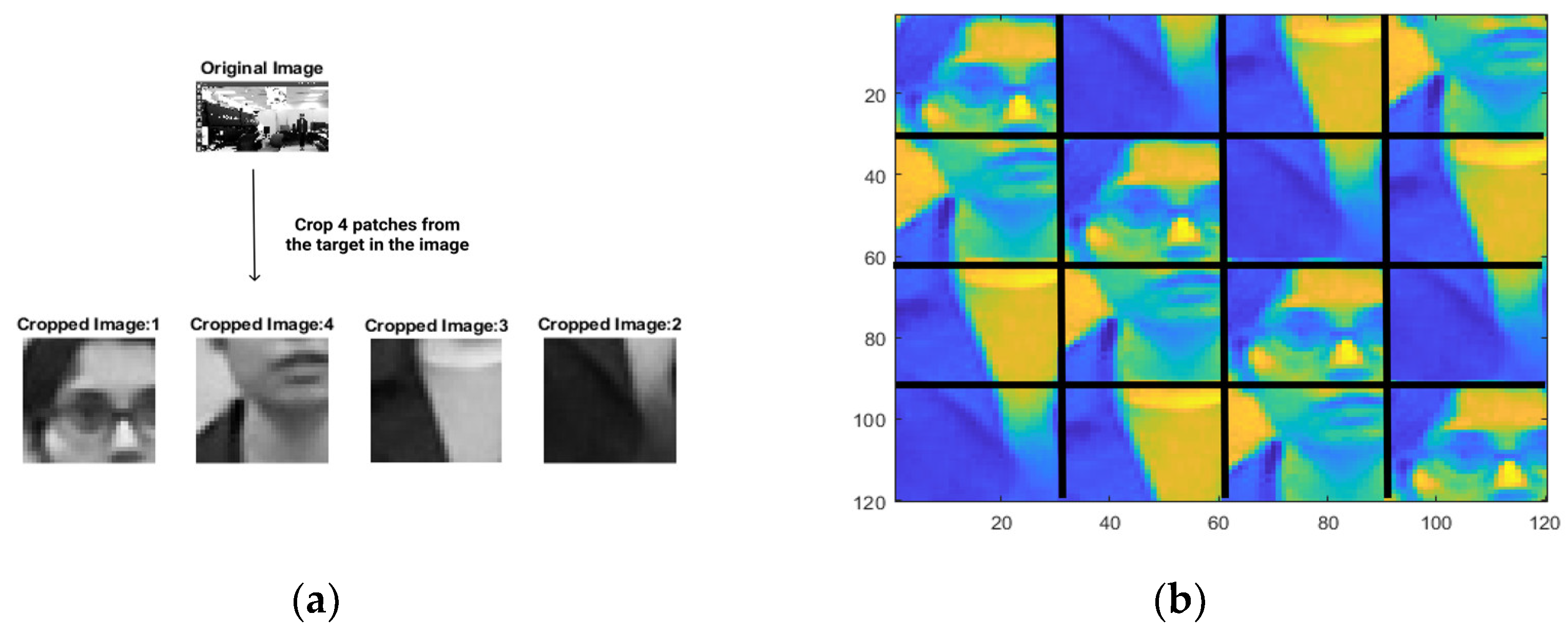
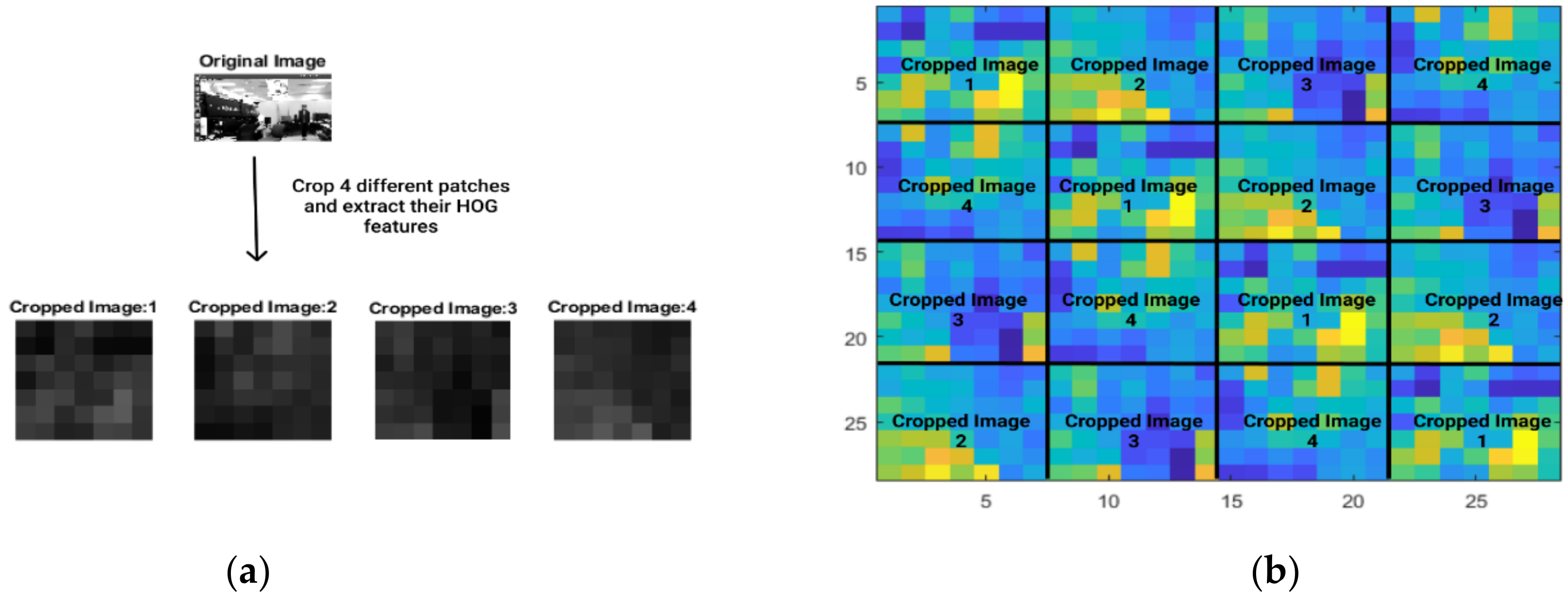








| Scenarios | Subjects | Data (No of Frames) |
|---|---|---|
| Clutter | 6 | 1677 |
| Deformation | 6 | 1494 |
| Normal | 6 | 900 |
| Occlusion | 6 | 663 |
| Motion | 6 | 784 |
| Out of view | 6 | 620 |
| Total | 6138 | |
| Clutter | Deformation | Motion | Normal | Occlusion | Out-of-View | |
|---|---|---|---|---|---|---|
| Dataset-1 | 0.9808 | 0.9168 | 1.0 | 0.9718 | 0.4958 | 0.7480 |
| Dataset-2 | 0.9841 | 0.6005 | 0.9123 | 1.0 | 0.7857 | 0.8717 |
| Dataset-3 | 0.9843 | 0.7731 | 0.8852 | 0.9927 | 0.8436 | 0.8577 |
| Dataset-4 | 0.7093 | 0.7274 | 0.8884 | 1.0 | 0.6784 | 0.8798 |
| Average | 0.9038 | 0.7544 | 0.9213 | 0.9911 | 0.7008 | 0.8393 |
| IV | IPR | LR | OCC | OPR | OV | SV | MB | FM | DEF | BC | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| ELMACF [31] | 55.7 | 59.1 | 38.1 | 62.5 | 62.2 | 51.3 | 52.8 | 58.1 | 54.0 | 64.0 | 59.6 |
| ACFN [32] | 55.7 | 56.5 | 35.2 | 60.4 | 60.0 | 62.4 | 59.2 | 52.1 | 52.7 | 63.2 | 54.6 |
| FCN [33] | 59.8 | 55.5 | 51.4 | 57.1 | 58.1 | 59.2 | 55.8 | 58.0 | 56.5 | 64.4 | 56.4 |
| DDCF [29] | 63.8 | 48.8 | 44.8 | 44.4 | 46.1 | 44.3 | 48.3 | 53.3 | 52.3 | 41.2 | 54.5 |
| SAMF [30] | 46.3 | 45.8 | 44.0 | 47.8 | 48.1 | 39.5 | 44.6 | 44.0 | 42.8 | 44.0 | 43.8 |
| DSST [26] | 51.7 | 44.0 | 37.3 | 43.2 | 40.2 | 32.3 | 41.7 | 40.5 | 36.6 | 40.9 | 49.1 |
| KCF [8] | 43.3 | 38.9 | 28.5 | 39.6 | 39.6 | 32.7 | 35.3 | 40.8 | 38.9 | 40.0 | 41.7 |
| Struck [28] | 33.0 | 37.6 | 31.9 | 33.2 | 33.5 | 32.7 | 35.9 | 39.9 | 40.4 | 32.3 | 35.6 |
| Tracker | Accuracy | Robustness | Speed |
|---|---|---|---|
| RAJSSC [34] | 0.57 | 1.63 | 2.12 |
| SRDCF [35] | 0.56 | 1.24 | 1.99 |
| DeepSRDCF [36] | 0.56 | 1.05 | 0.38 |
| NSAMF [34] | 0.53 | 1.29 | 5.47 |
| MKCF+ [38] | 0.52 | 1.83 | 0.21 |
| MvCFT [34] | 0.52 | 1.72 | 2.24 |
| LDP [37] | 0.51 | 1.84 | 4.36 |
| KCFDP [34] | 0.49 | 2.34 | 4.80 |
| MTSA-KCF [34] | 0.49 | 2.29 | 2.83 |
| sKCF [34] | 0.48 | 2.68 | 66.22 |
| KCF2 [34] | 0.48 | 2.17 | 4.60 |
| KCFv2 [34] | 0.48 | 1.95 | 10.90 |
| Baseline | Real-Time | |||||
|---|---|---|---|---|---|---|
| EOA | A | R | EOA | A | R | |
| LSRDFT [39] | 0.317 | 0.531 | 0.312 | 0.087 | 0.455 | 1.741 |
| TDE [39] | 0.256 | 0.534 | 0.465 | 0.086 | 0.308 | 1.274 |
| SSRCCOT [39] | 0.234 | 0.495 | 0.507 | 0.081 | 0.360 | 1.505 |
| CSRDCF [40] | 0.201 | 0.496 | 0.632 | 0.100 | 0.478 | 1.405 |
| CSRpp [39] | 0.187 | 0.468 | 0.662 | 0.172 | 0.468 | 0.727 |
| FSC2F [41] | 0.185 | 0.480 | 0.752 | 0.077 | 0.461 | 1.836 |
| M2C2F [41] | 0.177 | 0.486 | 0.747 | 0.068 | 0.424 | 1.896 |
| TCLCF [39] | 0.170 | 0.480 | 0.843 | 0.170 | 0.480 | 0.843 |
| WSCF-ST [39] | 0.162 | 0.534 | 0.963 | 0.160 | 0.532 | 0.968 |
| DPT [42] | 0.153 | 0.488 | 1.008 | 0.136 | 0.488 | 1.159 |
| CISRDCF [39] | 0.153 | 0.420 | 0.883 | 0.146 | 0.421 | 0.928 |
| KCF [8] | 0.110 | 0.441 | 1.279 | 0.108 | 0.440 | 1.294 |
| Struck [28] | 0.094 | 0.417 | 1.726 | 0.088 | 0.428 | 1.926 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yadav, S.; Payandeh, S. Critical Overview of Visual Tracking with Kernel Correlation Filter. Technologies 2021, 9, 93. https://doi.org/10.3390/technologies9040093
Yadav S, Payandeh S. Critical Overview of Visual Tracking with Kernel Correlation Filter. Technologies. 2021; 9(4):93. https://doi.org/10.3390/technologies9040093
Chicago/Turabian StyleYadav, Srishti, and Shahram Payandeh. 2021. "Critical Overview of Visual Tracking with Kernel Correlation Filter" Technologies 9, no. 4: 93. https://doi.org/10.3390/technologies9040093
APA StyleYadav, S., & Payandeh, S. (2021). Critical Overview of Visual Tracking with Kernel Correlation Filter. Technologies, 9(4), 93. https://doi.org/10.3390/technologies9040093






