Incremental Lagrangian Relaxation Based Discrete Gate Sizing and Threshold Voltage Assignment †
Abstract
:1. Introduction
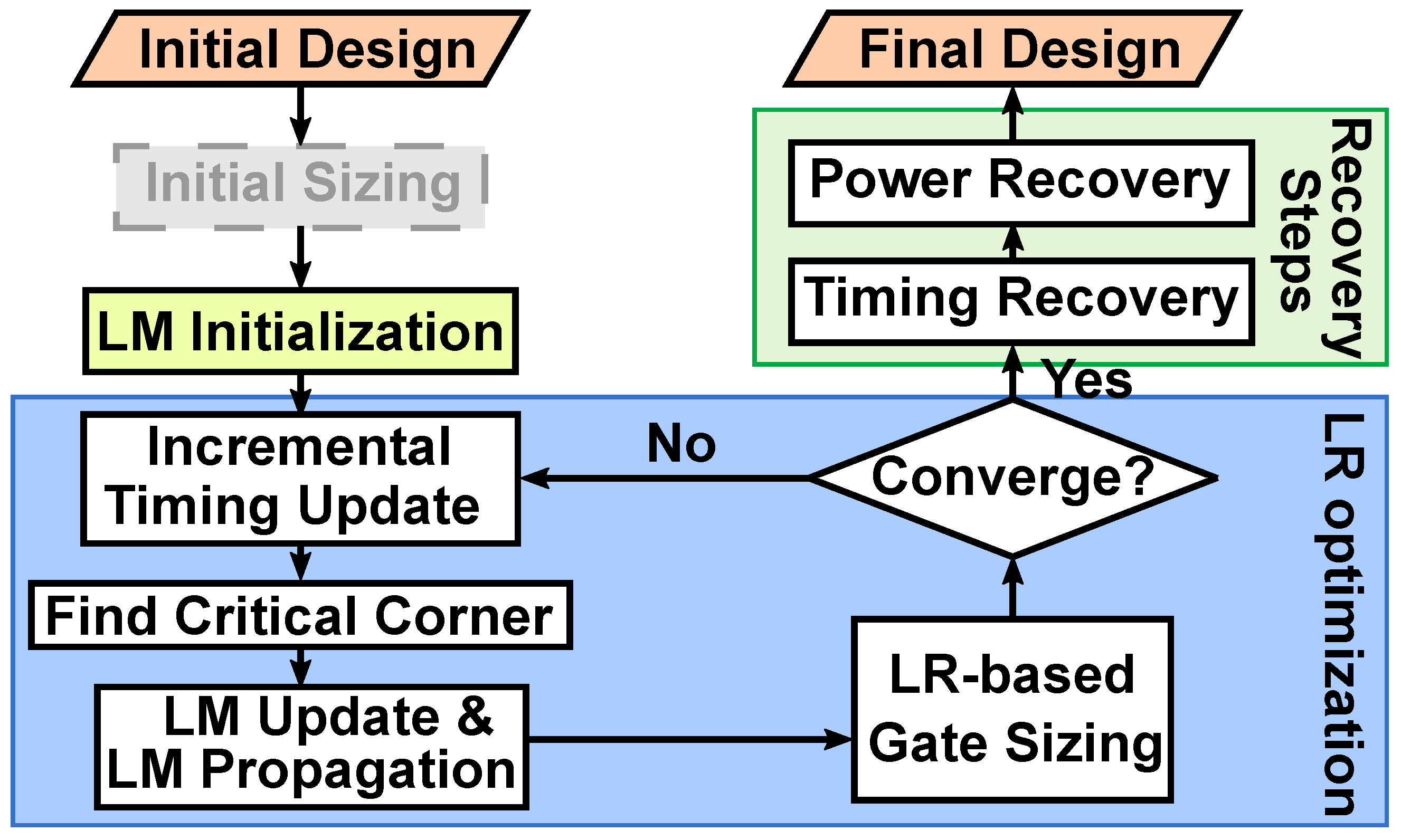
2. Basics of LR-Based Gate Sizing
| Algorithm 1: Find best size for gate g. |
 |
3. Incremental LR-Based Gate Sizing
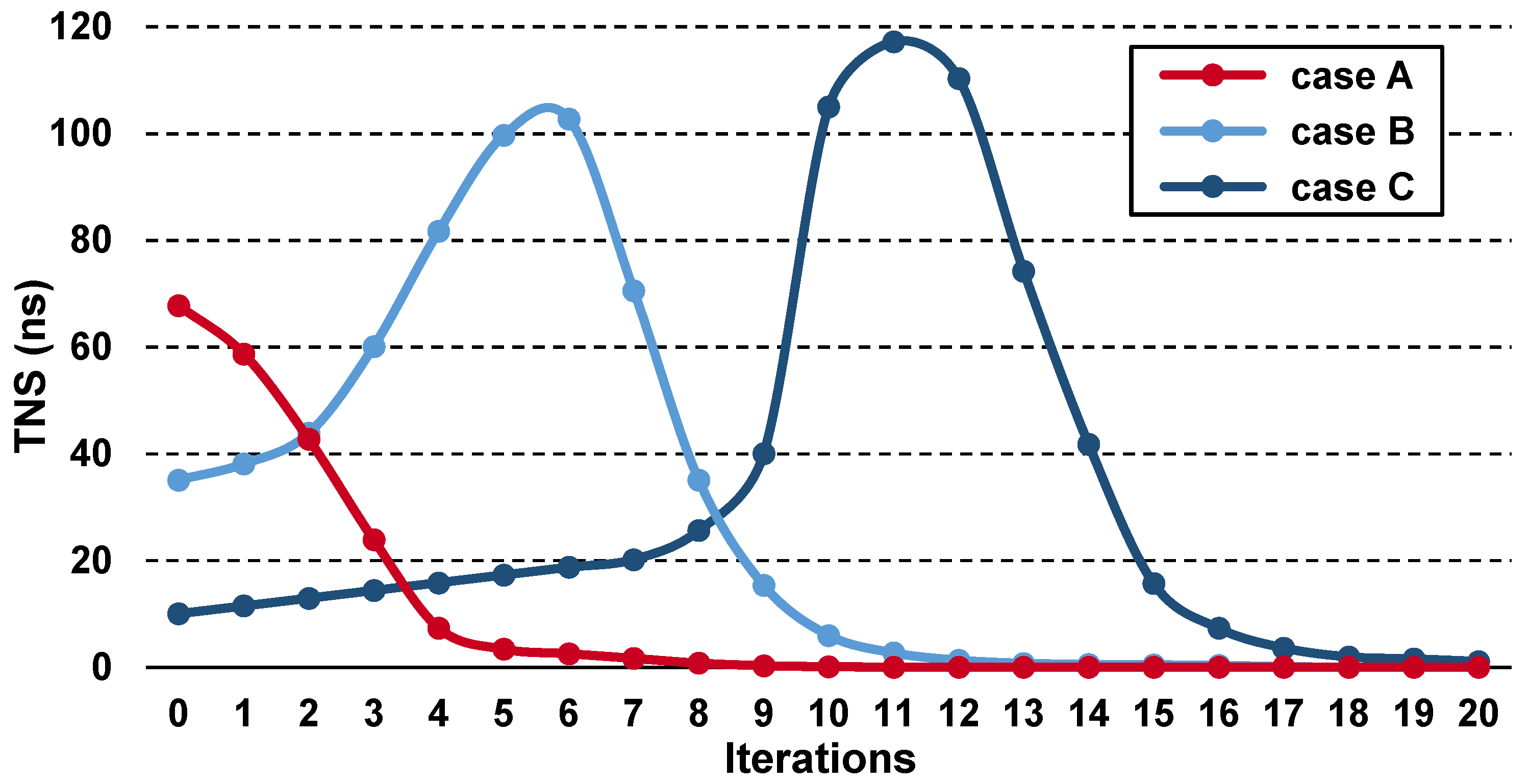
3.1. What Is the Problem?
3.2. What Can We Do about It?
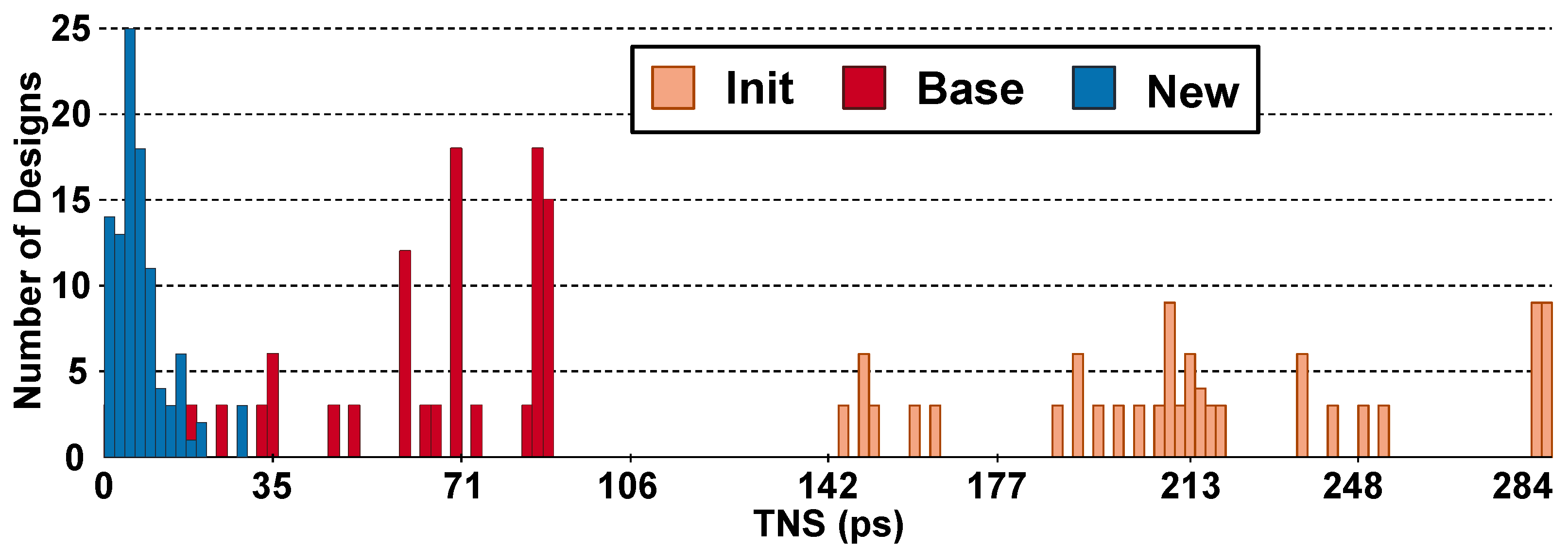
4. Results
4.1. Quality-of-Results and Runtime Comparisons
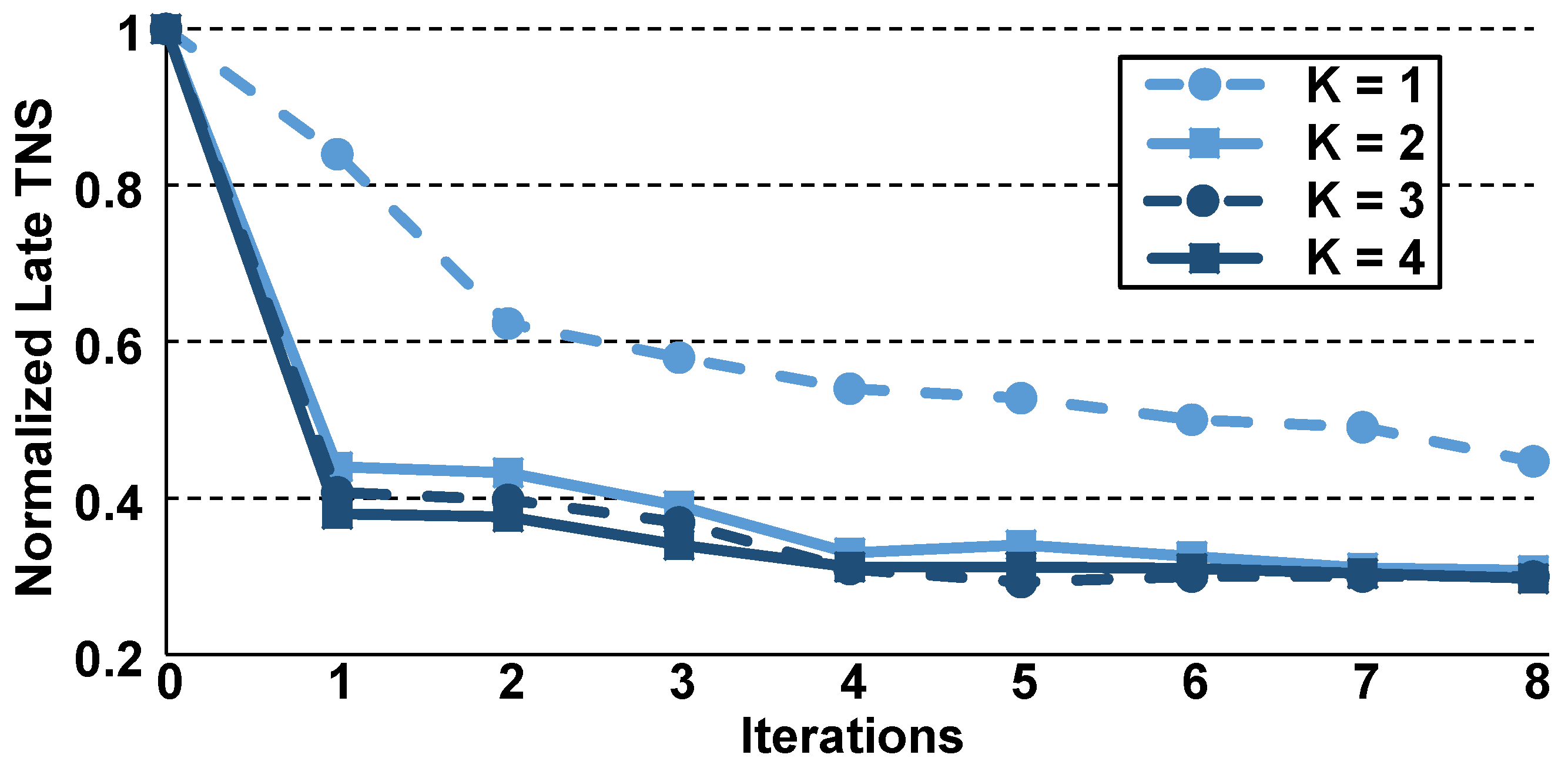
4.2. Exploring in Depth the Proposed LM Initialization
4.3. Optimization with a Restricted Number of Available Gate Sizes
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lavagno, L.; Martin, G.; Markov, I.L.; Scheffer, L.K. Electronic Design Automation for IC Implementation, Circuit Design, and Process Technology; Taylor and Francis Group: Boca Raton, FL, USA, 2016. [Google Scholar]
- Liu, Y.; Hu, J.; Shi, W. Multi-Scenario Buffer Insertion in Multi-Core Processor Designs. In Proceedings of the 2008 International Symposium on Physical Design, Portland, OR, USA, 13–16 April 2008; pp. 15–22. [Google Scholar]
- Roy, S.; Liu, D.; Um, J.; Pan, D.Z. OSFA: A new paradigm of gate-sizing for power/performance optimizations under multiple operating conditions. In Proceedings of the Design Automation Conference (DAC), San Francisco, CA, USA, 8–12 June 2015; pp. 1–6. [Google Scholar]
- MacDonald, N.D. Timing Closure in Deep Submicron Designs. In Proceedings of the Design Automation Conference (DAC), Anaheim, CA, USA, 13–18 July 2010. [Google Scholar]
- Chinnery, D.G.; Keutzer, K. Linear Programming for Sizing, Vth and Vdd Assignment. In Proceedings of the International Symposium on Low Power Electronics and Design (ISLPED), San Diego, CA, USA, 8–10 August 2005; pp. 149–154. [Google Scholar]
- Spindler, P.; Schlichtmann, U.; Johannes, F.M. Abacus: Fast legalization of standard cell circuits with minimal movement. In Proceedings of the International Symposium on Physical Design (ISPD), Portland, OR, USA, 13–16 April 2008; pp. 47–53. [Google Scholar]
- Puget, J.C.; Flach, G.; Reis, R.; Johann, M. Jezz: An effective legalization algorithm for minimum displacement. In Proceedings of the Symposium on Integrated Circuits and Systems Design (SBCCI), Salvador, Brazil, 31 August–4 September 2015; pp. 1–5. [Google Scholar]
- Chowdhary, A.; Rajagopal, K.; Venkatesan, S.; Cao, T.; Tiourin, V.; Parasuram, Y.; Halpin, B. How Accurately Can We Model Timing in a Placement Engine? In Proceedings of the ACM/IEEE Design Automation Conference (DAC), Anaheim, CA, USA, 13–17 June 2005; pp. 801–806. [Google Scholar]
- Alpert, C.; Chu, C.; Gandham, G.; Hrkić, M.; Hu, J.; Kashyap, C.; Quay, S. Simultaneous Driver Sizing and Buffer Insertion Using a Delay Penalty Estimation Technique. In Proceedings of the International Symposium on Physical Design (ISPD), San Diego, CA, USA, 7–10 April 2002; pp. 104–109. [Google Scholar]
- Stefanidis, A.; Mangiras, D.; Nicopoulos, C.; Chinnery, D.; Dimitrakopoulos, G. Autonomous Application of Netlist Transformations inside Lagrangian Relaxation-based Optimization. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2021, 40, 1672–1686. [Google Scholar] [CrossRef]
- Jiang, Y.; Sapatnekar, S.S.; Bamji, C.; Kim, J. Interleaving buffer insertion and transistor sizing into a single optimization. IEEE Trans. VLSI Syst. 1998, 6, 625–633. [Google Scholar] [CrossRef] [Green Version]
- Fishburn, J.P. Clock Skew Optimization. IEEE Trans. Comput. 1990, 39, 945–951. [Google Scholar] [CrossRef] [Green Version]
- Kim, S.; Do, S.; Kang, S. Fast Predictive Useful Skew Methodology for Timing-Driven Placement Optimization. In Proceedings of the ACM/IEEE Design Automation Conference (DAC), Austin, TX, USA, 18–22 June 2017; pp. 55:1–55:6. [Google Scholar]
- Fishburn, J.P.; Dunlop, A.E. TILOS: A posynomial programming approach to transistor sizing. In ICCAD 2003; Springer: Boston, MA, USA, 2003. [Google Scholar]
- Ozdal, M.M.; Burns, S.; Hu, J. Algorithms for Gate Sizing and Device Parameter Selection for High-Performance Designs. IEEE Trans. CAD 2012, 31, 1558–1571. [Google Scholar] [CrossRef]
- Coudert, O. Gate Sizing for Constrained Delay/Power/Area Optimization. IEEE Trans. VLSI Syst. 1997, 5, 465–472. [Google Scholar] [CrossRef] [Green Version]
- Nguyen, D.; Davare, A.; Orshansky, M.; Chinnery, D.; Thompson, B.; Keutzer, K. Minimization of Dynamic and Static Power Through Joint Assignment of Threshold Voltages and Sizing Optimization. In Proceedings of the 2003 International Symposium on Low Power Electronics and Design (ISLPED ’03), Seoul, Korea, 25–27 August 2003; pp. 158–163. [Google Scholar]
- Bhattacharya, K.; Ranganathan, N. A Linear Programming Formulation for Security-Aware Gate Sizing. In Proceedings of the ACM Great Lakes Symposium on VLSI (GLSVLSI ’08), Orlando, FL, USA, 4–6 May 2008; pp. 273–278. [Google Scholar]
- Berkelaar, M.; Jess, J. Gate sizing in MOS digital circuits with linear programming. In Proceedings of the European Design Automation Conference, Glasgow, UK, 12–15 March 1990; pp. 217–221. [Google Scholar]
- Jeong, K.; Kahng, A.B.; Yao, H. Revisiting the linear programming framework for leakage power vs. performance optimization. In Proceedings of the 2009 10th International Symposium on Quality Electronic Design, San Jose, CA, USA, 16–18 March 2009; pp. 127–134. [Google Scholar]
- Reimann, T.; Posser, G.; Flach, G.; Johann, M.; Reis, R. Simultaneous gate sizing and Vt assignment using Fanin/Fanout ratio and Simulated Annealing. In Proceedings of the 2013 IEEE International Symposium on Circuits and Systems (ISCAS), Beijing, China, 19–23 May 2013; pp. 2549–2552. [Google Scholar]
- Daboul, S.; Hähnle, N.; Held, S.; Schorr, U. Provably Fast and Near-Optimum Gate Sizing. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2018, 37, 3163–3176. [Google Scholar] [CrossRef]
- Hu, S.; Ketkar, M.; Hu, J. Gate Sizing For Cell Library-Based Designs. In Proceedings of the 2007 44th ACM/IEEE Design Automation Conference, San Diego, CA, USA, 4–8 June 2007; pp. 847–852. [Google Scholar]
- Ozdal, M.M.; Burns, S.; Hu, J. Gate sizing and device technology selection algorithms for high-performance industrial designs. In Proceedings of the 2011 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 7–10 November 2011; pp. 724–731. [Google Scholar]
- Rahman, M.; Tennakoon, H.; Sechen, C. Library-Based Cell-Size Selection Using Extended Logical Effort. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2013, 32, 1086–1099. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, J. A New Algorithm for Simultaneous Gate Sizing and Threshold Voltage Assignment. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2010, 29, 223–234. [Google Scholar] [CrossRef] [Green Version]
- Hu, J.; Kahng, A.B.; Kang, S.; Kim, M.C.; Markov, I.L. Sensitivity-guided metaheuristics for accurate discrete gate sizing. In Proceedings of the IEEE International Conference CAD, San Jose, CA, USA, 5–8 November 2012; pp. 233–239. [Google Scholar]
- Kahng, A.B.; Kang, S.; Lee, H.; Markov, I.L.; Thapar, P. High-performance Gate Sizing with a Signoff Timer. In Proceedings of the International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 18–21 November 2013; pp. 450–457. [Google Scholar]
- Fatemi, H.; Kahng, A.B.; Lee, H.; Li, J.; Pineda de Gyvez, J. Enhancing sensitivity-based power reduction for an industry IC design context. Integration 2019, 66, 96–111. [Google Scholar] [CrossRef]
- Lu, Y.C.; Nath, S.; Khandelwal, V.; Lim, S.K. RL-Sizer: VLSI Gate Sizing for Timing Optimization using Deep Reinforcement Learning. In Proceedings of the 2021 58th ACM/IEEE Design Automation Conference (DAC), San Francisco, CA, USA, 5–9 December 2021; pp. 733–738. [Google Scholar]
- Flach, G.; Reimann, T.; Posser, G.; Johann, M.; Reis, R. Effective Method for Simultaneous Gate Sizing and Vth Assignment Using Lagrangian Relaxation. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2014, 33, 546–557. [Google Scholar] [CrossRef]
- Sharma, A.; Chinnery, D.; Bhardwaj, S.; Chu, C. Fast Lagrangian Relaxation Based Gate Sizing Using Multi-Threading. In Proceedings of the IEEE Inter. Conf. on Computer-Aided Design, Austin, TX, USA, 2–6 November 2015; pp. 426–433. [Google Scholar]
- Sharma, A.; Chinnery, D.; Dhamdhere, S.; Chu, C. Rapid gate sizing with fewer iterations of Lagrangian Relaxation. In Proceedings of the 2017 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Irvine, CA, USA, 13–16 November 2017; pp. 337–343. [Google Scholar]
- Livramento, V.S.; Guth, C.; Güntzel, J.L.; Johann, M.O. A Hybrid Technique for Discrete Gate Sizing Based on Lagrangian Relaxation. ACM Trans. Des. Autom. Electron. Syst. 2014, 19. [Google Scholar] [CrossRef]
- Shklover, G.; Emanuel, B. Simultaneous Clock and Data Gate Sizing Algorithm with Common Global Objective. In Proceedings of the 2012 ACM International Symposium on International Symposium on Physical Design, Napa, CA, USA, 25–28 March 2012; pp. 145–152. [Google Scholar]
- Li, L.; Kang, P.; Lu, Y.; Zhou, H. An efficient algorithm for library-based cell-type selection in high-performance. In Proceedings of the 2012 IEEE/ACM International Conference on Computer-Aided Design (ICCAD), San Jose, CA, USA, 5–8 November 2012; pp. 226–232. [Google Scholar]
- Ozdal, M.; Amin, C.; Ayupov, A.; Burns, S.M.; Wilke, G.R.; Zhuo, C. An Improved Benchmark Suite for the ISPD-2013 Discrete Cell Sizing Contest. In Proceedings of the International Symposium on Physical Design, Stateline, NV, USA, 24–27 March 2013; pp. 168–170. [Google Scholar]
- Mangiras, D.; Dimitrakopoulos, G. Incremental Lagrangian Relaxation based Discrete Gate Sizing and Threshold Voltage Assignment. In Proceedings of the 2021 10th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 5–7 July 2021; pp. 1–5. [Google Scholar]
- Bhasker, J.; Chadha, R. Static Timing Analysis for Nanometer Designs: A Practical Approach; Springer: Boston, MA, USA, 2009. [Google Scholar]
- Mangiras, D.; Stefanidis, A.; Seitanidis, I.; Nicopoulos, C.; Dimitrakopoulos, G. Timing-Driven Placement Optimization Facilitated by Timing-Compatibility Flip-Flop Clustering. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2020, 39, 2835–2848. [Google Scholar] [CrossRef]
- Berkelaar, M.; Buurman, P.; Jess, J. Computing the entire active area/power consumption versus delay tradeoff curve for gate sizing with a piecewise linear simulator. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 1996, 15, 1424–1434. [Google Scholar] [CrossRef]
- Montiel-Nelson, J.; Sosa, J.; Navarro, H.; Sarmiento, R.; Núñez, A. Efficient method to obtain the entire active area against circuit delay time trade-off curve in gate sizing. IEE Proc.-Circuits Dev. Syst. 2005, 152, 133–145. [Google Scholar] [CrossRef]
- Tennakoon, H.; Sechen, C. Nonconvex Gate Delay Modeling and Delay Optimization. IEEE Trans. Comput.-Aided Des. Integr. Circuits Syst. 2008, 27, 1583–1594. [Google Scholar] [CrossRef]
- Flach, G.; Fogaça, M.; Monteiro, J.; Johann, M.; Reis, R. Rsyn: An Extensible Physical Synthesis Framework. In Proceedings of the International Symposium on Physical Design, Portland, OR, USA, 19–22 March 2017; pp. 33–40. [Google Scholar]
- Huang, T.W.; Wong, M.D.F. OpenTimer: A high-performance timing analysis tool. In Proceedings of the IEEE/ACM International Conference on Computer-Aided Design (ICCAD), Austin, TX, USA, 2–6 November 2015; pp. 895–902. [Google Scholar]


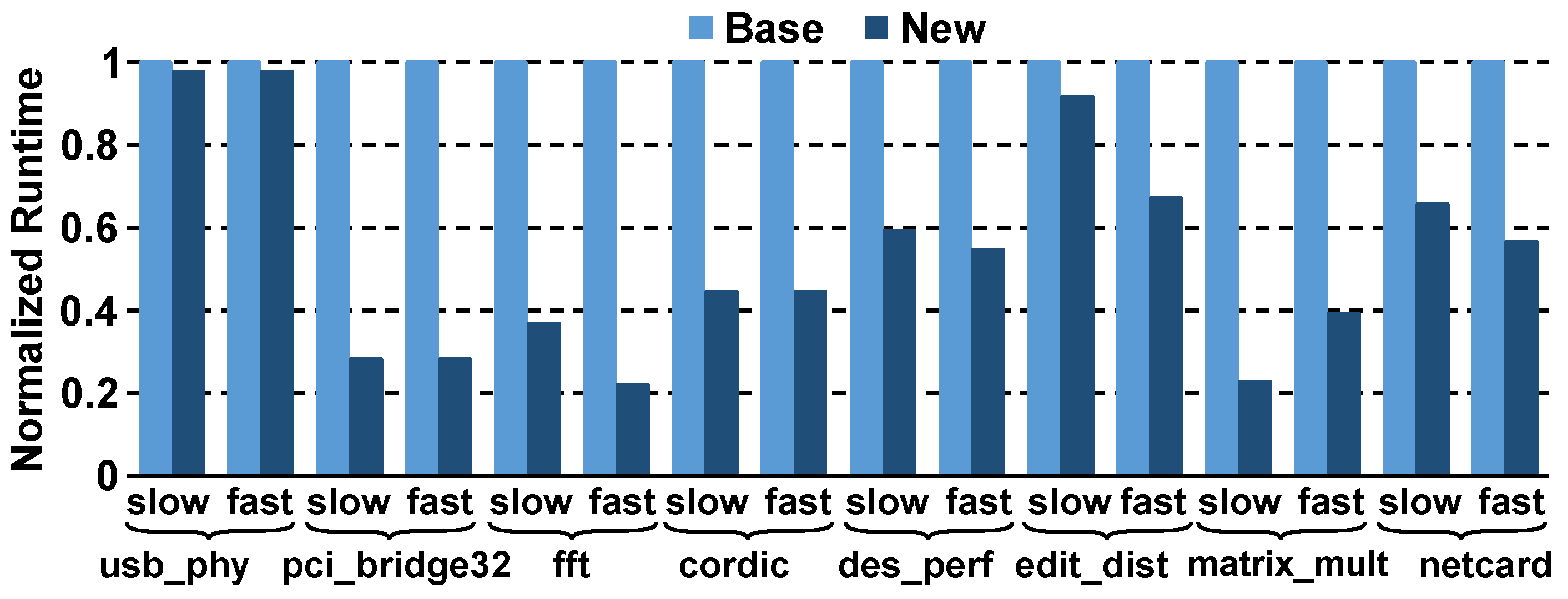
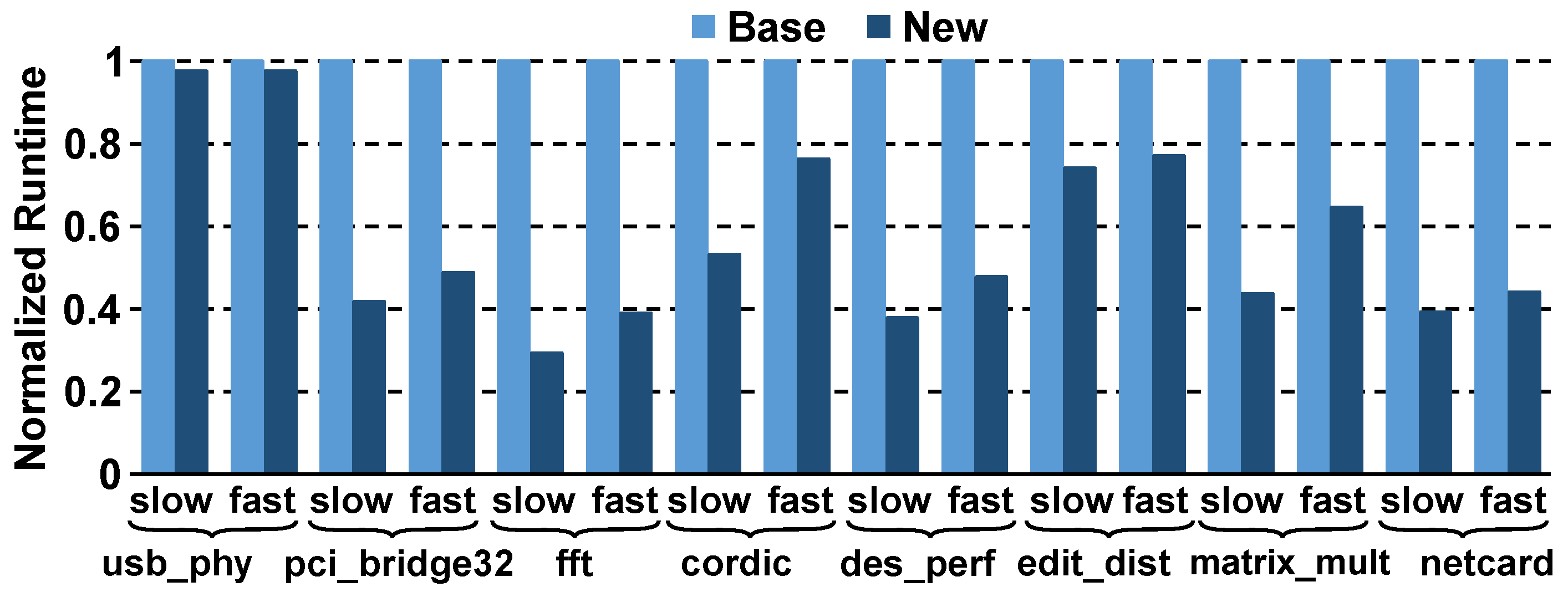

| Design | #Cells | Single Corner | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Late WNS (ps) | Late TNS (ps) | Leakage (mW) | ||||||||
| Init | Base | New | Init | Base | New | Init | Base | New | ||
| usb_phy_slow | 623 | −1.53 | 0.00 | 0.00 | −1.53 | 0.00 | 0.00 | 1 | 1 | 1 |
| usb_phy_fast | −0.61 | 0.00 | 0.00 | −0.61 | 0.00 | 0.00 | 2 | 2 | 2 | |
| pci_bridge32_slow | 30,763 | −11.21 | 0.00 | 0.00 | −333.10 | 0.00 | 0.00 | 58 | 58 | 58 |
| pci_bridge32_fast | −16.66 | −0.44 | 0.00 | −614.66 | −0.96 | 0.00 | 98 | 97 | 100 | |
| fft_slow | 33,792 | −16.35 | 0.00 | 0.00 | −320.92 | 0.00 | 0.00 | 88 | 88 | 87 |
| fft_fast | −18.18 | −6.58 | −1.88 | −234.28 | −63.37 | −4.25 | 217 | 228 | 228 | |
| cordic_slow | 42,937 | −13.99 | −14.43 | −1.24 | −801.84 | −116.70 | −2.11 | 306 | 349 | 309 |
| cordic_fast | −13.26 | −4.26 | −6.94 | −752.72 | −30.00 | −31.40 | 1139 | 1142 | 933 | |
| des_perf_slow | 113,346 | −30.40 | −1.88 | 0.00 | −11,920.00 | −5.26 | 0.00 | 449 | 410 | 420 |
| des_perf_fast | −25.80 | −3.51 | −4.10 | −11,412.20 | −49.94 | −8.69 | 609 | 522 | 556 | |
| edit_dist_slow | 129,227 | −54.44 | 0.00 | 0.00 | −21,881.50 | 0.00 | 0.00 | 452 | 447 | 445 |
| edit_dist_fast | −63.59 | −3.34 | 0.00 | −36,639.50 | −15.16 | 0.00 | 624 | 630 | 610 | |
| matrix_mult_slow | 159,642 | −44.00 | 0.00 | 0.00 | −3292.93 | 0.00 | 0.00 | 481 | 487 | 476 |
| matrix_mult_fast | −33.07 | 0.00 | 0.00 | −2694.75 | 0.00 | 0.00 | 1056 | 1230 | 1020 | |
| netcard_slow | 984,094 | −30.19 | 0.00 | 0.00 | −1477.58 | 0.00 | 0.00 | 5160 | 5101 | 5102 |
| netcard_fast | −28.97 | 0.00 | 0.00 | −6394.27 | 0.00 | 0.00 | 5203 | 5144 | 5141 | |
| Average | −25.14 | −2.15 | −0.89 | −6173.27 | −17.59 | −2.90 | 996 | 996 | 968 | |
| Design | Multiple Corners | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Late WNS (ps) | Late TNS (ps) | Leakage (mW) | |||||||
| Init | Base | New | Init | Base | New | Init | Base | New | |
| usb_phy_slow | −0.03 | 0.00 | 0.00 | −0.03 | 0.00 | 0.00 | 1 | 1 | 1 |
| usb_phy_fast | −6.38 | −4.99 | 0.00 | −14.39 | −8.57 | 0.00 | 3 | 2 | 3 |
| pci_bridge32_slow | −14.76 | 0.00 | 0.00 | −485.44 | 0.00 | 0.00 | 60 | 59 | 59 |
| pci_bridge32_fast | −21.40 | −4.25 | 0.00 | −280.77 | −14.78 | 0.00 | 194 | 151 | 153 |
| fft_slow | −10.74 | −0.14 | 0.00 | −194.37 | −0.27 | 0.00 | 96 | 97 | 98 |
| fft_fast | −8.21 | 0.00 | 0.00 | −449.16 | 0.00 | 0.00 | 356 | 426 | 391 |
| cordic_slow | −24.57 | −0.68 | −2.06 | −1000.51 | −1.09 | −2.06 | 518 | 561 | 527 |
| cordic_fast | −122.26 | −92.07 | −66.50 | −5412.47 | −2954.33 | −1710.28 | 2604 | 3189 | 3220 |
| des_perf_slow | −34.07 | −29.24 | −14.08 | −11,391.80 | −42.13 | −26.27 | 723 | 704 | 715 |
| des_perf_fast | −77.49 | −46.25 | −33.07 | −19,884.50 | −737.60 | −216.15 | 1272 | 926 | 1038 |
| edit_dist_slow | −67.66 | 0.00 | 0.00 | −36,892.70 | 0.00 | 0.00 | 477 | 473 | 471 |
| edit_dist_fast | −68.96 | −11.22 | 0.00 | −39,745.10 | −77.41 | 0.00 | 766 | 791 | 754 |
| matrix_mult_slow | −43.79 | 0.00 | 0.00 | −3254.51 | 0.00 | 0.00 | 576 | 591 | 574 |
| matrix_mult_fast | −36.16 | −45.23 | −33.02 | −3243.41 | −107.50 | −41.07 | 1876 | 2357 | 2302 |
| netcard_slow | −42.25 | 0.00 | 0.00 | −2251.09 | 0.00 | 0.00 | 5163 | 5105 | 5105 |
| netcard_fast | −28.96 | −1.23 | 0.00 | −10,606.80 | −2.34 | 0.00 | 5245 | 5187 | 5183 |
| Average | −37.98 | −14.71 | −9.3 | −8444.19 | −246.63 | −124.74 | 1246 | 1289 | 1287 |
| Design | Single Corner | |||||
|---|---|---|---|---|---|---|
| Late WNS (ps) | Late TNS (ps) | Leakage (mW) | ||||
| Base | New | Base | New | Base | New | |
| usb_phy_slow | 0.00 | 0.00 | 0.00 | 0.00 | 1 | 1 |
| usb_phy_fast | 0.00 | 0.00 | 0.00 | 0.00 | 2 | 2 |
| pci_bridge32_slow | 0.00 | 0.00 | 0.00 | 0.00 | 58 | 58 |
| pci_bridge32_fast | −1.65 | 0.00 | −6.13 | 0.00 | 98 | 98 |
| fft_slow | 0.00 | 0.00 | 0.00 | 0.00 | 88 | 87 |
| fft_fast | −6.87 | −1.01 | −20.18 | −2.24 | 224 | 221 |
| cordic_slow | −8.79 | −2.96 | −67.21 | −2.96 | 378 | 310 |
| cordic_fast | −17.06 | −2.73 | −133.10 | −4.81 | 1209 | 942 |
| des_perf_slow | −27.50 | −1.40 | −67.53 | −4.52 | 480 | 464 |
| des_perf_fast | −14.41 | −7.61 | −47.42 | −23.30 | 637 | 611 |
| edit_dist_slow | 0.00 | 0.00 | 0.00 | 0.00 | 450 | 449 |
| edit_dist_fast | −20.77 | −1.95 | −698.80 | −2.16 | 623 | 619 |
| matrix_mult_slow | 0.00 | 0.00 | 0.00 | 0.00 | 478 | 479 |
| matrix_mult_fast | 0.00 | 0.00 | 0.00 | 0.00 | 1174 | 1020 |
| netcard_slow | 0.00 | 0.00 | 0.00 | 0.00 | 5152 | 5153 |
| netcard_fast | 0.00 | 0.00 | 0.00 | 0.00 | 5197 | 5194 |
| Average | −6.07 | −1.10 | −65.02 | −2.50 | 1016 | 982 |
| Design | Multiple Corners | |||||
|---|---|---|---|---|---|---|
| Late WNS (ps) | Late TNS (ps) | Leakage (mW) | ||||
| Base | New | Base | New | Base | New | |
| usb_phy_slow | 0.00 | 0.00 | 0.00 | 0.00 | 1 | 1 |
| usb_phy_fast | −12.81 | 0.00 | −42.00 | 0.00 | 2 | 2 |
| pci_bridge32_slow | 0.00 | 0.00 | 0.00 | 0.00 | 62 | 60 |
| pci_bridge32_fast | −22.20 | −21.24 | −189.58 | −154.97 | 170 | 170 |
| fft_slow | 0.00 | 0.00 | 0.00 | 0.00 | 100 | 98 |
| fft_fast | −22.48 | 0.00 | −92.88 | 0.00 | 366 | 365 |
| cordic_slow | −1.48 | 0.00 | −1.86 | 0.00 | 705 | 516 |
| cordic_fast | −113.97 | −112.70 | −5604.24 | −4867.80 | 3325 | 3389 |
| des_perf_slow | −30.88 | −18.45 | −207.30 | −125.34 | 728 | 713 |
| des_perf_fast | −68.24 | −47.37 | −1520.11 | −386.81 | 1205 | 1229 |
| edit_dist_slow | 0.00 | 0.00 | 0.00 | 0.00 | 478 | 477 |
| edit_dist_fast | −3.11 | −0.48 | −3.11 | −0.85 | 824 | 758 |
| matrix_mult_slow | 0.00 | 0.00 | 0.00 | 0.00 | 602 | 580 |
| matrix_mult_fast | −26.23 | −27.31 | −42.98 | −43.54 | 2214 | 2154 |
| netcard_slow | 0.00 | 0.00 | 0.00 | 0.00 | 5172 | 5158 |
| netcard_fast | −4.70 | 0.00 | −7.60 | 0.00 | 5250 | 5236 |
| Average | −19.13 | −14.22 | −481.98 | −348.71 | 1325 | 1307 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mangiras, D.; Dimitrakopoulos, G. Incremental Lagrangian Relaxation Based Discrete Gate Sizing and Threshold Voltage Assignment. Technologies 2021, 9, 92. https://doi.org/10.3390/technologies9040092
Mangiras D, Dimitrakopoulos G. Incremental Lagrangian Relaxation Based Discrete Gate Sizing and Threshold Voltage Assignment. Technologies. 2021; 9(4):92. https://doi.org/10.3390/technologies9040092
Chicago/Turabian StyleMangiras, Dimitrios, and Giorgos Dimitrakopoulos. 2021. "Incremental Lagrangian Relaxation Based Discrete Gate Sizing and Threshold Voltage Assignment" Technologies 9, no. 4: 92. https://doi.org/10.3390/technologies9040092
APA StyleMangiras, D., & Dimitrakopoulos, G. (2021). Incremental Lagrangian Relaxation Based Discrete Gate Sizing and Threshold Voltage Assignment. Technologies, 9(4), 92. https://doi.org/10.3390/technologies9040092







