Multiobjective Ant Lion Approaches Applied to Electromagnetic Device Optimization

Abstract

Nature-inspired metaheuristics of the swarm intelligence field are a powerful approach to solve electromagnetic optimization problems. Ant lion optimizer (ALO) is a nature-inspired stochastic metaheuristic that mimics the hunting behavior of ant lions using steps of random walk of ants, building traps, entrapment of ants in traps, catching preys, and re-building traps. To extend the classical single-objective ALO, this paper proposes four multiobjective ALO (MOALO) approaches using crowding distance, dominance concept for selecting the elite, and tournament selection mechanism with different schemes to select the leader. Numerical results from a multiobjective constrained brushless direct current (DC) motor design problem show that some MOALO approaches present promising performance in terms of Pareto-optimal solutions.

1. Introduction

Population-based metaheuristics such as evolutionary algorithms and swarm-based intelligence (SI) algorithms have gained prominence to solve different kinds of electromagnetic optimization problems [1,2,3,4,5,6,7,8,9,10] involving nonlinear, non-convex, multi-modal, and non-differentiable functions mainly due to advantages when compared with single-point search algorithms of mathematical programming in terms of no need to objective function be differentiable and continuous, and global searching capability.

SI has the features of natural distribution and self-organization. SI algorithms typically simulate animal behaviors in terms of social hierarchy, collaboration, and collective activities. A wide array of swarm-based methods was suggested in the literature [11] and implemented to a variety of engineering problems.

A promising metaheuristic linked to the SI field recently proposed by Mirjalili [12] is the ant lion optimizer (ALO). It is a nature-inspired stochastic metaheuristic algorithm that mimics hunting mechanisms of the ant lions’ larvae in catching its preferred prey in nature. One of the advantages of ALO is that it has few parameters to tune, making it a flexible algorithm for solving diverse problems [13].

Different from the single-objective optimization problems where the optimal solution is clearly defined, in multicriteria or multiobjective problems (MOPs) there exists, in general, a set of trade-offs giving rise to numerous solutions (often conflicting) instead of a unique optimal solution. The optimal solutions of a MOP constitute possibly an infinite set of compromise solutions, known as Pareto optimal solutions or non-dominated solutions. However, it is not easy to obtain a proper result in a large solution space where multiobjective algorithms need to explore and collect a set of optimal solutions at the same time to satisfy all objectives.

In the latest years, solving MOPs has become important in electromagnetic optimization and metaheuristic optimization methods have shown their popularity and effectiveness in tackling MOPs (see examples in [14,15,16,17,18]).

By extending the basic ideas from the single-objective ALO, a multiobjective ALO (MOALO) approach using crowding distance [19] and the dominance concept for selecting the elite of ant lions, and a tournament mechanism to select the ant lions to perform the random walk is proposed. Different leader selection schemes were evaluated to improve the population convergence and diversity of the MOALO. A brushless direct current (DC) wheel motor benchmark presented in [20] and with the Matlab source code for computing the objective function is publicly available [21] is used to investigate the performance of the MOALO. A major problem is to design a DC wheel motor so that it operates optimally in the sense of producing maximum efficiency with minimal material cost, and also satisfy inequality constraints simultaneously. In this context, MOALO can be useful to obtain a well-distributed set of Pareto-optimal solutions.

The remaining of this paper is arranged as follows. Section 2 explains the fundamentals of the ALO and the proposed MOALO. After, the description of the brushless DC wheel motor benchmark problem and results are presented in Section 3 and Section 4, respectively. Finally, the conclusions and future research issues are given in Section 5 followed by references.

2. Fundamentals of the ALO and MOALO

In nature, ant lions move along a circular track in sand and dig pits using their lower jaws to trap ants. In the ALO, ants and antlions as search agents are proposed to find solutions. When ants randomly move into pits, ant lions will catch ants, rebuild their pits as trap form and wait for the next prey (another ant) [22]. The ALO algorithm [12] mimics the interaction between ant lions and ants in the trap. To model such interactions, ants are required to move over the search space and ant lions are expected to hunt them and become fitter using traps. Since ants move stochastically in nature when searching for food, a random walk is chosen for modeling ants’ movement in the original ALO. The steps of the ALO for single-objective optimization are briefly described in Figure 1, where NP is the only hyperparameter of the algorithm.

In general, multiobjective optimization refers to a set of objective functions that are taken and optimized concurrently. Therefore, a set of many solutions that present a good tradeoff between the objectives is to find, which means that multiple optimal solutions can be found in a single run. In general, multiobjective optimization algorithms use space objectives to guide their exploration in the search space. However, an appropriate balance between convergence and diversity is essential in a multiobjective metaheuristic optimization method. The tradeoff can be also defined between exploitation and exploration with a focus on a well-converged and well-distributed set of Pareto-optimal solutions, where exploitation is the process of neighborhood searching, and exploration is the process within the entire space.

Differently from other multiobjective algorithms from literature that use discrete grids or anchors, the MOALO is a multiobjective version of the ALO that uses the crowding distance [19], the dominance strategy for selecting the elite of the ant lions, and a tournament mechanism to select the ant lions to perform the random walk. The crowding distance is based on the cardinality of the solution sets and their distance to the solution boundaries. Accordingly, the solutions which are in a promising less crowded region in the objective space are given preference concerning others, once the MOALO aims to diversify the solutions.

The MOALO operates by the notion of following a leader when there are many local optimal fronts. In such a situation, the MOALO may get stuck to a local Pareto-optimal front, which is a set of solutions sub-dominated among themselves but still not efficient enough to compose the global Pareto-optimal front. It means that MOALO can prematurely converge onto a local set of solutions rather than finding the global set.

In this context, four leader selection schemes were proposed and evaluated to improve the population convergence and diversity of the MOALO—in the original single-objective ALO, the leader is the solution with the best fitness, which cannot be directly applied to multiobjective optimization. The original equations from ALO are kept and only the leaders are updated every iteration: (i) each ant lion follows another random ant lion from the sub-population formed by the non-dominated ones; (ii) all ant lions follow the first one of the ranking, which is based on the non-domination and crowding distance criteria; (iii) the entire population follows the same random ant lion from the whole population; and (iv) each ant lion follows a different random one from the sub-population formed by the Nc best-ranked solutions using the same ranking criteria of approach (iii). The only hyperparameter of MOALO is the population size, NP.

3. Brushless DC Wheel Motor Design Problem

Brushless DC motors, also known as electronically commutated motor and synchronous DC motors, are synchronous motors driven by DC electricity through an inverter or switching power supply which produces an alternating electric current to drive each phase of the motor through a closed-loop controller. Brushless DC motors are widely used due to their advantages such as better power-weight and torque-current ratio compared to permanent magnet synchronous motor. They are adopted as actuators in many aerospace applications, robotics, medical instruments, automotive industry, and electronic applications.

In this paper, a brushless DC wheel motor design problem [20] was evaluated. The problem is composed of 78 nonlinear equations implemented with five design variables (see

Table 1. Design parameters in the brushless DC motor benchmark.

Symbol	Meaning	Minimum Value	Maximum Value
Ds (m)	Bore (stator) diameter	0.15	0.33
Be (T)	Air gap induction	0.50	0.76
δ (A/m2)	Conductor current density	2.0 × 106	5.0 × 106
Bd (T)	Teeth magnetic induction	0.9	1.8
Bcs (T)	Stator back iron induction	0.6	1.6

for the range of optimization variables) subject to six inequality constraints, which are related to technological, operational, and considerations regarding the wheel motor. Here, the objectives are the minimization of f₁ = 1-η, where η is the efficiency, and f₂ = M_total, where M_total is the total mass of the active parts, which has the constraint M_total ≤ 15 kg.

A third objective function f₃ to be minimized related to the number of infeasible solutions is adopted in the optimization procedure. It increases the complexity of the problem while it helps to avoid premature convergence by exploring a wider range of regions in the search space. The focus is to obtain only feasible solutions (f₃ equal to zero) i.e., a solution set that satisfies the constraints called the feasible set. Solutions that do not satisfy at least one of the constraints are called infeasible solutions. In other words, a solution is infeasible if there exists no solution value that satisfies all of the constraints.

Table 2. Inequality constraints, g_i where i = 1, …, nc in the brushless DC motor benchmark.

Symbol	Meaning	Minimum Value	Maximum Value
Dext (mm)	Outer diameter	g1	Dext-340 ≤ 0
Din (mm)	Inner diameter	g2	76-Din ≤ 0
Imax (A)	Maximum current in the phases	g3	125-Imax ≤ 0
discr (Ds, δ, Bd, Be)	Determinant used for the calculation of the slot height	g4	−discr ≤ 0
Ta (°C)	Motor temperature	g5	Ta-120 ≤ 0
Mtot (kg)	Total mass	g6	Mtot-15 ≤ 0

presents the inequality constraints in the brushless DC motor benchmark.

If the infeasible solutions were completely disregarded during the MOALO optimization cycle, the diversity and adequate convergence may be lost during the early stages of the search process leading to a locally optimal or partial Pareto front.

The outer diameter of the brushless DC wheel motor must be lower to 340 mm so that the motor fits into the rim of a wheel, the inner diameter must be superior to 76 mm for mechanical reasons, the magnets shall support a phase current of 125 A without demagnetization and the temperature of the magnets shall be less than 120 °C. The geometry of the brushless DC wheel motor is presented in Figure 2 [20].

4. Results

The proposed MOALO approaches are applied to the brushless DC motor design problem using a population size of 100 and a stopping criterion of 300,000 function evaluations in each run. The MOALO has been designed with four different approaches to select the elite in the population.

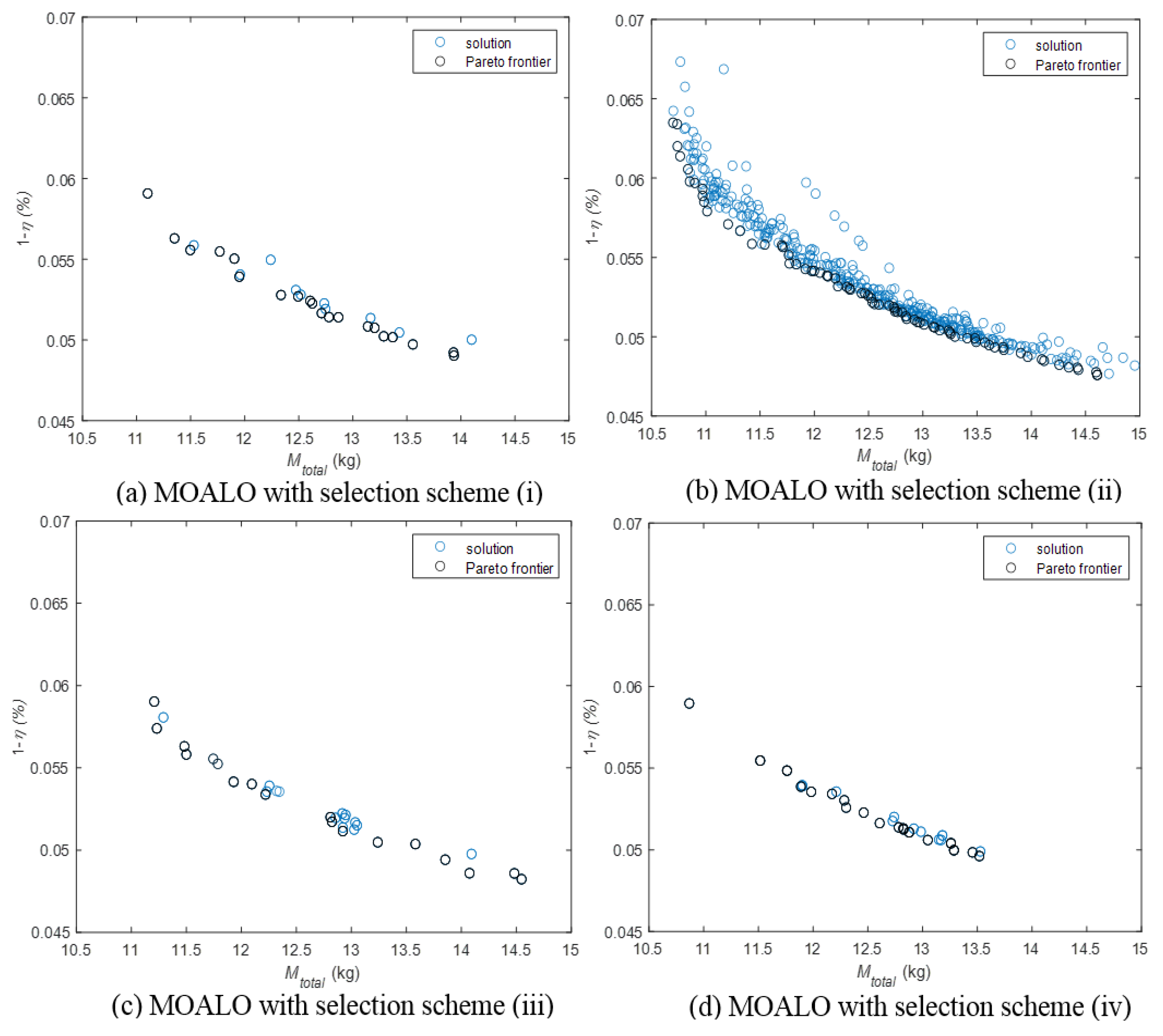
Results are illustrated in Figure 2 shows the obtained Pareto fronts filtered after 30 runs with different and random initial conditions considering only the feasible solutions. The 1-η axis is expressed as a percentage and M_total is expressed in kg. According to the simulation results, the MOALO with the leader selection scheme (ii) presented promising results in terms of spacing and solutions in the Pareto frontier.

The algorithms were evaluated according to the number of feasible solutions, being evaluated the number of non-dominated solutions, the hypervolume to the Nadir point (1, 1) (which is computed as the area formed from the Nadir point—the worst objective values of extreme Pareto points—up to every single point of the Pareto front, approximated by the discrete integral calculation), the mean Euclidean distance to the origin, and the spacing. The hypervolume, the Euclidean distance, and the spacing were calculated using normalized values inside the interval (0, 1), that is why the Nadir point is (1, 1). It is important to highlight that the optimal value for hypervolume would be 1 if the entire Pareto front were inside the axis with one solution in the origin. These results are shown in

Table 3. Performance metrics for MOALO with four selection schemes (30 runs).

Metrics for the MOALO	Scheme (i)	Scheme (ii)	Scheme (iii)	Scheme (iv)
Pareto solutions	60	417	60	66
Non-dominated solutions	40	76	34	43
Hypervolume	0.5930	0.6768	0.6200	0.5273
Normalized Euclidean distance using (f1, f2) values to the origin	0.7319	0.6800	0.7367	0.7630
Normalized spacing between the (f1, f2) values	3.73 × 10−6	1.23 × 10−2	9.69 × 10−3	3.57 × 10−6

, where the Pareto solutions include all feasible solutions before filtering the non-dominated ones.

Taking as reference the number of feasible solutions, scheme (ii) has found more solutions than the other schemes, which has also resulted in the higher number of non-dominated solutions, the higher hypervolume, and the smaller mean Euclidean distance to the origin. On the other hand, the scheme (iv) has found a smaller spacing, which means a better distribution of the solution along the Pareto front.

The best feasible solution for MOALO with scheme (ii) related to the mass is with (f₁, f₂) = (0.0635, 10.6975) and the one related to the best 1-η is (f₁, f₂) = (0.0476, 14.6076). A tradeoff feasible solution using the mean of the normalized of the f₁ and f₂ values is also a promising solution with (f₁, f₂) = (0.0559, 11.4251). The solutions related to these objective function values are shown in

Table 4. Results in terms of decision variables for MOALO.

Scheme (i)	Ds (m)	Be (T)	δ (A/m2)	Bd (T)	Bcs (T)
Best Mtotal	0.1822	0.6575	3.22 × 106	1.7205	1.5138
Best 1-η	0.1969	0.6580	2.15 × 106	1.7832	1.4608
Mean (f1, f2)	0.1816	0.6715	2.72 × 106	1.7843	1.4319
Scheme (ii)	Ds (m)	Be (T)	δ (A/m2)	Bd (T)	Bcs (T)
Best Mtotal	0.1865	0.6664	3.64 × 106	1.8000	1.6000
Best 1-η	0.2003	0.6545	2.08 × 106	1.7837	1.1230
Mean (f1, f2)	0.1774	0.6815	2.90 × 106	1.8000	1.5117
Scheme (iii)	Ds (m)	Be (T)	δ (A/m2)	Bd (T)	Bcs (T)
Best Mtotal	0.1795	0.6796	3.32 × 106	1.7402	1.2680
Best 1-η	0.1964	0.6881	2.26 × 106	1.7269	1.0568
Mean (f1, f2)	0.1815	0.6845	2.76 × 106	1.7921	1.5220
Scheme (iv)	Ds (m)	Be (T)	δ (A/m2)	Bd (T)	Bcs (T)
Best Mtotal	0.1787	0.6632	3.16 × 106	1.7820	1.5928
Best 1-η	0.1943	0.6518	2.23 × 106	1.7917	1.4059
Mean (f1, f2)	0.1821	0.6603	2.67 × 106	1.7976	1.4802

.

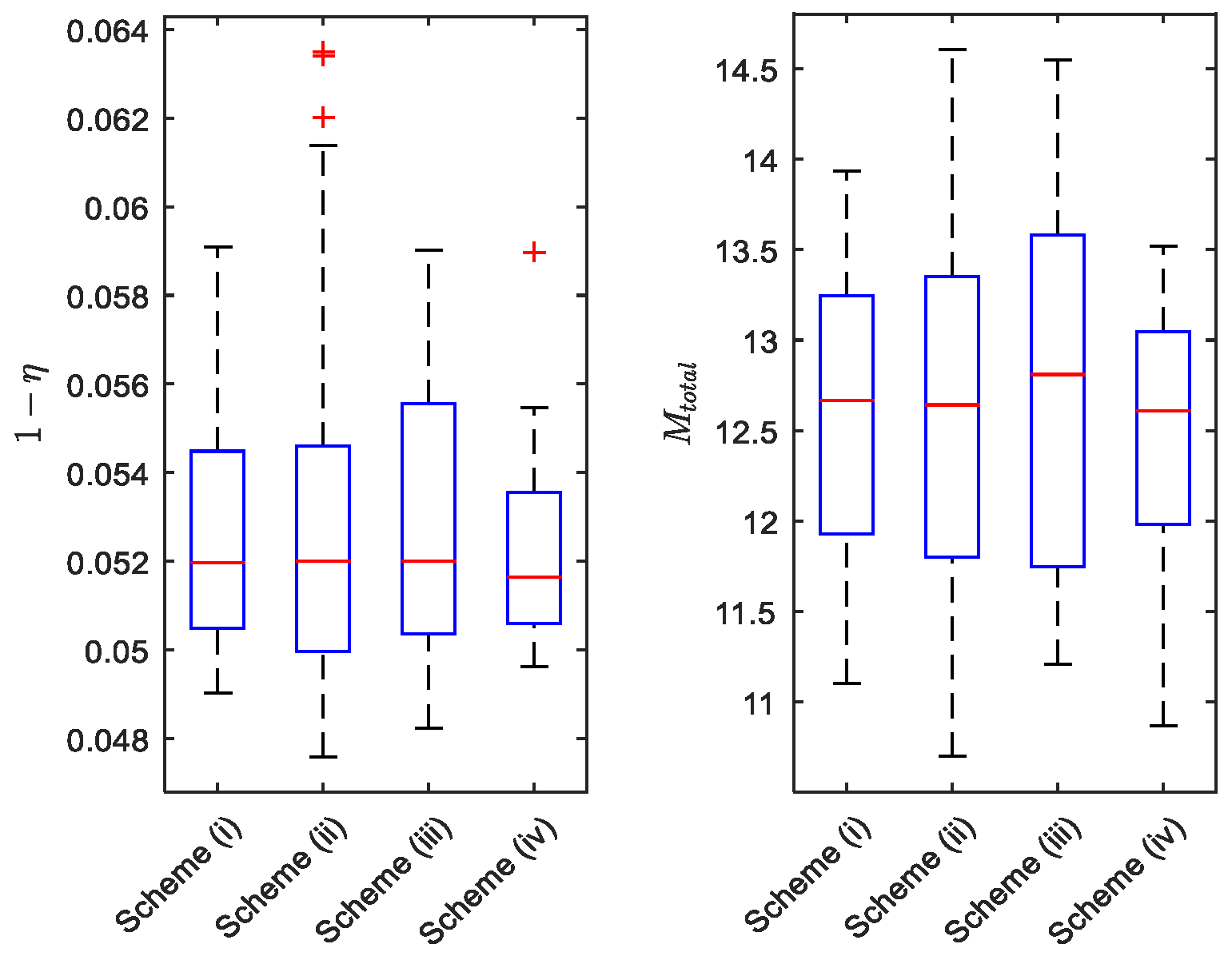
Analyzing the fitness result distribution, one can see the solution density in the variable space. Figure 3 presents the graphical distribution for MOALO approaches concerning the output variables. On the right-hand side, there are the mass values and on the left-hand side, there are the efficiency results. It is possible to conclude the scheme (iv) outcomes are more concentrated than the MOSOS ones, which is explained by the normalized spacing shown in Table 3. Having a bigger normalized spacing coefficient and having a more feasible solutions scheme (ii) can cover a wider range of values when compared to the other schemes. About median results, the values presented by all schemes are nearly similar. Checking for the decision variables selected concerning the feasible solutions presented by the problem, it is possible to see among the 30 runs how the variables are spread. 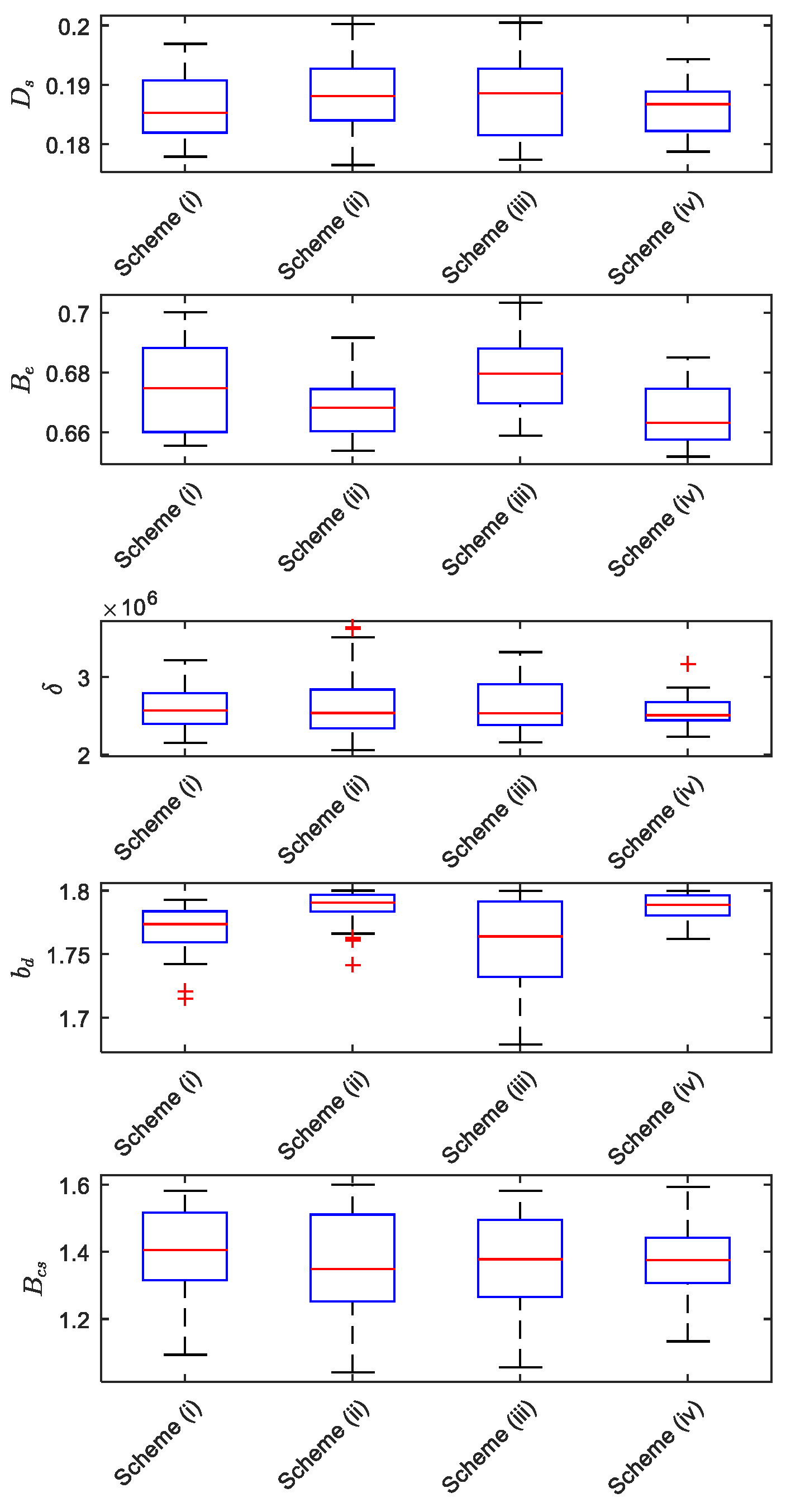Figure 4 shows the results for the 30 runs for each one of the decision variables comparing the proposed algorithms.

Regarding median values, the results seem to be equivalent. Taking the B_d, scheme (iii) presented a wider range of values and even the percentiles are wider than the other schemes. On the other hand, schemes (ii) and (iv) have presented a smaller range compared to the other schemes. Considering B_e, these schemes have presented slightly smaller values than the other schemes. The conductor current density given by δ range of scheme (iv) is lower than the other schemes, while the absolute values seem to be similar for all schemes.

5. Conclusions and Future Research

In this paper, MOALO with different leader selection schemes has been proposed and evaluated to a brushless DC motor multiobjective design problem. MOALO approaches presented promising results for the benchmark problem tested showing a wider range of feasible solutions. MOALO with the leader selection scheme (ii) provided promising results for 30 runs in terms of mean values of a spacing measure, the number of solutions in the Pareto front, and normalized Euclidean distances to the origin. Additionally, MOALO approaches shown a wider range of feasible solutions.

Taking the normalized spacing measure into consideration, the scheme (iv) presented a better performance. Besides, it has achieved the best median performance. Nevertheless, scheme (ii) achieved the best performance than the other schemes regarding the remaining metrics. For future studies, we are planning to investigate the recently-proposed optimizers [23,24,25] to electromagnetic optimization and also other approaches as an alternative for the crowding distance. Furthermore, another direction of research will be the realization of significance statistical tests and convergence analysis of the MOALO applied to multiobjective optimization benchmarks.