Circuit Implementation of a Modified Chaotic System with Hyperbolic Sine Nonlinearities Using Bi-Color LED ^†

Abstract

In this paper, a chaotic three dimansional dynamical system is proposed, that is a modification of the system in Volos et al. (2017). The new system has two hyperbolic sine nonlinear terms, as opposed to the original system that only included one, in order to optimize system’s chaotic behavior, which is confirmed by the calculation of the maximal Lyapunov exponents and Kaplan-Yorke dimension. The system is experimentally realized, using Bi-color LEDs to emulate the hyperbolic sine functions. An extended dynamical analysis is then performed, by computing numerically the system’s bifurcation and continuation diagrams, Lyapunov exponents and phase portraits, and comparing the numerical simulations with the circuit simulations. A series of interesting phenomena are unmasked, like period doubling route to chaos, coexisting attractors and antimonotonicity, which are all verified from the circuit realization of the system. Hence, the circuit setup accurately emulates the chaotic dynamics of the proposed system.

1. Introduction

During the last six decades, the theory of chaotic systems has been a prominent field of study for physicists, mathematicians, and analog circuit design engineers. By knowing the set of differential equations describing a system, a circuit that emulates its behavior can be constructed, to experimentally verify the chaotic behavior. Many works on how to build chaotic circuits are available, see for example [1,2,3], as well as the works referenced therein.

Chaos has so far been observed in systems related to mechanics, physics, chemistry, biology, circuits, economics and more, and the chaotic behavior has been verified via well-known theoretical and numerical tools, such as the bifurcation diagrams and the algorithm for calculating the Lyapunov Exponents (LEs). Chaotic attractors were observed and numerically confirmed in the case of Colpitts [4], Hartley [5], Wien-bridge [6] harmonic oscillator, Chua circuit [7] and other memristive systems [8], Van der Pol oscillator [9], phase-locked loops [10], dc-dc converters [11], and more.

In addition to the emergence of chaos in modelling physical phenomena, as indicated above, chaotic systems have found use in applications related to encryption, like random bit generators, signal masking, secure communications and more [12,13,14]. The suitability of chaotic systems for such applications is attributed to their simple structure that can yield complex dynamics with high unpredictability. Thus, many research teams are constantly working on developing new chaotic systems with rich dynamics. This is often done by considering existing systems and enriching their dynamics by modifying the differential/difference equations that describe them. The aim is to derive systems with more complex behavior, which can be indicated by higher values of the Maximum Lyapunov Exponent (MLE), Kaplan-Yorke dimension, and also the emergence of phenomena like multistability, coexisting attractors and antimonotonicity.

In the existing literature, the approaches for optimizing a system’s chaotic behavior can be summed up in three basic methodologies:

• In the first method, one of the system’s nonlinear terms can be replaced by a higher order one, for example by changing a product term to an exponential or logarithmic function [15,16].
• In the second method an existing nonlinear term is adjusted, without affecting its order [17,18].
• In the third approach, additional nonlinear terms and variables are added in the system, increasing its complexity and order [19,20].

Recently, many chaotic circuits with a hyperbolic sine term as a nonlinearity, have been developed [14,21,22,23,24,25,26]. To implement this nonlinear term in a circuit, two antiparallel diodes can be used. Due to the nature of the $i-v$ characteristic of this term, phenomena like a period doubling route to chaos, coexisting attractors, antimonotonicity and intermittency have been observed in the above systems.

In this work, the third method mentioned above is adopted for enhancing the complexity of the system proposed in [21]. The original system had a hyperbolic sine term in its third differential equation. The modified system is enhanced by adding a hyperbolic sine term in the second differential equation as well. The linear terms are also multiplied by control parameters, so the system now is in its general parametric form. The system is then emulated in a circuit, where the hyperbolic sine nonlinearities are implemented with simple Bi-color LEDs, in contrast to using antiparallel diodes. The use of Bi-color LEDs is very promising, since the resulting circuit has a simple structure, which can make it more suitable in the aforementioned chaos related applications.

After the circuit is designed, extensive simulations are performed with respect to three different bifurcation parameters. First, the dynamical characteristics are studied, like dissipation, symmetry, and equilibria. Then, calculation of the bifurcation diagrams, Lyapunov exponents diagram and phase portraits unmask interesting phenomena for the system, like period doubling route to chaos, antimonotonicity, coexisting attractors and a higher Kaplan-Yorke dimension compared to the original system. The numerical simulations are compared with the experimental circuit simulations and it is seen that the circuit accurately emulates the dynamics of the system. The present paper extends the results of [27], with a more detailed dynamical analysis and a plethora of new simulations performed.

The rest of the work is structured as follows: In Section 2 the dynamical system and its corresponding circuit are presented. In Section 3, the dynamical characteristics of the system are studied. Section 4 presents extensive simulation results regarding the behavior of the system with respect to different parameters. Finally, Section 5 closes the paper with a note on future topics of study.

2. The Proposed Chaotic Circuit

2.1. The Chaotic System of Differential Equations

In 2017, the following three dimensional chaotic jerk system was proposed in [21]:

$$\left\{\begin{array}{c}\dot{x}=-y\hfill \\ \dot{y}=-z\hfill \\ \dot{z}=-x-bz+asinh\left(y\right)\hfill \end{array}\right.$$

(1)

This was one of the first chaotic systems to use a hyperbolic sine function as a nonlinearity. Here, a modification of the system is proposed by adding one more hyperbolic sine function ($csinh\left(z\right)$) in the second equation of (1), and also multiplying the linear terms by adjustable parameters $d,e$.

$$\left\{\begin{array}{c}\dot{x}=-y\hfill \\ \dot{y}=-dz-csinh\left(z\right)\hfill \\ \dot{z}=-ex-bz+asinh\left(y\right)\hfill \end{array}\right.$$

(2)

The system now has two nonlinear hyperbolic sine functions, and five parameters $a,b,c,d,e$.

2.2. The Chaotic Circuit

The developed circuit that emulates (2) consists of three capacitors, ten resistors and five operational amplifiers (TL084CN), three of which ($U_1-U_3$) are configured as integrators. The nonlinear elements used are two Bi-color LEDs. The current, through each of the Bi-color LEDs, is given by:

$$I=2I_{S}sinh\left(\frac{\upsilon }{n{V}_T}\right)$$

(3)

This is derived by applying Kirchhoff’s current law and the known Shockley diode equation for the two antiparallel LEDs that consists the Bi-color LED. In (3), n is a diode ideality factor, $I_S$ is the reverse bias saturation current, $\upsilon$ is a voltage over the LEDs and $V_T$ is a thermal voltage.

The designed circuit is presented in Figure 1. Figure 2 shows the experimental realization of the circuit. The mathematical model of (2) is obtained by applying Kirchhoff’s laws into the circuit of Figure 1, as

$$\left\{\begin{array}{c}\frac{d{\upsilon }_{C_1}}{dt}=\frac{1}{RC}(-{\upsilon }_{C_2})\hfill \\ \frac{d{\upsilon }_{C_2}}{dt}=\frac{1}{RC}\left(-\frac{R}{R_d}{\upsilon }_{C_3}-2R{I}_{S}sinh\left(\frac{{\upsilon }_{C_3}}{n{V}_T}\right)\right)\hfill \\ \frac{d{\upsilon }_{C_3}}{dt}=\frac{1}{RC}\left(-\frac{R}{R_e}{\upsilon }_{C_1}+2R_a{I}_{S}sinh\left(\frac{{\upsilon }_{C_2}}{n{V}_T}\right)-\frac{R}{R_b}{\upsilon }_{C_3}\right)\hfill \end{array}\right.$$

(4)

by applying scale transformation for the variables and physical parameters, as follows

$$\begin{array}{c}x=\frac{{\upsilon }_{C_1}}{n{V}_T},y=\frac{{\upsilon }_{C_2}}{n{V}_T},z=\frac{{\upsilon }_{C_3}}{n{V}_T},\tau =\frac{t}{RC},a=\frac{2R_a{I}_s}{n{V}_T},b=\frac{R}{R_b},c=\frac{2R{I}_S}{n{V}_T},d=\frac{R}{R_d},e=\frac{R}{R_e}\end{array}$$

(5)

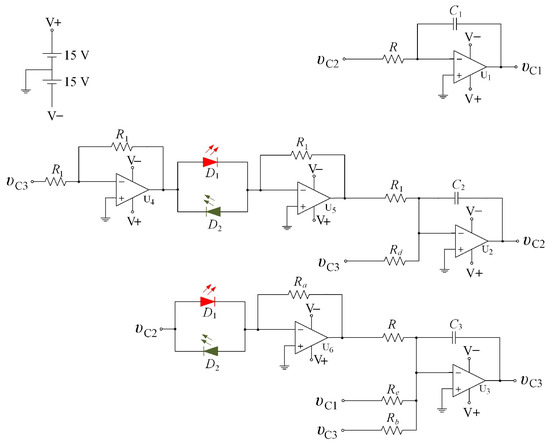
Figure 1. Schematic of the proposed circuit of system (2).

Figure 2. (a) The experimental setup and (b) the realization of the proposed circuit of Figure 1.

Using Bi-color LEDs, the parameter values a, c are fixed as: $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$, according to the Bi-color LEDs specifications ($I_S=1$ nA, $V_T=26$ mV and $n=2$), while parameters $d=e=1$. Note that the system’s behavior can be controlled by changing parameters $b,d,e$, which does not affect the Bi-color LEDs (3). The rest of the circuit’s elements are: $C_1=C_2=C_3=10$ nF, $R=10$ k$\mathrm{\Omega }$, $R_1=1$ M$\mathrm{\Omega }$, $R_a=10.4$ k$\mathrm{\Omega }$, $R_d=R_e=10$ k$\mathrm{\Omega }$ and $R_b$: variable resistor, while the power supply is $\pm 15$ V.

3. Theoretical Study of The System

The divergence of system (2) is defined as:

$$\nabla V=\frac{\partial \dot{x}}{\partial x}+\frac{\partial \dot{y}}{\partial y}+\frac{\partial \dot{z}}{\partial z}=-b$$

(6)

where V is the phase volume. Since $\nabla V<0$, $\forall x,y,z$ and $\forall b>0$, the system is bounded. So system (2) is dissipative and converges in the index

$$\frac{dV}{dt}=e^{-bt}$$

(7)

The interpretation of this index is that each volume, containing the trajectories of (2), will reduce to zero as time approaches infinity, at an exponential rate of $V_0{e}^{-bt}$. Thus, each trajectory of (2) is ultimately confined to a particular subset having zero volume, and its asymptotic motion of (2) is arranged to an attractor.

Moreover, the coordinate transformation $(x,y,z)\to (-x,-y,-z)$ leaves the system invariant. So, if $(x,y,z)$ is a solution of (2) for a choice of parameters, then $(-x,-y,-z)$ is also a solution for the same parameter values. This means that the shape of the attractors is symmetrically inverted with respect to the origin. This symmetry could justify the phenomenon of several coexisting attractors in the state space.

Finally, for $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$, $d=e=1$, the system’s equilibria are computed as $E{q}_1=(-10.946b,0,-10.946)$, $E{q}_2=(0,0,0)$ and $E{q}_3=(10.946b,0,10.946)$.

4. Circuit’s Dynamical Analysis

In this section, the system (2) is studied with respect to the bifurcation parameters $b,d,e$ is performed.

4.1. Dyncamical Behavior with Respect to b

For the analysis of system (2) with respect to b, the other parameter values are chosen as: $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$ and $d=e=1$, with initial conditions $(x_0,y_0,z_0)=(0,0.1,0)$. For this study, system (2) is solved using the 4th order Runge-Kutta algorithm, with fixed time step $\Delta t=0.001$. The continuation diagram with respect to parameter b is shown in Figure 3. The continuation diagram differs from the bifurcation diagram as to the choice of initial conditions. In the bifurcation diagram, the initial conditions in each iteration are kept the same, while in the continuation diagram, the last values of the variables in each iteration play the role of initial conditions in the next iteration.

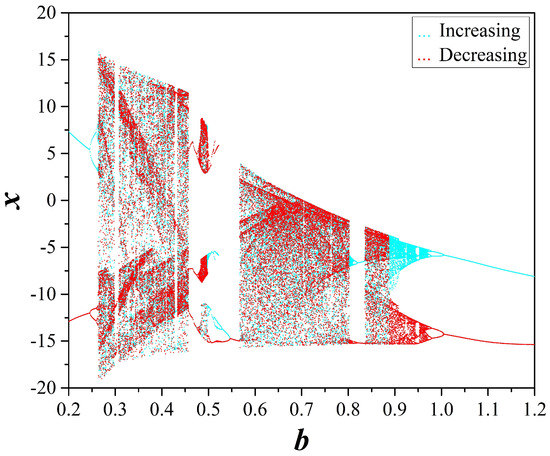
Figure 3. Continuation diagrams of system (2), when parameter b is increased (red) and decreased (blue).

The diagram is plotted both for increasing, and decreasing values of b. The diagram of Lyapunov Exponents (LE) spectrum is also shown in Figure 4, from which the chaotic behavior of the system is verified by the positive values of the Maximal Lyapunov Exponent (MLE).

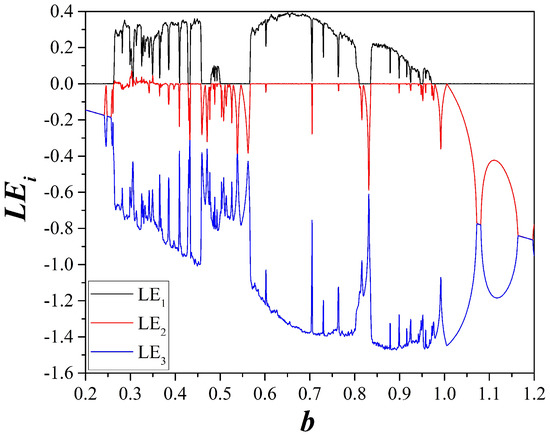
Figure 4. Spectrum of Lyapunov exponents of system (2), when varying b, for $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$ and $d=e=1$.

The experimental phase portraits of ${\upsilon }_{C_2}$ versus ${\upsilon }_{C_1}$, for various values of the resistor $R_b$ are produced and displayed using a digital oscilloscope, in order to verify the behaviors observed from the continuation diagram of Figure 3. In Figure 5 the agreement between the numerical simulation and the experimental observation of the circuit for the phase portrait for $b=0.625$ is verified.

Figure 5. Chaotic phase portraits of y versus x, for $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$, $d=e=1$ and $b=0.625$ $(R_b=16$ k$\mathrm{\Omega })$, produced (a) from system’s (2) simulation and (b) experimentally from the circuit of Figure 2.

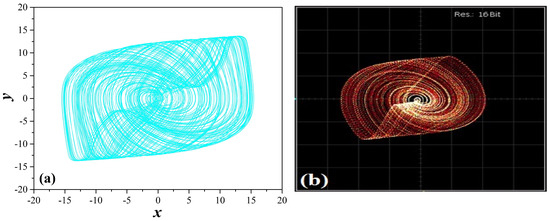
Additionally, the maximum value of the MLE of the proposed system (2) is $ML{E}_{max}=0.3904$, which is computed for $b=0.625$, while the max MLE value of the original system [21], was $ML{E}_{max}=0.2250$ for $b=0.634$. So, it can be seen that the MLE achieves a higher value in the modified system. Also, the maximum value of Kaplan-Yorke dimension [28] of the chaotic system (2) is calculated, for $b=0.287$, as:

$$D_{KY}=2+\frac{L{E}_1+L{E}_2}{|L{E}_3|}=2.4464$$

(8)

while, in the case of the system with one hyperbolic sinusoidal term the respective maximum value of Kaplan-Yorke dimension is $D_{KY}=2.2168$, for $b=0.508$. Indeed, a significant increase of the system’s chaoticity is verified. So, it is concluded that adopting the third method mentioned in the Introduction for modifying an existing system by adding more terms, leads to increase in the system’s complexity.

As for the chaotic phenomena observed from the continuation diagrams of Figure 3, first it must be noted that the period doubling route to chaos as the value of d decreases is observed in both diagrams. This phenomenon is the most common example of route to chaos, appearing in many well known systems, like the logistic map.

Also, another interesting behavior can be observed in the continuation diagrams of Figure 3. For lower and higher values of parameter b, coexisting attractors appear, which are experimentally verified from the phase portraits of Figure 6, for $R_b=50$ k$\mathrm{\Omega }$ $(b=0.2)$, in which two symmetric coexisting periodic attractors have been produced by turning on and off the power supply. As mentioned in Section 3, this coexistence is a consequence of system’s symmetry under the transformation $(x,y,z)\to (-x,-y,-z)$. So starting from different initial conditions, the attractor is positioned differently in the phase plane.

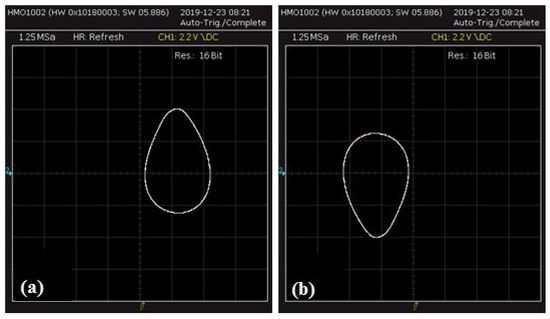
Figure 6. (a,b) Experimentally observed coexisting period-1 phase portraits of ${\upsilon }_{C_1}$ versus ${\upsilon }_{C_2}$, for $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$, $d=e=1$ and $b=0.2$ ($R_b=50$ k$\mathrm{\Omega }$).

Moreover, taking a look at Figure 3, the phenomenon of antimonotonicity is observed. Antimonotonicity, introduced by Dawson et al. [29], is the phenomenon where the system traverses to chaotic behavior as the bifurcation parameter increases, starting from a period of 1 and following a period doubling route to chaos (i.e., period-1 → period-2 → period-4 → ... → chaos) and then leaves the chaotic region, falling back into period-1, by following a reverse period halving route (i.e., chaos→ ... → period-4 → period-2 → period-1). This phenomenon is distinctly depicted in the continuation diagram by a bubble shape. This behavior is again confirmed from the circuit implementation in Figure 7 as the circuit enters chaos by following a period doubling sequence (Figure 7a–d and exits from chaos by following a reverse period halving sequence Figure 7h–j.

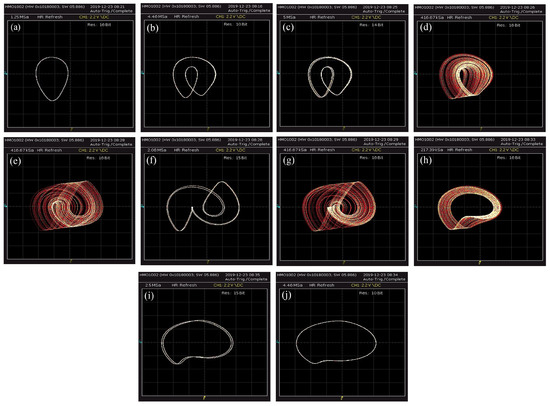
Figure 7. Experimental observation of ${\upsilon }_{C_2}$ versus ${\upsilon }_{C_1}$, of (a) period-1 phase portrait for $R_b=50$ k$\mathrm{\Omega }$ ($b=0.2$), (b) period-2 phase portrait for $R_b=40$ k$\mathrm{\Omega }$ ($b=0.25$), (c) period-4 phase portrait for $R_b=38.16k\mathrm{\Omega }$ ($b=0.262$), (d) chaotic phase portrait for $R_b=38$ k$\mathrm{\Omega }$ ($b=0.263$), (e) chaotic phase portrait for $R_b=25$ k$\mathrm{\Omega }$ ($b=0.4$), (f) period-2 phase portrait for $R_b=19.05$ k$\mathrm{\Omega }$ ($b=0.525$), (g) chaotic phase portrait for $R_b=14.3$ k$\mathrm{\Omega }$ ($b=0.699$), (h) chaotic phase portrait for $R_b=11$ k$\mathrm{\Omega }$ ($b=0.909$), (i) period-2 phase portrait for $R_b=10.1$ k$\mathrm{\Omega }$ ($b=0.99$), and (j) period-1 phase portrait for $R_b=9.09$ k$\mathrm{\Omega }$ ($b=1.1$). The rest of parameters are $a=4\times {10}^{-4}$, $c=3.846\times {10}^{-4}$ and $d=e=1$.

Finally, a periodic window appears in the continuation diagram around $b=0.55$. This is experimentally captured in Figure 7f. This periodic behavior appears in-between two chaotic regions, which are also captured in Figure 7e,g.

4.2. Dynamical Behavior with Respect to d

Considering the dynamical behavior with respect to d, the rest of the parameters are chosen as: $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$ and $e=1$, with initial conditions $(x_0,y_0,z_0)=(0,0.1,0)$, while d plays the role of the control parameter.

Figure 8 shows the bifurcation and continuation diagram of variable x versus parameter d, which takes values in the range $d\in [1,20]$. By studying this figure the route to chaos through the mechanism of period doubling as the value of parameter d is decreased, is observed from both the diagrams.

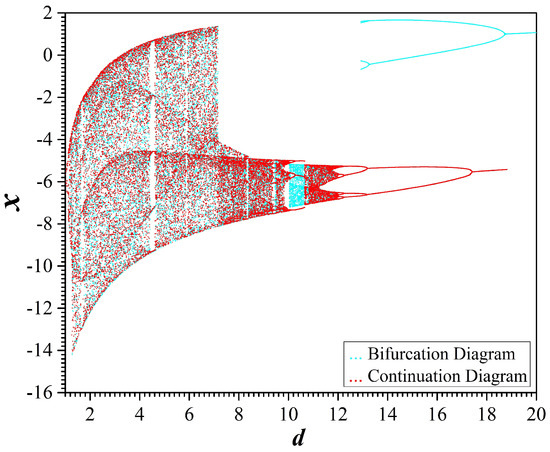
Figure 8. Bifurcation diagram (cyan) and continuation diagram (red) of system (2), when parameter d is increased, for $a=4\times {10}^{-4}$, $b=$ 1, $c=3.846\times {10}^{-4}$ and $e=1$, when parameter d is increased.

Also, comparing the bifurcation and continuation diagrams of variable x versus parameter d (Figure 8), another interesting feature arises. The coexistence of different system’s attractors in two ranges ($[10.02,10.61]$ and $[12.89,20]$) of values of parameter d can be observed. In Figure 9, Figure 10, Figure 11, Figure 12 and Figure 13 five different couples of attractors for various values in the aforementioned ranges and for different initial conditions are depicted, confirming the phenomenon of coexisting attractors. The coexisting attractors, as well as their values of d, have been cited in Table 1.

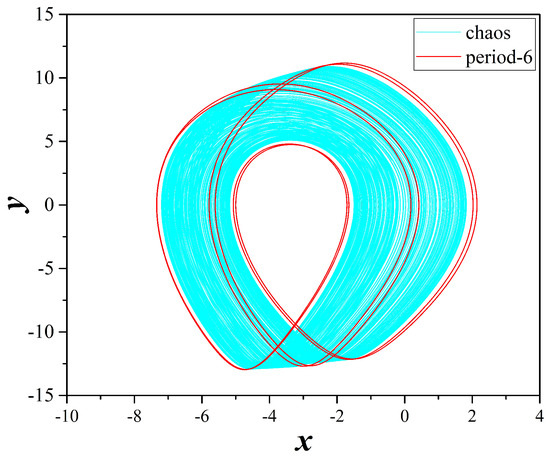
Figure 9. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $e=1$ and $d=10.1$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a chaotic attractor, while with red color and $(x_0,y_0,z_0)=(-5.7896825,0,2.9007334)$ a period-6 attractor.

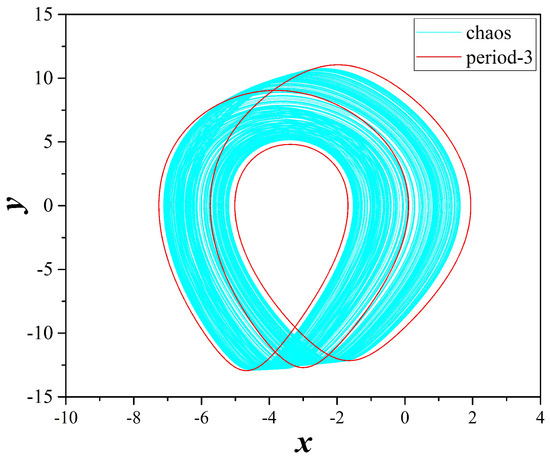
Figure 10. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $e=1$ and $d=10.5$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a chaotic attractor, while with red color and $(x_0,y_0,z_0)=(-5.7439696,0,2.8417025)$ a period-6 attractor.

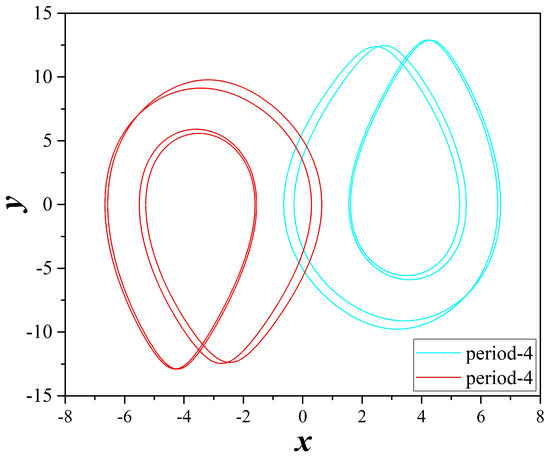
Figure 11. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $e=1$ and $d=13$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a period-4 attractor, while with red color and $(x_0,y_0,z_0)=(-6.5697976,0,2.5822365)$ a symmetric period-4 attractor.

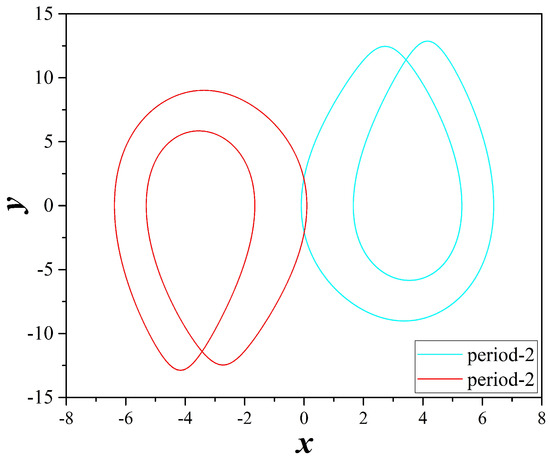
Figure 12. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $e=1$ and $d=15$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a period-2 attractor, while with red color and $(x_0,y_0,z_0)=(-5.3107692,0,1.7241613)$ a symmetric period-2 attractor.

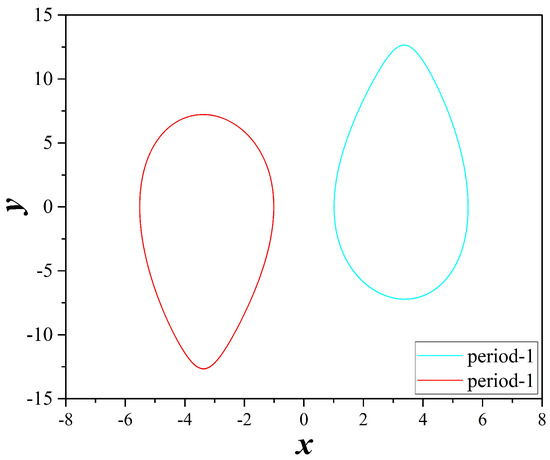
Figure 13. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $e=1$ and $d=19$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a period-1 attractor, while with red color and $(x_0,y_0,z_0)=(-5.5160634,0,1.737452)$ a symmetric period-1 attractor.

Table 1. Coexisting attractors as they are observed from the comparison of the bifurcation diagram with the respective continuation diagram of variable x versus the parameter d, for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $e=1$.

Value of Parameter d	Behavior from the Bifurcation Diagram	Behavior from the Continuation Diagram
10.1	Chaos	Period-6
10.5	Chaos	Period-3
13.0	Period-4	Period-4 (symmetric)
15.0	Period-2	Period-2 (symmetric)
19.0	Period-1	Period-1 (symmetric)

4.3. Dynamical Behavior with Respect to e

The same behavior has been observed from the comparison of the bifurcation diagram with the respective continuation diagram of variable x versus the parameter e (Figure 14). As parameter e increases the system is driven to chaos through the mechanism of period doubling. However, the coexistence of different attractors is revealed in some regions of values of the parameter e, especially at its route to chaos (Figure 15, Figure 16, Figure 17 and Figure 18). Table 2 presents the coexisting attractors in four different values of parameter e.

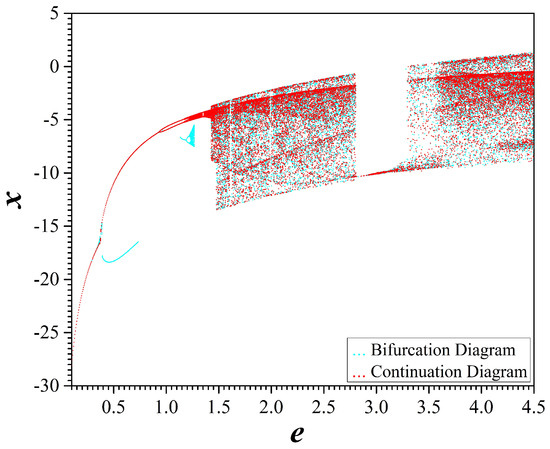
Figure 14. Bifurcation diagram (cyan) and continuation diagram (red) of system (2), when parameter e is increased, for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$ and $d=1$, when parameter e is increased.

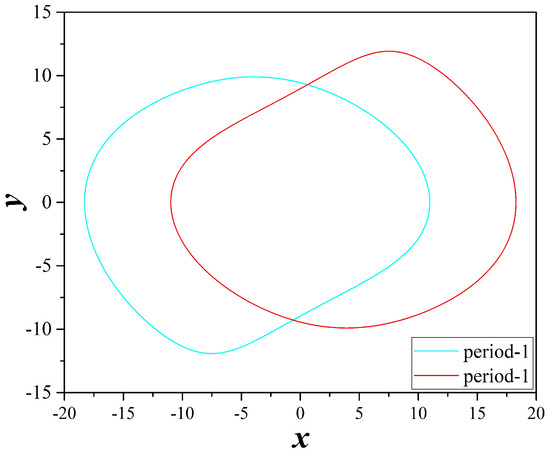
Figure 15. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $d=1$ and $e=0.50$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a period-1 attractor, while with red color and $(x_0,y_0,z_0)=(-10.969297,0,4.5870237)$ a symmetric period-1 attractor.

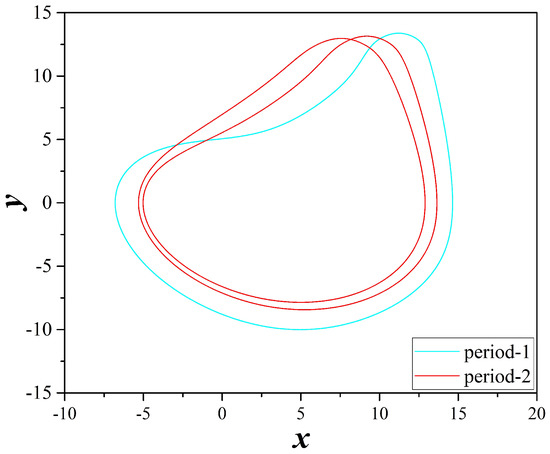
Figure 16. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $d=1$ and $e=1.15$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a period-1 attractor, while with red color and $(x_0,y_0,z_0)=(-5.3168311,0,4.9638148)$ a period-2 attractor.

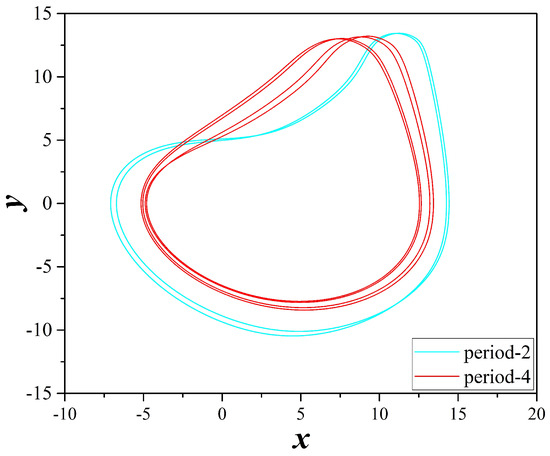
Figure 17. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $d=1$ and $e=1.20$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a period-2 attractor, while with red color and $(x_0,y_0,z_0)=(-4.7922951,0,4.3626296)$ a period-4 attractor.

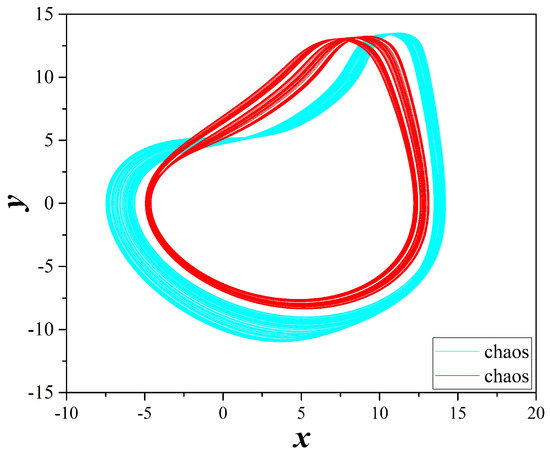
Figure 18. Coexisting attractors of system (2), for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $d=1$ and $e=1.26$. With cyan color and for $(x_0,y_0,z_0)=(0,0.1,0)$ a chaotic attractor, while with red color and $(x_0,y_0,z_0)=(-4.6300732,0,4.5716944)$ a different chaotic attractor.

Table 2. Coexisting attractors as they are observed from the comparison of the bifurcation diagram with the respective continuation diagram of variable x versus the parameter e, for $a=4\times {10}^{-4}$, $b=1$, $c=3.846\times {10}^{-4}$, $d=1$.

Value of Parameter e	Behavior from the Bifurcation Diagram	Behavior from the Continuation Diagram
0.50	Period-1	Period-1 (symmetric)
1.15	Period-1	Period-2
1.20	Period-2	Period-4
1.26	Chaos	Chaos (symmetric)

5. Conclusions

In this work, an optimization method of a circuit’s chaoticity was presented. For this reason an autonomous chaotic circuit, with a single nonlinear element, which was a bi-color LED described by a hyperbolic sine function, was used. In this circuit one more bi-color LED was added. The three dimensional dynamical system, which described the new nonlinear autonomous circuit, presented a collection of chaotic phenomena, like antimonotonicity, period doubling route to chaos and coexisting attractors. Also, the addition of the second nonlinear term in the system has as a consequence the increase of system’s chaoticity, which was confirmed by the calculation of the maximal Lyapunov exponents and the Kaplan-Yorke dimension. Finally, the resulting circuit, having complex dynamics, albeit a simple structure, is suitable for use in applications related to chaos synchronization and secure communications. Thus, it is among our future research interests to utilize the system in such a design. Firing phenomena can also be explored [30]. Also, fractional versions of the system can be developed and also implemented in circuits, which is another promising field of study [3,31].