1. Introduction
Phase-locked loops (PLLs) are widely implemented in radio, wired and wireless telecommunication, clock generation, and other electronic applications. Because high-performance system-on-chip (SoC) requires multiple simultaneously generated frequencies, several frequency generators need to be implemented in the system. These frequencies can be generated and synchronised by using a PLL. It is a closed-loop system that uses the phase-locking technique to align the output signal phase in phase with the input signal phase.
PLLs are classified into analogue and digital PLLs [
1]. Analogue PLLs provide good phase-noise performance and high accuracy with the cost of a large chip size and high power consumption due to the analogue nature of the loop filter [
2]. In contrast to an analogue PLL, digital PLLs consume less power and area while compromising linearity, as the generated frequency can only be varied in discrete steps limited by the resolution of the control bits [
3]. On the other hand, the digital PLL provides short locking time and strong robustness against process, voltage, and temperature (PVT) changes due to the lack of analogue components [
4]. Digital PLL can benefit for the shorter locking time depends on their controller type such as SAR [
5]. Because of their larger locking step, they can reach correct locking point faster compared to analogue PLL despite digital PLL suffers from limited resolution. On the other hand, analogue PLL has an infinite resolution, therefore it provides much smaller locking step to achieve correct locking point with smaller phase error compared to digital PLL [
6]. At the same time, a digital PLL suffers from several disadvantages in terms of jitter and phase-noise performance when compared to an analogue PLL.
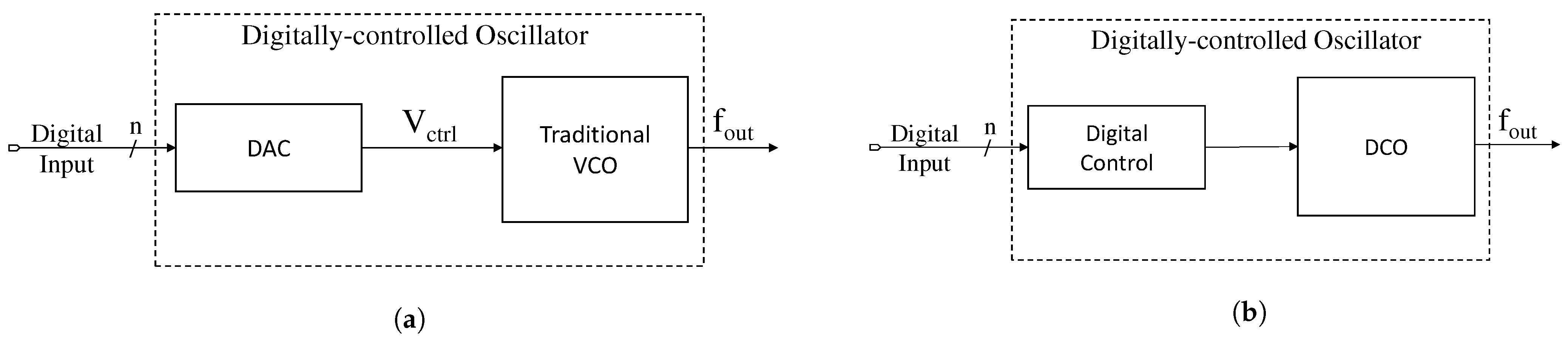
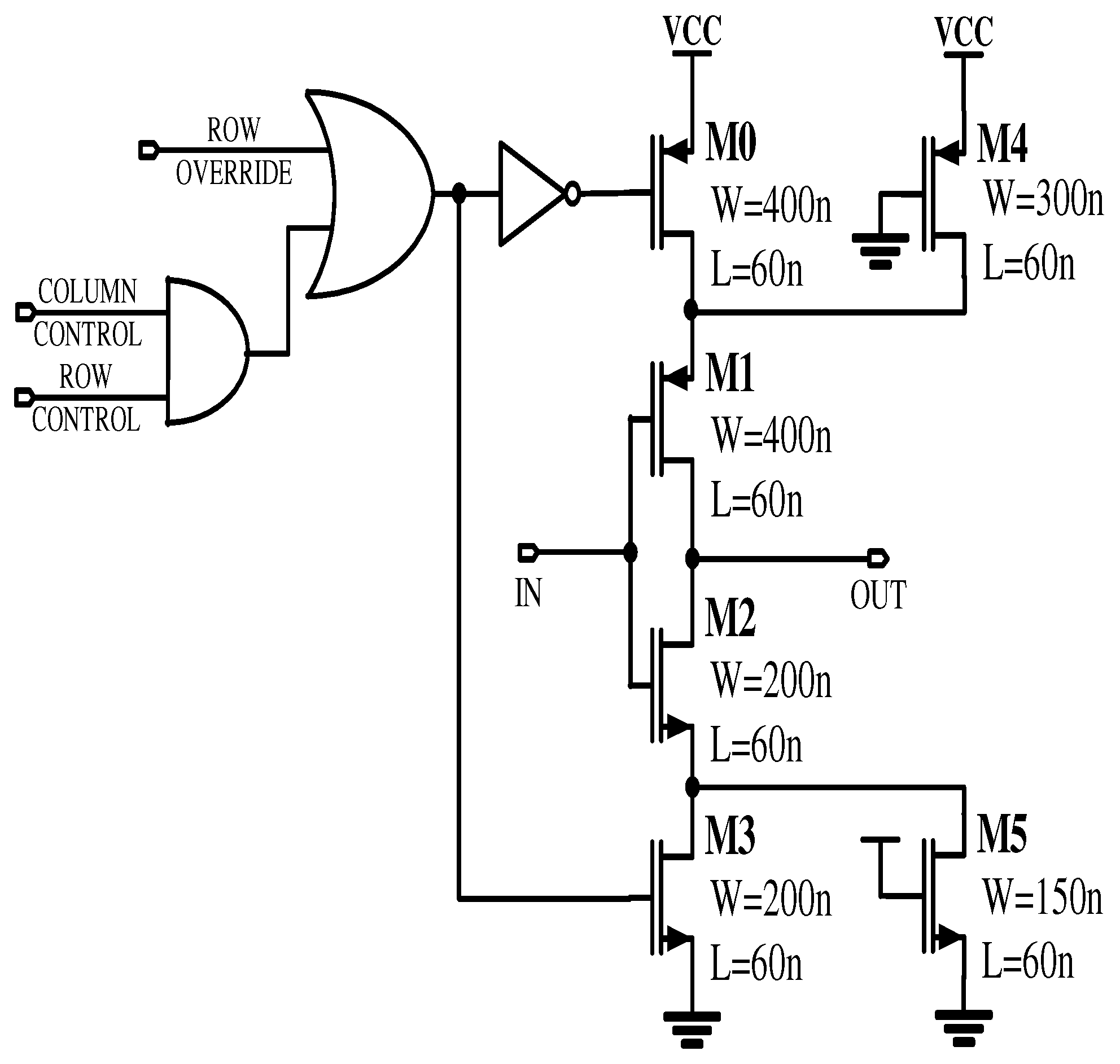
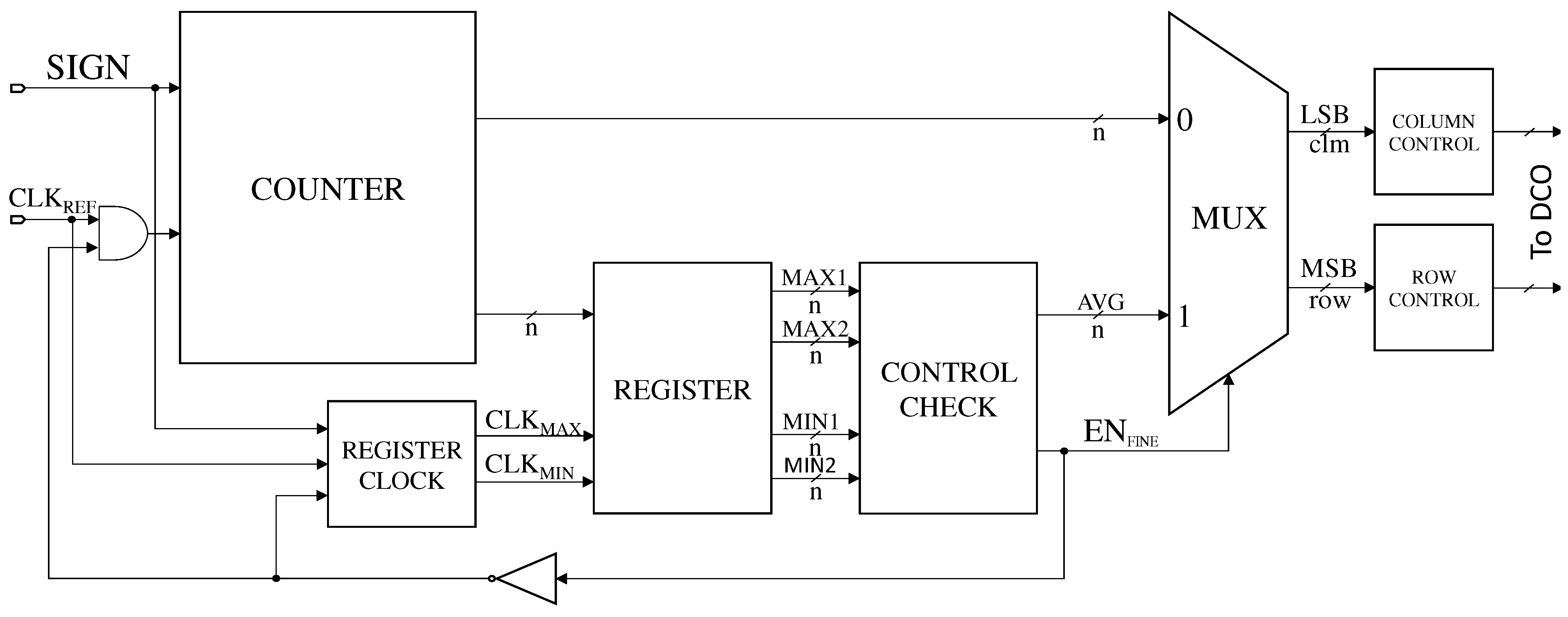
The most crucial part of the digital PLL is the digitally-controlled oscillator (DCO) that generates a periodic signal whose frequency is achieved by digital control input code. It decides the overall performance, such as phase noise and jitter, tuning range, power consumption, and the total occupied area. In this regard, two common types of DCO exist: LC-based DCOs and ring-oscillator based DCOs. The LC-based DCO gives better phase-noise performance and resolution, but it occupies a larger chip area, consumes more power, and suffers from higher degree of mutual coupling between oscillators. A ring-oscillator based DCO occupies a significantly smaller area and it is less susceptible towards PVT changes. A DCO can be realised in two different approaches, as presented in
Figure 1. The first approach, as seen in
Figure 1a, is a hybrid approach, where the traditional voltage-controlled oscillator (VCO) is used with a digital-to-analogue converter (DAC) to be integrated with the rest of the digital PLL. The advantage of this system is that the VCO requires a minimal redesign from analogue to digital PLL to adapt to the control voltage that is given by the DAC. However, the performance of these components strongly depends on their analogue behaviour of the DAC, restricting the key advantage of the digital PLL system. The second approach, as shown in
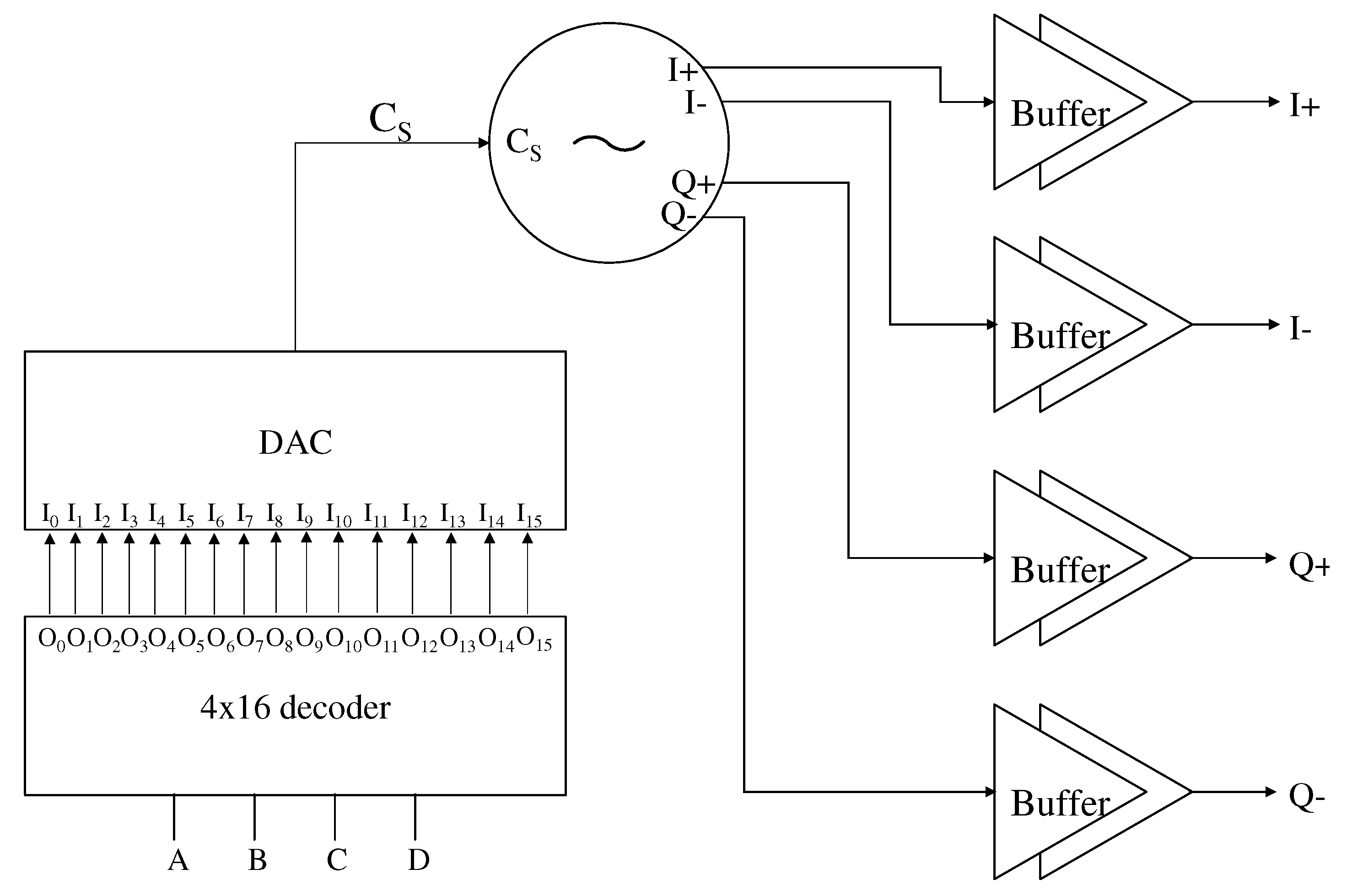
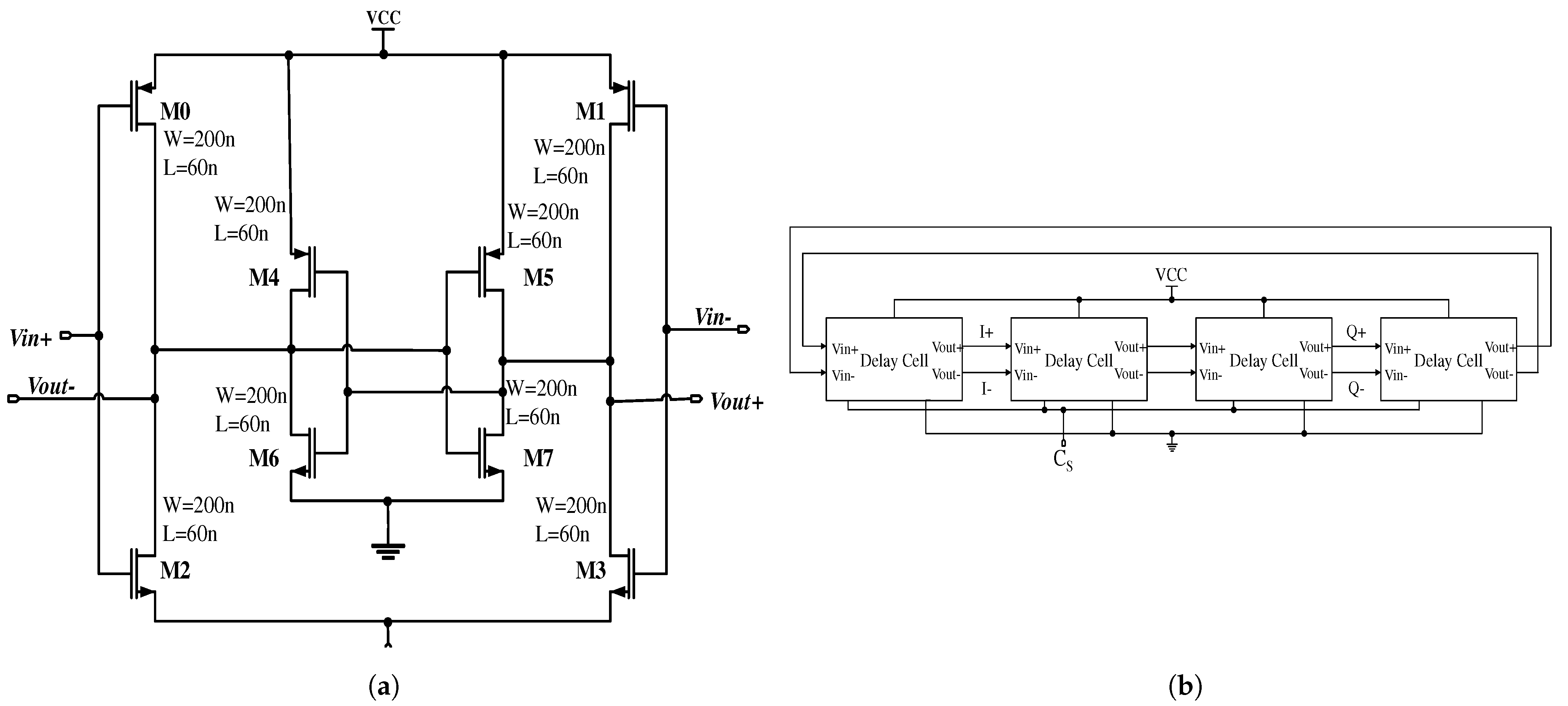
Figure 1b, utilises a digital control mechanism for frequency tuning. In inverter-based ring oscillators, inverters that make the ring are classified into addressable components. The frequency is then tuned by increasing or decreasing the effective delay in the inverters. This is achieved by turning on or off the transistors that can tune the total delay time of each cell in the ring oscillator. This paper compares the performance of the DCO that is controlled by the analogue and digital behaviour of the system.
The paper is structured, as follows:
Section 2 describes the two different implementation for the DCO. The simulation result and comparison of the two implementations are presented in
Section 3 and, finally, conclusions are given in
Section 4.
3. Layout and Simulation Results
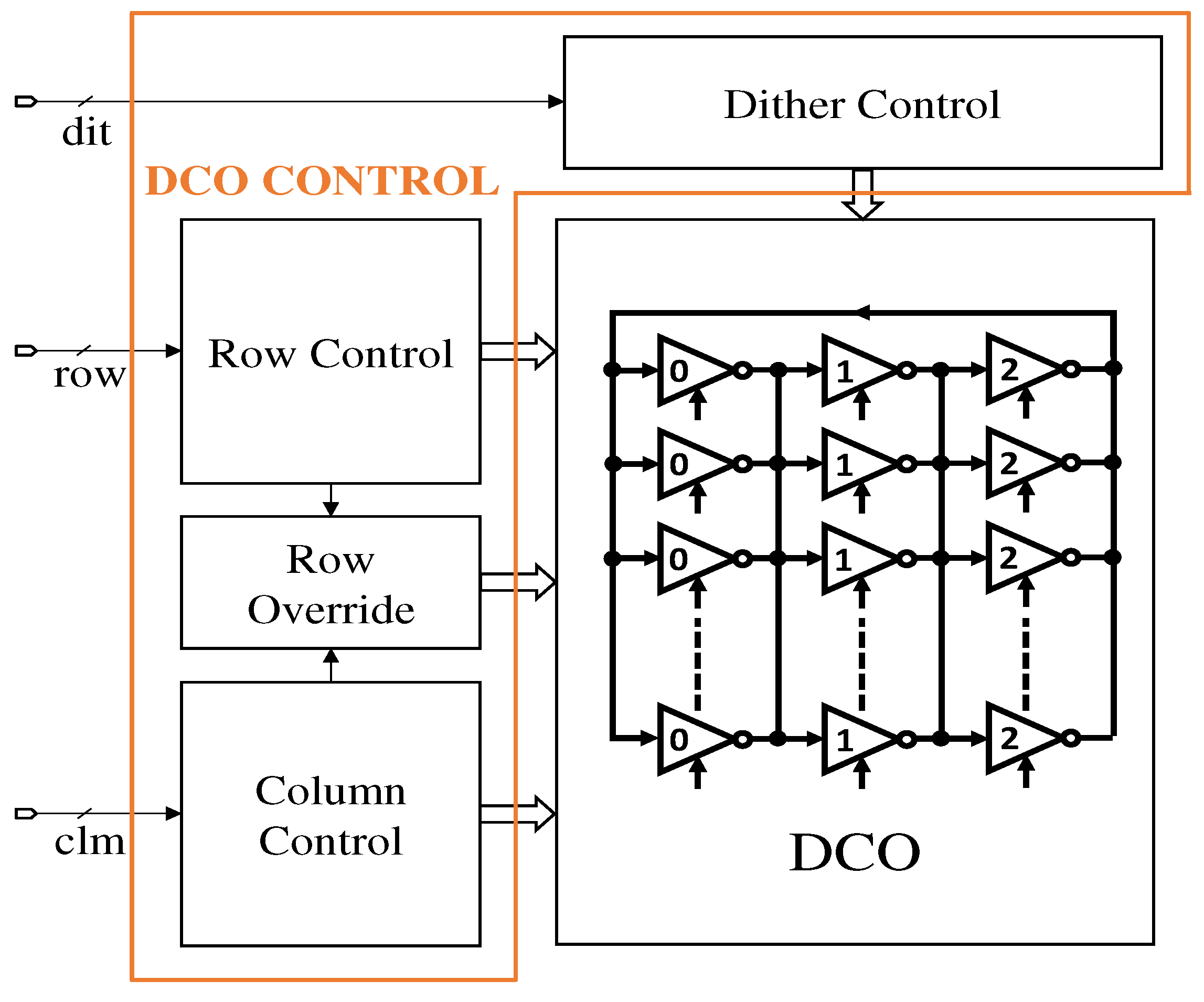
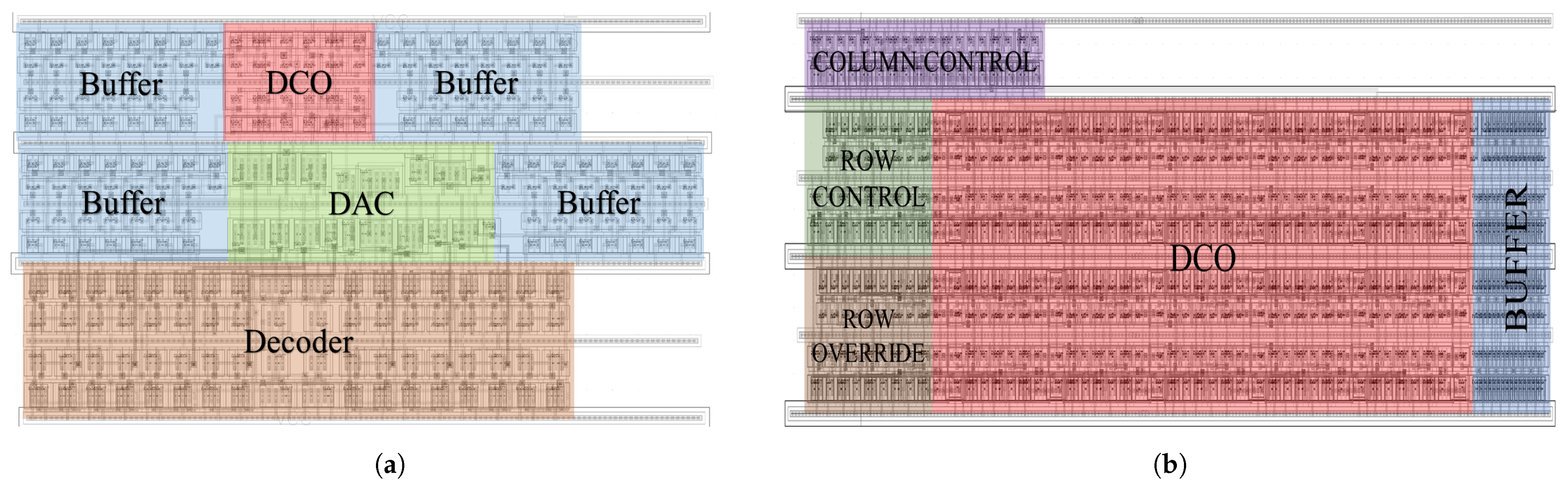
The layouts of the DAC-based DCO and the controller-based DCO with an area of 36.33 μm
2 and 550 μm
2 in TSMC 65 nm CMOS technology, respectively, are shown in
Figure 8. The blank space on the top in the controller-based DCO can be used for implementing the dither control, which makes the layout more compact. All of the simulations are performed with extracted RC parasitics from the layout. Whereas, the DAC-based differential ring oscillator oscillates between
and
, consuming an average power of
. The designed controller-based DCO operates between
and
, and it consumes an average power of
. Both of the oscillators operates from
and the power is measured with the oscillators running at their highest frequency along with their control circuit and the buffers.
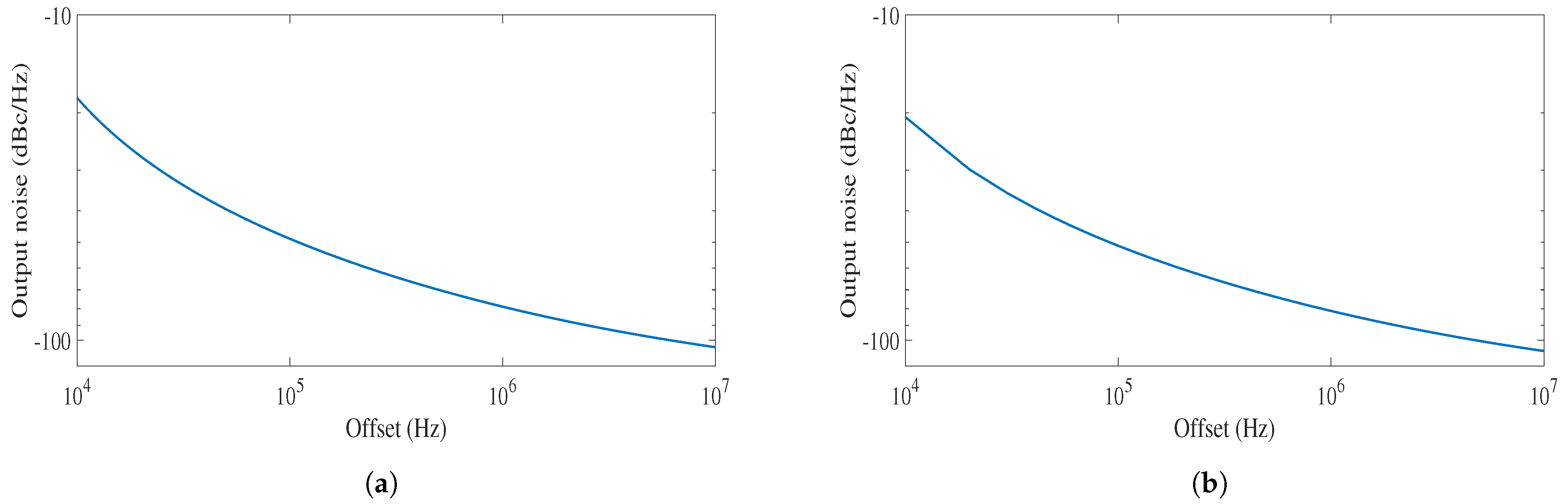
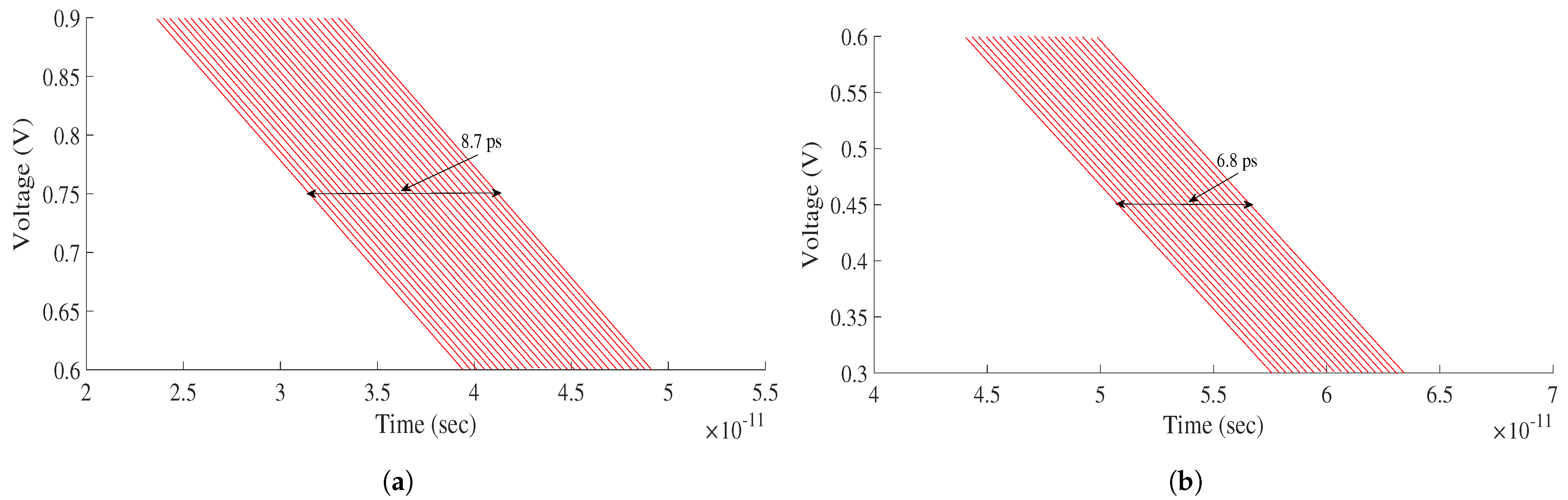
Figure 9 sows the phase noise characteristics of the free running oscillator in both types. The phase noise performance can be improved by using the DCO in a closed-loop system with proper loop filter adjustment. The phase noise of the DAC-based DCO and controller-based DCO at 2.2 GHz and 6.4 GHz is −78.9 dBc/Hz and −81.3 dBc/Hz at 1 MHz offset, respectively. The jitter performance of the DCOs is measured from the eye diagram at their highest operating frequency. The peak-to-peak jitter obtained for the DAC-based DCO is 8.7 ps and for the controller-based DCO is 6.8 ps at 2.2 GHz and 6.4 GHz, respectively, as shown in
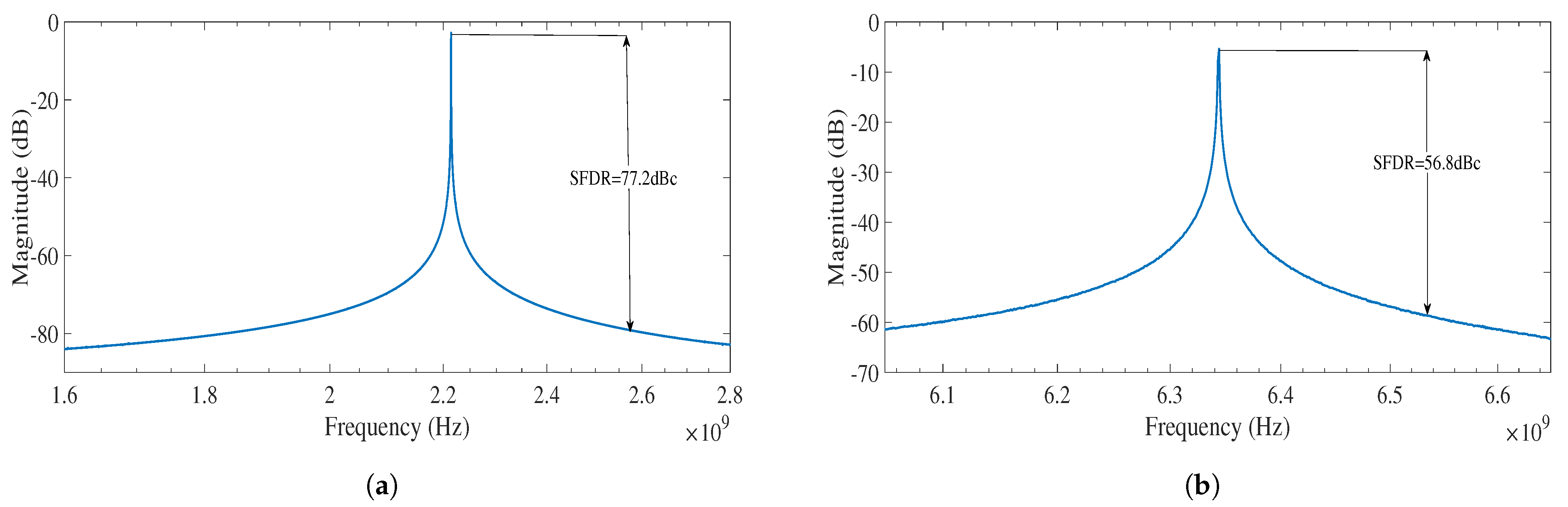
Figure 10. The spectrum of the DAC-based DAC at 2.2 GHz and controller-based DCO at 6.34 GHz is shown in
Figure 11. The spectrum is a measure of distortions to the signal by other noise sources. The Spurious Free Dynamic Range (SFDR) of the DAC-based and controller-based DCO at 125 MHz is 77.2 dBc and 56.8 dBc, respectively. DAC-based and controller-based DCOs both show a linear behaviour with increase in input control bits. Monte Carlo simulations are performed for both the DAC-based and controller-based DCOs, and the deviation of 7.4% and 8.5% was observed in the output frequency.
Table 1 shows a comparison with state-of-the-art ADPLL. The DAC-based DCO and controller-based DCO outperform the state-of-the-art designs in terms of area and power consumption. The implemented DAC-based DCO gives an advantage in terms of the resolution and step size of the frequency shifting of the ring oscillator due to the analogue behaviour of the design. On the other hand, the proposed design may suffer from the process variation since the size relation between current charging transistors in the DAC directly affect the analogue output control voltage that changes based on digital input data. The second implementation which is the fully digital controller-based DCO does not require any precise current charging capability. Thus, the process variation can have a less effect on the working principle of the proposed controller. Additionally, since this locking step primarily controlled by the SIGN signal generated by a conventional phase detector, the robustness of the controller is further improved against process variation as compared to the conventional time-to-digital converter (TDC) based controller, which makes them sensitive to the any changes in resolution. The Figure-of-Merit for jitter (FOM
jitter) of the DAC-based and controller-based DCO outperform [
8], and they are almost the same with [
9]. The [
10] is based on the schematic simulation, hence the FOM
jitter is better than the proposed designs. The DCO in [
11] is designed using 28
technology and it uses LC-tank based architecture. Hence, the phase noise performance of [
11] is better than the DAC-based and controller-based DCO. However, its active area is much larger than the proposed DAC-based and controller-based DCO in spite of the DCO that was implemented in 28
. The DAC-based DCO and controller-based DCO outperform [
8,
9] in terms of peak-to-peak jitter performance. The proposed design uses a simple architecture and it occupies a less active area. Hence, for SoC applications where multiple PLLs are required, the introduced locking techniques, especially the fully digital controller-based DCO, occupy smaller active with comparable performance compared to state-of-the-art designs.
4. Conclusions
A DAC-based DCO and controller-based DCO are designed using TSMC 65 CMOS technology. The DAC-based DCO is designed with four digitally-controlled differential stages leading to a tuning range from to . The controller-based DCO is designed with three digitally-controlled stages that can be tuned from to . The DAC-based DCO provides better resolution than the controller-based DCO, as the DAC-based architecture is analogue in nature. However, the resolution of the controller-based architecture can be increased by adding dithering stages controlled by a delta-sigma modulator. For both architectures, the layout is constructed, verified with DRS and LVS, and the parasitic components of the layout version are extracted. The designs are checked for their phase noise performance, peak-to-peak distortions, and for their jitter performance. The designs are small in size and are linear in nature.