Electrical Breakdown Spectroscopy of Nano-/Micro-Thermites
Abstract
1. Introduction
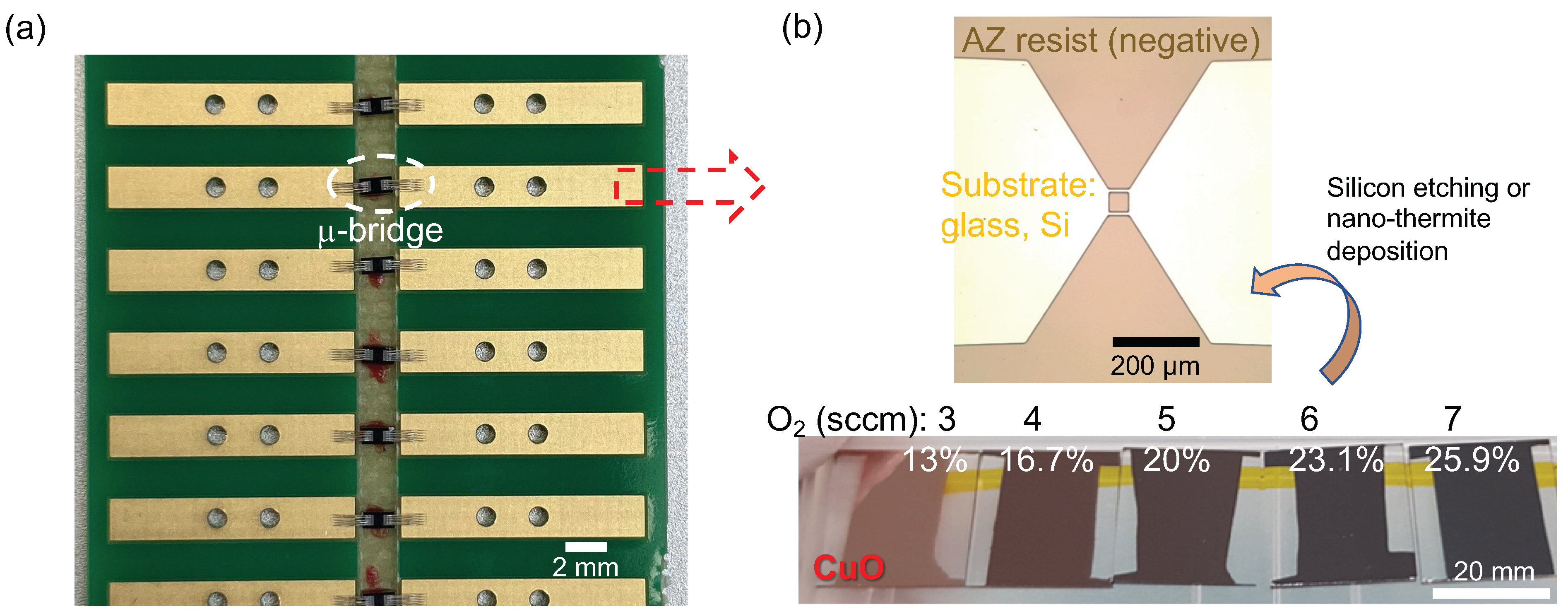
2. Experimental
3. Results and Discussion
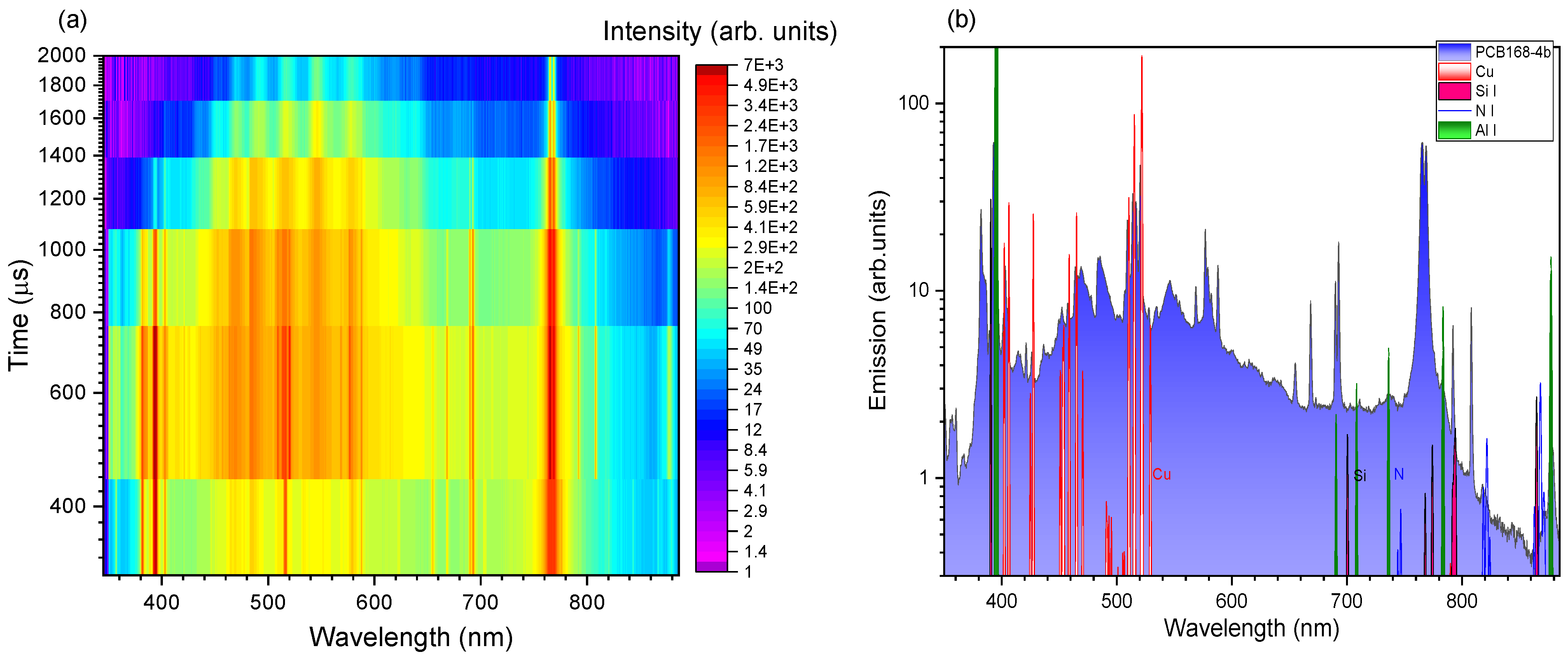
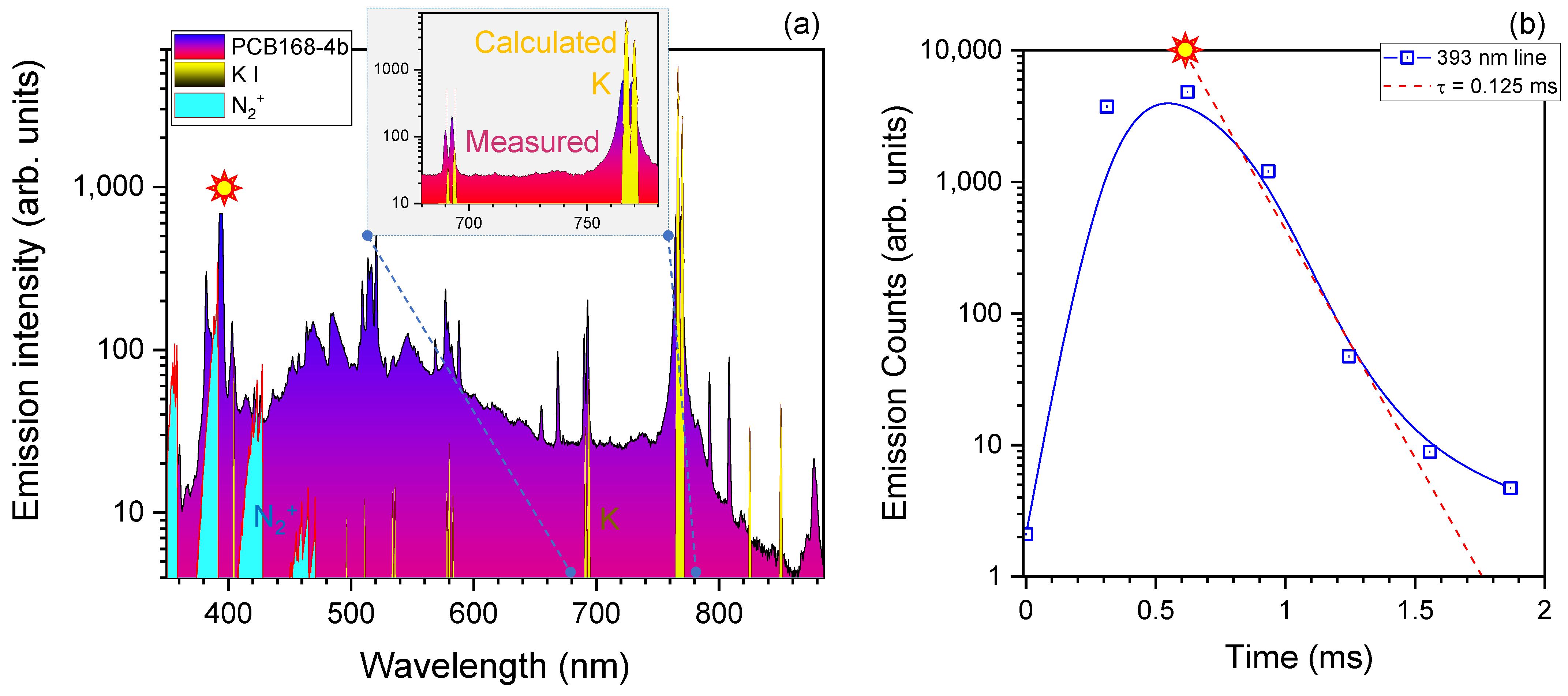
3.1. Optical Signature of Electrical -Thermite’s Breakdown
3.2. Electrical Signature of Plasma Formation
3.3. Scaling Insights from Analytical Formulae and Applications
4. Conclusions and Outlook
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. The Black-Body Radiation Temperature
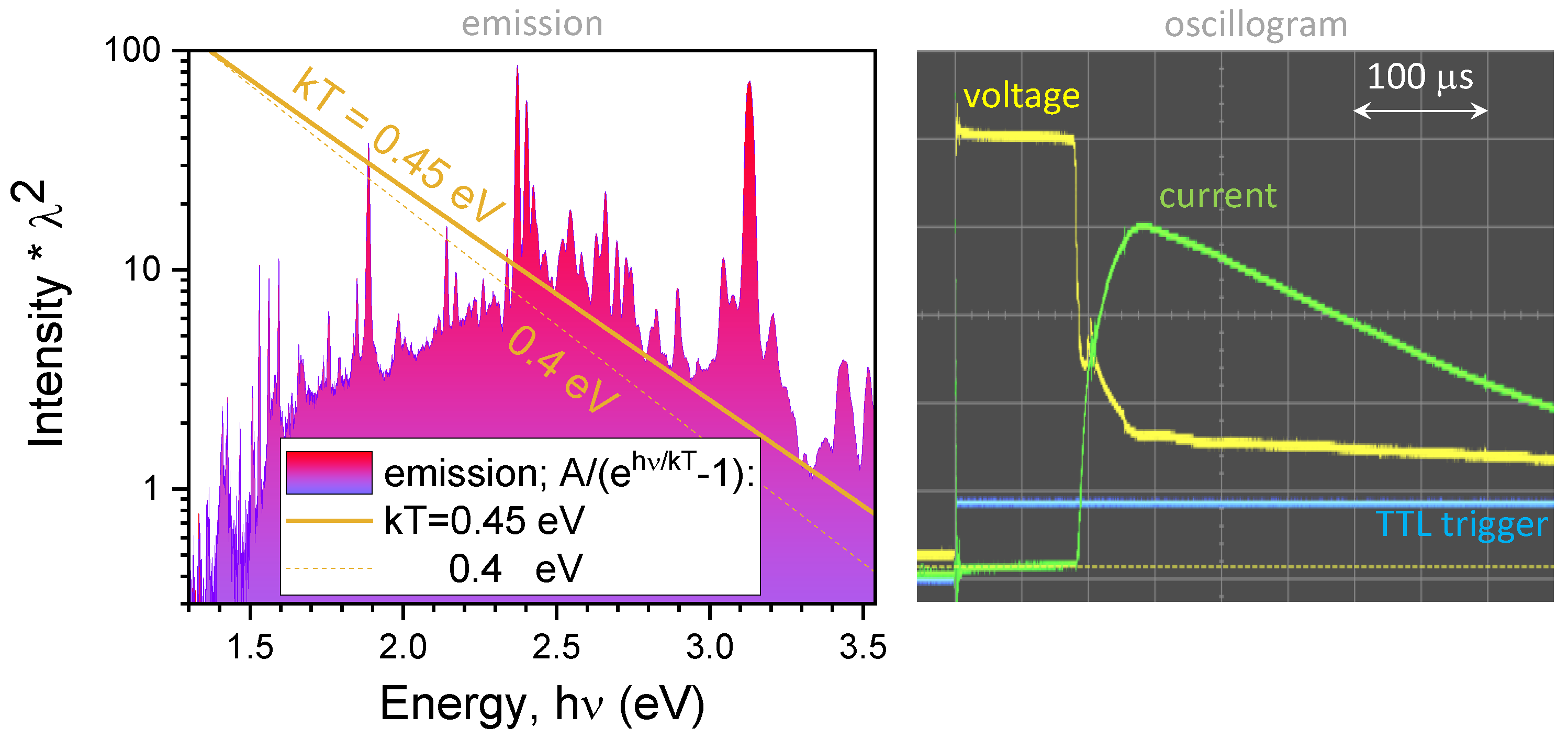
Appendix B. Energy Balance
References
- Betti, R.; Hurricane, O.A. Inertial-confinement fusion with lasers. Nat. Phys. 2016, 12, 435–448. [Google Scholar] [CrossRef]
- Mourou, G.; Tajima, T.; Bulanov, S. Optics in the relativistic regime. Rev. Mod. Phys. 2006, 78, 309–371. [Google Scholar] [CrossRef]
- Gibbon, P.; Förster, E. Short-pulse laser–plasma interactions. Plasma Phys. Control. Fusion 1996, 38, 769–793. [Google Scholar] [CrossRef]
- Torretti, F.; Sheil, J.; Schupp, R.; Basko, M.M.; Bayraktar, M.; Meijer, R.A.; Witte, S.; Ubachs, W.; Hoekstra, R.; Versolato, O.O.; et al. Prominent radiative contributions from multiply-excited states in laser-produced tin plasma for nanolithography. Nat. Commun. 2020, 11, 2334. [Google Scholar] [CrossRef] [PubMed]
- Gorbunov, L.M.; Kirsanov, V.I. Excitation of plasma waves by an electromagnetic wave packet. Sov. Phys. JETP 1987, 66, 290–294. [Google Scholar]
- Schwoerer, H. Particle acceleration with lasers. S. Afr. J. Sci. 2008, 104, 299–304. [Google Scholar]
- Charles, C. Plasmas for spacecraft propulsion. J. Phys. D Appl. Phys. 2009, 42, 163001. [Google Scholar] [CrossRef]
- Gamaly, E.G.; Rode, A.V. Ultrafast re-structuring of the electronic landscape of transparent dielectrics: New material states (Die-Met). Appl. Phys. A 2018, 124, 278. [Google Scholar] [CrossRef]
- Luo, Z.; Li, D.; Su, B.; Zhang, S.; Deng, J. On the time coupling analysis of explosion pressure and intermediate generation for multiple flammable gases. Energy 2020, 198, 117329. [Google Scholar] [CrossRef]
- Maurice, S.; Clegg, S.M.; Wiens, R.C.; Gasnault, O.; Rapin, W.; Forni, O.; Cousin, A.; Sautter, V.; Mangold, N.; Le Deit, L.; et al. ChemCam activities and discoveries during the nominal mission of the Mars Science Laboratory in Gale crater, Mars. J. Anal. At. Spectrom. 2016, 31, 863–889. [Google Scholar] [CrossRef]
- Lasue, J.; Wiens, R.C.; Clegg, S.M.; Vaniman, D.T.; Joy, K.H.; Humphries, S.; Mezzacappa, A.; Melikechi, N.; McInroy, R.E.; Bender, S. Remote laser-induced breakdown spectroscopy (LIBS) for lunar exploration. J. Geophys. Res. 2012, 117, E01002. [Google Scholar] [CrossRef]
- Russo, R.; Mao, X.; Liu, H.; Yoo, J.; Mao, S. Time-resolved plasma diagnostics and mass removal during single-pulse laser ablation. Appl. Phys. A 1999, 69, S887–S894. [Google Scholar] [CrossRef]
- Baginski, T.A.; Systems, R.; Taliaferro, S.L.; Fahey, W.D. Novel Electroexplosive Device Incorporating a Reactive Laminated Metallic Bridge. J. Propuls. Power 2001, 17, 184–189. [Google Scholar] [CrossRef]
- Marín, L.; Nanayakkara, C.E.; Veyan, J.F.; Warot-Fonrose, B.; Joulie, S.; Esteìve, A.; Tenailleau, C.; Chabal, Y.J.; Rossi, C. Enhancing the Reactivity of Al/CuO Nanolaminates by Cu Incorporation at the Interfaces. ACS Appl. Mater. Interfaces 2015. [Google Scholar] [CrossRef]
- Lundgaard, S.; Ng, S.H.; Cahill, D.; Dahlberg, J.; Ruan, D.; Cole, N.; Stoddart, P.R.; Juodkazis, S. Towards Safer Primers: A Review. Technologies 2019, 7, 75. [Google Scholar] [CrossRef]
- Anand, V.; Ng, S.H.; Katkus, T.; Juodkazis, S. Spatio-Spectral-Temporal Imaging of Fast Transient Phenomena Using a Random Array of Pinholes. Adv. Photonics Res. 2020, 1, 2000032. [Google Scholar]
- Atomic Spectra Database. NIST Standard Reference Database 78 (Ver. 5.8). Nat. Inst. Stand. Technol. 2020. [CrossRef]
- Effenberger, A.J., Jr.; Scott, J.R. Effect of Atmospheric Conditions on LIBS Spectra. Sensors 2010, 10, 4907–4925. [Google Scholar] [CrossRef]
- Kaladė, J.; Rinkunas, R.; Purlys, R.; Žilinskas, P.J.; Lozovski, T.; Poškus, A. The Dynamics of the Electric Field Distribution in the Surface of Insulating Film Irradiated by Air Ions. Mater. Sci. 2016, 22, 126–131. [Google Scholar] [CrossRef][Green Version]
- Levchenko, I.; Xu, S.; Cherkun, O.; Baranov, O.; Bazaka, K. Plasma meets metamatertials: Three ways to advance space micropropulsion systems. Adv. Phys. X 2020, 6, 1834452. [Google Scholar]
- Juodkazis, S.; Murazawa, N.; Wakatsuki, H.; Misawa, H. Laser irradiation induced disintegration of a bubble in a glass melt. Appl. Phys. A 2007, 87, 41–45. [Google Scholar] [CrossRef]
- Laux, C.; Spence, T.; Kruger, C.; Zare, R. Optical diagnostics of atmospheric pressure air plasmas. Plasma Sources Sci. Technol. 2003, 12, 125–138. [Google Scholar] [CrossRef]
- Pawłat, J.; Terebun, P.; Kwiatkowski, M.; Tarabová, B.; Kovaľová, Z.; Kučerová, K.; Machala, Z.; Janda, M.; Hensel, K. Evaluation of Oxidative Species in Gaseous and Liquid Phase Generated by Mini-Gliding Arc Discharge. Plasma Chem. Plasma Process. 2019, 39, 627–642. [Google Scholar] [CrossRef]
- Lee, J.; Kim, T.; Ryu, S.U.; Choi, K.; Ahn, G.H.; Paik, J.G.; Ryu, B.; Park, T.; Won, Y.S. Study on the Aging Mechanism of Boron Potassium Nitrate (BKNO3) for Sustainable Efficiency in Pyrotechnic Mechanical Devices. Sci. Rep. 2018, 8, 1–9. [Google Scholar] [CrossRef]
- Žukauskas, A.; Malinauskas, M.; Kadys, A.; Gervinskas, G.; Seniutinas, G.; Kandasamy, S.; Juodkazis, S. Black silicon: Substrate for laser 3D micro/nano-polymerization. Opt. Express 2013, 21, 6901–6909. [Google Scholar] [CrossRef]
- Gervinskas, G.; Seniutinas, G.; Hartley, J.S.; Kandasamy, S.; Stoddart, P.R.; Juodkazis, S. Surface-enhanced Raman scattering sensing on black silicon. Annal. Phys. 2013, 525, 907–914. [Google Scholar] [CrossRef]
- Federation of American Scientists. Military Analysis Network. ES310. Introduction to Naval Weapons Engineering. Course Syllabus: Chemistry. 1998. Available online: https://fas.org/man/dod-101/navy/docs/es310/chemstry/chemstry.htm (accessed on 1 January 2021).
- Sinha, S.; Piekiel, N.; Smith, G.; Morris, C. Investigating aging effects for porous silicon energetic materials. Combust. Flame 2017, 181, 164–171. [Google Scholar] [CrossRef]
- Hora, H. Laser Plasma Physics: Forces and the Nonlinearity Principle; SPIE Press: Bellingham, WA, USA, 2000. [Google Scholar]
- Fujisawa, H.; Ryu, M.; Lundgaard, S.; Linklater, D.; Ivanova, E.; Nishijima, Y.; Juodkazis, S.; Morikawa, J. Direct Measurement of Temperature Diffusivity of Nanocellulose-Doped Biodegradable Composite Films. Micromachines 2011, 11, 738. [Google Scholar] [CrossRef]
- Cebe, P.; Hu, X.; Kaplan, D.; Zhuravlev, E.; Wurm, A.; Arbeiter, D.; Schick, C. Beating the Heat—Fast Scanning Melts Silk Beta Sheet Crystals. Sci. Rep. 2013, 3, 1130. [Google Scholar] [CrossRef]
- Minakova, A.; Morikawa, J.; Ryu, M.; Zhuravlev, E.; Schick, C. Variations of interfacial thermal conductance at melting and crystallization of an indium micro-particle in contact with a solid. Mater. Des. 2021, 201, 109475. [Google Scholar] [CrossRef]
- Lundgaard, S.; Ng, S.H.; Nishijima, Y.; Mazilu, M.; Juodkazis, S. Black Metals: Optical Absorbers. Micromachines 2020, 11, 256. [Google Scholar] [CrossRef] [PubMed]
- Toulouse, A.; Drozella, J.; Thiele, S.; Giessen, H.; Herkommer, A. 3D-printed miniature spectrometer for the visible range with a 100 × 100 μm2 footprint. Light Adv. Manuf. 2020, 1, 5. [Google Scholar]
- Falcinelli, S.; Rosi, M. Production and Characterization of Molecular Dications: Experimental and Theoretical Efforts. Molecules 2020, 25, 4157. [Google Scholar] [CrossRef] [PubMed]
- Mathur, D. Structure and dynamics of molecules in high charge states. Phys. Rep. 2004, 391, 1–1187. [Google Scholar] [CrossRef]
- Juodkazis, K.; Juodkazytė, J.; Grigucevičienė, A.; Juodkazis, S. Hydrogen species within the metals: Role of molecular hydrogen ion . Appl. Surf. Sci. 2011, 258, 743–747. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lundgaard, S.; Ng, S.H.; Cahill, D.; Dahlberg, J.; Allender, J.; Barber, M.; Stephens, J.; Juodkazis, S. Electrical Breakdown Spectroscopy of Nano-/Micro-Thermites. Technologies 2021, 9, 34. https://doi.org/10.3390/technologies9020034
Lundgaard S, Ng SH, Cahill D, Dahlberg J, Allender J, Barber M, Stephens J, Juodkazis S. Electrical Breakdown Spectroscopy of Nano-/Micro-Thermites. Technologies. 2021; 9(2):34. https://doi.org/10.3390/technologies9020034
Chicago/Turabian StyleLundgaard, Stefan, Soon Hock Ng, Damien Cahill, Johan Dahlberg, Jamie Allender, Michael Barber, Joshua Stephens, and Saulius Juodkazis. 2021. "Electrical Breakdown Spectroscopy of Nano-/Micro-Thermites" Technologies 9, no. 2: 34. https://doi.org/10.3390/technologies9020034
APA StyleLundgaard, S., Ng, S. H., Cahill, D., Dahlberg, J., Allender, J., Barber, M., Stephens, J., & Juodkazis, S. (2021). Electrical Breakdown Spectroscopy of Nano-/Micro-Thermites. Technologies, 9(2), 34. https://doi.org/10.3390/technologies9020034






