A Space-Time Correlation Model for MRC Receivers in Rayleigh Fading Channels
Abstract
1. Introduction
2. Background and Previous Works
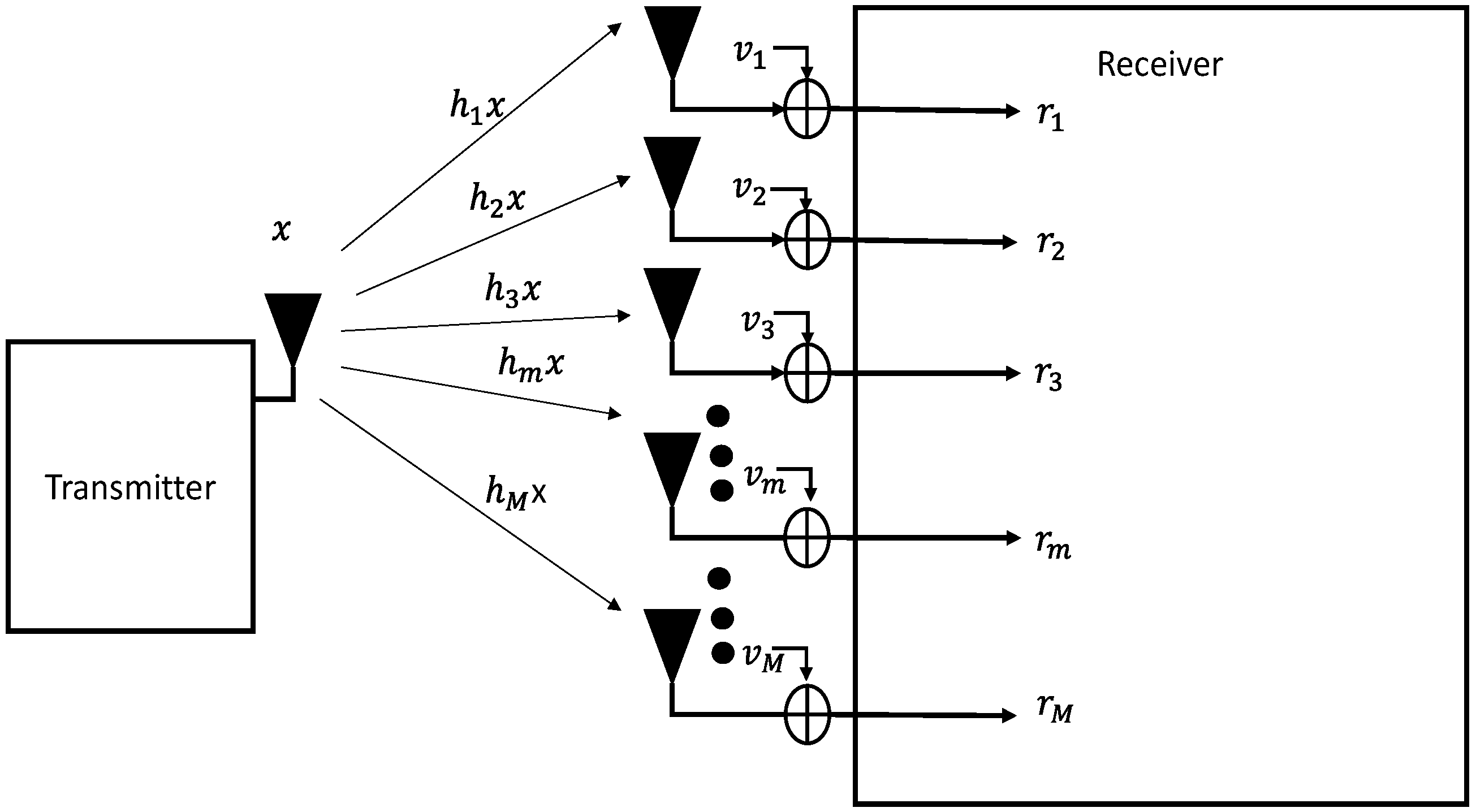
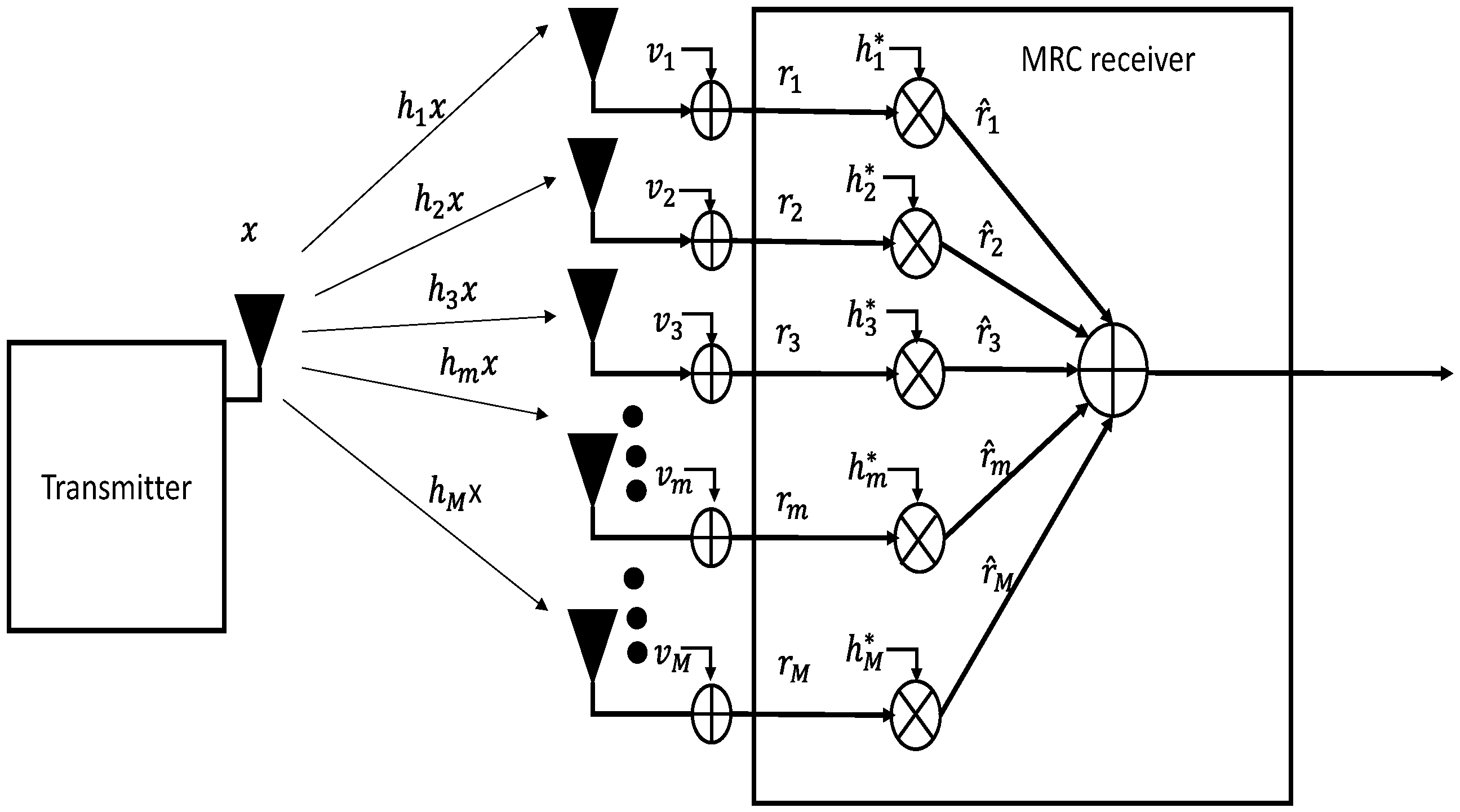
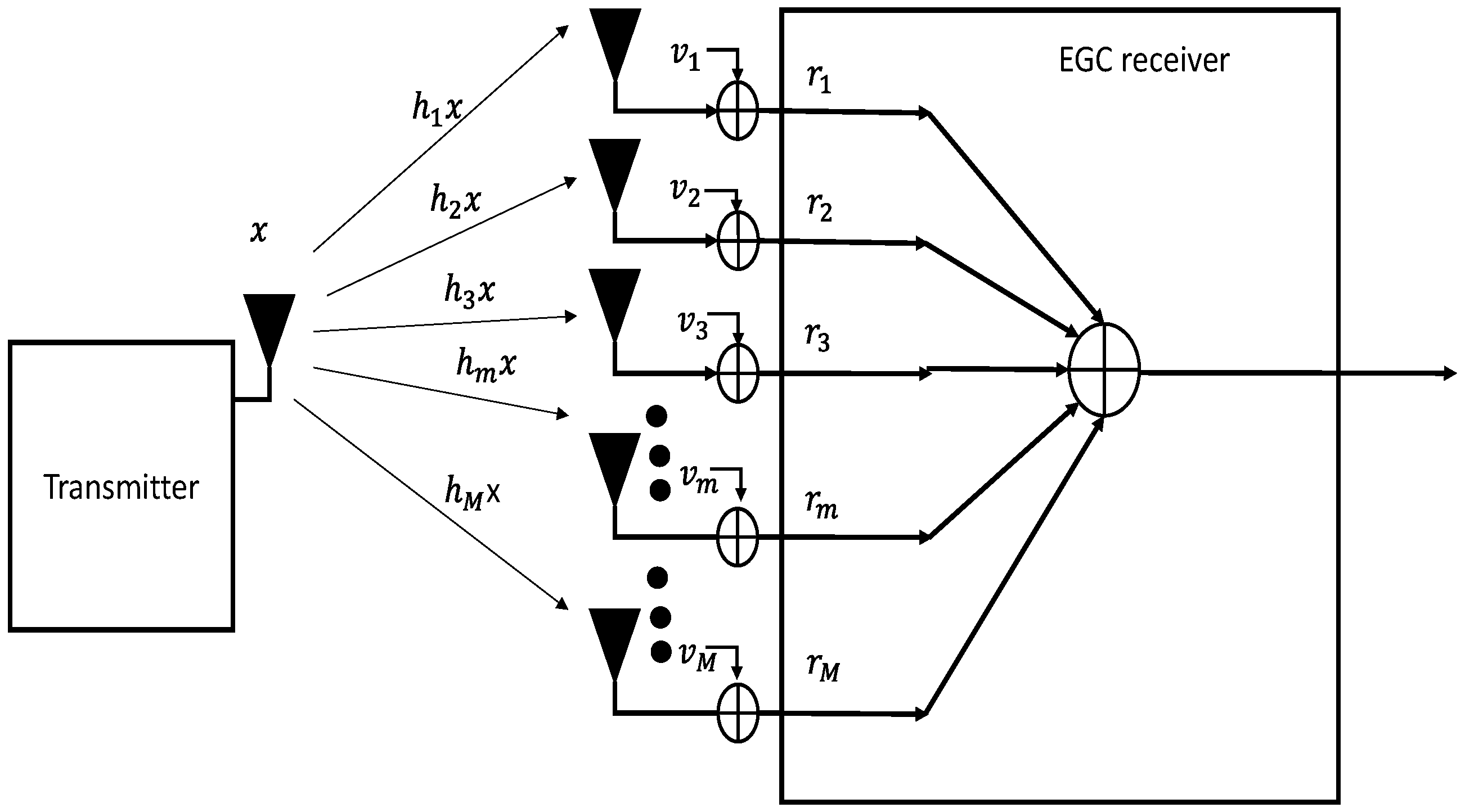
2.1. MRC Receiver Formulation
2.2. Previous Works
- Extension of MRC receivers (conventionally analyzed in the space domain) to the time domain. This means the use of either a retransmission diversity mechanism or a space-time coding repetition approach.
- The MRC performance model uses spatial and temporal correlation coefficients. To the best of our knowledge, this is not commonly used in the literature of MRC receivers, and
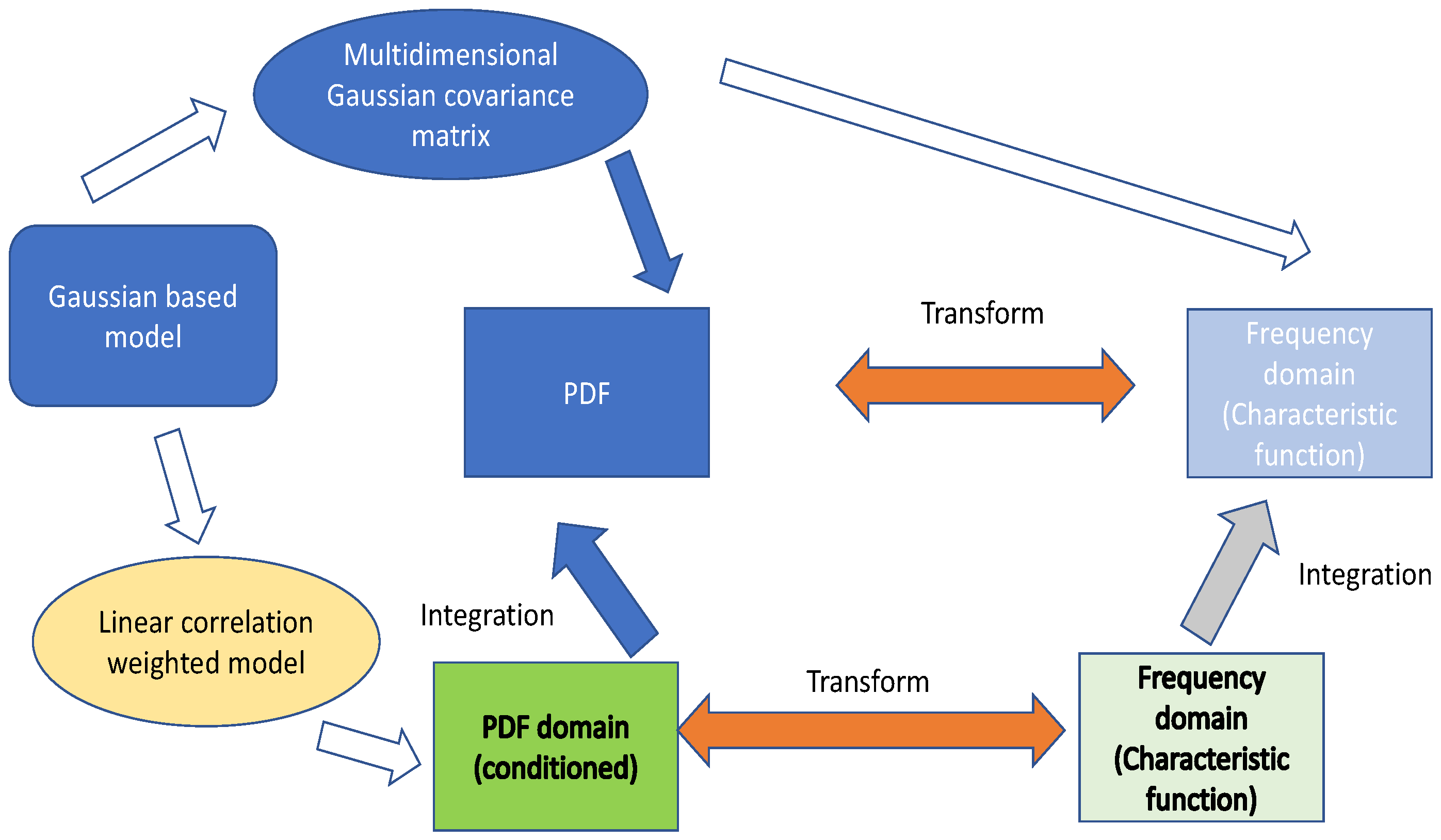
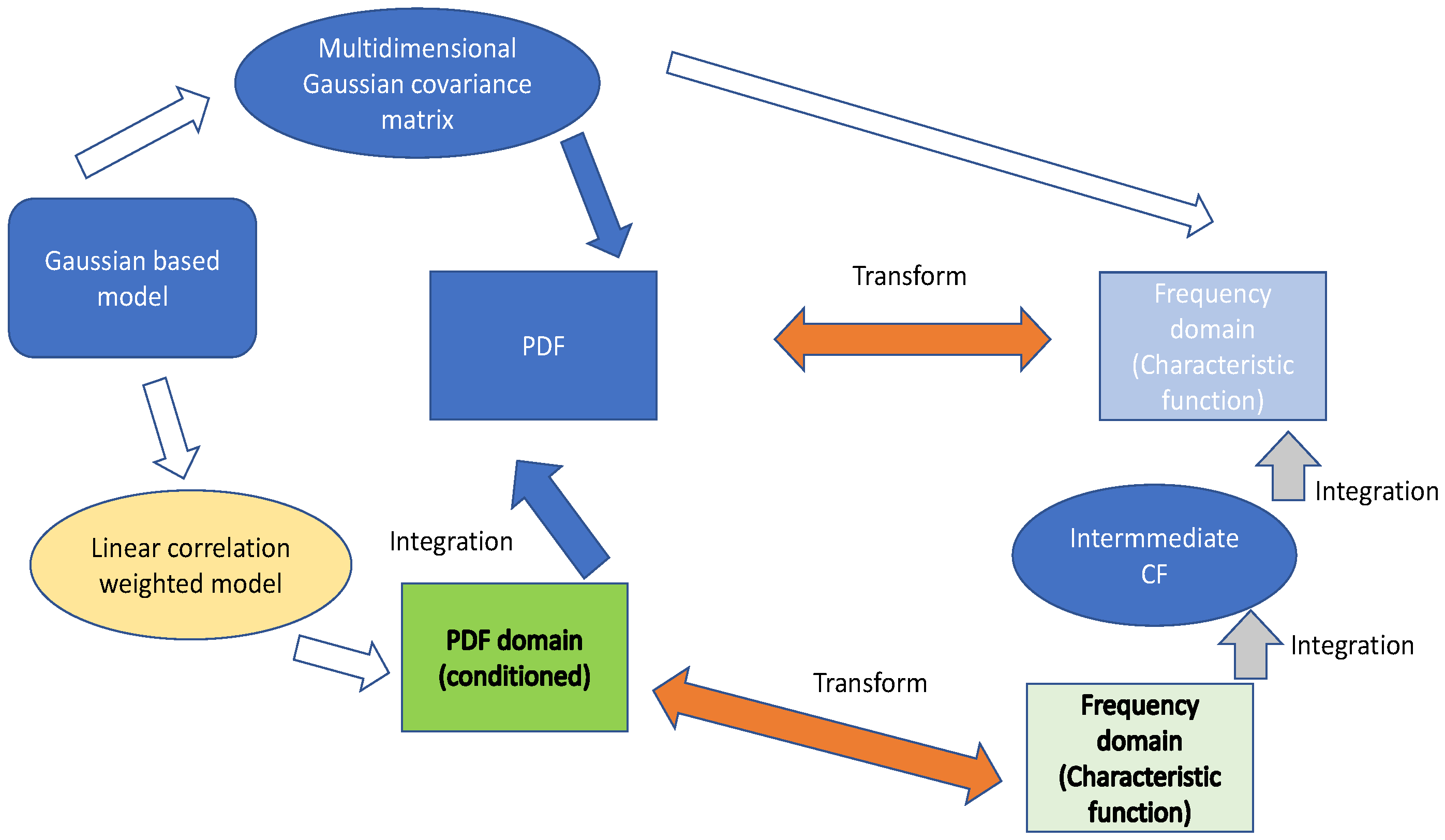
- A frequency-domain approach (via the characteristic function) is used to calculate the statistics of the space-time MRC receiver. The result is a polynomial function whose roots can be obtained via numerical methods. The inverse transform is then used to obtain the exact probability density function (PDF). This is opposed to conventional methodologies where all conditioning and integration work are conducted exclusively in the PDF domain, which in some cases can lead to complex infinite series expressions.
3. System Model
4. Statistics Derivation
4.1. First Stage
4.2. Second Stage
4.3. Third Stage
4.4. Final Statistics
4.5. Adaptive Activation
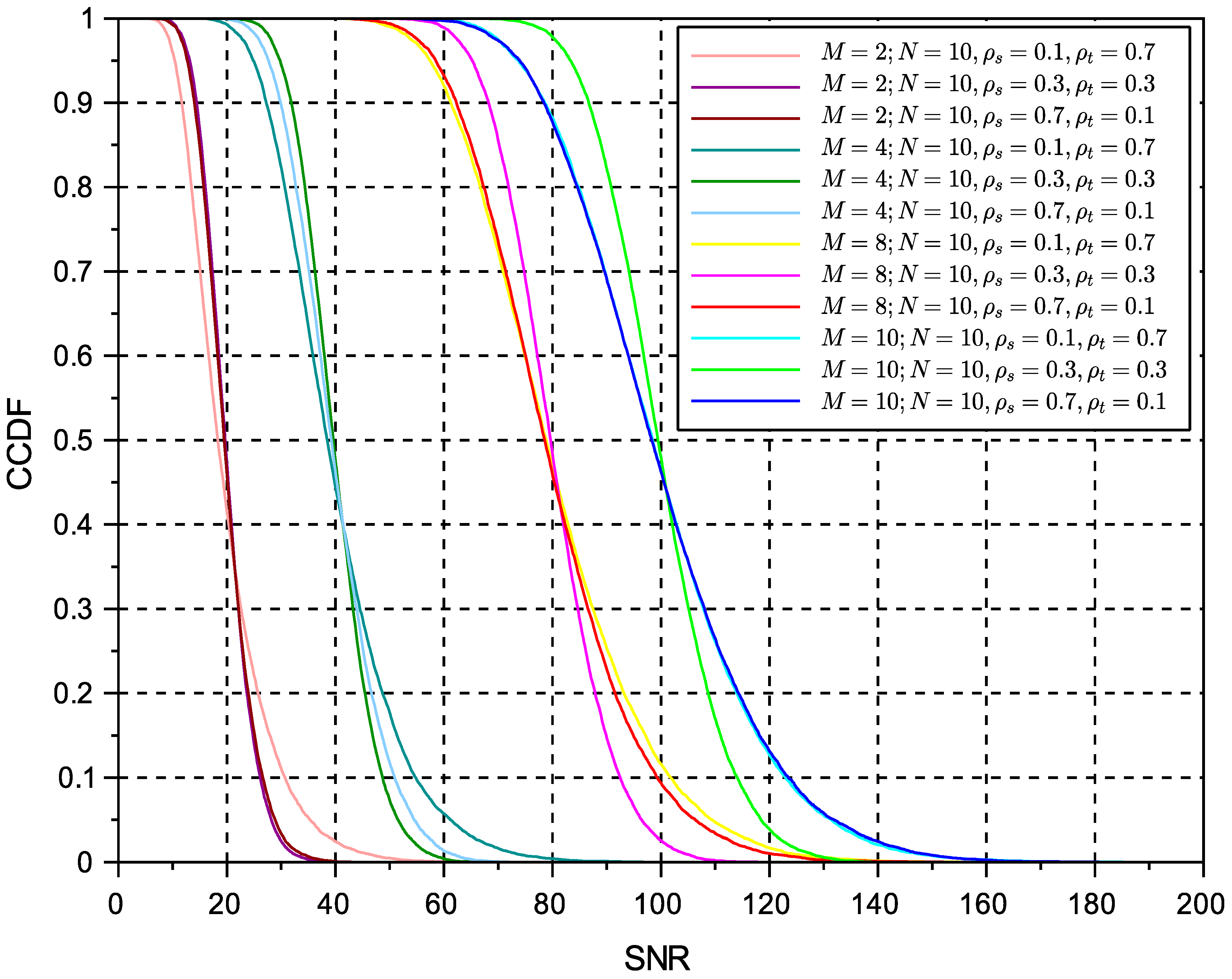
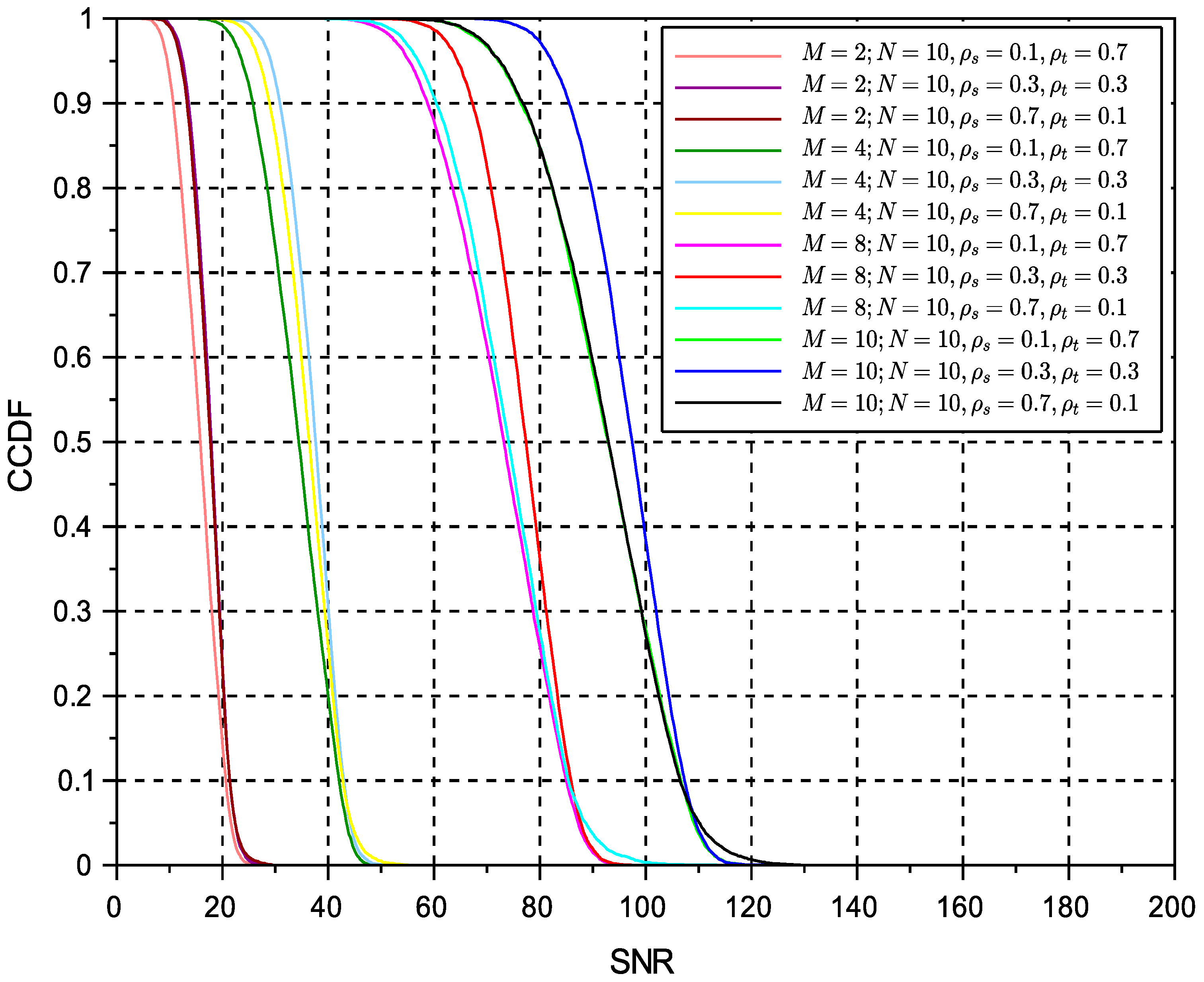
5. Results
6. Conclusions
Funding
Conflicts of Interest
Appendix A. CF Calculation in (26)
Appendix B. Derivation of the Conditioned CCDF in (30)
References
- Sisinni, E.; Saifullah, A.; Han, S.; Jennehag, U.; Gidlund, M. Industrial Internet of Things: Challenges, Opportunities, and Directions. IEEE Trans. Ind. Inform. 2018, 14, 4724–4734. [Google Scholar] [CrossRef]
- Xu, H.; Yu, W.; Griffith, D.; Golmie, N. A Survey on Industrial Internet of Things: A Cyber-Physical Systems Perspective. IEEE Access 2018, 6, 78238–78259. [Google Scholar] [CrossRef]
- Ferrari, P.; Flammini, A.; Sisinni, E.; Rinaldi, S.; Brandão, D.; Rocha, M.S. Delay Estimation of Industrial IoT Applications Based on Messaging Protocols. IEEE Trans. Instrum. Meas. 2018, 67, 2188–2199. [Google Scholar] [CrossRef]
- Bai, L.; Wang, C.X.; Wu, S.; Lopez, C.F.; Gao, X.; Zhang, W.; Liu, Y. Performance comparison of six massive MIMO channel models. In Proceedings of the 2017 IEEE/CIC International Conference on Communications in China (ICCC), Qingdao, China, 22–24 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Lu, L.; Li, G.Y.; Swindlehurst, A.L.; Ashikhmin, A.; Zhang, R. An Overview of Massive MIMO: Benefits and Challenges. IEEE J-STSP 2014, 8, 742–758. [Google Scholar] [CrossRef]
- Ghosh, A.; Maeder, A.; Baker, M.; Chandramouli, D. 5G Evolution: A View on 5G Cellular Technology Beyond 3GPP Release 15. IEEE Access 2019, 7, 127639–127651. [Google Scholar] [CrossRef]
- Dietrich, F.A.; Utschick, W. Maximum ratio combining of correlated Rayleigh fading channels with imperfect channel knowledge. IEEE Commun. Lett. 2003, 7, 419–421. [Google Scholar] [CrossRef]
- Ma, Y.; Schober, R.; Pasupathy, S. Effect of channel estimation errors on MRC diversity in Rician fading channels. IEEE Trans. Veh. Technol. 2005, 54, 2137–2142. [Google Scholar] [CrossRef]
- Samano-Robles, R.; Lavendelis, E.; Tovar, E. Performance Analysis of MRC Receivers with Adaptive Modulation and Coding in Rayleigh Fading Correlated Channels with Imperfect CSIT. IEEE Trans. Veh. Technol. 2016, 2016, 6940368. [Google Scholar] [CrossRef]
- Bithas, P.; Maliatsos, K.; Kanatas, A. The bivariate double Rayleigh distribution for multichannel time-varying systems. IEEE Wirel. Commun. Lett. 2019. [Google Scholar] [CrossRef]
- Ma, Y. Impact of correlated diversity branches in Rician fading channels. In Proceedings of the IEEE International Conference on Communications, Seoul, Korea, 16–20 May 2005; Volume 1, pp. 473–477. [Google Scholar]
- Hui, H.T. The performance of the maximum ratio combining method in correlated Rician-Fading channels for antenna-diversity signal combining. IEEE Trans. Antennas Propag. 2009, 53, 958–964. [Google Scholar] [CrossRef]
- Loskot, P.; Beaulieu, N.C. A unified approach to computing error probabilities of diversity combining schemes over correlated fading channels. IEEE Trans. Commun. 2009, 57, 2031–2041. [Google Scholar] [CrossRef]
- Beauliu, N.C.; Zhang, X. On selecting the number of receiver diversity antennas in Ricean fading cochannel interference. In Proceedings of the IEEE Global Telecommunications Conference (Globecom), San Francisco, CA, USA, 27 November–1 December 2006; pp. 1–6. [Google Scholar]
- Beauliu, N.C.; Zhang, X. On the maximum number of receiver diversity antennas that can be usefully deployed in a cochannel interference dominated environment. IEEE Trans. Signal Process. 2007, 55, 3349–3359. [Google Scholar] [CrossRef]
- Beauliu, N.C.; Zhang, X. On the maximum useful number of receiver antennas for MRC diversity in cochannel interference and noise. In Proceedings of the 2007 IEEE International Conference on Communications, Glasgow, UK, 24–28 June 2007; pp. 5103–5108. [Google Scholar] [CrossRef]
- Dong, Y.; Hughes, B.L.; Lazzi, G. Performance analysis of maximum ratio combining with imperfect channel estimation in the presence of cochannel interferences. IEEE Trans. Wirel. Commun. 2009, 8, 1080–1085. [Google Scholar]
- Le, K.N. A review of selection combining receivers over correlated Rician fading. In Digital Signal Processing; Elsevier: Amsterdam, The Netherlands, 2019; Volume 88, pp. 1–22. [Google Scholar]
- Samano-Robles, R. Joint Beamforming, Terminal Scheduling, and Adaptive Modulation with Imperfect CSIT in Rice Fading Correlated Channels with non-persistent Co-channel Interference. IJATES 2017, 10, 186–195. [Google Scholar]
- Hemachandra, K.T.; Beaulieu, N.C. Novel representations for the equicorrelated multivariate non-central chi-square distribution and applications to MIMO systems in correlated Rician fading. IEEE Trans. Commun. 2011, 59, 2349–2354. [Google Scholar] [CrossRef]
- Beaulieu, N.C.; Hemachandra, K.T. Novel simple representations for Gaussian class multivariate distributions with generalized correlation. IEEE Trans. Inf. Theory 2011, 57, 8072–8083. [Google Scholar] [CrossRef]
- Samano-Robles, R.; Lavendelis, E. Performance model for MRC receivers with adaptive modulation and coding in Rayleigh fading correlated channels with imperfect CSIT. In Proceedings of the 2015 Advances in Wireless and Optical Communications (RTUWO), Riga, Latvia, 5–6 November 2015; pp. 26–29. [Google Scholar]
- Samano-Robles, R.; Gameiro, A. A performance model for maximum ratio combining receivers with adaptive modulation and coding in Rice fading correlated channels. In Proceedings of the 2014 IEEE Symposium on Computers and Communications (ISCC), Funchal, Portugal, 23–26 June 2014; pp. 1–6. [Google Scholar]
- Karagiannidis, G.K.; Zogas, D.A.; Kotsopoulos, S.A. On the multivariate Nakagami-mdistribution with exponential correlation. IEEE Trans. Commun. 2003, 51, 1240–1244. [Google Scholar] [CrossRef]

| Variable | Meaning |
|---|---|
| Channel between the terminal and antenna m in time slot n | |
| M | Number of Rx antennas. |
| N | Number of time slots. |
| Channel variance | |
| Space correlation coefficient | |
| Temporal correlation coefficient | |
| Rx Signal | |
| Noise vector at the receiver |
| Variable | Value |
|---|---|
| M | Variable from 2 to 10 |
| 1. | |
| . | |
| Variable: 0.1, 0.3, 0.7 | |
| Variable: 0.1, 0.3, 0.7 | |
| N | set to 10 time slots |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sámano-Robles, R. A Space-Time Correlation Model for MRC Receivers in Rayleigh Fading Channels. Technologies 2020, 8, 41. https://doi.org/10.3390/technologies8030041
Sámano-Robles R. A Space-Time Correlation Model for MRC Receivers in Rayleigh Fading Channels. Technologies. 2020; 8(3):41. https://doi.org/10.3390/technologies8030041
Chicago/Turabian StyleSámano-Robles, Ramiro. 2020. "A Space-Time Correlation Model for MRC Receivers in Rayleigh Fading Channels" Technologies 8, no. 3: 41. https://doi.org/10.3390/technologies8030041
APA StyleSámano-Robles, R. (2020). A Space-Time Correlation Model for MRC Receivers in Rayleigh Fading Channels. Technologies, 8(3), 41. https://doi.org/10.3390/technologies8030041




