Engineering Micropatterned Surfaces for Controlling the Evaporation Process of Sessile Droplets
Abstract
1. Introduction
2. Materials and Methods
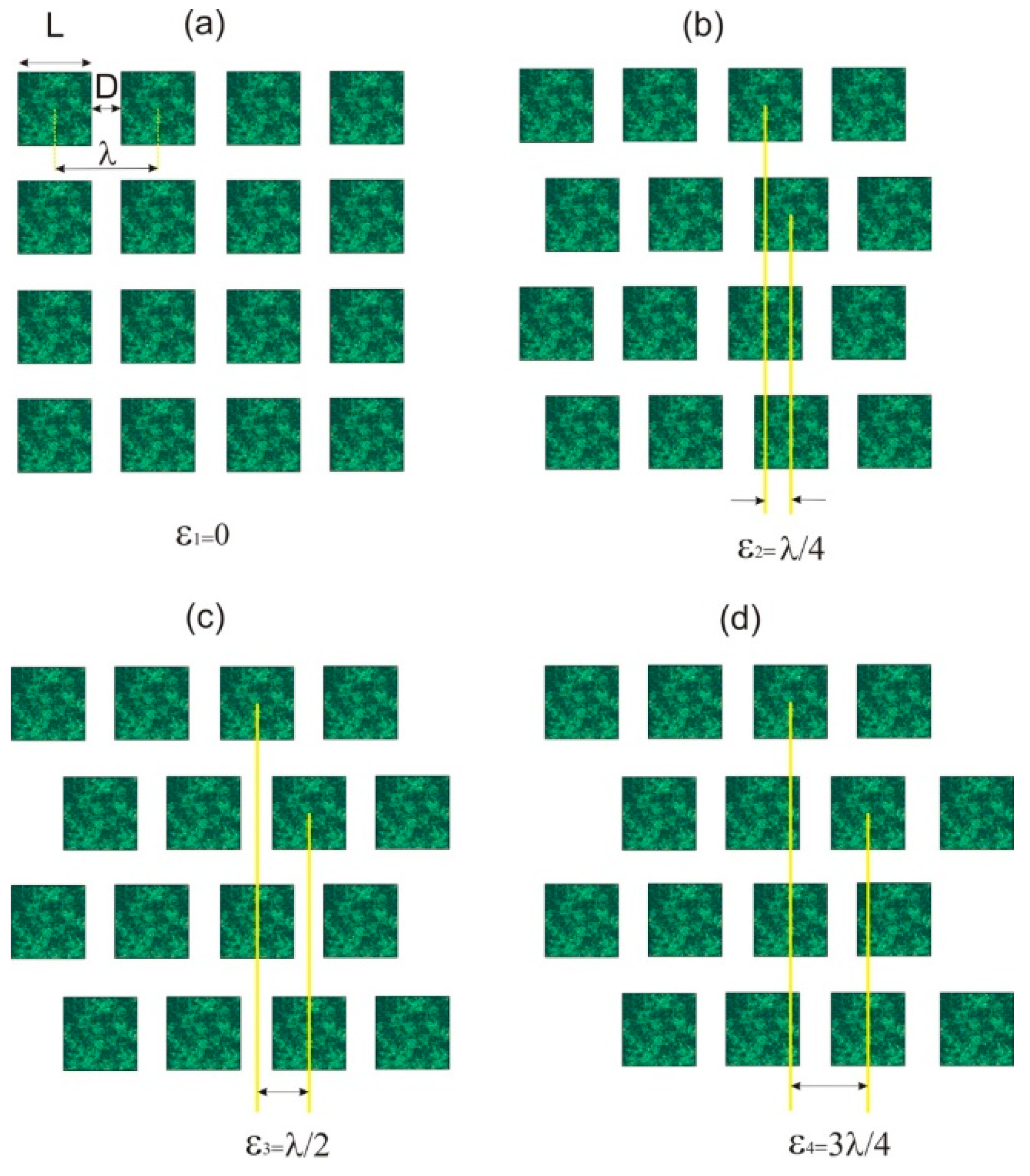
2.1. Design of Micropatterned Surfaces
2.2. Fabrication of Micropatterned Surfaces
2.3. Monitoring the Droplet Evaporation
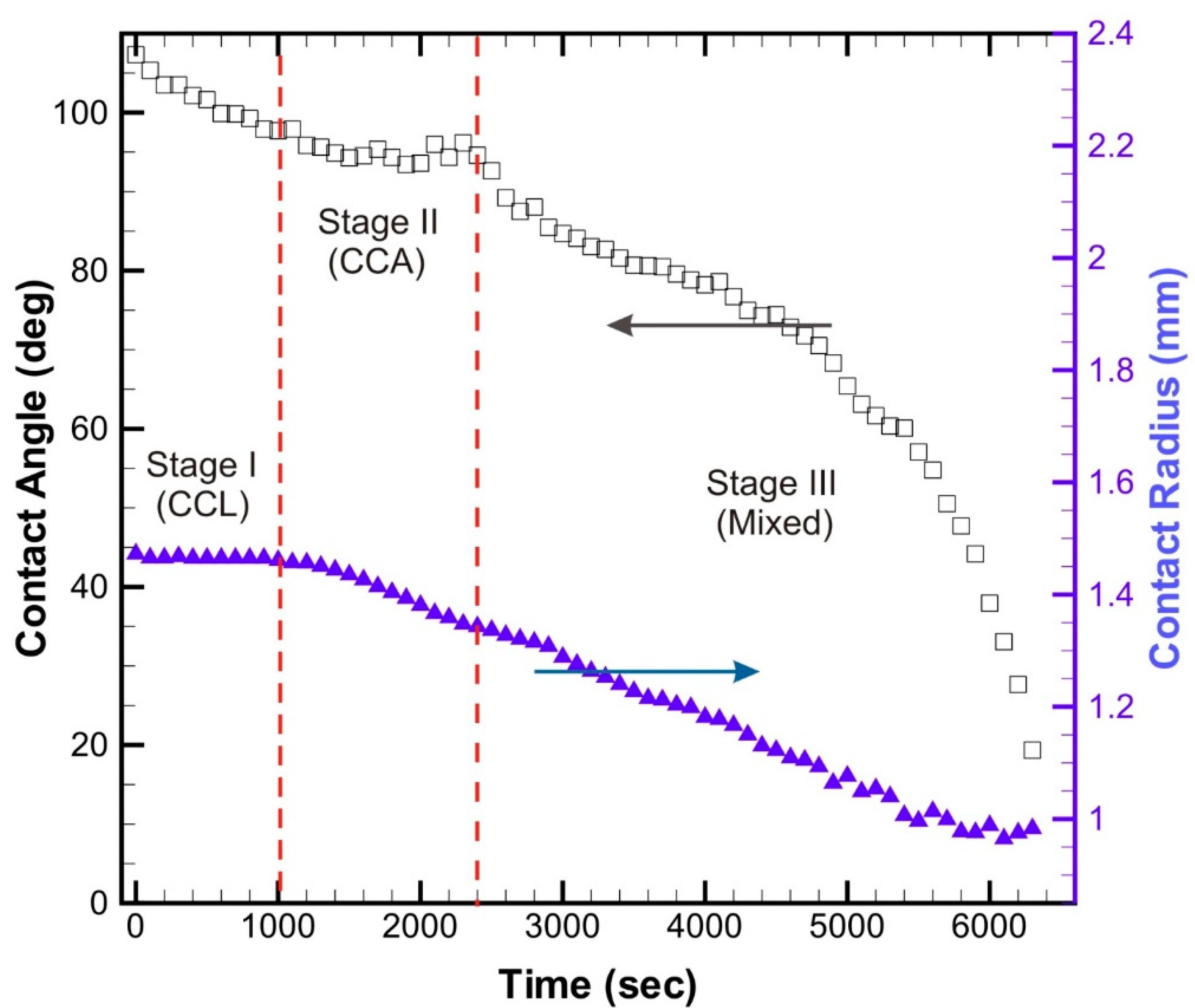
3. Results and Discussions
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Majumder, M.; Rendall, C.; Li, M.; Behabtu, N.; Eukel, J.A.; Hauge, R.H.; Schmidt, H.K.; Pasquali, M. Insights into the physics of spray coating of SWNT films. Chem. Eng. Sci. 2010, 65, 2000–2008. [Google Scholar] [CrossRef]
- Jia, W.; Qiu, H.H. Experimental investigation of droplet dynamics and heat transfer in spray cooling. Exp. Therm. Fluid Sci. 2003, 27, 829–838. [Google Scholar] [CrossRef]
- Lim, T.; Han, S.; Chung, J.; Chung, J.T.; Ko, S.; Grigoropoulos, C.P. Experimental study on spreading and evaporation of inkjet printed pico-liter droplet on a heated substrate. Int. J. Heat Mass Transf. 2009, 52, 431–441. [Google Scholar] [CrossRef]
- Yu, Y.; Zhu, H.; Ozkan, H.; Derksen, R.; Krause, C. Evaporation and deposition coverage area of droplets containing insecticides and spray additives on hydrophilic, hydrophobic, and crabapple leaf surfaces. Trans. ASAE (Am. Soc. Agric. Eng.) 2009, 52, 39. [Google Scholar] [CrossRef]
- Dugas, V.; Broutin, J.; Souteyrand, E. Droplet evaporation study applied to DNA chip manufacturing. Langmuir 2005, 21, 9130–9136. [Google Scholar] [CrossRef]
- Moghadas, H.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.-T. A high-performance polydimethylsiloxane electrospun membrane for cell culture in lab-on-a-chip. Biomicrofluidics 2018, 12, 024117. [Google Scholar] [CrossRef] [PubMed]
- Barisam, M.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.-T. Prediction of necrotic core and hypoxic zone of multicellular spheroids in a microbioreactor with a u-shaped barrier. Micromachines 2018, 9, 94. [Google Scholar] [CrossRef]
- Moghadas, H.; Saidi, M.S.; Kashaninejad, N.; Nguyen, N.-T. Challenge in particle delivery to cells in a microfluidic device. Drug Deliv. Transl. Res. 2018, 8, 830–842. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Chan, W.K.; Nguyen, N.-T. Fluid mechanics of flow through rectangular hydrophobic microchannels. In Proceedings of the ASME 2011 9th International Conference on Nanochannels, Microchannels, and Minichannels, Edmonton, AB, Canada, 19–22 June 2011; Volume 1, pp. 647–655. [Google Scholar] [CrossRef]
- Rostami, P.; Kashaninejad, N.; Moshksayan, K.; Saidi, M.S.; Firoozabadi, B.; Nguyen, N.-T. Novel approaches in cancer management with circulating tumor cell clusters. J. Sci. Adv. Mater. Devices 2019, 4, 1–18. [Google Scholar] [CrossRef]
- Vadivelu, R.; Kashaninejad, N.; Sreejith, K.R.; Bhattacharjee, R.; Cock, I.; Nguyen, N.-T. Cryoprotectant-free freezing of cells using liquid marbles filled with hydrogel. ACS Appl. Mater. Interfaces 2018, 10, 43439–43449. [Google Scholar] [CrossRef]
- Cheng, W.; Park, N.; Walter, M.T.; Hartman, M.R.; Luo, D. Nanopatterning self-assembled nanoparticle superlattices by moulding microdroplets. Nat. Nano 2008, 3, 682–690. [Google Scholar] [CrossRef] [PubMed]
- Maxwell, J. Diffusion, Collected Scientific Papers; Encyclopedia Britannica: Cambridge, UK, 1877. [Google Scholar]
- Picknett, R.G.; Bexon, R. The evaporation of sessile or pendant drops in still air. J. Colloid Interface Sci. 1977, 61, 336–350. [Google Scholar] [CrossRef]
- Rowan, S.M.; Newton, M.I.; McHale, G. Evaporation of microdroplets and the wetting of solid surfaces. J. Phys. Chem. 1995, 99, 13268–13271. [Google Scholar] [CrossRef]
- Erbil, H.Y.; Meric, R.A. Evaporation of sessile drops on polymer surfaces: Ellipsoidal cap geometry. J. Phys. Chem. B 1997, 101, 6867–6873. [Google Scholar] [CrossRef]
- Erbil, H.Y.; McHale, G.; Newton, M.I. Drop evaporation on solid surfaces: Constant contact angle mode. Langmuir 2002, 18, 2636–2641. [Google Scholar] [CrossRef]
- Bourges-Monnier, C.; Shanahan, M.E.R. Influence of evaporation on contact angle. Langmuir 1995, 11, 2820–2829. [Google Scholar] [CrossRef]
- Erbil, H.Y. Evaporation of pure liquid sessile and spherical suspended drops: A review. Adv. Colloid Interface Sci. 2012, 170, 67–86. [Google Scholar] [CrossRef]
- Song, H.; Lee, Y.; Jin, S.; Kim, H.Y.; Yoo, J.Y. Prediction of sessile drop evaporation considering surface wettability. Microelectron. Eng. 2011, 88, 3249–3255. [Google Scholar] [CrossRef]
- Yu, Y.-S.; Wang, Z.; Zhao, Y.-P. Experimental and theoretical investigations of evaporation of sessile water droplet on hydrophobic surfaces. J. Colloid Interface Sci. 2012, 365, 254–259. [Google Scholar] [CrossRef]
- McHale, G.; Aqil, S.; Shirtcliffe, N.J.; Newton, M.I.; Erbil, H.Y. Analysis of droplet evaporation on a superhydrophobic surface. Langmuir 2005, 21, 11053–11060. [Google Scholar] [CrossRef]
- Cassie, A.; Baxter, S. Wettability of porous surfaces. Trans. Faraday Soc. 1944, 40, 546–551. [Google Scholar] [CrossRef]
- Wenzel, R. Resistance of solid surfaces to wetting by water. Ind. Eng. Chem. 1936, 28, 988–994. [Google Scholar] [CrossRef]
- Zhang, X.; Tan, S.; Zhao, N.; Guo, X.; Zhang, X.; Zhang, Y.; Xu, J. Evaporation of sessile water droplets on superhydrophobic natural lotus and biomimetic polymer surfaces. ChemPhysChem 2006, 7, 2067–2070. [Google Scholar] [CrossRef] [PubMed]
- Gelderblom, H.; Marín, Á.G.; Nair, H.; van Houselt, A.; Lefferts, L.; Snoeijer, J.H.; Lohse, D. How water droplets evaporate on a superhydrophobic substrate. Phys. Rev. E 2011, 83, 026306. [Google Scholar] [CrossRef]
- Popov, Y.O. Evaporative deposition patterns: Spatial dimensions of the deposit. Phys. Rev. E 2005, 71, 036313. [Google Scholar] [CrossRef]
- Chen, X.; Ma, R.; Li, J.; Hao, C.; Guo, W.; Luk, B.L.; Li, S.C.; Yao, S.; Wang, Z. Evaporation of droplets on superhydrophobic surfaces: Surface roughness and small droplet size effects. Phys. Rev. Lett. 2012, 109, 116101. [Google Scholar] [CrossRef]
- Zhang, C.; Zhu, X.; Zhou, L. Morphology tunable pinning force and evaporation modes of water droplets on PDMS spherical cap micron-arrays. Chem. Phys. Lett. 2011, 508, 134–138. [Google Scholar] [CrossRef]
- Xu, W.; Choi, C.-H. Effects of surface topography and colloid particles on the evaporation kinetics of sessile droplets on superhydrophobic surfaces. J. Heat Transf. 2012, 134, 051022–051027. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Chan, W.K.; Nguyen, N.-T. Eccentricity effect of micropatterned surface on contact angle. Langmuir 2012, 28, 4793–4799. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Nguyen, N.-T.; Chan, W.K. The three-phase contact line shape and eccentricity effect of anisotropic wetting on hydrophobic surfaces. Soft Matter 2013, 9, 527–535. [Google Scholar] [CrossRef]
- Kashaninejad, N.; Nguyen, N.-T.; Chan, W.K. Eccentricity effects of microhole arrays on drag reduction efficiency of microchannels with a hydrophobic wall. Phys. Fluids 2012, 24, 112004–112018. [Google Scholar] [CrossRef]
- Lee, M.; Lee, D.; Jung, N.; Yun, M.; Yim, C.; Jeon, S. Evaporation of water droplets from hydrophobic and hydrophilic nanoporous microcantilevers. Appl. Phys. Lett. 2011, 98, 013107. [Google Scholar] [CrossRef][Green Version]
- Kulinich, S.A.; Farzaneh, M. Effect of contact angle hysteresis on water droplet evaporation from super-hydrophobic surfaces. Appl. Surf. Sci. 2009, 255, 4056–4060. [Google Scholar] [CrossRef]
- Kashaninejad, N. Fluid Mechanics of Flow through Microchannels; Nanyang Technological University: Singapore, 2013. [Google Scholar]
- Drelich, J.; Miller, J.D. Modification of the cassie equation. Langmuir 1993, 9, 619–621. [Google Scholar] [CrossRef]



| 2.5 | 6 | 0,2,4,6 | 0, 0.25, 0.5, 0.75 |
| 0 | 0.25 | 0.5 | 0.75 | |
|---|---|---|---|---|
| CAH |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kashaninejad, N.; Nguyen, N.-T.; Chan, W.K. Engineering Micropatterned Surfaces for Controlling the Evaporation Process of Sessile Droplets. Technologies 2020, 8, 29. https://doi.org/10.3390/technologies8020029
Kashaninejad N, Nguyen N-T, Chan WK. Engineering Micropatterned Surfaces for Controlling the Evaporation Process of Sessile Droplets. Technologies. 2020; 8(2):29. https://doi.org/10.3390/technologies8020029
Chicago/Turabian StyleKashaninejad, Navid, Nam-Trung Nguyen, and Weng Kong Chan. 2020. "Engineering Micropatterned Surfaces for Controlling the Evaporation Process of Sessile Droplets" Technologies 8, no. 2: 29. https://doi.org/10.3390/technologies8020029
APA StyleKashaninejad, N., Nguyen, N.-T., & Chan, W. K. (2020). Engineering Micropatterned Surfaces for Controlling the Evaporation Process of Sessile Droplets. Technologies, 8(2), 29. https://doi.org/10.3390/technologies8020029







