Abstract
The performance of an underwater optical wireless communication link is investigated by taking into account—for the first time and to the best of our knowledge—the simultaneous influence of the chromatic dispersion, the time jitter and the turbulence effects, by assuming chirped longitudinal Gaussian pulse propagation as information carriers. The estimation procedure is presented and a novel probability density function is extracted in order to describe the irradiance fluctuations at the receiver side. Furthermore, the availability of the link is investigated by means of its probability of fade and various numerical results are presented using typical parameters for the underwater optical wireless communication systems.
1. Introduction
Underwater optical wireless communication (UOWC) systems have attracted significant research and commercial interest in recent years due to their very significant advantages that they offer. More specifically, the UOWC links, due to their very large bandwidth, can achieve very high data rates and real time communications inside the water, with low energy consumption and very high security standards. Many recent theoretical and experimental works have been done in order to estimate the effectiveness of the transmitter/receivers, link, modulation formats, etc. that are used in these systems [1,2,3,4,5,6,7,8,9,10]. However, the performance of these systems is dominated by the characteristics of the medium, where the pulses are propagating. Thus, the water strongly attenuates the information signal and consequently their effective link length is of some tens of meters. Additionally, the turbulence of the fluid, water purity and dispersion significantly affect the performance and the operation of the wireless communication link. Furthermore, due to their capability for ultrafast data transmission, the time jitter effect also affects their characteristics [1,11,12,13].
Many statistical models have been presented in order to describe the turbulence effect, especially in the atmospheric environment. However, it has been proven that most of these models are also accurate for the underwater environment [14,15,16,17]. Thus, the gamma–gamma distribution is accurate enough for weak to strong turbulence conditions; the log-normal and the gamma are appropriate for weak turbulence, while the K distribution and the negative exponential one can be used for strong and saturated turbulence, respectively [18,19,20].
The influence of the time jitter effect can be considered as a significant factor for ultra-high data rate communication systems due to the fact that the longitudinal pulses, used by these systems, are very short. Thus, any delayed arrival or time desynchronization at the receiver can cause the detection of the optical pulse earlier or later than the “correct” time of the detection. This effect results in the performance mitigation of the link, because it increases the negative influence of the scintillation effect, due to the increased intensity of the fluid turbulence and the negative affection on the systems characteristics [21,22,23,24,25,26,27].
Another effect that can significantly decrease the performance of the underwater optical communication links is the chromatic dispersion. More specifically, due to the dependence of the refractive index of the seawater on the wavelength and taking into account that the typical optical pulses used in the optical communication systems cannot be monochromatic, the longitudinal pulse shape changes along its propagation, and thus the detection procedure at the receiver becomes more difficult and erroneous [28,29,30,31,32,33].
In this work—for the first time and to the best of our knowledge—the simultaneous influence of turbulence, time jitter and chromatic dispersion is investigated for an UOWC link. It is assumed that the communication system uses longitudinal chirped Gaussian pulses as information carriers and that the fluid turbulence is weak. Thus, the log-normal distribution model has been used for the representation of the fluid turbulence effect, while the influence of the group velocity dispersion (GVD) is studied for both signs of a pulse’s chirp. Additionally, as far as the time jitter effect is concerned, it has been assumed here that the probability of detecting a pulse earlier is equal to detecting it later, and the normal distribution has been chosen in order to investigate its influence. The joint influence of all the above effect is estimated and the corresponding probability distribution function (PDF) is extracted. Then, using the derived mathematical expression for the PDF, the performance of the link is estimated by means of its probability of fade and the relative numerical results are presented, using typical values for the UOWC links.
The remainder of this work is organized as follows: in the next section, the underwater channel is presented and the fluid turbulence effect is introduced, while in Section 3, the chromatic dispersion effect is studied. Next, in Section 4, the time jitter effect is investigated and in Section 5, the simultaneous influence of all the aforementioned effects is presented. Moreover, in Section 6, the probability of fade of the link is obtained, while the numerical results and the conclusions of this work are presented in Section 7 and Section 8, respectively.
2. The Underwater Channel Model
The optical information pulse is assumed to propagate through the turbulent underwater environment of the UOWC system, with additive white Gaussian noise (AWGN), n, of zero mean value and variance σn2. Additionally, the channel is considered as memoryless, stationary and ergodic. Thus, the signal which arrives at the input of the receiver, y, is given as [34,35]:
where η stands for the effective photocurrent efficiency, x is the modulated transmitted signal and I represents the instantaneous normalized irradiance at the receiver. The normalized irradiance, I, depends on both the effects of the water turbulence, It, along with the influence of the time jitter effect, Ij. Thus, the total normalized irradiance of (1), is expressed as [35,36,37,38]:
with Il being the signal losses due to the medium’s attenuation, but without loss of generality, in this work, it is assumed to be equal to unity [36,37,38].
The turbulence effect plays a very significant role in the terrestrial optical wireless links [39,40,41,42]. However, in the corresponding underwater systems, turbulence is still a significant mitigation factor for their performance [18,43,44]. More specifically, by assuming weak water turbulence, the irradiance fluctuations at the receiver of the UOWC link can be studied through the log-normal (LN) distribution. The probability distribution function (PDF) of the LN model as a function of the instantaneous normalized irradiance at the receiver, It, is given as [18,44,45]:
with σ2 being the log-irradiance variance [45,46,47], which depends on the channel’s characteristics.
3. The Chromatic Dispersion Effect
Taking into account that the optical pulses of the UOWC links are not monochromatic and the refractive index of the seawater depends on the optical signal’s frequency, the chromatic dispersion effect appears during the signal’s propagation. In order to estimate its influence, the refractive index as a function of the link’s characteristics should be estimated. Thus, by using the empirical model introduced by McNeil [48], and by substituting the wavelength, λ, in nm, of the optical beam, with the corresponding angular frequency, ω, in rad/sec, i.e. , with v being the speed of light in the water in m/sec, the refractive index of the underwater environment will be given through the following expression as a function of the link’s parameters [27]:
where Pr is the water pressure in kg/cm2, Te is the temperature in Celsius degrees, while Sa stands for the salinity of the seawater in ‰, [27,48].
Next, by substituting the refractive index into the propagation constant, i.e., , with c being the speed of light in vacuum, in m/sec [28,33], and by expanding it in a Taylor series around the angular frequency and keeping terms up to the second order [28], with for q = 1,2, ... [28], the value of , which represents the inverse group velocity [28], is estimated, while , which represents the GVD parameter, is given in ps2/km as [28]:
Then, by taking into account (4) and (5), the values of the refractive index, and β2 are presented in the following Table 1, for various values of the wavelength of the UOWC systems and by assuming typical values of water temperature and salinity, i.e., , Te = 0 °C [27,48]. It should be mentioned here that for the specific temperature and salinity values, it has been proven that the pressure can be accurately estimated as [48], where d represents the underwater depth in meters and takes the value of 100 m.

Table 1.
Refractive index and GVD parameter values for various wavelengths for , Te = 0 °C and d = 100 m.
By using the GVD parameter, β2, obtained in (5), the evolution of the normalized amplitude, U(z,T), of a pulse propagating along axis z, in km, inside a dispersive medium, can be estimated through the following equation [28]:
where T stands for the retarded time, in ps, which is defined as , representing a time frame of the pulse propagating with the group velocity along the pulse [28,31,32,49].
In order to estimate the influence of the GVD at the performance of the link, we assume longitudinal chirped Gaussian pulses as information carriers of the UOWC, which have the following initial condition [28]:
where C is the chirp effect parameter and T0 stands for the parameter, which represents the half width at 1/e intensity of the pulse [21,28]. Furthermore, from (7) using (6), after propagation distance z, the envelope of the longitudinal chirped Gaussian pulse will have the form [33,50]:
while, its pulsewitdh is given as [28]:
4. The Time Jitter Effect
By assuming the propagation of the longitudinal chirped Gaussian pulse through the dispersive medium, its instantaneous normalized irradiance at the receiver, Ij, is obtained from (8) and given as [27,51]:
with and , [50].
The retarded time T, as mentioned above, represents, in practice, the deviation from the center of the longitudinal pulse. Thus, the value T=0 ps refers exactly at the center of the Gaussian pulse. Thus, if the detection of each bit does not happen exactly at the correct time, i.e., at T=0 ps, then the Ij value will be lower than expected. More specifically, while the throughput of the optical wireless links increases and the duration of each information bit decreases, the probability of pulse detection before or after the “ideal” moment, which corresponds at the center of the pulse, increases due to various desynchronization reasons concerning either the electronic circuits of the communication system or the propagation characteristics of the optical beam. Consequently, the time jitter effect is getting stronger.
By assuming the time jitter as a probabilistic effect, with the same probability to detect each specific bit before or after, T=0 ps, it could be statistically described by a normal distribution with mean value equal to zero. Thus, the PDF of the normal distribution model with mean value, , and variance is given as [52,53]:
The PDF of (11) is expressed as a function of T parameter and in order to make the needed random variable (RV) transformation with Ij, the value of T should be obtained from (10) as:
Next, using the above equation (12), the PDF of (11) as a function of Ij is given as:
and by substituting (11) and (12) into (13), the PDF of the Ij factor caused by the GVD and the time jitter effect is obtained by:
5. The Joint Influence of GVD, Time Jitter and Turbulence
The total simultaneous influence of the chromatic dispersion, time jitter and water turbulence effects on the performance of the UOWC link can be estimated, from (3) and (14), through the extraction of the corresponding joint PDF as [37,54,55]:
where stands for the conditional probability. By substituting (3) and (14) into (15) the joint PDF, which corresponds to the LN-turbulence with the simultaneous influence of the time jitter and the GVD effects, is given as:
and if the variable of the integral is transformed as , and by assuming that the mean value for the time jitter effect is zero, as mentioned above, after some simplifications, (16) can take the following form:
Next, by expressing the second exponential term of the integral of (17), through the infinite summation, i.e., , we conclude to the following expression:
Finally, by solving the integral of (18), we obtain the following mathematical form for the joint PDF of the UOWC link:
The mathematical expression that has been derived in (19) corresponds to a new, joint PDF, which describes the simultaneous influence of the chromatic dispersion, the water turbulence, modeled with the log-normal distribution model and the time jitter effects, for the case of longitudinal Gaussian chirped pulses being used as information carriers for the underwater optical wireless communication link.
6. The Probability of Fade
A significant performance metric for the communication systems is their probability of fade. This quantity represents the availability of the link and gives the probability that the signal’s irradiance at the receiver falls below a specific threshold, Ith, which constitutes a characteristic technical parameter of the receiver of each link and is given as [50,56,57]:
where the function fI(I) represents the PDF, which describes the irradiance fluctuations of the information signal at the input of the link’s receiver.
Thus, using (19) and (20), the probability of fade of an UOWC link, which is using longitudinal Gaussian chirped pulses as information carriers, taking into account the influence of the seawater turbulence, the time jitter and the GVD is given as:
7. Numerical Results
In this work, the joint influence of time jitter, log-normal turbulence and chromatic dispersion in an UOWC system was studied, which uses longitudinal Gaussian chirped pulses as information carrier. Through the above procedure, a novel joint PDF was derived (19) in order to describe the irradiance fluctuations at the receiver, due to their simultaneous effect. Moreover, the fade probability of the system can be estimated from (21). For the numerical results presented below, typical values of water temperature and salinity, i.e., , Te = 0 °C [27,48], have been chosen, while the underwater depth is fixed at 100 m and the corresponding pressure is estimated through the expression [48], as mentioned above. Moreover, the information pulse duration, T0, values are varying from 2 ps to 6 ps and the operational wavelength, λ, is taken to be 470 nm, which is a typical value for the UOWC systems. Furthermore, the chirp parameter, C, is assigned the values −10 or 10 and the horizontal propagation link is assumed to have length either 40 m or 50 m [58,59,60]. Furthermore, the parameter , which depends on the turbulence strength, takes three values, i.e., 8.0×10−15 m−2/3, 1.6×10−14 m−2/3 and 2.4×10−14 m−2/3. Finally, the variation of the time jitter effect, σΤ, is set at 5 ps while the receiver’s irradiance threshold is assumed to be Ith = 0.5.
A very significant issue concerning this work is the influence of the GVD on the pulse’s shape depending on the sign of its chirp. More specifically, as it can be observed from (10), the pulse’s amplitude, i.e. the value of B, depends strongly on the value of the chirp. Thus, it can be seen that if the chirp value is negative the amplitude of the pulse initially increases and after a maximum value, decreases with the propagation distance. On the other hand, for positive chirp values, the value of B decreases monotonically when the link length increases. The opposite behavior is observed for the width of the pulse. Thus, from (9), it can be seen that for positive chirp, the pulsewidth increases monotonically, while for negative values, it decreases initially, reaches a minimum value (which corresponds to the maximum value of amplitude) increases after that, as well. From (9), it arises that the critical propagation distance, z, where the monotonicity changes, depends on the parameters of the channel and the initial shape of the pulse.
In Figure 1, the amplitude of Ij from (8) is plotted as a function of the propagation distance, for various pulse widths, T0, and for positive and negative chirp values. As it can be seen in Figure 1, for C = −10, the amplitude of the optical pulses increases in the first meters of the propagation path, then achieves a maximum value and after that the value of B decreases when z increases. On the contrary, for C = 10, the value of B decreases always when z increases. It should be mentioned that when the pulse’s amplitude increases, due to the GVD effect, its pulsewidth decreases, respectively, and vice versa. The corresponding behavior concerning the width of the optical pulse is shown in Figure 2, where the influence can be seen of the chirp, the wavelength and the propagation distance.
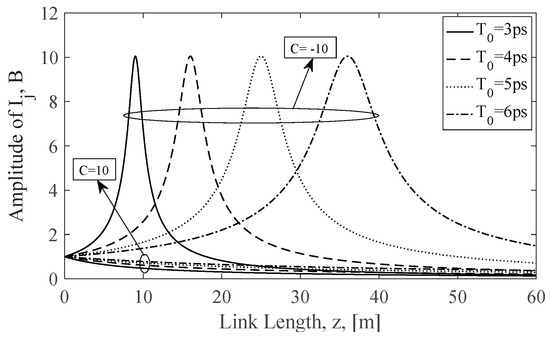
Figure 1.
Amplitude of the optical pulse, i.e., B parameter, as a function of the propagation distance.
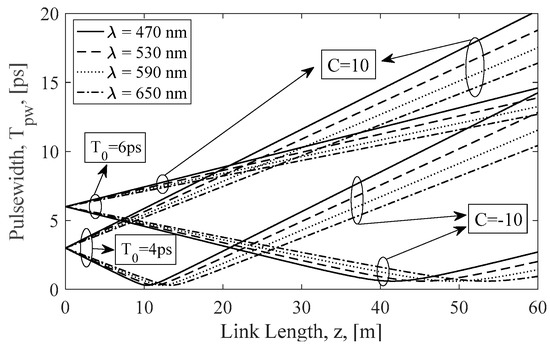
Figure 2.
Width of the optical pulse, i.e., Tpw, as a function of the propagation distance, z.
Taking into account the behavior of the amplitude of a longitudinal Gaussian pulse, due to the GVD effect depending on the chirp’s sign, we plot the probability of fade of the optical wireless system in Figure 3, considering the GVD effect, the time jitter and the fluid turbulence modeled with the log-normal distribution by using the expression obtained in (21). In the specific figure, the probability of fade of a UOWC link is plotted as a function of the longitudinal Gaussian pulsewidth, for a propagation distance z equal to 40 m and assuming typical water values for salinity, temperature and Ith, as mentioned above. The influence of the atmospheric turbulence strength can be observed, while the chirp value and its sign play a very important role. More specifically, the negative chirped pulses help the UOWC link to have better performance and availability capabilities, because the probability of fade is much lower than the probability obtained for positive chirp. Additionally, from Figure 1 and Figure 3, it can be seen that the best probability of fade performance is achieved for link lengths where the larger amplitude value B, appears.
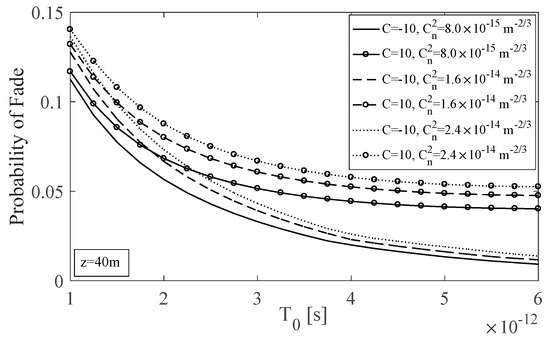
Figure 3.
Probability of fade for a UOWC system under the joint action of GVD, time jitter and fluid turbulence effect, as a function of the longitudinal pulsewidth of the Gaussian pulse for a 40-m horizontal propagation distance and 100-m depth.
Next, in Figure 4, the probability of fade of a UOWC link with longer link length is presented. Due to the fluid turbulence, the outage probability performance decreases when the intensity of the effect is getting stronger and the chirp value significantly affects its value. Here, the link length is assumed to be z = 50 m with the same irradiance threshold as in the previous case. By comparing Figure 3 and Figure 4, and by taking into account the outcomes that have been presented in Figure 1, it can be seen that the positive influence of the negative value of chirp is getting weaker as the probability of fade is estimated away from the maximum amplitude of the pulse due to the GVD effect, i.e. the value of B. However, even for longer distances, the negative chirp value can improve the performance characteristics of the underwater optical wireless link.
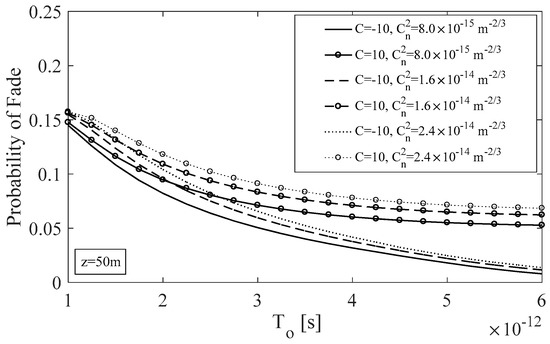
Figure 4.
Probability of fade for a UOWC system under the joint action of GVD, time jitter and fluid turbulence effect, as a function of the longitudinal pulsewidth of the Gaussian pulse for a 50-m horizontal propagation distance and 100-m depth.
In both Figure 3 and Figure 4, it can be seen that the influence of the chirp effect is significant especially for link distances near the critical link length for the negative chirp pulses. Additionally, the influence of the atmospheric turbulence effect can significantly mitigate the performance of the link, while, as shown in Figure 2, the link’s wavelength affects the quality of the connection and its availability. Thus, taking into account the obtained conclusions and using the above derived expressions (19) and (21), the most effective UOWC system can be designed depending on the characteristics of the underwater optical channel and the required link performance.
8. Conclusions
In this work, for first time to the best of our knowledge, the performance of an underwater optical wireless communication system with longitudinal chirped Gaussian pulses as data carriers and taking into account the simultaneous influence of the effects of chromatic dispersion, time jitter and turbulence, has been studied. For the latter effect, the log-normal distribution has been used. For this UOWC link, a novel probability density function was derived in order to describe the irradiance fluctuations at the system’s receiver due to the joint influence of the above-mentioned effects and we presented the expression for the estimation of its availability by means of its probability of fade. Finally, using typical parameter values for the UOWC systems and by using the above-derived expressions, we presented the corresponding numerical results and conclusions concerning the amplitude and the width of the pulse and their dependence of the effects studied above, the new joint PDF and the probability of fade of the link.
Author Contributions
Conceptualization, G.D.R., H.E.N., G.S.T.; methodology, G.D.R., H.E.N., A.N.S., G.K.V.; software, G.D.R., H.E.N., A.N.S., G.K.V., A.D.T.; validation, G.D.R., H.E.N., A.N.S., G.K.V., A.D.T.; formal analysis, G.D.R., H.E.N., A.N.S., G.K.V., A.D.T.; investigation, G.D.R., H.E.N., A.N.S., G.K.V., A.D.T., G.S.T.; resources, G.D.R., H.E.N., A.N.S., G.K.V., A.D.T.; writing—original draft preparation, G.D.R., H.E.N., A.N.S.; writing—review and editing, H.E.N., G.S.T.; supervision, H.E.N. All authors have read and agreed to the published version of the manuscript.
Acknowledgments
G.D.R. acknowledges that this research is co-financed by Greece and the European Union (European Social Fund- ESF) through the Operational Program “Human Resources Development, Education and Lifelong Learning” in the context of the project “Strengthening Human Resources Research Potential via Doctorate Research” (MIS-5000432), implemented by the State Scholarships Foundation (ΙΚΥ).
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Arnon, S. Underwater Optical Wireless Communication Network. Opt. Eng. 2010, 49, 015001. [Google Scholar] [CrossRef]
- Tsonev, D.; Chun, H.; Rajbhandari, S.; McKendry, J.J.D.; Videv, S.; Gu, E.; Haji, M.; Watson, S.; Kelly, A.E.; Faulkner, G.; et al. A 3-Gb/s Single-LED OFDM-Based Wireless VLC Link Using a Gallium Nitride μLED. IEEE Photonics Technol. Lett. 2014, 26, 637–640. [Google Scholar] [CrossRef]
- Wu, T.C.; Chi, Y.C.; Wang, H.Y.; Tsai, C.T.; Lin, G.R. Blue laser diode enables underwater communication at 12.4 gbps. Sci. Rep. 2017, 7, 1–10. [Google Scholar] [CrossRef] [PubMed]
- Kaushal, H.; Kaddoum, G. Underwater Optical Wireless Communication. IEEE Access 2016, 4, 1518–1547. [Google Scholar] [CrossRef]
- Chi, Y.-C.; Hsieh, D.-H.; Tsai, C.-T.; Chen, H.-Y.; Kuo, H.-C.; Lin, G.-R. 450-nm GaN laser diode enables high-speed visible light communication with 9-Gbps QAM-OFDM. Opt. Express 2015, 23, 13051. [Google Scholar] [CrossRef]
- Gkoura, L.K.; Roumelas, G.D.; Nistazakis, H.E.; Sandalidis, H.G.; Vavoulas, A.; Tsigopoulos, A.D.; Tombras, G.S. Underwater Optical Wireless Communication Systems: A Concise Review. In Turbulence Modelling Approaches—Current State, Development Prospects, Applications; Volkov, K., Ed.; InTech: Vienna, Austria, 2017. [Google Scholar] [CrossRef]
- Huang, Y.-F.; Tsai, C.-T.; Chi, Y.-C.; Huang, D.-W.; Lin, G.-R. Filtered Multicarrier OFDM Encoding on Blue Laser Diode for 14.8-Gbps Seawater Transmission. J. Light. Technol. 2018, 36, 1739–1745. [Google Scholar] [CrossRef]
- Saeed, N.; Celik, A.; Al-Naffouri, T.Y.; Alouini, M.-S. Underwater optical wireless communications, networking, and localization: A survey. Ad Hoc Netw. 2019, 94, 101935. [Google Scholar] [CrossRef]
- Coello, Y.; Xu, B.; Miller, T.L.; Lozovoy, V.V.; Dantus, M. Group-velocity dispersion measurements of water, seawater, and ocular components using multiphoton intrapulse interference phase scan. Appl. Opt. 2007, 46, 8394–8401. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Shen, C.-C.; Kao, H.-Y.; Hsieh, D.-H.; Wang, H.-Y.; Yeh, Y.-W.; Lu, Y.-T.; Huang Chen, S.-W.; Tsai, C.-T.; Chi, Y.-C.; et al. 850/940-nm VCSEL for optical communication and 3D sensing. Opto-Electronic Adv. 2018, 1, 18000501–18000511. [Google Scholar] [CrossRef]
- Mullen, L.; Alley, D.; Cochenour, B. Investigation of the effect of scattering agent and scattering albedo on modulated light propagation in water. Appl. Opt. 2011, 50, 1396–1404. [Google Scholar] [CrossRef]
- Cochenour, B.; Mullen, L.; Laux, A. Spatial and temporal dispersion in high bandwidth underwater laser communication links. In MILCOM 2008—2008 IEEE Military Communications Conference; IEEE: Piscataway, NJ, USA, 2008; pp. 1–7. ISBN 978-1-42-442676-8. [Google Scholar]
- Liu, L.; Zhou, S.; Cui, J. Prospects and Problems of Wireless Communication for Underwater Sensor Networks. Wirel. Commun. Mob. Comput. 2008, 8, 977–994. [Google Scholar] [CrossRef]
- Baykal, Y. Signal-to-noise ratio reduction due to oceanic turbulence in oceanic wireless optical communication links. Opt. Commun. 2018, 427, 44–47. [Google Scholar] [CrossRef]
- Baykal, Y. Scintillations of optical plane and spherical waves in underwater turbulence. J. Opt. Soc. Am. A 2014, 31, 1552–1556. [Google Scholar] [CrossRef]
- Korotkova, O.; Farwell, N.; Shchepakina, E. Light scintillation in oceanic turbulence. Waves Random Complex Media 2012, 22, 260–266. [Google Scholar] [CrossRef]
- Andrews, L.C.; Phillips, R.L.; Hopen, C.Y. Laser Beam Scintillation with Applications; SPIE: Bellingham, WA, USA, 2001; ISBN 978-0-81-944103-4. [Google Scholar]
- Jamali, M.V.; Khorramshahi, P.; Tashakori, A.; Chizari, A.; Shahsavari, S.; Abdollahramezani, S.; Fazelian, M.; Bahrani, S.; Salehi, J.A. Statistical distribution of intensity fluctuations for underwater wireless optical channels in the presence of air bubbles. IWCIT 2016 Iran Workshop Commun. Inf. Theory 2016. [Google Scholar] [CrossRef]
- Arpali, S.; Baykal, Y.; Arpali, C. BER evaluations for multimode beams in underwater turbulence. J. Mod. Opt. 2016, 340, 1–4. [Google Scholar] [CrossRef]
- Liu, J.; Dong, Y. On capacity of underwater optical wireless links under weak oceanic turbulence. Ocean. 2016 Shanghai 2016. [Google Scholar] [CrossRef]
- Agrawal, G.P. Fiber-Optic Communication Systems; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2010; Volume 6. [Google Scholar]
- Underhill, M.J. Time jitter and phase noise—Now and in the future? In 2012 IEEE International Frequency Control Symposium Proceedings; IEEE: Piscataway, NJ, USA, 2012; pp. 1–8. [Google Scholar]
- Grigoryan, V.S.; Menyuk, C.R.; Mu, R.M. Calculation of timing and amplitude jitter in dispersion-managed optical fiber communications using linearization. J. Light. Technol. 1999, 17, 1347–1356. [Google Scholar] [CrossRef]
- Gnauck, A.H.; Mecozzi, A.; Clausen, C.B.; Sang-Gyu, P.; Shtaif, M. Cancellation of timing and amplitude jitter in symmetric links using highly dispersed pulses. IEEE Photonics Technol. Lett. 2002, 13, 445–447. [Google Scholar] [CrossRef]
- Santhanam, J.; Agrawal, G.P. Raman-induced timing jitter in dispersion-managed optical communication systems. IEEE J. Sel. Top. Quantum Electron. 2002, 8, 632–639. [Google Scholar] [CrossRef]
- Ghassemlooy, Z.; Arnon, S.; Uysal, M.; Xu, Z.; Cheng, J. Emerging Optical Wireless Communications-Advances and Challenges. IEEE J. Sel. Areas Commun. 2015, 33, 1738–1749. [Google Scholar] [CrossRef]
- Roumelas, G.D.; Nistazakis, H.E.; Stassinakis, A.N.; Volos, C.K.; Tsigopoulos, A.D. Underwater Optical Wireless Communications with Chromatic Dispersion and Time Jitter. Computation 2019, 7, 35. [Google Scholar] [CrossRef]
- Agrawal, G.G.P. Nonlinear Fiber Optics, 3rd ed.; Academic Press: San Diego, CA, USA, 2001. [Google Scholar]
- Crisp, J. Introduction to Fiber Optics, 2nd ed.; Newnes: Oxford, UK, 2001; Volume 1, ISBN 0750650303. [Google Scholar]
- Lu, H.; Zhao, W.; Xie, X. Analysis of temporal broadening of optical pulses by atmospheric dispersion in laser communication system. Opt. Commun. 2012, 285, 3169–3173. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Frantzeskakis, D.J.; Atai, J.; Malomed, B.A.; Efremidis, N.; Hizanidis, K. Multichannel pulse dynamics in a stabilized Ginzburg-Landau system. Phys. Rev. E Stat. Phys. Plasma Fluids Relat. Interdiscip. Top. 2002, 65, 1–12. [Google Scholar] [CrossRef] [PubMed]
- Hizanidis, K.; Malomed, B.A.; Nistazakis, H.E.; Frantzeskakis, D.J. Stabilizing soliton transmission by third-order dispersion in dispersion-compensated fibre links. Pure Appl. Opt. 1998, 7, 57–62. [Google Scholar] [CrossRef]
- Stassinakis, A.N.; Nistazakis, H.E.; Peppas, K.P.; Tombras, G.S. Improving the availability of terrestrial FSO links over log-normal atmospheric turbulence channels using dispersive chirped Gaussian pulses. Opt. Laser Technol. 2013, 54, 329–334. [Google Scholar] [CrossRef]
- Djordjevic, G.T.; Petkovic, M.I.; Spasic, M.; Antic, D.S. Outage capacity of FSO link with pointing errors and link blockage. Opt. Express 2016, 24, 219–230. [Google Scholar] [CrossRef]
- Gappmair, W.; Hranilovic, S.; Leitgeb, E. Performance of PPM on terrestrial FSO links with turbulence and pointing errors. IEEE Commun. Lett. 2010, 14, 468–470. [Google Scholar] [CrossRef]
- Aarthi, G.; Ramachandra Reddy, G. Average spectral efficiency analysis of FSO links over turbulence channel with adaptive transmissions and aperture averaging. Opt. Commun. 2018, 410, 896–902. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO optical wireless links with nonzero boresight pointing errors over M modeled turbulence channels. Opt. Commun. 2017, 403, 391–400. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Gappmair, W.; Sandalidis, H.G.; Tombras, G.S. DF relayed subcarrier FSO links over Malaga turbulence channels with phase noise and non-zero boresight pointing errors. Appl. Sci. 2018, 8, 664. [Google Scholar] [CrossRef]
- Jagadeesh, V.K.; Palliyembil, V.; Ansari, I.S.; Muthuchidambaranathan, P.; Qaraqe, K.A. Performance Analysis of Relaying FSO System over M -Distributed Turbulent Channel with Variable Gain AF Protocol. In Law and Regulation of Common Carriers in the Communications Industry, 2nd ed.; Springer: Singapore, 2019; ISBN 978-0-42-996785-6. [Google Scholar]
- Prabu, K.; Kumar, D.S.; Srinivas, T. Performance analysis of FSO links under Strong atmospheric turbulence conditions using various modulation schemes. Optik (Stuttg) 2014, 125, 5573–5581. [Google Scholar] [CrossRef]
- Sandalidis, H.G.; Tsiftsis, T.A. Outage probability and ergodic capacity of free-space optical links over strong turbulence. Electron. Lett. 2008, 44, 46–47. [Google Scholar] [CrossRef]
- Gappmair, W. Novel results on pulse-position modulation performance for terrestrial free-space optical links impaired by turbulent atmosphere and pointing errors. IET Commun. 2012, 6, 1300–1305. [Google Scholar] [CrossRef]
- Li, Y.; Liang, H.; Gao, C.; Miao, M.; Li, X. Temporal dispersion compensation for turbid underwater optical wireless communication links. Opt. Commun. 2019, 435, 355–361. [Google Scholar] [CrossRef]
- Vali, Z.; Gholami, A.; Ghassemlooy, Z.; Michelson, D.G. System parameters effect on the turbulent underwater optical wireless communications link. Optik (Stuttg) 2019, 198, 163153. [Google Scholar] [CrossRef]
- Majumdar, A.K. Advanced Free Space Optics (Fso)—A System Approach; Springer: New York, NY, USA, 2015; Volume 140. [Google Scholar]
- Kaushik, R.; Khandelwal, V.; Jain, R.C. A New Closed Form Approximation for BER for Optical Wireless Systems in Weak Atmospheric Turbulence. J. Opt. Commun. 2018, 39, 247–253. [Google Scholar] [CrossRef]
- Katsis, A.; Nistazakis, H.E.; Tombras, G.S. Bayesian and frequentist estimation of the performance of free space optical channels under weak turbulence conditions. J. Franklin Inst. 2009, 346, 315–327. [Google Scholar] [CrossRef]
- McNeil, G.T. Metrical Fundamentals of Underwater Lens System. Opt. Eng. 1977, 16, 162128. [Google Scholar] [CrossRef]
- Driben, R.; Malomed, B.A.; Chu, P.L. Transmission of pulses in a dispersion-managed fiber link with extra nonlinear segments. Opt. Commun. 2005, 245, 227–236. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Volos, C.K.; Tombras, G.S. FSO links with diversity pointing errors and temporal broadening of the pulses over weak to strong atmospheric turbulence channels. Optik (Stuttg) 2016, 127, 3402–3409. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Stassinakis, A.N.; Nistazakis, H.E.; Tsigopoulos, A.D.; Peppas, K.P.; Aidinis, C.J.; Tombras, G.S. Probability of fade estimation for FSO links with time dispersion and turbulence modeled with the gamma–gamma or the I-K distribution. Optik (Stuttg) 2014, 125, 7191–7197. [Google Scholar] [CrossRef]
- Papoulis, A. Probability, Random Variables, and Stochastic Processes, 3rd ed.; McGraw-Hill, Inc.: New York, NY, USA, 1991; ISBN 0070484775. [Google Scholar]
- Weber, H.; Arfken, G.B. Essentials of Math Methods for Physicists; Elsevier: Amsterdam, The Netherlands, 1966; ISBN 978-1-48-320059-0. [Google Scholar]
- Farid, A.A.; Hranilovic, S. Outage capacity optimization for free-space optical links with pointing errors. J. Light. Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Ninos, M.P.; Nistazakis, H.E.; Tombras, G.S. On the BER performance of FSO links with multiple receivers and spatial jitter over gamma-gamma or exponential turbulence channels. Optik (Stuttg) 2017, 138, 269–279. [Google Scholar] [CrossRef]
- Barrios, R.; Dios, F. Probability of fade and BER performance of FSO links over the exponentiated Weibull fading channel under aperture averaging. Unmanned/Unattended Sens. Sens. Netw. IX 2012, 8540, 85400D. [Google Scholar] [CrossRef]
- Vetelino, F.S.; Young, C.; Andrews, L. Fade statistics and aperture averaging for Gaussian beam waves in moderate-to-strong turbulence. Appl. Opt. 2007, 46, 3780–3789. [Google Scholar] [CrossRef]
- Wang, C.; Yu, H.-Y.; Zhu, Y.-J. A Long Distance Underwater Visible Light Communication System With Single Photon Avalanche Diode. IEEE Photonics J. 2016, 8, 1–11. [Google Scholar] [CrossRef]
- Partan, J.; Kurose, J.; Levine, B.N. A survey of practical issues in underwater networks. ACM SIGMOBILE Mob. Comput. Commun. Rev. 2007, 11, 23. [Google Scholar] [CrossRef]
- Farr, N.; Chave, A.D.; Freitag, L.; Preisig, J.; White, S.N.; Yoerger, D.; Sonnichsen, F. Optical Modem Technology for Seafloor Observatories. In OCEANS 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–6. ISBN 1424401143. [Google Scholar]
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).