A New Simplified Model and Parameter Estimations for a HfO2-Based Memristor †
Abstract
1. Introduction
2. A Description of the Proposed Hafnium Dioxide Memristor Model
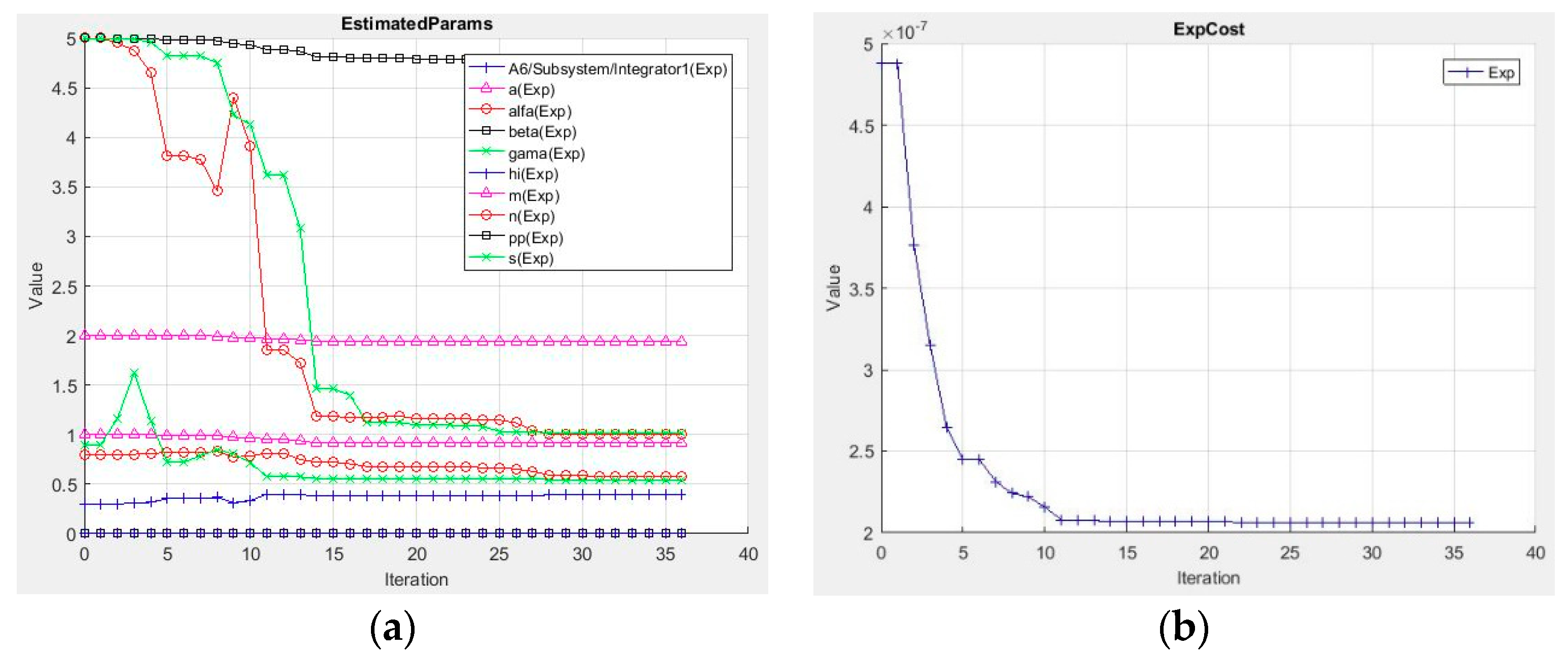
3. Parameter Estimations of the Considered Memristor Model
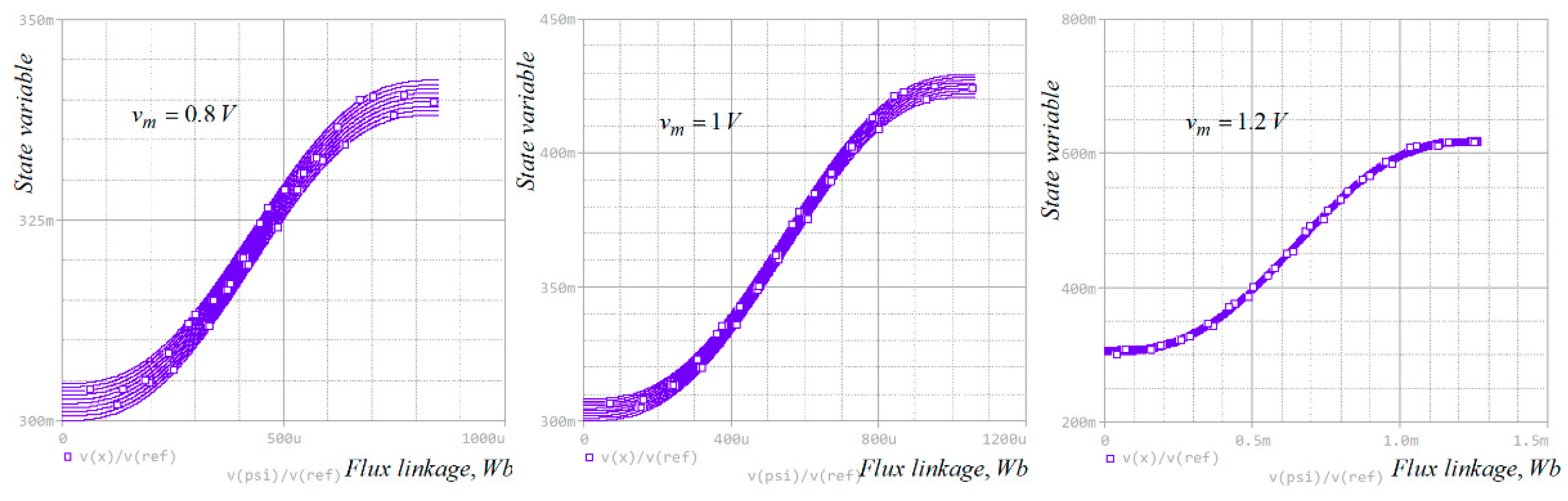
4. Analysis of the Considered Hafnium Oxide Memristor Model in the PSpice Environment
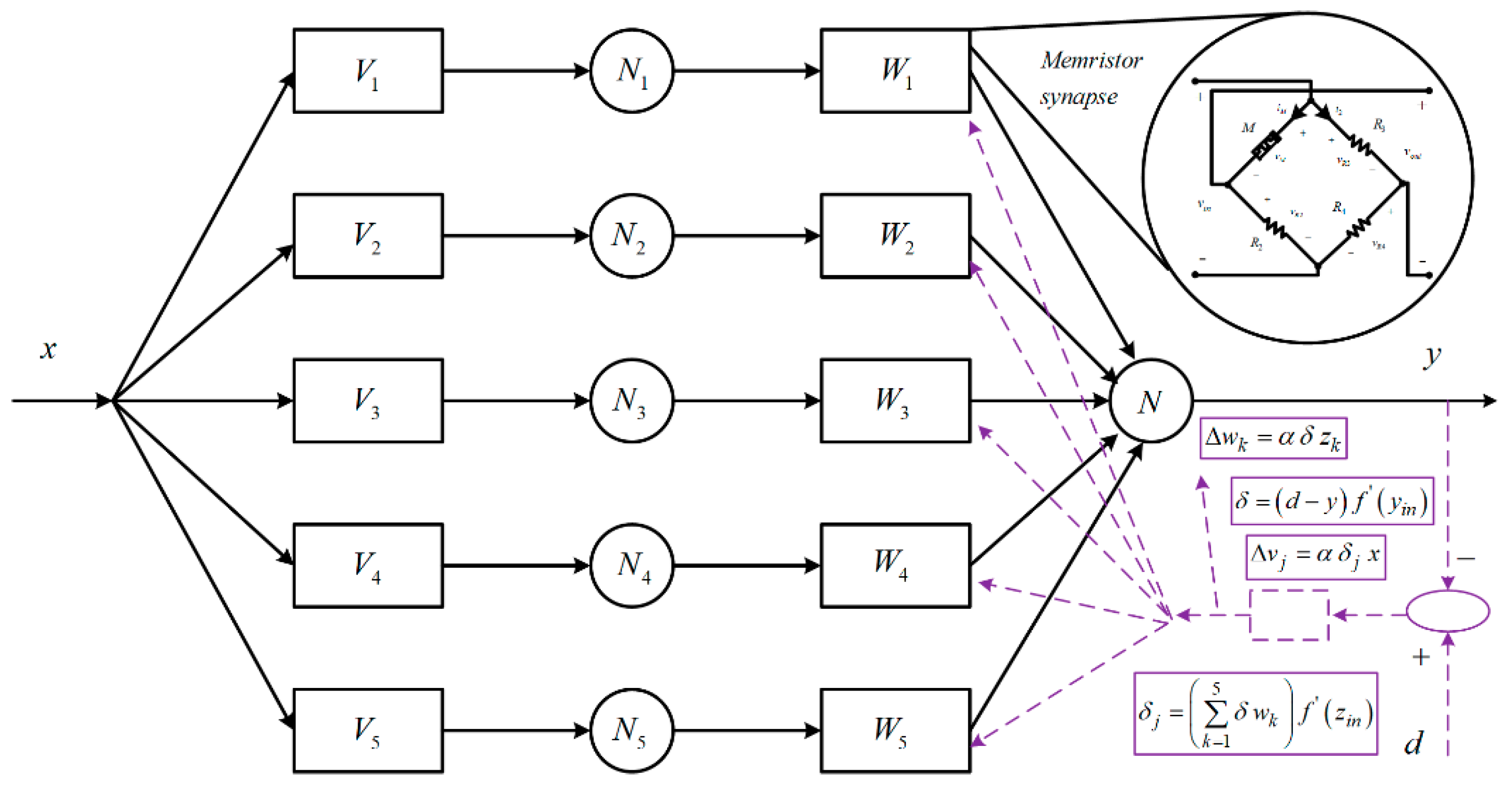
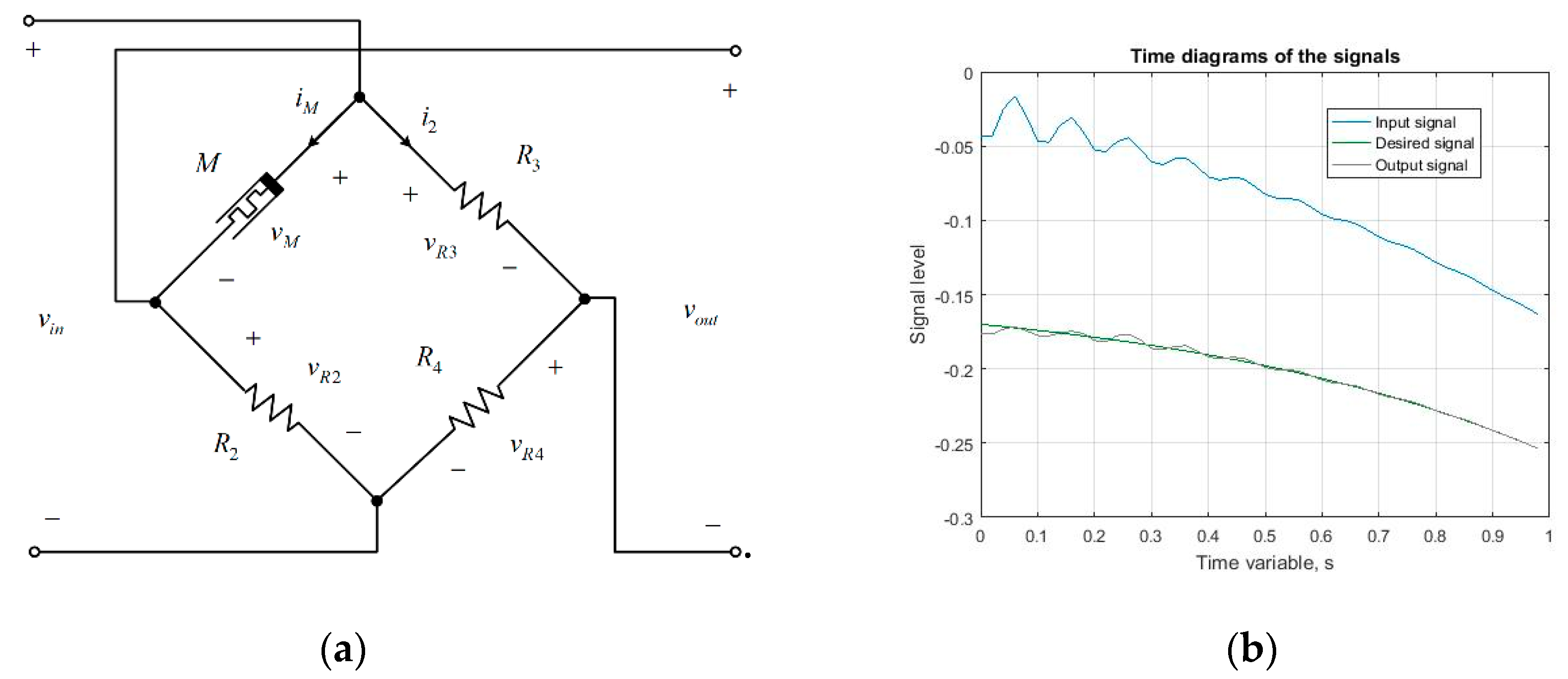
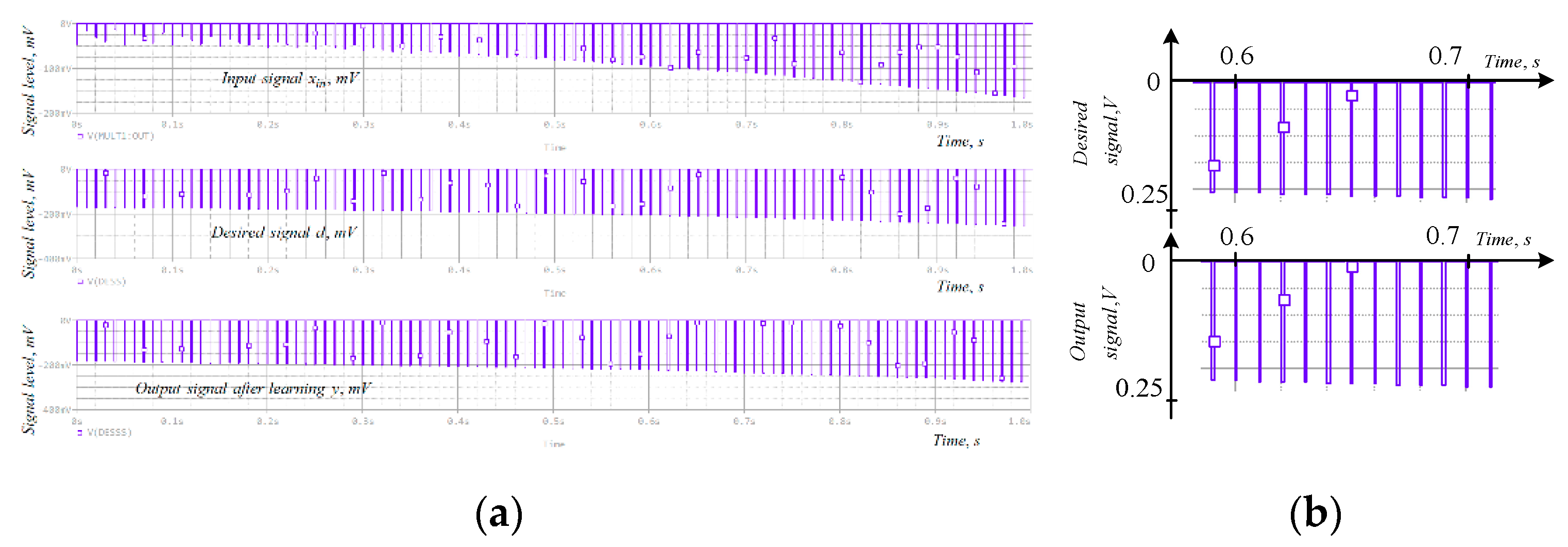
5. Application and Testing of the Proposed Hafnium Oxide Memristor Model
6. Conclusions
Funding
Conflicts of Interest
Appendix A
References
- Chua, L. Memristor—The Missing Circuit Element. IEEE Trans. Circuit Theory 1971, 18, 507–519. [Google Scholar] [CrossRef]
- Strukov, D.; Snider, G.; Stewart, D.; Williams, R. The Missing Memristor Found. Nat. Lett. 2008, 453, 80–83. [Google Scholar] [CrossRef] [PubMed]
- Joglekar, Y.; Wolf, S. The Elusive Memristor: Properties of Basic Electrical Circuits. Eur. J. Phys. 2009, 30, 661–675. [Google Scholar] [CrossRef]
- Biolek, Z.; Biolek, D.; Biolkova, V. SPICE Model of Memristor with Nonlinear Dopant Drift. Radioengineering 2009, 18, 210–214. [Google Scholar]
- Mladenov, V. A New Simplified Model for HfO2-Based Memristor. In Proceedings of the 2019 8th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 13–15 May 2019. [Google Scholar]
- Strukov, D.; Williams, R.S. Exponential ionic drift: Fast switching and low volatility of thin-film memristors. Appl. Phys. A 2009, 4, 515–519. [Google Scholar] [CrossRef]
- Yang, J.; Pickett, M.; Li, X.; Ohlberg, D.; Stewart, D.; Williams, R. Memristive switching mechanism for metal/oxide/metal nanodevices. Nat. Nanotechnol. 2008, 3, 429–433. [Google Scholar] [CrossRef] [PubMed]
- Lehtonen, E.; Laiho, M. CNN using memristors for neighborhood connections. In Proceedings of the 2010 12th International Workshop on Cellular Nanoscale Networks and their Applications, Berkeley, CA, USA, 3–5 February 2010. [Google Scholar]
- Mohammad, B.; Jaoude, M.; Kumar, V.; Homouz, D.; Nahla, H.; Al-Qutayri, M.; Christoforou, N. State of the art of metal oxide memristor devices. Nanotechnol. Rev. 2016, 5, 311–329. [Google Scholar] [CrossRef]
- Lupo, N.; Bonizzoni, E.; Pérez, E.; Wenger, C.; Maloberti, F. A Voltage–Time Model for Memristive Devices. IEEE Trans. Very Large Scale Integr. Syst. 2018, 26, 1452–1460. [Google Scholar] [CrossRef]
- Amer, С.; Sayyaparaju, S.; Rose, G.; Beckmann, K.; Cady, N. A practical hafnium-oxide memristor model suitable for circuit design and simulation. In Proceedings of the 2017 IEEE International Symposium on Circuits and Systems (ISCAS), Baltimore, MD, USA, 28–31 May 2017; pp. 1–5. [Google Scholar]
- Matveyev, Y.; Kirtaev, R.; Fetisova, A.; Zakharchenko, S.; Negrov, D.; Zenkevich, A. Crossbar Nanoscale HfO2-Based Electronic Synapses. Nanoscale Res. Lett. 2016, 11, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Kumar, S.; Wang, Z.; Huang, X.; Kumari, N.; Davila, N.; Strachan, J.; Vine, D.; Kilcoyne, A.; Nishi, Y.; Williams, R. Oxygen migration during resistance switching and failure of hafnium oxide memristors. Appl. Phys. Lett. 2017, 110, 103503. [Google Scholar] [CrossRef]
- Mladenov, V.; Kirilov, S. A Nonlinear Drift Memristor Model with a Modified Biolek Window Function and Activation Threshold. Electronics 2017, 6, 77. [Google Scholar] [CrossRef]
- Zhou, J.; Shi, J. A comprehensive multi-factor analysis on RFID localization capability. Adv. Eng. Inform. 2011, 25, 32–40. [Google Scholar] [CrossRef]
- Chen, S.; Billings, A.; Luo, W. Orthogonal least squares methods and their application to non-linear system identification. Int. J. Control 1989, 50, 1873–1896. [Google Scholar] [CrossRef]
- Ntinas, V.; Ascoli, A.; Tetzlaff, R.; Sirakoulis, G. Transformation techniques applied to a TaO memristor model to enable stable device simulations. In Proceedings of the 2017 European Conference on Circuit Theory and Design, Catania, Italy, 4–6 September 2017. [Google Scholar]
- Palm, W. Introduction to MATLAB for Engineers; McGraw-Hill: New York, NY, USA, 2011; ISBN 978-1-259-01205-1. [Google Scholar]
- Rashid, M. Introduction to PSpice Using OrCAD for Circuits and Electronics, 3rd ed.; Prentice Hall: Upper Saddle River, NJ, USA, 2004; ISBN 0-13-101988-0. [Google Scholar]
- Fausett, L. Fundamentals of Neural Networks; Prentice Hall: Upper Saddle River, NJ, USA, 1994; ISBN 0130422509. [Google Scholar]
- Mladenov, V. Synthesis and Analysis of a Memristor-Based Artificial Neuron. In Proceedings of the 16th International Workshop on Cellular Nanoscale Networks and their Applications, Budapest, Hungary, 28–30 August 2018. [Google Scholar]
- Mladenov, V.; Kirilov, S. Learning of an Artificial Neuron with Resistor-Memristor Synapses. In Proceedings of the Advances in Neural Networks and Applications, St. Konstantin, Bulgaria, 15–17 September 2018. [Google Scholar]
- Mladenov, V. Advanced Memristor Modeling—Memristor Circuits and Networks; MDPI: Basel, Switzerland, 2019; ISBN 978-3-03897-104-7. [Google Scholar]
- Liberti, L. Introduction to Global Optimization; LIX, Ecole Polytechnique: Palaiseau, France, 2008. [Google Scholar]
- Haddock, J.; Mittenthal, J. Simulation optimization using simulated annealing. Comput. Ind. Eng. 1992, 22, 387–395. [Google Scholar] [CrossRef]
- Chua, L. Resistance switching memories are memristors. Appl. Phys. A Mater. Sci. Process. 2011, 5, 765–783. [Google Scholar] [CrossRef]
- Walsh, A.; Carley, R.; Feely, O.; Ascoli, A. Memristor circuit investigation through a new tutorial toolbox. In Proceedings of the 2013 European Conference on Circuit Theory and Design, Dresden, Germany, 8–12 September 2013. [Google Scholar]
- Ascoli, A.; Tetzlaff, R.; Biolek, Z.; Kolka, Z.; Biolkovà, V.; Biolek, D. The Art of Finding Accurate Memristor Model Solutions. IEEE J. Emerg. Sel. Top. Circuits Syst. 2015, 5, 133–142. [Google Scholar] [CrossRef]


| n | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| b1n | −0.45 | −0.45 | 0.01 | 0.05 | 0.31 |
| b1 | −0.0052 | - | - | - | - |
| v1n | 0.5997 | 0.9652 | −0.1571 | 0,1110 | 0.3220 |
| w1n | 0.0744 | 0.0720 | −0.2898 | 0.5309 | 0.1276 |
| Mb1n | 10450 | 10450 | 528.4 | 450 | 129.01 |
| Mb2 | 561.6 | - | - | - | - |
| Mv1n | 149.8 | 174.62 | 1053.96 | 350.16 | 119.09 |
| Mw1n | 407.52 | 411.53 | 2066.55 | 160.48 | 326.35 |
© 2020 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mladenov, V.
A New Simplified Model and Parameter Estimations for a HfO2-Based Memristor
Mladenov V.
A New Simplified Model and Parameter Estimations for a HfO2-Based Memristor
Mladenov, Valeri.
2020. "A New Simplified Model and Parameter Estimations for a HfO2-Based Memristor
Mladenov, V.
(2020). A New Simplified Model and Parameter Estimations for a HfO2-Based Memristor





