Comparison of Time Delay Estimation Methods Used for Fast Pipeline Leak Localization in High-Noise Environment

Abstract

Pipeline networks are one of the most efficient and extensively used means for transporting fluid products. However, they suffer from a serious problem that threatens their normal and secure operation, which is the occurrence of leaks. In this article, an acoustic technique for the localization of leaks in pipelines placed in the high-noise environment of an oil refinery is described. This technique is based on the estimation of the time delay between the moments at which an acoustic signal produced by a leak reaches two sensors mounted on the external surface of the pipeline at a certain distance between them. For this reason, three different time delay estimation methods, based on the cross-correlation procedure, are studied in this article. These methods are tested for their accuracy in the estimation of the leak position, as well as for their ability to work with measurements of short duration and the results are compared. This is important because the acquisition duration affects directly the response time of the leak localization system, which is a crucial parameter for the targeted applications. Finally, an algorithm for fast and accurate identification of the leak point is proposed.

1. Introduction

A large number of applications both in the industrial world and in our everyday life require the use of pipeline networks. These networks have been utilized and tested for many years and have been proven very efficient and reliable in transporting fluid products in long distances. In addition, they can be built almost everywhere. They can be constructed above the ground (like it happens in refineries), underground (e.g., water supply networks in the cities), or even underwater (as in the case where fluid products need to be transferred between neighboring countries or continents).

However, there is a serious problem that impedes the normal operation of a pipeline network. This problem is the appearance of leaks. Leaks in a pipeline system can occur due to many reasons, like faulty valves (which are often responsible for small leaks difficult to be identified), poor maintenance of the pipelines, material corrosion, industrial accidents, harsh environmental conditions etc. Since leaks are responsible for product loss, environmental pollution, problems in the cities (e.g., in the water supply network) and even dangerous accidents (e.g., when the carried product is flammable), it is more than obvious that there is an urgent need for the development of proper leak detection and localization systems.

Particular safety problems for staff and facilities can arise from leaks in over ground pipeline structures in petrochemical plants that treat flammable fluids. In case where pipes pass through high-risk areas (e.g., high relative temperature, rotating parts with potential for sparks), a leak can mean ignition and immediate danger. In this case, immediate information about the appearance of a leak is necessary as it can lead to automatic and instantaneous risk-averse decisions by stopping the flow in the pipe. It is also critical to detect the location of the leak in order to activate appropriate measures for adjacent units with the least impact on the normal operation of the plant. Pipeline structures in such environments usually correspond to a few tens or hundreds of meters.

Over the past years, many different methods for detecting and localizing leaks in pipelines have been reported [1,2,3,4]. Some examples are: fiber optic method, vapor sampling method, infrared thermography, electromechanical impedance-based methods, fluorescence method, capacitive sensing, visual/biological methods, negative pressure wave method, and state estimators/observers method, among others. Another method for which considerable research work has been done in the past is the acoustic method, where the acoustic phenomena that arise when a leak is present are detected and processed [5,6,7,8,9,10,11,12]. Meng et al. [7] and Liu et al. [11] use the acoustic method to detect and localize leaks in pipelines. The basis of the localization process is the estimation of the time difference of arrival of the acoustic waves at two sensors located at the upstream and downstream of the pipe, by using the cross-correlation algorithm. In order to improve the accuracy in the estimation of the leak position, they included the velocity of the contained fluid in the mathematical expression for the position of the leak point.

Another study about the localization of a leak, based on the time difference of arrival, is the one conducted by Liu et al. [12]. They proposed an improved method, which combines the Wavelet Transform (WT) with the Blind Source Separation (BSS), in order to calculate this time difference more accurately. However, the employment of WT and BSS adds a computational complexity to this method, which in turn affects the response time of a leak localization system utilizing this method.

On the other hand, Lee et al. [13] presented a leak localization method, which uses the impulse response function (IRF). Specifically, the identification of the leak position is based on the estimation of the time interval needed for a transient signal to reach the leak point, reflect off the leak, and then travel to the measurement system. The use of the IRF allows the sharpening of the peaks of the reflected signals, which results in a better estimation of the time delays. However, the additional requirement for the extraction of the IRF of the system (apart from the calculation of the propagation velocity, which is needed in most of the traditional acoustic methods) increases the complexity of this method, since the IRF of a system is not always easy to determine.

Duan et al. [14] conducted a research concerning the transient-based leak detection methods. From this research, it was found that this kind of method relies on the presence of leak-reflected signals in the pipeline and can provide accurate results for the location of the leak. The downside is that the accuracy of these methods drops significantly when non-leak induced reflections (e.g., due to variations in the pipe geometry) appear in the pipe. Furthermore, in order for clear reflections to be produced, additional devices (like solenoid valves) need to be installed to the pipelines. Therefore, these transient-based leak detection methods cannot be considered as non-invasive techniques, which are often required in many practical applications in the field.

Moreover, Zhang et al. [15] presented a hybrid technique, which combines the real-time transient modeling method (RTTM) with the stimulus-response method (SM). The leak is detected by the use of the RTTM method and when its occurrence is confirmed, the SM method is employed in order for the position of the leak point to be determined. However, like the transient-based leak detection methods discussed earlier, this hybrid technique also requires the installation of additional devices to existing pipelines; therefore, it cannot be included in the category of non-invasive methods.

Another basic aspect that the methods mentioned above have not provided results for is the relationship between their accuracy and the number of the required signal samples needed to be measured (acquisition duration) which affects the response time of the method, a critical parameter for some applications. The method proposed in this article fills this gap by determining the optimal measurement duration that ensures accurate results in a short amount of time. It has to be mentioned that such a, rather simple, study has been presented in [16], where the kurtosis of the normalized autocorrelation of monitored signals is used as a metric for the detection of leakages. The effect of the acquisition time on the value of kurtosis is determined and the influence on the robustness of the method is recorded. However, in [16], only the existence of leakages is examined and not their location.

In this article, a non-invasive leak localization method, which falls into the category of acoustic techniques, is presented. This method has been developed for the high-noise environment of the process area of an oil refinery, the Hellenic Petroleum company in Thessaloniki (and it has been tested in a laboratory setup). Our method for detecting the existence of leaks in such an environment has been presented in [17]. The proposed leak localization method relies on the calculation of the difference between the time instances at which the leak signal arrives at two acoustic sensors mounted on the external surface of the pipeline at a certain distance between them. Cross-correlation is the basis of this calculation [7]. Specifically, three different time delay estimation methods based on the cross-correlation technique are studied. The efficiency of these methods in terms of the response time and the accuracy in the identification of the leak position is provided. Simple algorithms with relatively low processing requirements are used. In this way, the response time is mainly defined by the number of required signal samples (measurement window) needed for accurate decision making. Furthermore, a procedure which deals with the statistical nature of the leak measurements is proposed.

2. Materials and Methods

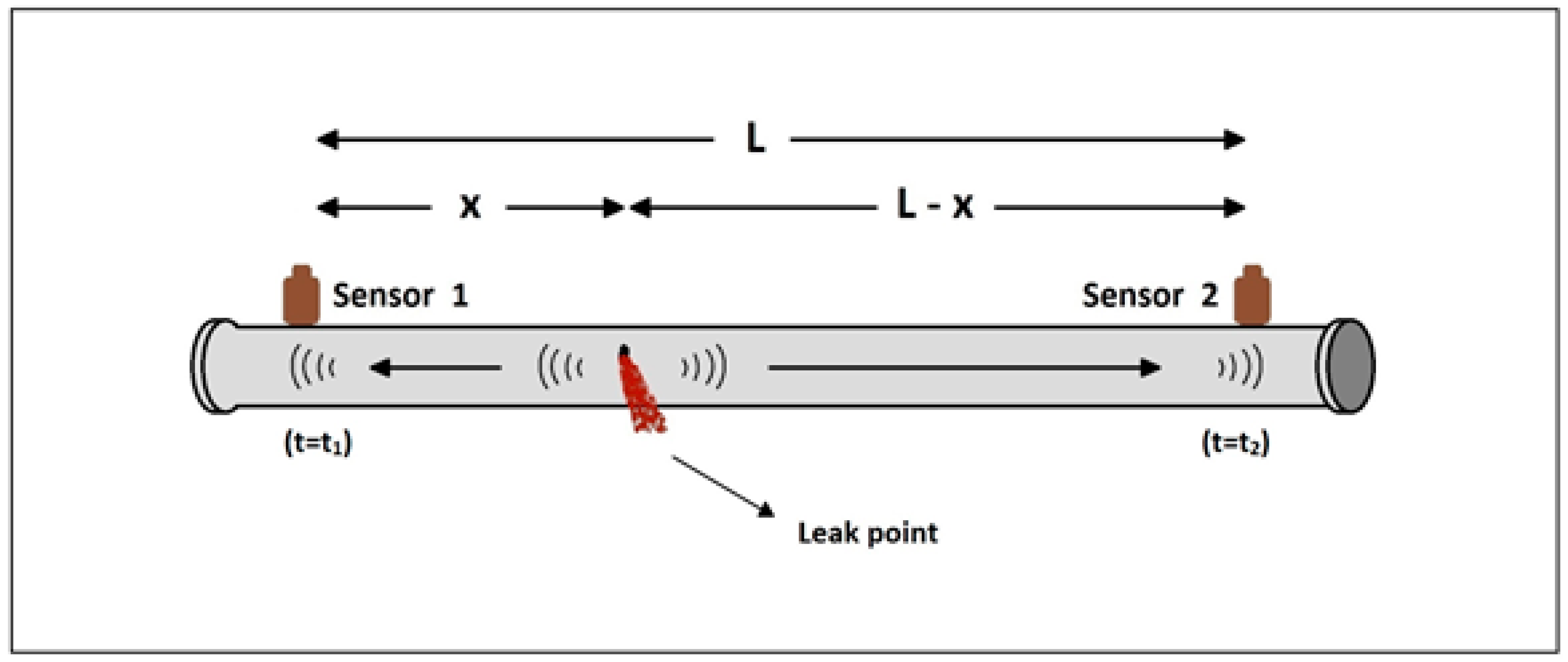
As was mentioned earlier, in this project, the localization of leaks in a pipeline is based on the calculation of the time difference between the moments of arrival of the leak signal at the two sensors. In order for this to be explained, let us consider the setup depicted in Figure 1. When a leak appears in the pipeline, the acoustic wave that propagates towards sensor 1 arrives at the location of the sensor at a specific time instance t₁. Similarly, the acoustic wave that travels towards the other direction reaches sensor 2 at another time instance t₂. As it is frequently mentioned in the literature [18], if the time difference Δt = t₁ − t₂ is determined, the position x of the leak point can be calculated by the following mathematical formula:

$$x=\frac{L+u\cdot \Delta t}{2}$$

(1)

where L is the distance between the sensors and u is the propagation velocity of the acoustic waves. This velocity can be determined by emulating a leak at a known point on the pipeline, calculating the time difference Δt and then solving for u in Equation (1).

In this article, three different methods for the estimation of the time difference Δt, based on real measurements, are going to be examined: the Cross Correlation (CC) method, the Generalized Cross Correlation—BCC (BCC) method, and the Generalized Cross Correlation—Roth (Roth) method. Their efficiency in the calculation of the leak position in a noisy pipe and their ability to work properly with short measurements will be determined. The computational requirements of the algorithms will also be investigated. Such a study is substantial for defining the response time for each of the above approaches, which is critical for the targeted applications.

2.1. Time Delay Estimation Methods

The time delay estimation methods described in this article rely on the cross-correlation function. Specifically, by observing at which sample this function shows its maximum value, the time delay Δt between the signals obtained by the two sensors can be determined. The difference among these methods lies in the form of the cross-correlation function.

2.1.1. Cross Correlation (CC) Method

In this method, the cross-correlation function between the discrete time signals x₁[m] (from sensor 1) and x₂[m] (from sensor 2) that is used is described by the following expression:

$$R[n]=\frac{{\displaystyle \sum _{m=0}^{N-1}{x}_1[m]\cdot x_2[m-n]}}{\sqrt{{\displaystyle \sum _{m=0}^{N-1}{x}_1{}^2[m]}}\cdot \sqrt{{\displaystyle \sum _{m=0}^{N-1}{x}_2{}^2[m]}}}$$

(2)

where N is the number of samples of each signal and for the integer variable n we have: $n\in (-N,N)$.

The time difference Δt between the signals x₁ and x₂ can be easily identified from the function R[n]. If the total maximum of this function appears at a specific sample with index n, the time delay Δt can be found by the following expression:

$$\Delta t=n\cdot T_S=\frac{n}{f_S}$$

(3)

where T_S and f_S are the sampling period and the sampling frequency, respectively. This means that the selected sampling frequency defines the resolution of the method in the estimation of the time differences and, therefore, in the calculation of the leak position.

2.1.2. BCC and Roth Methods

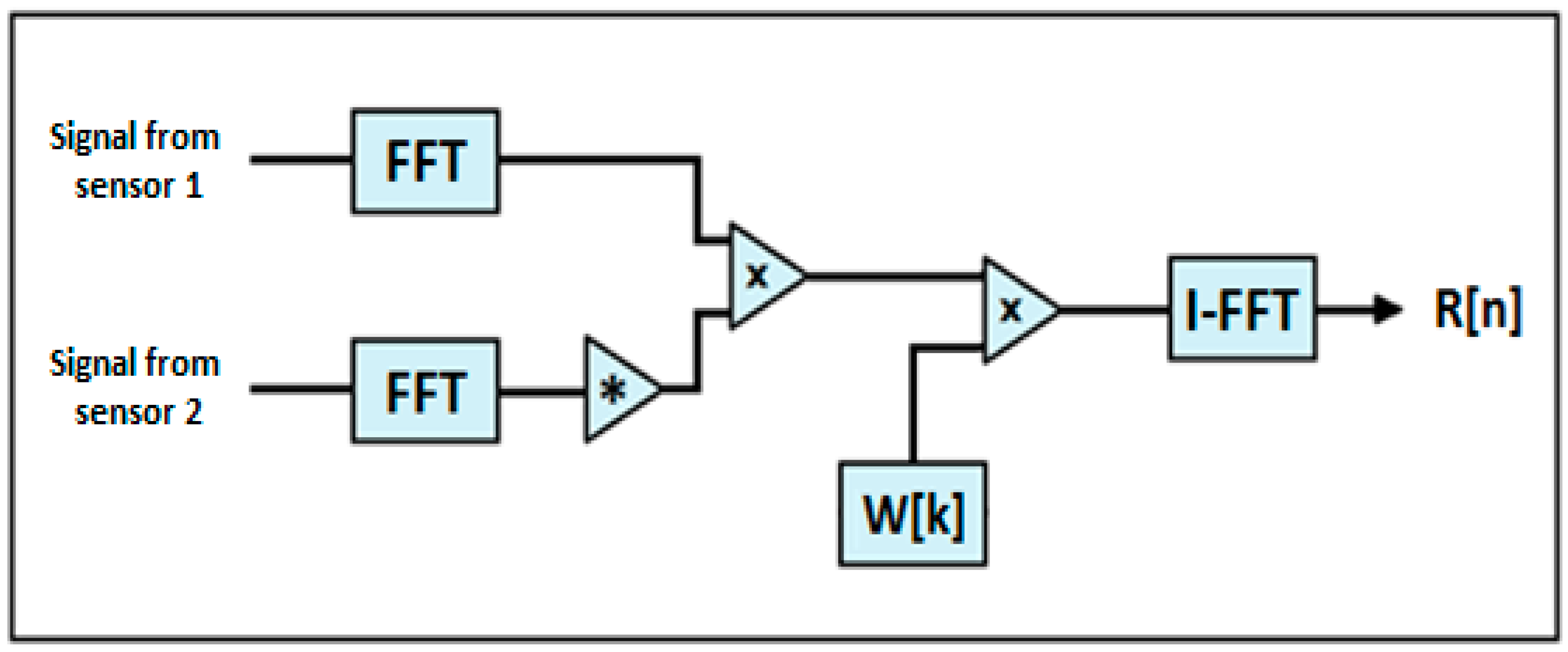
These two methods belong to the category of the generalized cross correlations techniques. The procedure for the calculation of the time difference Δt by using these methods is similar to the one followed in the CC method. However, the cross-correlation function R[n] is constructed in the following way:

• Step 1: Calculation of the Fast Fourier Transforms (FFTs) of the signals obtained by the two sensors.
• Step 2: Calculation of the cross spectral density of the two signals (which is the product of the FFT of the first signal and the complex conjugate of the FFT of the second signal).
• Step 3: Multiplication of the cross spectral density with a weighting function W[k].
• Step 4: Calculation of the Inverse FFT (I-FFT) of the complex function created in the previous step, which results in the creation of the cross-correlation function R[n].

The aforementioned steps, which are illustrated in Figure 2, lead to the following expression for the cross-correlation function [19]:

$$R[n]={\displaystyle \sum _{k=0}^{N-1}W[k]\cdot S_1[k]S_2{}^{*}[k]}\cdot e^{i\cdot 2\pi \cdot \frac{kn}{N}}$$

(4)

where n is the index in the time domain, k is the index in the frequency domain, S₁ and S₂ are the FFTs of the signals from sensors 1 and 2, respectively, and W[k] is the weighting function. In the case of the BCC method, the weighting function is W[k] = 1, so the cross correlation function is described by Equation (5), and in the case of the Roth method, the weighting function is W[k] = 1/|S₁[k]|² and the cross correlation function is given by Equation (6).

$$R_{BCC}[n]={\displaystyle \sum _{k=0}^{N-1}{S}_1[k]S_2{}^{*}[k]}\cdot e^{i\cdot 2\pi \cdot \frac{kn}{N}}$$

(5)

$$R_{Roth}[n]={\displaystyle \sum _{k=0}^{N-1}\frac{1}{{\left|S_1[k]\right|}^2}\cdot S_1[k]S_2{}^{*}[k]}\cdot e^{i\cdot 2\pi \cdot \frac{kn}{N}}$$

(6)

The different calculations needed for the functions defined in Equations (2), (5) and (6) will influence their accuracy in the localization of a leak, the number of the required samples per measurement (i.e., the measurement duration) and the computational time. At this point, it should be mentioned that the BCC method is the counterpart of the CC method in the frequency domain. However, as will be shown later, the results from these two methods for the leak position are slightly different, so they are examined separately.

2.2. Experimental Setup

For the experimental testing of the studied methods, a laboratory setup was employed. This setup includes a steel pipeline with a diameter of three inches, which contains water. This system is equipped with a proper pump in order for the circulation of the water to be possible.

The pipeline is also equipped with a number of valves, by the help of which leaks can be emulated. More specifically, there are five groups of valves. Each group contains a set of valves with different diameters. For this article, two diameters were chosen: 0.5 mm (about 6 mL/s outflow rate) and 2 mm (about 91 mL/s outflow rate) valves. In addition, two cases for the distance L between the sensors were employed: L = 8.5 m and L = 15 m. In

Table 1. Positions of the utilized valves on the pipeline.

		Positions of the 1st Group Valves (m)	Positions of the 2nd Group Valves (m)	Positions of the 3rd Group Valves (m)	Positions of the 4th Group Valves (m)	Positions of the 5th Group Valves (m)
L = 8.5 m	0.5 mm valve	0.70	2.21	4.24	5.26	7.28
	2 mm valve	0.78	2.29	4.31	5.36	7.36
L = 15 m	0.5 mm valve	7.20	8.71	10.74	11.76	13.78
	2 mm valve	7.28	8.79	10.81	11.86	13.86

, the positions of the chosen valves from each group are presented. These (leak) positions are defined as distances from sensor 1. During the measurements, the pressure inside the pipeline was set at 6 bars and the flow rate at 12.5 L/s. A picture of the experimental setup is shown in Figure 3.

The measurement system that was utilized in the laboratory setup consists of the following components:

• NI-9232 module: this is a 3-channel data acquisition card [20], which contains Analog-to-Digital Converters (ADCs). These ADCs have a voltage rage of ±30 V, 24-bit resolution, and a maximum sampling frequency of 102.4 kHz (in this project a sampling frequency of 25.6 kHz was used).
• NI cDAQ-9174 module: this is a 4-slot chassis [21] on which the NI-9232 module is connected.
• PCB 352C33: this is a ceramic shear ICP accelerometer [22] with a sensitivity of 100 mV/g and a flat frequency response. Two sensors of this type are used in this project. These sensors are connected to the NI-9232 module.
• Computer: a computer (laptop) is connected to the NI cDAQ-9174 chassis and receives the data acquired in the measurements.

Before proceeding to the results, it should be mentioned that the efficiency of the studied time delay estimation methods was tested for measurements both without and with noise, which is the case in the field (i.e., the refinery). The measurements that include noise were created from the initial ones, conducted in the experimental setup, by adding (in LabVIEW 2018) measured noise from the field (i.e., from pipelines in the oil refinery) to them. For the dataset with the noisy measurements, proper filtering was performed prior to the application of the time delay estimation methods. The filtering algorithm is described in our previous work referred in [17] and it involves the following steps:

• Step 1: Application of a bandpass filter with lower cutoff at 250 Hz and upper cutoff at 11 kHz to a measurement (of 1 s duration) containing noise from the field.
• Step 2: Division of the remaining spectrum into frequency bands of 250 Hz width and calculation of the spectral energy in each of these bands (E_i), as well as the total spectral energy (E_tot) of the noise signal, which remained after the bandpass filtering (at step 1).
• Step 3: Calculation of the quotient E_i/E_tot for each band and the percentage that this quotient corresponds to.
• Step 4: Steps 1–3 are repeated for another nine noise measurements and a mean value for each of the percentages calculated in step 3 is computed.
• Step 5: If the mean value of the percentage corresponding to a particular band is greater than the percentage (1/n)∙100% (where n = 43 is the number of the frequency bands from 250 Hz to 11 kHz), this band is cut from the signal by the use of extra filters.

3. Results

In this section, the results regarding the efficiency of the three studied methods will be presented. Specifically, results from the two different leak sizes (0.5 mm and 2 mm) for each of the studied cases (8.5 m and 15 m distance between the sensors and leaks with or without flow) are provided. Furthermore, for each of these cases, two datasets are examined: one with the initial measurements from the experimental setup (leaks without noise) and another one containing these measurements with the noise from the field added to them (leaks with noise). In addition, a comparison of the tested methods will be made in relation to their accuracy in the localization of a leak and their ability to work efficiently with measurements of short duration. As has been mentioned, this is critical because the duration of the measurements has a direct impact on the response time of the leak localization system.

3.1. Results for the Leak Location

It has been mentioned earlier that in order for the identification of the leak position to be possible, the propagation velocity of the acoustic waves should be determined. For this reason, an initial measurement was conducted for a leak created at a known point in the pipeline and the value of the propagation velocity was computed with the help of Equation (1). Then, by using the five groups of valves with which the pipeline is equipped, a number of leaks were emulated at several points on the pipe and their location was estimated based on the three mentioned methods.

In

Table 2. Results from the CC method for 8.5 m distance between the sensors.

			Real Value of x (m)	Estimated Value of x (m)	Absolute Error Rate (%)
without noise	without flow	0.5 mm leak	2.21	2.58	4.4
		2 mm leak	7.36	7.31	0.6
	with flow	0.5 mm leak	2.21	2.94	8.6
		2 mm leak	2.29	2.79	5.9
with noise (filtered)	without flow	0.5 mm leak	0.70	0.17	6.2
		2 mm leak	7.36	7.78	4.9
	with flow	0.5 mm leak	0.70	0.29	4.8
		2 mm leak	2.29	2.56	3.2

and

Table 3. Results from the CC method for 15 m distance between the sensors.

			Real Value of x (m)	Estimated Value of x (m)	Absolute Error Rate (%)
without noise	without flow	0.5 mm leak	8.71	8.54	1.1
		2 mm leak	8.79	7.93	5.7
	with flow	0.5 mm leak	10.74	10.17	3.8
		2 mm leak	10.81	9.74	7.1
with noise (filtered)	without flow	0.5 mm leak	10.74	11.23	3.3
		2 mm leak	13.86	14.07	1.4
	with flow	0.5 mm leak	8.71	8.54	1.1
		2 mm leak	11.86	13.45	10.6

, results from the CC method are provided. These tables include indicative examples for both 0.5 mm and 2 mm leaks for each of the studied cases (with/without flow and with/without noise). Moreover, the results in Table 2 and Table 3 concern the sets of measurements with L = 8.5 m and L = 15 m, respectively. Similar results are provided for the BCC method in

Table 4. Results from the BCC method for 8.5 m distance between the sensors.

			Real Value of x (m)	Estimated Value of x (m)	Absolute Error Rate (%)
without noise	without flow	0.5 mm leak	2.21	2.58	4.4
		2 mm leak	5.36	5.16	2.4
	with flow	0.5 mm leak	2.21	2.94	8.6
		2 mm leak	7.36	7.66	3.5
with noise (filtered)	without flow	0.5 mm leak	0.70	0.17	6.2
		2 mm leak	2.29	3.20	10.7
	with flow	0.5 mm leak	2.21	2.62	4.8
		2 mm leak	2.29	2.56	3.2

and

Table 5. Results from the BCC method for 15 m distance between the sensors.

			Real Value of x (m)	Estimated Value of x (m)	Absolute Error Rate (%)
without noise	without flow	0.5 mm leak	11.76	11.74	0.1
		2 mm leak	8.79	7.93	5.7
	with flow	0.5 mm leak	10.74	10.17	3.8
		2 mm leak	10.81	9.74	7.1
with noise (filtered)	without flow	0.5 mm leak	10.74	11.23	3.3
		2 mm leak	11.86	13.45	10.6
	with flow	0.5 mm leak	7.20	6.15	7.0
		2 mm leak	11.86	13.45	10.6

and for the Roth method in

Table 6. Results from the Roth method for 8.5 m distance between the sensors.

			Real Value of x (m)	Estimated Value of x (m)	Absolute Error Rate (%)
without noise	without flow	0.5 mm leak	2.21	3.29	12.7
		2 mm leak	0.78	0.93	1.8
	with flow	0.5 mm leak	2.21	3.29	12.7
		2 mm leak	5.36	4.56	9.4
with noise (filtered)	without flow	0.5 mm leak	5.26	4.25	11.9
		2 mm leak	2.29	4.10	21.3
	with flow	0.5 mm leak	2.21	3.92	20.1
		2 mm leak	2.29	3.59	15.3

and

Table 7. Results from the Roth method for 15 m distance between the sensors.

			Real Value of x (m)	Estimated Value of x (m)	Absolute Error Rate (%)
without noise	without flow	0.5 mm leak	11.76	11.53	1.5
		2 mm leak	8.79	8.09	4.7
	with flow	0.5 mm leak	7.20	7.40	1.3
		2 mm leak	8.79	7.43	9.1
with noise (filtered)	without flow	0.5 mm leak	13.78	10.21	19.1
		2 mm leak	7.28	6.43	5.7
	with flow	0.5 mm leak	10.74	7.62	20.8
		2 mm leak	10.81	9.08	11.5

. At this point, the measurement window is defined at 5 sec (128,000 samples). The leak position (x) is measured from sensor 1 and the provided error rates (i.e., the absolute value of the error rates) are expressed as a percentage of the distance L between the sensors.

From Table 2, Table 3, Table 4, Table 5, Table 6 and Table 7, a general idea about the accuracy of the three studied methods in localizing a leak can be acquired. However, in order for the comparison between these methods to be clarified, the mean absolute error rates for each case of leaks that was examined are shown in

Table 8. Mean absolute error rates for the three studied methods.

			Mean Absolute Error Rate (%)
			CC Method	BCC Method	Roth Method
L = 8.5 m	without noise	without flow	3.7	3.7	8.2
		with flow	6.1	7	9.6
	with noise (filtered)	without flow	7.1	7.1	17.0
		with flow	8.5	8.5	18.6
L = 15 m	without noise	without flow	4.1	4.1	3.8
		with flow	5.3	6.4	4.1
	with noise (filtered)	without flow	5.7	5.7	11.8
		with flow	5.7	6.4	12.3
For all cases			5.8	6.1	10.7

. In this table, the mean error rate for each case is calculated from the corresponding set of measurements, concerning both 0.5 mm and 2 mm leaks. Specifically, each set contains measurements from leaks at ten different positions on the pipe (described in Table 1) and for each of them the measurement was repeated three times. As it can be observed, the case of leaks without noise shows slightly higher accuracy than the one with noise. Furthermore, the existence of flow in the pipe results in a small increase in the leak location error. For this issue, a correction in Equation (1) that takes into account the velocity of the fluid in the pipe [6] can be done, but it does not decrease the location error significantly. Moreover, the CC and the BCC methods present better accuracy than the Roth method (apart from some minor exceptions). A result similar to that was found by Almeida et al. in [23]. Specifically, they observed that the occurrence of resonances in plastic pipes increases the time delay estimation error of the PHAT method (which is another generalized cross-correlation method), while it does not affect the error of the BCC method. Apart from that, Choi et al. [24] refer that the Roth method cannot work efficiently in cases with low SNR (Signal-to-Noise Ratio). However, in Table 8, it can be seen that for L = 8.5 m even in the case without noise (and therefore high SNR), this method presents larger error rates compared to the other two methods.

The total mean error rate (taking into account all cases of leaks mentioned in Table 8) is approximately 5.8% for the CC method, 6.1% for the BCC method and 10.7% for the Roth method.

3.2. Results for the Measurement Duration and the Execution Time of the Algorithms

Apart from the accuracy in the estimation of the leak position, the ability of the studied methods to work with the same efficiency for measurements of shorter duration and the execution time of the algorithms of these methods are examined. A short measurement duration is very important, because it contributes to the decrease of the response time of the leak localization system, which is required for fast identification of the leak position (and therefore the avoidance of any hazardous situations caused by the leak). In

Table 9. Estimation of the time difference Δt for several measurement durations.

Measurement Duration (s)	CC Method		BCC Method		Roth Method
	Leak 1 Δt (ms)	Leak 2 Δt (ms)	Leak 1 Δt (ms)	Leak 2 Δt (ms)	Leak 1 Δt (ms)	Leak 2 Δt (ms)
5	8.13	12.58	8.13	12.58	8.24	12.58
3	8.16	12.62	8.13	12.58	8.24	12.58
1	8.16	12.62	8.13	12.58	6.48	6.95
0.8	8.16	12.62	8.13	12.58	7.77	26.76
0.5	8.16	12.62	8.13	12.58	3.52	7.03
0.3	8.16	12.62	8.13	12.58	7.77	−0.16
0.1	8.13	12.58	8.13	12.58	3.52	2.07
0.08	8.59	12.62	8.01	13.63	−1.60	0

, the time difference Δt for two different cases of leak is estimated for several measurement durations. It can be observed that as the duration of the measurement decreases, the value of Δt remains quite stable for the CC and the BCC methods, which is not the case for the Roth method. Specifically, while the Roth method cannot work properly for measurements under 3 s, the other two methods are able to estimate the time difference Δt, with low or no deviation from the initial value (obtained by the 5 s measurement), even for measurements with a duration of 0.1 s. Based on this finding and on the fact that the CC and the BCC methods present better accuracy in the estimation of the leak position, these methods are preferred for the leak localization procedure.

Moreover, working with short measurements is also important for another reason. An isolated system for pipeline leakage detection and localization consists of two wireless sensors placed at the edges of the pipe under protection (Figure 1). Both sensors acquire data simultaneously, but the one which acts as a slave has to transmit its measured data to the other one that operates as a master, in order to proceed with the calculations. The measurement duration affects the transmitting time of the data, as well as the execution time of the algorithm that is used, which are two of the three basic parameters of the response time of the system (the third one being the measurement duration itself). The shorter the duration of the measurement, the lower the execution and transmitting times will be. In

Table 10. Execution time for different measurement durations.

Measurement Duration (s)	Execution Time for CC (ms)	Execution Time for BCC (ms)
1	740.98	26.23
0.8	485.54	25.44
0.5	186.39	10.84
0.1	8.38	1.76

, the execution time of the two preferred methods (CC and BCC) for several measurement durations is computed in Matlab R2019b. It can be seen that as the measurement duration decreases, the execution time for both methods is decreased even more (especially for the CC method), therefore improving the response time of the system. At this point, it should be mentioned that an analysis about the transmitting time of the data is not included because for a fixed measurement duration (i.e., fixed amount of data) the transmitting time is stable and independent of the method that is used. This is also valid for the time needed for the filtering of the data (in case of noisy measurements).

3.3. Algorithm for Fast and Accurate Leak Localization

It is often mentioned in the literature [25] that the results of the cross-correlation algorithms are enhanced and stabilized if the number of samples (therefore the measurement duration) is increased. However, as it has been explained, long measurements are not desired for the targeted applications, so a proper study about the accuracy and the stability of the two preferred methods (CC and BCC) for the case of 0.1 s measurements had to be done. The statistical nature of the leak signals, which is present even in the case of long-duration signals, imposes the use of a set of measurements, instead of one single measurement. These measurements, in general, may provide different values for Δt. Taking the average of these values was found to give inaccurate results. Besides, it has been observed that for a large number of measurements, the most frequently appeared value of Δt is the one that provides the best accuracy for the time difference Δt.

By conducting a large number of measurement sets and varying the number of measurements per set, it was found that, for a set of ten measurements (of 0.1 s duration each), if the rate of appearance of the most frequently encountered value of Δt (hit rate) is greater or equal to 70%, then this value of Δt is correct (i.e., it results in an accurate estimation of the leak position). On the other hand, if this hit rate is less than 40%, the estimated value of Δt is not reliable. Finally, if the hit rate is greater or equal to 40% and less than 70%, then the validity of the estimated value of Δt is not clear. Based on this finding, the following algorithm, which provides fast and accurate estimation of the value of Δt, is proposed: a set of measurements is conducted and the hit rate of the most frequently appeared value of Δt is calculated. If this hit rate is greater or equal to 70%, then the value of Δt is considered reliable and the time difference estimation process ends here. If this is not the case, then the set of measurements is repeated, one or more times, until one of the following conditions is satisfied:

(a)

A hit rate of 50% or more is achieved two times for this value of Δt.

(b)

A hit rate of 40% or more is achieved three times for this value of Δt.

(c)

A hit rate of 70% or more is achieved for another value of Δt.

(d)

One of the conditions (a) and (b) is satisfied for another value of Δt.

(e)

If ten successive measurement sets have been conducted and none of the conditions (a) to (d) is satisfied, then the most frequently appeared value of Δt (regardless of its hit rate) is taken into account for the estimation of the leak position.

In

Table 11. Measurement sets with significant error for different hit rates.

Hit Rate	CC Method		BCC Method
	Number of Measurement Sets with Faulty Value of Δt	Measurement Sets with Faulty Value of Δt (Percentage)	Number of Measurement Sets with Faulty Value of Δt	Measurement sets with Faulty Value of Δt (Percentage)
≥40%	7	2.92%	8	3.33%
≥50%	4	1.67%	4	1.67%
≥60%	3	1.25%	2	0.83%
≥70%	0	0%	0	0%

, results concerning the rate of appearance of faulty values for Δt in our experiment are provided. These results correspond to a number of 240 measurement sets. In this table, the number of sets with faulty value of Δt for different hit rates is presented, as well as the percentage of the total number of sets that this number corresponds to. For example, in the case of the CC method, only 7 out of 240 sets (2.92%) presented a hit rate greater than 40% and resulted in a faulty value of Δt. For hit rates greater than 70%, the percentage of cases with faulty values goes to 0%. Therefore, it is shown that the probability of obtaining a faulty value is minimal and it decreases even more by the use of the proposed algorithm.

At this point, it should be mentioned that apart from the statistical nature of the leak signals, another reason for selecting ten measurements of 0.1 s duration (i.e., total duration of 1 s), instead of one single measurement of 1 s duration, is the need for low execution time. Specifically, as can be seen in Table 10, the execution time for a measurement of 1 s is much larger than what it is for ten measurements of 0.1 s, especially in the case of the CC method.

4. Discussions

In this article, the localization of leaks in a pipeline was studied. The identification of the leak point was based on time delay estimation methods. Three such methods were examined: the CC method, the BCC method, and the Roth method. These methods were tested for their accuracy in the estimation of the leak position and for their ability to work as expected with measurements of short duration.

It is very important that the leak point is identified quickly, so that hazardous situations are avoided. Therefore, the leak localization system should be able to estimate the position of the leak immediately, which allows it to send a command to the adjacent factory units to stop working (or stop the flow of the contained, possibly flammable fluids), in order for the safety of the staff and the facilities to be ensured. For this reason, a study about the minimum measurement duration that the three mentioned time delay estimation methods can work with was conducted. This study showed that while the Roth method cannot function properly with measurements under 3 s, the CC and the BCC methods can provide reliable results even for a measurement duration of 0.1 s, which in turn leads to a low execution time. Specifically, the execution time for a 0.1 s measurement was found to be 8.38 ms for the CC method and 1.76 ms for the BCC method. These time intervals are very small, compared to the measurement duration. This leads to a similar response time for these two methods, allowing both of them to be used for the implementation of a fast leak localization system.

Moreover, the CC and the BCC methods provided better results in the accuracy of the leak position estimation, especially when there is (filtered) noise in the pipeline. At this point, it should be added that the studied methods were tested even with noisy measurements without filtering. It was found that in this case the CC and the BCC methods cannot work properly and the Roth method can provide some acceptable results for the leak location. However, this method is not able to function with short measurements, which makes it unsuitable for the targeted applications. The mean error rates of the CC and the BCC methods are 5.8% and 6.1%, respectively, which are comparable to results for the location error, from similar or different methods, encountered in the literature [8,26]. In addition, the existence of flow in the pipe has a negative effect on the accuracy of the three studied methods, since the error rates for the leak position are slightly higher in the case with flow. In addition, the results for the leak localization obtained for the case of L = 15 m seem to be a little better than the one with L = 8.5 m, but it should be taken into account that in Table 8 the errors are expressed as percentages of the distance L. Thus, the same error in position gives greater error rate for the case of L = 8.5 m, while the error for this case expressed as an absolute number is actually smaller.

Finally, the stability of the two preferred methods (CC and BCC) in the estimation of the time difference Δt, for the case of 0.1 s measurements, was studied. It was observed that the statistical nature of the leak signals sometimes causes deviations from the correct value of Δt. For this reason, an algorithm which deals with this statistical nature and provides fast response with sufficient accuracy in the identification of the time difference was proposed. This algorithm was tested in the laboratory setup and it provided sufficient results.

5. Conclusions

In this article, a comparison of three different time delay estimation methods (the CC, the BCC, and the Roth methods), used for pipeline leak localization, was performed. This comparison was made in terms of localization accuracy and, especially, fast response. The latter is of major importance for the targeted applications, i.e., monitoring of pipeline networks in potentially hazardous environments, like a refinery. As it was found, the CC and the BCC methods provide more efficient results, both from the accuracy and from the response time point of view. Specifically, the mean error rate for these two methods in the estimation of the leak position is around 6% and it was found that the acquisition duration can be reduced to 0.1 s without decreasing the accuracy of these methods. Moreover, in order to overcome the ambiguity introduced by the statistical nature of the problem, a proper algorithm was proposed, by the help of which sufficiently accurate results for the leak position are achieved in a quite short amount of time.