A Self-Deformation Robot Design Incorporating Bending-Type Pneumatic Artificial Muscles
Abstract
1. Introduction
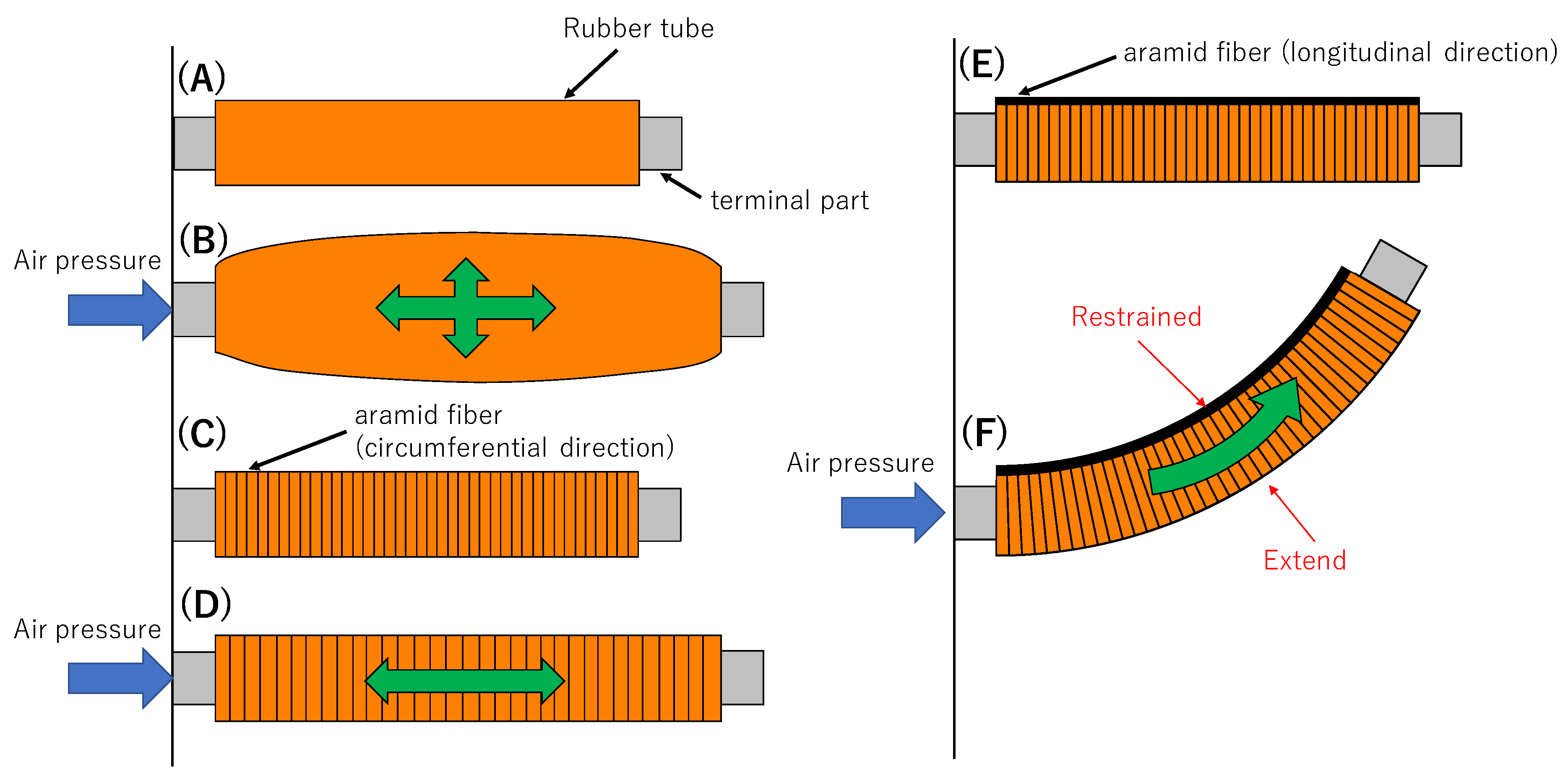
2. Bending-Type Pneumatic Rubber Artificial Muscle
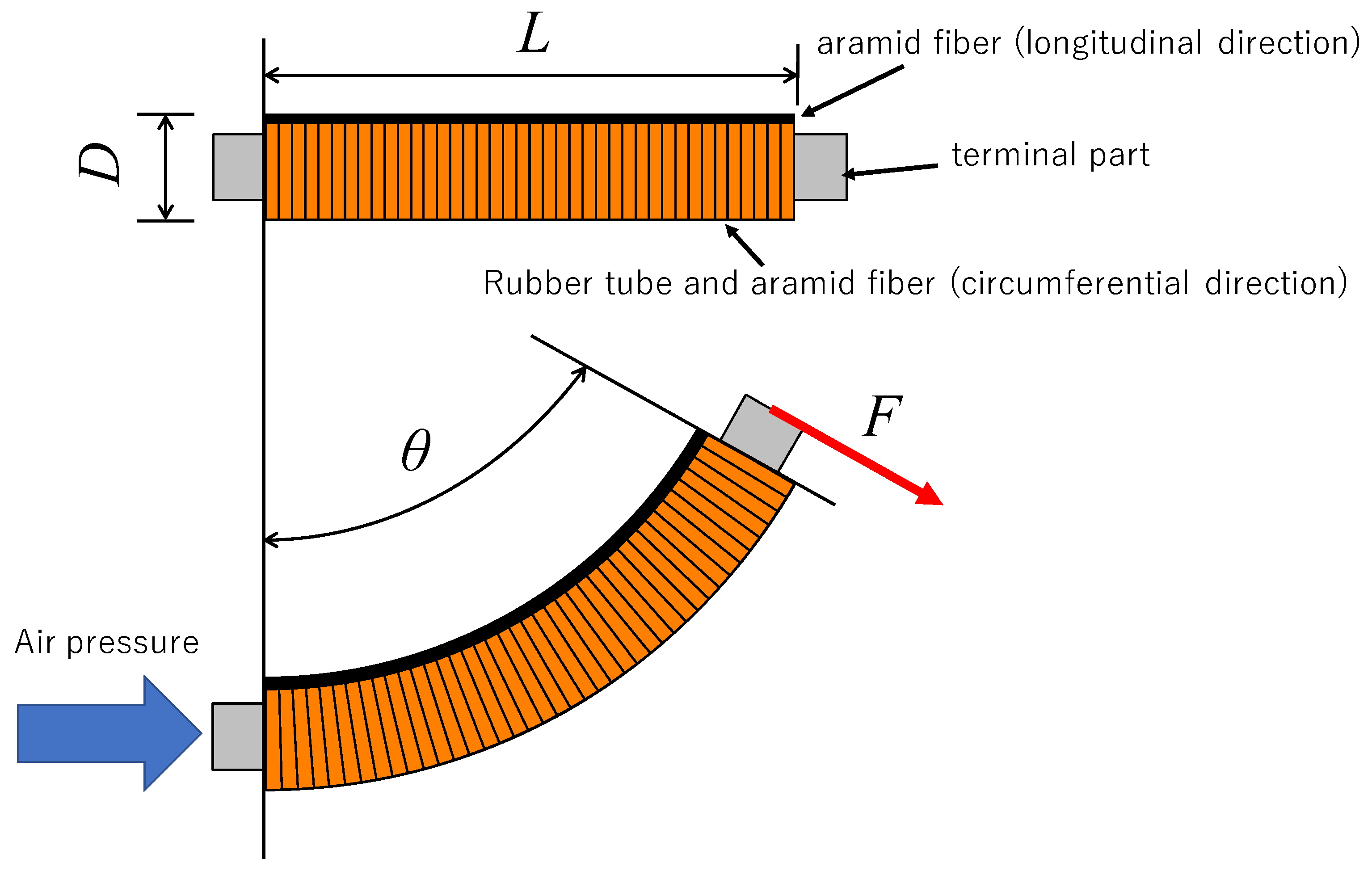
2.1. Mechanism of the BPAM
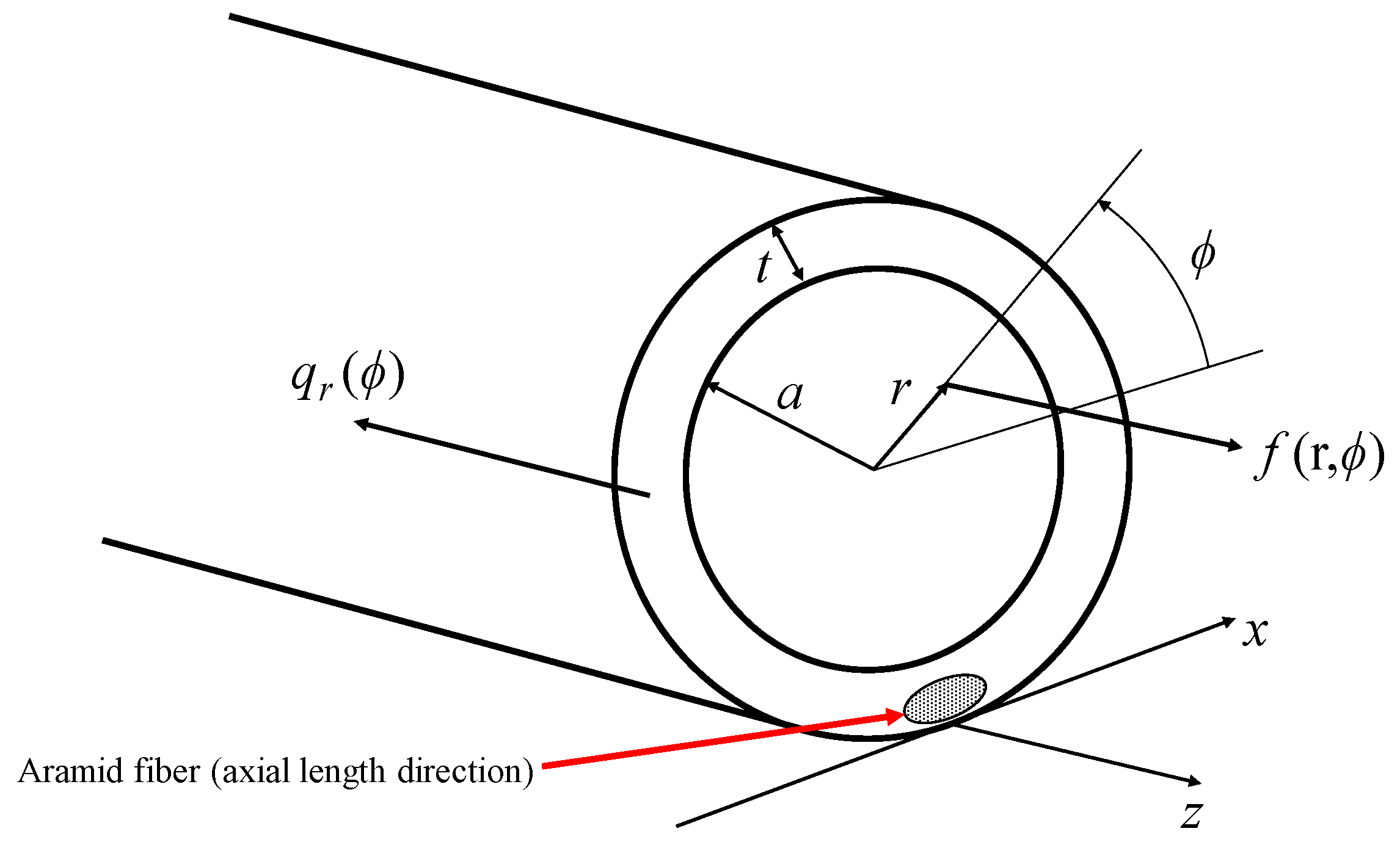
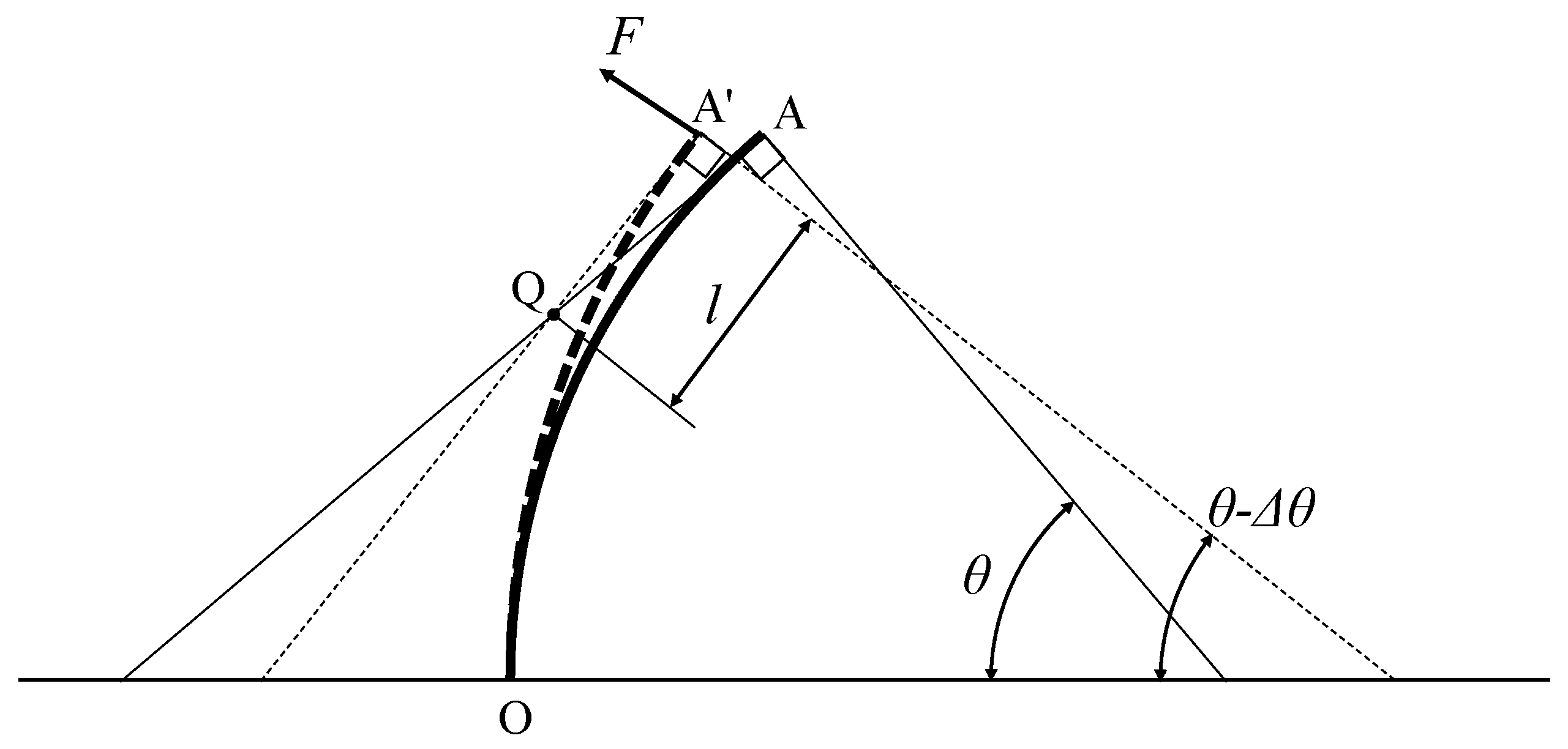
2.2. Static Characteristics Model of BPAM
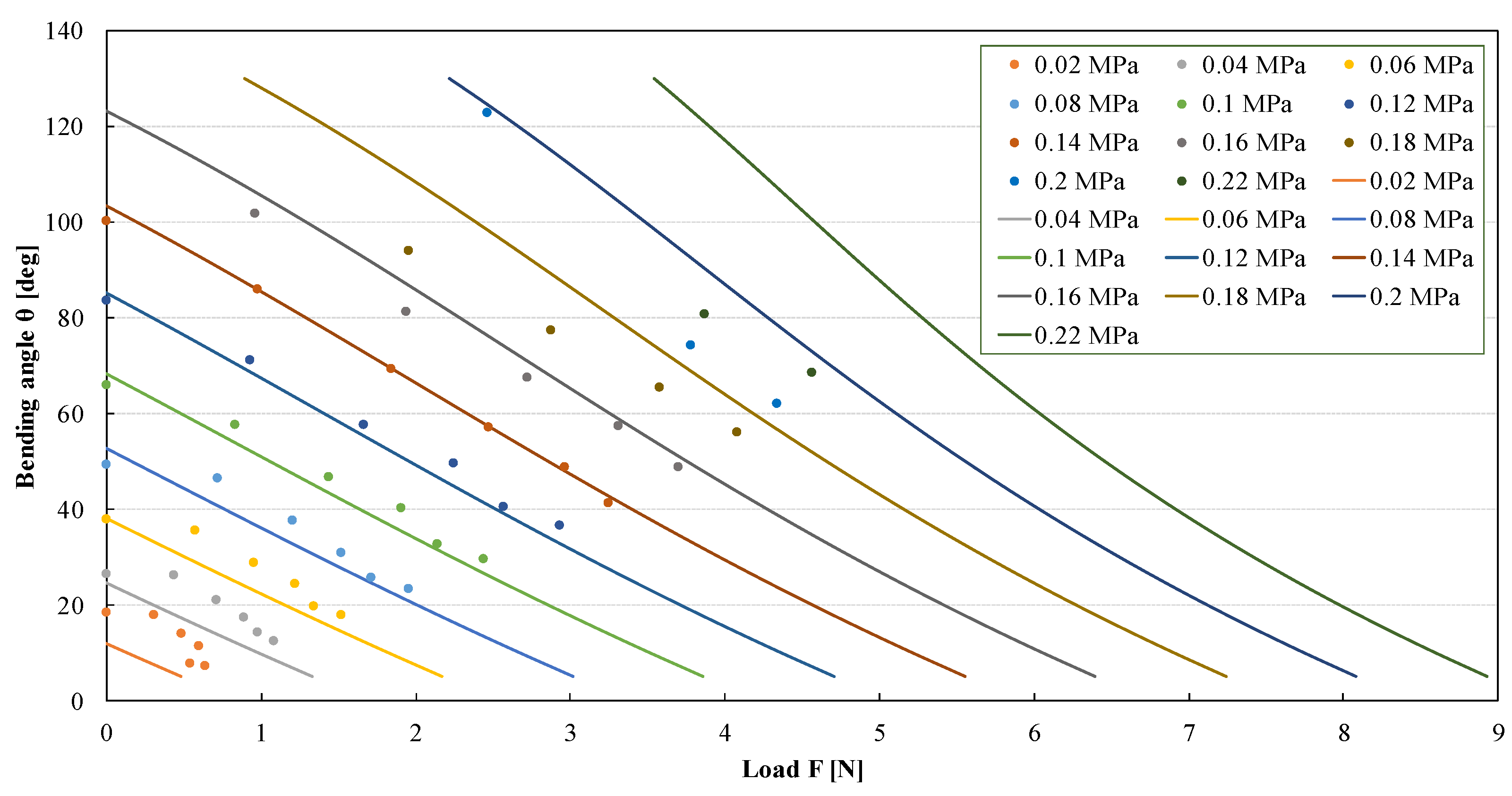
2.3. Static Characteristics Experiments
3. Self-Deformation Robot (SDR)
3.1. Robot Design
3.2. Proposed Locomotion Method
- BPAM(BF) and BPAM(CG) bent (1).
- BPAM(AB), BPAM(CD), BPAM(EF), and BPAM(GH) bent (2).
- Air pressure in BPAM(BF) and BPAM(CG) was released; these BPAMs become unactuated (3). Next, the SDR rolled (4).
- Finally, air pressure in BPAM(AB), BPAM(CD), BPAM(EF), and BPAM(GH) was released.
4. Locomotion Demonstration
5. Discussion
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ragaglia, M.; Zanchettin, A.M.; Rocco, P. Trajectory generation algorithm for safe human-robot collaboration based on multiple depth sensor measurements. Mechatronics 2018, 55, 267–281. [Google Scholar] [CrossRef]
- Sim, O.; Oh, J.; Lee, K.; Oh, J.H. Collision detection and safe reaction algorithm for non-backdrivable manipulator with single force/torque sensor. J. Intell. Robot. Syst. 2018, 91, 403–412. [Google Scholar] [CrossRef]
- Yang, H.; Xu, M.; Li, W.; Zhang, S. Design and Implementation of a soft robotic arm driven by SMA coils. IEEE Trans. Ind. Electron. 2019, 66, 6108–6116. [Google Scholar] [CrossRef]
- Takeichi, M.; Suzumori, K.; Endo, G.; Nabae, H. Development of a 20-m-long giacometti arm with balloon body based on kinematic model with air resistance. In Proceedings of the 2017 IEEE/RSJ International Conference on Intelligent Robots and Systems, Vancouver, BC, Canada, 24–28 September 2017; pp. 2710–2716. [Google Scholar]
- Ansari, Y.; Manti, M.; Falotico, E.; Mollard, Y.; Cianchetti, M.; Laschi, C. Towards the development of a soft manipulator as an assistive robot for personal care of elderly people. Int. J. Adv. Robot. Syst. 2017, 14, 1–17. [Google Scholar] [CrossRef]
- Ward-Cherrier, B.; Pestell, N.; Cramphorn, L.; Winstone, B.; Giannaccini, M.E.; Rossiter, J.; Lepora, N.F. The TacTip Family: Soft Optical Tactile Sensors with 3D-Printed Biomimetic Morphologies. Soft Robot. 2018, 5, 216–227. [Google Scholar] [CrossRef] [PubMed]
- Ortiz, D.; Gravish, N.; Tolley, M.T. Soft Robot Actuation Strategies for Locomotion in Granular Substrates. IEEE Robot. Autom. Lett. 2019, 4, 2630–2636. [Google Scholar] [CrossRef]
- Suzumori, K.; Abe, A. Applying flexible microactuators to pipeline inspection robots. In Proceedings of the IMACS/SICE International Symposium on Robotics, Mechatronics and Manufacturing Systems, Tempe, AZ, USA, 15–17 March 1993; pp. 515–520. [Google Scholar]
- Hawkes, E.W.; Blumenschein, L.H.; Greer, J.D.; Okamura, A.M. A soft robot that navigates its environment through growth. Sci. Robot. 2017, 2, eaan3028. [Google Scholar] [CrossRef]
- Digumarti, K.M.; Conn, A.T.; Rossiter, J. Pellicular Morphing Surfaces for Soft Robots. IEEE Robot. Autom. Lett. 2019, 4, 2304–2309. [Google Scholar] [CrossRef]
- Bolson, N.; Singh, D.; Lube, V.; Lubineau, G. All-polymer based polymorph skin with controllable surface texture. Smart Mater. Struct. 2019, 28, 075011. [Google Scholar] [CrossRef]
- Thuruthel, T.G.; Shih, B.; Laschi, C.; Tolley, M.T. Soft robot perception using embedded soft sensors and recurrent neural networks. Sci. Robot. 2019, 4, eaav1488. [Google Scholar] [CrossRef]
- Shiblee, M.N.; Ahmed, K.; Kawakami, M.; Furukawa, H. 4D Printing of shape-memory hydrogels for soft-robotic functions. Int. J. Adv. Mater. Technol. 2019, 4, 1900071. [Google Scholar] [CrossRef]
- Akbari, S.; Sakhaei, A.H.; Panjwani, S.; Kowsari, K.; Serjourei, A.; Ge, Q. Multimaterial 3D printed soft actuators powered by shape memory alloy wires. Sens. Actuators A Phys. 2019, 290, 177–189. [Google Scholar] [CrossRef]
- Sung, W.Y.; Oh, I.K. A biomimetic jellyfish robot based on ionic polymer metal composite actuators. Smart Mater. Struct. 2009, 18, 085002. [Google Scholar]
- White, B.T.; Long, T.E. Advances in Polymeric Materials for Electromechanical Devices. Macromol. Rapid Commun. 2019, 40, 1800521. [Google Scholar] [CrossRef] [PubMed]
- Alici, G.; Devaud, V.; Renaud, P.; Spinks, G. Conducting polymer microactuators operating in air. J Micromech. Microeng. 2009, 19, 025017. [Google Scholar] [CrossRef]
- Yan, S.Z.; Yang, T.F.; Liu, X.J.; Wang, R.C. Tactile feedback control for a gripper driven by SMA springs. AIP Adv. 2012, 2, 032134. [Google Scholar] [CrossRef]
- Kongahage, D.; Foroughi, J. Actuator Materials: Review on Recent Advances and Future Outlook for Smart Textiles. Fibers 2019, 7, 21. [Google Scholar] [CrossRef]
- Sarosi, J. Elimination of the hysteresis effect of pam actuator: Modelling and experimental studies. Tech. Gaz. 2015, 22, 1489–1494. [Google Scholar]
- Deaconescu, T.; Deaconescu, A. Pneumatic muscle actuated isokinetic equipment for the rehabilitation of patients with disabilities of the bearing joints. In Proceedings of the International MultiConference of Engineers and Computer Scientists, Hong Kong, China, 18–20 March 2009; Volume 2, pp. 1823–1827. [Google Scholar]
- Li, X.; Xia, H.; Guan, T. Development of legs rehabilitation exercise system driven by pneumatic muscle actuator. In Proceedings of the 2008 2nd International Conference on Bioinformatics and Biomedical Engineering, Shanghai, China, 16–18 May 2008; pp. 1309–1311. [Google Scholar]
- Zhao, L.; Liu, X.; Wang, T. Trajectory tracking control for double-joint manipulator systems driven by pneumatic artificial muscles based on a nonlinear extended state observer. Mech. Syst. Signal Process. 2019, 122, 307–320. [Google Scholar] [CrossRef]
- Tondu, B.; Ippolito, S.; Guiochet, J.; Daidie, A. A Seven-degree-of-freedom robot-arm driven by pneumatic artificial muscles for humanoid robots. Int. J. Robot. Res. 2005, 24, 257–274. [Google Scholar] [CrossRef]
- Miyagawa, T.; Toya, K.; Kubota, Y. Static Characteristics of pneumatic soft actuator using fiber reinforced rubber. In Proceedings of the 2007 JSME Conference on Robotics and Mechatronics, Akita, Japan, 10–12 May 2007; pp. 1A2–A01. (In Japanese). [Google Scholar]






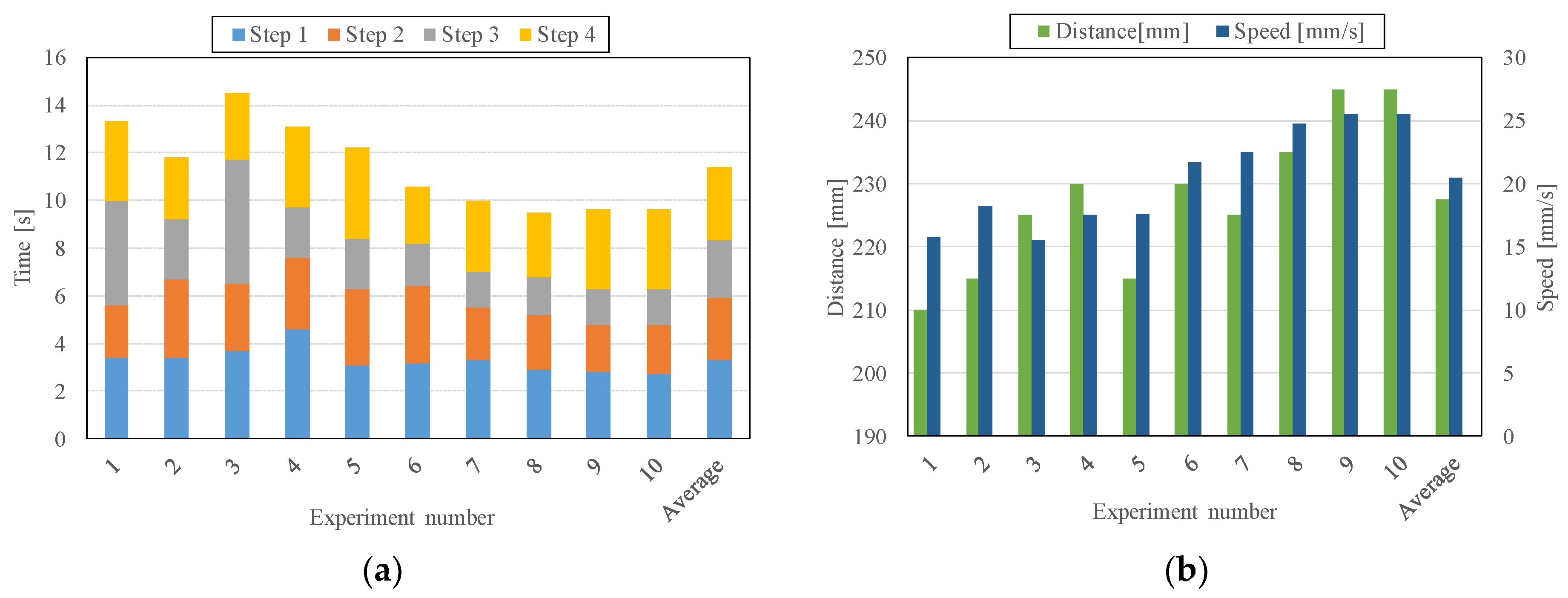
| Parameter | Specification |
|---|---|
| Length (mm) | 100 |
| Outer diameter (mm) | 21 |
| Inner diameter (mm) | 16 |
| Weight (kg) | 0.05 |
| Air Pressure (Mpa) | MSE | Air Pressure (MPa) | MSE |
|---|---|---|---|
| 0.02 | 56.87 | 0.14 | 2.17 |
| 0.04 | 34.23 | 0.16 | 15.39 |
| 0.06 | 22.33 | 0.18 | 115.61 |
| 0.08 | 14.77 | 0.20 | 202.07 |
| 0.10 | 11.77 | 0.22 | 1316.83 |
| 0.12 | 9.13 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tomori, H.; Hiyoshi, K.; Kimura, S.; Ishiguri, N.; Iwata, T. A Self-Deformation Robot Design Incorporating Bending-Type Pneumatic Artificial Muscles. Technologies 2019, 7, 51. https://doi.org/10.3390/technologies7030051
Tomori H, Hiyoshi K, Kimura S, Ishiguri N, Iwata T. A Self-Deformation Robot Design Incorporating Bending-Type Pneumatic Artificial Muscles. Technologies. 2019; 7(3):51. https://doi.org/10.3390/technologies7030051
Chicago/Turabian StyleTomori, Hiroki, Kenta Hiyoshi, Shonosuke Kimura, Naoya Ishiguri, and Taisei Iwata. 2019. "A Self-Deformation Robot Design Incorporating Bending-Type Pneumatic Artificial Muscles" Technologies 7, no. 3: 51. https://doi.org/10.3390/technologies7030051
APA StyleTomori, H., Hiyoshi, K., Kimura, S., Ishiguri, N., & Iwata, T. (2019). A Self-Deformation Robot Design Incorporating Bending-Type Pneumatic Artificial Muscles. Technologies, 7(3), 51. https://doi.org/10.3390/technologies7030051





