A Verifiable Fully Homomorphic Encryption Scheme for Cloud Computing Security

Abstract

Performing smart computations in a context of cloud computing and big data is highly appreciated today. It allows customers to fully benefit from cloud computing capacities (such as processing or storage) without losing confidentiality of sensitive data. Fully homomorphic encryption (FHE) is a smart category of encryption schemes that enables working with the data in its encrypted form. It permits us to preserve confidentiality of our sensible data and to benefit from cloud computing capabilities. While FHE is combined with verifiable computation, it offers efficient procedures for outsourcing computations over encrypted data to a remote, but non-trusted, cloud server. The resulting scheme is called Verifiable Fully Homomorphic Encryption (VFHE). Currently, it has been demonstrated by many existing schemes that the theory is feasible but the efficiency needs to be dramatically improved in order to make it usable for real applications. One subtle difficulty is how to efficiently handle the noise. This paper aims to introduce an efficient and symmetric verifiable FHE based on a new mathematic structure that is noise free. In our encryption scheme, the noise is constant and does not depend on homomorphic evaluation of ciphertexts. The homomorphy of our scheme is obtained from simple matrix operations (addition and multiplication). The running time of the multiplication operation of our encryption scheme in a cloud environment has an order of a few milliseconds.

1. Introduction

Cloud computing has developed as a powerful computing model in the last decade, with numerous advantages both to clients and providers. One of the obvious huge advantage is that clients can delegate their complex computations and benefit from the best technologies and computation powers with low costs. The benefits compared to the costs presented by cloud technologies are one of the major arguments that justify the spreading of cloud computing in many industries. During the last few years, an enterprise culture of accepting cloud computing was developed and many companies had shown their readiness to utilize the cloud and benefit from its capacities, but businesses are now finding that there are a number of security issues that have to be addressed when venturing into the cloud.

Privacy of sensible data is one of most important security issues. Leakage of some data can cause huge damage to its owners. In general, to save privacy of our data it is advised to encrypt it before storing it on a remote cloud server. Using classical encryption schemes as RSA, AES, and 3DES allows clients to preserve data privacy during transmission to the cloud, but if a client requests the cloud to perform a complex treatment on its data, he should share his private key with the remote cloud server. This traditional use of cryptography may not be the best solution in terms of privacy, especially if we consider the cloud as an untrusted domain.

One solution to this problem is doing smart computations on encrypted data. This idea was introduced by Rivest, Adleman and Dertozous in 1978 [1], where the authors conjectured the existence of a privacy homomorphism. Today we are using the notion of Fully Homomorphic Encryption (FHE) rather than privacy homomorphism.

FHE schemes (Figure 1) are considered as the next generation algorithms for cryptography. FHE is a type of smart encryption cryptosystem that supports arbitrary computations on ciphertexts without ever needing to decrypt or reveal it. In the context of cloud computing and distributed computation, this is a highly precious power. In fact, a significant application of fully homomorphic encryption is for big data and cloud computing. Generally, FHE is used for outsourcing complex computations on sensitive data stored in a cloud as it can be employed in specific applications for big data like a secure search on encrypted big data and private information retrieval. Such outsourcing was a major problem until the revolutionary work of Gentry in 2009 [2]. In his thesis, Gentry proposed the first adequate fully homomorphic encryption scheme by exploiting properties of ideal lattices.

Gentry’s construction is based on his bootstrapping theorem which provides that given a somewhat homomorphic encryption scheme (SWHE) that can homomorphically evaluate its own decryption circuit and an additional NAND gate, we can pass to a “levelled” fully homomorphic encryption scheme and so obtain an FHE scheme by assuming circular security. The purpose of using a bootstrapping technique is to allow refreshment of ciphertexts and reduce noise after its growth.

Gentry’s construction is not a single algorithm, but rather it is considered as a framework that inspires cryptologists to build new fully homomorphic encryption schemes [3,4,5,6]. An FHE cryptosystem that uses Gentry’s bootstrapping technique can be classified in the category of noise-based fully homomorphic encryption schemes [7]. If this class of cryptosystems has the advantage of being robust and more secure, it also has the drawback of not being efficient in terms of runtime and ciphertext size. In several works that followed Gentry’s one, many techniques of noise management are invented to improve runtime efficiency and to minimize ciphertext and key size’s [8,9,10], but the problem of designing a practical and efficient fully homomorphic encryption scheme has remained the same until now.

In the literature we can locate a second category called free-noise fully homomorphic encryption schemes which do not need a technique of noise management to refresh ciphertexts. In a free-noise fully homomorphic encryption scheme one can an infinite number of operations on the same ciphertext without noise growing. This class of encryption schemes is known as being faster than the previous one, involves simple operations to evaluate circuits on ciphertexts and does not require a noise management technique, but it suffers from security problems because the majority of designed schemes are cryptanalyzed today.

A verifiable encryption scheme is a cryptosystem that allows us to prove some properties about an encrypted value without disclosing it. If the verification option is combined with homomorphic capacities in the same encryption scheme, it becomes a verifiable fully homomorphic encryption scheme (VFHE). Consequently, a VFHE scheme (Figure 2) is a very smart scheme that we can use to outsource complex computations on sensible data to a remote cloud server. It allows the client to verify the correctness of its delegated computations.

In this work, we will adopt the free-noise approach to design an efficient verifiable fully homomorphic encryption scheme. We will try to overcome the problem of weak security by using the ring of quaternions. For that reason, we will begin by providing some definitions in the second, third and fourth sections. The fifth part is dedicated to our main contribution, in particular we will present a verifiable fully homomorphic encryption scheme that is noise free and quaternionic based. In the sixth section we will demonstrate its security and in the seventh and eighth sections we will provide some comparisons with other schemes and implementation results.

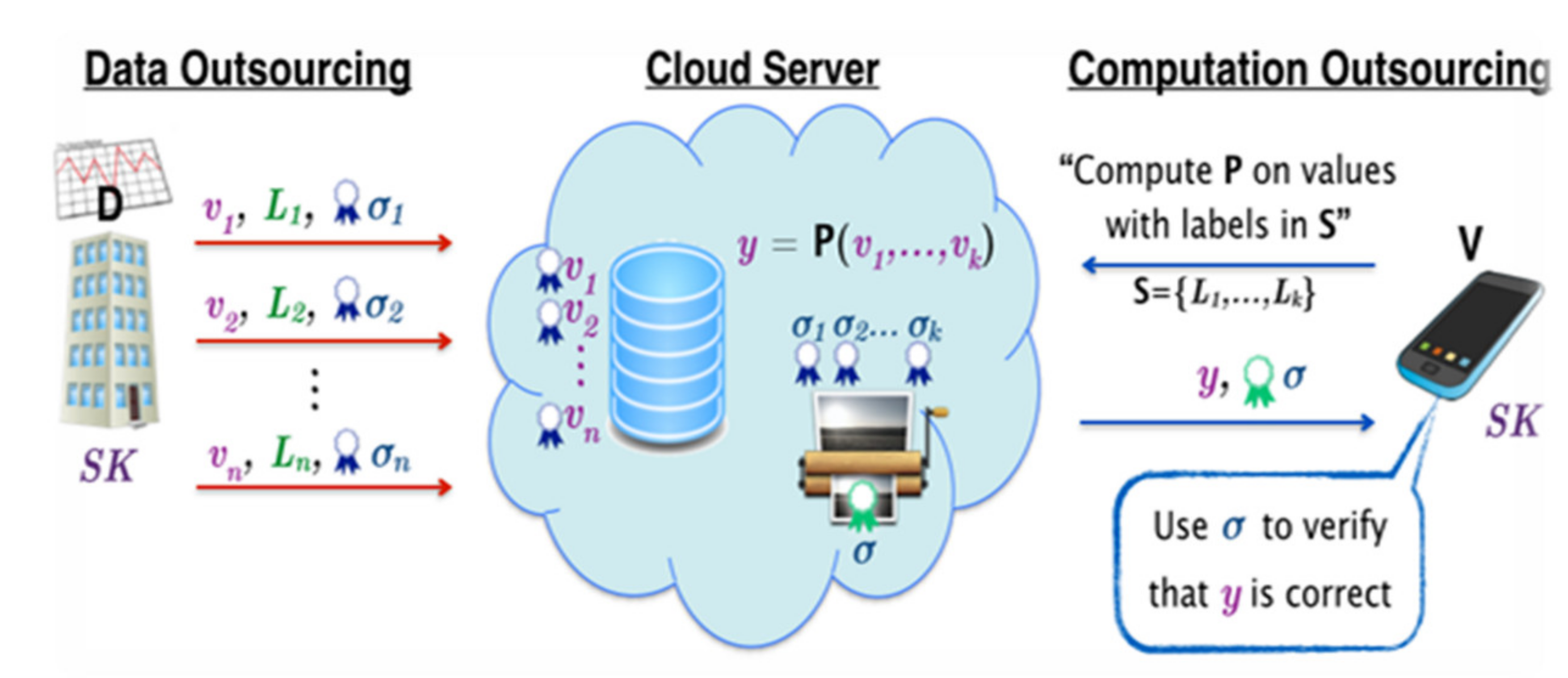
2. Problem Definition

2.1. The Three Main Phases of a Verifiable Computation Scheme

Gennaro et al. [10] defined the notion of a verifiable computational scheme as a protocol between two parts, having a polynomial execution time, which collaborate in the computation of a function $f:{\left\{0,1\right\}}^n\to {\left\{0,1\right\}}^m$. This scheme includes three main phases:

• Pretreatment: the client performs this step in order to calculate some auxiliary information associated with f. Some of this information is public and shared with the server while the rest is private and kept at the client’s side.
• Preparation of inputs: At this stage, the client calculates auxiliary information on the input of the function f. Some of this information is public while the rest is private and kept at the client’s side. The public information is sent to the server to calculate f on the inputs.
• Output computation and verification: In this step, the server uses the public information associated with f and the inputs of f, which were computed in the two preceding phases, to calculate an output of the function f applied to the inputs provided. This result is then returned to the client to verify its accuracy by calculating the actual value of the output by decoding the result returned by the server using the private information calculated in the previous phases.

The concept of verifiable computation scheme defined by Gennaro et al. [10] minimizes the interaction between the client and the server in exactly two messages (Figure 3), where a single message is sent from each party to the other party during the different phases of the protocol.

In a very broad way, a verifiable computation scheme is a protocol that allows a client to delegate a calculation to a server while having the assurance that the calculation has been correctly performed. Since homomorphic encryption allows to delegate calculations on encrypted data to a remote server, it would be wise to extend the verification property to this type of encryption to allow a prover (cloud server for example) to convince an auditor. (the client who has requested the evaluation of the function f on its encrypted data ($c_1,c_2,\dots ,c_n$) that a given ciphertext $C=f\left(c_1,c_2,\dots ,c_n\right)$ is an encryption of the message $m=f\left(m_1,m_2,\dots ,m_n\right)$ under the same encryption key of the message $m_i$ knowing that we already know that $c_i=E\left(k,m_i\right)$ where k is the encryption key used in this context. On the one hand, the proof built by the server must demonstrate the accuracy of the calculations made. On the other hand, the client must be able to simply verify the said proof with a minimum of resources, knowing that it already has low computing and storage capacities.

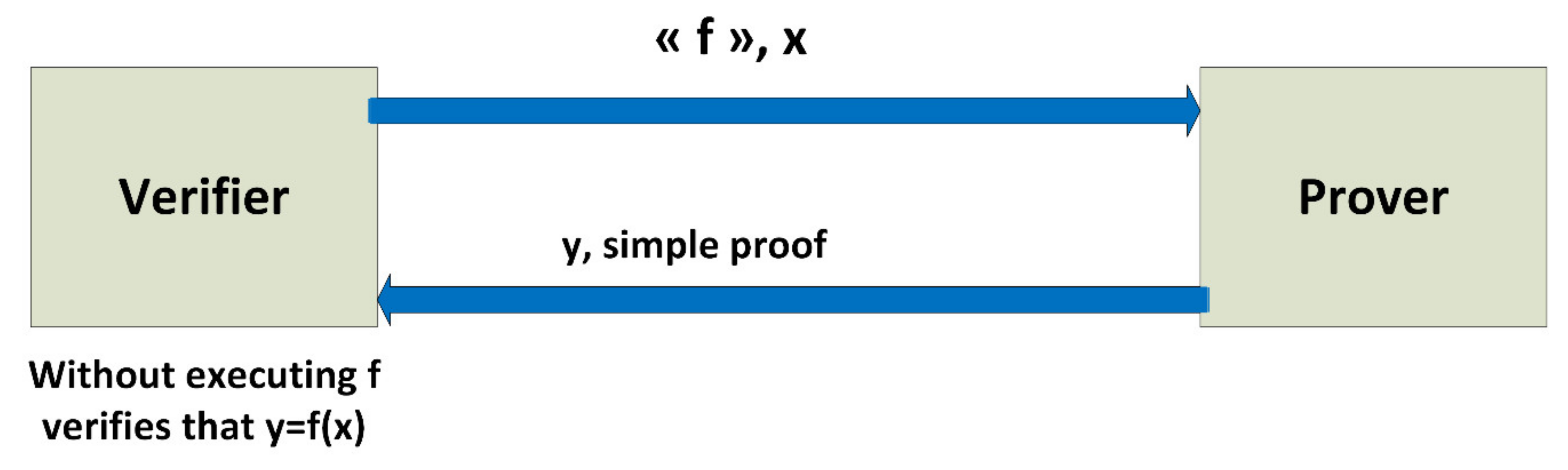
2.2. Definition of a Verifiable Computation Scheme

According to Gennaro et al. [10], a verifiable calculation scheme $VC=\left(\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n},\mathit{P}\mathit{r}\mathit{o}\mathit{b}\mathit{G}\mathit{e}\mathit{n},\mathit{C}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e},\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}\right)$ is a quadruplet of algorithms defined as follows:

• $\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(f,\lambda \right)\to \left(PK,SK\right)$: Based on security parameter λ, the key generation algorithm randomly generates a public key PK (which encodes the target function f) which is used by the server to compute f. It also calculates a corresponding secret key SK, which is kept private by the customer.
• $\mathit{P}\mathit{r}\mathit{o}\mathit{b}\mathit{G}\mathit{e}\mathit{n}\left(SK,x\right)\to \left({\sigma }_x,{\tau }_x\right)$: The problem generation algorithm uses the secret key SK to code the input x as a public value ${\sigma }_x$ which is given to the server to calculate, and a secret value ${\tau }_x$ which is kept private by the client.
• $\mathit{C}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e}\left(PK,{\sigma }_x\right)\to {\sigma }_y$: Using the client’s public key and coded entry, the server calculates an encoded version of the output of the function y = f (x).
• $\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}\left(SK,{\tau }_x,{\sigma }_y\right)\to \left(acc,y\right)$: Using the secret key SK and the secret ${\tau }_x$, the verification algorithm converts the output of the server into an acc bit and a y string. If acc = 1 we say that the client accepts y = f (x), if acc = 0 we say that the client rejects.

A verifiable computation scheme should be both efficient and secure. A scheme is effective if the problem generation algorithm produces values that allow an honest server to compute values that will be successfully verified and that match the evaluation of f on those inputs.

2.3. Properties of a Verifiable Computation Scheme

The most important properties of verifiable computation schemes [11] are: the level of security, confidentiality and efficiency, the type of verifiability and the class of functions provided.

• The security level: A verifiable computation scheme is secure if a malicious server will not be able to convince a verifier of the accuracy of a calculation even though the result is not correct. The level of security provided describes an adversary’s ability to attack the system.
• Level of confidentiality: The level of confidentiality includes different aspects. It depends on the point of view where he is related, whether to servers or to verifiers. In both cases, confidentiality means that both parties do not learn anything about inputs, output, or even the input and output of a calculation. Such a feature is desirable when processing sensitive data, e.g. medical data, government data, commercial data and military data. For example, a cloud can store medical records and perform statistics on them. In this scenario, the cloud (the server) and the auditors should not learn the health status of individual patients during the processing and verification of calculations.
• Efficiency: Efficiency considers the work required by the client (the client is the one with the verifier) and the verifier. Usually, the client must perform a preprocessing which is an additional input to the calculations made by the server. If both preprocessing and verification are more efficient than performing the calculation locally, a verifiable computation scheme is considered effective. However, efficiency is often considered in a depreciated sense, that is, the customer has installation costs that are executed once and then several operations can be performed and verified. Thus, schemes for which at least the verification process is more efficient than performing the calculations are expected to provide depreciated efficiency.
• The type of verifiability: There are two types of verifiability. If the verification can be done by a third party, then we are talking about public verifiability. If the verification requires secret information from the client then we are talking about private verifiability.
• The class of provided functions: The class of provided functions determines the expressivity of the calculations that can be performed by the verifiable computation scheme. While some systems cover only arithmetic circuits of fixed degree, others can handle arbitrary arithmetic circuits.

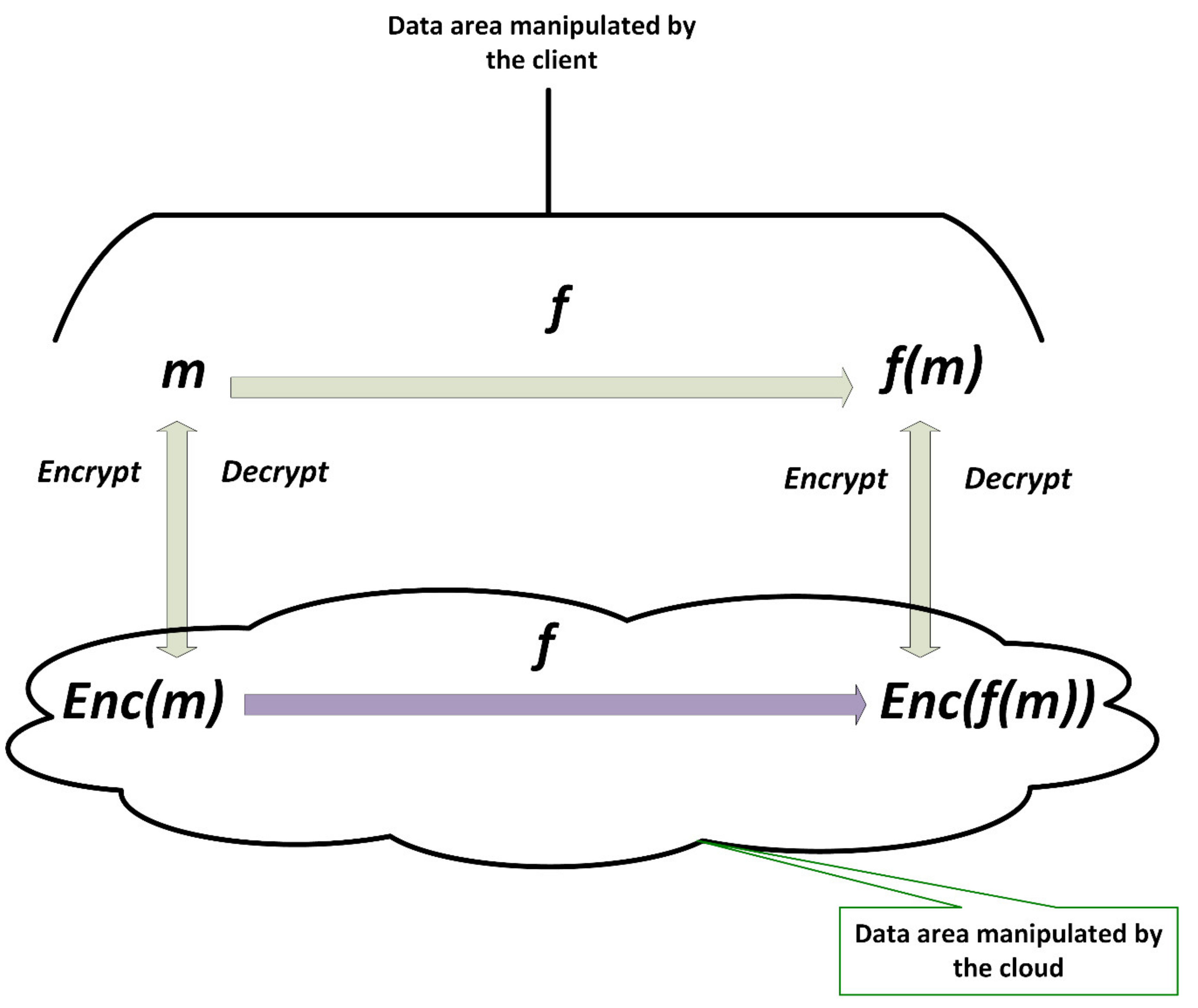
3. Definition of Fully Homomorphic Encryption

Mathematically, a fully homomorphic encryption scheme is a quadruplet of polynomial algorithms $\left(\mathit{G}\mathit{e}\mathit{n},\mathit{E}\mathit{n}\mathit{c},\mathit{D}\mathit{e}\mathit{c},\mathit{E}\mathit{v}\mathit{a}\mathit{l}\right)$ verifying:

• $\mathit{G}\mathit{e}\mathit{n}\left(\mathit{\lambda }\right):$ Is an algorithm of key generation, takes as input a security parameter $\lambda$ and outputs public and secret keys $\left(pk,sk\right).$
• $\mathit{E}\mathit{n}\mathit{c}\left(\mathit{m},\mathit{p}\mathit{k}\right):$ Is an encryption algorithm, takes as input a plaintext $m$ and a public key $pk$ and outputs a ciphertext $c$.
• $\mathit{D}\mathit{e}\mathit{c}\left(\mathit{c},\mathit{s}\mathit{k}\right):$ Is a decryption algorithm, takes as input a ciphertext $c$ and a secret key $sk$ and outputs a plaintext $m$.
• $\mathit{E}\mathit{v}\mathit{a}\mathit{l}\left(\mathit{C},{\mathit{c}}_{\mathbf{1}},\dots ,{\mathit{c}}_{\mathit{n}}\right):$ Is an evaluation algorithm, takes as input a circuit $C$ and ciphertexts $c_1,\dots ,c_n$ and verifies $Dec\left(Eval\left(C,c_1,\dots ,c_n\right),sk\right)=C\left(m_1,\dots ,m_n\right)$. Anyone can evaluate $Eval$, since it does not require the secret key $sk$.

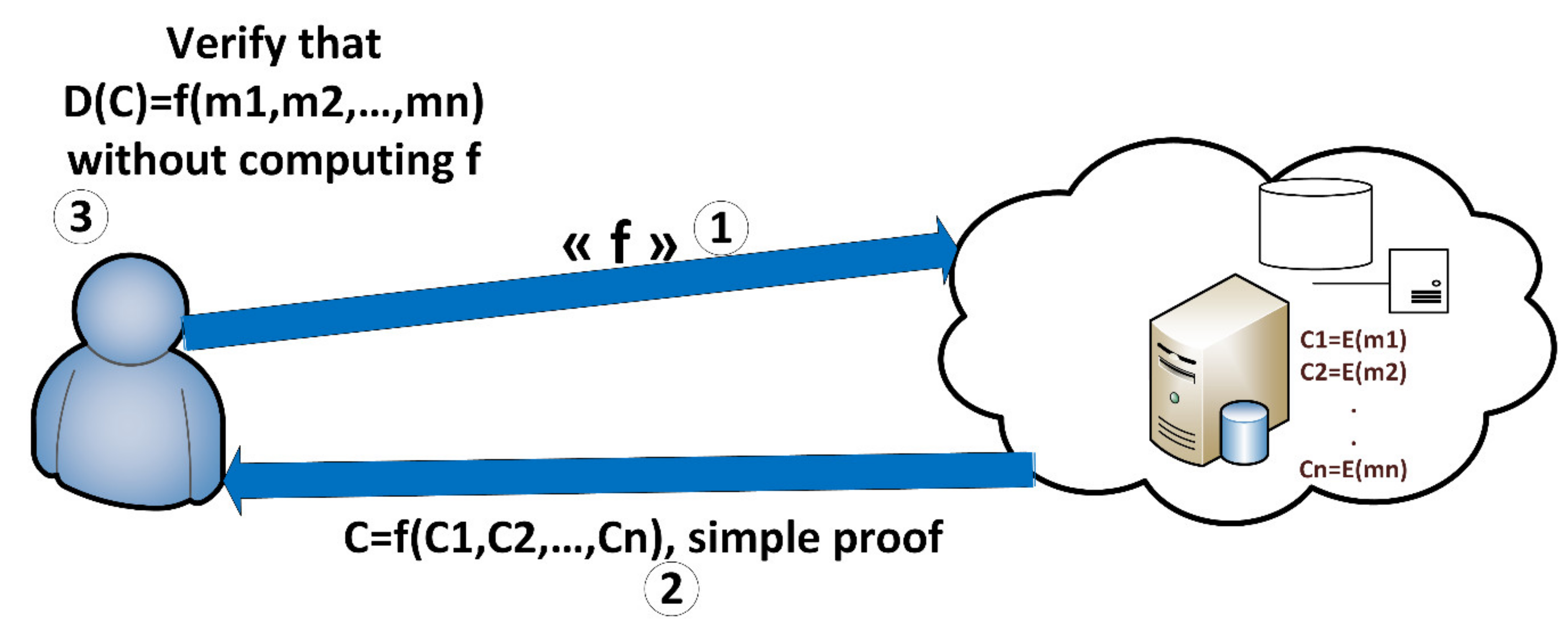
4. Definition of Verifiable Fully Homomorphic Encryption

The definition of verifiable fully homomorphic encryption [12] is based on the two definitions of fully homomorphic encryption and verifiable computation.

Let$\mathit{F}\mathit{H}\mathit{E}=\left(\mathit{F}\mathit{H}\mathit{E}.\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n},\mathit{F}\mathit{H}\mathit{E}.\mathit{E}\mathit{n}\mathit{c},\mathit{F}\mathit{H}\mathit{E}.\mathit{D}\mathit{e}\mathit{c},\mathit{F}\mathit{H}\mathit{E}.\mathit{E}\mathit{v}\mathit{a}\mathit{l}\right)$a fully homomorphic encryption scheme and$\mathit{V}\mathit{C}=\left(\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n},\mathit{P}\mathit{r}\mathit{o}\mathit{b}\mathit{G}\mathit{e}\mathit{n},\mathit{C}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e},\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}\right)$a verifiable computation scheme.

We can describe, from the previous tools, a new verifiable calculation scheme $\mathit{V}\mathit{F}\mathit{H}\mathit{E}=\left(\mathit{P}\mathit{r}\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n},\mathit{P}\mathit{r}\mathit{P}\mathit{r}\mathit{o}\mathit{b}\mathit{G}\mathit{e}\mathit{n},\mathit{P}\mathit{r}\mathit{C}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e},\mathit{P}\mathit{r}\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}\right)$ called also verifiable fully homomorphic encryption scheme:

• $\mathit{P}\mathit{r}\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(\mathit{f},\mathit{\lambda }\right)\to \left(P{K}_P,S{K}_P\right)$:
  • Execute $\mathit{F}\mathit{H}\mathit{E}.\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(\mathit{\lambda }\right)$ to generate $\left(\mathit{p}\mathit{k},\mathit{s}\mathit{k}\right)$ the FHE keys.
  • Execute $\mathit{K}\mathit{e}\mathit{y}\mathit{G}\mathit{e}\mathit{n}\left(eva{l}_{\mathit{f}},\mathit{\lambda }\right)$ to generate $\left(PK,SK\right)$ the VC keys. Knowing that $eva{l}_{\mathit{f}}$ is a function that takes as input $\mathit{F}\mathit{H}\mathit{E}.\mathit{E}\mathit{n}\mathit{c}\left(\mathit{p}\mathit{k},\mathit{x}\right)$ and gives as output $\mathit{F}\mathit{H}\mathit{E}.\mathit{E}\mathit{n}\mathit{c}\left(\mathit{p}\mathit{k},\mathit{f}\left(x\right)\right)$. This function is efficiently calculable from the algorithm $\mathit{F}\mathit{H}\mathit{E}.\mathit{E}\mathit{v}\mathit{a}\mathit{l}$.
  • Take $P{K}_P=\left(PK,pk\right)$ and $S{K}_P=\left(P{K}_P,SK,sk\right)$
• $\mathit{P}\mathit{r}\mathit{P}\mathit{r}\mathit{o}\mathit{b}\mathit{G}\mathit{e}\mathit{n}\left(S{K}_P,x\right)\to \left({\sigma }_x,{\tau }_x\right)$:
  • Calculate $C_x=FHE.Enc\left(PK,x\right)$
  • Execute $\mathit{P}\mathit{r}\mathit{o}\mathit{b}\mathit{G}\mathit{e}\mathit{n}\left(\mathit{S}\mathit{K},C_x\right)$ to obtain $\left({\sigma }_x,{\tau }_x\right)$.
• $\mathit{P}\mathit{r}\mathit{C}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e}\left(P{K}_P,{\sigma }_x\right)\to {\sigma }_y$:
  • Execute $\mathit{C}\mathit{o}\mathit{m}\mathit{p}\mathit{u}\mathit{t}\mathit{e}\left(\mathit{P}\mathit{K},{\sigma }_x\right)$ to compute ${\sigma }_y$. Note that ${\sigma }_y$ is an encoding of $C_y=\mathit{F}\mathit{H}\mathit{E}.\mathit{E}\mathit{v}\mathit{a}\mathit{l}\left(\mathit{f},C_x\right)$.
• $\mathit{P}\mathit{r}\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}\left(S{K}_P,{\tau }_x,{\sigma }_y\right)\to \left(acc,y\right)$:
  • Execute $\mathit{V}\mathit{e}\mathit{r}\mathit{i}\mathit{f}\mathit{y}\left(\mathit{S}\mathit{K},{\tau }_x,{\sigma }_y\right)$ to obtain $\left(acc,C\right)$.
  • If $acc=0$ reject. Si $acc=1$, decrypt $y=\mathit{F}\mathit{H}\mathit{E}.\mathit{D}\mathit{e}\mathit{c}\left(sk,C\right)$.

In a very simple way, we can schematize the verifiable fully homomorphic encryption between a verifier client and a Prover cloud server as follows (Figure 4):

5. Our Techniques and Results

We propose an efficient and verifiable noise-free fully homomorphic encryption scheme that uses the ring of Lipschitz’s quaternions and permits computations over encrypted data under a symmetric key; our scheme permits us to verify if the computation was performed in its correct form. We exploit properties of non-commutativity of Lipschitz integers to build our efficient encryption scheme.

5.1. Mathematical Background

5.1.1. Quaternionique Field ℍ

A quaternion is a number in a general sense. Quaternions encompass real and complex numbers in a number system where multiplication is no longer a commutative law.

The quaternions were introduced by the Irish mathematician William Rowan Hamilton in 1843. They now find applications in mathematics, physics, computer science and engineering.

Mathematically, the set of quaternions ℍ is a non-commutative associative algebra on the field of real numbers ℝ generated by three elements 𝒾, 𝒿 and 𝓀 satisfying relations: ${𝒾}^2={𝒿}^2={𝓀}^2=𝒾.𝒿.𝓀=-1$. Concretely, any quaternion $q$ is written uniquely in the form: $q=a+b𝒾+c𝒿+d𝓀$ where $a,b,c\mathrm{and}d$ are real numbers.

The operations of addition and multiplication by a real scalar are trivially done term to term, whereas the multiplication between two quaternions is termed by respecting the non-commutativity and the rules proper to 𝒾, 𝒿 and 𝓀. For example, given $q=a+b𝒾+c𝒿+d𝓀$ and $q\prime =a\prime +b\prime 𝒾+c\prime 𝒿+d\prime 𝓀$ we have $qq\prime =a_0+b_0𝒾+c_0𝒿+d_0𝓀$ such that: $a_0=aa\prime -\left(bb\prime +cc\prime +dd\prime \right)$, $b_0=ab\prime +a\prime b+cd\prime -c\prime d$, $c_0=ac\prime -bd\prime +ca\prime +db\prime$ and $d_0=ad\prime +bc\prime -cb\prime +a\prime d$.

The quaternion $\overline{q}=a-b𝒾-c𝒿-d𝓀$ is the conjugate of $q$.

$\left|q\right|=\sqrt{q\overline{q}}=\sqrt{a^2+b^2+c^2+d^2}$ is the module of $q$. The real part of $q$ is $Re\left(q\right)=\frac{q+\overline{q}}{2}=a$ and the imaginary part is $Im\left(q\right)=\frac{q-\overline{q}}{2}=b𝒾+c𝒿+d𝓀$.

A quaternion is invertible if and only if its modulus is non-zero, and we have $q^{-1}=\frac{1}{{\left|q\right|}^2}\overline{q}$.

5.1.2. Reduced Form of Quaternion

Quaternion can be represented in a more economical way, which considerably alleviates the calculations and highlights interesting results. Indeed, it is easy to see that ℍ is a ℝ-vectorial space of dimension 4, of which $\left(1,𝒾, 𝒿 ,𝓀\right)$ constitutes a direct orthonormal basis. We can thus separate the real component of the pure components, and we have for $q\in \text{ℍ}, q=\left(a,\mathit{u}\right)$ such that $\mathit{u}$ is a vector of ${\text{ℝ}}^3$. Therefore, for $q=\left(a,\mathit{u}\right) , q\prime =\left(a\prime ,\mathit{v}\right)\in \text{ℍ}$ and $\lambda \in \text{ℝ}$ we obtain:

• $q+q\prime =\left(a+a\prime ,\mathit{u}+\mathit{v}\right)$ and $\lambda q=\left(\lambda a,\lambda \mathit{u}\right)$
• $qq\prime =\left(aa\prime -\mathit{u}.\mathit{v},av+a\prime \mathit{u}+\mathit{u}\wedge \mathit{v}\right)$ where $\wedge$ is the cross product of ${\text{ℝ}}^3$.
• $\overline{q}=\left(a,-\mathit{u}\right)$ and ${\left|q\right|}^2=a^2+{\mathit{u}}^2$.

5.1.3. Ring of Lipschitz Integers

The set of quaternions defined as follows:

$\text{ℍ}\left(\text{ℤ}\right)=\left\{q=a+b𝒾+c𝒿+d𝓀/\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\in \text{ℤ}\right\}$ has a ring structure called the ring of Lipschitz integers, $\text{ℍ}\left(\text{ℤ}\right)$ is trivially non-commutative.

For r $n\in {\text{ℕ}}^{*}$, the set of quaternions:

$\text{ℍ}\left(\text{ℤ}/n\text{ℤ}\right)=\left\{q=a+b𝒾+c𝒿+d𝓀/\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\in \text{ℤ}/n\text{ℤ}\right\}$ has the structure of a non-commutative ring.

A modular quaternion of Lipschitz $\mathrm{q}\in \text{ℍ}\left(\text{ℤ}/\mathrm{n}\text{ℤ}\right)$ is invertible if and only if its module and the integer $\mathit{n}$ are coprime numbers, i.e., ${\left|\mathrm{q}\right|}^2\wedge \mathrm{n}=1$.

5.1.4. Quaternionique Matrices ${\mathbb{M}}_2\left(\text{ℍ}\left(\text{ℤ}/\mathrm{n}\text{ℤ}\right)\right)$

The set of matrices ${\mathbb{M}}_2\left(\text{ℍ}\left(\text{ℤ}/\mathit{n}\text{ℤ}\right)\right)$ describes the matrices with four inputs (two rows and two columns) which are quaternions of $\text{ℍ}\left(\text{ℤ}/\mathit{n}\text{ℤ}\right).$ This set has a non-commutative ring structure.

There are two ways of multiplying the quaternion matrices: The Hamiltonian product, which respects the order of the factors, and the octonionique product, which does not respect it.

The Hamiltonian product is defined as for all matrices with coefficients in a ring (not necessarily commutative). For example:

$$U=\left(\begin{array}{cc}{u}_{11}& u_{12}\\ u_{21}& u_{22}\end{array}\right), V=\left(\begin{array}{cc}{v}_{11}& v_{12}\\ v_{21}& v_{22}\end{array}\right) \Rightarrow UV=\left(\begin{array}{cc}{u}_{11}{v}_{11}+u_{12}{v}_{21}& u_{11}{v}_{12}+u_{12}{v}_{22}\\ u_{21}{v}_{11}+u_{22}{v}_{21}& u_{21}{v}_{12}+u_{22}{v}_{22}\end{array}\right)$$

The octonionique product does not respect the order of the factors: on the main diagonal, there is commutativity of the second products and on the second diagonal there is commutativity of the first products.

$$U=\left(\begin{array}{cc}{u}_{11}& u_{12}\\ u_{21}& u_{22}\end{array}\right), V=\left(\begin{array}{cc}{v}_{11}& v_{12}\\ v_{21}& v_{22}\end{array}\right)\Rightarrow UV=\left(\begin{array}{cc}{u}_{11}{v}_{11}+v_{21}{u}_{12}& v_{12}{u}_{11}+u_{12}{v}_{22}\\ v_{11}{u}_{21}+u_{22}{v}_{21}& u_{21}{v}_{12}+v_{22}{u}_{22}\end{array}\right)$$

In our article we will adopt the Hamiltonian product as an operation of multiplication of the quaternionique matrices.

5.1.5. Schur Complement and Inversibility of Quaternionique Matrices

Let $ℛ$ be an arbitrary associative ring, a matrix $M\in {ℛ}^{n\times n}$ is supposed to be invertible if $\exists N\in {ℛ}^{n\times n}$ such that $MN=NM=I_n$ where $N$ is necessarily unique.

The Schur complement method is a very powerful tool for calculating inverse of matrices in rings. Let $M\in {ℛ}^{n\times n}$ be a matrix per block satisfying:

$M=\left(\begin{array}{cc}A& B\\ C& D\end{array}\right)$ such that $A\in {ℛ}^{k\times k}$.

Suppose that $A$ is invertible, we have:

$M=\left(\begin{array}{cc}{I}_k& 0\\ C{A}^{-1}& I_{n-k}\end{array}\right)\left(\begin{array}{cc}A& 0\\ 0& A_s\end{array}\right)\left(\begin{array}{cc}{I}_k& A^{-1}B\\ 0& I_{n-k}\end{array}\right)$ where

$A_s=D-C{A}^{-1}B$ is the Schur complement of $A$ in $M$.

The inversibility of $A$ ensures that the matrix $M$ is invertible if and only if $A_s$ is invertible. The inverse of $M$ is:

$M^{-1}=\left(\begin{array}{cc}{I}_k& -A^{-1}B\\ 0& I_{n-k}\end{array}\right)\left(\begin{array}{cc}{A}^{-1}& 0\\ 0& A_s^{-1}\end{array}\right)\left(\begin{array}{cc}{I}_k& 0\\ -C{A}^{-1}& I_{n-k}\end{array}\right) =\left(\begin{array}{cc}{A}^{-1}+A^{-1}B{A}_s^{-1}C{A}^{-1}& -A^{-1}B{A}_s^{-1}\\ -A_s^{-1}C{A}^{-1}& A_s^{-1}\end{array}\right)$.

For a quaternionique matrix

$M=\left(\begin{array}{cc}a& b\\ c& d\end{array}\right)\in {ℛ}^{2\times 2}={\mathbb{M}}_2\left(\text{ℍ}\left(\text{ℤ}/\mathit{n}\text{ℤ}\right)\right)$ where the quaternion $a$ is invertible as well as its Schur complement $a_s=d-c{a}^{-1}b$ we have $M$ is invertible and: $M^{-1}=\left(\begin{array}{cc}{a}^{-1}+a^{-1}b{a}_s^{-1}c{a}^{-1}& -a^{-1}b{a}_s^{-1}\\ -a_s^{-1}c{a}^{-1}& a_s^{-1}\end{array}\right)$.

Therefore, to randomly generate an invertible quaternionique matrix, it suffices to:

• Choose randomly three quaternions $a, b \mathrm{and} c$ for which $a$ is invertible.
• Select randomly the fourth quaternion $d$ such that the Schur complement $a_s=d-c{a}^{-1}b$ of $a$ in $M$ is invertible.

5.2. A Verifiable FHE Scheme

We place ourselves in a context where Bob wants to store confidential data in a very powerful but non-confident cloud. Bob will later need to execute complex processing on his data, of which he does not have the necessary computing powers to perform it. At this level he thinks, at first, of the encryption of his sensitive data to avoid any fraudulent action. But he knows that the ordinary encryption does not allow the cloud to process his calculation requests without having decrypted the data stored beforehand, which impairs their confidentiality. Bob asks if there is a convenient and efficient type of encryption to process his data without revealing it to the cloud. The answer to Bob’s question is a favorable one, in fact since 2009 so-called fully homomorphic encryption have existed, the principle of which is quite simple: doing computations on encrypted data without thinking of any previous decryption.

As the cloud is unconfident, computations over encrypted data may be false or done incorrectly. Bob must have tools to verify the veracity of the demanded computations. For this purpose, the cloud must show Bob a proof, which can be verified by Bob on receipt, of the exactitude of the performed operations. This proof is an additional service offered by the used fully homomorphic scheme.

In order to profitably benefit from the technological advance of the cloud computing and to outsource its heavy calculations comfortably, Bob needs a robust highly secure and verifiable fully homomorphic encryption scheme. With this FHE scheme, addition and multiplication are done in a judicious time, the generated noise during a treatment is manageable and of which Bob has a proof of exactitude of the performed operations on encrypted data.

To help Bob take full advantage of the powers of the cloud, we introduce a probabilistic symmetric and verifiable fully homomorphic encryption scheme without noise. The addition and multiplication operations generate no noise. We can describe our cryptosystem as follows:

5.2.1. Key Generation

• Bob generates randomly two big prime numbers p and q.
• Then, he calculates $\mathit{N}=\mathrm{p}.\mathrm{q}$.
• Bob generates randomly an invertible matrix
  $K=\left(\begin{array}{cc}{k}_1& k_2\\ k_3& k_4\end{array}\right)=\left(\begin{array}{cc}\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}& \begin{array}{cc}{a}_{13}& a_{14}\\ a_{23}& a_{24}\end{array}\\ \begin{array}{cc}{a}_{31}& a_{32}\\ a_{41}& a_{42}\end{array}& \begin{array}{cc}{a}_{33}& a_{34}\\ a_{43}& a_{44}\end{array}\end{array}\right)\in {\mathbb{M}}_4\left(\text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\right)$ such that $k_1$ is an invertible matrix.
• Bob calculates the inverse of $K$ and $k_1$, Which will be denoted $K^{-1}$ and $k_1^{-1}$.
• The secrete key is $\left(k_1,k_1^{-1},K,K^{-1}\right)$.

5.2.2. Encryption

Lets $\sigma \in \text{ℤ}/{\mathrm{N}}^2\text{ℤ}$ be a clear text. To encrypt $\sigma$ Bob proceed as follows:

• Bob transforms $\sigma$ into a quaternion:

  $$m=\sigma +\alpha Ni+\beta Nj+\gamma Nk\in \text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\mathrm{such}\mathrm{that}\alpha ,\beta ,\gamma \in \text{ℤ}/\mathit{N}\text{ℤ}.$$
• Bob generates a matrix: $M=\left(\begin{array}{cc}m& r_1\\ 0& r_2\end{array}\right)\in {\mathbb{M}}_2\left(\text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\right)$ such that $r_1$ and $r_2\in \text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)$ are randomly generated.
• Bob calculates $M\prime =k_{1}M{k}_1^{-1}$.
• Bob transforms $\sigma$ into a quaternion:

  $$m\prime =\sigma +\alpha \prime Ni+\beta \prime Nj+\gamma \prime Nk\in \text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right).$$
• Bob generates a matrix $M\prime \prime =\left(\begin{array}{cc}m\prime & r_1\prime \\ 0& 0\end{array}\right)\in {\mathbb{M}}_2\left(\text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\right)$ such that $r_1\prime \in \text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)$
• The ciphertext of $\sigma$ is:
  $C=Enc\left(\sigma \right)=K\left(\begin{array}{cc}M\prime & R\\ 0& M″\end{array}\right)K^{-1}\in {\mathbb{M}}_4\left(\text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\right)$ such that $R\in {\mathbb{M}}_2\left(\text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\right)$ is randomly generated.

5.2.3. Decryption and Verification

Lets $C\in {\mathbb{M}}_4\left(\text{ℍ}\left(\text{ℤ}/{\mathit{N}}^2\text{ℤ}\right)\right)$ be a ciphertext. To decrypt $C$, using his secrete key $\left(k_1,k_1^{-1},K,K^{-1}\right)$, Bob proceed as follows:

• He calculates $\left(\begin{array}{cc}M\prime & R\\ 0& M″\end{array}\right)=K^{-1}CK$.
• He computes $M=k_1^{-1}M\prime k_1$.
• Then he takes the first inputs of the resulting matrices $m={\left(M\right)}_{1,1}$ and $m\prime ={\left(M\prime \right)}_{1,1}$
• Finally, he recovers his clear message by verifying if $\sigma =mmodN=m\prime modN$. If the verification is true, then the clear message returned is σ otherwise the ciphertext has been modified.

5.2.4. Addition and Multiplication

Let ${\sigma }_1$ and ${\sigma }_2$ be two clear texts and $C_1=Enc\left({\sigma }_1\right)$ and $C_2=Enc\left({\sigma }_2\right)$ be their ciphertexts respectively.

It is easy to verify that:

(1)

$C_{mult}=C_1\times C_{2}mod N^2=Enc\left({\sigma }_1\right)\times Enc\left({\sigma }_2\right)mod N^2$ = $Enc\left({\sigma }_1\times {\sigma }_2\right)$.

(2)

$C_{add}=C_1+C_{2}mod N^2=Enc\left({\sigma }_1\right)+Enc\left({\sigma }_2\right)mod N^2$ = $Enc\left({\sigma }_1+{\sigma }_2\right)$.

6. Security of the Proposed Scheme

The security of our scheme can be seen from two different angles, the first is the semantic security –named also Indistinguishability– of the algorithm while the second is the security of the secret key of the system. Ciphertext indistinguishability is an important security property of many encryption schemes. Intuitively, if a cryptosystem possesses the property of indistinguishability, then an adversary will be unable to distinguish pairs of ciphertexts based on the message they encrypt. Since our cryptosystem is designed to be fully homomorphic i.e. it supports operations on encrypted data, the resistance against chosen ciphertexts attacks (IND-CCA1) is very sought and it is the best level of security that can be achieved for this category of cryptosystems. It is easy to see that a fully homomorphic encryption scheme cannot be secure against adaptive chosen ciphertext attacks (IND-CCA2).

Regarding the security of the secret key, it is essential for any type of cryptosystems. Otherwise, we will have an FHE scheme that does not even reach the basic level of security, which is breakability, and it falls in the case of the total breaking of the algorithm.

6.1. Semantic Security

6.1.1. The Adversary:

We are protecting ourselves from an adversary $\mathcal{A}$, who:

• Is a probabilistic polynomial time Turing machine.
• Has all the algorithms.
• Has full access to communication media.

6.1.2. Chosen Ciphertext Attack

In this model, the attack assumes that the adversary $\mathcal{A}$ has access to an encryption oracle and that the adversary can choose an arbitrary number of plaintexts to be encrypted and obtain the corresponding ciphertexts. In addition, the adversary $\mathcal{A}$ gains access to a decryption oracle, which decrypts arbitrary ciphertexts at the adversary’s request, returning the plaintext.

Startup

• The challenger generates a secret key $Sk$ based on some security parameter $k$ (e.g., a key size in bits) and retains it.
• The adversary $\mathcal{A}$ may ask the encryption oracle for any number of encryptions, calls to the decryption oracle based on arbitrary ciphertexts, or other operations.
• Eventually, the adversary $\mathcal{A}$ submits two distinct chosen plaintexts $m_0$, $m_1$ to the challenger.

The Challenge

• The challenger selects a bit $b\in \left\{0,1\right\}$ uniformly at random, and sends the “challenge” ciphertext $C=Enc\left(Sk,m_b\right)$ back to the adversary. The adversary is free to perform any number of additional computations or encryptions.
  • In the non-adaptive case (IND-CCA), the adversary may not make further calls to the decryption oracle before guessing.
  • In the adaptive case (IND-CCA2), the adversary may make further calls to the decryption oracle, but may not submit the challenge ciphertext C.
• In the end it will guess the value of $b$.

The Result

• Again, the adversary $\mathcal{A}$ wins the game if it guesses the bit $b$.
• A cryptosystem is indistinguishable under chosen ciphertext attack if no adversary can win the above game with probability $p$ greater than $\frac{1}{2}+\epsilon$ where is a negligible function in the security parameter $k$.
• If $p>\frac{1}{2}$ then the difference $p-\frac{1}{2}$ is the advantage of the given adversary in distinguishing the ciphertext.

In Our Situation

• The adversary $\mathcal{A}$ should distinguish an encryption of zero from an encryption of one after asking the encryption oracle of a number of encryptions and the decryption oracle to decrypt arbitrary ciphertexts.
• The adversary $\mathcal{A}$ can do operations on the two given ciphertexts to distinguish zero from one.
• As he can do operations on the entire ciphertext matrices or just to use some entrees (the diagonal of ciphertexts matrices, computations on the trace and the diagonal).
• In our case, even if the diagonal of $M$ completely determines the invertibility of $C$, an encryption of a bit $\sigma \in \left\{0,1\right\}$ is always non invertible because of the choice of the random $r{\prime }_2$ ($\left|r_2^{\prime }\right|\equiv 0\left[\mathit{n}\right]$) which gives always det(C) = 0.

Therefore, an adversary cannot then distinguish encryptions of units from encryptions of non-units. Consequently, the attack proposed on Li-Wang’s scheme [13] in Reference [14] does not work for our case. Based on these assumptions, we believe that our fully homomorphic encryption scheme is indistinguishable under chosen ciphertext attacks (IND-CCA1).

6.2. Breakability

Concerning the security of the secret key:

Given a random secret key of our encryption scheme: $K=\left(\begin{array}{cc}{k}_1& k_2\\ k_3& k_4\end{array}\right)=\left(\begin{array}{cc}\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}& \begin{array}{cc}{a}_{13}& a_{14}\\ a_{23}& a_{24}\end{array}\\ \begin{array}{cc}{a}_{31}& a_{32}\\ a_{41}& a_{42}\end{array}& \begin{array}{cc}{a}_{33}& a_{34}\\ a_{43}& a_{44}\end{array}\end{array}\right)$ and $K^{-1}=\left(\begin{array}{cc}\overline{k_1}& \overline{k_2}\\ \overline{k_3}& \overline{k_4}\end{array}\right)=\left(\begin{array}{cc}\begin{array}{cc}\overline{a_{11}}& \overline{a_{12}}\\ \overline{a_{21}}& \overline{a_{22}}\end{array}& \begin{array}{cc}\overline{a_{13}}& \overline{a_{14}}\\ \overline{a_{23}}& \overline{a_{24}}\end{array}\\ \begin{array}{cc}\overline{a_{31}}& \overline{a_{32}}\\ \overline{a_{41}}& \overline{a_{42}}\end{array}& \begin{array}{cc}\overline{a_{33}}& \overline{a_{34}}\\ \overline{a_{43}}& \overline{a_{44}}\end{array}\end{array}\right)$

And a clear text $\sigma \in \left\{0,1\right\}$.

A ciphertext of $m=bitToQuatern\left(\sigma \right)$ is determined by: $C=Enc\left(\sigma \right)=K\left(\begin{array}{cc}N& R\\ 0& M^{\prime }\end{array}\right) K^{-1}=\left(\begin{array}{cc}\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}& \begin{array}{cc}{c}_{13}& c_{14}\\ c_{23}& c_{24}\end{array}\\ \begin{array}{cc}{c}_{31}& c_{32}\\ c_{41}& c_{42}\end{array}& \begin{array}{cc}{c}_{33}& c_{34}\\ c_{43}& c_{44}\end{array}\end{array}\right)$ such that $M\prime =\left(\begin{array}{cc}m\prime & r_1\prime \\ 0& r_2\prime \end{array}\right)$ and $N=\left(\begin{array}{cc}{n}_{11}& n_{12}\\ n_{21}& n_{22}\end{array}\right)=k_1\left(\begin{array}{cc}m& r_1\\ 0& r_2\end{array}\right)k_1^{-1}$ where $m\prime$ is the clear message transformed into a quaternion using bitToQuatern transform.

As a result, we have the following equality:

$\left(\begin{array}{cc}\begin{array}{cc}{c}_{11}& c_{12}\\ c_{21}& c_{22}\end{array}& \begin{array}{cc}{c}_{13}& c_{14}\\ c_{23}& c_{24}\end{array}\\ \begin{array}{cc}{c}_{31}& c_{32}\\ c_{41}& c_{42}\end{array}& \begin{array}{cc}{c}_{33}& c_{34}\\ c_{43}& c_{44}\end{array}\end{array}\right)=\left(\begin{array}{cc}\begin{array}{cc}{a}_{11}& a_{12}\\ a_{21}& a_{22}\end{array}& \begin{array}{cc}{a}_{13}& a_{14}\\ a_{23}& a_{24}\end{array}\\ \begin{array}{cc}{a}_{31}& a_{32}\\ a_{41}& a_{42}\end{array}& \begin{array}{cc}{a}_{33}& a_{34}\\ a_{43}& a_{44}\end{array}\end{array}\right)\left(\begin{array}{cccc}{n}_{11}& n_{12}& r_3& r_5\\ n_{21}& n_{22}& r_4& r_6\\ 0& 0& m\prime & r_1\prime \\ 0& 0& 0& r_2\prime \end{array}\right)\left(\begin{array}{cc}\begin{array}{cc}\overline{a_{11}}& \overline{a_{12}}\\ \overline{a_{21}}& \overline{a_{22}}\end{array}& \begin{array}{cc}\overline{a_{13}}& \overline{a_{14}}\\ \overline{a_{23}}& \overline{a_{24}}\end{array}\\ \begin{array}{cc}\overline{a_{31}}& \overline{a_{32}}\\ \overline{a_{41}}& \overline{a_{42}}\end{array}& \begin{array}{cc}\overline{a_{33}}& \overline{a_{34}}\\ \overline{a_{43}}& \overline{a_{44}}\end{array}\end{array}\right)$.

Therefore, we obtain the sixteen following equations:

(1)

$c_{1,1}=\left(a_{1,1}{n}_{11}+a_{1,2}{n}_{21}\right)\overline{a_{1,1}}+\left(a_{1,1}{n}_{12}+a_{1,2}{n}_{22}\right)\overline{a_{2,1}}+\left(a_{1,1}{r}_3+a_{1,2}{r}_4+a_{1,3}m\prime \right)\overline{a_{3,1}}+\left(a_{1,1}{r}_5+a_{1,2}{r}_6+a_{1,3}{r}_1\prime +a_{1,4}{r}_2\prime \right)\overline{a_{4,1}}$

(2)

$c_{1,2}=\left(a_{1,1}{n}_{11}+a_{1,2}{n}_{21}\right)\overline{a_{1,2}}+\left(a_{1,1}{n}_{12}+a_{1,2}{n}_{22}\right)\overline{a_{2,2}}+\left(a_{1,1}{r}_3+a_{1,2}{r}_4+a_{1,3}m\prime \right)\overline{a_{3,2}}+\left(a_{1,1}{r}_5+a_{1,2}{r}_6+a_{1,3}{r}_1\prime +a_{1,4}{r}_2\prime \right)\overline{a_{4,2}}$

(3)

$c_{1,3}=\left(a_{1,1}{n}_{11}+a_{1,2}{n}_{21}\right)\overline{a_{1,3}}+\left(a_{1,1}{n}_{12}+a_{1,2}{n}_{22}\right)\overline{a_{2,3}}+\left(a_{1,1}{r}_3+a_{1,2}{r}_4+a_{1,3}m\prime \right)\overline{a_{3,3}}+\left(a_{1,1}{r}_5+a_{1,2}{r}_6+a_{1,3}{r}_1\prime +a_{1,4}{r}_2\prime \right)\overline{a_{4,3}}$

(4)

$c_{1,4}=\left(a_{1,1}{n}_{11}+a_{1,2}{n}_{21}\right)\overline{a_{1,4}}+\left(a_{1,1}{n}_{12}+a_{1,2}{n}_{22}\right)\overline{a_{2,4}}+\left(a_{1,1}{r}_3+a_{1,2}{r}_4+a_{1,3}m\prime \right)\overline{a_{3,4}}+\left(a_{1,1}{r}_5+a_{1,2}{r}_6+a_{1,3}{r}_1\prime +a_{1,4}{r}_2\prime \right)\overline{a_{4,4}}$

(5)

$c_{2,1}=\left(a_{2,1}{n}_{11}+a_{2,2}{n}_{21}\right)\overline{a_{1,1}}+\left(a_{2,1}{n}_{12}+a_{2,2}{n}_{22}\right)\overline{a_{2,1}}+\left(a_{2,1}{r}_3+a_{2,2}{r}_4+a_{2,3}m\prime \right)\overline{a_{3,1}}+\left(a_{2,1}{r}_5+a_{2,2}{r}_6+a_{2,3}{r}_1\prime +a_{2,4}{r}_2\prime \right)\overline{a_{4,1}}$

(6)

$c_{2,2}=\left(a_{2,1}{n}_{11}+a_{2,2}{n}_{21}\right)\overline{a_{1,2}}+\left(a_{2,1}{n}_{12}+a_{2,2}{n}_{22}\right)\overline{a_{2,2}}+\left(a_{2,1}{r}_3+a_{2,2}{r}_4+a_{2,3}{m}^{\prime }\right)\overline{a_{3,2}}+\left(a_{2,1}{r}_5+a_{2,2}{r}_6+a_{2,3}{r}_1{}^{\prime }+a_{2,4}{r}_2{}^{\prime }\right)\overline{a_{4,2}}$

(7)

$c_{2,3}=\left(a_{2,1}{n}_{11}+a_{2,2}{n}_{21}\right)\overline{a_{1,3}}+\left(a_{2,1}{n}_{12}+a_{2,2}{n}_{22}\right)\overline{a_{2,3}}+\left(a_{2,1}{r}_3+a_{2,2}{r}_4+a_{2,3}{m}^{\prime }\right)\overline{a_{3,3}}+\left(a_{2,1}{r}_5+a_{2,2}{r}_6+a_{2,3}{r}_1{}^{\prime }+a_{2,4}{r}_2{}^{\prime }\right)\overline{a_{4,3}}$

(8)

$c_{2,4}=\left(a_{2,1}{n}_{11}+a_{2,2}{n}_{21}\right)\overline{a_{1,4}}+\left(a_{2,1}{n}_{12}+a_{2,2}{n}_{22}\right)\overline{a_{2,4}}+\left(a_{2,1}{r}_3+a_{2,2}{r}_4+a_{2,3}{m}^{\prime }\right)\overline{a_{3,4}}+\left(a_{2,1}{r}_5+a_{2,2}{r}_6+a_{2,3}{r}_1{}^{\prime }+a_{2,4}{r}_2{}^{\prime }\right)\overline{a_{4,4}}$

(9)

$c_{3,1}=\left(a_{3,1}{n}_{11}+a_{3,2}{n}_{21}\right)\overline{a_{1,1}}+\left(a_{3,1}{n}_{12}+a_{3,2}{n}_{22}\right)\overline{a_{2,1}}+\left(a_{3,1}{r}_3+a_{3,2}{r}_4+a_{3,3}{m}^{\prime }\right)\overline{a_{3,1}}+\left(a_{3,1}{r}_5+a_{3,2}{r}_6+a_{3,3}{r}_1{}^{\prime }+a_{3,4}{r}_2{}^{\prime }\right)\overline{a_{4,1}}$

(10)

$c_{3,2}=\left(a_{3,1}{n}_{11}+a_{3,2}{n}_{21}\right)\overline{a_{1,2}}+\left(a_{3,1}{n}_{12}+a_{3,2}{n}_{22}\right)\overline{a_{2,2}}+\left(a_{3,1}{r}_3+a_{3,2}{r}_4+a_{3,3}{m}^{\prime }\right)\overline{a_{3,2}}+\left(a_{3,1}{r}_5+a_{3,2}{r}_6+a_{3,3}{r}_1{}^{\prime }+a_{3,4}{r}_2{}^{\prime }\right)\overline{a_{4,2}}$

(11)

$c_{3,3}=\left(a_{3,1}{n}_{11}+a_{3,2}{n}_{21}\right)\overline{a_{1,3}}+\left(a_{3,1}{n}_{12}+a_{3,2}{n}_{22}\right)\overline{a_{2,3}}+\left(a_{3,1}{r}_3+a_{3,2}{r}_4+a_{3,3}{m}^{\prime }\right)\overline{a_{3,3}}+\left(a_{3,1}{r}_5+a_{3,2}{r}_6+a_{3,3}{r}_1{}^{\prime }+a_{3,4}{r}_2{}^{\prime }\right)\overline{a_{4,3}}$

(12)

$c_{3,4}=\left(a_{3,1}{n}_{11}+a_{3,2}{n}_{21}\right)\overline{a_{1,4}}+\left(a_{3,1}{n}_{12}+a_{3,2}{n}_{22}\right)\overline{a_{2,4}}+\left(a_{3,1}{r}_3+a_{3,2}{r}_4+a_{3,3}m\prime \right)\overline{a_{3,4}}+\left(a_{3,1}{r}_5+a_{3,2}{r}_6+a_{3,3}{r}_1\prime +a_{3,4}{r}_2\prime \right)\overline{a_{4,4}}$

(13)

$c_{4,1}=\left(a_{4,1}{n}_{11}+a_{4,2}{n}_{21}\right)\overline{a_{1,1}}+\left(a_{4,1}{n}_{12}+a_{4,2}{n}_{22}\right)\overline{a_{2,1}}+\left(a_{4,1}{r}_3+a_{4,2}{r}_4+a_{4,3}m\prime \right)\overline{a_{3,1}}+\left(a_{4,1}{r}_5+a_{4,2}{r}_6+a_{4,3}{r}_1\prime +a_{4,4}{r}_2\prime \right)\overline{a_{4,1}}$

(14)

$c_{4,2}=\left(a_{4,1}{n}_{11}+a_{4,2}{n}_{21}\right)\overline{a_{1,2}}+\left(a_{4,1}{n}_{12}+a_{4,2}{n}_{22}\right)\overline{a_{2,2}}+\left(a_{4,1}{r}_3+a_{4,2}{r}_4+a_{4,3}m\prime \right)\overline{a_{3,2}}+\left(a_{4,1}{r}_5+a_{4,2}{r}_6+a_{4,3}{r}_1\prime +a_{4,4}{r}_2\prime \right)\overline{a_{4,2}}$

(15)

$c_{4,3}=\left(a_{4,1}{n}_{11}+a_{4,2}{n}_{21}\right)\overline{a_{1,3}}+\left(a_{4,1}{n}_{12}+a_{4,2}{n}_{22}\right)\overline{a_{2,3}}+\left(a_{4,1}{r}_3+a_{4,2}{r}_4+a_{4,3}{m}^{\prime }\right)\overline{a_{3,3}}+\left(a_{4,1}{r}_5+a_{4,2}{r}_6+a_{4,3}{r}_1{}^{\prime }+a_{4,4}{r}_2{}^{\prime }\right)\overline{a_{4,3}}$

(16)

$c_{4,4}=\left(a_{4,1}{n}_{11}+a_{4,2}{n}_{21}\right)\overline{a_{1,4}}+\left(a_{4,1}{n}_{12}+a_{4,2}{n}_{22}\right)\overline{a_{2,4}}+\left(a_{4,1}{r}_3+a_{4,2}{r}_4+a_{4,3}m\prime \right)\overline{a_{3,4}}+\left(a_{4,1}{r}_5+a_{4,2}{r}_6+a_{4,3}{r}_1\prime +a_{4,4}{r}_2\prime \right)\overline{a_{4,4}}$

According to the decryption algorithm, the plaintext $m$ can be obtained by the equation:

(17)

$m\prime =\left(\overline{a_{3,1}}{\mathrm{c}}_{1,1}+\overline{a_{3,2}}{\mathrm{c}}_{2,1}+\overline{a_{3,3}}{\mathrm{c}}_{3,1}+\overline{a_{3,4}}{\mathrm{c}}_{4,1}\right)a_{1,3}+\left(\overline{a_{3,1}}{\mathrm{c}}_{1,2}+\overline{a_{3,2}}{\mathrm{c}}_{2,2}+\overline{a_{3,3}}{\mathrm{c}}_{3,2}+\overline{a_{3,4}}{\mathrm{c}}_{4,2}\right)a_{2,3}+\left(\overline{a_{3,1}}{\mathrm{c}}_{1,3}+\overline{a_{3,2}}{\mathrm{c}}_{2,3}+\overline{a_{3,3}}{\mathrm{c}}_{3,3}+\overline{a_{3,4}}{\mathrm{c}}_{3,4}\right)a_{3,3}+\left(\overline{a_{3,1}}{\mathrm{c}}_{1,4}+\overline{a_{3,2}}{\mathrm{c}}_{2,4}+\overline{a_{3,3}}{\mathrm{c}}_{3,4}+\overline{a_{3,4}}{\mathrm{c}}_{3,4}\right)a_{4,3}$

An adversary who possesses the ciphertext $C$ and wants to find the cleartext m or the secret key from the above nine equations should, at least, extract the secret components $\overline{a_{3,1}}$, $\overline{a_{3,2}}$, $\overline{a_{3,3}}$, $\overline{a_{3,4}}$, $a_{1,3}$, $a_{2,3}$, $a_{3,3}$ and $a_{4,3}$ according to the Equation (17). Since our fully homomorphic encryption scheme is probabilistic, these sixteen equations are randomly independent even if the encrypted messages are the same one. Therefore, finding the secret key is equivalent to a problem of solving an over-defined system of quadratic multivariate polynomial equations in a non-commutative ring.

7. Comparison with Other Schemes

As is shown in

Table 1. Comparison of the performances of VFHE scheme (N is a security parameter).

Algorithm	Cleartext	Secrete Key	Public Key	Ciphertext
Gentry [2]	{0,1}	$N^7$	$N^3$	$N^{1.5}$
Smart-Verc [3]	{0,1}	$O\left(N^3\right)$	$N^3$	$O\left(N^{1.5}\right)$
DGHV [4]	{0,1}	$\tilde{O}\left(N^{10}\right)$	$\tilde{O}\left(N^2\right)$	$\tilde{O}\left(N^5\right)$
CMNT [8]	{0,1}	$\tilde{O}\left(N^7\right)$	$\tilde{O}\left(N^2\right)$	$\tilde{O}\left(N^5\right)$
BatchDGHV [9]	${\left\{0,1\right\}}^l$	$\tilde{O}\left(N^7\right)$	$l.\tilde{O}\left(N^2\right)$	$l.\tilde{O}\left(N^5\right)$
LI-WANG [13]	$\text{ℤ}/N\text{ℤ}$	$O\left(3N\right)$	$NA$	$O\left(3N\right)$
Our scheme	$\text{ℤ}/{\mathrm{N}}^2\text{ℤ}$	$O\left(16{\mathrm{N}}^2\right)$	$NA$	$O\left(16{\mathrm{N}}^2\right)$

, our cryptosystem presents good performances compared to other existing schemes. Its ciphertext and key sizes depend linearly to clear text space dimension. The other schemes use a small clear text space which influences the runtime of the algorithm. In our case we are using a large clear text space which allows us to encrypt big messages and perform computations directly on ciphertexts.

We can observe that the complexity of Li-Wang’s scheme is smaller than ours. This difference of complexities is normal, because our scheme offers an additional property of verification, which is not offered by Li-Wang’s homomorphic encryption scheme. To obtain verification property for our scheme we have augmented the order of matrices and used a larger clear text space. Using a larger clear text space can be seen as a supplementary advantage of our encryption scheme because it is highly appreciated in a context of big data security in the cloud.

8. Implementation and Tests

We present in this part the results of implementation of our verifiable fully homomorphic encryption scheme. The tests are performed within the Microsoft Azure cloud using a VM with features: 2vCPU running at 2.40 GHz, with L2 cache of 256 KB and 7 GB of RAM.

The implementation of the algorithm was done using the JAVA programming language, based on the library we had already implemented for the first cryptosystem. This library contains the basic objects of our cryptosystems, namely: Lipschitz quaternions and quaternionic matrices.

The basic results of our tests are summarized in the table above (

Table 2. Implementation result of our verifiable fully homomorphic encryption scheme.

Security Param (bits)	Key Gen (ms)	Enc (ms)	Dec (ms)	Verification (ms)	Add (ms)	Mult (ms)	Secrete Key (kbits)	Cleartext (kbits)	Ciphertext (kbits)
256	67	10	1	<<1	<<1	<<1	40	0.5	16
512	166	26	3	1	<<1	<<1	80	1	32
1024	718	111	9	2	<<1	2	160	2	64
2048	5209	849	28	8	<<1	8	320	4	128
4096	63,516	10,075	84	18	<<1	23	640	8	256

); these results correspond to the different sizes of the security parameter n used to generate the secret key. In this table, we have summarized the fundamental operations of our verifiable fully homomorphic cryptosystem.

On the one hand, we observed that, even though the encryption and decryption algorithms have almost the same mathematical formulations, the execution time of encryption is significantly higher than that of decryption. This excessive difference between the two operations is due to the bitToQuatern transform used during the encryption, we confirm that the majority of the encryption time is dedicated to transform a bit σ∈ {0,1} into a Lipschitz quaternion. With regard to the evaluation operations, we have observed that the addition is always done in less than a millisecond while the multiplication is done in an optimal time. This is very reasonable given the fact that matrix operations are simple. Therefore, these temporal complexities are practical in a context of cloud computing with unlimited computing capabilities.

The verification is done in a reasonable time for all the sizes of the keys. It of the same order as the decryption operation, except that the latter uses quaternionic matrices of order 4 so for the verification, we use quaternionic matrices of order 2. One thing that is well shown in the results: verification requires half the time of decryption.

On the other hand, we noticed that the size of the secret key is of the order of a few kilobytes for a given security parameter n while the size of the ciphertext is about half the size of the secret key. This is because the secret key consists of two matrices, but the ciphertext consists of only one matrix. All sizes of ciphertexts are fixed because we use a noise-free fully homomorphic encryption scheme.

9. Conclusions

In this paper, we presented a new verifiable fully homomorphic encryption scheme. It is a symmetric, noise free and probabilistic cryptosystem, for which the ciphertext space is non-commutative ring quaternionic based. The clear text is a large number $\sigma \in \text{ℤ}/{\mathrm{N}}^2\text{ℤ}$. Our encryption scheme finds its effective applications in the domain of smart computations on encrypted data in cloud computing as it can also be applied to big data security. It is an efficient and practical scheme for which the security is based on the problem of solving an over-defined system of quadratic multivariate polynomial equations in a non-commutative ring. The two most important features of our scheme are homomorphy and verifiability. This scheme allows a remote, non-confident, cloud computing to perform complex computations over encrypted data, and permits the client to verify the exactitude of its outsourced operations during the decryption.

We have also presented an implementation of this new encryption scheme using the JAVA programming language and Microsoft Azure as Cloud computing environment. We have obtained ambitious results after testing the algorithm. We have tested the algorithm for different key sizes in the cloud. The obtained results, for different key sizes, show that our cryptosystem is powerful and efficient. It gives runtime execution of the order of a few milliseconds for an acceptable security level. In our next work, we will focus on the integration of this scheme with Hadoop framework for big data security in the cloud.