A Preconditioned Iterative Approach for Efficient Full Chip Thermal Analysis on Massively Parallel Platforms ^†

Abstract

Efficient full-chip thermal simulation is among the most challenging problems facing the EDA industry today, especially for modern 3D integrated circuits, due to the huge linear systems resulting from thermal modeling approaches that require unreasonably long computational times. While the formulation problem, by applying a thermal equivalent circuit, is prevalent and can be easily constructed, the corresponding 3D equations network has an undesirable time-consuming numerical simulation. Direct linear solvers are not capable of handling such huge problems, and iterative methods are the only feasible approach. In this paper, we propose a computationally-efficient iterative method with a parallel preconditioned technique that exploits the resources of massively-parallel architectures such as Graphic Processor Units (GPUs). Experimental results demonstrate that the proposed method achieves a speedup of 2.2× in CPU execution and a 26.93× speedup in GPU execution over the state-of-the-art iterative method.

1. Introduction

The evolution of the manufacturing technology of Integrated Circuits (ICs) has continued unabated over the past fifty years, according to the predictions of Moore’s law and has led to extremely complex circuits (modern processors contain several billion transistors and are easily the most complex human construction), but also to analogous escalation of the problems related to the analysis and simulation of such circuits. Therefore, thermal analysis is one of the most critical challenges arising from the technological evolution. The continuous effort for smaller sizes, in the sub-45-nm era, and greater performance, as well as the new 3D structures have begun to outpace the ability of heat sinks to dissipate the on-chip power.

In particular, aggravation of thermal effects is an inevitable consequence of the continuous scaling trend. High temperature has a significant impact on chip performance and functionality, leading to slower transistor speed, more leakage power, higher interconnect resistance, and reduced reliability [1]. The problem becomes more pronounced in modern technologies due to the multilayer 3D stacking, and the use of new device technologies, like FinFETsand Silicon on Insulator (SOI), which are more sensitive to the self-heating effect [2]. Furthermore, as heat generation is nonuniform, local hotspots and spatial gradients appear. Stacking multiple layers in a 3D chip promises density and performance enhancement. However, it requires extensive thermal analysis as the power density and temperature of these architectures can be quite high. For the above reasons, full chip thermal analysis is a vital, but extremely difficult problem due to the size of the systems that need to be solved for multiple time points and remains a key issue for future microprocessors and ICs [3,4]. Due to this fact, IC thermal analysis problems have drawn considerable attention over the past two decades. To deal with these challenges, prior approaches have focused on the formulation of the problem and the fast steady-state and transient thermal simulation in order to compute the temperature across the whole chip.

Direct methods (based on matrix factorization) have been widely used in the past for solving the resulting linear systems, mainly because of their robustness in most types of problems. Unfortunately, these methods do not scale well with the dimension of the linear system and are prohibitively expensive, while the thermal problems are becoming larger, in both execution time and memory requirements. On the other hand, iterative Krylov-subspace methods such as Conjugate Gradients (CG) involve only inner products and matrix-vector products and constitute a better alternative for large sparse linear systems in many respects, being more computationally- and memory-efficient.

Moving beyond conventional direct solvers, our early work in [5] introduced an approach for full chip thermal analysis that is based on the Finite Difference Method (FDM) or the formulation of an RC equivalent electrical network in conjunction with a highly parallel iterative Krylov-subspace Preconditioned Conjugate Gradient (PCG) method, which overcomes the computational demands for the very large systems arising from the thermal modeling. In particular, the contributions of this paper to the problem of thermal analysis are:

• Accelerated solution of thermal grids: The proposed thermal simulator uses FDM with preconditioned CG, which is well-suited, offers faster solution times, and uses less memory than sparse direct solvers.
• Highly parallel preconditioned mechanism: The specialized structures of thermal grids allow the usage of fast transform solvers as a preconditioned mechanism in the CG method, which are highly parallel and can be easily ported to GPUs.
• Fast convergence to the solution: Fast transform solvers can handle different matrix blocks, which offers a good preconditioner approximation. This results in considerably more accurate preconditioners that can approximate thermal grids and make CG converge to the final solution in a few iterations.

Experimental results demonstrate that our method achieves speedups of around 20× on GPU and around 2× on CPU for a 10 M node thermal grid over a state-of-the-art iterative method, like Incomplete Cholesky Preconditioned Conjugate Gradient (ICCG) on a CPU.

The rest of the paper, is organized as follows. Section 2 describes the related work on the thermal simulation problem. Section 3 introduces the thermal model that was used in the present work. Section 4 provides a brief description of the 3D fast transform solver. Section 5 describes the proposed approach, combining the methods presented in the two previous sections. Finally, Section 6 presents the results and a discussion about the advantages of the method, followed by the conclusions in Section 7.

2. Related Work

The growing need to simulate large-scale thermal models in technology nodes below 45 nm has led to some important research in the fast thermal estimation of the IC chips. In this section, we briefly review some of these methods. Most transient thermal analysis methodologies have so far relied on solving the entire system, using different modeling techniques, based mainly on the Finite Element Method (FEM), the Finite Difference Method (FDM), and Green’s functions. The research work in [6,7] adopted the FDM method, with a multigrid approach in order to speed up the simulation process, and the FDM method with temporal and spatial adaptation to further accelerate thermal analysis was proposed in [8,9]. Similarly, in [10], the full-chip thermal transient equations were solved in a similar manner using an Alternating Direction Implicit (ADI) method for enhanced computational efficiency. Furthermore, in [11,12], the FDM approach and the RCequivalent were used along with modeling of the fluids for micro-cooling 3D structures. In [13], FEM was adopted for 2D and 3D geometries along with a multigrid preconditioning method and automatic mesh generation for chip geometries. Finally, Green’s functions were used in [14] with discrete cosine transform and its inversion in order to accelerate the numerical computation of the homogeneous and inhomogeneous solution. However, these method are efficient for a limited range of problems, since they have limited potential for parallelism.

Besides the previous conventional approaches, different methods like a Neural Net (NN) approach were used in [15], but since it was based in predictions, it did not always provide an accurate solution to the crucial problem of thermal analysis. Moreover, a Look Up Table (LUT) method based on the power thermal relation, which develops a double-mesh scheme to capture thermal characteristics and store the results in library files, was presented in [16]. However, currently, chips can lead to huge library files due to the highly complex combined heat maps. Furthermore, the reduction of the problem size, through a Model Order Reduction (MOR) process, was proposed in [17,18], which can be useful in addressing the performance of individual devices, but in some cases, it is not enough to address all the reliability issues.

Finally, the authors in [19] provided a parallel iterative Generalized Minimal RESidual (GMRES) method for FDM and micro-cooling problems, but without any special preconditioning approach. Clearly, the concept of a dedicated fully-parallel preconditioned technique has not yet been introduced in the context of transient thermal analysis.

3. On-Chip Thermal Modeling and Analysis

There are three modes of heat transfer: conduction, convection, and radiation. The primary mechanism of heat transfer in solids is by conduction, and the others can be neglected. The starting point for thermal analysis is Fourier’s law of heat conduction [20]:

$$\mathbf{q}(\mathbf{r},t)=-k_t\nabla T(\mathbf{r},t)$$

(1)

which states that the vector of heat flux density $\mathbf{q}$ (heat flow per unit area and unit time) is proportional to the negative gradient of temperature T at every spacial point $\mathbf{r}={[x,y,z]}^T$ and time t, where $k_t$ is the thermal conductivity of the material.

The conservation of energy also states that the divergence of the heat flux $\mathbf{q}$ equals the difference between the power generated by external heat sources and the rate of change of temperature, i.e.,

$$\begin{array}{c}\hfill \nabla ·\mathbf{q}(\mathbf{r},t)=g(\mathbf{r},t)-\rho c_p\frac{\partial T(\mathbf{r},t)}{\partial t}\end{array}$$

(2)

where $g(\mathbf{r},t)$ is the power density of the heat sources, $c_p$ is the specific heat capacity of the material, and $\rho$ is the density of the material. By combining (1) and (2), we have:

$$\begin{array}{c}\hfill -k_t{\nabla }^{2}T(\mathbf{r},t)=g(\mathbf{r},t)-\rho c_p\frac{\partial T(\mathbf{r},t)}{\partial t}\end{array}$$

(3)

which may be rewritten as the following parabolic Partial Differential Equation (PDE):

$$\begin{array}{c}\hfill \rho c_p\frac{\partial T(\mathbf{r},t)}{\partial t}=k_t{\nabla }^{2}T(\mathbf{r},t)+g(\mathbf{r},t)\\ \hfill =k_t(\frac{{\partial }^{2}T(\mathbf{r},t)}{\partial x^2}+\frac{{\partial }^{2}T(\mathbf{r},t)}{\partial y^2}+\frac{{\partial }^{2}T(\mathbf{r},t)}{\partial z^2})+g(\mathbf{r},t)\end{array}$$

(4)

(normally accompanied by appropriate boundary conditions [21]).

A common procedure for the numerical solution of (4) is by discretization along the three spatial coordinates with steps $\Delta x,\Delta y$, and $\Delta z$ and substitution of the spatial second-order derivatives by finite difference approximations, leading to the following expression for temperature $T_{i,j,k}$ at each discrete point $(i,j,k)$ in relation to its neighboring points:

$$\begin{array}{c}\hfill \rho c_p\frac{d{T}_{i,j,k}}{dt}=k_t\frac{T_{i+1,j,k}-2T_{i,j,k}+T_{i-1,j,k}}{\Delta x^2}\\ \hfill +k_t\frac{T_{i,j+1,k}-2T_{i,j,k}+T_{i,j-1,k}}{\Delta y^2}\\ \hfill +k_t\frac{T_{i,j,k+1}-2T_{i,j,k}+T_{i,j,k-1}}{\Delta z^2}+g_{i,j,k}\end{array}$$

(5)

or by multiplying by $\Delta x\Delta y\Delta z$:

$$\begin{array}{c}\hfill \rho c_p(\Delta x\Delta y\Delta z)\frac{d{T}_{i,j,k}}{dt}\\ \hfill -k_t\frac{\Delta y\Delta z}{\Delta x}(T_{i+1,j,k}-2T_{i,j,k}+T_{i-1,j,k})\\ \hfill -k_t\frac{\Delta x\Delta z}{\Delta y}(T_{i,j+1,k}-2T_{i,j,k}+T_{i,j-1,k})\\ \hfill -k_t\frac{\Delta x\Delta y}{\Delta z}(T_{i,j,k+1}-2T_{i,j,k}+T_{i,j,k-1})\\ \hfill =g_{i,j,k}(\Delta x\Delta y\Delta z)\end{array}$$

(6)

There is a well-known analogy between thermal and electrical conduction, where temperature corresponds to voltage and heat flow corresponds to current (see

Table 1. Analogy between electrical and thermal circuits.

Electrical Circuit	Thermal Circuit
Voltage	Temperature
Current	Heat Flow
Electrical Conductance	Thermal Conductance
Electrical Resistance	Thermal Resistance
Electrical Capacitance	Thermal Capacitance
Current Source	Heat Source

).

In light of this analogy, Equation (6) has a direct correspondence to an electrical circuit where there is a node at every discrete point or cell in the thermal grid (see Figure 1). Every circuit node is connected to spatially-neighboring nodes via conductances in the directions x, y, z with values:

$$G_x\equiv \frac{k_t\Delta y\Delta z}{\Delta x},G_y\equiv \frac{k_t\Delta x\Delta z}{\Delta y},G_z\equiv \frac{k_t\Delta x\Delta y}{\Delta z}$$

(7)

and there is a capacitance to ground at every node or thermal cell with value:

$$C\equiv \rho c_p(\Delta x\Delta y\Delta z)$$

(8)

The heat sources constitute input excitations and are modeled in the equivalent circuit as the current sources with values:

$$I_{i,j,k}\equiv g_{i,j,k}(\Delta x\Delta y\Delta z)$$

(9)

The above current sources are connected at the specific points $(i,j,k)$ or circuit nodes where there is heat flow (i.e., power dissipation from the underlying chip logic blocks).

The resulting electrical equivalent circuit is described in the time domain, using the Modified Nodal Analysis (MNA) framework, by a system of Ordinary Differential Equations (ODE):

$$\mathbf{G}\mathbf{x}\left(t\right)+\mathbf{C}\frac{d\mathbf{x}\left(t\right)}{dt}=\mathbf{u}\left(t\right)$$

(10)

where $\mathbf{G}\in {\mathcal{R}}^{n\times n}$ is a symmetric and positive definite matrix of the conductances (7), $\mathbf{C}\in {\mathcal{R}}^{n\times n}$ is a diagonal matrix of cell capacitances (8), $\mathbf{x}\in {\mathcal{R}}^n$ is the vector of unknown temperatures $T_{i,j,k}$ at all discretization points (constituting internal states of the system), and $\mathbf{u}\in {\mathcal{R}}^p$ is the vector of input excitations from the current sources $I_{i,j,k}$ of (9).

For transient simulation, we can discretize the time interval into time instants $t_k$, $k=1,2,\cdots$ and use the backward-Euler numerical integration method for the calculation of temperature in each discrete time instant $t_k$:

$$(\mathbf{G}+\frac{\mathbf{C}}{h_k})\mathbf{x}\left(t_k\right)=\frac{\mathbf{C}}{h_k}\mathbf{x}\left(t_{k-1}\right)+\mathbf{u}\left(t_k\right)$$

(11)

where $h_k=t_k-t_{k-1}$, $k=1,2,\cdots$ is the time step of time $t_k$ (which may in general vary during transient analysis). The above equation involves the solution of a very large sparse linear system in each time instant $t_k$.

Direct methods (based on matrix factorization) have been widely used in the past for solving the resulting linear systems, mainly because of their robustness in most types of problems. Unfortunately, these methods do not scale well with the dimension of the linear system and become prohibitively expensive for large-scale networks. Iterative methods involve only inner products and matrix-vector products and constitute a better alternative for large sparse linear systems in many respects, being more computationally and memory efficient. In this work, we employ iterative methods for the solution of large-scale networks arising from the 3D discretization of the chip for thermal analysis. The system matrices arising from the modeling of the thermal grid can also be shown to be Symmetric and Positive Definite (SPD), which allows the use of the efficient method of the Conjugate Gradient (CG) for the solution of the corresponding linear systems. The CG method is well known [22], and its implementation is shown in Algorithm 1.

Algorithm 1 Preconditioned conjugate gradient.

1: $\mathbf{x}=$ initial guess ${\mathbf{x}}^{\left(0\right)}$ 2: $\mathbf{r}=\mathbf{b}-\mathbf{A}\mathbf{x}$ 3: $iter=0$ 4: repeat 5:     $iter=iter+1$ 6:     Solve $\mathbf{M}\mathbf{z}=\mathbf{r}$    (Preconditioner-Solve Step) 7:     $\rho =\mathbf{r}·\mathbf{z}$ 8:     if $iter==1$ then 9:         $\mathbf{p}=\mathbf{z}$ 10:     else 11:         $\beta =\rho /\rho 1$ 12:         $\mathbf{p}=\mathbf{z}+\beta \mathbf{p}$ 13:     end if 14:     $\rho 1=\rho$ 15:     $\mathbf{q}=\mathbf{A}\mathbf{p}$ 16:     $\alpha =\rho /(\mathbf{p}·\mathbf{q})$ 17:     $\mathbf{x}=\mathbf{x}+\alpha \mathbf{p}$ 18:     $\mathbf{r}=\mathbf{r}-\alpha \mathbf{q}$ 19: until$\frac{\left|\right|\mathbf{b}-\mathbf{Ax}\left|\right|}{\left|\right|\mathbf{b}\left|\right|}<tol$

Regarding the convergence rate of CG, it can be shown [23] that the required number of iterations (for a given initial guess and convergence tolerance) is bounded in terms of the spectral condition number $k_2\left(\mathbf{A}\right)={\left|\right|\mathbf{A}\left|\right|}_2\left|\right|{\mathbf{A}}^{-1}{\left|\right|}_2\ge 1$; specifically, it is $O\left(\sqrt{k_2\left(\mathbf{A}\right)}\right)$, which for SPD matrices becomes $k_2\left(\mathbf{A}\right)=\frac{{\lambda }_{max}\left(\mathbf{A}\right)}{{\lambda }_{min}\left(\mathbf{A}\right)}$ where ${\lambda }_{max}\left(\mathbf{A}\right)$, ${\lambda }_{min}\left(\mathbf{A}\right)$ are the maximum and minimum eigenvalues of $\mathbf{A}$, respectively. This means that convergence of CG is fast when $k_2\left(\mathbf{A}\right)\approx 1$ and slow when $k_2\left(\mathbf{A}\right)>>1$.

To improve the convergence speed, it is necessary to apply a preconditioning mechanism, which transforms the initial linear system into an equivalent one with a more favorable spectral condition number. The so-called preconditioner is a matrix $\mathbf{M}$ that approximates $\mathbf{A}$ in some way, such that the transformed system ${\mathbf{M}}^{-1}\mathbf{Ax}={\mathbf{M}}^{-1}\mathbf{b}$ (which obviously has the same solution as the initial $\mathbf{Ax}=\mathbf{b}$) exhibits condition number $k_2\left({\mathbf{M}}^{-\mathbf{1}}\mathbf{A}\right)=k_2\left(\mathbf{I}\right)=1$. In practice, it is not necessary to invert the preconditioner $\mathbf{M}$ and apply it directly at the system $\mathbf{Ax}=\mathbf{b}$. It can be shown that the same thing can be accomplished by introducing an extra computational step within the iterative method, which entails solving a system $\mathbf{Mz}=\mathbf{r}$ with known Right-Hand Side (RHS) vector $\mathbf{r}$ and unknown vector $\mathbf{z}$ in every iteration [23].

From the above, it follows that a good preconditioner $\mathbf{M}$ must satisfy two key properties:

• The fast convergence rate of the preconditioned.
• A linear system involving $\mathbf{M}$ is solved much more efficiently than the original system that involves $\mathbf{A}$.

where “more efficiently” can mean with less asymptotic complexity—ideally, an optimal or near-optimal complexity of $O\left(N\right)$ or $O\left(NlogN\right)$—and/or significantly more parallelism in the solution procedure. If the preconditioner is faithful enough to reduce the iterations substantially, then the whole burden of the algorithm is transferred to the preconditioner-solve step $\mathbf{Mz}=\mathbf{r}$. The next section will describe the proposed form of the preconditioner matrices for 3D thermal networks, as well as the solution of the corresponding linear systems via two series of fast transforms and inverse fast transforms.

4. Fast Transform Preconditioners for 3D Thermal Networks

Recent implementations of fast transform solvers have shown great potential for the solution of block-tridiagonal systems with a special structure [24,25]. This section describes such an algorithm for the solution of an appropriate preconditioner system $\mathbf{M}\mathbf{z}=\mathbf{r}$ by the use of a fast transform solver in a near-optimal number of operations.

Let $\mathbf{M}$ be an $N\times N$ block-tridiagonal matrix with l diagonal blocks of size $mn\times mn$ each (overall $N=lmn$), where l is very small (typically 5–8 depending on the material layers (metal and insulator) of the chip), with the following form:

$$\begin{array}{cc}\hfill \mathbf{M}& =\left[\begin{array}{ccccc}{\mathbf{M}}_1& -{\delta }_1{\mathbf{I}}_{mn}& & & \\ -{\delta }_1{\mathbf{I}}_{mn}& {\mathbf{M}}_2& -{\delta }_2{\mathbf{I}}_{mn}& & \\ & ·& ·& ·& \\ & & -{\delta }_{l-2}{\mathbf{I}}_{mn}& {\mathbf{M}}_{l-1}& -{\delta }_{l-1}{\mathbf{I}}_{mn}\\ & & & -{\delta }_{l-1}{\mathbf{I}}_{mn}& {\mathbf{M}}_l\end{array}\right]\hfill \end{array}$$

(12)

where ${\mathbf{I}}_{\mathbf{mn}}$ is the $mn\times mn$ identity matrix and ${\mathbf{M}}_i$, $i=1,\cdots ,l$, are block tridiagonal $mn\times mn$ matrices of the form:

$$\begin{array}{cc}\hfill {\mathbf{M}}_i& =\left[\begin{array}{ccccc}{\mathbf{T}}_i+{\gamma }_i{\mathbf{I}}_n& -{\gamma }_i{\mathbf{I}}_n& & & \\ -{\gamma }_i{\mathbf{I}}_n& {\mathbf{T}}_i+2{\gamma }_i{\mathbf{I}}_n& -{\gamma }_i{\mathbf{I}}_n& & \\ & ·& ·& ·& \\ & & -{\gamma }_i{\mathbf{I}}_n& {\mathbf{T}}_i+{\gamma }_i{\mathbf{I}}_n& -{\gamma }_i{\mathbf{I}}_n\\ & & & -{\gamma }_i{\mathbf{I}}_n& {\mathbf{T}}_i+{\gamma }_i{\mathbf{I}}_n\end{array}\right]\hfill \end{array}$$

(13)

where ${\mathbf{I}}_n$ is the $n\times n$ identity matrix and ${\mathbf{T}}_i$, $i=1,\cdots ,m$ are $n\times n$ tridiagonal matrices with the following form:

$$\begin{array}{cc}\hfill {\mathbf{T}}_i& =\left[\begin{array}{ccccc}{\alpha }_i+{\beta }_i& -{\alpha }_i& & & \\ -{\alpha }_i& 2{\alpha }_i+{\beta }_i& -{\alpha }_i& & \\ & ·& ·& ·& \\ & & -{\alpha }_i& 2{\alpha }_i+{\beta }_i& -{\alpha }_i\\ & & & -{\alpha }_i& {\alpha }_i+{\beta }_i\end{array}\right]=\hfill \end{array}$$

$${\alpha }_i\left[\begin{array}{ccccc}1& -1& & & \\ -1& 2& -1& & \\ & ·& ·& ·& \\ & & -1& 2& -1\\ & & & -1& 1\end{array}\right]+{\beta }_i\mathbf{I}$$

(14)

This class of tridiagonal matrices has a beforehand known eigen-decomposition. Specifically, it can be shown [26] that each ${\mathbf{T}}_i$ has n distinct eigenvalues ${\lambda }_{i,j},j=1,\cdots ,n$, which are given by:

$$\begin{array}{c}\hfill {\lambda }_{i,j}={\beta }_i+4{\alpha }_{i}si{n}^2(\frac{(j-1)\pi }{2n})={\beta }_i+{\alpha }_i(2cos(\frac{(j-1)\pi }{n})-2)\end{array}$$

(15)

and a set of n orthonormal eigenvectors ${\mathbf{q}}_j,j=1,\cdots ,n$, with elements:

$$q_{j,k}=\left\{\begin{array}{cc}\sqrt{\frac{1}{n}}cos\frac{(2k-1)(j-1)\pi }{2n},\hfill & j=1,k=1,\cdots ,n\hfill \\ \sqrt{\frac{2}{n}}cos\frac{(2k-1)(j-1)\pi }{2n},\hfill & j=2,\cdots ,n,k=1,\cdots ,n\hfill \end{array}\right.$$

(16)

Note that, the eigenvectors do not depend on the values ${\alpha }_i$ and ${\beta }_i$ and are the same for every matrix ${\mathbf{T}}_i$. If ${\mathbf{Q}}_n=[{\mathbf{q}}_1,\cdots ,{\mathbf{q}}_n]$ denotes the matrix whose columns are the eigenvectors ${\mathbf{q}}_j$, then due to the eigen-decomposition of ${\mathbf{T}}_i$, we have ${\mathbf{Q}}_n^T{\mathbf{T}}_i{\mathbf{Q}}_n={\mathsf{\Lambda }}_i=diag({\lambda }_{i,1},\cdots ,{\lambda }_{i,n})$. By exploiting the diagonalization of the matrix ${\mathbf{T}}_i$ and considering that ${\mathbf{Q}}_n^T{\mathbf{Q}}_n=\mathbf{I}$, the system $\mathbf{Mz}=\mathbf{r}$ is equivalent to the following system:

$$\begin{array}{cc}\hfill \left[\begin{array}{ccc}{\mathbf{Q}}_n^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_n^T\end{array}\right]\mathbf{M}\left[\begin{array}{ccc}{\mathbf{Q}}_n& & \\ & \ddots & \\ & & {\mathbf{Q}}_n\end{array}\right]& \left[\begin{array}{ccc}{\mathbf{Q}}_n^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_n^T\end{array}\right]\mathbf{z}\hfill \\ \hfill =\left[\begin{array}{ccc}{\mathbf{Q}}_n^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_n^T\end{array}\right]& \mathbf{r}\iff \hfill \end{array}$$

(17)

$$\left[\begin{array}{ccccc}{\tilde{\mathbf{M}}}_1& -{\delta }_1{\mathbf{I}}_{mn}& & & \\ -{\delta }_1{\mathbf{I}}_{mn}& {\tilde{\mathbf{M}}}_2& -{\delta }_2{\mathbf{I}}_{mn}& & \\ & ·& ·& ·& \\ & & -{\delta }_{l-2}{\mathbf{I}}_{mn}& {\tilde{\mathbf{M}}}_{l-1}& -{\delta }_{l-1}{\mathbf{I}}_{mn}\\ & & & -{\delta }_{l-1}{\mathbf{I}}_{mn}& {\tilde{\mathbf{M}}}_l\end{array}\right]\tilde{\mathbf{z}}=\tilde{\mathbf{r}}$$

(18)

where:

$${\tilde{\mathbf{M}}}_{\mathbf{i}}=\left[\begin{array}{ccccc}{\mathsf{\Lambda }}_i^{\left(1\right)}& -{\gamma }_i\mathbf{I}& & & \\ -{\gamma }_i\mathbf{I}& {\mathsf{\Lambda }}_i^{\left(2\right)}& -{\gamma }_i\mathbf{I}& & \\ & ·& ·& ·& \\ & & -{\gamma }_i\mathbf{I}& {\mathsf{\Lambda }}_i^{\left(2\right)}& -{\gamma }_i\mathbf{I}\\ & & & -{\gamma }_i\mathbf{I}& {\mathsf{\Lambda }}_i^{\left(1\right)}\end{array}\right]$$

(19)

$$\tilde{\mathbf{z}}=\left[\begin{array}{ccc}{\mathbf{Q}}_n^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_n^T\end{array}\right]\mathbf{z},\tilde{\mathbf{r}}=\left[\begin{array}{ccc}{\mathbf{Q}}_n^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_n^T\end{array}\right]\mathbf{r}$$

and ${\mathsf{\Lambda }}_i^{\left(1\right)}=diag({\lambda }_{i,1}^{\left(1\right)},\cdots ,{\lambda }_{i,n}^{\left(1\right)})$ and ${\mathsf{\Lambda }}_i^{\left(2\right)}=diag({\lambda }_{i,1}^{\left(2\right)},\cdots ,{\lambda }_{i,n}^{\left(2\right)})$ are diagonal matrices with the eigenvalues of ${\mathbf{T}}_i+{\gamma }_i{\mathbf{I}}_n$, ${\mathbf{T}}_i+2{\gamma }_i{\mathbf{I}}_n$, which are the following:

$$\begin{array}{c}\hfill {\lambda }_{i,j}^{\left(1\right)}={\gamma }_i+{\beta }_i+{\alpha }_i(2cos(\frac{(j-1)\pi }{n})-2)j=1,\cdots ,n,\\ \hfill {\lambda }_{i,j}^{\left(2\right)}=2{\gamma }_i+{\beta }_i+{\alpha }_i(2cos(\frac{(j-1)\pi }{n})-2)j=1,\cdots ,n,\end{array}$$

(20)

If the $N\times 1$ vectors $\mathbf{r}$, $\mathbf{z}$, $\tilde{\mathbf{r}}$, $\tilde{\mathbf{z}}$ are also partitioned into m blocks of size $n\times 1$ each, i.e.,

$$\mathbf{r}=\left[\begin{array}{c}{\mathbf{r}}_1\\ ⋮\\ {\mathbf{r}}_m\end{array}\right],\mathbf{z}=\left[\begin{array}{c}{\mathbf{z}}_1\\ ⋮\\ {\mathbf{z}}_m\end{array}\right],\tilde{\mathbf{r}}=\left[\begin{array}{c}{\tilde{\mathbf{r}}}_1\\ ⋮\\ {\tilde{\mathbf{r}}}_m\end{array}\right],\tilde{\mathbf{z}}=\left[\begin{array}{c}{\tilde{\mathbf{z}}}_1\\ ⋮\\ {\tilde{\mathbf{z}}}_m\end{array}\right]$$

then we have: ${\tilde{\mathbf{r}}}_i={\mathbf{Q}}_n^T{\mathbf{r}}_i$ and ${\tilde{\mathbf{z}}}_i={\mathbf{Q}}_n^T{\mathbf{z}}_i\iff {\mathbf{z}}_i={\mathbf{Q}}_n{\tilde{\mathbf{z}}}_i,i=1,\cdots ,m$.

However, it can be shown [27] that each product ${\mathbf{Q}}_n^T{\mathbf{r}}_i={\tilde{\mathbf{r}}}_i$ corresponds to a Discrete Cosine Transform of Type-II (DCT-II) on ${\mathbf{r}}_i$, and each product ${\mathbf{Q}}_n{\tilde{\mathbf{z}}}_i={\mathbf{z}}_i$ corresponds to an Inverse Discrete Cosine Transform of Type-II (IDCT-II) on ${\tilde{\mathbf{z}}}_i$. This means that the computation of the whole vector $\tilde{\mathbf{r}}$ from $\mathbf{r}$ amounts to m independent DCT-II transforms of size n, and the computation of the whole vector $\mathbf{z}$ from $\tilde{\mathbf{z}}$ amounts to m independent IDCT-II transforms of size n. A modification of the Fast Fourier Transform (FFT) can be employed for each of the $lm$ independent DCT-II/IDCT-II transforms [27], giving a total near-optimal operation count of $\mathcal{O}(mnlogn)=\mathcal{O}(Nlogn)$.

If now, $\mathbf{P}$ is a permutation matrix of size $mn\times mn$ that reorders the elements of a vector or the rows of a matrix as $1,n+1,\cdots ,(m-1)n+1,2,n+2,\cdots ,(m-1)n+2,\cdots ,n,n+n,\cdots ,(m-1)n+n$ and ${\mathbf{P}}_1$, ${\mathbf{P}}_1^T$ are the block-diagonal $lmn\times lmn$ permutation matrices ${\mathbf{P}}_1=diag(\mathbf{P},\cdots ,\mathbf{P})$, ${\mathbf{P}}_1^T=diag({\mathbf{P}}^T,\cdots ,{\mathbf{P}}^T)$, then the system at (18) is transformed into:

$${\mathbf{P}}_1\left[\begin{array}{ccccc}{\tilde{\mathbf{M}}}_1& -{\delta }_1{\mathbf{I}}_{mn}& & & \\ -{\delta }_1{\mathbf{I}}_{mn}& {\tilde{\mathbf{M}}}_2& -{\delta }_2{\mathbf{I}}_{mn}& & \\ & ·& ·& ·& \\ & & -{\delta }_{l-2}{\mathbf{I}}_{mn}& {\tilde{\mathbf{M}}}_{l-1}& -{\delta }_{l-1}{\mathbf{I}}_{mn}\\ & & & -{\delta }_{l-1}{\mathbf{I}}_{mn}& {\tilde{\mathbf{M}}}_l\end{array}\right]{\mathbf{P}}_1^T{\mathbf{P}}_1\tilde{\mathbf{z}}={\mathbf{P}}_1\tilde{\mathbf{r}}\iff$$

$$\left[\begin{array}{ccccc}{\mathbf{D}}_1& -{\delta }_1{\mathbf{I}}_{mn}& & & \\ -{\delta }_1{\mathbf{I}}_{mn}& {\mathbf{D}}_2& -{\delta }_2{\mathbf{I}}_{mn}& & \\ & ·& ·& ·& \\ & & -{\delta }_{l-2}{\mathbf{I}}_{mn}& {\mathbf{D}}_{l-1}& -{\delta }_{l-1}{\mathbf{I}}_{mn}\\ & & & -{\delta }_{l-1}{\mathbf{I}}_{mn}& {\mathbf{D}}_l\end{array}\right]{\tilde{\mathbf{z}}}^{{\mathbf{P}}_1}={\tilde{\mathbf{r}}}^{{\mathbf{P}}_1}$$

(21)

where ${\mathbf{D}}_1=diag({\tilde{\mathbf{T}}}_{i,1},\cdots ,{\tilde{\mathbf{T}}}_{i,n})$, $i=1,\cdots ,l$, with ${\tilde{\mathbf{T}}}_{i,j}$, $j=1,\cdots ,n$ being $m\times m$ tridiagonal matrices of the form:

$$\begin{array}{cc}\hfill {\tilde{\mathbf{T}}}_{i,j}& =\left[\begin{array}{ccccc}{\lambda }_{i,j}^{\left(1\right)}& -{\gamma }_i& & & \\ -{\gamma }_i& {\lambda }_{i,j}^{\left(2\right)}& -{\gamma }_i& & \\ & ·& ·& ·& \\ & & -{\gamma }_i& {\lambda }_{i,j}^{\left(2\right)}& -{\gamma }_i\\ & & & -{\gamma }_i& {\lambda }_{i,j}^{\left(1\right)}\end{array}\right]=\hfill \end{array}$$

$${\gamma }_i\left[\begin{array}{ccccc}1& -1& & & \\ -1& 2& -1& & \\ & ·& ·& ·& \\ & & -1& 2& -1\\ & & & -1& 1\end{array}\right]+({\beta }_i+{\alpha }_i(2cos(\frac{(j-1)\pi }{n})-2)){\mathbf{I}}_m$$

(22)

and ${\tilde{\mathbf{z}}}^{{\mathbf{P}}_1}={\mathbf{P}}_1\tilde{\mathbf{z}}$, ${\tilde{\mathbf{r}}}^{{\mathbf{P}}_1}={\mathbf{P}}_1\tilde{\mathbf{r}}$. If ${\tilde{\mathsf{\Lambda }}}_{i,j}=diag({\tilde{\lambda }}_{i,j,1},\cdots ,{\tilde{\lambda }}_{i,j,m})$ is the diagonal matrix with the eigenvalues of ${\tilde{\mathbf{T}}}_{i,j}$, which are:

$$\begin{array}{c}\hfill {\tilde{\lambda }}_{i,j,k}={\gamma }_i(2cos(\frac{(k-1)\pi }{n})-2)+{\beta }_i+{\alpha }_i(2cos(\frac{(j-1)\pi }{n})-2),k=1,\cdots ,m\end{array}$$

(23)

and ${\mathbf{Q}}_m$ is the common matrix of eigenvectors for all ${\tilde{\mathbf{T}}}_{i,j}$, then by similar reasoning as in (17), the system (21) is equivalent to:

$$\left[\begin{array}{ccccc}{\tilde{\mathbf{D}}}_1& -{\delta }_1{\mathbf{I}}_{mn}& & & \\ -{\delta }_1{\mathbf{I}}_{mn}& {\tilde{\mathbf{D}}}_2& -{\delta }_2{\mathbf{I}}_{mn}& & \\ & ·& ·& ·& \\ & & -{\delta }_{l-2}{\mathbf{I}}_{mn}& {\tilde{\mathbf{D}}}_{l-1}& -{\delta }_{l-1}{\mathbf{I}}_{mn}\\ & & & -{\delta }_{l-1}{\mathbf{I}}_{mn}& {\tilde{\mathbf{D}}}_l\end{array}\right]\widetilde{\tilde{\mathbf{z}}}=\widetilde{\tilde{\mathbf{r}}}$$

(24)

where ${\tilde{\mathbf{D}}}_i=diag({\tilde{\mathsf{\Lambda }}}_{i,1},\cdots ,{\tilde{\mathsf{\Lambda }}}_{i,n})$ and:

$$\widetilde{\tilde{\mathbf{z}}}=\left[\begin{array}{ccc}{\mathbf{Q}}_m^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_m^T\end{array}\right]{\tilde{\mathbf{z}}}_1^{\mathbf{P}},\widetilde{\tilde{\mathbf{r}}}=\left[\begin{array}{ccc}{\mathbf{Q}}_m^T& & \\ & \ddots & \\ & & {\mathbf{Q}}_m^T\end{array}\right]{\tilde{\mathbf{r}}}_1^{\mathbf{P}}$$

In a similar way as previously, the $N\times 1$ vectors ${\tilde{\mathbf{z}}}^{{\mathbf{P}}_1}$, ${\tilde{\mathbf{r}}}^{{\mathbf{P}}_1}$, $\widetilde{\tilde{\mathbf{z}}}$, and $\widetilde{\tilde{\mathbf{r}}}$ can be partitioned into $ln$ sub-vectors of size $m\times 1$ each, and the DCT-II and IDCT-II are performed accordingly, giving a total near-optimal operation count of $\mathcal{O}(lmnlogn)=\mathcal{O}(Nlogn)$.

If now, ${\mathbf{P}}_2$ is a permutation matrix of size $N\times N$ that reorders the elements of a vector or the rows of a matrix as $1,mn+1,2mn+1,\cdots ,(l-1)mn+1,2,mn+2,2mn+2,\cdots ,(l-1)mn+2,\cdots ,mn,mn+mn,2mn+mn,\cdots ,(l-1)mn+mn$, and ${\mathbf{P}}_2^T$ is the inverse permutation matrix, then System (24) is equivalent to:

$$\widetilde{\tilde{\mathbf{M}}}{\widetilde{\tilde{\mathbf{z}}}}^{{\mathbf{P}}_2}={\widetilde{\tilde{\mathbf{r}}}}^{{\mathbf{P}}_2}$$

(25)

where $\widetilde{\tilde{\mathbf{M}}}=diag({\widetilde{\tilde{\mathbf{T}}}}_{1,1},{\widetilde{\tilde{\mathbf{T}}}}_{1,2},\cdots ,{\widetilde{\tilde{\mathbf{T}}}}_{1,m},{\widetilde{\tilde{\mathbf{T}}}}_{2,1},{\widetilde{\tilde{\mathbf{T}}}}_{2,2},\cdots ,{\widetilde{\tilde{\mathbf{T}}}}_{2,m},\cdots {\widetilde{\tilde{\mathbf{T}}}}_{n,m})$, with ${\widetilde{\tilde{\mathbf{T}}}}_{j,k}$, $j=1,\cdots ,n$, $k=1,\cdots ,m$ being $l\times l$ tridiagonal matrices of the form:

$$\begin{array}{cc}\hfill {\widetilde{\tilde{\mathbf{T}}}}_{j,k}& =\left[\begin{array}{ccccc}{\tilde{\lambda }}_{1,i,k}& -{\delta }_1& & & \\ -{\delta }_1& {\tilde{\lambda }}_{2,i,k}& -{\delta }_2& & \\ & ·& ·& ·& \\ & & -{\delta }_{l-1}& {\tilde{\lambda }}_{l-1,i,k}& -{\delta }_l\\ & & & -{\delta }_l& {\tilde{\lambda }}_{l,i,k}\end{array}\right]\hfill \end{array}$$

(26)

and ${\widetilde{\tilde{\mathbf{z}}}}^{{\mathbf{P}}_2}={\mathbf{P}}_2\widetilde{\tilde{\mathbf{z}}}$, ${\widetilde{\tilde{\mathbf{r}}}}^{{\mathbf{P}}_2}={\mathbf{P}}_2\widetilde{\tilde{\mathbf{r}}}$.

Taking into account the above equations and by applying permutation matrices in order to reorder the elements of the $\mathbf{Mz}=\mathbf{r}$ system, a fast solution for the preconditioner solve step can be obtained as shown in Algorithm 2.

Algorithm 2 Preconditioner solution for the thermal grid.

1: Partition vector $\mathbf{r}$ into $lm$ sub-vectors ${\mathbf{r}}_i$ of size n, and perform DCT-II transform (${\mathbf{Q}}_n^T{\mathbf{r}}_i$ ) on each sub-vector to obtain transformed vector $\tilde{\mathbf{r}}$. 2: Partition vector $\tilde{\mathbf{r}}$ into l sub-vectors $\widetilde{{\mathbf{r}}_i}$ of size $mn$, and permute each subvector by permutation $\mathbf{P}$, which orders elements as $1,n+1,\cdots ,(m-1)n+1,2,n+2,\cdots ,(m-1)n+2,\cdots ,n,n+n,\cdots ,(m-1)n+n$, in order to obtain vector ${\tilde{\mathbf{r}}}^{{\mathbf{P}}_1}$. 3: Partition vector ${\tilde{\mathbf{r}}}^{{\mathbf{P}}_1}$ into ln sub-vectors ${\widetilde{{\mathbf{r}}_{\mathbf{i}}}}^{{\mathbf{P}}_1}$ of size m, and perform DCT-II transform (${\mathbf{Q}}_m^T{\widetilde{{\mathbf{r}}_{\mathbf{i}}}}^{{\mathbf{P}}_1}$) on each sub-vector to obtain transformed vector $\widetilde{\tilde{\mathbf{r}}}$. 4: Permute vector $\widetilde{\tilde{\mathbf{r}}}$ by applying permutation ${\mathbf{P}}_2$, which orders elements as $1,mn+1,2mn+1,\cdots ,(l-1)mn+1,2,mn+2,2mn+2,\cdots ,(l-1)mn+2,\cdots ,mn,mn+mn,2mn+mn,\cdots ,(l-1)mn+mn$, in order to obtain vector ${\widetilde{\tilde{\mathbf{r}}}}^{{\mathbf{P}}_2}$. 5: Calculate elements of matrices ${\tilde{\mathbf{T}}}_{n,m}$, and solve the $mn$ tridiagonal systems, in order to obtain vector ${\widetilde{\tilde{\mathbf{z}}}}^{{\mathbf{P}}_2}$. 6: Apply inverse permutation ${\mathbf{P}}_2^T$ on vector ${\widetilde{\tilde{\mathbf{z}}}}^{{\mathbf{P}}_2}$ so as to obtain vector $\widetilde{\tilde{\mathbf{z}}}$. 7: Partition vector $\widetilde{\tilde{\mathbf{z}}}$ into $ln$ sub-vectors $\tilde{\widetilde{{\mathbf{z}}_i}}$ of size m, and perform IDCT-II transform (${\mathbf{Q}}_m\tilde{\widetilde{{\mathbf{z}}_i}}$) on each sub-vector to obtain vector ${\tilde{\mathbf{z}}}^{{\mathbf{P}}_1}$. 8: Partition vector ${\tilde{\mathbf{z}}}^{{\mathbf{P}}_1}$ into l sub-vectors ${\widetilde{{\mathbf{z}}_i}}^{{\mathbf{P}}_1}$ of size $mn$, and apply inverse permutation ${\mathbf{P}}^T$ on each sub-vector to obtain vector $\tilde{\mathbf{z}}$. 9: Partition vector $\tilde{\mathbf{z}}$ into $lm$ sub-vectors $\widetilde{{\mathbf{z}}_i}$ of size n, and perform IDCT-II transform (${\mathbf{Q}}_n{\mathbf{z}}_i$) on each sub-vector to obtain final solution vector $\mathbf{z}$.

5. Methodology for Full Chip Thermal Analysis

This section applies the theoretical background that was analyzed before for the computation of the temperatures across the chip. The complete methodology consists of the following steps:

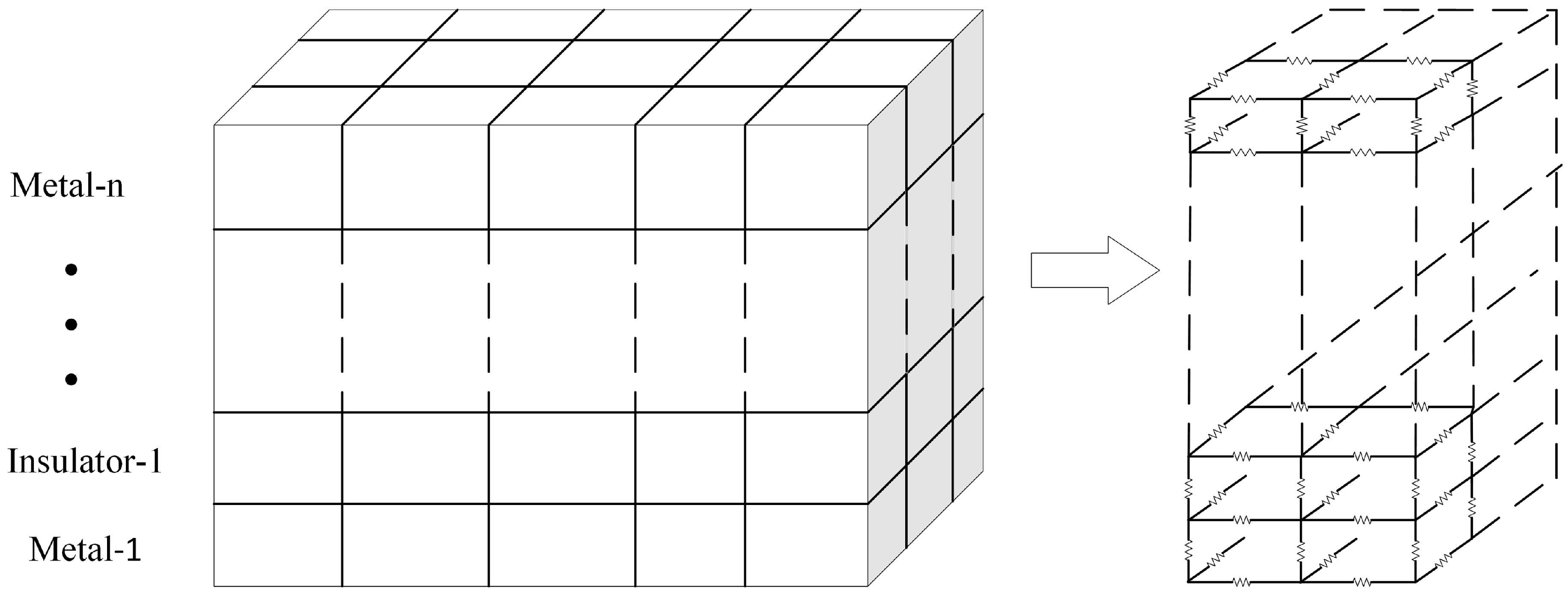
• 3D discretization of the chip: The spatial steps $\Delta x$, $\Delta y$ in the x- and y-direction are user defined, but the step $\Delta z$ along the z-direction is typically chosen to coincide with the interface between successive layers (metal and insulator). The discretization procedure naturally covers multiple layers in the z-direction and can be easily extended to model heterogeneous structures that can be found in modern chips (e.g., heat sinks).
• Construction of equivalent electrical circuit: The RC elements of the electrical equivalent are calculated by (7) and (8).
• Estimation of the power consumption profile of chip logic blocks. This determines the location and the time behavior of heat sources and the value of current sources (9) that constitute the vector $\mathbf{u}\left(t\right)$ in (10).
• Formulation of equivalent circuit description: Using modified nodal analysis, the equivalent circuit is described by the ODE system (10).
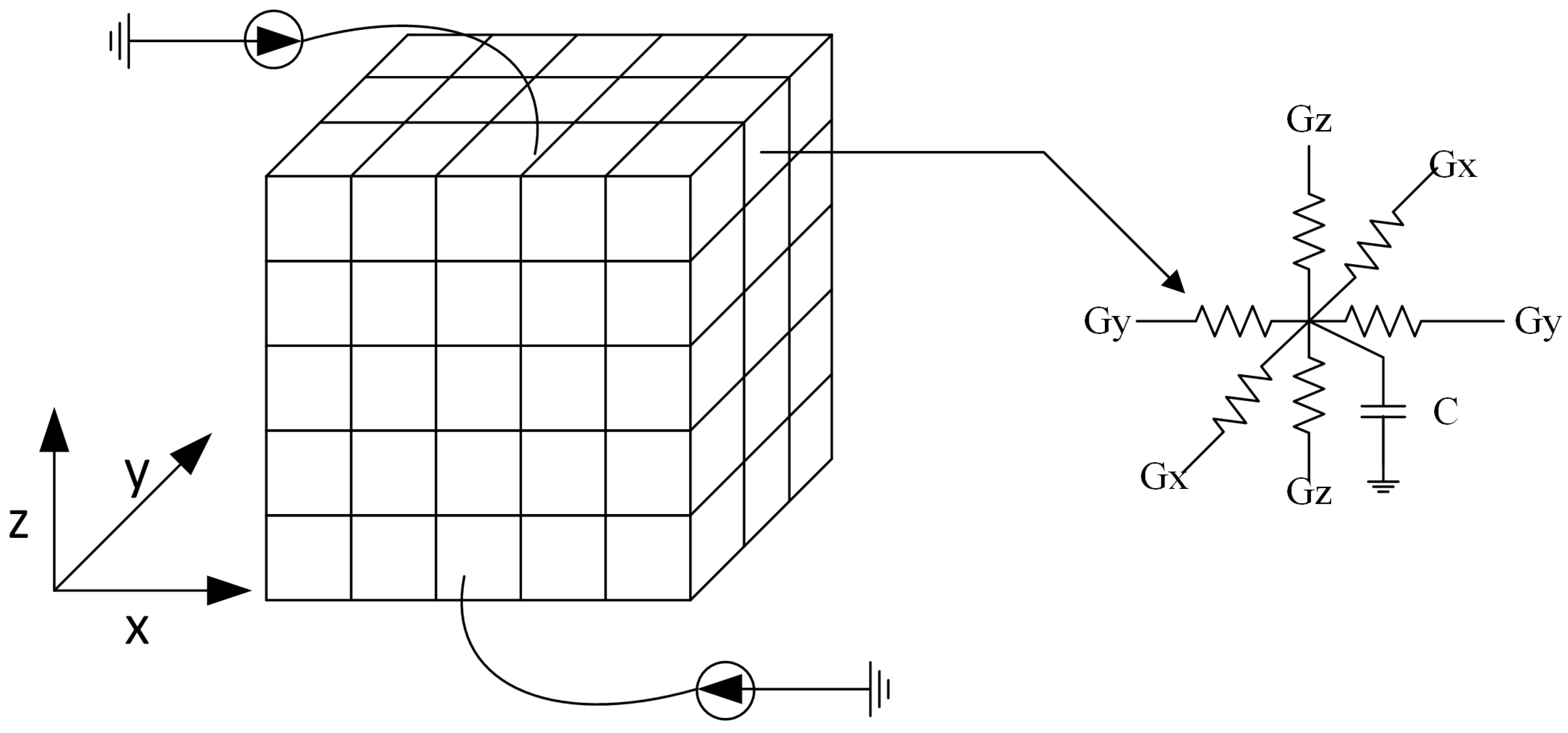
• Construction of the preconditioner matrix: Based on the algorithm described in the previous section, the preconditioner matrix is constructed based on [24], and the preconditioner-solve step is performed with the fast transform solver. More specifically, the thermal grid is equivalent to a highly regular resistive network, as depicted in Figure 2, with resistive branches connecting nodes in the x, y, and z axis. To create a preconditioner that will approximate the grid matrix, we substitute each horizontal and vertical thermal conductance with its average value in the corresponding layer. Moreover, we substitute each thermal conductance connecting nodes in adjacent layers (z axis) with their average value between the two layers.
• Compute either the DC or transient solution: The solution is obtained with the iterative PCG method in both cases. Note that in the case of the transient solution, the backward-Euler numerical integration method as in (11) is employed for the calculation of temperature in each discrete time instant. The convergence of the method is accelerated with the highly parallel fast transform solver that is used in preconditioner-solve step in Algorithm 1.

The proposed methodology offers significant advantages over the established thermal simulation methods. Firstly, iterative methods can handle large-scale problems in contrast to direct methods that do not scale well with the matrix dimension and can only be applied to a narrow range of problems. Furthermore, the fast preconditioned solution step exhibits near-optimal computational complexity, low memory requirements, and great potential for parallelism, which can harness the computational power of parallel architectures, such as multicore processors or GPUs, thus further reducing the amount of time required for simulation.

6. Experimental Results

Due to the lack of availability of benchmarks for full chip thermal analysis and in order to evaluate the efficiency of the proposed methodology for thermal simulation, we have created a set of artificial benchmark circuits that represent simplified microprocessor designs (like MIPS and LEON) with a random control logic and datapath, based on the theory described in Section 3. The technology node that was used for this work was 32 nm. Similarly, one can form the linear set of equations for different technology-specific parameters of Equations (7) and (8). Despite the fact that the benchmarks were artificially created, the problems that would arise from a real design would be represented by a similar set of linear equations.

In

Table 2. Runtime results for the three solvers. Bench. is the name of the benchmark, Discr. Point. is the number of points that correspond to the x and y axis, Layers is the number of layers of each chip and corresponds to the z axis, Time (s) denotes the average time required for the solution at each iteration, Iter. is the average number of iterations required for the convergence of each iterative method, while Speedup denotes the speedup of our method over the ICCG.

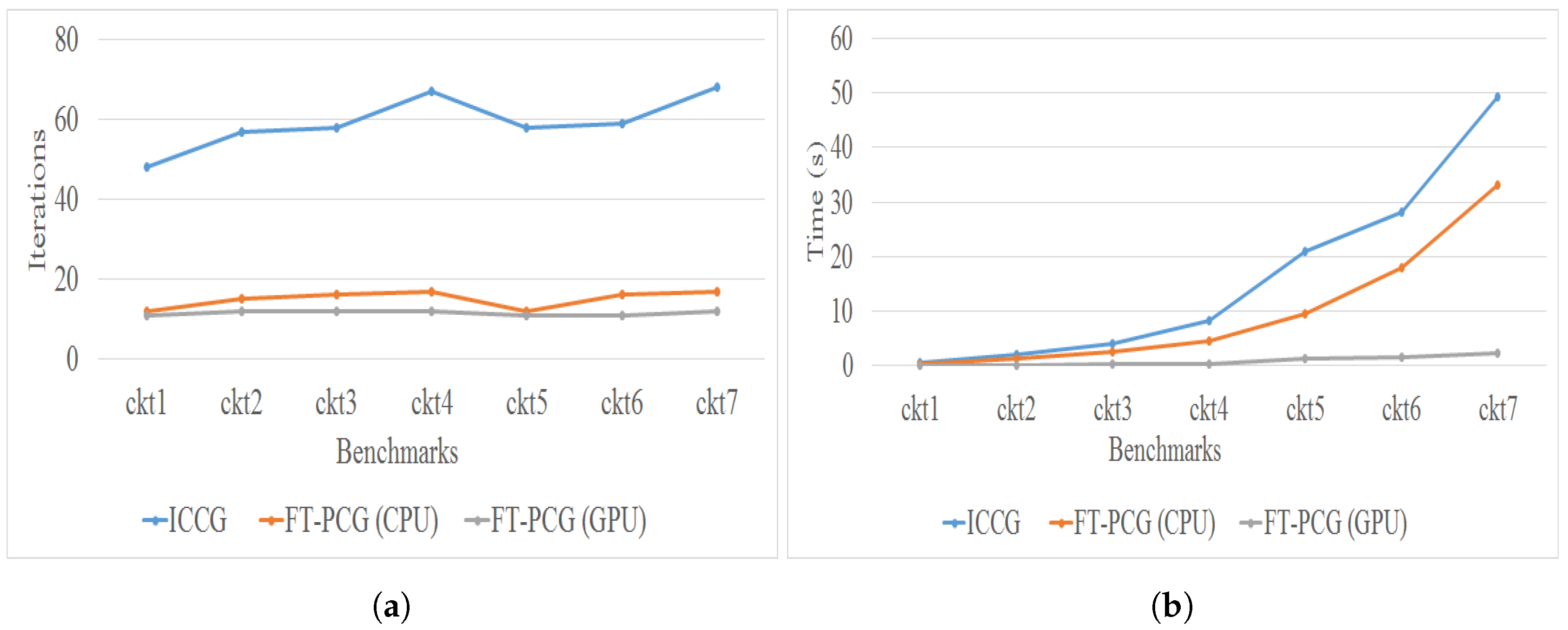
Bench.	Discr. Points	Layers	ICCG		FT-PCG (CPU)			FT-PCG (GPU)
			Iter.	Time (s)	Iter.	Time (s)	Speedup	Iter.	Time (s)	Speedup
ckt1	175	5	48	0.48	12	0.31	1.54×	11	0.03	16×
ckt2	320	5	57	1.98	15	1.23	1.6×	12	0.08	24.75×
ckt3	410	6	58	4.20	16	2.64	1.59×	12	0.23	18.26×
ckt4	500	7	67	8.35	17	4.51	1.85×	12	0.31	26.93×
ckt5	845	7	58	21.07	12	9.48	2.22×	11	1.34	15.72×
ckt6	946	7	59	28.27	16	17.94	1.57×	11	1.60	17.65×
ckt7	1118	8	68	49.35	17	33.07	1.49×	12	2.39	20.64×

discretization points are the number of discretizations in each axis, while layers are the number of layers that each benchmark has. Moreover, the matrix dimensions can be calculated by multiplying the square of the discretization points by the number of layers. All experiments were executed on a Linux workstation, comprised of an Intel Core i7 processor running at 2.4 GHz (six cores and 24 GB main memory) and an NVIDIA Tesla C2075 GPU with 6 GB of main memory. We have used the CUDA library [28] (Version 5.5, along with the CUBLAS, CUSPARSE, and CUFFT libraries) for mapping the proposed Fast-Transform PCG (FT-PCG) algorithm on the GPU. The ICCG was executed on the CPU since it would not be beneficial to port it on the GPU due many irregular memory transfers. The convergence tolerance ($tol$) for iterative solvers was set to ${10}^{-6}$, which is typically sufficient to yield perfect accuracy, and convergence was achieved in all cases. Table 2 presents the results from the evaluation of the aforementioned methods on the set of benchmark circuits. The number Iter. is the number of iterations that the algorithm needed to converge, while Time (s) refers to the time in seconds that were needed to compute the final solution. Both the number of iterations and time represent either the DC solution of the system or the average iterations and time of a time instant in transient analysis.

Comparing the iterative methods, it can be observed that the proposed method was able to reduce the number of iterations required for convergence greatly, as shown in Figure 3a. Compared with general purpose preconditioning methods such as ICCG, the proposed preconditioners take into account the topology characteristics of the thermal grid. As a result, they are able to approximate it faithfully enough and reduce the required number of iterations. Moreover, owing to their inherent parallelism, the proposed preconditioners can utilize the vast amount of computational resources found in massively-parallel architectures, such as GPUs. Thus, their efficiency is increased with the increasing circuit size, by greatly reducing the runtime for each time-step, as depicted in Figure 3b. FT-PCG was able to achieve a speed-up ranging between 1.5× and 2.2× in CPU execution and 16× and 26.93× in GPU execution over ICCG.

7. Conclusions

In this paper, we presented a fast thermal simulation method based on the RC equivalent, which uses fast transform solvers and preconditioned Krylov-subspace iterative solvers. The preconditioned iterative solvers offer linear scaling in simulation time as the thermal grid is increased. Experimental evaluation of the proposed method on a set of thermal benchmarks with the size ranging from 0.15 M–10 M nodes showed that the proposed methodology achieved a speedup ranging between 15.72× and 26.93× over a preconditioned iterative method with an incomplete Cholesky factorization preconditioner when GPUs are utilized.