Design of a Quick Switching Sampling System Based on the Coefficient of Variation
Abstract
1. Introduction
2. QSS System Based on CV
The Proposed Methodology
- (1)
- Step 1: Begin with the normal inspection. Take a random sample of size from the lot and compute.
- (2)
- Step 2: Accept the lot if and continue the normal inspection for the next lot, where is the critical acceptance value under the normal inspection. Otherwise, switch to the tightened inspection as in Step 3 for the next lot.
- (3)
- Step 3: During the tightened inspection, take a random sample of size from the lot and compute.
- (4)
- Step 4: Accept the lot if and switch to the normal inspection as in Step 1 for the next lot, where is the critical acceptance value under the tightened inspection and < Otherwise, continue the tightened inspection as in Step 3 for the next lot.
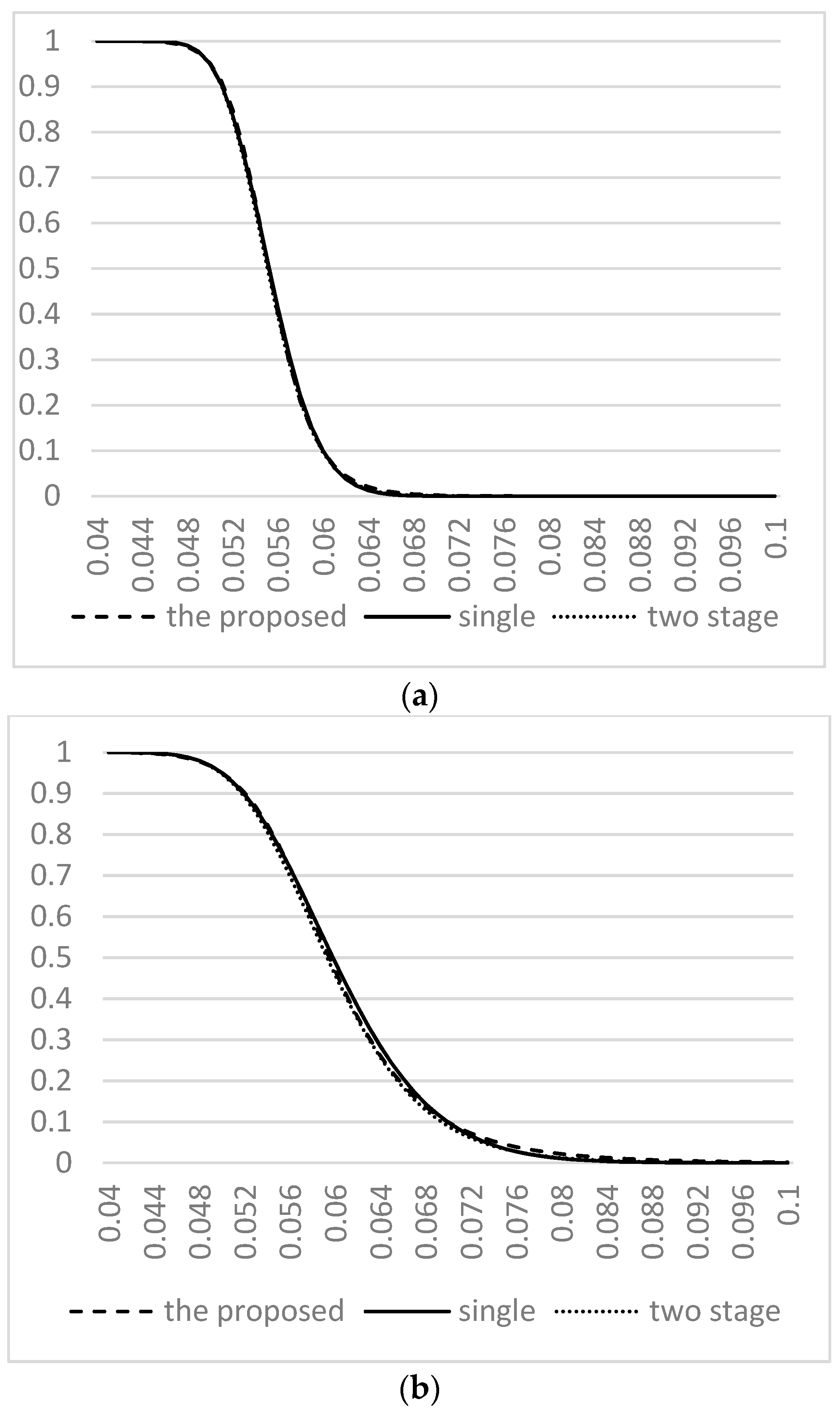
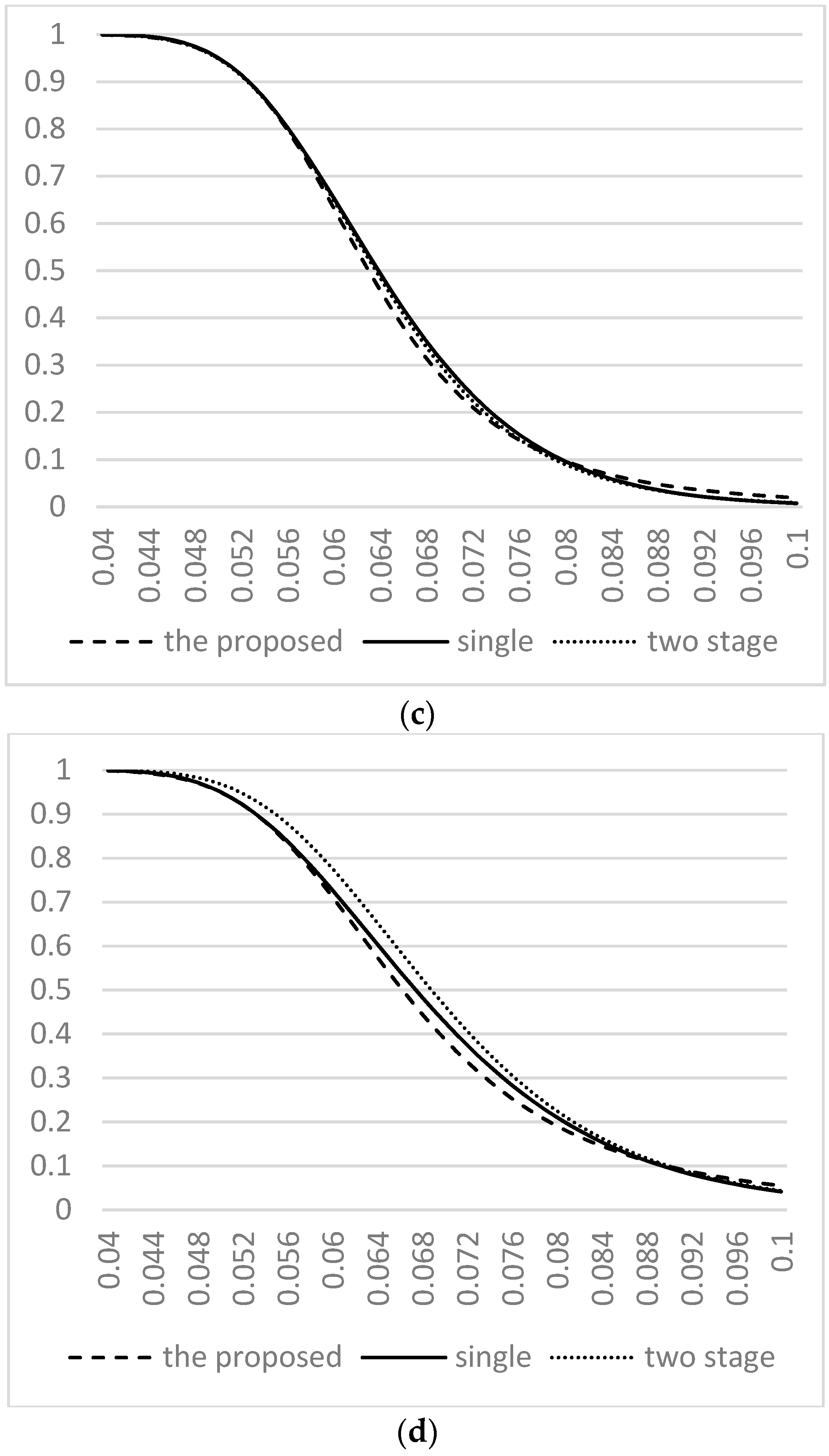
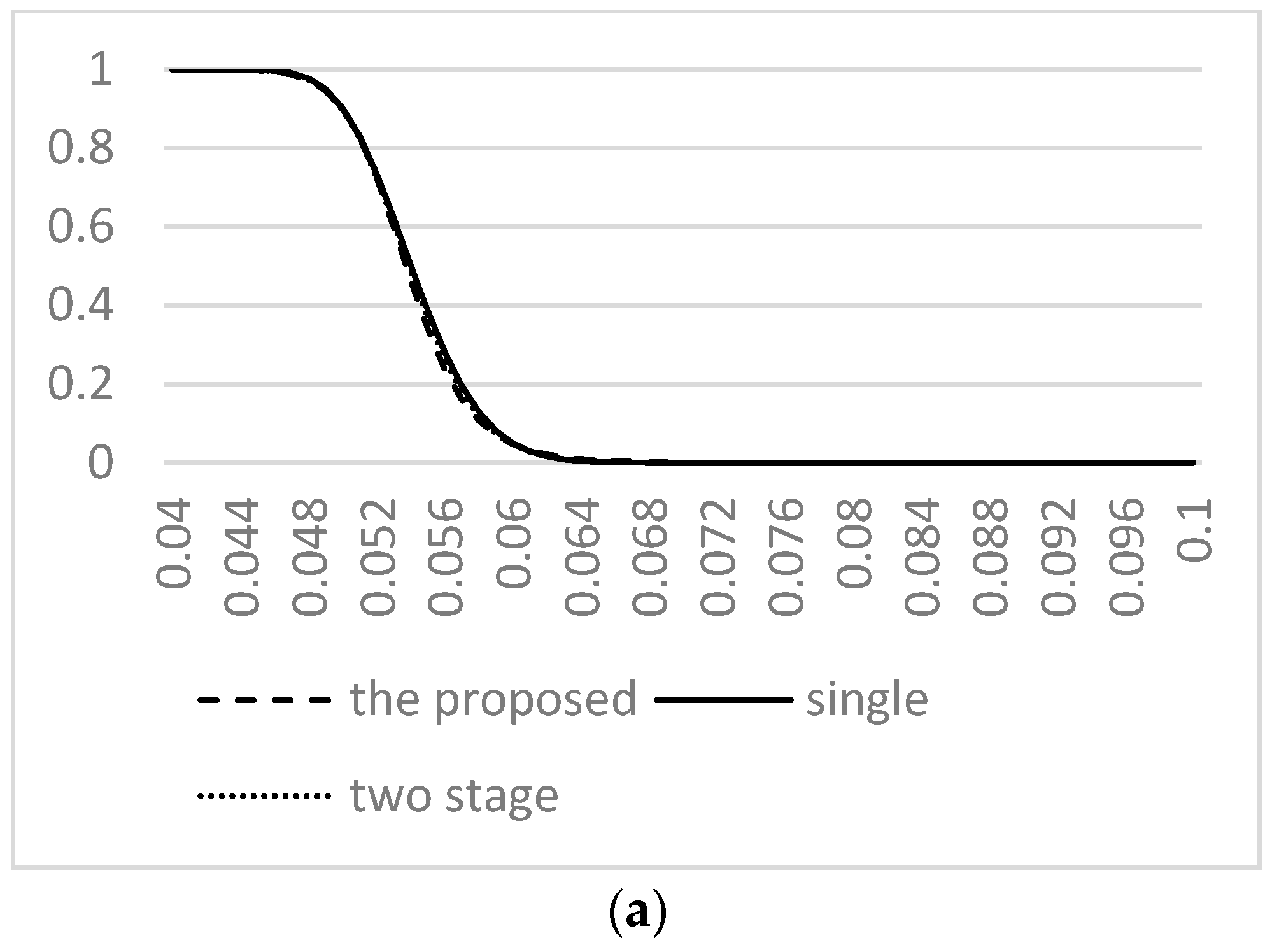
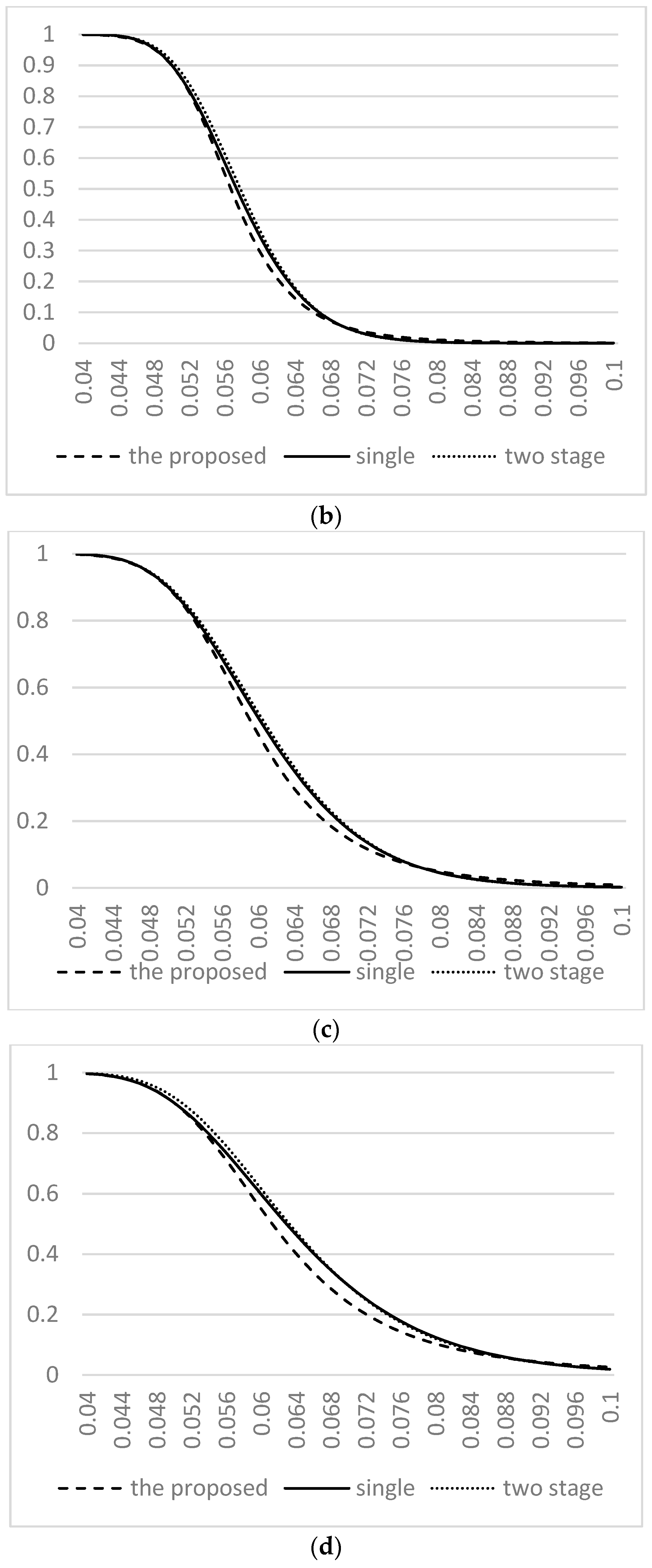
3. Comparison and Analysis
4. An Example in Industry
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Montgomery, D.C. Introduction to Statistical Quality Control; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Balamurali, S.; Jun, C. Repetitive group sampling procedure for variables inspection. J. Appl. Stat. 2006, 33, 327–338. [Google Scholar] [CrossRef]
- Wu, C.-W.; Pearn, W.L. A variables sampling plan based on Cpmk for product acceptance determination. Eur. J. Oper. Res. 2008, 184, 549–560. [Google Scholar] [CrossRef]
- Yen, C.-H.; Aslam, M.; Jun, C.-H. A lot inspection sampling plan based on EWMA yield index. Int. J. Adv. Manuf. Technol. 2014, 75, 861–868. [Google Scholar] [CrossRef]
- Kurniati, N.; Yeh, R.-H.; Wu, C.-W. A sampling scheme for resubmitted lots based on one-sided capability indices. Qual. Technol. Quant. Manag. 2015, 12, 501–515. [Google Scholar] [CrossRef]
- Aslam, M.; Azam, M.; Jun, C.-H. Acceptance sampling plans for multi-stage process based on time-truncated test for weibull distribution. Int. J. Adv. Manuf. Technol. 2015, 79, 1779–1785. [Google Scholar] [CrossRef]
- Dodge, H.F. A New Dual System of Acceptance Sampling; The Statistics Center, Technical Report No. 16; The Statistics Center, Rutgers—The State University: New Brunswick, NJ, USA, 1967. [Google Scholar]
- Romboski, L.D. An Investigation of Quick Switching Acceptance Sampling System. Ph.D. Thesis, Rutgers–The State University, New Jersey, NJ, USA, 1969. [Google Scholar]
- Calvin, T.W. TNT Zero Acceptance Number Sampling. Available online: http://asq.org/qic/display-item/index.html?item=1973 (accessed on 28 October 2018).
- Soundararajan, V.; Vijayaraghavan, R. Construction and selection of tightened-normal-tightened sampling inspection scheme of type TNT-(n1, n2; c). J. Appl. Stat. 1992, 19, 339–349. [Google Scholar] [CrossRef]
- Vijayaraghavan, R.; Soundararajan, V. Procedures and tables for the selection of tightened-normal-tightened (TNT-(n; c 1, c 2)) sampling schemes. J. Appl. Stat. 1996, 23, 69–80. [Google Scholar] [CrossRef]
- Muthuraj, D.; Senthilkumar, D. Designing and construction of tightened-normal-tightened variables sampling scheme. J. Appl. Stat. 2006, 33, 101–111. [Google Scholar] [CrossRef]
- Senthilkumar, D.; Muthuraj, D. Construction and selection of tightened–normal–tightened variables sampling scheme of type TNTVSS (n1, n2; k). J. Appl. Stat. 2010, 37, 375–390. [Google Scholar] [CrossRef]
- Aslam, M.; Balamurali, S.; Jun, C.-H.; Ahmad, M. A two-plan sampling system for life testing under weibull distribution. Ind. Eng. Manag. Syst. 2010, 9, 54–59. [Google Scholar] [CrossRef]
- Castagliola, P.; Amdouni, A.; Taleb, H.; Celano, G. One-sided shewhart-type charts for monitoring the coefficient of variation in short production runs. Qual. Technol. Quant. Manag. 2015, 12, 53–67. [Google Scholar] [CrossRef]
- Gomez, K.A.; Gomez, K.A.; Gomez, A.A. Statistical Procedures for Agricultural Research; John Wiley and Sons: Hoboken, NJ, USA, 1984. [Google Scholar]
- Steel, R.G.D.; Torrie, J.H. Principles and Procedures of Statistics: A Biometrical Approach, 2nd ed.; McGraw-Hill: New York, NY, USA, 1980. [Google Scholar]
- Taye, G.; Njuho, P. Monitoring field variability using confidence interval for coefficient of variation. Commun. Stat. Theory Methods 2008, 37, 831–846. [Google Scholar] [CrossRef]
- Kang, C.W.; Lee, M.S.; Seong, Y.J. A Control Chart for the Coefficient of Variation. J. Qual. Technol. 2007, 39, 151–158. [Google Scholar] [CrossRef]
- Calzada, M.E.; Scariano, S.M. A synthetic control chart for the coefficient of variation. J. Stat. Comput. Simul. 2013, 83, 853–867. [Google Scholar] [CrossRef]
- Tong, Y.; Chen, Q. Sampling inspection by variables for coefficient of variation. Math. Theory Appl. Probab. 1991, 3, 315–327. [Google Scholar]
- Wang, J.Q.; Xiao, H.G. A variable single sampling inspection using the coefficient of variation as the quality index. J. Quant. Tech. Econ. 2001, 3, 117–119. [Google Scholar]
- Yan, A.; Liu, S.; Dong, X. Designing a multiple dependent state sampling plan based on the coefficient of variation. SpringerPlus 2016, 5, 1447. [Google Scholar] [CrossRef] [PubMed]
- Yan, A.; Liu, S.; Dong, X. Variables two stage sampling plans based on the coefficient of variation. J. Adv. Mech. Des. Syst. 2016, 10. [Google Scholar] [CrossRef]
- Iglewicz, B.; Myers, R.; Howe, R. On the percentage points of the sample coefficient of variation. Biometrika 1968, 55, 580–581. [Google Scholar] [CrossRef]
| n | kT | kN | ||
|---|---|---|---|---|
| 0.05 | 0.06 | 50 | 0.0501 | 0.0597 |
| 0.07 | 14 | 0.0472 | 0.0695 | |
| 0.08 | 8 | 0.0449 | 0.0766 | |
| 0.09 | 6 | 0.0449 | 0.0806 | |
| 0.10 | 5 | 0.0448 | 0.0836 | |
| 0.06 | 0.07 | 69 | 0.0601 | 0.0699 |
| 0.08 | 19 | 0.0576 | 0.0798 | |
| 0.09 | 10 | 0.0549 | 0.0883 | |
| 0.10 | 7 | 0.053 | 0.0945 | |
| 0.11 | 6 | 0.0519 | 0.0977 | |
| 0.07 | 0.08 | 92 | 0.0703 | 0.0799 |
| 0.09 | 25 | 0.0684 | 0.0898 | |
| 0.10 | 13 | 0.0659 | 0.0984 | |
| 0.11 | 8 | 0.0611 | 0.1082 | |
| 0.12 | 7 | 0.0651 | 0.1089 | |
| 0.08 | 0.09 | 118 | 0.0804 | 0.0899 |
| 0.10 | 32 | 0.079 | 0.0998 | |
| 0.11 | 16 | 0.0768 | 0.1088 | |
| 0.12 | 10 | 0.073 | 0.118 | |
| 0.13 | 8 | 0.0739 | 0.1219 | |
| 0.09 | 0.10 | 151 | 0.0906 | 0.0999 |
| 0.11 | 40 | 0.0894 | 0.1098 | |
| 0.12 | 19 | 0.0866 | 0.1198 | |
| 0.13 | 14 | 0.0893 | 0.1236 | |
| 0.14 | 9 | 0.0819 | 0.1352 |
| n | kT | kN | ||
|---|---|---|---|---|
| 0.05 | 0.06 | 43 | 0.0471 | 0.0598 |
| 0.07 | 13 | 0.0423 | 0.0691 | |
| 0.08 | 9 | 0.0432 | 0.0714 | |
| 0.09 | 7 | 0.0436 | 0.0735 | |
| 0.10 | 6 | 0.0448 | 0.0745 | |
| 0.06 | 0.07 | 60 | 0.0574 | 0.0698 |
| 0.08 | 17 | 0.0522 | 0.0799 | |
| 0.09 | 11 | 0.0524 | 0.0834 | |
| 0.10 | 8 | 0.0513 | 0.0873 | |
| 0.11 | 7 | 0.0537 | 0.0875 | |
| 0.07 | 0.08 | 80 | 0.0674 | 0.0799 |
| 0.09 | 23 | 0.0635 | 0.0892 | |
| 0.10 | 15 | 0.062 | 0.937 | |
| 0.11 | 10 | 0.0624 | 0.0977 | |
| 0.12 | 8 | 0.0624 | 0.1005 | |
| 0.08 | 0.09 | 103 | 0.0776 | 0.0899 |
| 0.10 | 29 | 0.0738 | 0.0994 | |
| 0.11 | 16 | 0.071 | 0.1064 | |
| 0.12 | 12 | 0.0719 | 0.1091 | |
| 0.13 | 9 | 0.0706 | 0.1136 | |
| 0.09 | 0.10 | 129 | 0.0877 | 0.0999 |
| 0.11 | 36 | 0.0842 | 0.1094 | |
| 0.12 | 19 | 0.0814 | 0.1169 | |
| 0.13 | 14 | 0.0825 | 0.1199 | |
| 0.14 | 11 | 0.0819 | 0.1235 |
| n | kT | kN | ||
|---|---|---|---|---|
| 0.05 | 0.06 | 54 | 0.0486 | 0.0599 |
| 0.07 | 16 | 0.0451 | 0.0693 | |
| 0.08 | 9 | 0.042 | 0.0766 | |
| 0.09 | 7 | 0.0423 | 0.0796 | |
| 0.10 | 6 | 0.0436 | 0.0812 | |
| 0.06 | 0.07 | 76 | 0.0588 | 0.0699 |
| 0.08 | 22 | 0.059 | 0.0792 | |
| 0.09 | 12 | 0.0534 | 0.0867 | |
| 0.10 | 9 | 0.0537 | 0.0903 | |
| 0.11 | 7 | 0.0524 | 0.0948 | |
| 0.07 | 0.08 | 103 | 0.0689 | 0.0799 |
| 0.09 | 29 | 0.0664 | 0.0893 | |
| 0.10 | 15 | 0.0636 | 0.0976 | |
| 0.11 | 10 | 0.0607 | 0.1047 | |
| 0.12 | 8 | 0.0607 | 0.1084 | |
| 0.08 | 0.09 | 132 | 0.0791 | 0.0899 |
| 0.10 | 36 | 0.0765 | 0.0997 | |
| 0.11 | 18 | 0.0731 | 0.1089 | |
| 0.12 | 12 | 0.0709 | 0.1159 | |
| 0.13 | 10 | 0.0732 | 0.1179 | |
| 0.09 | 0.10 | 167 | 0.0892 | 0.0999 |
| 0.11 | 46 | 0.0873 | 0.1093 | |
| 0.12 | 22 | 0.0837 | 0.1191 | |
| 0.13 | 14 | 0.0806 | 0.1274 | |
| 0.14 | 11 | 0.0809 | 0.1316 |
| n | kT | kN | ||
|---|---|---|---|---|
| 0.05 | 0.06 | 37 | 0.0484 | 0.0598 |
| 0.07 | 11 | 0.044 | 0.0693 | |
| 0.08 | 7 | 0.0431 | 0.0738 | |
| 0.09 | 6 | 0.0469 | 0.0735 | |
| 0.10 | 5 | 0.047 | 0.0756 | |
| 0.06 | 0.07 | 52 | 0.0586 | 0.0698 |
| 0.08 | 15 | 0.0549 | 0.0794 | |
| 0.09 | 9 | 0.0529 | 0.0851 | |
| 0.10 | 7 | 0.0554 | 0.0867 | |
| 0.11 | 6 | 0.0578 | 0.0876 | |
| 0.07 | 0.08 | 69 | 0.0687 | 0.799 |
| 0.09 | 19 | 0.065 | 0.0899 | |
| 0.10 | 11 | 0.0638 | 0.0959 | |
| 0.11 | 8 | 0.063 | 0.1002 | |
| 0.12 | 6 | 0.0605 | 0.1056 | |
| 0.08 | 0.09 | 90 | 0.0789 | 0.0899 |
| 0.10 | 25 | 0.0762 | 0.0994 | |
| 0.11 | 13 | 0.0731 | 0.1075 | |
| 0.12 | 9 | 0.0718 | 0.113 | |
| 0.13 | 7 | 0.0706 | 0.1174 | |
| 0.09 | 0.10 | 113 | 0.089 | 0.0999 |
| 0.11 | 31 | 0.0866 | 0.1094 | |
| 0.12 | 16 | 0.0842 | 0.1174 | |
| 0.13 | 11 | 0.0835 | 0.1227 | |
| 0.14 | 8 | 0.0803 | 0.1294 |
| Quality Level | α = 0.05, β = 0.1 | α = 0.1, β = 0.05 | |||||
|---|---|---|---|---|---|---|---|
| Single | Two Stage | The Proposed | Single | Two Stage | The Proposed | ||
| n | ASN | n | n | ASN | n | ||
| 0.05 | 0.06 | 131 | 104.34 | 50 | 134 | 106.65 | 43 |
| 0.07 | 39 | 32.35 | 14 | 41 | 35.64 | 13 | |
| 0.08 | 20 | 17.42 | 8 | 23 | 19.71 | 9 | |
| 0.09 | 14 | 12.32 | 6 | 15 | 13.15 | 7 | |
| 0.10 | 11 | 8.78 | 5 | 12 | 10.14 | 6 | |
| 0.06 | 0.07 | 182 | 149.3 | 69 | 186 | 160 | 60 |
| 0.08 | 53 | 47.10 | 19 | 56 | 47.41 | 17 | |
| 0.09 | 28 | 22.88 | 10 | 28 | 26.23 | 11 | |
| 0.10 | 17 | 15.03 | 7 | 20 | 16.70 | 8 | |
| 0.11 | 14 | 11.30 | 6 | 15 | 11.87 | 7 | |
| 0.07 | 0.08 | 242 | 201.85 | 92 | 248 | 208.45 | 80 |
| 0.09 | 69 | 57.36 | 25 | 72 | 62.22 | 23 | |
| 0.10 | 35 | 28.41 | 13 | 36 | 33.61 | 15 | |
| 0.11 | 23 | 19.71 | 8 | 25 | 20.74 | 10 | |
| 0.12 | 17 | 14.04 | 7 | 17 | 15.23 | 8 | |
| 0.08 | 0.09 | 311 | 271.33 | 118 | 318 | 256.93 | 103 |
| 0.10 | 88 | 71.48 | 32 | 91 | 76.48 | 29 | |
| 0.11 | 44 | 38.55 | 16 | 46 | 39.42 | 16 | |
| 0.12 | 28 | 23.28 | 10 | 30 | 24.65 | 12 | |
| 0.09 | 0.10 | 327 | 317.43 | 151 | 336 | 324.45 | 129 |
| 0.11 | 109 | 92.62 | 40 | 112 | 93.51 | 36 | |
| 0.12 | 55 | 43.41 | 19 | 56 | 48.63 | 19 | |
| Quality Level | The Proposed Method | Two Stage Sampling | ||||||
|---|---|---|---|---|---|---|---|---|
| CVAQL | CVLTPD | n | kT | kN | n1 = n2 = n | ka1 | ka2 | kr |
| 0.05 | 0.06 | 50 | 0.0501 | 0.0597 | 90 | 0.0535 | 0.0540 | 0.0569 |
| 0.07 | 14 | 0.0472 | 0.0695 | 28 | 0.0558 | 0.0570 | 0.0625 | |
| 0.08 | 8 | 0.0449 | 0.0766 | 15 | 0.0561 | 0.0658 | 0.0658 | |
| 0.09 | 6 | 0.0449 | 0.0806 | 10 | 0.0556 | 0.0703 | 0.0735 | |
| 0.10 | 5 | 0.0448 | 0.0836 | 7 | 0.0533 | 0.0723 | 0.0751 | |
| The Proposed Method | |||||||||||||
| Quality Level | The Probability of Acceptance or Rejection under CVAQL | The Probability of Acceptance or Rejection under CVLTPD | |||||||||||
| CVAQL | CVLTPD | NA | NR | TA | TR | AP | ASN | NA | NR | TA | TR | LP | ASN |
| 0.05 | 0.06 | 0.9188 | 0.0289 | 0.0289 | 0.0234 | 0.9477 | 50.00 | 0.0484 | 0.0477 | 0.0476 | 0.8563 | 0.096 | 50.00 |
| 0.07 | 0.9263 | 0.0215 | 0.0215 | 0.0307 | 0.9478 | 14.00 | 0.0544 | 0.0444 | 0.0443 | 0.8569 | 0.0987 | 14.00 | |
| 0.08 | 0.9305 | 0.0213 | 0.0213 | 0.0269 | 0.9518 | 8.00 | 0.0532 | 0.0502 | 0.0501 | 0.8465 | 0.1033 | 8.00 | |
| 0.09 | 0.9257 | 0.0223 | 0.0223 | 0.0297 | 0.948 | 6.00 | 0.0483 | 0.0557 | 0.0557 | 0.8403 | 0.104 | 6.00 | |
| 0.10 | 0.9273 | 0.0235 | 0.0235 | 0.0257 | 0.9508 | 5.00 | 0.0421 | 0.0595 | 0.0594 | 0.839 | 0.1015 | 5.00 | |
| Two Stage Sampling Plan | |||||||||||||
| Quality Level | The Probability of Acceptance or Rejection under CVAQL | The Probability of Acceptance or Rejection under CVLTPD | |||||||||||
| CVAQL | CVLTPD | FA | FR | SA | SR | AP | ASN | FA | FR | SA | SR | LP | ASN |
| 0.05 | 0.06 | 0.8351 | 0.0359 | 0.1034 | 0.0256 | 0.9385 | 101.61 | 0.0733 | 0.7401 | 0.0093 | 0.1773 | 0.0826 | 106.79 |
| 0.07 | 0.8226 | 0.0365 | 0.1125 | 0.0284 | 0.9351 | 31.95 | 0.0708 | 0.7534 | 0.0088 | 0.167 | 0.0796 | 32.92 | |
| 0.08 | 0.7833 | 0.0463 | 0.1675 | 0.0029 | 0.9508 | 17.56 | 0.0642 | 0.7995 | 0.037 | 0.0993 | 0.1012 | 17.04 | |
| 0.09 | 0.7247 | 0.0225 | 0.2489 | 0.0039 | 0.9736 | 12.53 | 0.0597 | 0.7339 | 0.0604 | 0.146 | 0.1201 | 12.06 | |
| 0.10 | 0.6609 | 0.0372 | 0.2963 | 0.0056 | 0.9572 | 9.11 | 0.0546 | 0.758 | 0.0554 | 0.132 | 0.11 | 8.31 | |
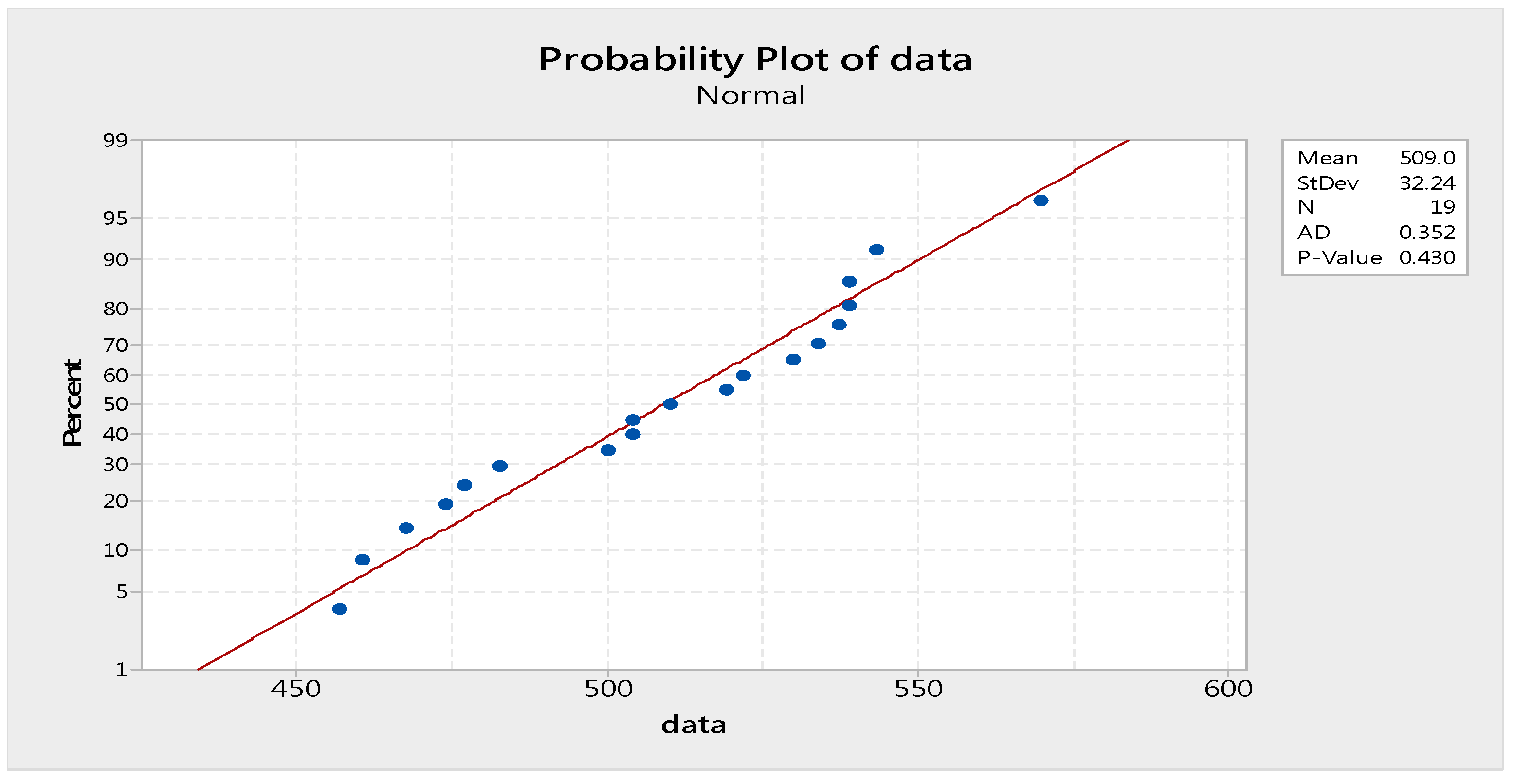
| 519.21 | 537.28 | 482.7 | 533.78 | 460.56 | 504.2 | 504.22 |
| 476.83 | 467.39 | 510.01 | 473.92 | 539.05 | 456.92 | 569.96 |
| 530.03 | 539.1 | 543.41 | 500.11 | 521.86 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yen, C.-H.; Aslam, M.; Chang, C.-H.; Khan, M.Z.; Jun, C.-H. Design of a Quick Switching Sampling System Based on the Coefficient of Variation. Technologies 2018, 6, 98. https://doi.org/10.3390/technologies6040098
Yen C-H, Aslam M, Chang C-H, Khan MZ, Jun C-H. Design of a Quick Switching Sampling System Based on the Coefficient of Variation. Technologies. 2018; 6(4):98. https://doi.org/10.3390/technologies6040098
Chicago/Turabian StyleYen, Ching-Ho, Muhammad Aslam, Chia-Hao Chang, Muhammad Zahir Khan, and Chi-Hyuck Jun. 2018. "Design of a Quick Switching Sampling System Based on the Coefficient of Variation" Technologies 6, no. 4: 98. https://doi.org/10.3390/technologies6040098
APA StyleYen, C.-H., Aslam, M., Chang, C.-H., Khan, M. Z., & Jun, C.-H. (2018). Design of a Quick Switching Sampling System Based on the Coefficient of Variation. Technologies, 6(4), 98. https://doi.org/10.3390/technologies6040098





