Filling the Joints: Completion and Recovery of Incomplete 3D Human Poses †
Abstract
1. Introduction
2. Literature Overview
3. Design of Comparative Study
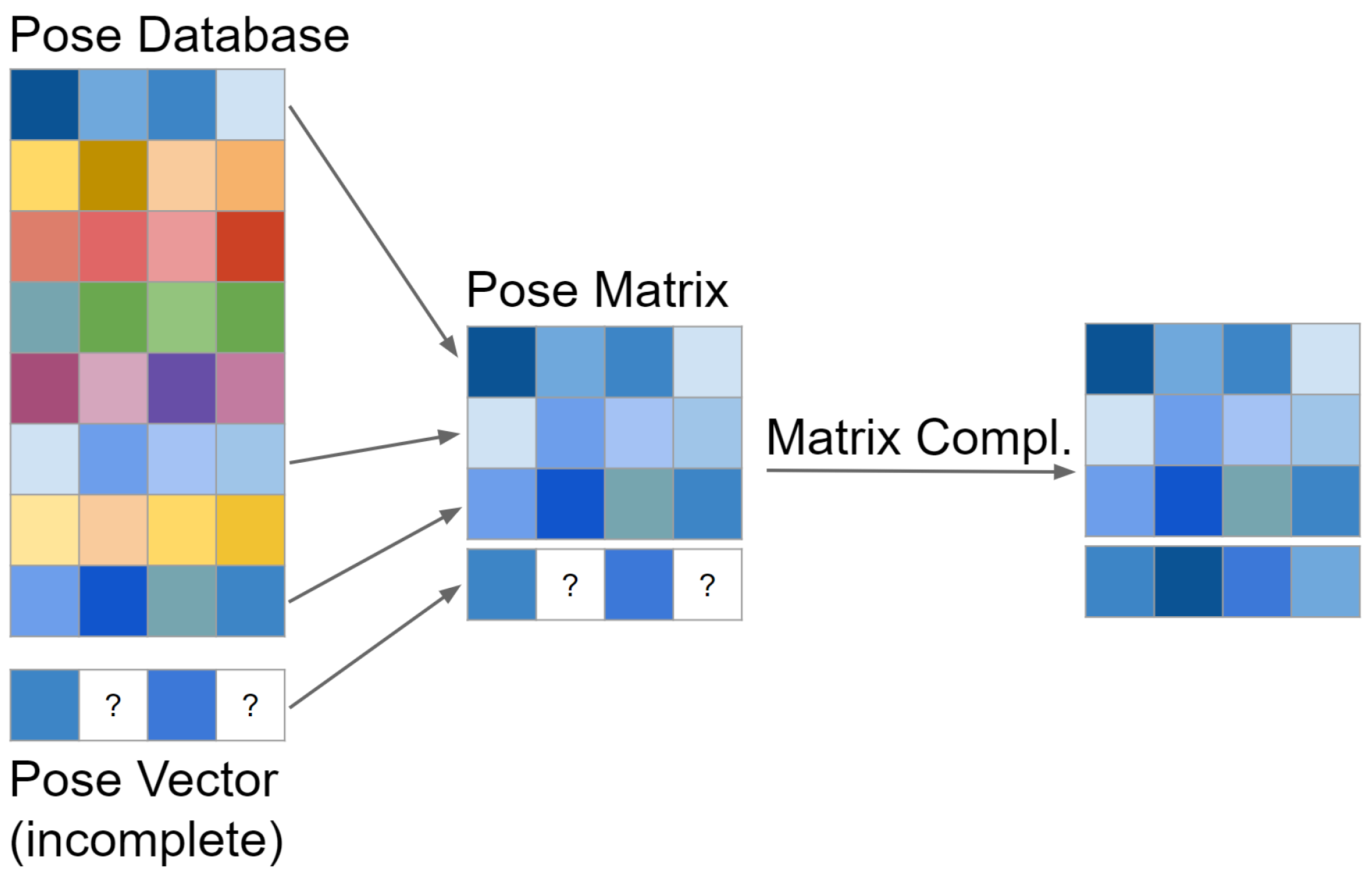
3.1. Matrix Completion and Recovery
3.1.1. Inversion-Based Matrix Completion (IBMC)
3.1.2. Gradient Descent Matrix Completion (GDMC)
3.1.3. Matrix Recovery with Lagrange Multipliers (MRLM)
3.2. Conducting the Experiments
3.2.1. Simulated Experiments
3.2.2. Real World Experiments
4. Results
4.1. Results from Simulation Experiments
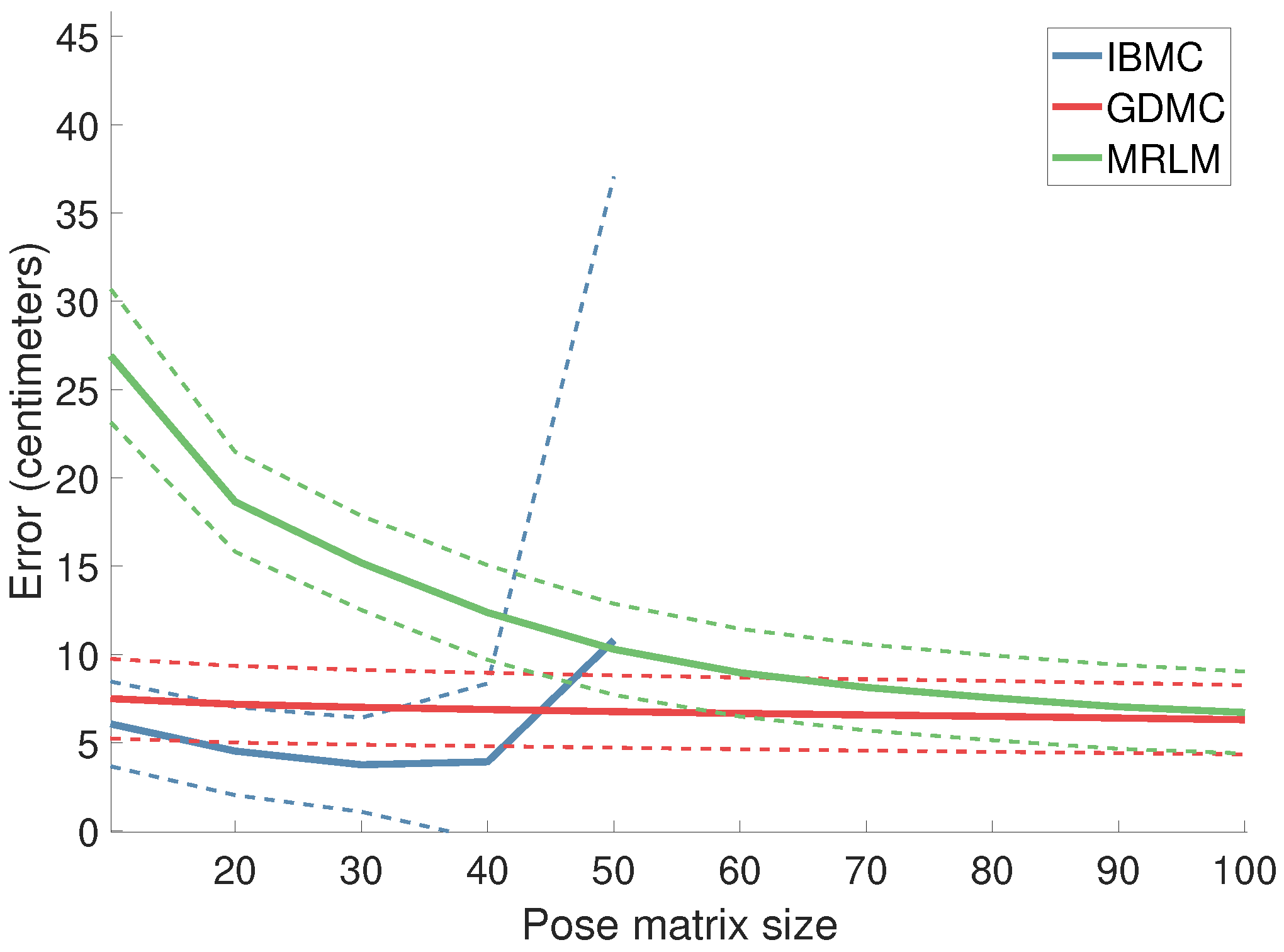
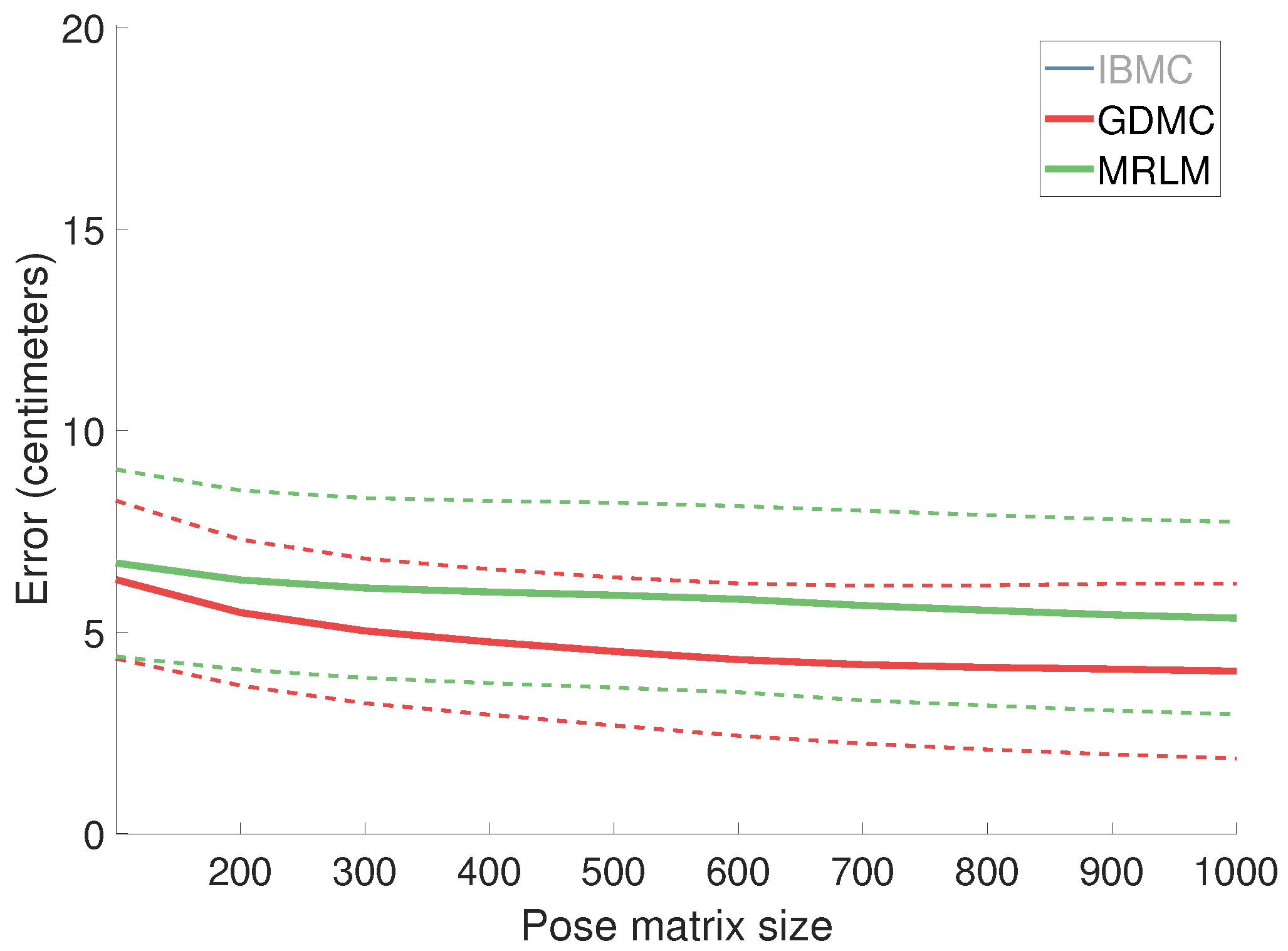
4.1.1. Estimation Error as a Function of the Pose Matrix Size
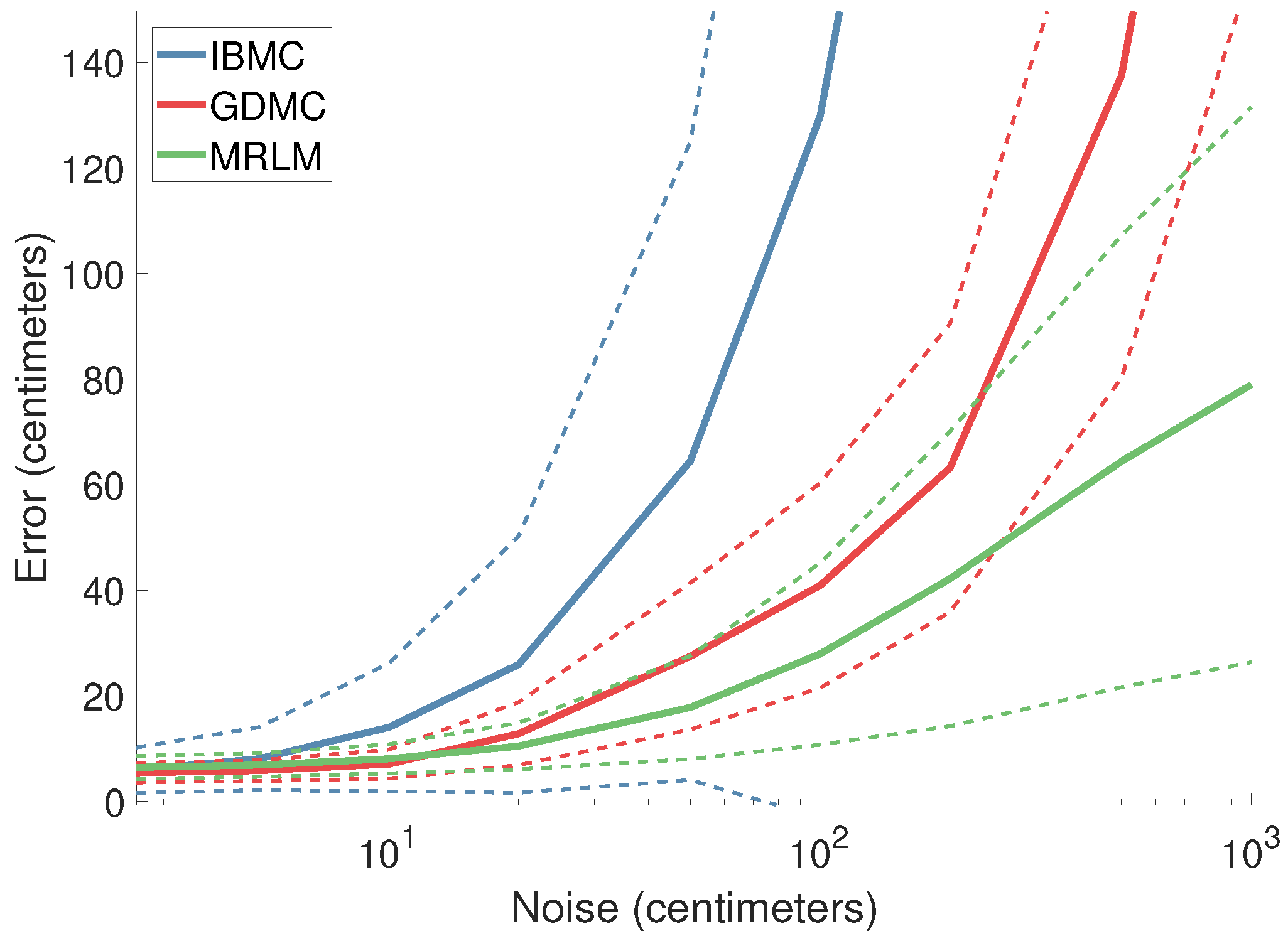
4.1.2. Estimation Error as a Function of Noise
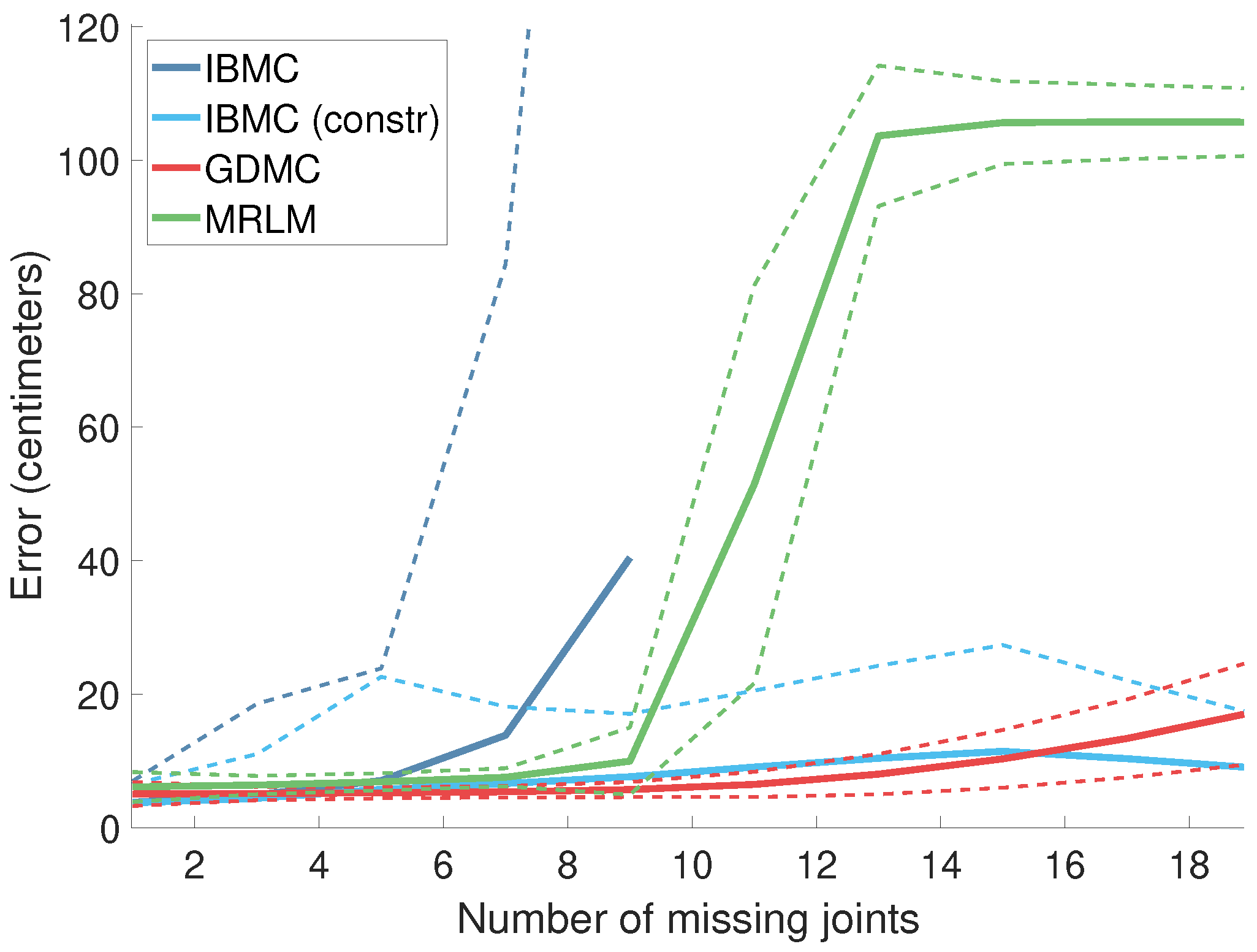
4.1.3. Error as a Function of the Number of Missing Joints
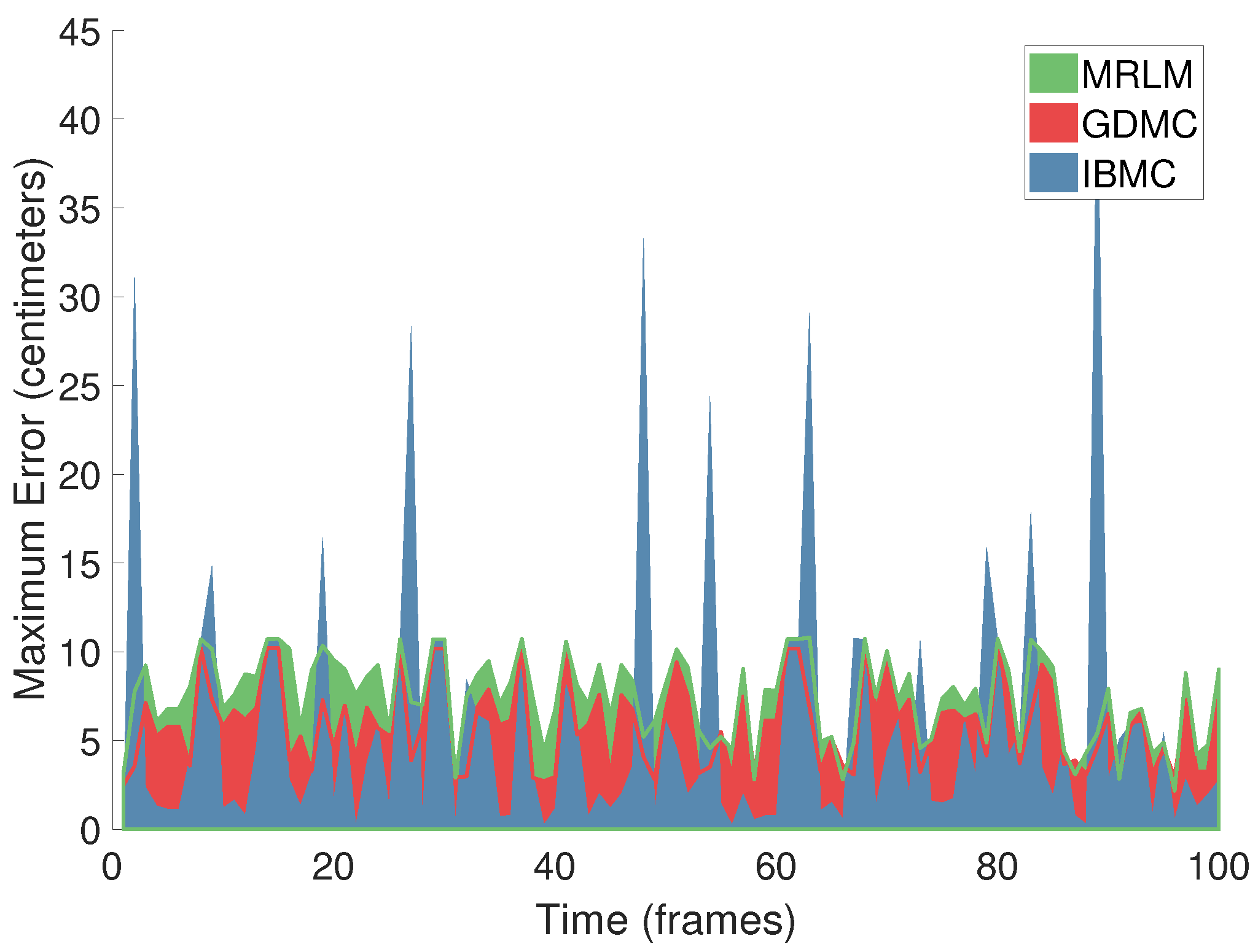
4.1.4. Estimation Error as a Function of Time
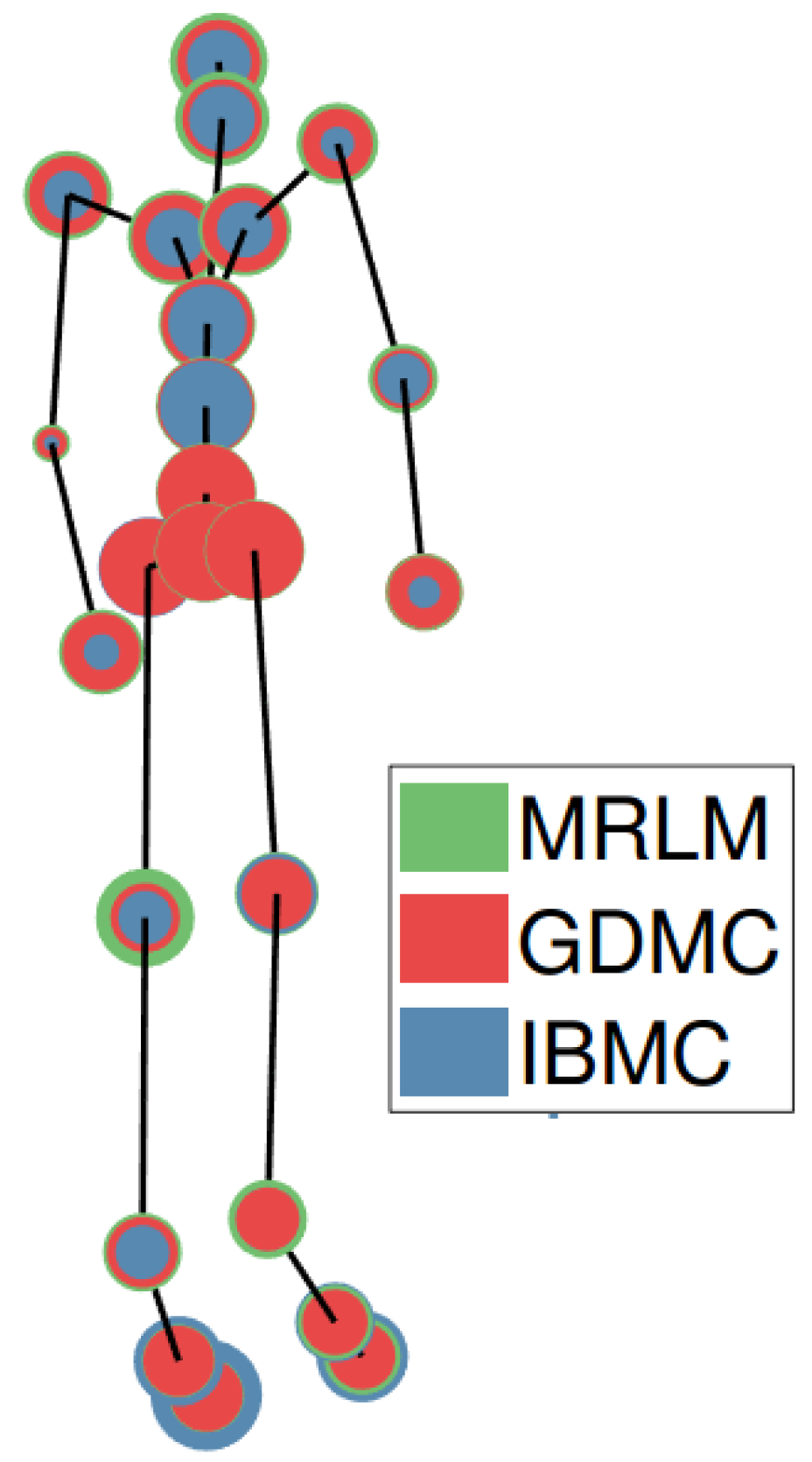
4.1.5. Estimation Error per Joint
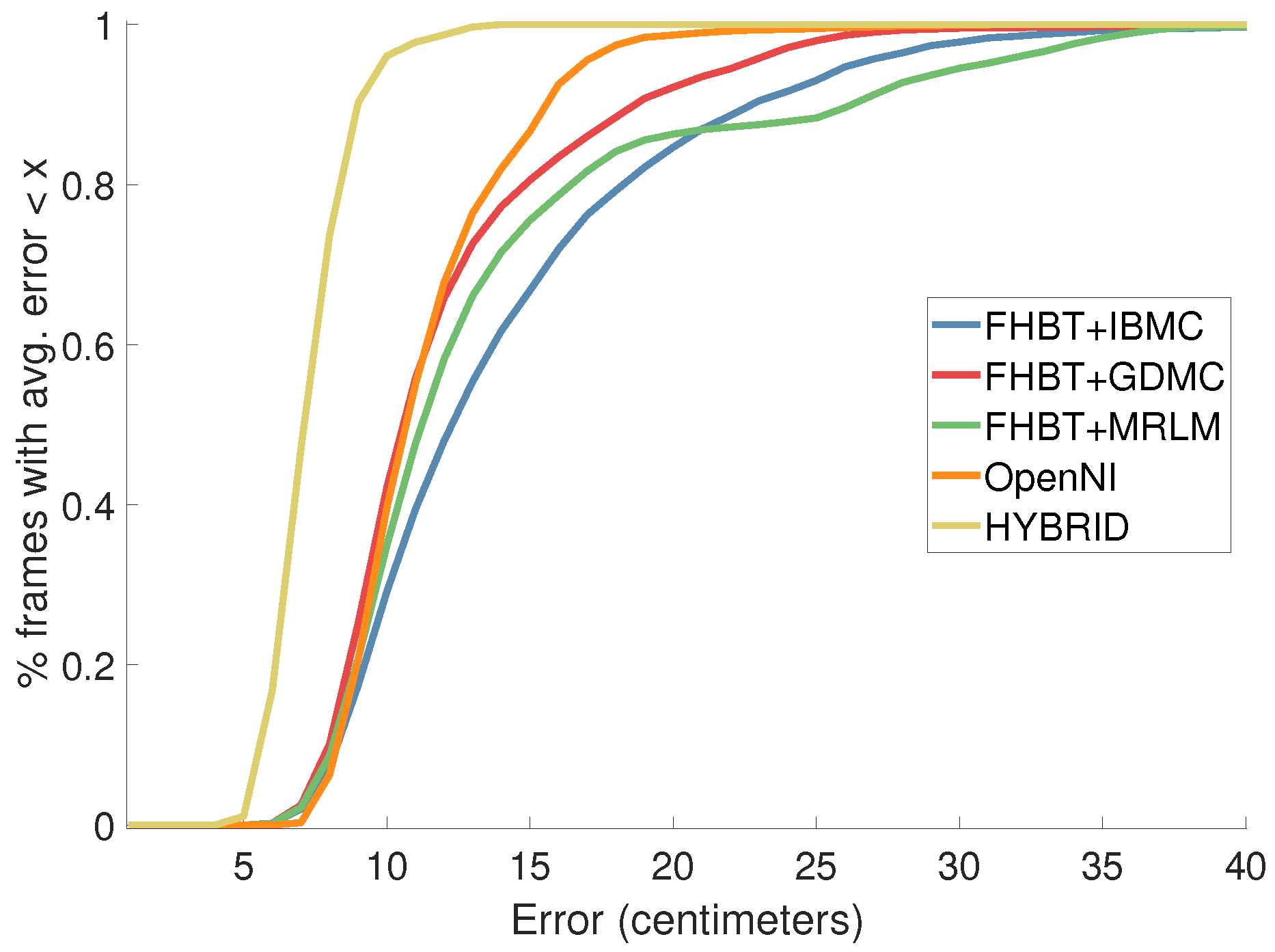
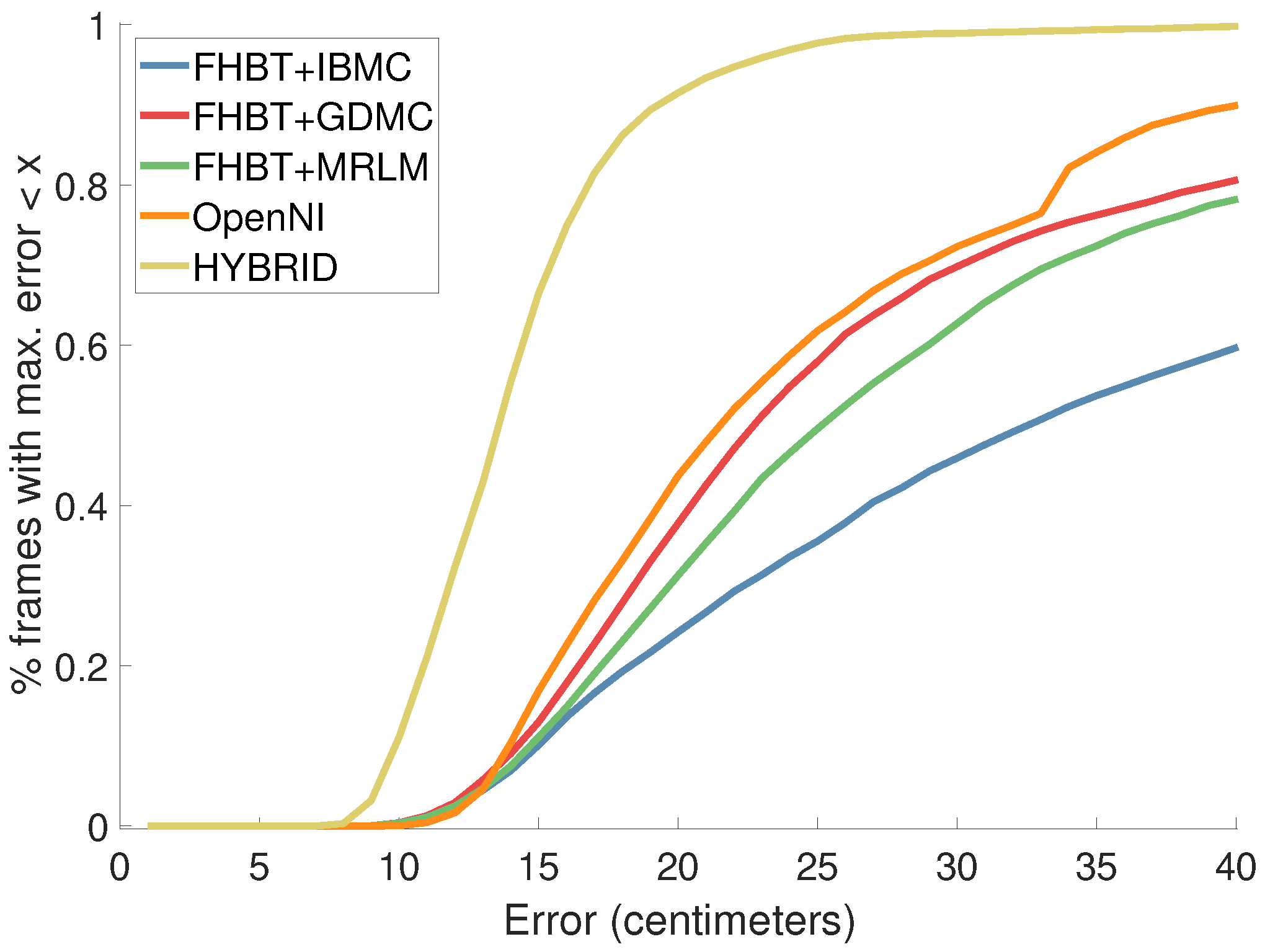
4.2. Results from Completing FHBT
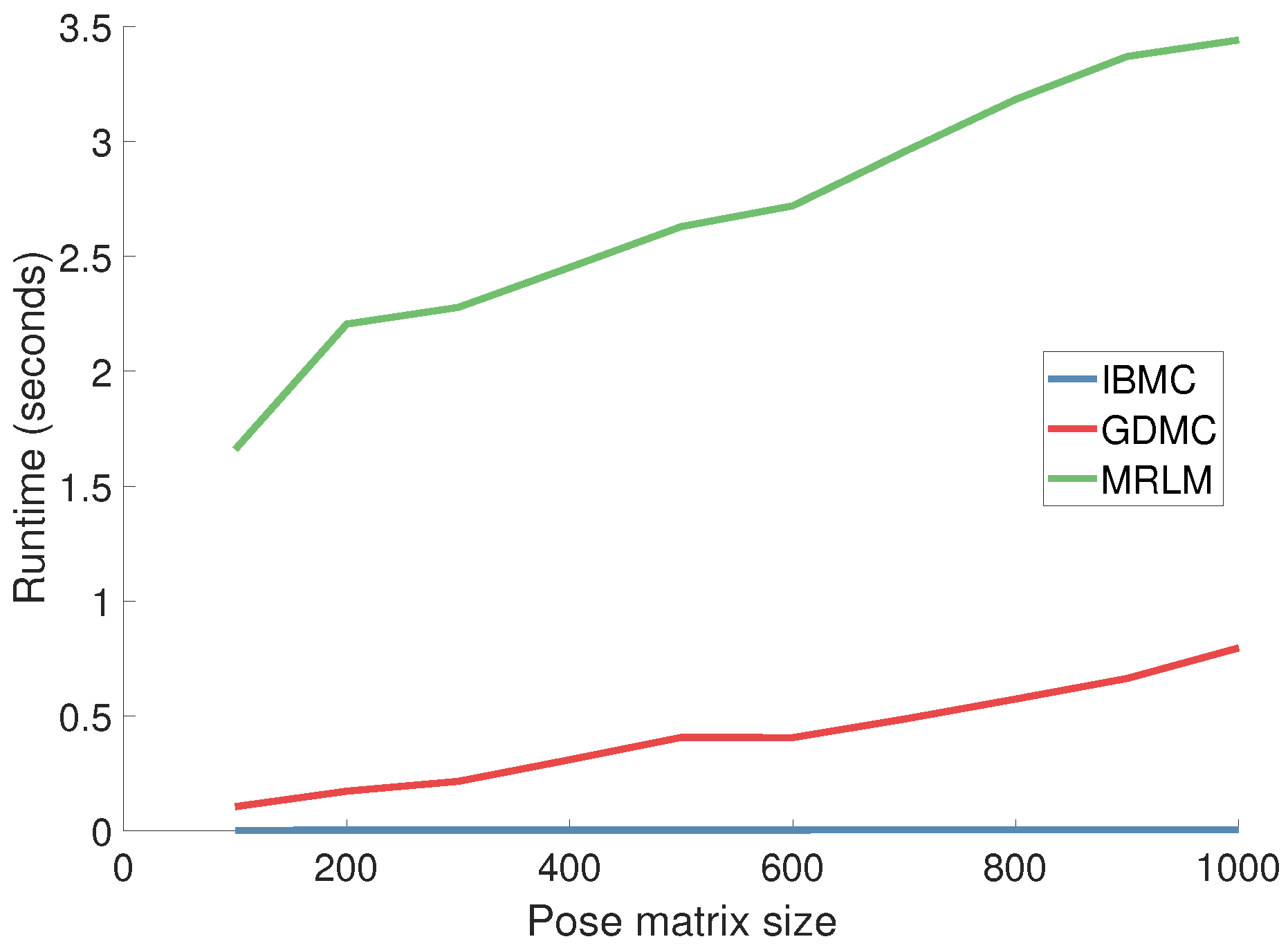
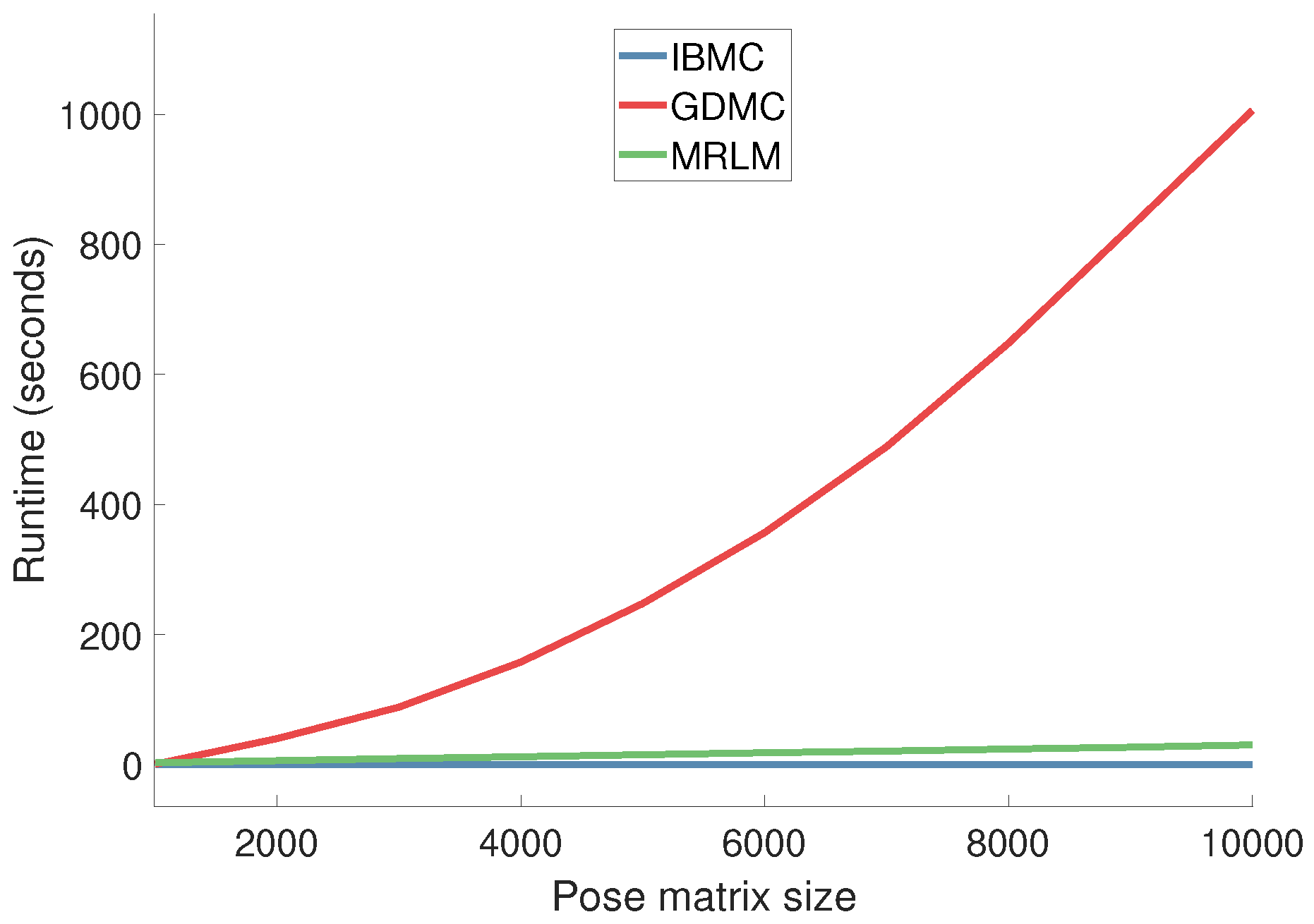
4.3. Runtime
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Moeslund, T.B.; Granum, E. A survey of computer vision-based human motion capture. Comput. Vis. Image Underst. 2001, 81, 231–268. [Google Scholar] [CrossRef]
- Gong, W.; Zhang, X.; Gonzàlez, J.; Sobral, A.; Bouwmans, T.; Tu, C.; Zahzah, E. Human Pose Estimation from Monocular Images: A Comprehensive Survey. Sensors 2016, 16, 1966. [Google Scholar] [CrossRef] [PubMed]
- Erol, A.; Bebis, G.; Nicolescu, M.; Boyle, R.D.; Twombly, X. Vision-based hand pose estimation: A review. Comput. Vis. Image Underst. 2007, 108, 52–73. [Google Scholar] [CrossRef]
- Microsoft Corporation. Available online: https://en.wikipedia.org/wiki/Kinect (accessed on 26 October 2018).
- Lecun, Y.; Bengio, Y.; Hinton, G. Deep learning. Nature 2015, 521, 436–444. [Google Scholar] [CrossRef] [PubMed]
- Michel, D.; Argyros, A.A. Apparatuses, Methods and Systems for Recovering a 3-Dimensional Skeletal Model of the Human Body. U.S. Patent 20160086350A1, 24 March 2016. [Google Scholar]
- Michel, D.; Qammaz, A.; Argyros, A.A. Markerless 3D Human Pose Estimation and Tracking based on RGBD Cameras: An Experimental Evaluation. In Proceedings of the International Conference on Pervasive Technologies Related to Assistive Environments (PETRA 2017), Rhodes, Greece, 21–23 June 2017; pp. 115–122. [Google Scholar]
- Foukarakis, M.; Adami, I.; Ioannidi, D.; Leonidis, A.; Michel, D.; Qammaz, A.; Papoutsakis, K.; Antona, M.; Argyros, A.A. A Robot-based Application for Physical Exercise Training. In Proceedings of the International Conference on Information and Communication Technologies for Ageing Well and e-Health (ICT4AWE 2016), Rome, Italy, 21–22 April 2016; pp. 45–52. [Google Scholar]
- Panteleris, P.; Argyros, A.A. Monitoring and Interpreting Human Motion to Support Clinical Applications of a Smart Walker. Available online: http://users.ics.forth.gr/~argyros/mypapers/2016_05_IETWorkshop_acanto.pdf (accessed on 29 October 2018).
- Sobral, A.; Bouwmans, T.; Zahzah, E. LRSLibrary: Low-Rank and Sparse tools for Background Modeling and Subtraction in Videos. In Robust Low-Rank and Sparse Matrix Decomposition: Applications in Image and Video Processing; Bouwmans, T., Sobral, A., Zahzah, E., Eds.; CRC Press: Boca Raton, FL, USA, 2015. [Google Scholar]
- Sinha, A.; Choi, C.; Ramani, K. DeepHand: Robust Hand Pose Estimation by Completing a Matrix Imputed with Deep Features. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4150–4158. [Google Scholar] [CrossRef]
- Bouwmans, T.; Javed, S.; Zhang, H.; Lin, Z.; Otazo, R. On the Applications of Robust PCA in Image and Video Processing. Proc. IEEE 2018, 106, 1427–1457. [Google Scholar] [CrossRef]
- Bouwmans, T.; Sobral, A.; Javed, S.; Jung, S.K.; Zahzah, E.H. Decomposition into low-rank plus additive matrices for background/foreground separation: A review for a comparative evaluation with a large-scale dataset. Sci. Comput. Rev. 2017, 23, 1–71. [Google Scholar] [CrossRef]
- Mansour, H.; Vetro, A. Video background subtraction using semi-supervised robust matrix completion. In Proceedings of the 2014 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Florence, Italy, 4–9 May 2014; pp. 6528–6532. [Google Scholar]
- Rezaei, B.; Ostadabbas, S. Background Subtraction via Fast Robust Matrix Completion. In Proceedings of the 2017 IEEE International Conference on Computer Vision Workshops, Venice, Italy, 22–29 October 2017; pp. 1871–1879. [Google Scholar]
- Candès, E.J.; Recht, B. Exact matrix completion via convex optimization. Found. Comput. Math. 2009, 9, 717–772. [Google Scholar] [CrossRef]
- Lin, Z.; Chen, M.; Ma, Y. The Augmented Lagrange Multiplier Method for Exact Recovery of Corrupted Low-Rank Matrices. arXiv, 2010; arXiv:1009.5055. [Google Scholar]
- Bautembach, D.; Oikonomidis, I.; Argyros, A.A. A Comparative Study of Matrix Completion and Recovery Techniques for Human Pose Estimation. In Proceedings of the 11th PErvasive Technologies Related to Assistive Environments Conference (PETRA 2018), Corfu, Greece, 26–29 June 2018. [Google Scholar]
- Organization, O. OpenNI User Guide. Available online: https://www.bibsonomy.org/bibtex/2d7953305373f5ce2ec6ab43e80306fdc/lightraven (accessed on 29 October 2018).
- Michel, D.; Panagiotakis, C.; Argyros, A.A. Tracking the articulated motion of the human body with two RGBD cameras. Mach. Vis. Appl. 2015, 26, 41–54. [Google Scholar] [CrossRef]
- Shotton, J.; Fitzgibbon, A.; Cook, M.; Sharp, T.; Finocchio, M.; Moore, R.; Kipman, A.; Blake, A. Real-Time Human Pose Recognition in Parts from Single Depth Images. In Proceedings of the IEEE Computer Vision and Pattern Recognition (CVPR) 2011, Colorado Springs, CO, USA, 20–25 June 2011; pp. 1297–1304. [Google Scholar]
- Andriluka, M.; Pishchulin, L.; Gehler, P.; Schiele, B. 2D Human Pose Estimation: New Benchmark and State of the Art Analysis. In Proceedings of the IEEE Conference on computer Vision and Pattern Recognition, Columbus, OH, USA, 24–27 June 2014; pp. 3686–3693. [Google Scholar] [CrossRef]
- Cao, Z.; Simon, T.; Wei, S.E.; Sheikh, Y. Realtime Multi-Person 2D Pose Estimation using Part Affinity Fields. arXiv, 2016; arXiv:1611.08050. [Google Scholar]
- Tompson, J.; Stein, M.; Lecun, Y.; Perlin, K. Real-Time Continuous Pose Recovery of Human Hands Using Convolutional Networks. ACM Trans. Graph. 2014, 33, 1–10. [Google Scholar] [CrossRef]
- Tang, D.; Taylor, J.; Kohli, P.; Keskin, C.; Kim, T.K.; Shotton, J. Opening the Black Box: Hierarchical Sampling Optimization for Estimating Human Hand Pose. Proceedings of 2015 IEEE International Conference on Computer Vision (ICCV), Santiago, Chile, 7–13 December 2015; pp. 3325–3333. [Google Scholar] [CrossRef]
- Oberweger, M.; Lepetit, V. DeepPrior++: Improving Fast and Accurate 3D Hand Pose Estimation. Proceedings of 2017 IEEE International Conference on Computer Vision Workshops (ICCVW), Venice, Italy, 22–29 October 2017; Volume 840, p. 2. [Google Scholar] [CrossRef]
- Vicon. Motion Capture Systems|Vicon. Available online: https://www.vicon.com/ (accessed on 29 October 2018).
- OptiTrack. OptiTrack—Motion Capture Systems. Available online: https://optitrack.com/ (accessed on 29 October 2018).
- Wang, R.Y.; Popović, J. Real-time hand-tracking with a color glove. ACM Trans. Graph. 2009, 28, 63. [Google Scholar] [CrossRef]
- Joo, H.; Simon, T.; Sheikh, Y. Total Capture: A 3D Deformation Model for Tracking Faces, Hands, and Bodies. arXiv, 2018; arXiv:1801.01615. [Google Scholar]
- Romero, J.; Tzionas, D.; Black, M.J. Embodied hands: Modeling and Capturing Hands and Bodies Together. ACM Trans. Graph. 2017, 36, 1–17. [Google Scholar] [CrossRef]
- Tekin, B.; Katircioglu, I.; Salzmann, M.; Lepetit, V.; Fua, P. Structured Prediction of 3D Human Pose with Deep Neural Networks. arXiv, 2016; arXiv:1605.05180. [Google Scholar]
- Oberweger, M.; Wohlhart, P.; Lepetit, V. Hands Deep in Deep Learning for Hand Pose Estimation. arXiv, 2015; arXiv:1502.06807. [Google Scholar]
- Ciotti, S.; Battaglia, E.; Oikonomidis, I.; Makris, A.; Tsoli, A.; Bicchi, A.; Argyros, A.A.; Bianchi, M. Synergy-driven Performance Enhancement of Vision-based 3D Hand Pose Reconstruction. In Proceedings of the International Conference on Wireless Mobile Communication and Healthcare, Milan, Italy, 14–16 November 2018; pp. 328–336. [Google Scholar] [CrossRef]
- Kyriazis, N.; Argyros, A.A. Physically Plausible 3D Scene Tracking: The Single Actor Hypothesis. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR 2013), Portland, OR, USA, 25–27 June 2013; pp. 9–16. [Google Scholar] [CrossRef]
- Melax, S.; Keselman, L.; Orsten, S. Dynamics Based 3D Skeletal Hand Tracking. Proceedings of Graphics Interface 2013, Regina, SK, Canada, 29–31 May 2013; pp. 63–70. [Google Scholar]
- Tzionas, D.; Ballan, L.; Srikantha, A.; Aponte, P.; Pollefeys, M.; Gall, J. Capturing Hands in Action Using Discriminative Salient Points and Physics Simulation. Int. J. Comput. Vis. 2016, 118, 172–193. [Google Scholar] [CrossRef]
- Fleishman, S.; Kliger, M.; Lerner, A.; Kutliroff, G. ICPIK: Inverse Kinematics based articulated-ICP. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Boston, MA, USA, 7–12 June 2015; pp. 28–35. [Google Scholar] [CrossRef]
- Sun, X.; Wei, Y.; Liang, S.; Tang, X.; Sun, J. Cascaded hand pose regression. In Proceedings of the 2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 824–832. [Google Scholar] [CrossRef]
- Douvantzis, P.; Oikonomidis, I.; Kyriazis, N.; Argyros, A.A. Dimensionality Reduction for Efficient Single Frame Hand Pose Estimation. In Proceedings of the International Conference on Computer Vision Systems, St. Petersburg, Russia, 16–18 July 2013; pp. 143–152. [Google Scholar]
- Roditakis, K.; Makris, A.; Argyros, A.A. Generative 3D Hand Tracking with Spatially Constrained Pose Sampling. In Proceedings of the British Machine Vision Conference (BMVC 2017), London, UK, 4–7 September 2017. [Google Scholar]
- Johnson, S.; Everingham, M. Learning effective human pose estimation from inaccurate annotation. In Proceedings of the Computer Vision and Pattern Recognition (CVPR 2011), Colorado Springs, CO, USA, 20–25 June 2011; pp. 1465–1472. [Google Scholar] [CrossRef]
- Simo-Serra, E.; Torras, C.; Moreno-Noguer, F. Lie algebra-based kinematic prior for 3D human pose tracking. In Proceedings of the 2015 14th IAPR International Conference on Machine Vision Applications (MVA), Tokyo, Japan, 18–22 May 2015; pp. 394–397. [Google Scholar]
- Lifshitz, I.; Fetaya, E.; Ullman, S. Human Pose Estimation using Deep Consensus Voting. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2018; pp. 246–260. [Google Scholar] [CrossRef]
- Brau, E.; Jiang, H. 3D Human Pose Estimation via Deep Learning from 2D Annotations. Proceedings of 2016 Fourth International Conference on 3D Vision (3DV), Stanford, CA, USA, 25–28 October 2016; pp. 582–591. [Google Scholar] [CrossRef]
- Pavlakos, G.; Zhou, X.; Derpanis, K.G.; Daniilidis, K. Coarse-to-Fine Volumetric Prediction for Single-Image 3D Human Pose. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1263–1272. [Google Scholar] [CrossRef]
- Insafutdinov, E.; Pishchulin, L.; Andres, B.; Andriluka, M.; Schiele, B. Deepercut: A deeper, stronger, and faster multi-person pose estimation model. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 34–50. [Google Scholar] [CrossRef]
- Newell, A.; Yang, K.; Deng, J. Stacked Hourglass Networks for Human Pose Estimation. In Proceedings of the European Conference on Computer Vision, Amsterdam, The Netherlands, 8–16 October 2016; pp. 483–499. [Google Scholar] [CrossRef]
- Baak, A.; Muller, M.; Bharaj, G.; Seidel, H.P.; Theobalt, C. A data-driven approach for real-time full body pose reconstruction from a depth camera. In Proceedings of the 2011 International Conference on Computer Vision, Barcelona, Spain, 6–13 November 2011; pp. 1092–1099. [Google Scholar] [CrossRef]
- Moreno-Noguer, F. 3D Human Pose Estimation from a Single Image via Distance Matrix Regression. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 1561–1570. [Google Scholar] [CrossRef]
- Mehta, D.; Sridhar, S.; Sotnychenko, O.; Rhodin, H.; Shafiei, M.; Seidel, H.P.; Xu, W.; Casas, D.; Theobalt, C. VNect: Real-time 3D Human Pose Estimation with a Single RGB Camera. ACM Trans. Graph. 2017, 36, 44. [Google Scholar] [CrossRef]
- Zhou, X.; Huang, Q.; Sun, X.; Xue, X.; Wei, Y. Towards 3D Human Pose Estimation in the Wild: A Weakly-supervised Approach. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 398–407. [Google Scholar] [CrossRef]
- Elhayek, A.; De Aguiar, E.; Jain, A.; Thompson, J.; Pishchulin, L.; Andriluka, M.; Bregler, C.; Schiele, B.; Theobalt, C. MARCOnI - ConvNet-Based MARker-less motion capture in outdoor and indoor scenes. IEEE Trans. Pattern Anal. Mach. Intell. 2017, 39, 501–514. [Google Scholar] [CrossRef] [PubMed]
- Tekin, B.; Rozantsev, A.; Lepetit, V.; Fua, P. Direct Prediction of 3D Body Poses from Motion Compensated Sequences. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 991–1000. [Google Scholar] [CrossRef]
- Yu, T.; Guo, K.; Xu, F.; Dong, Y.; Su, Z.; Zhao, J.; Li, J.; Dai, Q.; Liu, Y. BodyFusion: Real-time Capture of Human Motion and Surface Geometry Using a Single Depth Camera. In Proceedings of the 2017 IEEE International Conference on Computer Vision (ICCV), Venice, Italy, 22–29 October 2017; pp. 910–919. [Google Scholar] [CrossRef]
- Owen, A.B.; Perry, P.O. Bi-cross-validation of the SVD and the nonnegative matrix factorization. Ann. Appl. Stat. 2009, 3, 564–594. [Google Scholar] [CrossRef]
- Ofli, F.; Chaudhry, R.; Kurillo, G.; Vidal, R.; Bajcsy, R. Berkeley MHAD: A comprehensive Multimodal Human Action Database. In Proceedings of the 2013 IEEE Workshop on Applications of Computer Vision (WACV), Tampa, FL, USA, 15–17 January 2013; pp. 53–60. [Google Scholar] [CrossRef]
- Horn, B.K.P. Closed-form solution of absolute orientation using unit quaternions. J. Opt. Soc. Am. A 1987, 4, 629. [Google Scholar] [CrossRef]

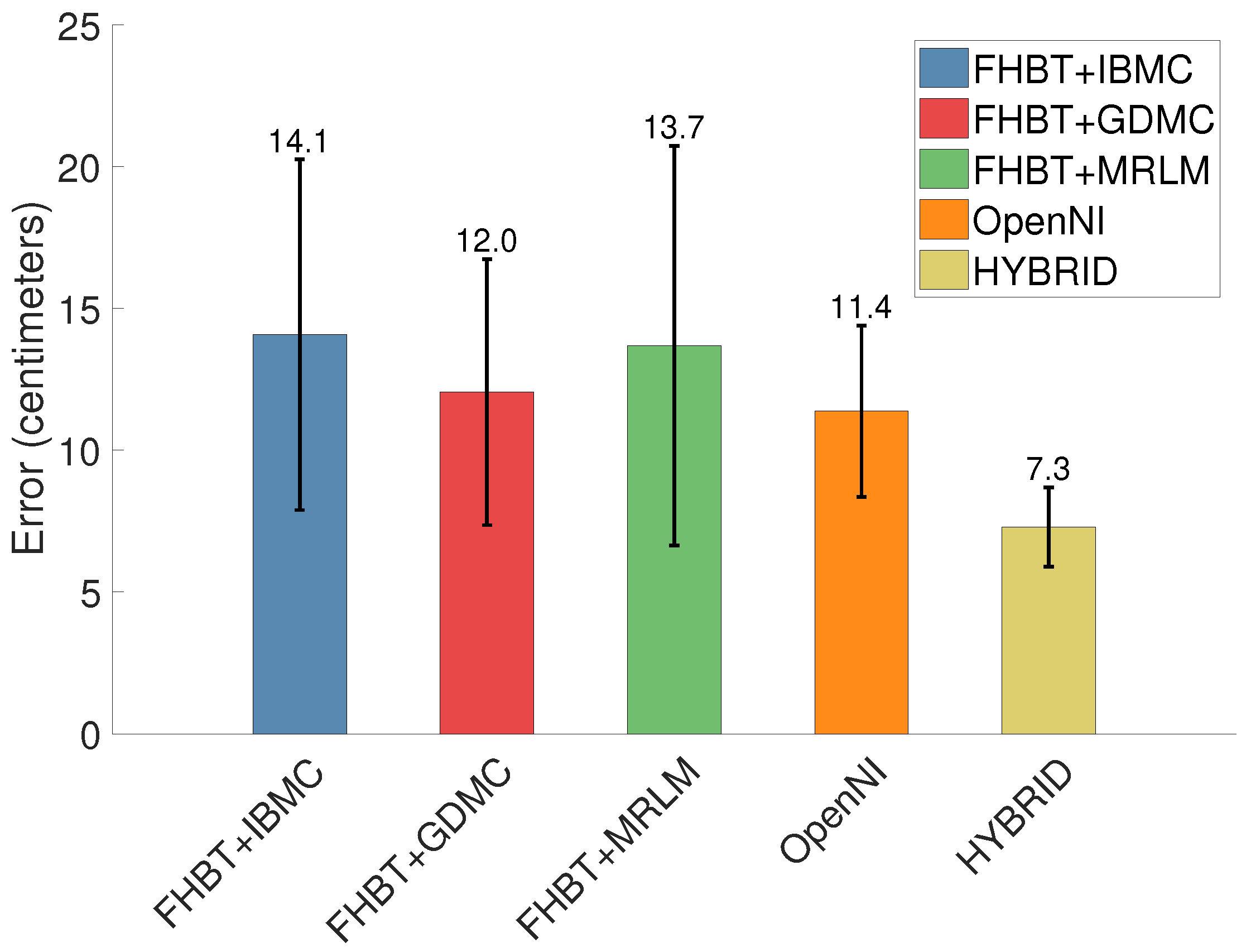
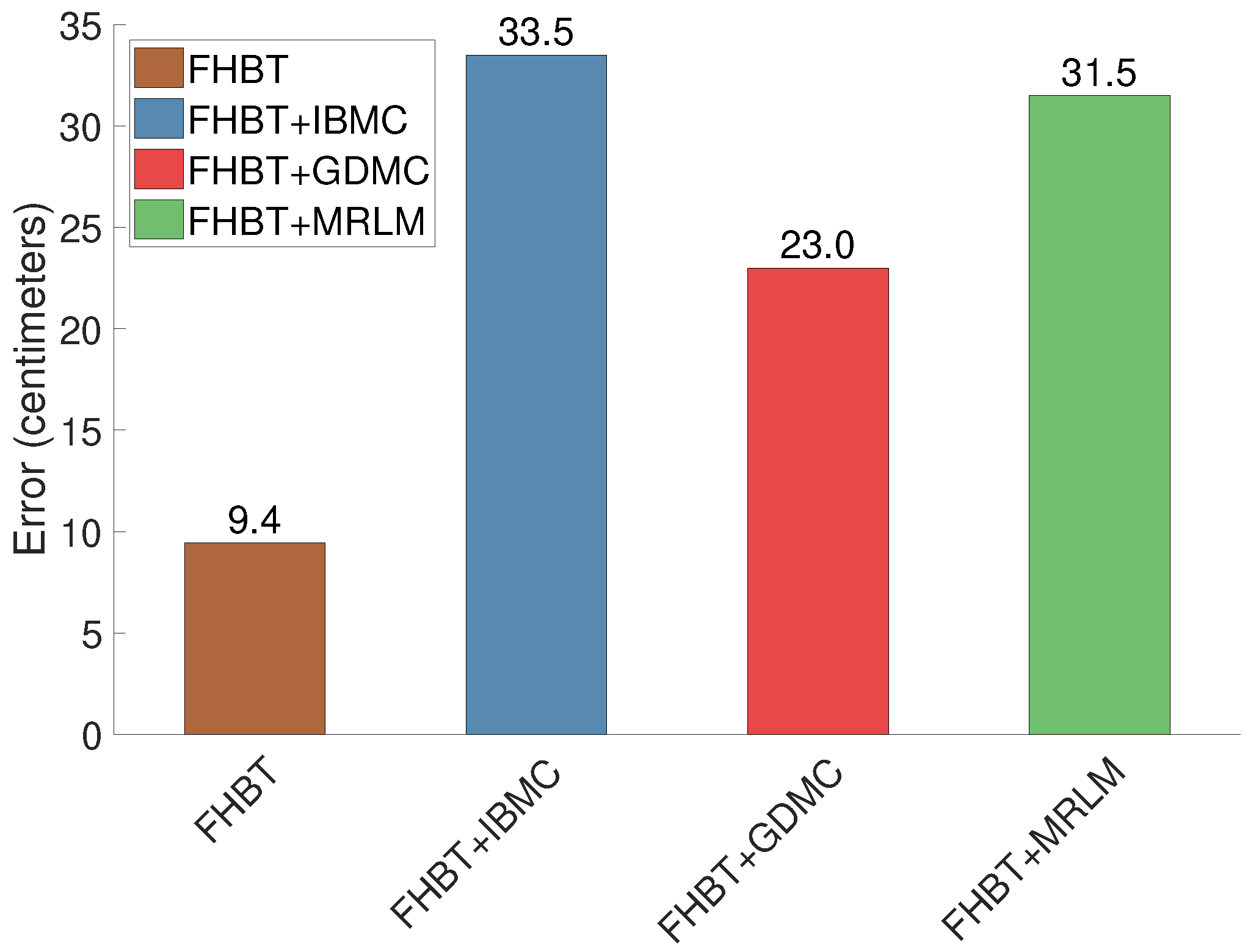
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bautembach, D.; Oikonomidis, I.; Argyros, A. Filling the Joints: Completion and Recovery of Incomplete 3D Human Poses. Technologies 2018, 6, 97. https://doi.org/10.3390/technologies6040097
Bautembach D, Oikonomidis I, Argyros A. Filling the Joints: Completion and Recovery of Incomplete 3D Human Poses. Technologies. 2018; 6(4):97. https://doi.org/10.3390/technologies6040097
Chicago/Turabian StyleBautembach, Dennis, Iason Oikonomidis, and Antonis Argyros. 2018. "Filling the Joints: Completion and Recovery of Incomplete 3D Human Poses" Technologies 6, no. 4: 97. https://doi.org/10.3390/technologies6040097
APA StyleBautembach, D., Oikonomidis, I., & Argyros, A. (2018). Filling the Joints: Completion and Recovery of Incomplete 3D Human Poses. Technologies, 6(4), 97. https://doi.org/10.3390/technologies6040097




