Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels
Abstract
1. Introduction
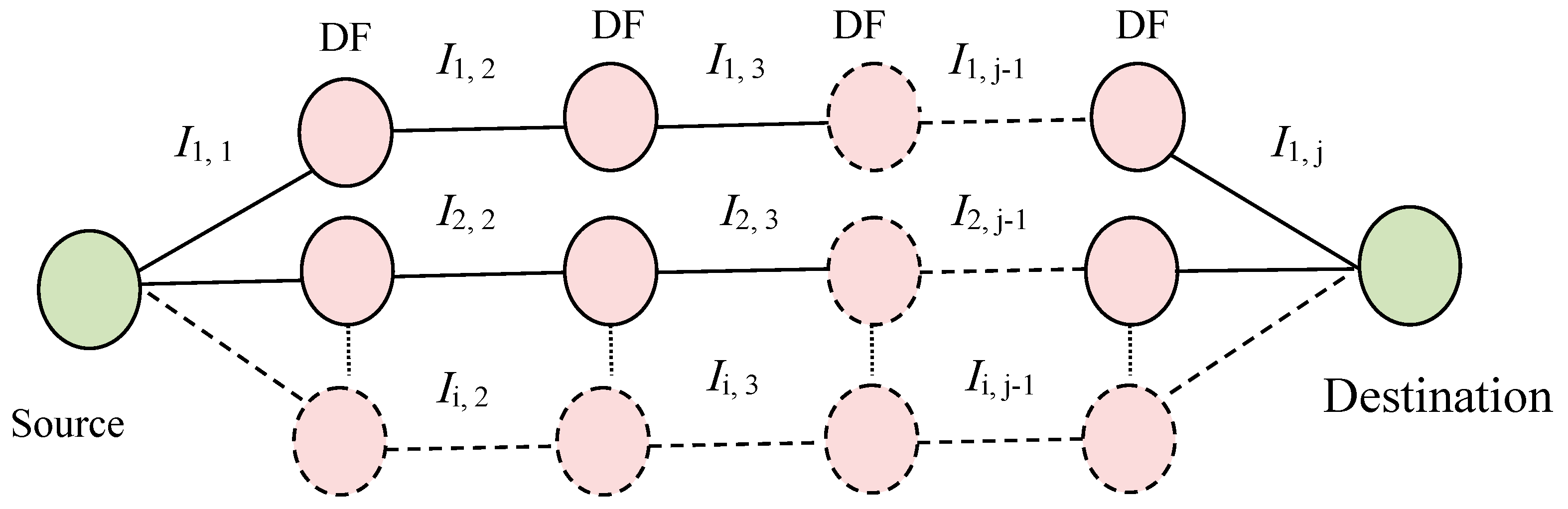
2. System and Channel Model
2.1. Signal and System Assumptions
2.2. The Atmospheric Turbulence Effect
2.3. Generalized Pointing Errors
2.4. Joint Turbulence and Pointing Errors Effects
3. Outage Probability Estimation
4. Mean Outage Duration Estimation
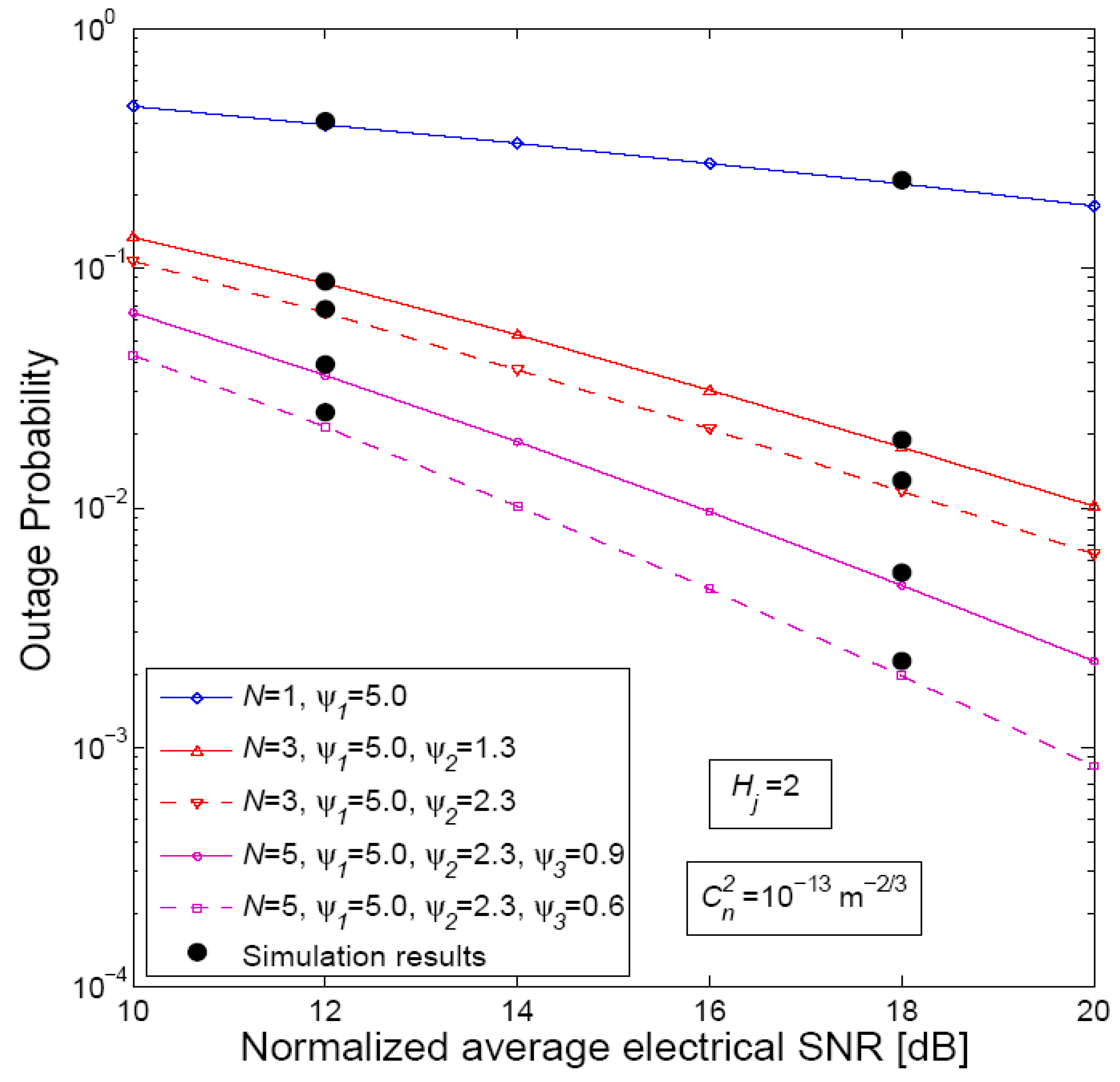
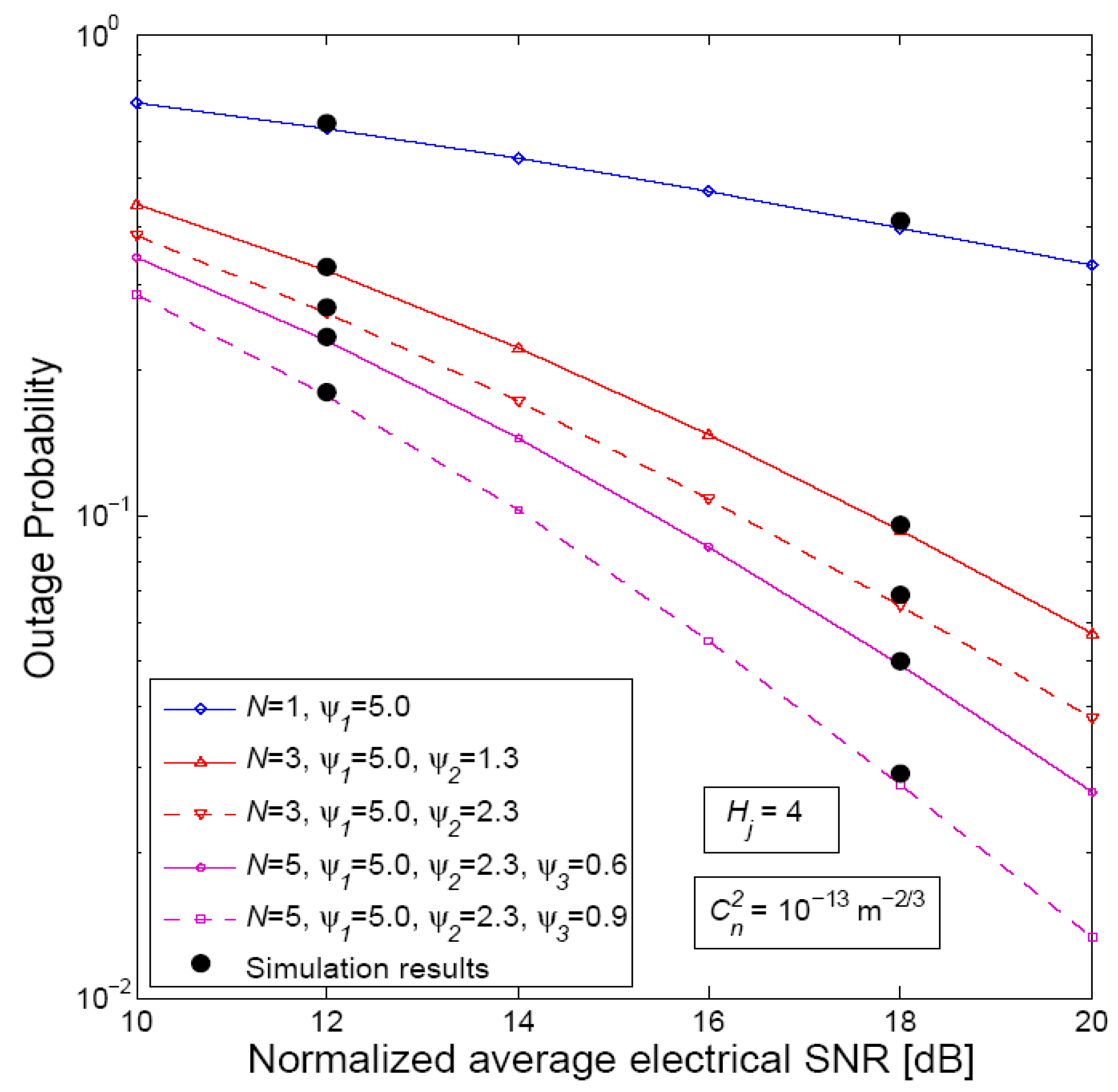
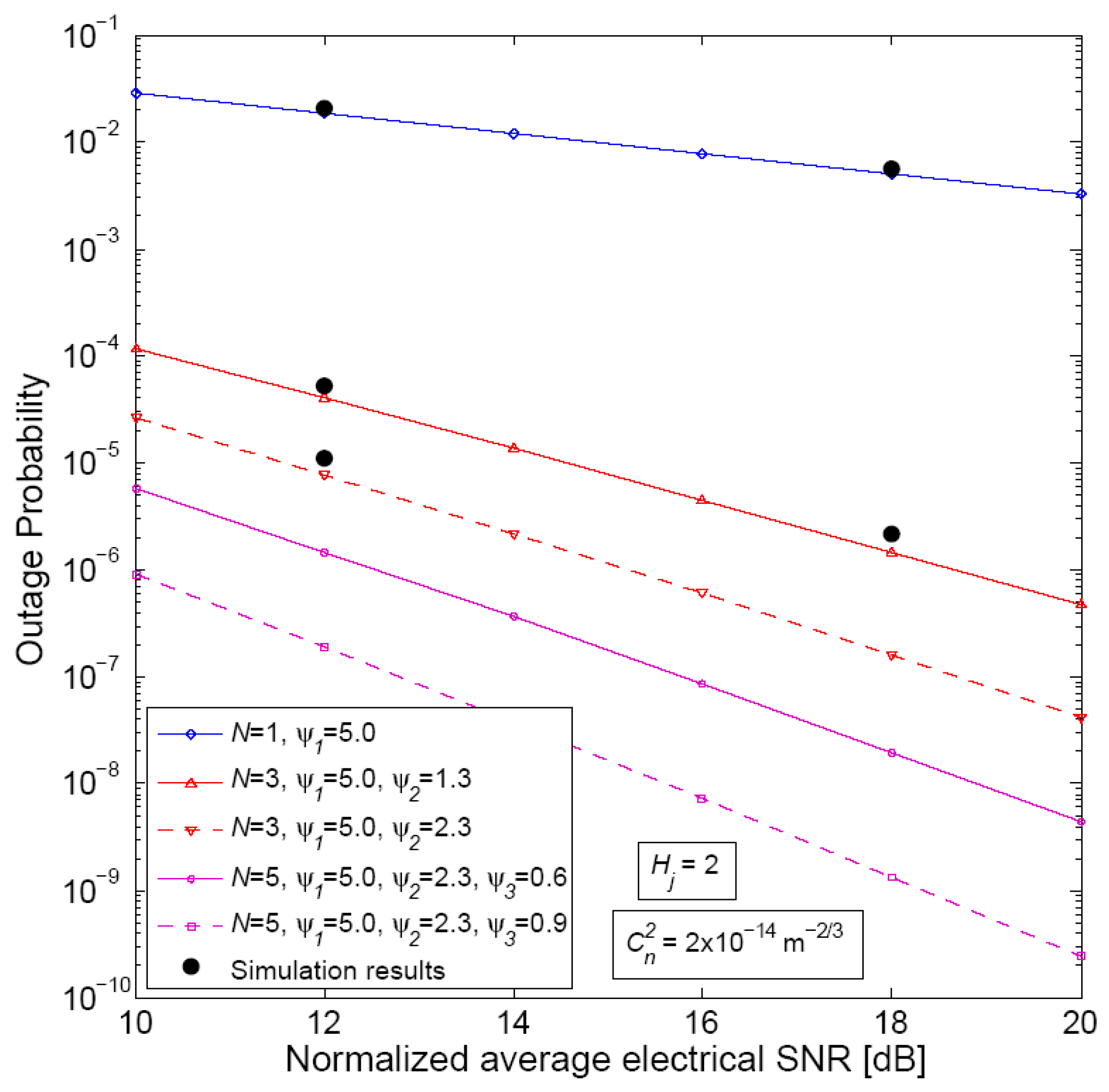
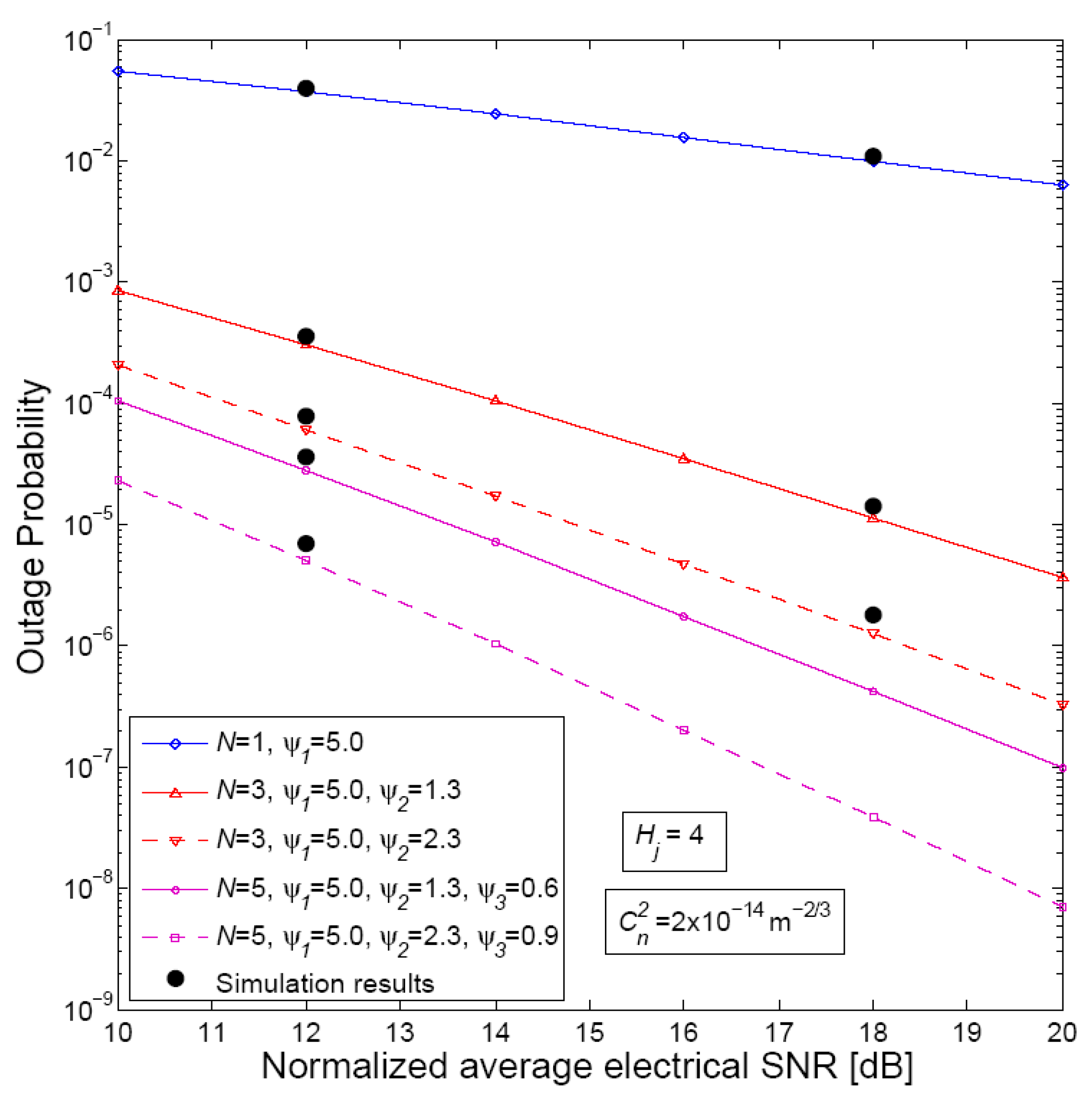
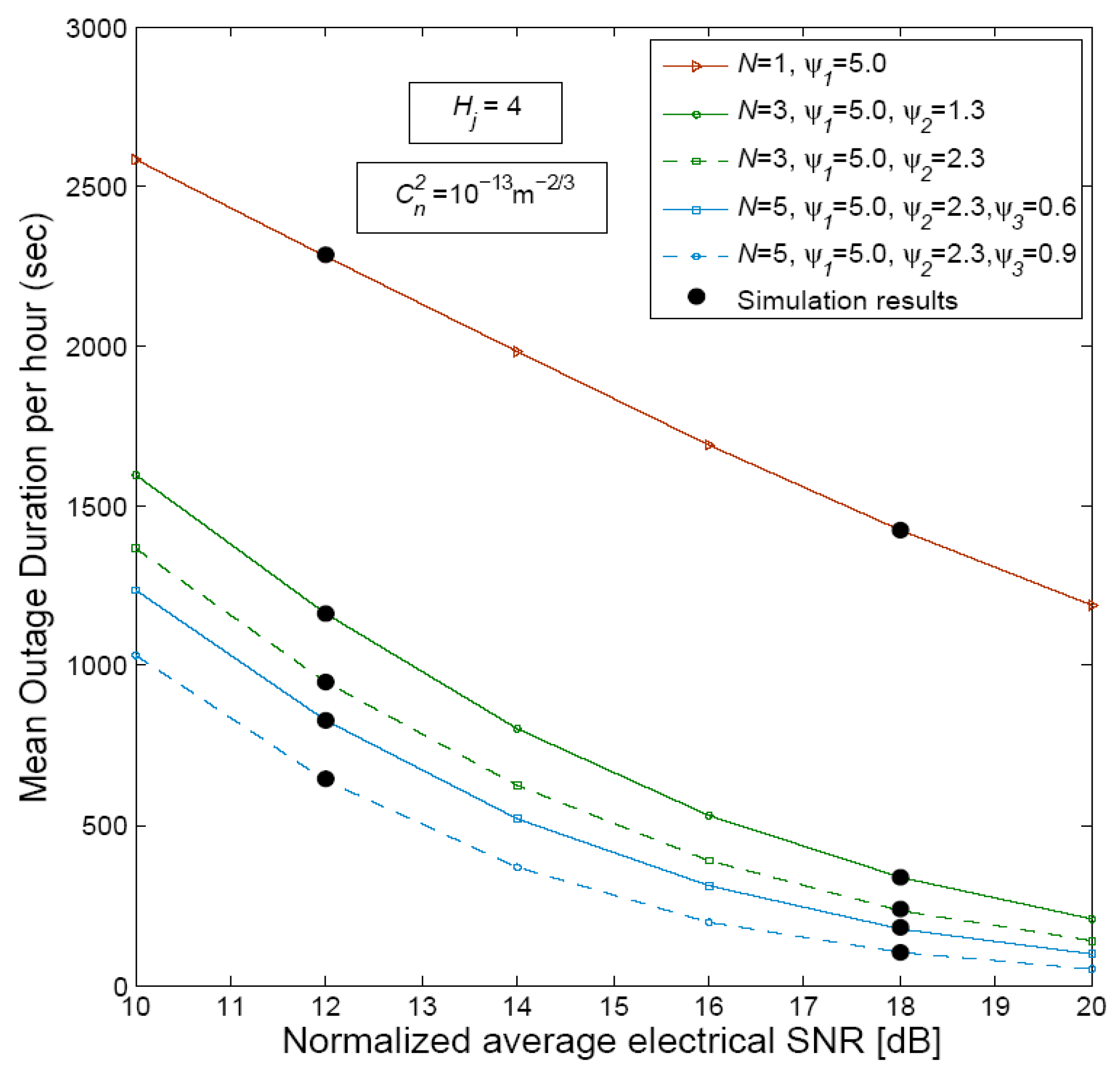
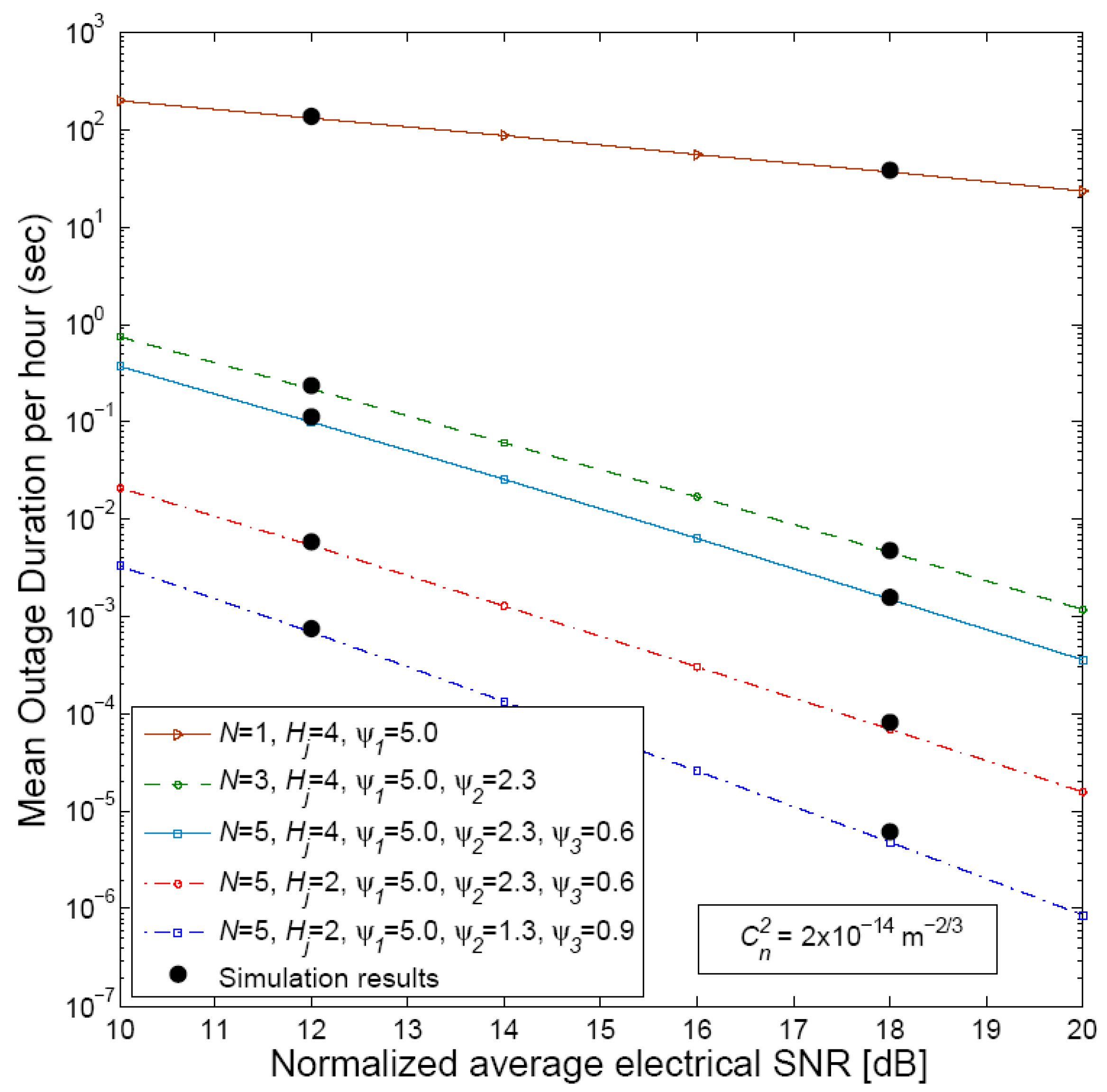
5. Numerical Results
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Ghassemlooy, Z.; Popoola, W.O. Terrestrial Free-Space Optical Communications. In Mobile and Wireless Communications: Network Layer and Circuit Level Design; Fares, S.A., Adachi, F., Eds.; InTech: London, UK, 2010; pp. 355–392. [Google Scholar]
- Henniger, H.; Wilfert, O. An Introduction to Free-Space Optical Communications. Radioengineering 2010, 19, 203–212. [Google Scholar]
- Varotsos, G.K.; Nistazakis, H.E.; Volos, C.K.; Tombras, G.S. FSO links with diversity pointing errors and temporal broadening of the pulses over weak to strong atmospheric turbulence channels. Elsevier Opt. 2016, 127, 3402–3409. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Petkovic, M.I.; Djordjevic, G.T.; Tombras, G.S. SIMO optical wireless links with nonzero boresight pointing error over M modeled turbulence channels. Opt. Commun. 2017, 303, 391–400. [Google Scholar] [CrossRef]
- Zhu, X.; Kahn, J.M. Free-space optical communication through atmospheric turbulence channels. IEEE Trans. Commun. 2002, 50, 1293–1300. [Google Scholar]
- Arnon, S. Effects of atmospheric turbulence and building sway on optical wireles-communication systems. Opt. Lett. 2003, 28, 129–131. [Google Scholar] [CrossRef] [PubMed]
- Farid, A.; Hranilovic, S. Outage capacity optimization for free-space optical links with pointing errors. J. Lightwave Technol. 2007, 25, 1702–1710. [Google Scholar] [CrossRef]
- Yang, F.; Cheng, J.; Tsiftsis, T.A. Free-space optical communication with nonzero boresight pointing errors. IEEE Trans. Commun. 2014, 62, 713–725. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; Garcia-Zambrana, A.; Castillo-Vazquez, B.; Castillo-Vazquez, C. Impact of nonzeroboresight pointing error on ergodic capacity of MIMO FSO communication systems. Opt. Express 2016, 24, 3513–3534. [Google Scholar] [CrossRef] [PubMed]
- Prabu, K.; Kumar, D.S. Outage Analysis of Relay-Assisted BPSK-SIM Based FSO Systems over Strong Atmospheric turbulence with Pointing errors. Int. J. Comput. Commun. Eng. 2014, 3, 317–320. [Google Scholar] [CrossRef]
- Acampora, A.S.; Krishnamurthy, S.V. A broadband wireless access network based on mesh-connected free-space optical links. IEEE Pers. Commun. 1999, 6, 62–65. [Google Scholar] [CrossRef]
- Tsiftsis, T.A.; Sandalidis, H.G.; Karagiannidis, G.K.; Sagias, N.C. Multihop free-space optical communications over strong turbulence channels. In Proceedings of the 2006 IEEE International Conference on Communications, Istanbul, Turkey, 11–15 June 2006; Volume 6, pp. 2755–2759. [Google Scholar]
- Karagiannidis, G.K.; Tsiftsis, T.A.; Sandalidis, H.G. Outage probability of relayed free space optical communication systems. Electron. Lett. 2006, 42, 994–996. [Google Scholar] [CrossRef]
- Safari, M.; Uysal, M. Relay-assisted free-space optical communication. IEEE Trans. Wirel. Commun. 2008, 7, 5441–5449. [Google Scholar] [CrossRef]
- Feng, M.; Wang, J.B.; Sheng, M.; Cao, L.L.; Xie, X.X.; Chen, M. Outage performance for parallel relay-assisted free-space optical communications in strong turbulence with pointing errors. In Proceedings of the 2011 International Conference on Wireless Communications and Signal Processing, Nanjing, China, 9–11 November 2011; pp. 1–5. [Google Scholar]
- Wang, P.; Wang, R.; Guo, L.; Cao, T.; Yang, Y. On the performances of relay-aided FSO system over M distribution with pointing errors in presence of various weather conditions. Opt. Commun. 2016, 367, 59–67. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Nistazakis, H.E.; Stassinakis, A.N.; Tombras, G.S.; Christofilakis, V.; Volos, C.K. Outage performance of mixed, parallel and serial DF relayed FSO links over weak turbulence channels with nonzero boresight pointing errors. In Proceedings of the 2018 7th International Conference in Modern Circuits and Systems Technologies (MOCAST2018), Thessaloniki, Greece, 7–9 May 2018; p. 4. [Google Scholar]
- Epple, B. Simplified channel model for simulation of free-space optical communications. IEEE/OSA J. Opt. Commun. Netw. 2010, 2, 293–304. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; Garcia-Zambrana, A.; Castillo-Vazquez, C.; Castillo-Vazquez, B. Novel approximation of misalignment fading modeled by Beckmann distribution on free-space optical links. Opt. Express 2016, 24, 22635–22649. [Google Scholar] [CrossRef]
- Al-Habash, M.A.; Andrews, L.C.; Phillips, R.L. Mathematical model for the irradiance probability density function of a laser beam propagating through turbulent media. Opt. Eng. 2001, 40, 1554–1562. [Google Scholar] [CrossRef]
- Popoola, W.O.; Ghassemlooy, Z.; Ahmadi, V. Performance of sub-carrier modulated free-space optical communication link in negative exponential atmospheric turbulence environment. Int. J. Auton. Adapt. Commun. Syst. 2008, 1, 342–355. [Google Scholar] [CrossRef]
- Nistazakis, H.E.; Stassinakis, A.N.; Muhammad, S.S.; Tombras, G.S. BER Estimation for Multi Hop RoFSO QAM or PSK OFDM Communication Systems Over Gamma Gamma or Exponentially Modeled Turbulence Channels. Elsevier Opt. Laser Technol. 2014, 64, 106–112. [Google Scholar] [CrossRef]
- Muhammad, S.S.; Köhldorfer, P.; Leitgeb, E. Channel Modeling for Terrestrial Free Optical Links. In Proceedings of the 7th International Conference on Transparent Optical Networks ICTON 2005, Barcelona, Spain, 3–7 July 2005; pp. 407–410. [Google Scholar]
- Gappmair, W. Novel results on pulse-position modulation performance for terrestrial free-space optical links impaired by turbulent atmosphere and pointing errors. IET Commun. 2012, 6, 1300–1305. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products, 6th ed.; Academic: New York, NY, USA, 2008. [Google Scholar]
- Gappmair, W.; Nistazakis, H.E. Subcarrier PSK performance in terrestrial FSO links impaired by Gamma-Gamma fading, pointing errors, and phase noise. J. Lightwave Technol. 2017, 35, 1624–1632. [Google Scholar] [CrossRef]
- Varotsos, G.K.; Stassinakis, A.N.; Nistazakis, H.E.; Tsigopoulos, A.D.; Peppas, K.P.; Aidinis, C.J.; Tombras, G.S. Probability of fade estimation for FSO links with time dispersion and turbulence modeled with the gamma–gamma or the IK distribution. Opt. Int. J. Light Electron Opt. 2014, 125, 7191–7197. [Google Scholar] [CrossRef]
- Garcia-Zambrana, A.; Castillo-Vazquez, B.; Castillo-Vazquez, C. Average Capacity of FSO Links with Transmit Laser Selection Using Non-Uniform OOK Signaling Over Exponential Atmospheric Turbulence Channels. Opt. Express 2010, 18, 20445–20454. [Google Scholar] [CrossRef] [PubMed]
- Varotsos, G.K.; Nistazakis, H.E.; Gappmair, W.; Sandalidis, H.G.; Tombras, G.S. DF Relayed Subcarrier FSO Links over Malaga Turbulence Channels with Phase Noise and Non-Zero Boresight Pointing Errors. Appl. Sci. 2018, 8, 664. [Google Scholar] [CrossRef]
- The Wolfram Functions Site. 2008. Available online: http:/functions.wolfram.com (accessed on 20 October 2018).
- Sandalidis, H.G.; Tsiftsis, T.A.; Karagiannidis, G.K. Optical wireless communications with heterodyne detection over turbulence channels with pointing errors. J. Lightwave Technol. 2009, 27, 4440–4445. [Google Scholar] [CrossRef]
- Adamchik, V.S.; Marichev, O.I. The Algorithm for Calculating Integrals of Hypergeometric Type Function and its Realization in Reduce System. In Proceedings of the International Conference on Symbolic and Algebraic Computation, Tokyo, Japan, 20–24 August 1990; pp. 212–224. [Google Scholar]
- Ninos, M.P.; Nistazakis, H.E.; Tombras, G.S. On the BER performance of FSO links with multiple receivers and spatial jitter over gamma-gamma or exponential turbulence channels. Opt. Int. J. Light Electron Opt. 2017, 138, 269–279. [Google Scholar] [CrossRef]
- Ansari, I.S.; Yilmaz, F.; Alouini, M.S. Performance Analysis of Free-Space Optical Links Over Málaga Turbulence Channels with Pointing Errors. IEEE Trans. Wirel. Commun. 2016, 15, 91–102. [Google Scholar] [CrossRef]
- Djordjevic, G.T.; Petkovic, M.I. Average BER performance of FSO SIM-QAM systems in the presence of atmospheric turbulence and pointing errors. J. Mod. Opt. 2016, 63, 715–723. [Google Scholar] [CrossRef]
- Proakis, J.G. Digital Communications; McGraw-Hill: New York, NY, USA, 1989. [Google Scholar]
- Davis, J.; Tango, W. Measurement of the atmospheric coherence time. Publ. Astron. Soc. Pac. 1996, 108, 456. [Google Scholar] [CrossRef]
- Popoola, W.O.; Ghassemlooy, Z.; Lee, C.G.; Boucouvalas, A.C. Scintillation effect on intensity modulated laser communication systems—A laboratory demonstration. Opt. Laser Technol. 2010, 42, 682–692. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Varotsos, G.K.; Nistazakis, H.E.; Stassinakis, A.N.; Volos, C.K.; Christofilakis, V.; Tombras, G.S. Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels. Technologies 2018, 6, 121. https://doi.org/10.3390/technologies6040121
Varotsos GK, Nistazakis HE, Stassinakis AN, Volos CK, Christofilakis V, Tombras GS. Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels. Technologies. 2018; 6(4):121. https://doi.org/10.3390/technologies6040121
Chicago/Turabian StyleVarotsos, George K., Hector E. Nistazakis, Argyris N. Stassinakis, Christos K. Volos, Vasileios Christofilakis, and George S. Tombras. 2018. "Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels" Technologies 6, no. 4: 121. https://doi.org/10.3390/technologies6040121
APA StyleVarotsos, G. K., Nistazakis, H. E., Stassinakis, A. N., Volos, C. K., Christofilakis, V., & Tombras, G. S. (2018). Mixed Topology of DF Relayed Terrestrial Optical Wireless Links with Generalized Pointing Errors over Turbulence Channels. Technologies, 6(4), 121. https://doi.org/10.3390/technologies6040121







