Characterization of Fading Statistics of mmWave (28 GHz and 38 GHz) Outdoor and Indoor Radio Propagation Channels †
Abstract
1. Introduction
2. Overview of Measurement Setup and Used Data-Extraction Method
2.1. Case 1: Outdoor Urban Environment at 38 GHz
2.2. Case 2: Indoor Corridor Environment at 28 GHz and 38 GHz
2.3. Case 3: Indoor Office Environment at 28 GHz
2.4. Data Extraction and Calibration
3. Channel Statistics
3.1. Definition of Angular Spread Quantifiers
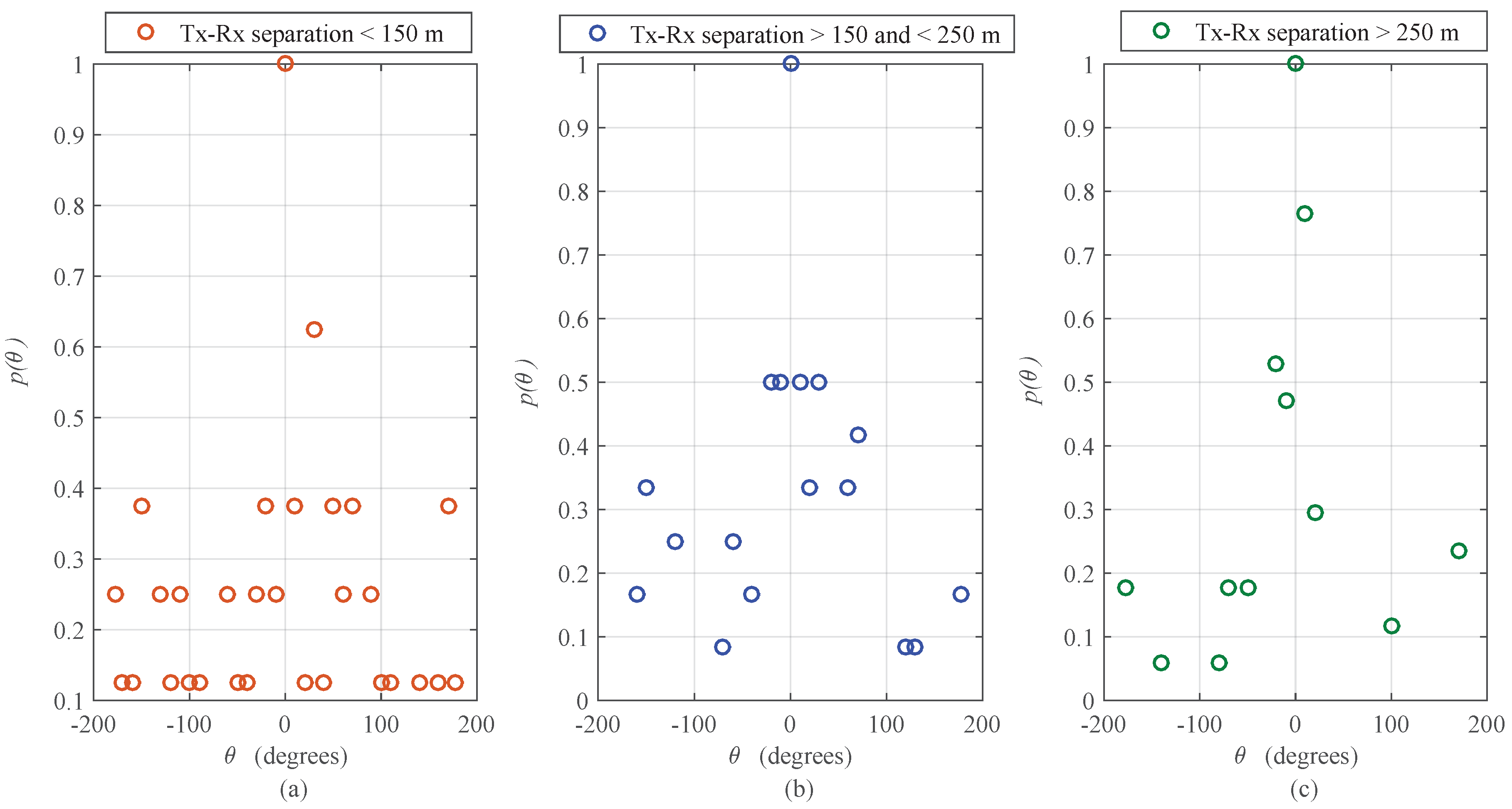
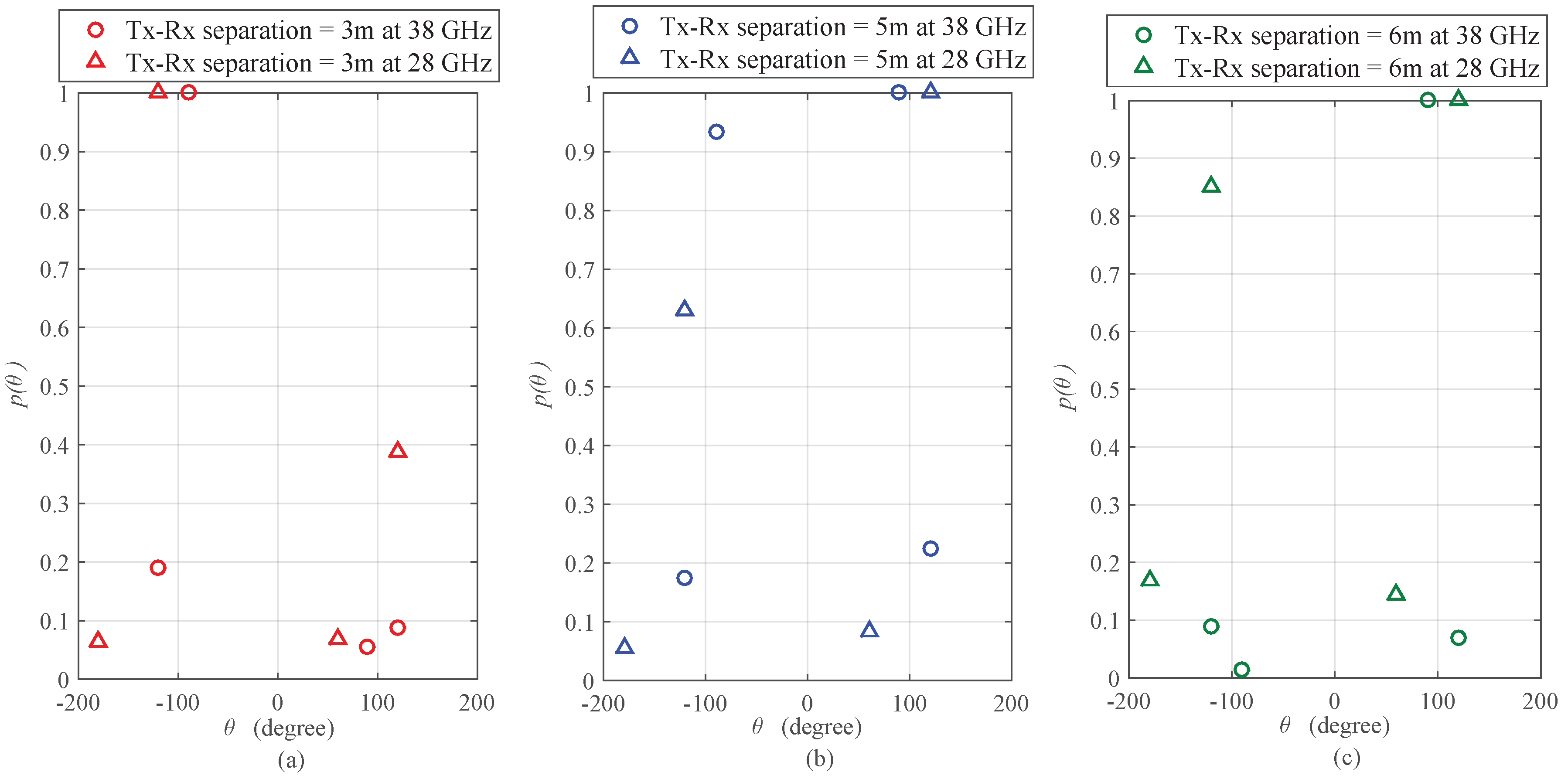
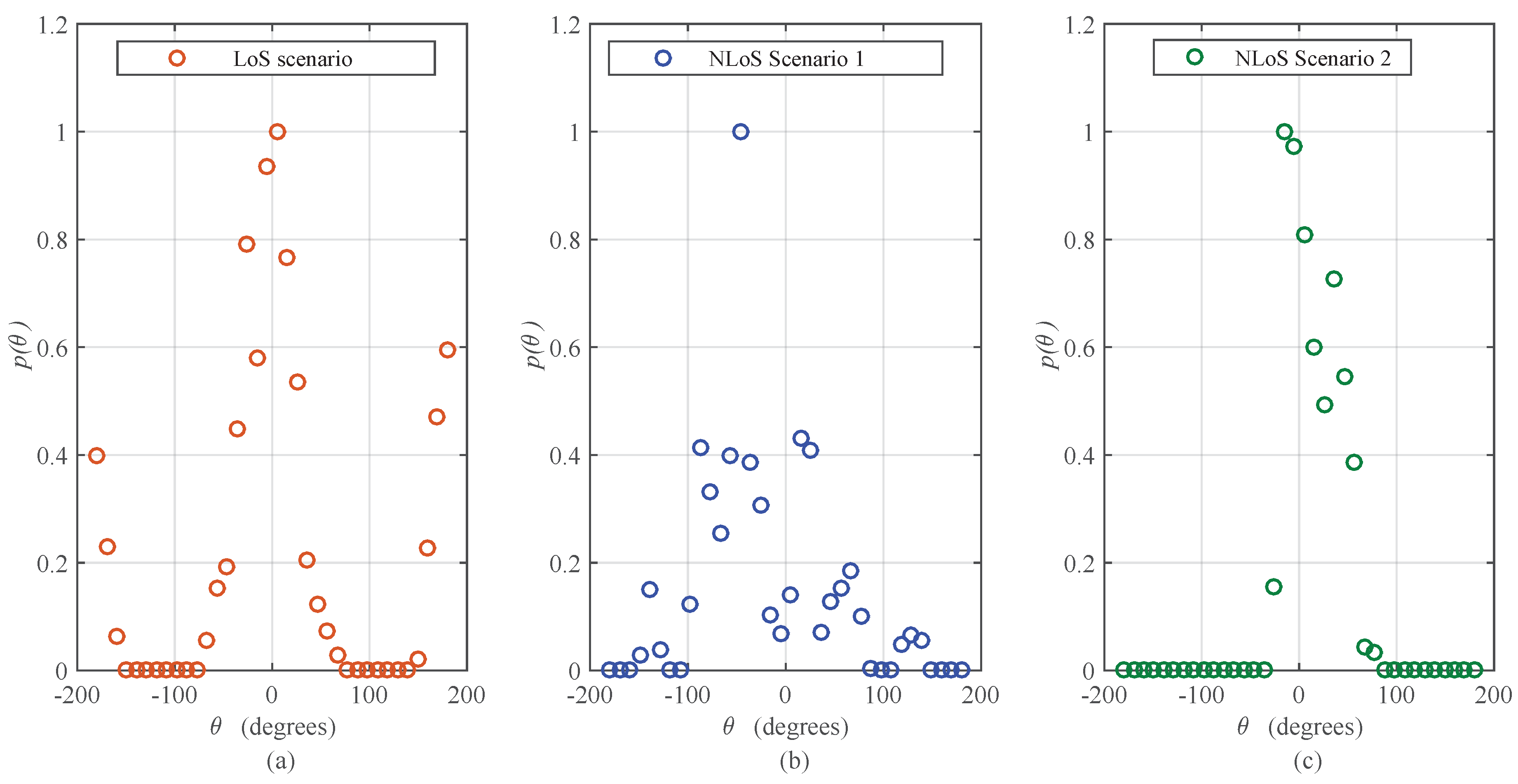
3.2. Characterization of Angular Spread for Outdoor and Indoor Radio Propagation Channels
3.3. Definition of SOFS Quantifiers
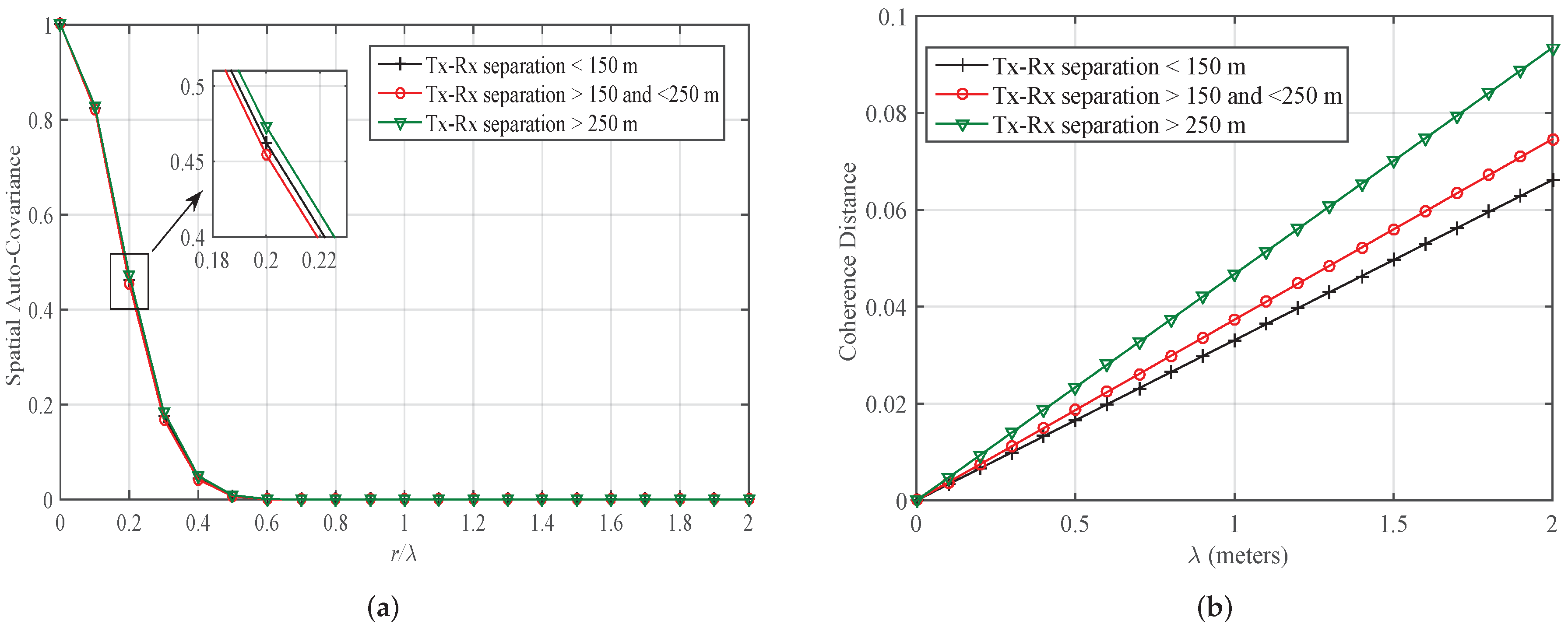
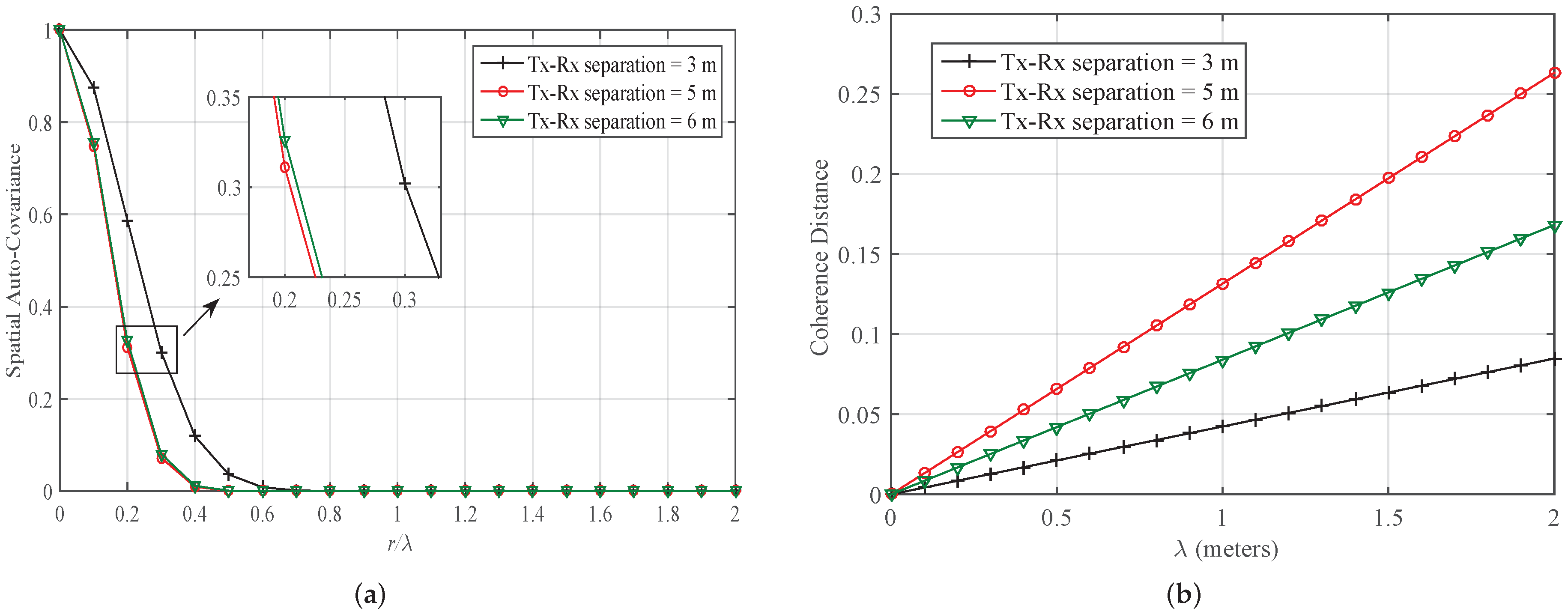
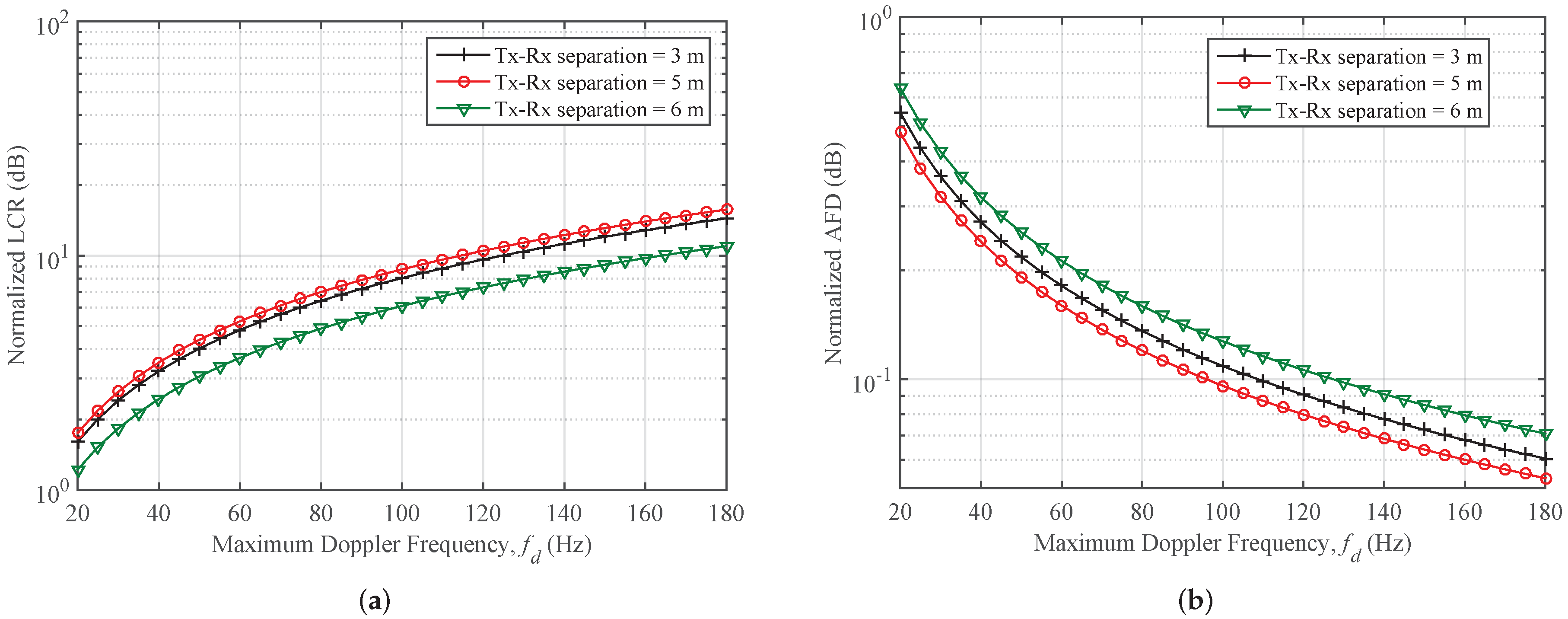
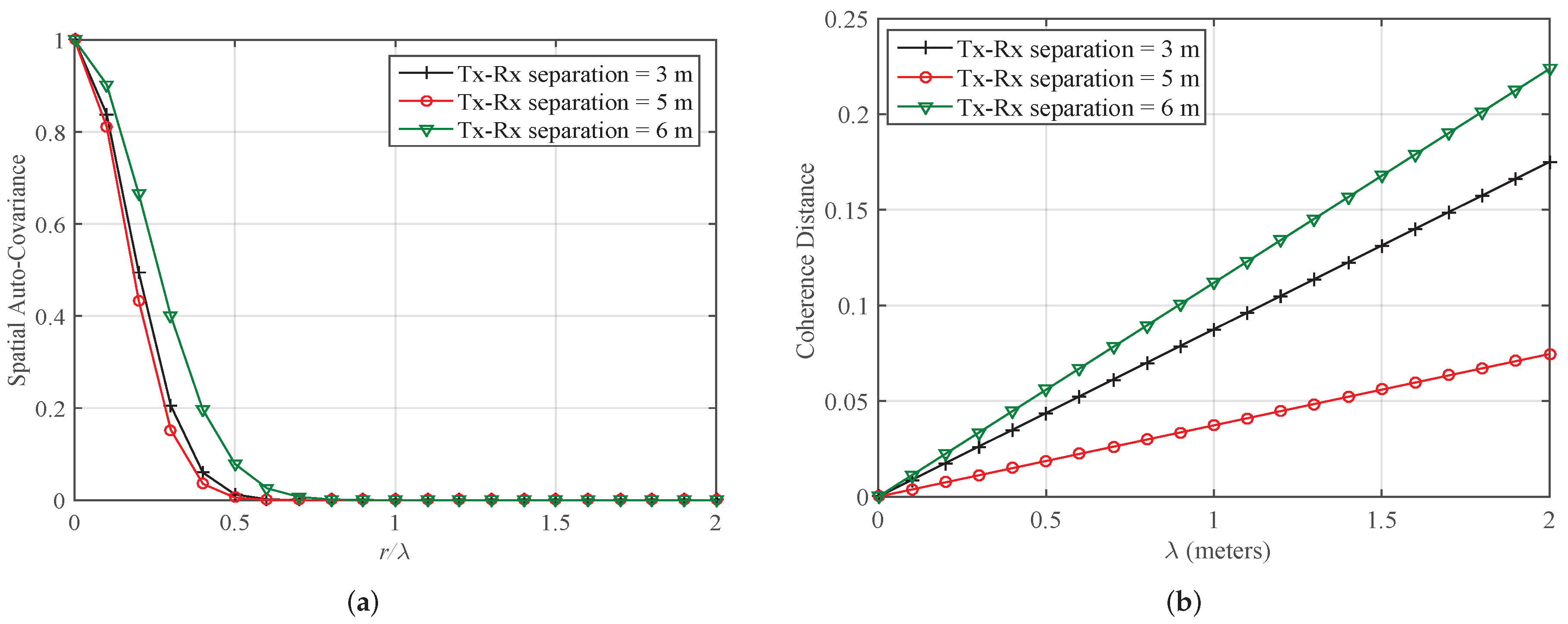
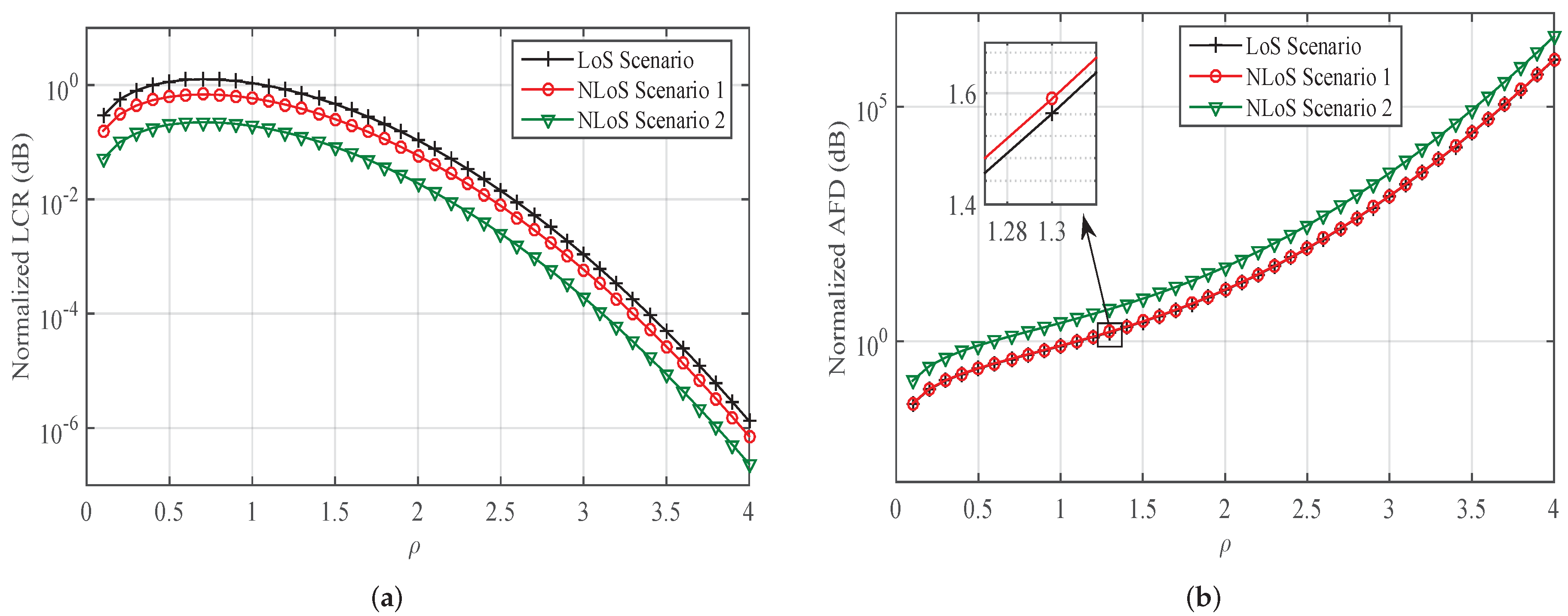
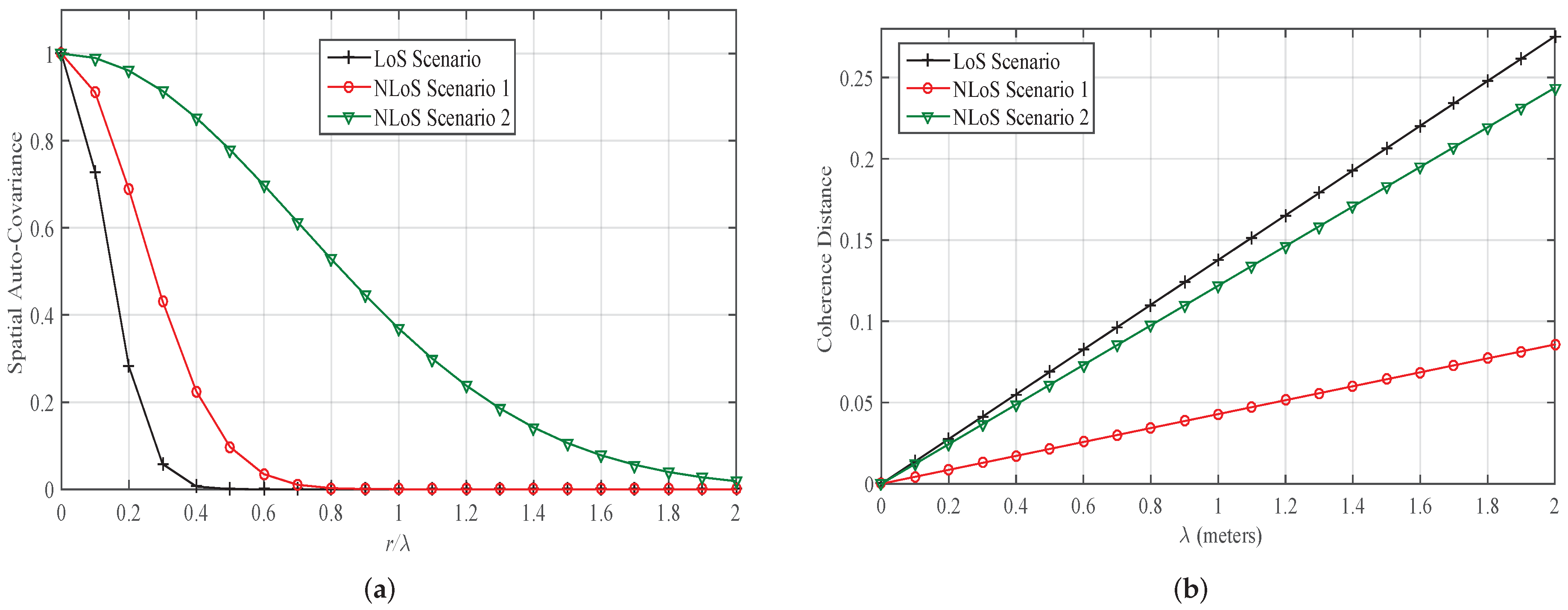
3.4. Characterization of SOFS for Outdoor and Indoor Radio Propagation Channels
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Vatalaro, F.; Forcella, A. Doppler spectrum in mobile-to-mobile communications in the presence of three-dimensional multipath scattering. IEEE Trans. Veh. Technol. 1997, 46, 213–219. [Google Scholar] [CrossRef]
- Nawaz, S.J.; Khan, N.M.; Patwary, M.N.; Moniri, M. Effect of directional antenna on the Doppler spectrum in 3-D mobile radio propagation environment. IEEE Trans. Veh. Technol. 2011, 60, 2895–2903. [Google Scholar] [CrossRef]
- Azar, Y.; Wong, G.N.; Wang, K.; Mayzus, R.; Schulz, J.K.; Zhao, H.; Gutierrez, F.; Hwang, D.; Rappaport, T.S. 28 GHz propagation measurements for outdoor cellular communications using steerable beam antennas in New York city. In Proceedings of the IEEE International Conference on Communications (ICC), Budapest, Hungary, 9–13 June 2013; pp. 5143–5147. [Google Scholar]
- Rappaport, T.S.; Gutierrez, F.; Ben-Dor, E.; Murdock, J.N.; Qiao, Y.; Tamir, J.I. Broadband Millimeter-Wave Propagation Measurements and Models Using Adaptive-Beam Antennas for Outdoor Urban Cellular Communications. IEEE Trans. Antenn. Propag. 2013, 61, 1850–1859. [Google Scholar] [CrossRef]
- Eldowek, B.M.; El-atty, S.M.A.; El-Rabaie, E.S.M.; El-Samie, F.E.A. Second-Order Statistics Channel Model for 5G Millimeter-Wave Mobile Communications. Arab. J. Sci. Eng. 2017, 43, 2833–2842. [Google Scholar] [CrossRef]
- Yin, X.; Ling, C.; Kim, M.D. Experimental Multipath-Cluster Characteristics of 28-GHz Propagation Channel. IEEE Access 2015, 3, 3138–3150. [Google Scholar] [CrossRef]
- Al-samman, A.M.; Abd Rahman, T.; Azmi, M.H. Indoor Corridor Wideband Radio Propagation Measurements and Channel Models for 5G Millimeter Wave Wireless Communications at 19 GHz, 28 GHz, and 38 GHz Bands. Wirel. Commun. Mob. Comput. 2018, 2018, 6369517. [Google Scholar] [CrossRef]
- Nawaz, S.J.; Wyne, S.; Baltzis, K.B.; Gulfam, S.M.; Cumanan, K. A tunable 3-D statistical channel model for spatio-temporal characteristics of wireless communication networks. Trans. Emerg. Telecommun. Technol. 2017, 28, e3213. [Google Scholar] [CrossRef]
- Durgin, G.D.; Rappaport, T.S. Effects of multipath angular spread on the spatial cross-correlation of received voltage envelopes. In Proceedings of the IEEE Vehicular Technology Conference, Houston, TX, USA, 16–20 May 1999; Volume 2, pp. 996–1000. [Google Scholar]
- Durgin, G.D.; Rappaport, T.S. Theory of multipath shape factors for small-scale fading wireless channels. IEEE Trans. Antenn. Propag. 2000, 48, 682–693. [Google Scholar] [CrossRef]
- Zajic, A.G.; Stuber, G.L. Three-dimensional modeling, simulation, and capacity analysis of space–time correlated mobile-to-mobile channels. IEEE Trans. Veh. Technol. 2008, 57, 2042–2054. [Google Scholar] [CrossRef]
- Ziolkowski, C.; Kelner, J.M. Statistical evaluation of the azimuth and elevation angles seen at the output of the receiving antenna. IEEE Trans. Antennas Propag. 2018, 66, 2165–2169. [Google Scholar] [CrossRef]
- Ziolkowski, C.; Kelner, J.M. Antenna pattern in three-dimensional modelling of the arrival angle in simulation studies of wireless channels. IET Microw. Antennas Propag. 2017, 11, 898–906. [Google Scholar] [CrossRef]
- Valchev, D.G. Spatial Modeling of Three-Dimensional Multipath Wireless Channels. Ph.D. Thesis, Northeastern University, Boston, MA, USA, 2008. [Google Scholar]
- Valchev, D.G.; Brady, D. Three-dimensional multipath shape factors for spatial modeling of wireless channels. IEEE Trans. Wirel. Commun. 2009, 8, 5542–5551. [Google Scholar] [CrossRef]
- Nawaz, S.J.; Khan, N.M.; Ramer, R. 3-D Spatial Spread Quantifiers for Multipath Fading Wireless Channels. IEEE Wireless Commun. Lett. 2016, 5, 484–487. [Google Scholar] [CrossRef]
- Khan, N.M. Modeling and Characterization of Multipath Fading Channels in Cellular Mobile Communication System. Ph.D. Thesis, School of Electrical Engineering and Telecommunication, University of New South Wales, Sydney, Australia, 2006. [Google Scholar]
- Lu, J.; Han, Y. Application of multipath shape factors in Nakagami-m fading channel. In Proceedings of the International Conference on Wireless Communications & Signal Processing, Nanjing, China, 13–15 November 2009; pp. 1–4. [Google Scholar]
- Youssef, N.; Wang, C.X.; Patzold, M. A Study on the Second Order Statistics of Nakagami-Hoyt Mobile Fading Channels. IEEE Trans. Veh. Technol. 2005, 54, 1259–1265. [Google Scholar] [CrossRef]
- Filho, J.; Yacoub, M. On the second-order statistics of Nakagami fading simulators. IEEE Trans. Commun. 2009, 57, 3543–3546. [Google Scholar] [CrossRef]
- Loni, Z.M.; Khan, N.M. Analysis of fading statistics in cellular mobile communication systems. J. Supercomput. 2013, 64, 295–309. [Google Scholar] [CrossRef]
- Gulfam, S.M.; Nawaz, S.J.; Ahmed, A.; Patwary, M.N. Analysis on multipath shape factors of air-to-ground radio communication channels. In Proceedings of the 2016 Wireless Telecommunications Symposium (WTS), London, UK, 18–20 April 2016; pp. 1–5. [Google Scholar]
- Gulfam, S.M.; Nawaz, S.J.; Ahmed, A.; Patwary, M.N.; Ni, Q. A Novel 3D Analytical Scattering Model for Air-to-Ground Fading Channels. Appl. Sci. 2016, 6, 207. [Google Scholar] [CrossRef]
- Ahmed, A.; Nawaz, S.J.; Gulfam, S.M. A 3-D Propagation Model for Emerging Land Mobile Radio Cellular Environments. PLoS ONE 2015, 10, e0132555. [Google Scholar] [CrossRef]
- Waseer, W.I.; Junaid Nawaz, S.; Gulfam, S.M.; Mughal, M.J. Second-order fading statistics of massive-MIMO vehicular radio communication channels. Trans. Emerg. Telecommun. Technol. 2018, 29, e3487. [Google Scholar] [CrossRef]
- Iqbal, T. Statistical Fading Analysis of Millimeter Waves for Mobile Channel. Master’s Thesis, Department of Electronic Engineering, Mohammad Ali Jinnah University, Islamabad, Pakistan, 2015. [Google Scholar]
- Gulfam, S.M.; Nawaz, S.J.; Baltzis, K.B. Characterization of second-order fading statistics of 28 GHz indoor radio propagation channels. In Proceedings of the 7th International Conference on Modern Circuits and Systems Technologies (MOCAST), Thessaloniki, Greece, 7–9 May 2018; pp. 1–4. [Google Scholar]
- Nawaz, S.J.; Ahmed, A.; Wyne, S.; Cumanan, K.; Ding, Z. 3-D Spatial Modeling of Network Interference in Two-Tier Heterogeneous Networks. IEEE Access 2017, 5, 24040–24053. [Google Scholar] [CrossRef]
- Chen, Y.; Mucchi, L.; Wang, R.; Huang, K. Modeling Network Interference in the Angular Domain: Interference Azimuth Spectrum. IEEE Trans. Commun. 2014, 62, 2107–2120. [Google Scholar] [CrossRef]
- Jameel, F.; Wyne, S.; Syed, J.N.; Chang, Z. Propagation Channels for mmWave Vehicular Communications: State-of-the-art and Future Research Directions. arXiv, 2018; arXiv:1812.02483. [Google Scholar]


| Measurement Scenario | Propagation Environment | Frequency Band | Channel Statistics | |
|---|---|---|---|---|
| Available | Proposed Extension | |||
| Case 1 [4] | Outdoor Urban | 38 GHz | Path Loss, Root Mean Square (RMS) Delay Spread, AoA | Azimuthal Spread Quantification, LCR, AFD, CD, Auto-Correlations |
| Case 2 [7] | Indoor Corridor | 28 and 38 GHz | Path Loss, RMS Delay Spread, AoA | Azimuthal Spread Quantification, LCR, AFD, CD, Auto-Correlations |
| Case 3 [6] | Indoor Office | 28 GHz | Delay Spread, AoA, Time of Arrival | Azimuthal Spread Quantification, LCR, AFD, CD, Auto-Correlations |
| Angular Spread Quantifiers | Quantifiers and Measurement Details | Angular Spread [10] | True Standard Deviation [16,17] | Angular Constriction [10] | Direction of Maximum Fading [10] |
| Mathematical Expression: | |||||
| Range of Quantifier: | 0∼1. | 0∼2 (∼) | 0∼1 | ∼ (∼) | |
| Description: | Denotes concentration of multipaths around a single direction. 0 indicates the concentration of energy around exactly one path, while 1 indicates no bias. | Denotes measure of energy dispersion in angular domain. Measures the spread in true scientific notation, i.e., radians or degrees. | Denotes concentration of multipaths about two directions. 1 indicates the concentration of energy about exactly two paths, while 0 indicates no bias. | Denotes the physical direction of maximum fading in radians. | |
| Case 1: Outdoor Urban Environment at 38 GHz | Tx-Rx separation < 150 m | 0.9829 | 0.163 | ||
| Tx-Rx separation > 150 m and < 250 m | 0.955 | 0.0941 | |||
| Tx-Rx separation > 250 m | 0.891 | 0.0698 | |||
| Case 2 (a): Indoor Corridor Environment at 28 GHz | Tx-Rx separation = 3 m | 0.8463 | 0.7297 | ||
| Tx-Rx separation = 5 m | 0.8789 | 0.74 | |||
| Tx-Rx separation = 6 m | 0.9077 | 0.6605 | |||
| Case 2 (b): Indoor Corridor Environment at 38 GHz | Tx-Rx separation = 3 m | 0.767 | 0.705 | ||
| Tx-Rx separation = 5 m | 0.969 | 0.322 | |||
| Tx-Rx separation = 6 m | 0.619 | 0.852 | |||
| Case 3: Indoor Office Environment at 28 GHz | LoS Scenario (Figure 8b of [6]) | 0.9049 | 0.6834 | ||
| NLoS Scenario 1 (Figure 8e of [6]) | 0.7906 | 0.3881 | |||
| NLoS Scenario 2 (Figure 8h of [6]) | 0.4125 | 0.9212 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gulfam, S.M.; Nawaz, S.J.; Baltzis, K.B.; Ahmed, A.; Khan, a.N.M. Characterization of Fading Statistics of mmWave (28 GHz and 38 GHz) Outdoor and Indoor Radio Propagation Channels. Technologies 2019, 7, 9. https://doi.org/10.3390/technologies7010009
Gulfam SM, Nawaz SJ, Baltzis KB, Ahmed A, Khan aNM. Characterization of Fading Statistics of mmWave (28 GHz and 38 GHz) Outdoor and Indoor Radio Propagation Channels. Technologies. 2019; 7(1):9. https://doi.org/10.3390/technologies7010009
Chicago/Turabian StyleGulfam, Sardar Muhammad, Syed Junaid Nawaz, Konstantinos B. Baltzis, Abrar Ahmed, and and Noor M. Khan. 2019. "Characterization of Fading Statistics of mmWave (28 GHz and 38 GHz) Outdoor and Indoor Radio Propagation Channels" Technologies 7, no. 1: 9. https://doi.org/10.3390/technologies7010009
APA StyleGulfam, S. M., Nawaz, S. J., Baltzis, K. B., Ahmed, A., & Khan, a. N. M. (2019). Characterization of Fading Statistics of mmWave (28 GHz and 38 GHz) Outdoor and Indoor Radio Propagation Channels. Technologies, 7(1), 9. https://doi.org/10.3390/technologies7010009





