Localization Meets Uncertainty: Uncertainty-Aware Multi-Modal Localization

Abstract

Reliable localization is critical for robot navigation in complex indoor environments. In this paper, we propose an uncertainty-aware localization method that enhances the reliability of localization outputs without modifying the prediction model itself. This study introduces a percentile-based rejection strategy that filters out unreliable 3-degree-of-freedom pose predictions based on aleatoric and epistemic uncertainties the network estimates. We apply this approach to a multi-modal end-to-end localization that fuses RGB images and 2D LiDAR data, and we evaluate it across three real-world datasets collected using a commercialized serving robot. Experimental results show that applying stricter uncertainty thresholds consistently improves pose accuracy. Specifically, the mean position error, calculated as the average Euclidean distance between the predicted and ground-truth (x, y) coordinates, is reduced by 41.0%, 56.7%, and 69.4%, and the mean orientation error, representing the average angular deviation between the predicted and ground-truth yaw angles, is reduced by 55.6%, 65.7%, and 73.3%, when percentile thresholds of 90%, 80%, and 70% are applied, respectively. Furthermore, the rejection strategy effectively removes extreme outliers, resulting in better alignment with ground truth trajectories. To the best of our knowledge, this is the first study to quantitatively demonstrate the benefits of percentile-based uncertainty rejection in multi-modal and end-to-end localization tasks. Our approach provides a practical means to enhance the reliability and accuracy of localization systems in real-world deployments.

1. Introduction

Localization is a classical problem in the robotics literature. With simultaneous localization and mapping (SLAM) [1,2] and its related technologies [3,4], localization techniques have been constantly developed, and the advances have led to some commercial services using mobile robots and self-driving cars. In particular, service robots have been widely used in indoor environments such as hotels, hospitals, and restaurants for tasks like food delivery or guest assistance in recent years. In such dynamic environments, robots frequently encounter localization challenges such as occlusions, dynamic obstacles, or map drift. These issues can lead to localization failure, causing the robot to become lost or deliver items to incorrect locations. One of the most well-known failure scenarios is the kidnapped robot problem, where a robot is unexpectedly displaced without any sensor trace, making recovery difficult for conventional SLAM-based approaches. To ensure robust and uninterrupted operation, especially after initialization or recovery from failure, global localization—where a robot must estimate its pose from scratch without prior information—plays a critical role in these scenarios. End-to-end localization based on a deep neural network can be a promising solution to global localization.

PoseNet [5] is the first study on the deep learning-based end-to-end localization method. It estimates a six-dimensional pose directly from sensor data (image) using neural networks in an end-to-end manner. Since PoseNet, the following studies have been conducted based on images [6,7,8], 3D point clouds [9,10,11,12], inertial information [13], and the fusion of images and 2D point clouds [14]. These end-to-end localization methods are known to be more robust against sensor data variations such as noise and illumination. However, it is difficult to use them solely because they generally provide relatively higher localization errors compared to the matching-based localization methods. Meanwhile, Jo and Kim [15] utilized PoseNet to obtain an initial pose for a particle filter-based localization. However, they overlooked how much confidence we can have in the output of PoseNet. If a localization result with a large error is served as the initial pose, the navigation system may fail to operate properly. In detail, due to factors such as complex environments, sensor noise, or data inconsistency, the estimated pose can suddenly jump or become unstable. Such issues may cause the localization failure, causing a serious risk to safe robot operation.

In this paper, we propose an uncertainty-aware multi-modal end-to-end network that can quantitatively estimate both the pose and its associated uncertainty, along with an uncertainty-based percentile rejection mechanism. The proposed network is built on the FusionLoc architecture, extending it to estimate both aleatoric and epistemic uncertainty. Specifically, the regression branch is augmented to predict the variance representing aleatoric uncertainty, while Monte Carlo (MC) dropout [16] is employed to approximate the model posteriors for estimating epistemic uncertainty. Furthermore, going beyond the findings of Li et al. [12], which demonstrated a strong correlation between the measured uncertainty and localization error, we apply a percentile rejection method based on the predicted uncertainty. This approach effectively reduces localization errors and enhances the reliability of localization results by filtering out unreliable localization results with large errors. As a result, it can improve safety and practical utility in safety-critical scenarios such as adaptive Monte Carlo localization (AMCL) initialization or recovery from localization failures. Experiments using our datasets collected by a 2D LiDAR and a camera demonstrate that the uncertainty-based rejection effectively reduces position and orientation errors. More specifically, our uncertainty-based rejection method reduces the position error by up to 69.4% and the orientation error by 73.3%. In particular, experimental results show that our strategy can exclude the outputs with significant position and orientation errors. This means that the passed outputs are reliable enough for the results of global localization. To the best of our knowledge, this is the first study that systematically utilizes uncertainty-based thresholds to reject unreliable localization results predicted in an end-to-end manner and improves the accuracy and confidence of pose estimates. The main contributions of this paper are as follows:

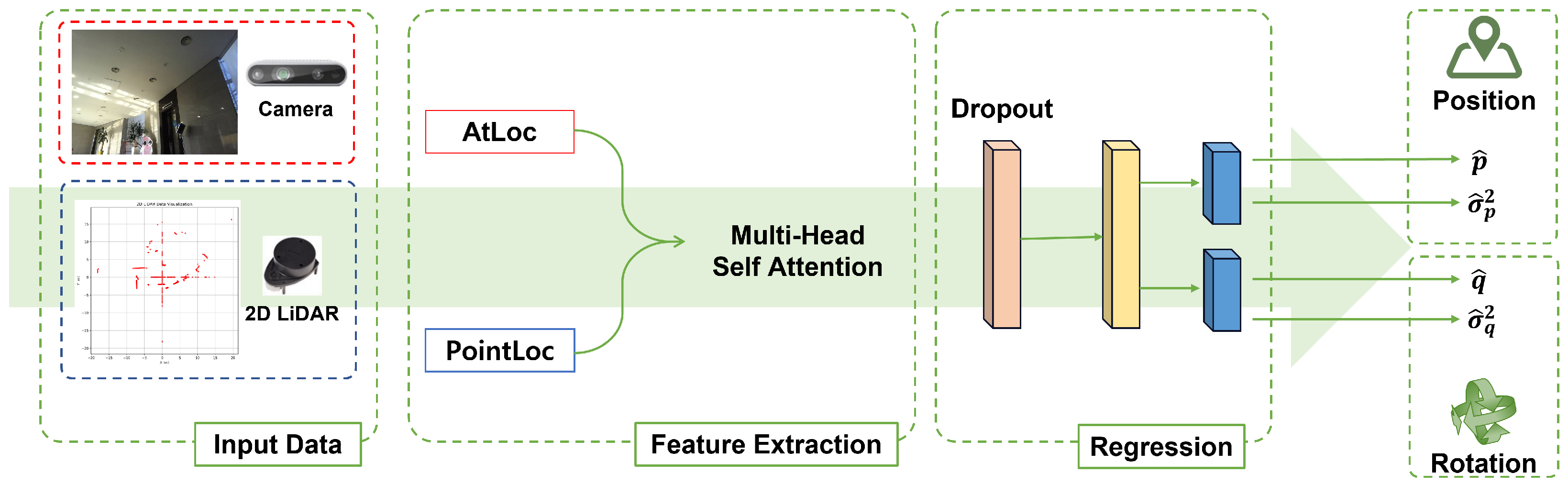
• A novel uncertainty-aware multi-modal end-to-end localization framework that not only estimates the robot’s 3-DoF pose but also quantifies uncertainty associated with the predictions. The original FusionLoc architecture is extended to output uncertainty values by integrating MC dropout for epistemic uncertainty and direct variance regression for aleatoric uncertainty, enabling a more reliable and informative localization result.
• We introduce a percentile-based rejection method using the thresholds (e.g., 70%, 80%, and 90%) to reject low-confidence pose estimations, thereby improving localization robustness and safety in uncertain environments.
• The proposed approach is validated on three indoor datasets under various environmental conditions, demonstrating the effectiveness of uncertainty-aware localization over standard approaches.

The remainder of this paper is organized as follows. Section 2 reviews related works on end-to-end localization and uncertainty quantification. Section 3 describes the proposed method, including the original FusionLoc architecture and the extensions introduced for measuring uncertainty. Section 4 presents the datasets used and the experimental results. Finally, Section 5 concludes the paper and provides future work.

2. Related Works

2.1. End-to-End Localization

End-to-end localization, also known as absolute pose regression, directly predicts the pose of a robot or a sensor from its data using deep neural networks, without conventional procedures such as feature detection and matching. It can serve as a solution for global localization, particularly in environments where GPS is unavailable. Depending on the type of sensors used for localization, it can be categorized into camera, LiDAR, and multi-modal localizations.

Visual localization estimates the current pose using only images captured by a camera in indoor or outdoor environments. Initially, convolutional neural networks (CNNs) are primarily leveraged to extract salient features. However, recent studies have introduced various techniques in their models. Kendall et al. [5] developed a CNN-based 6-DoF pose regression model that allows localization without relying on feature matching or keyframes. Meanwhile, Wang et al. [6] employed the self-attention technique [17] to improve the accuracy of the end-to-end localization. Moreover, Transformer architectures [17] have also been utilized for end-to-end camera localization [7,8]. Also, Wang et al. [18] integrated CNNs, self-attention, and long short-term memory (LSTM) modules in a unified architecture to extract static features, which can lead to more effective 6-DoF pose estimation compared to using dynamic features. Recently, Zheng et al. [19] introduced a more advanced algorithm than the end-to-end localization methods, called scene-agnostic pose regression. It is noteworthy that it does not require the collection of new datasets or retraining for deployment in previously unseen environments.

LiDAR-based end-to-end localization leverages 3D structural information, making it robust in textureless environments. Wang et al. [9] introduced the first LiDAR-based 6-DoF pose regression model, enhancing feature learning with the self-attention mechanism. Yu et al. [10] proposed a deep neural network for pose regression that consists of two modules: a universal encoder for scene feature extraction and a regressor for pose estimation. They also demonstrated the relationship between the regression capability and the number of hidden units in the regression module. Yu et al. [20] introduced additional classification headers alongside the original regression headers, together with a feature aggregation module based on temporal attention for spatial and temporal constraints. Ibrahim et al. [21] presented a self-supervised learning approach utilizing a Transformer-based backbone for LiDAR-based end-to-end localization. Also, SGLoc [11] enhanced pose regression accuracy by incorporating scene geometry encoding. Recently, Li et al. [12] proposed measuring uncertainty from the outputs of their proposed method, DiffLoc, a diffusion model for localization to estimate the 6-DoF pose of a 3D LiDAR sensor from a point cloud. Their approach further improves accuracy by applying an iterative denoising process based on a diffusion model to the pose regression. Yu et al. [22] proposed a 3D LiDAR localization method inspired by neurobiological mechanisms of three different cells in mammalian brains. Yang et al. [23] utilized semantic awareness to mitigate negative effects caused by dynamic objects and repeating structures so that they improved the localization accuracy and robustness.

Some studies have combined complementary information from multiple modalities to improve the robustness of localization. For instance, Lai et al. [24] proposed leveraging both visual and LiDAR features to achieve more accurate and robust place recognition. Wang et al. [25] developed a vision-assisted LiDAR localization method that effectively utilizes visual information to address issues related to 2D LiDAR-based localization drift. Additionally, Nakamura et al. [26] incorporated a fisheye camera together with a 2D LiDAR system to enhance localization fault detection. However, the methods mentioned above do not fall under the category of end-to-end localization techniques. FusionLoc [14] is an end-to-end localization method that utilizes multi-modality. It was demonstrated that taking both RGB images and 2D LiDAR point clouds as input could provide superior performance compared to a mono-modal input, either image or 2D LiDAR point cloud, by effectively leveraging complementary information from each modality. Table 1 provides a brief comparison of the previous studies mentioned above. In this study, we present a FusionLoc-based approach to make localization more reliable by rejecting network outputs with significant errors.

2.2. Uncertainty Quantification

Uncertainty quantification is a well-established topic in pattern recognition and machine learning. While it did not receive much attention during the early stages of the deep learning revolution—especially in comparison to efforts to enhance the accuracy of deep learning algorithms—its importance is becoming increasingly recognized, particularly in safety-critical applications. A Bayesian approach is one of the most comprehensive frameworks for managing uncertainty. However, developing and implementing a Bayesian deep neural network for regression tasks is very challenging because it is often impractical to determine posterior probabilities accurately. Fortunately, Gal and Ghahramani [16] presented dropout as an alternative to Bayesian approximation. Additionally, Kendall and Gal [27] proposed using the MC dropout to quantify both aleatoric and epistemic uncertainties in regression tasks, such as pixel-wise depth estimation.

After the groundbreaking studies, the following researchers focused on network calibration, which aims to align estimated uncertainty values with empirical results. Kuleshov et al. [28] introduced a simple, algorithm-agnostic method inspired by Platt scaling [29]. Cui et al. [30] utilized the maximum mean discrepancy, viewing calibration as a form of distribution matching. Similarly, Bhatt et al. [31] applied the f-divergence with the same perspective. In another approach, Yu et al. [32] proposed an auxiliary network branch to estimate uncertainty alongside the main branch used for the original regression task. This method is similar to the work of [33], which also employs additional network branches to estimate uncertainty or confidence in classification problems. For more details on uncertainty quantification in deep neural networks, refer to [34,35].

However, none of the studies mentioned above addressed the localization problem. Chen et al. [36] recently proposed a method for quantifying uncertainty in visual localization. However, their approach estimates the pose of a query image through keypoint matching rather than in an end-to-end manner. Unfortunately, the matching-based approaches are known to be more sensitive to variations such as illumination change and dynamic objects compared to the end-to-end approaches of the proposed method. In contrast, Li et al. [12] suggested an end-to-end localization approach using a diffusion model. However, their work primarily focused on the relationship between quantified uncertainties (variance) and positional errors, lacking qualitative experimental results. Unlike [12,36], this study aims to quantify uncertainty in the results of an end-to-end localization method. We will also demonstrate how this quantification can effectively reject network outputs with significant errors, ultimately improving the localization performance.

Table 1. Summary of related works on end-to-end localization.

Reference	Sensor Modality	Localization	Uncertainty
Kendall et al. [5]	RGB Camera	✓	✘
Wang et al. [6]	RGB Camera	✓	✘
Li and Ling [7]	Multi-view Camera	✓	✘
Qiao et al. [8]	RGB Camera	✓	✘
Wang et al. [18]	RGB Camera	✓	✘
Wang et al. [9]	3D LiDAR	✓	✘
Yu et al. [10]	3D LiDAR	✓	✘
Yu et al. [20]	3D LiDAR	✓	✘
Ibrahim et al. [21]	3D LiDAR	✓	✘
Li et al. [11]	3D LiDAR	✓	✘
Lai et al. [24]	RGB Camera + 3D LiDAR	✓	✘
Wang et al. [25]	RGB Camera + 2D LiDAR	✓	✘
Nakamura et al. [26]	Fisheye RGB Camera + 2D LiDAR	✓	✘
Lee et al. [14]	RGB Camera + 2D LiDAR	✓	✘
Chen et al. [36]	RGB Camera	✓	✓
Li et al. [12]	3D LiDAR	✓	✓
Ours	RGB Camera + 2D LiDAR	✓	✓

Table 1. Summary of related works on end-to-end localization.

Reference	Sensor Modality	Localization	Uncertainty
Kendall et al. [5]	RGB Camera	✓	✘
Wang et al. [6]	RGB Camera	✓	✘
Li and Ling [7]	Multi-view Camera	✓	✘
Qiao et al. [8]	RGB Camera	✓	✘
Wang et al. [18]	RGB Camera	✓	✘
Wang et al. [9]	3D LiDAR	✓	✘
Yu et al. [10]	3D LiDAR	✓	✘
Yu et al. [20]	3D LiDAR	✓	✘
Ibrahim et al. [21]	3D LiDAR	✓	✘
Li et al. [11]	3D LiDAR	✓	✘
Lai et al. [24]	RGB Camera + 3D LiDAR	✓	✘
Wang et al. [25]	RGB Camera + 2D LiDAR	✓	✘
Nakamura et al. [26]	Fisheye RGB Camera + 2D LiDAR	✓	✘
Lee et al. [14]	RGB Camera + 2D LiDAR	✓	✘
Chen et al. [36]	RGB Camera	✓	✓
Li et al. [12]	3D LiDAR	✓	✓
Ours	RGB Camera + 2D LiDAR	✓	✓

3. Method

3.1. Measuring Uncertainty

Deep learning has shown remarkable performance on various complex tasks, primarily focused on enhancing predictive accuracy. However, real-world applications often face uncertainty due to some factors, such as incomplete information and ambiguities. This complexity makes it difficult to assess the performance of the model solely on the basis of accuracy [30]. Therefore, quantifying uncertainty is crucial to improve prediction reliability, improve model robustness, and ensure safety.

Uncertainty can be divided into two categories: epistemic uncertainty and aleatoric uncertainty [27]. Epistemic uncertainty arises from limitations in the model’s knowledge or training process, typically due to insufficient data. This uncertainty can be reduced by incorporating additional training data or enhancing the model architecture. In contrast, aleatoric uncertainty stems from sensor noise, measurement errors, or inherent randomness in the data collection procedure. Unlike epistemic uncertainty, aleatoric uncertainty cannot be eliminated through additional training, as it originates from data sensing. Both types of uncertainty can be estimated using Bayesian neural networks (BNNs). BNNs treat model weights as probabilistic distributions to quantify uncertainty. However, computing the exact posterior distribution in high-dimensional spaces is almost impractical. In this study, we use MC dropout [27] to approximate Bayesian inference and provide uncertainty estimation.

Let us consider a regression task with N data pairs of input $\mathbf{x}$ and output y, i.e., ${\left\{\left({\mathbf{x}}_i,y_i\right)\right\}}_{i=1}^N$. To quantify aleatoric and epistemic uncertainties in this task, we consider a BNN model $\mathbf{f}$ to infer the posterior distribution. From an input $\mathbf{x}$, it provides a model output $\widehat{y}$ together with a variance ${\widehat{\sigma }}^2$ of the aleatoric uncertainty. In contrast, to estimate the epistemic uncertainty, we employ the MC dropout to approximate the posterior over the model. By representing the model weights as $\widehat{\mathbf{W}}$ from the approximate posterior, the model provides both the predictive mean and the variance, i.e., $[\widehat{y},{\widehat{\sigma }}^2]={\mathbf{f}}^{\widehat{\mathbf{W}}}\left(\mathbf{x}\right)$. The objective function of learning the model can be defined without the regularization term as follows:

$${\displaystyle \frac{1}{N}}\sum _{i=1}^N\left[{\displaystyle \frac{1}{2{\widehat{\sigma }}_i^2}}{∥y_i-{\widehat{y}}_i∥}^2+{\displaystyle \frac{1}{2}}log{\widehat{\sigma }}_i^2\right]={\displaystyle \frac{1}{2N}}\sum _{i=1}^N\left[exp(-s_i){∥y_i-{\widehat{y}}_i∥}^2+s_i\right],$$

where $s_i=log{\widehat{\sigma }}_i^2$. Here, the second equation is more numerically stable for the case of division by zero. After training, we can estimate the uncertainty of an output $\widehat{y}$ by T times multiple inferences for a given input as follows:

$${\displaystyle \frac{1}{T}}\sum _{t=1}^T\left[{\widehat{y}}_t^2-{\left({\displaystyle \frac{1}{T}}\sum _{t=1}^T{\widehat{y}}_t\right)}^2\right]+{\displaystyle \frac{1}{T}}\sum _{t=1}^T{\widehat{\sigma }}_t^2,$$

where $({\widehat{y}}_t,{\widehat{\sigma }}_t^2)$ is the t-th output of the model based on randomly determined weights by dropout. Note that the first and the second terms correspond to the epistemic and the aleatoric uncertainties of the output, respectively. More details are referred to as [27].

3.2. Uncertainty-Aware Localization Based on FusionLoc

In this section, we describe our uncertainty-aware localization method based on the fusion of RGB image and 2D LiDAR data captured from a commercialized serving robot. As shown in Figure 1, our approach builds upon FusionLoc [14], a deep learning-based framework that estimates a robot’s 3-DoF pose from RGB image and 2D LiDAR data. The proposed method extends FusionLoc by quantifying localization uncertainty and applying a percentile rejection method to improve safety and reliability in scenarios with large localization errors.

To better understand the underlying mechanism, we first describe the FusionLoc network architecture and its pose estimation process. FusionLoc takes the input data, consisting of an RGB image $\mathbf{I}$ and 2D LiDAR data $\mathbf{S}$, as shown in the input data part of Figure 1, and predicts the robot’s position $\widehat{\mathbf{p}}$ and orientation $\widehat{\mathbf{q}}$, which are the outputs of the original FusionLoc, as follows:

$$[\widehat{\mathbf{p}},\widehat{\mathbf{q}}]=\mathbf{f}(\mathbf{I},\mathbf{S}),$$

where $\widehat{\mathbf{p}}=[\widehat{x},\widehat{y}]$ is the 2D coordinates of the robot position, and $\widehat{\mathbf{q}}=[cos\widehat{\theta },sin\widehat{\theta }]$ corresponds to the robot orientation. The method computes an image feature from the input image using a feature extractor from AtLoc [6], while it calculates point features from the input LiDAR data using a different feature extractor from PointLoc [9]. To enhance the interaction between these two modalities, multi-head self-attention [17] is employed. This approach enables more effective multi-modality fusion than traditional methods such as concatenation or addition of the image and point features. Lastly, the output of the multi-head self-attention block is passed through the MLP layers, which consist of two branches in the regression part of Figure 1, each responsible for estimating the position and orientation. These branches predict the position $\widehat{\mathbf{p}}$ and the orientation $\widehat{\mathbf{q}}$.

Although the predicted pose obtained through this process generally reduces localization errors compared to mono-modal approaches, significant errors still occasionally occur. These large errors can cause the robot to navigate to incorrect locations, thereby compromising its operational safety and reliability. To address this issue, we assess the reliability of each estimated pose by quantifying the uncertainty of the estimated pose. To perform the uncertainty-aware localization, we modify the FusionLoc [14] architecture such that it has two more output nodes ${\widehat{\sigma }}_{\mathbf{p}}^2$ and ${\widehat{\sigma }}_{\mathbf{q}}^2$ to measure the aleatoric uncertainty. Thus, our model can be represented as the following:

$$[\widehat{\mathbf{p}},{\widehat{\sigma }}_{\mathbf{p}}^2,\widehat{\mathbf{q}},{\widehat{\sigma }}_{\mathbf{q}}^2]={\mathbf{f}}^{\widehat{\mathbf{W}}}(\mathbf{I},\mathbf{S}).$$

As mentioned above, we replace ${\widehat{\sigma }}_{\mathbf{p}}^2$ and ${\widehat{\sigma }}_{\mathbf{q}}^2$ by $s_{\mathbf{p}}=log{\widehat{\sigma }}_{\mathbf{p}}^2$ and $s_{\mathbf{q}}=log{\widehat{\sigma }}_{\mathbf{q}}^2$ for computational stability. Given N training samples ${\left\{({\mathbf{I}}_i,{\mathbf{S}}_i,{\mathbf{p}}_i,{\mathbf{q}}_i)\right\}}_{i=1}^N$, the loss function can be defined as the following:

$${\displaystyle \frac{1}{2N}}\sum _{i=1}^N\left[exp(-s_{\mathbf{p}i}){∥{\mathbf{p}}_i-{\widehat{\mathbf{p}}}_i∥}^2+s_{\mathbf{p}i}\right]+{\displaystyle \frac{1}{2N}}\sum _{i=1}^N\left[exp(-s_{\mathbf{q}i}){∥{\mathbf{q}}_i-{\widehat{\mathbf{q}}}_i∥}^2+s_{\mathbf{q}i}\right].$$

(1)

Another difference between the proposed method and the original FusionLoc is the dropout, which is applied to the output of the self-attention block in the original FusionLoc, as shown in Figure 1. It is important to note that the dropout is applied only in inference to measure the epistemic uncertainty. After finishing training process, we can predict the position ${\mathbf{p}}^{*}$ and orientation ${\mathbf{q}}^{*}$ of the robot by performing the inference T times using a pair of $(\mathbf{I},\mathbf{S})$ as the following:

$${\mathbf{p}}^{*}={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\widehat{\mathbf{p}}}_t,{\mathbf{q}}^{*}={\displaystyle \frac{1}{T}}\sum _{t=1}^T{\widehat{\mathbf{q}}}_t,$$

where ${\widehat{\mathbf{p}}}_t$ and ${\widehat{\mathbf{q}}}_t$ are the t-th position and orientation outputs obtained using dropout in the trained model. Due to the dropout, the network can output different values of $({\widehat{\mathbf{p}}}_t,s_{\mathbf{p}},{\widehat{\mathbf{q}}}_t,s_{\mathbf{q}})$ even if the input is the same for all t. And, their corresponding uncertainties $u_{\mathbf{p}}$ and $u_{\mathbf{q}}$ are computed as follows:

$$\begin{array}{cc}\hfill u_{\mathbf{p}}& ={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left[{\widehat{\mathbf{p}}}_t^2-{\left({\mathbf{p}}^{*}\right)}^2\right]+{\displaystyle \frac{1}{T}}\sum _{t=1}^T{\widehat{\sigma }}_{\mathbf{p}t}^2,\hfill \\ \hfill u_{\mathbf{q}}& ={\displaystyle \frac{1}{T}}\sum _{t=1}^T\left[{\widehat{\mathbf{q}}}_t^2-{\left({\mathbf{q}}^{*}\right)}^2\right]+{\displaystyle \frac{1}{T}}\sum _{t=1}^T{\widehat{\sigma }}_{\mathbf{q}t}^2,\hfill \end{array}$$

(2)

where the first and the second terms of $u_{\mathbf{p}}$ and $u_{\mathbf{q}}$ correspond to the epistemic and the aleatoric uncertainties of the output, respectively, as mentioned in the previous subsection.

Note that we cannot predict how much error the network output has, which may often lead to a serious problem in safety. Under the assumption that a network output with high uncertainty has a large localization error, we can select reliable outputs based on the uncertainty values computed as (2) as follows:

$$u_{\mathbf{p}}<{\eta }_{\mathbf{p}}\mathrm{and}{u}_{\mathbf{q}}<{\eta }_{\mathbf{q}},$$

(3)

where ${\eta }_{\mathbf{p}}$ and ${\eta }_{\mathbf{q}}$ are the rejection thresholds for the position and orientation, respectively. If one of $u_{\mathbf{p}}$ and $u_{\mathbf{q}}$ is greater than the corresponding threshold, the output $({\mathbf{p}}^{*},{\mathbf{q}}^{*})$ is rejected. By discarding results with high uncertainty, we ensure that the remaining outputs have comparatively lower errors.

Our approach utilizes a percentile-based thresholding method that rejects a portion of the network outputs that exceed predefined uncertainty thresholds. In this situation, it is crucial to determine the appropriate threshold value. We experiment with different percentile thresholds (100%, 90%, 80%, and 70%), progressively filtering the top 0%, 10%, 20%, and 30% of the most uncertain predictions. Although this thresholding approach is straightforward, it effectively rejects the network results corresponding to outliers, leading to a more reliable and precise localization system.

In the next section, we will present a detailed analysis of how the uncertainty-based rejection strategy improves localization performance.

4. Experiments

4.1. Datasets

For our experiments, we constructed three datasets from indoor environments named TheGardenParty, ETRI, and SusungHotel. For multi-modality, sensor data such as RGB images and 2D LiDAR scans were collected using a commercialized serving robot, Polaris3D Ereon (Polaris3D, Pohang, Republic of Korea), as shown in Figure 2. This robot is equipped with two cameras and a 2D LiDAR sensor. For our purposes, we utilized a lower-mounted camera to capture RGB images and the LiDAR sensor to gather 2D range data. We utilized an Intel RealSense D435 camera (Intel Corporation, Santa Clara, CA, USA) for collecting the TheGardenParty dataset and an Astra Stereo SU3 camera (Orbbec 3D, Troy, MI, USA) for the ETRI and SusungHotel datasets. The LiDAR sensor is the SLAMTEC RPLiDAR A1M8 (Shanghai SLAMTEC Co., Ltd., Shanghai, China), which operates at 8 Hz with a maximum range of 12 m and an angular resolution of 0.313$°$. It performs 360$°$ scans, generating up to 1150 2D points per scan. To effectively train and evaluate relocalization algorithms, it is essential to obtain robot poses aligned with sensor data such as images and point clouds. For this purpose, we first generated a map of our test environment using a 2D LiDAR-based SLAM approach. Then, we acquired the robot poses by running the SLAM system in localization mode. The collected datasets consist of RGB images that provide visual context, 2D LiDAR scans that capture structural and geometric information, and 3-DoF poses derived from these scans. We aimed to synchronize the images, 2D LiDAR data, and poses as closely in time as possible. These datasets were utilized for training and evaluating deep learning models focused on robot localization.

Figure 3 presents ground truth trajectories collected from three different datasets. In the figure, each color represents a different sequence, while the robot’s start and end positions are marked with the gold and downward stars, respectively. Table 2 compares the key characteristics of the three datasets and summarizes their features, including the number of samples and sequences used for training, evaluation, and validation. The TheGardenParty dataset provides images at a resolution of 320 × 240 pixels, and it was collected in a restaurant environment with predefined paths. This dataset consists of fragmented and partial sequences rather than full traversals of the environment. The dataset comprises 13,326 data tuples across 35 sequences, with 24 sequences used for training, 6 for evaluation, and 5 for validation. The ETRI dataset supports 640 × 480 pixels and it represents a more complex navigation environment, featuring a wide lobby space with three pillars where the robot navigates along several paths, including exploration and obstacle avoidance. Each sequence of this dataset covers the entire environment and was collected in a well-structured setting with minimal obstacles. As shown in Figure 4, the ETRI dataset features four distinct movement patterns:

• Straight corridor navigation: In this pattern, the robot navigates the entire space in a continuous loop before returning to its starting point.
• Zigzag movement: Here, the robot moves in a zigzag manner, weaving between obstacles.
• Repetitive back-and-forth motion: This pattern involves the robot moving back and forth within a confined space before proceeding with further exploration.
• Rotational maneuvers: In this last pattern, the robot performs in-place rotations at specific locations before retracing the same trajectory as in the first pattern.

The dataset comprises 19,014 tuples and 100 sequences, with 66 sequences designated for training, 16 for evaluation, and 16 for validation. The SusungHotel dataset also provides high-resolution images with a resolution of 640 × 480 pixels. It consists of a total of 9625 data tuples, collected from 20 distinct sequences. These sequences are categorized into 16 for training, 2 for validation, and 2 for evaluation. Notably, among the three datasets, the SusungHotel dataset features the longest continuous trajectories captured in a single recording session. This dataset contains sequences that cover the entire environment. However, the environment itself is narrow and takes the form of a long corridor. Furthermore, it contains some variations such as unpredictable dynamic obstacles, lighting conditions, and random perturbations to the robot’s movements.

Figure 3. Robot trajectories in each dataset. Each color represents a distinct sequence of data.

Figure 3. Robot trajectories in each dataset. Each color represents a distinct sequence of data.

Table 2. Summary of each dataset’s characteristics.

Attribute	TheGardenParty	ETRI	SusungHotel
Image resolution (pixels)	320 × 240	640 × 480	640 × 480
Robot movement type	Predefined	4 patterns	Predefined + random perturbation
Environment type	Restaurant	Wide lobby	Long and narrow curved corridor
Sequence type	Fragment	Full	Full
# Training tuples (# Sequences)	7848 (24)	12,688 (66)	7625 (16)
# Validation tuples (# Sequences)	2294 (5)	2964 (16)	1258 (2)
# Test tuples (# Sequences)	3184 (6)	2794 (16)	1276 (2)
Total tuples (# Sequences)	13,326 (35)	19,014 (100)	9625 (20)

Table 2. Summary of each dataset’s characteristics.

Attribute	TheGardenParty	ETRI	SusungHotel
Image resolution (pixels)	320 × 240	640 × 480	640 × 480
Robot movement type	Predefined	4 patterns	Predefined + random perturbation
Environment type	Restaurant	Wide lobby	Long and narrow curved corridor
Sequence type	Fragment	Full	Full
# Training tuples (# Sequences)	7848 (24)	12,688 (66)	7625 (16)
# Validation tuples (# Sequences)	2294 (5)	2964 (16)	1258 (2)
# Test tuples (# Sequences)	3184 (6)	2794 (16)	1276 (2)
Total tuples (# Sequences)	13,326 (35)	19,014 (100)	9625 (20)

Figure 4. Visualization of robot trajectories in different scenarios on the ETRI dataset. (a) Full-loop trajectory. (b) Zigzag navigation. (c) Localized back-and-forth motion. (d) In-place rotations at specific locations.

Figure 4. Visualization of robot trajectories in different scenarios on the ETRI dataset. (a) Full-loop trajectory. (b) Zigzag navigation. (c) Localized back-and-forth motion. (d) In-place rotations at specific locations.

4.2. Training and Inference Details

We implemented, trained, and inferred the network on a single NVIDIA GeForce RTX 4090 GPU (NVIDIA Corporation, Santa Clara, CA, USA) environment under the settings below. The input data consist of RGB images, 2D point clouds, and ground-truth trajectory information. The RGB images were resized to a resolution of $320\times 240$ and normalized using the mean and standard deviation computed during training. The point cloud was randomly sampled to a fixed number of points (e.g., 850), with each point represented by 2D coordinates $(x,y)$. The position vectors in the trajectory information were normalized using the mean and standard deviation of the training data and then fed into the model. The predicted outputs were subsequently un-normalized to recover real-world coordinates in meters. To keep the continuity of the rotational angle, the orientation was regressed in the form of ${[cos\widehat{\theta },sin\widehat{\theta }]}^T$ instead of $\widehat{\theta }$. Finally, the predicted yaw angle was reconstructed using the equation $\widehat{\theta }={tan}^{-1}(sin\widehat{\theta },cos\widehat{\theta })$.

The model was optimized using the Adam optimizer, and we set both the learning rate and weight decay to 0.0001. Training was conducted with a batch size of 128 for up to 1000 epochs. Model performance was evaluated at each epoch using a validation set, and only the model corresponding to the lowest validation loss was retained. Additionally, a dropout probability of 0.5 was applied during training to prevent overfitting. To enable the model to estimate predictive confidence alongside the output, we incorporated the aleatoric uncertainty into the regression loss function as in (1). In contrast, the epistemic uncertainty based on a BNN framework was not utilized during training. Instead, it was estimated at inference time by performing multiple forward passes using MC dropout and computing the variance of the predictions. Furthermore, the training loss function incorporates an $L_2$ loss weighted by aleatoric uncertainty through learnable log-variance terms. This approach allows the model to dynamically adjust the contribution of the position and orientation errors by scaling the loss according to the predicted uncertainty. As a result, the impact of high-error samples is mitigated, and the model is trained to jointly estimate both the target values and their associated confidence levels.

In this study, to evaluate the generalization performance of the proposed method, we designed a single-sequence inference procedure incorporating an uncertainty estimation mechanism based on MC dropout. During inference, the trained model parameters were loaded, and both an RGB image and a 2D LiDAR point cloud were provided as inputs to jointly predict the position and orientation. We performed inference applying the MC dropout technique using a dropout probability of 0.2. Multiple forward passes were conducted to compute the mean prediction and variance. In this context, the epistemic uncertainty is interpreted as the prediction variance estimated via the MC dropout, while the aleatoric uncertainty is directly obtained from the learned log-variance values. Both types of uncertainty were output alongside the predicted pose and were used to quantitatively assess the confidence level of the prediction results. For all inference samples, the epistemic uncertainty and aleatoric uncertainty were collected separately for both position and orientation. These two uncertainty measures were then combined to form a unified uncertainty score, which serves as a criterion for rejection. Specifically, for each sample, the epistemic and aleatoric uncertainties were summed as in (2) to compute a total uncertainty score for both position and orientation. Based on this score, only the samples falling below a specified percentile threshold are retained as in (3), allowing the evaluation to focus on high-confidence predictions.

4.3. Evaluation

In this subsection, we evaluate the performance of our localization method by applying the uncertainty-based rejection approach. To achieve this, we utilized the model mentioned in Section 3 and measured the epistemic and aleatoric uncertainties in the model’s predictions for position and orientation. We demonstrate the improvement in the reliability of position and orientation predictions by applying percentile-based thresholds using uncertainty values and discarding outputs that exceed these thresholds. Specifically, experiments were conducted using 100%, 90%, 80%, and 70% as thresholds, progressively rejecting the top 0%, 10%, 20%, and 30% of the outputs with the highest uncertainty. This rejection method retains only the reliable results, minimizing the influence of extreme outliers with high uncertainty. As a result, this approach finally leads to a more robust evaluation of the model’s performance.

To evaluate the impact of the rejection approach on localization performance, we compared the median and mean errors in position and orientation before and after applying the rejection based on uncertainty thresholding.

Table 3. Comparison of position and orientation metrics under different uncertainty thresholds across all datasets.

Dataset	Metric	Threshold	100% th.	90% th.	80% th.	70% th.
TheGardenParty	Position (m)	Min	0.072	0.074	0.069	0.098
		Median	0.573	0.567	0.552	0.523
		Max	5.559	5.288	4.317	4.192
		Mean	0.776	0.738	0.712	0.682
	Orientation ($°$)	Min	0.0204	0.017	0.003	0.015
		Median	2.672	2.544	2.512	2.299
		Max	72.738	54.508	49.384	48.397
		Mean	4.880	3.783	3.358	3.126
ETRI	Position (m)	Min	0.023	0.025	0.026	0.031
		Median	0.289	0.298	0.300	0.298
		Max	1.610	1.613	1.287	1.490
		Mean	0.324	0.326	0.327	0.327
	Orientation ($°$)	Min	0.013	0.012	0.008	0.010
		Median	1.127	1.052	0.978	0.902
		Max	26.224	16.182	15.569	11.024
		Mean	1.990	1.661	1.527	1.409
SusungHotel	Position (m)	Min	0.022	0.028	0.031	0.019
		Median	0.659	0.561	0.477	0.424
		Max	66.392	66.279	59.829	59.753
		Mean	4.262	2.788	2.211	1.575
	Orientation ($°$)	Min	0.004	0.008	0.009	0.008
		Median	2.732	2.466	2.168	2.020
		Max	179.385	174.738	173.323	127.828
		Mean	13.711	9.008	5.861	4.329

illustrates the changes in position and orientation errors under varying uncertainty thresholds applied to the TheGardenParty, ETRI, and SusungHotel datasets. The results demonstrate consistent reductions in mean position and orientation errors across all rejection thresholds (90%, 80%, and 70%). In the TheGardenParty dataset, applying a 70% uncertainty threshold led to a reduction in the mean position error by as much as 12.1% (from 0.776 m to 0.682 m) and a decrease in the mean orientation error by up to 36.0% (from 4.880$°$ to 3.126$°$). For the ETRI dataset under the same conditions, the position error slightly increased by approximately 0.9% (from 0.324 m to 0.327 m), while the orientation error decreased by 29.2% (from 1.990° to 1.409°). Notably, the effectiveness of the uncertainty-based rejection strategy was also observed in the SusungHotel datasets. For the dataset, the mean position error decreased from 4.262 m to 1.575 m, while the mean orientation error was reduced from 13.711$°$ to 4.329$°$, reflecting improvements of approximately 63.0% and 68.4%, respectively. These findings indicate that the TheGardenParty and SusungHotel datasets have more outliers and noise, which leads to more significant performance improvements with the uncertainty-based rejection strategy. In contrast, the ETRI dataset, likely collected in a relatively simple environment, shows lower errors even without applying the rejection method, resulting in relatively less impact from this approach. The differences in performance improvement across the datasets may be attributed to their spatial characteristics. The TheGardenParty dataset was collected from a restaurant with many tables and chairs, while the SusungHotel dataset was gathered from a long and curved corridor, which presents challenges for robot localization. In contrast, the environment in which the ETRI dataset was collected is relatively straightforward and typical. Additionally, the size of the datasets may have played a role in the observed performance differences. The ETRI dataset contains about 1.6 times more training data than the other datasets. It is also noticeable that, in the TheGardenParty dataset, the maximum position error decreased from 5.559 m to 4.192 m, and the maximum orientation error significantly dropped from 72.738$°$ to 48.397$°$. This demonstrates the effectiveness of the rejection method in addressing extreme localization errors. These results indicate our end-to-end localization with the uncertainty-based rejection method can be utilized as a global localization solution, which can also provide a reliable initial pose to conventional localization modules, e.g., AMCL.

Figure 5 illustrates the distribution of position and orientation errors after applying the uncertainty-based rejection approach. Each scatter plot shows error values on the x-axis and their corresponding uncertainties on the y-axis. The outputs from the network are color-coded to distinguish between low-uncertainty (more reliable) and high-uncertainty (potentially erroneous) outputs. In the figure, red dots represent outputs with low uncertainty (below the 70% threshold), which are considered reliable predictions. They remain after applying all thresholds (100%, 90%, 80%, and 70%). On the other hand, blue dots indicate high-uncertainty outputs that are rejected when the 90% threshold is applied, meaning a higher likelihood of being erroneous. Additionally, green and orange dots represent outputs with moderate uncertainty, positioned between the red and blue dots. The black dashed lines in each plot indicate the rejection thresholds applied at different percentages. As the threshold decreases (from 100% to 70%), the number of low-uncertainty outputs (red) increases, while high-uncertainty outputs (blue) are progressively discarded. On the right side of each plot, the first number represents the uncertainty threshold applied at that level, while the percentages and corresponding values indicate the number of the remaining outputs. Overall, we can see that this strategy can effectively enhance the reliability of the network outputs by rejecting those with high uncertainty. In Figure 5, we also observe that applying a 70% threshold led to the removal of 955 outputs from the TheGardenParty dataset, 838 outputs from the ETRI dataset, and 383 outputs from the SusungHotel dataset. This indicates that excessive rejection can result in data loss and require multiple inferences to provide a non-rejected output, while the rejection approach effectively reduces errors on average. Thus, it is crucial to determine an appropriate threshold. Experimental results indicate that the 70% threshold achieves a satisfactory rejection while maintaining a sufficient number of network outputs. However, in a specific application, the rejection ratio should be carefully adjusted to balance performance improvement and multiple inferences. Therefore, selecting an optimal threshold is essential to maximizing performance while preserving sufficient data for model learning.

To further illustrate the impact of uncertainty-based thresholding, we visualize the predicted trajectories with and without filtering in various test sequences. Figure 6 shows the predicted trajectories overlaid with ground truth paths, highlighting the effect of applying thresholds at 90%, 80%, and 70%. In these plots, the reduction of noisy predictions and the improved alignment with the ground truth after filtering are clearly observable.

5. Conclusions and Future Work

This study experimentally demonstrated that our uncertainty-based rejection can effectively enhance robot localization performance. By applying different rejection thresholds (90%, 80%, and 70%), we confirmed that discarding network outputs with high uncertainty reduces both positional and orientation errors, thereby improving the reliability of model evaluation. Unlike conventional end-to-end localization methods that treat all evaluations equally, the proposed approach improves the reliability of network outputs by selectively rejecting those with high uncertainty. This method can be applied to other localization techniques based on deep neural networks. However, it is essential to determine the appropriate value for the rejection threshold. Thus, dynamically adjusting the rejection threshold based on dataset characteristics is necessary.

Future work includes optimizing the uncertainty-based rejection method for real-time robotic applications and verifying its practicality through experiments on actual robots. In addition, we aim to enhance the correlation between prediction error and uncertainty through calibration techniques such as post-processing [28] and distribution matching [30,31]. It is also important to improve the relatively slow inference speed observed in the current model. These efforts are expected to further increase the reliability and accuracy of robot localization systems in real-world environments.