Tsukamoto Fuzzy Logic Controller for Motion Control Applications: Assessment of Energy Performance
Abstract
1. Introduction
- This work proposes and validates a motion controller based on Tsukamoto fuzzy inference, which aims to reduce energy consumption during trajectory execution without compromising tracking accuracy in a linear platform.
- The Tsukamoto fuzzy logic controller (TFLC), due to its modular and adaptable nature, facilitates direct implementation in microcontroller-based embedded systems. Thanks to its rule-based structure and well-defined membership functions, the TFLC can be integrated relatively easily into low-power and resource-limited platforms, without requiring advanced computing units or specialized hardware.
- A statistical validation methodology is proposed to evaluate the energy performance of the TFLC, using metrics such as the coefficient of variation (CV) and Welch’s t-test. This strategy enables the analysis of the consistency and statistical significance of the TFLC’s energy consumption improvements under various motion profiles and load conditions, thereby providing a rigorous framework to support the controller’s effectiveness in embedded and real-time applications.
2. Related Works
3. Materials and Methods
3.1. Motion Profiles
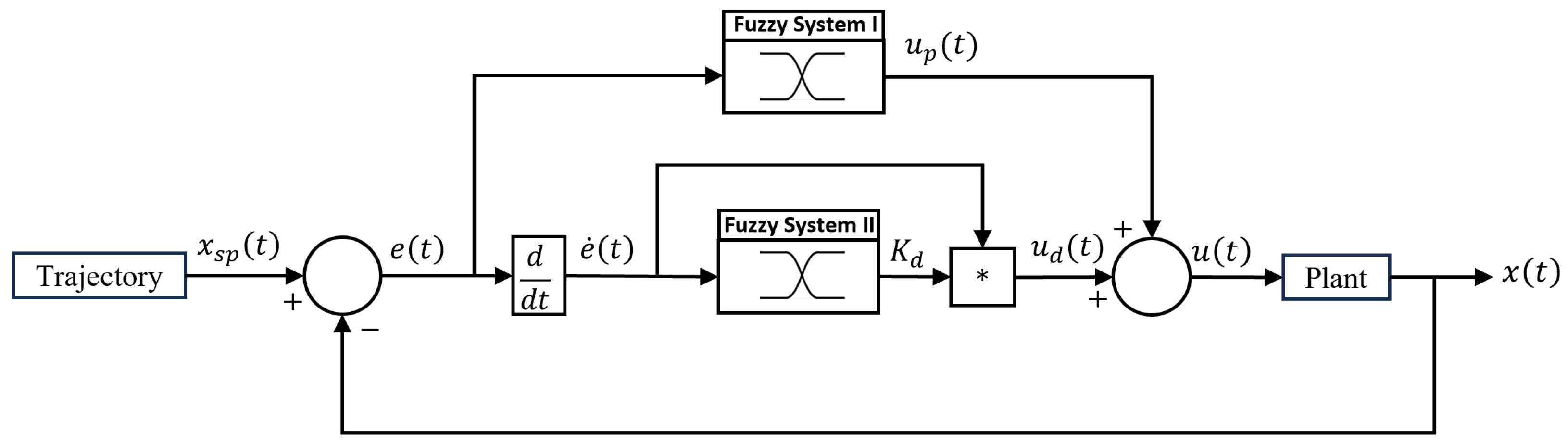
3.2. Tsukamoto Fuzzy Logic Controller Design
3.2.1. Fuzzy System I
3.2.2. Fuzzy System II
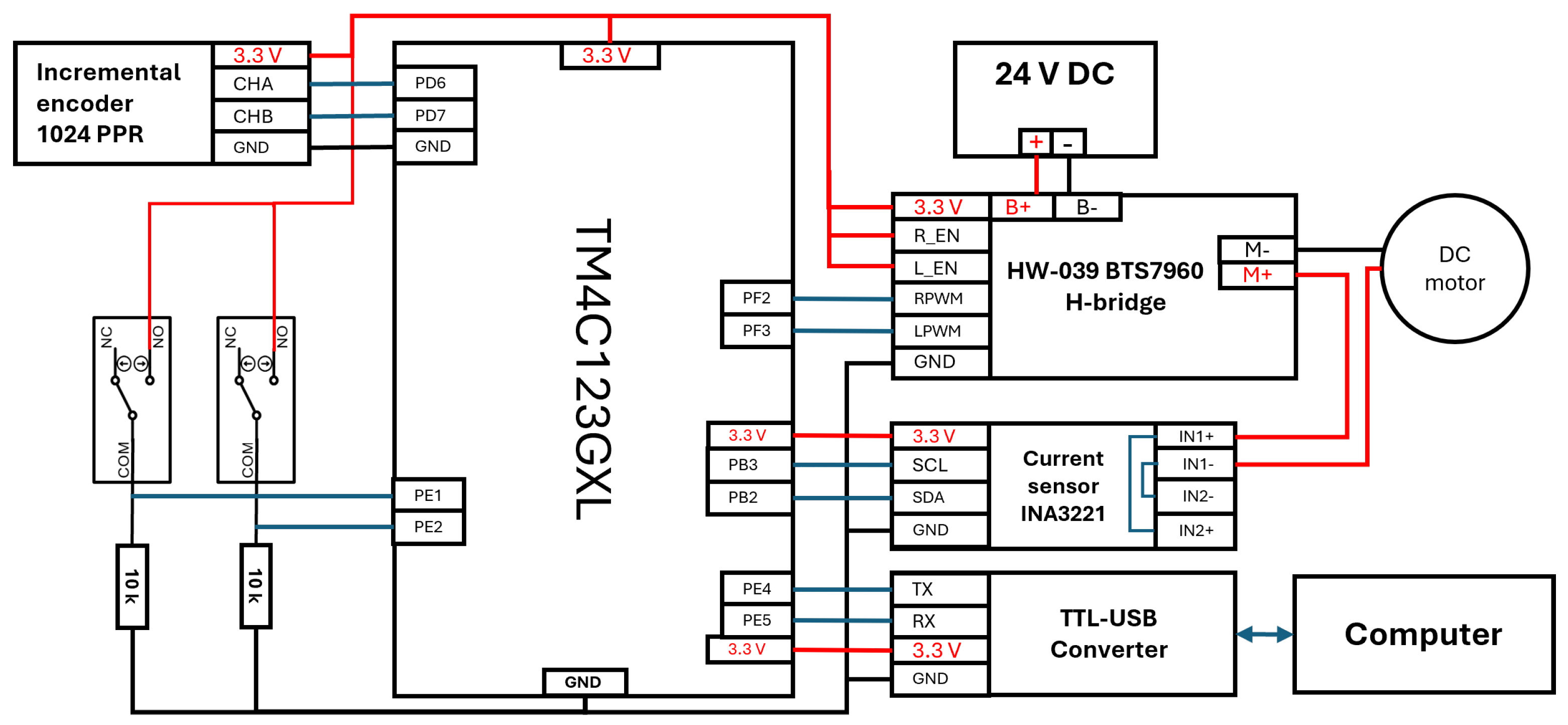
3.3. Test Platform Instrumentation
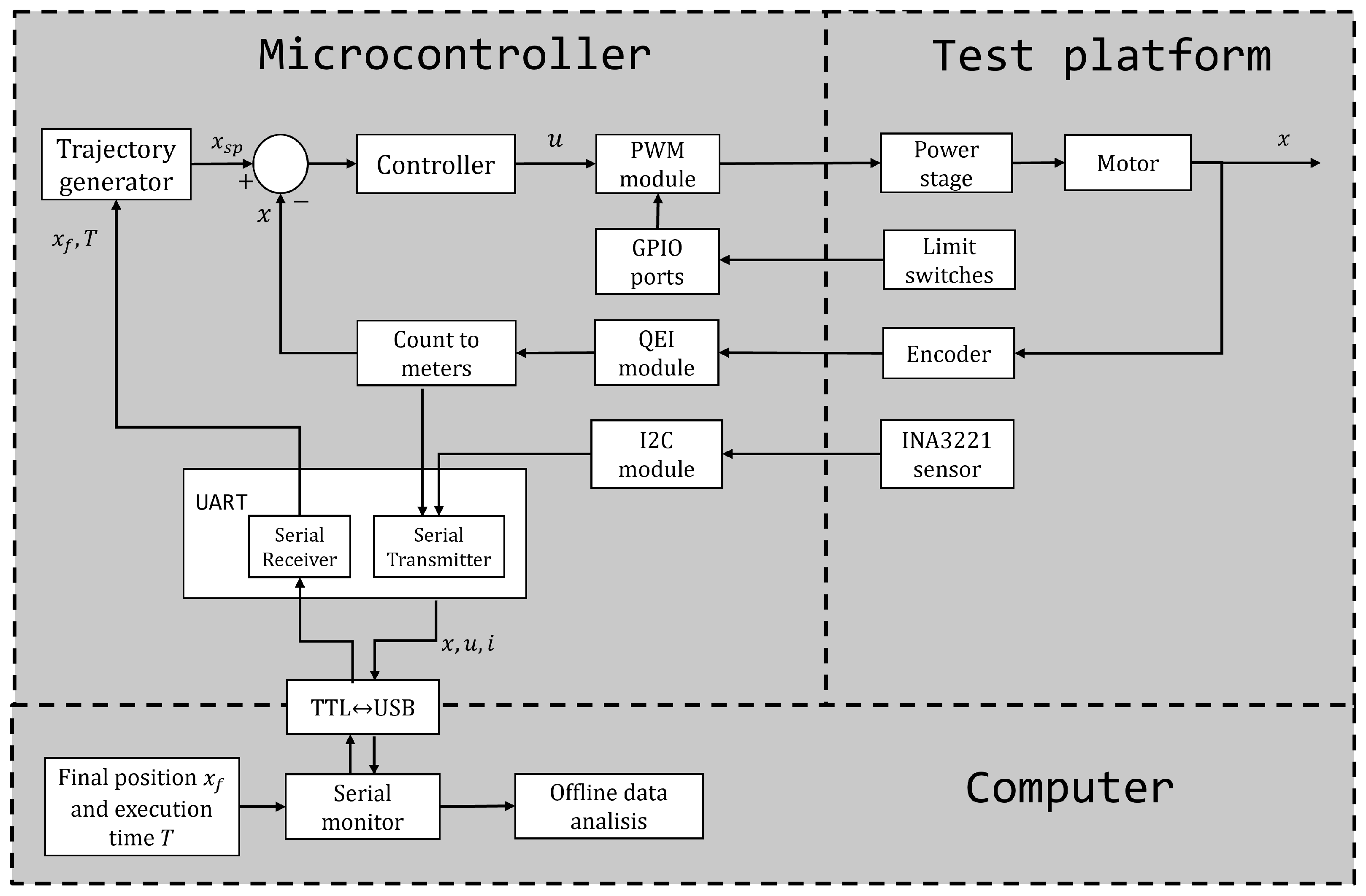
3.4. Control System Architecture
3.5. Embedded System Integration
| Algorithm 1 Embedded System Algorithm. |
|
3.5.1. Initial Configuration
- Operating frequency: 80 MHz;
- QEI module configured in quadrature mode, resulting in 4096 counts per revolution (CPR);
- PWM signals generated at 5 kHz with 10-bit resolution;
- UART communication set to 115,200 baud;
- General-purpose timer configured with a = 2 ms period.
3.5.2. Data Acquisition
3.5.3. Trajectory Generation
3.5.4. Control Signal Computation
| Algorithm 2 Sigmoid membership function. |
|
3.5.5. Data Transmission to PC
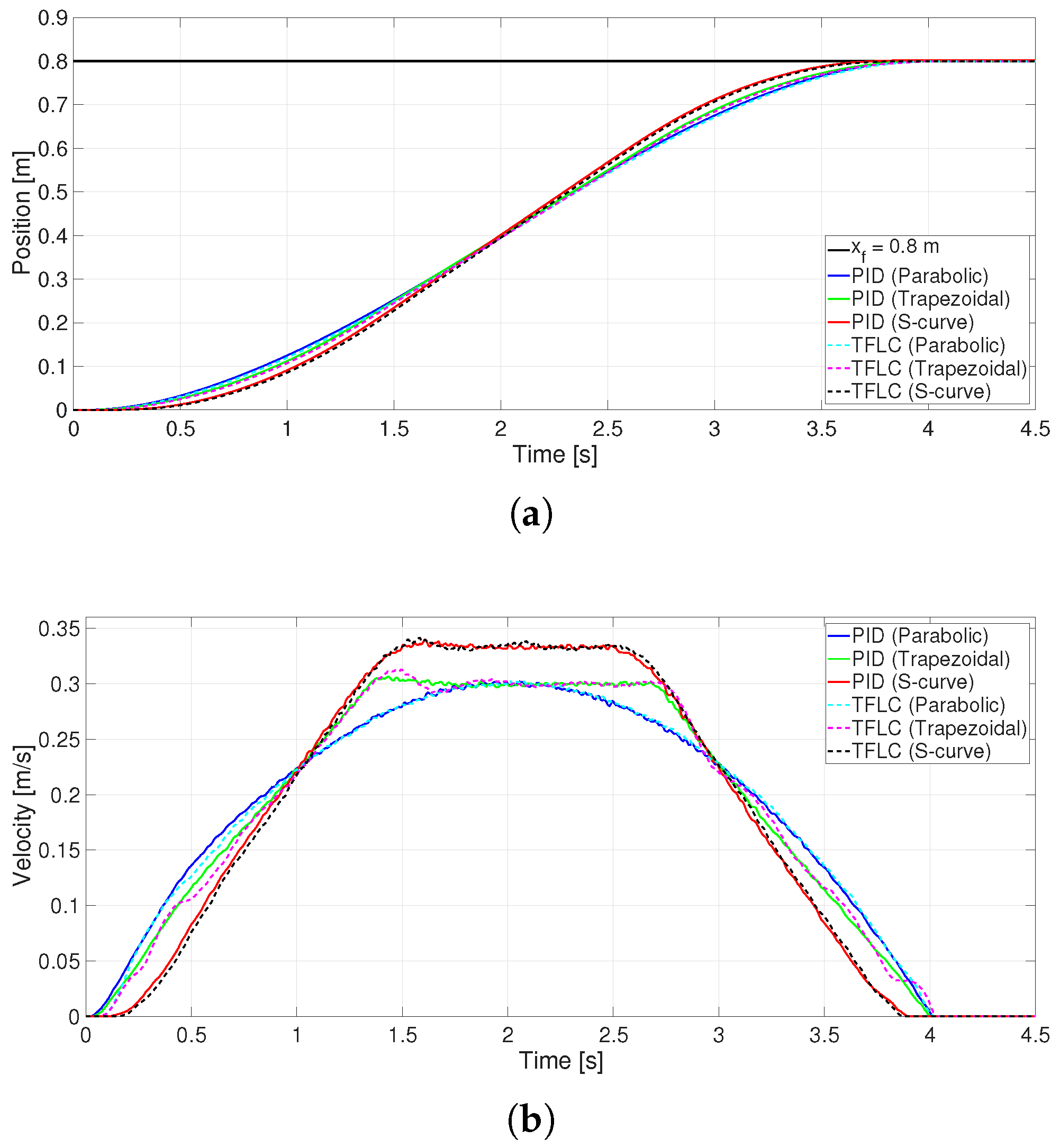
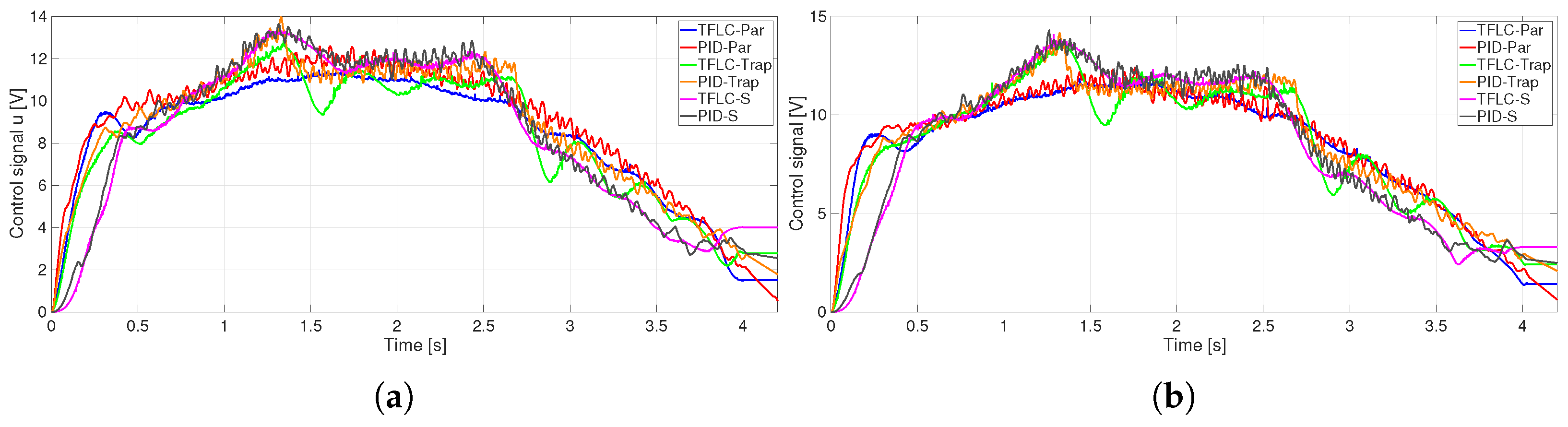
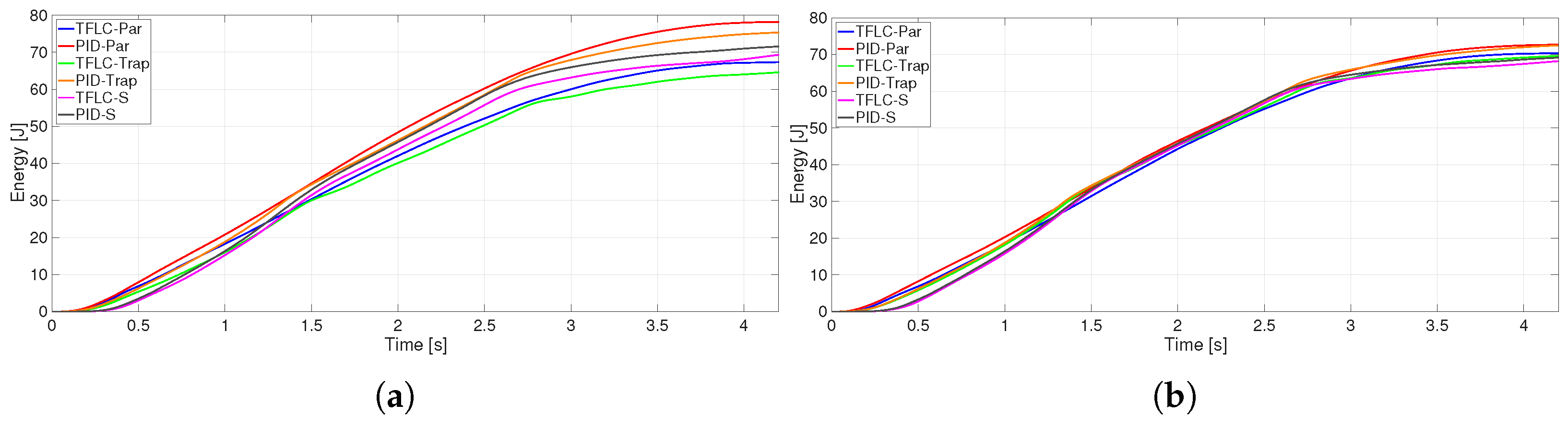
4. Results
Result Validation
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| TFLC | Tsukamoto Fuzzy Logic Controller |
| PID | Proportional–Integral–Derivative |
| QEI | Quadrature Encoder Interface |
| PWM | Pulse Width Modulation |
| UART | Universal Asynchronous Receiver–Transmitter |
| I2C | Inter-Integrated Circuit |
| CV | Coefficient of Variation |
| FIR | Finite Impulse Response |
| SSE | Steady-State Error |
| MTE | Maximum Tracking Error |
| PPR | Pulses Per Revolution |
| CPR | Counts Per Revolution |
| Ts | Sampling Time |
| PE/NE | Positive/Negative Error |
| PED/NED | Positive/Negative Error Derivative |
| PUP/NUP | Positive/Negative Control Action |
| HDG/LDG | High/Low Derivative Gain |
| HVAC | Heating, Ventilation, and Air Conditioning |
References
- De Laet, R.; Van Oosterwyck, N.; Cuyt, A.; Derammelaere, S. Global optimum motion profiles for enhanced energy efficiency in industrial positioning applications. Mechatronics 2025, 109, 103352. [Google Scholar] [CrossRef]
- Van Oosterwyck, N.; Vanbecelaere, F.; Knaepkens, F.; Monte, M.; Stockman, K.; Cuyt, A.; Derammelaere, S. Energy optimal point-to-point motion profile optimization. Mech. Based Des. Struct. Mach. 2024, 52, 239–256. [Google Scholar] [CrossRef]
- Huang, S.N.; Tan, K.K.; Lee, T.H. Adaptive motion control using neural network approximations. Automatica 2002, 38, 227–233. [Google Scholar] [CrossRef]
- Kyslan, K.; Smoleň, P.; Šlapák, V.; Ďurovský, F. A Nonlinear Controller for Point-to-Point Position Control. Energies 2023, 16, 6339. [Google Scholar] [CrossRef]
- Mehrabi, M. Design of a Fuzzy-Based Controller for Real-Time Control of CNC Machines. In Proceedings of the 2023 3rd International Conference on Electrical, Computer, Communications and Mechatronics Engineering (ICECCME), Tenerife, Spain, 19–21 July 2023; pp. 1–5. [Google Scholar]
- Gentili, P.L. The conformational contribution to molecular complexity and its implications for information processing in living beings and chemical artificial intelligence. Biomimetics 2024, 9, 121. [Google Scholar] [CrossRef] [PubMed]
- Yamakawa, T. Stabilization of an inverted pendulum by a high-speed fuzzy logic controller hardware system. Fuzzy Sets Syst. 1989, 32, 161–180. [Google Scholar] [CrossRef]
- Kandel, A.; Langholz, G. Fuzzy Hardware: Architectures and Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Niembro-Ceceña, J.A.; Gómez-Loenzo, R.A.; Rodríguez-Reséndiz, J. SoftCtrlDC-M: Embedded control software for brushed direct current motors. SoftwareX 2024, 25, 101643. [Google Scholar] [CrossRef]
- Urrea, C.; Saa, D. Design, Simulation, Implementation, and Comparison of Advanced Control Strategies Applied to a 6-DoF Planar Robot. Symmetry 2023, 15, 1070. [Google Scholar] [CrossRef]
- Tang, H.H.; Ahmad, N.S. Fuzzy Logic Approach for Controlling Uncertain and Nonlinear Systems: A Comprehensive Review of Applications and Advances. Syst. Sci. Control Eng. 2024, 12, 2394429. [Google Scholar] [CrossRef]
- Montes Rivera, M.; Olvera-Gonzalez, E.; Escalante-Garcia, N. UPAFuzzySystems: A Python Library for Control and Simulation with Fuzzy Inference Systems. Machines 2023, 11, 572. [Google Scholar] [CrossRef]
- Pop, M.-D.; Pescaru, D.; Micea, M.V. Mamdani vs. Takagi–Sugeno Fuzzy Inference Systems in the Calibration of Continuous-Time Car-Following Models. Sensors 2023, 23, 8791. [Google Scholar] [CrossRef]
- Michailidis, P.; Michailidis, I.; Vamvakas, D.; Kosmatopoulos, E. Model-Free HVAC Control in Buildings: A Review. Energies 2023, 16, 7124. [Google Scholar] [CrossRef]
- Carabin, G.; Vidoni, R. Energy-saving optimization method for point-to-point trajectories planned via standard primitives in 1-DoF mechatronic systems. Int. J. Adv. Manuf. Technol. 2021, 116, 331–344. [Google Scholar] [CrossRef]
- Hosseini, S.; Hahn, I. Nonlinear optimization of energy consumption in trajectory planning of a single-axis electrical drive. In Proceedings of the 2019 IEEE 28th International Symposium on Industrial Electronics (ISIE), Vancouver, BC, Canada, 12–14 June 2019; pp. 599–604. [Google Scholar]
- Montalvo, V.; Estévez-Bén, A.A.; Rodríguez-Reséndiz, J.; Macias-Bobadilla, G.; Mendiola-Santibáñez, J.D.; Camarillo-Gómez, K.A. FPGA-based architecture for sensing power consumption on parabolic and trapezoidal motion profiles. Electronics 2020, 9, 1301. [Google Scholar] [CrossRef]
- Tolochko, O.; Rozkariaka, P. Asymmetric reference trajectories for energy efficiency position electric drives. In Proceedings of the 2018 X International Conference on Electrical Power Drive Systems (ICEPDS), Moscow, Russia, 3–6 October 2018; pp. 1–7. [Google Scholar]
- Nshama, E.W.; Msukwa, M.R.; Uchiyama, N. A trade-off between energy saving and cycle time reduction by Pareto optimal corner smoothing in industrial feed drive systems. IEEE Access 2021, 9, 23579–23594. [Google Scholar] [CrossRef]
- Assad, F.; Rushforth, E.; Ahmad, M.; Ahmad, B.; Harrison, R. An approach of optimising s-curve trajectory for a better energy consumption. In Proceedings of the 2018 IEEE 14th International Conference on Automation Science and Engineering (CASE), Munich, Germany, 20–24 August 2018; pp. 98–103. [Google Scholar]
- Halinga, M.S.; Nyobuya, H.J.; Uchiyama, N. Generation of time and energy optimal coverage motion for industrial machines using a modified S-curve trajectory. In Proceedings of the 2023 IEEE/SICE International Symposium on System Integration (SII), Atlanta, GA, USA, 17–20 January 2023; pp. 1–6. [Google Scholar]
- Raisch, A.; Sawodny, O. Consumption minimization for electromechanical drives by energy-optimal feedforward control. In Proceedings of the 2019 IEEE International Conference on Systems, Man and Cybernetics (SMC), Bari, Italy, 6–9 October 2019; pp. 1557–1562. [Google Scholar]
- Wang, B.; Gou, M.; Yang, Z.; Qiu, S. A Synchronous Tracking Algorithm for Positioning Servo System with Double-loop Control. IEEE Trans. Ind. Appl. 2024, 61, 279–288. [Google Scholar] [CrossRef]
- Cicek, E.; Türker, T.; Akbati, O.; Sancak, K.V. Asymmetric S-curve generation and tracking under motion constraints: An experimental validation. In Proceedings of the 2022 Advances in Science and Engineering Technology International Conferences (ASET), Dubai, United Arab Emirates, 21–24 February 2022; pp. 1–6. [Google Scholar]
- Nguyen, A.T.; Nguyen, N.H.; Trinh, M.L. Fuzzy PD control for a quadrotor with experimental results. Results Control Optim. 2025, 19, 100568. [Google Scholar] [CrossRef]
- Lee, S.Y.; Kang, C.S.; Hyun, C.H.; Park, M. S-curve profile switching method using fuzzy system for position control of DC motor under uncertain load. In Proceedings of the 2012 12th International Conference on Control, Automation and Systems, Jeju Island, Republic of Korea, 17–21 October 2012; pp. 91–95. [Google Scholar]
- García-Martínez, J.R.; Cruz-Miguel, E.E.; Carrillo-Serrano, R.V.; Mendoza-Mondragón, F.; Toledano-Ayala, M.; Rodríguez-Reséndiz, J. A PID-type fuzzy logic controller-based approach for motion control applications. Sensors 2020, 20, 5323. [Google Scholar] [CrossRef]
- Meliani, H.; Ohamouddou, S.; El Afia, H.; Boulaich, M.H.; El Afia, A. Robot path planning using fuzzy Tsukamoto simulated annealing. In Proceedings of the 2024 Mediterranean Smart Cities Conference (MSCC), Tangier, Morocco, 2–4 May 2024; pp. 1–4. [Google Scholar]
- Khoukhi, A.; Baron, L.; Balazinski, M.; Demirli, K. Fuzzy-neuro optimal time-energy control of a three degrees of freedom planar manipulator. In Proceedings of the NAFIPS 2006 Annual Meeting of the North American Fuzzy Information Processing Society, Montreal, QC, Canada, 3–6 June 2006; pp. 247–252. [Google Scholar]
- Sunardi; Yudhana, A.; Furizal. Tsukamoto fuzzy inference system on Internet of Things-based for room temperature and humidity control. IEEE Access 2023, 11, 6209–6227. [Google Scholar] [CrossRef]
- Biagiotti, L.; Melchiorri, C. Trajectory Planning for Automatic Machines and Robots; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2008. [Google Scholar]
- Gurocak, H. Industrial Motion Control: Motor Selection, Drives, Controller Tuning, Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Kröger, T. On-Line Trajectory Generation in Robotic Systems: Basic Concepts for Instantaneous Reactions to Unforeseen (Sensor) Events; Springer Tracts in Advanced Robotics; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar]
- Gasparetto, A.; Boscariol, P.; Lanzutti, A.; Vidoni, R. Path planning and trajectory planning algorithms: A general overview. In Motion and Operation Planning of Robotic Systems; Springer: Berlin/Heidelberg, Germany, 2015; pp. 3–27. [Google Scholar]
- Crowder, R. Electric Drives and Electromechanical Systems: Applications and Control, 2nd ed.; Elsevier Science: Amsterdam, The Netherlands, 2019. [Google Scholar]
- Martínez, J.R.G.; Reséndiz, J.R.; Prado, M.Á.M.; Miguel, E.E.C. Assessment of jerk performance s-curve and trapezoidal velocity profiles. In Proceedings of the 2017 XIII International Engineering Congress (CONIIN), Santiago de Queretáro, Mexico, 15–19 May 2017; pp. 1–7. [Google Scholar]
- Ramos-Fernández, J.C.; López-Morales, V.; Márquez-Vera, M.A.; Pérez, J.M.X.; Suarez-Cansino, J. Neuro-fuzzy modelling and stable PD controller for angular position in steering systems. Int. J. Automot. Technol. 2021, 22, 1495–1503. [Google Scholar] [CrossRef]
- Baturone, I.; Barriga, A.; Jimenez-Fernandez, C.; Lopez, D.R.; Sanchez-Solano, S. Microelectronic Design of Fuzzy Logic-Based Systems; International Series on Computational Intelligence; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Siddique, N. Intelligent Control: A Hybrid Approach Based on Fuzzy Logic, Neural Networks and Genetic Algorithms; Studies in Computational Intelligence; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Ross, T.J. Fuzzy Logic with Engineering Applications, 4th ed.; Wiley: Hoboken, NJ, USA, 2016. [Google Scholar]
- Khan, A.A.; Rapal, N. Fuzzy PID controller: Design, tuning and comparison with conventional PID controller. In Proceedings of the 2006 IEEE International Conference on Engineering of Intelligent Systems, Islamabad, Pakistan, 22–23 April 2006; pp. 1–6. [Google Scholar] [CrossRef]
- Olmedo-García, L.F.; García-Martínez, J.R.; Cruz-Miguel, E.E.; Barra-Vázquez, O.A.; González-Lee, M.; Martínez-Sánchez, T. Real-time embedded system-based approach for sensing power consumption on motion profiles. Electronics 2023, 12, 3853. [Google Scholar] [CrossRef]
- Kishore, K.; Jaswal, V. Statistics corner: Comparing two unpaired groups. J. Postgrad. Med. Educ. Res. 2022, 56, 145–148. [Google Scholar] [CrossRef]
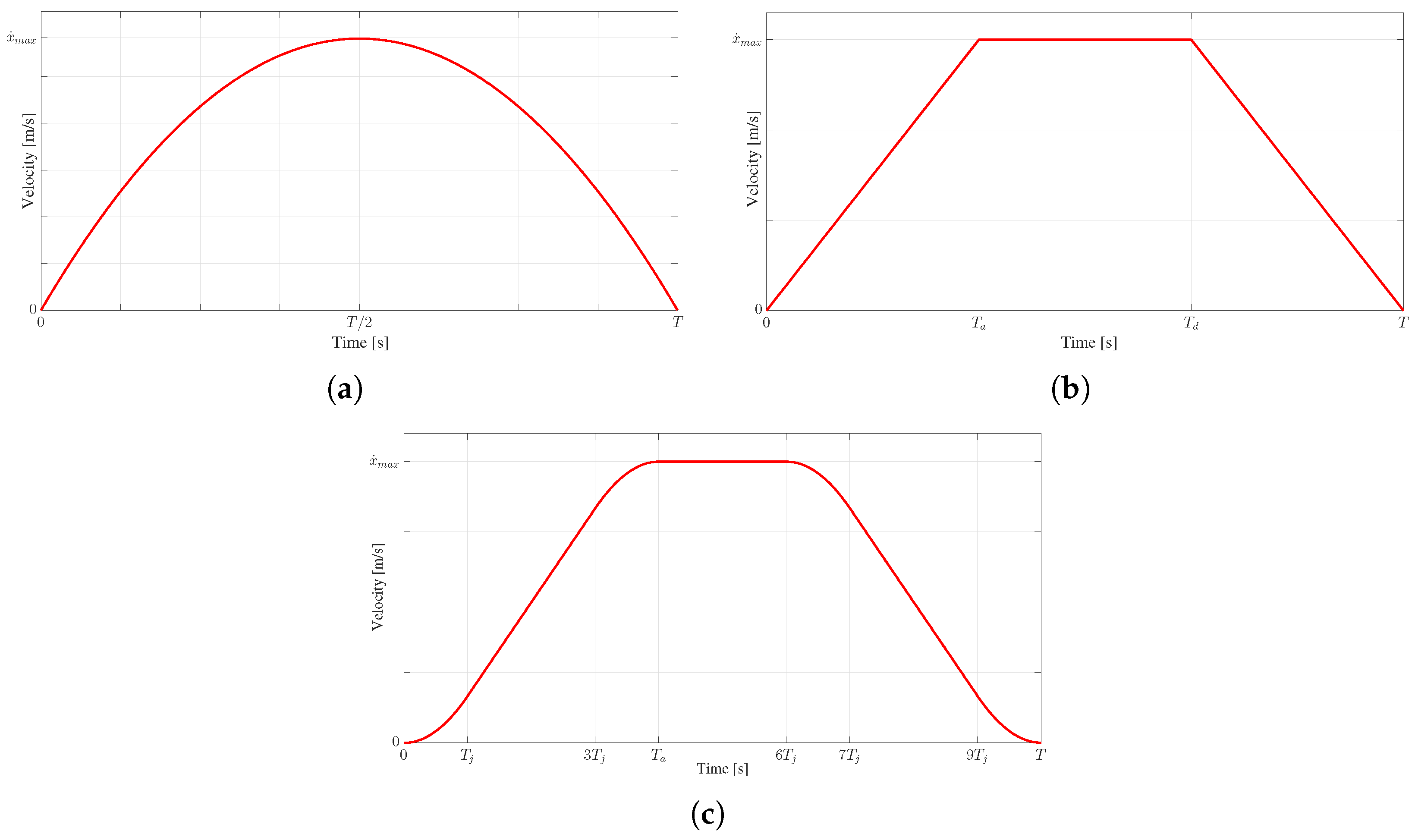
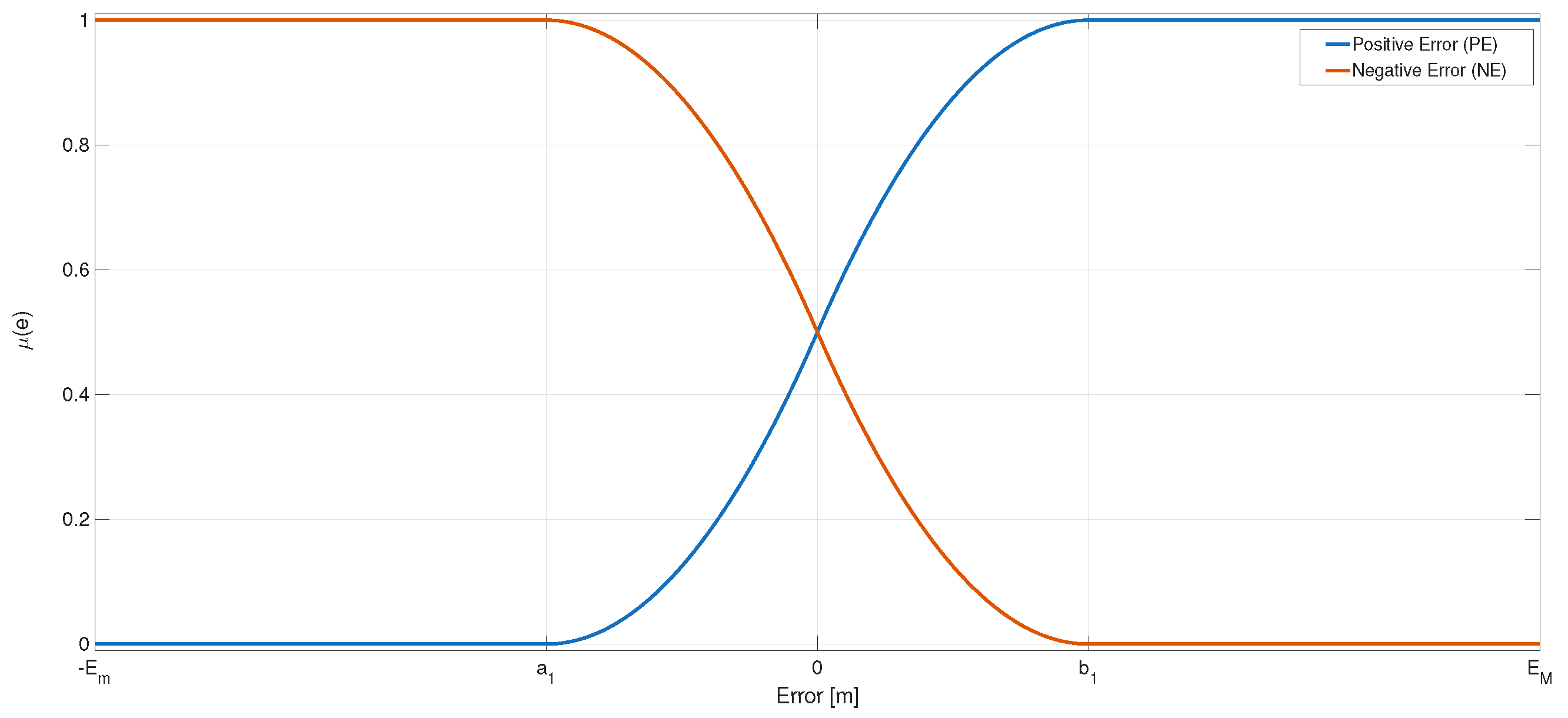


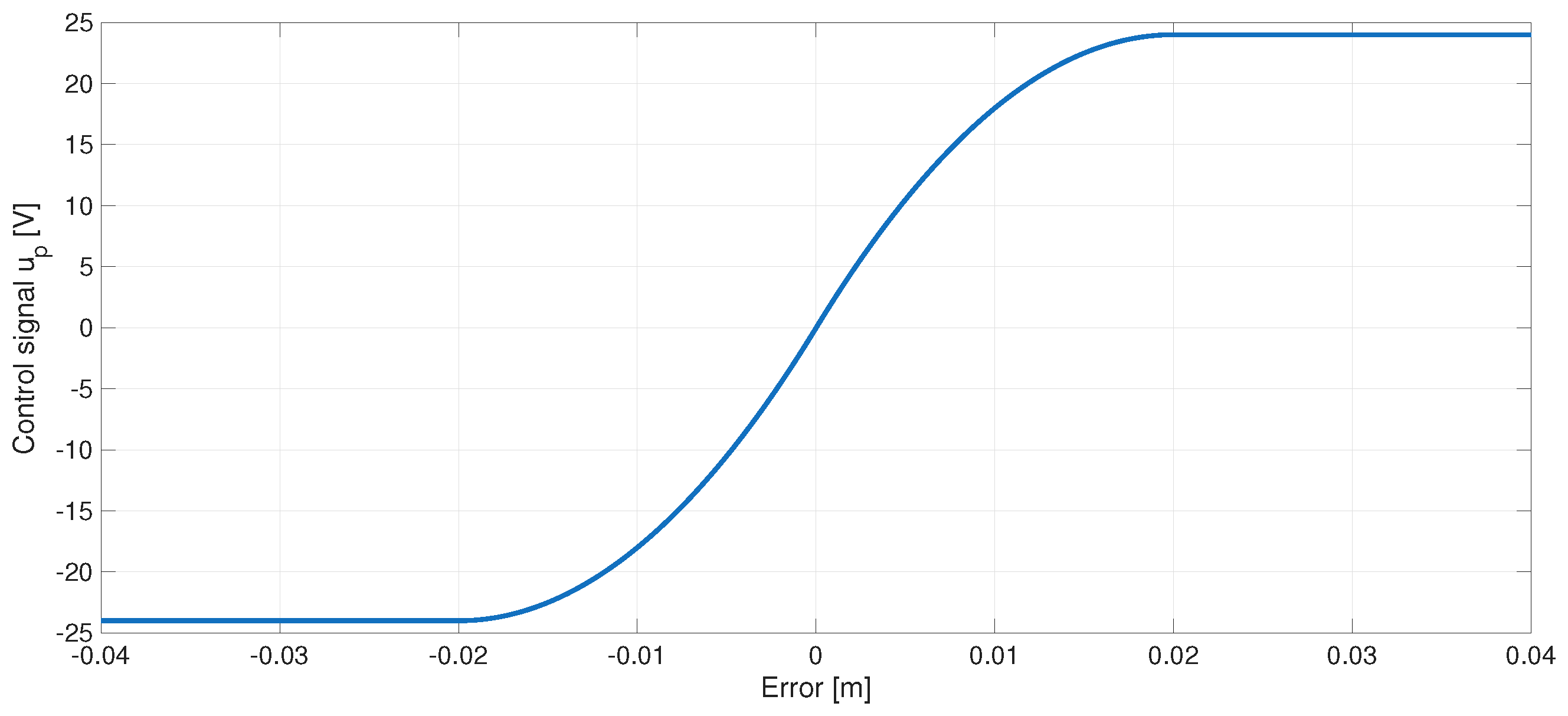
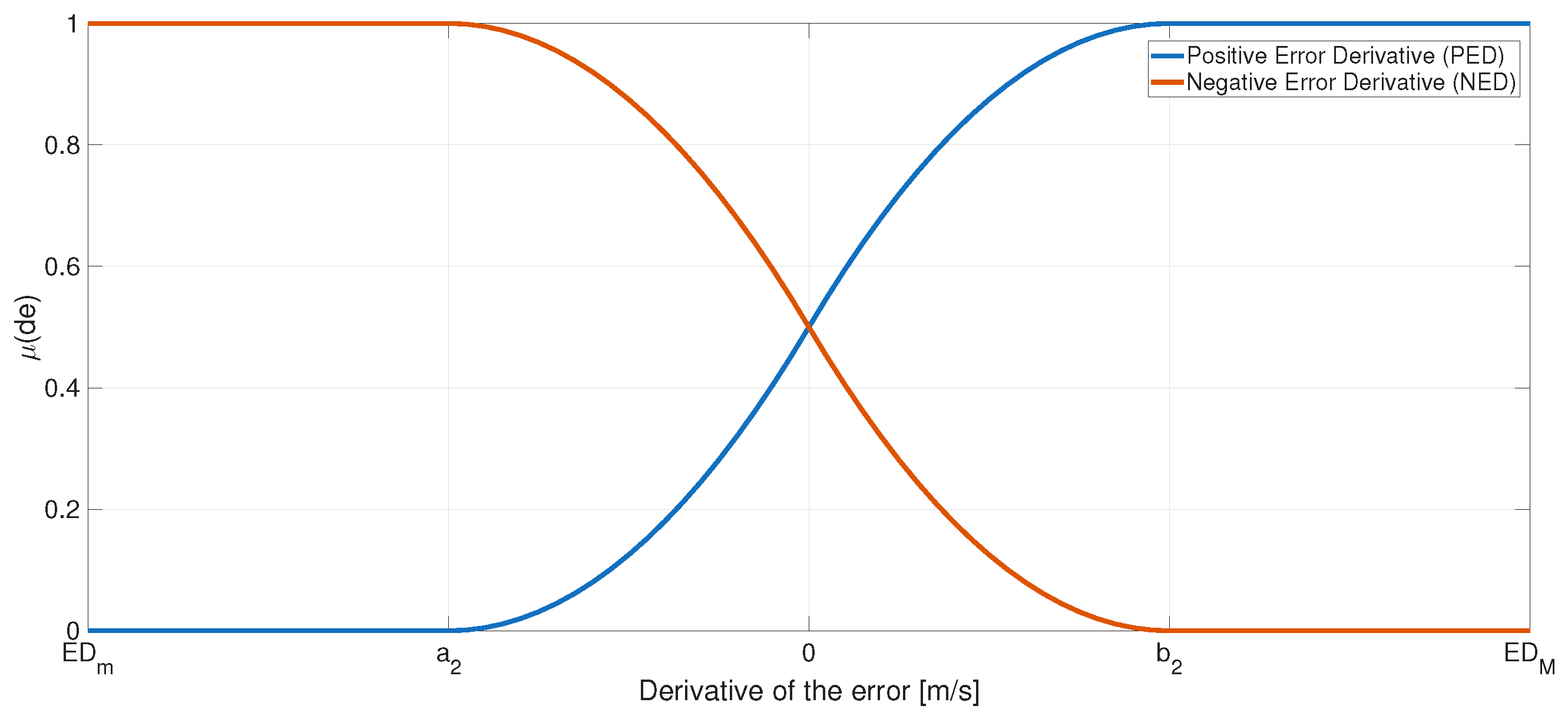
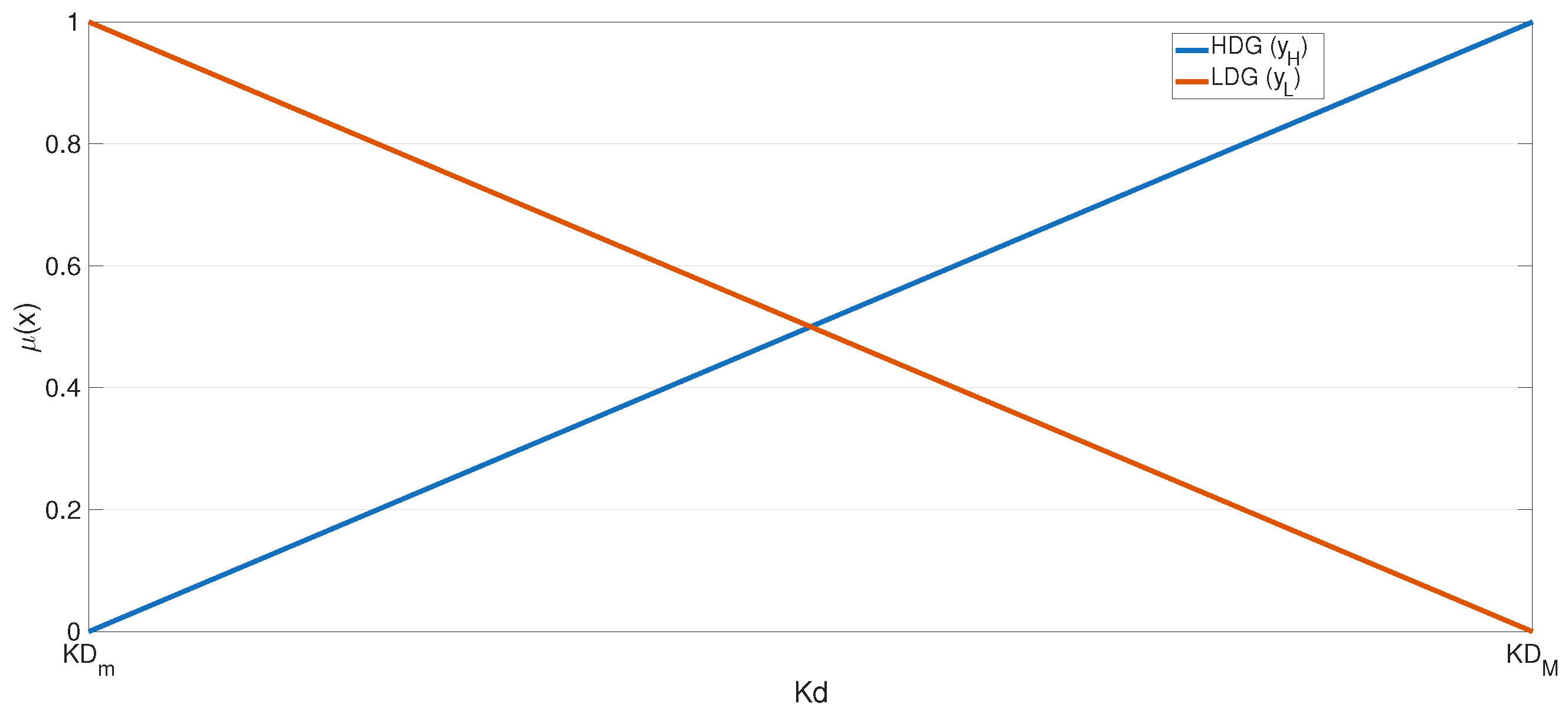




| Membership Function | [m] | [m] |
|---|---|---|
| Positive Error (P) | 0.02 | −0.02 |
| Negative Error (N) | −0.02 | 0.02 |
| Membership Function | [m/s] | m/s |
|---|---|---|
| Positive Error Derivative (PED) | 0.00015 | −0.00015 |
| Negative Error Derivative (NED) | −0.00015 | 0.00015 |
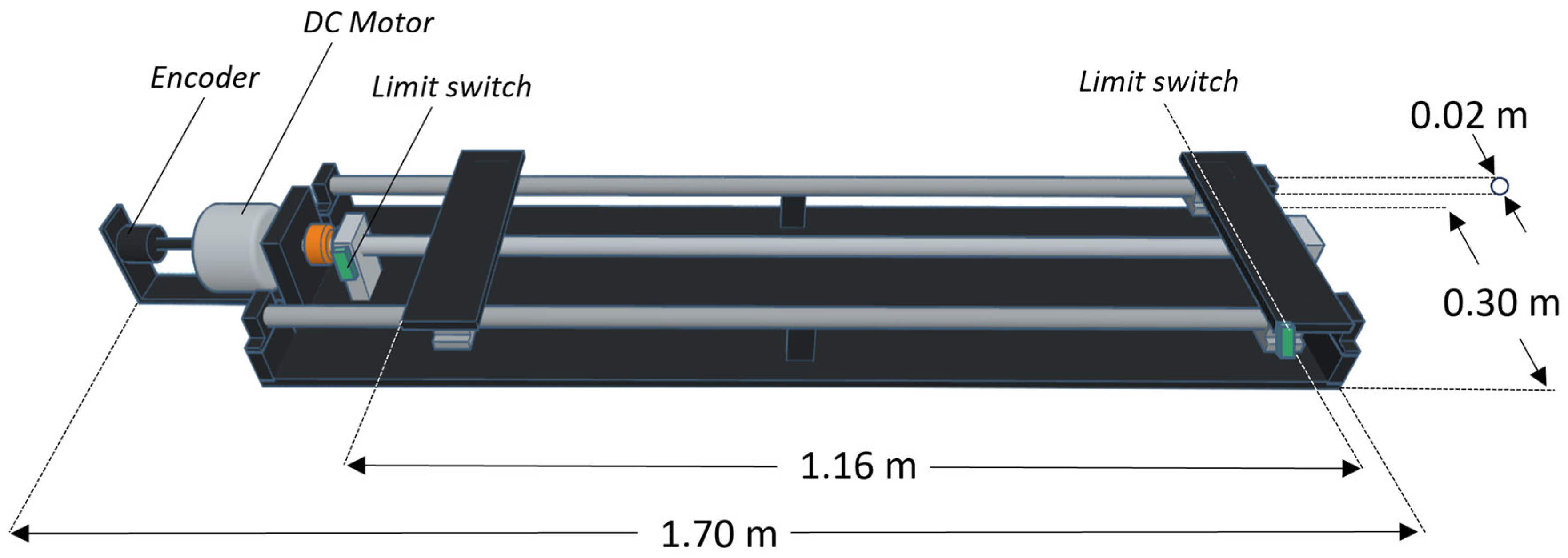
| Geometrical Parameter | Dimensions |
|---|---|
| Total length of the plant [m] | |
| Plant width [m] | |
| Carriage shaft [m] | |
| Rail linear guides [m] | |
| Round shaft linear guides [m] | |
| Coupling shaft flexible [m] | |
| Bearing balls [m] | × × |
| Feature | Description |
|---|---|
| Core | ARM Cortex-M4F |
| Performance | 80-MHz operation |
| UART | 8 modules |
| I2C | Four I2C modules with four transmission speeds, including high-speed mode |
| General-Purpose Timer (GPTM) | 6–16-/32-bit GPTM blocks and six 32/64-bit wide GPTM blocks |
| General-Purpose Input/Output (GPIO) | 6 physical GPIO blocks |
| PWM | 2 PWM modules, each with four PWM generator blocks and a control block, up to 16 PWM outputs |
| QEI | 2 QEI modules |
| Parameter | Parabolic | Trapezoidal | S-Curve |
|---|---|---|---|
| Final position () [m] | 0.8 | 0.8 | 0.8 |
| Total time for displacement (T) [s] | 4 | 4 | 4 |
| Acceleration time () [s] | – | 1.333 | 1.6 |
| Maximum velocity () [] | 0.3 | 0.3 | 0.333 |
| Maximum acceleration () [] | 0.3 | 0.225 | 0.277 |
| Profile | Controller | MTE [m] | SSE [m] | |
|---|---|---|---|---|
| Without Load | ||||
| Parabolic | PID | 0.00245 | 0.00080 | 0.100 |
| TFLC | 0.00541 | 0.00081 | 0.102 | |
| Trapezoidal | PID | 0.00221 | 0.00051 | 0.064 |
| TFLC | 0.00660 | 0.00089 | 0.112 | |
| S-curve | PID | 0.00193 | 0.00010 | 0.013 |
| TFLC | 0.00664 | 0.00180 | 0.226 | |
| With Load | ||||
| Parabolic | PID | 0.00960 | 0.00088 | 0.111 |
| TFLC | 0.00598 | 0.00087 | 0.109 | |
| Trapezoidal | PID | 0.00229 | 0.00038 | 0.048 |
| TFLC | 0.00695 | 0.00090 | 0.113 | |
| S-curve | PID | 0.00206 | 0.00011 | 0.014 |
| TFLC | 0.00694 | 0.00176 | 0.220 | |
| Profile | Controller | Max Current [A] | Max Voltage [V] | Max Power [W] |
|---|---|---|---|---|
| Without Load | ||||
| Parabolic | PID | 2.6192 | 12.4329 | 28.8797 |
| TFLC | 2.4996 | 11.4298 | 25.2190 | |
| Trapezoidal | PID | 2.6234 | 13.5946 | 35.5874 |
| TFLC | 2.4738 | 12.8834 | 31.8029 | |
| S-curve | PID | 2.6942 | 13.7301 | 36.8111 |
| TFLC | 2.6568 | 13.5802 | 35.8669 | |
| With Load | ||||
| Parabolic | PID | 2.6038 | 12.6425 | 29.8020 |
| TFLC | 2.5532 | 11.8505 | 27.3064 | |
| Trapezoidal | PID | 2.6844 | 13.9959 | 37.5539 |
| TFLC | 2.5964 | 13.4378 | 34.7456 | |
| S-curve | PID | 2.6940 | 14.1438 | 37.7888 |
| TFLC | 2.6882 | 14.0742 | 37.7467 | |
| Controller | Parabolic | Trapezoidal | S-Curve |
|---|---|---|---|
| Without Load | |||
| PID | 74.4293 | 70.7416 | 70.5947 |
| TFLC | 65.6661 ↓ | 64.1794 ↓ | 68.1557 ↓ |
| With Load | |||
| PID | 72.6189 | 71.2532 | 68.1431 |
| TFLC | 69.9805 ↓ | 65.7775 ↓ | 66.5385 ↓ |
| Condition | Profile | CVPID (%) | CVTFLC (%) | p-Value |
|---|---|---|---|---|
| No load | Parabolic | 2.71 | 1.86 | 0.00010 |
| Trapezoidal | 3.49 | 0.82 | 0.00332 | |
| S-curve | 1.76 | 0.48 | 0.01003 | |
| With load | Parabolic | 2.11 | 1.84 | 0.01903 |
| Trapezoidal | 3.00 | 2.98 | 0.00297 | |
| S-curve | 1.64 | 1.21 | 0.03373 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Olmedo-García, L.F.; García-Martínez, J.R.; Rodríguez-Reséndiz, J.; Dublan-Barragán, B.S.; Cruz-Miguel, E.E.; Barra-Vázquez, O.A. Tsukamoto Fuzzy Logic Controller for Motion Control Applications: Assessment of Energy Performance. Technologies 2025, 13, 387. https://doi.org/10.3390/technologies13090387
Olmedo-García LF, García-Martínez JR, Rodríguez-Reséndiz J, Dublan-Barragán BS, Cruz-Miguel EE, Barra-Vázquez OA. Tsukamoto Fuzzy Logic Controller for Motion Control Applications: Assessment of Energy Performance. Technologies. 2025; 13(9):387. https://doi.org/10.3390/technologies13090387
Chicago/Turabian StyleOlmedo-García, Luis F., José R. García-Martínez, Juvenal Rodríguez-Reséndiz, Brenda S. Dublan-Barragán, Edson E. Cruz-Miguel, and Omar A. Barra-Vázquez. 2025. "Tsukamoto Fuzzy Logic Controller for Motion Control Applications: Assessment of Energy Performance" Technologies 13, no. 9: 387. https://doi.org/10.3390/technologies13090387
APA StyleOlmedo-García, L. F., García-Martínez, J. R., Rodríguez-Reséndiz, J., Dublan-Barragán, B. S., Cruz-Miguel, E. E., & Barra-Vázquez, O. A. (2025). Tsukamoto Fuzzy Logic Controller for Motion Control Applications: Assessment of Energy Performance. Technologies, 13(9), 387. https://doi.org/10.3390/technologies13090387












