Double Wishbone Suspension: A Computational Framework for Parametric 3D Kinematic Modeling and Simulation Using Mathematica
Abstract
1. Introduction
2. Related Work
| System Type | Symbolic Method | Focus Area | Visualization | Interactivity |
|---|---|---|---|---|
| General suspensions [20] | Mixed Symbolic-Numerical | K&C modeling | ✗ | ✗ |
| Double wishbone [21] | Block-triangularization | Real-time dynamics | ✓ (simulator) | Partial |
| Generic link suspensions [22] | Symbolic sensitivity analysis | Design optimization | ✗ | ✗ |
| McPherson [23] | Mathematica-based symbolic kinematics | Static geometry | ✗ | ✗ |
| Double wishbone [24] | Coupled kineto-dynamics | Performance trade-offs | ✗ | ✗ |
| Double wishbone | Full symbolic + numerical solving | Real-time kinematics & visualization | ✓ (3D interactive) | ✓ (live parametric solver) |
3. Methodology
3.1. Coordinate Transformation
3.1.1. Rotation Matrix
- Rotation about the X-axis (pitch)This rotates a point or vector around the X-axis by an angle . It is used, for instance, to simulate the upper control arm’s pitch motion relative to chassis mounting points.
- Rotation about the Y-axis (yaw)This rotation is essential to simulate how the wheel steers around a vertical axis, such as when a vehicle turns left or right.
- Rotation about the Z-axis (roll)This represents rotation about the Z-axis, often used in modeling chassis roll or wheel tilt caused by lateral forces.
3.1.2. Combine 3D Rotation
- XYZ Order: Common for the lower control arm and other base-mounted parts.
- ZXY Order: Used for parts like the upper control arm where the rotation hierarchy differs.
3.2. Homogeneous Transformation
- Top-left block: the rotation matrix rot
- Top-right block: the translation vector trans
- Bottom row: a row vector
3.2.1. Numerical Considerations and Stability
3.2.2. Transformations from Chassis Frame to Upper and Lower Control Arm
- ACUCA[]: This constructs the transformation matrix for the upper control arm using the Z-X-Y (rot3DZXY) rotation sequence. This choice reflects a mounting configuration where roll (Z), camber/caster tilt (X), and toe or fore-aft direction (Y) are sequentially applied. This is often relevant to higher control arms whose mounts might be angled or non-orthogonal to the main chassis frame. The function returns a matrix representing the full pose (position and orientation) of the UCA frame in the chassis coordinate system.
- ACLCA[]: This defines the lower control arm transformation, using the Z-Y-X (rot3D) rotation sequence. This is a standard Euler sequence for typical orthogonal setups, where the LCA is mounted more parallel to the chassis axes. Likewise, it returns a homogeneous transformation matrix.
3.2.3. Transformations from UCA and LCA Frames to Upright Frame
- AUCUpright[]: This models the upper control arm to upright transformation. The transformation employs the Z-X-Y rotation order (rot3DZXY), which works best for systems that rotate first around the Z-axis, then translate along the X-axis, and finally rotate around the Y-axis. The matrix is composed with a translation vector , which specifies the physical mounting position of the upright relative to the UCA.
- ALCUpright[]: This transformation connects the lower control arm to the upright. It follows the Z-Y-X Euler sequence (rot3D), which is suitable for most mounting configurations where the upright moves vertically with LCA travel while also rotating due to steering input.
- ACRod[]: This transformation defines a rod or link, likely used as a tie rod or pushrod. The rotation is limited to the Y and Z axes, as given by rot3D[0, , ], indicating that the rod pivots only in the yaw and roll directions. This reflects typical tie rod behavior—steering left and right while allowing vertical compliance. Again, the translation vector defines the position of this rod base relative to the chassis frame or another reference component.
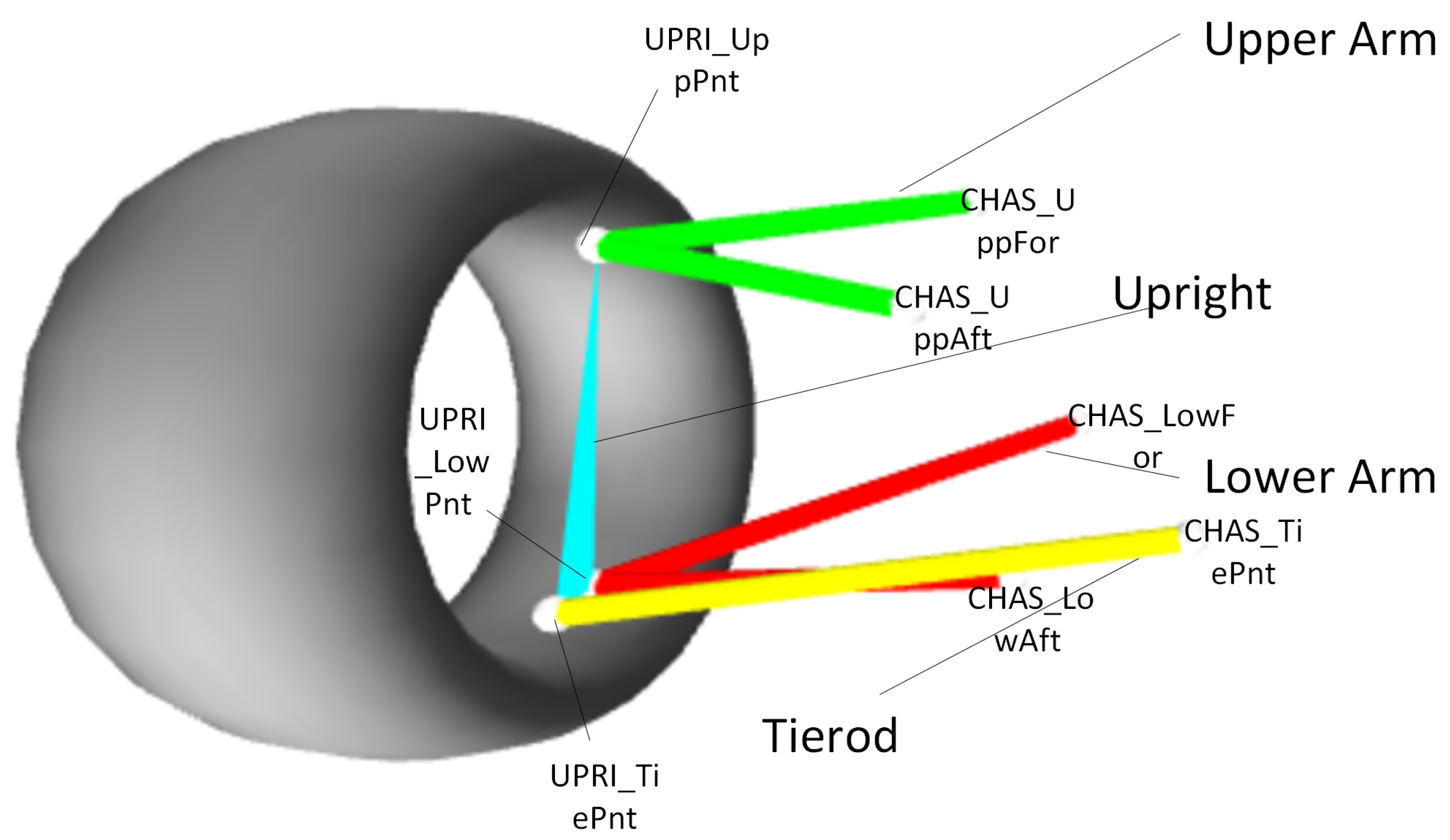
3.3. Local Frame Point
- Upper Control Arm (UCA): pUCAinF[] is the inboard (frame) mounting point of the UCA—typically attached to the chassis. pUCAinR[yUCAinR] is a parameterized inboard mounting on a rail, offset in the Y-axis. The parameter allows users to model various mount points. pUCAout[xUCAout, yUCAout] is the outer (upright) connection point of the UCA in its local frame.
- Tie Rod or Pushrod: pRodin[]: The base point of the rod in its frame (likely attached to the steering rack or chassis). pRodout[xRodout]: The upright-end attachment point of the rod, parameterized by X—commonly used in steering simulations.
- Upright: pUprightU[xUprightU] is the upper pivot point where the UCA connects to the upright. pUprightL[] is the lower pivot point of the upright, often aligned as the origin in its local frame. pUprightS[xUprightS, yUprightS] is a side point on the upright—likely for the tie rod or shock mount.
- Lower Control Arm (LCA): pLCAinF[] is the inboard (frame) mounting of the LCA. pLCAinR[yLCAinR] is another inboard option along the Y-axis. pLCAout[xLCAout, yLCAout] is the outer joint where the LCA connects to the upright.
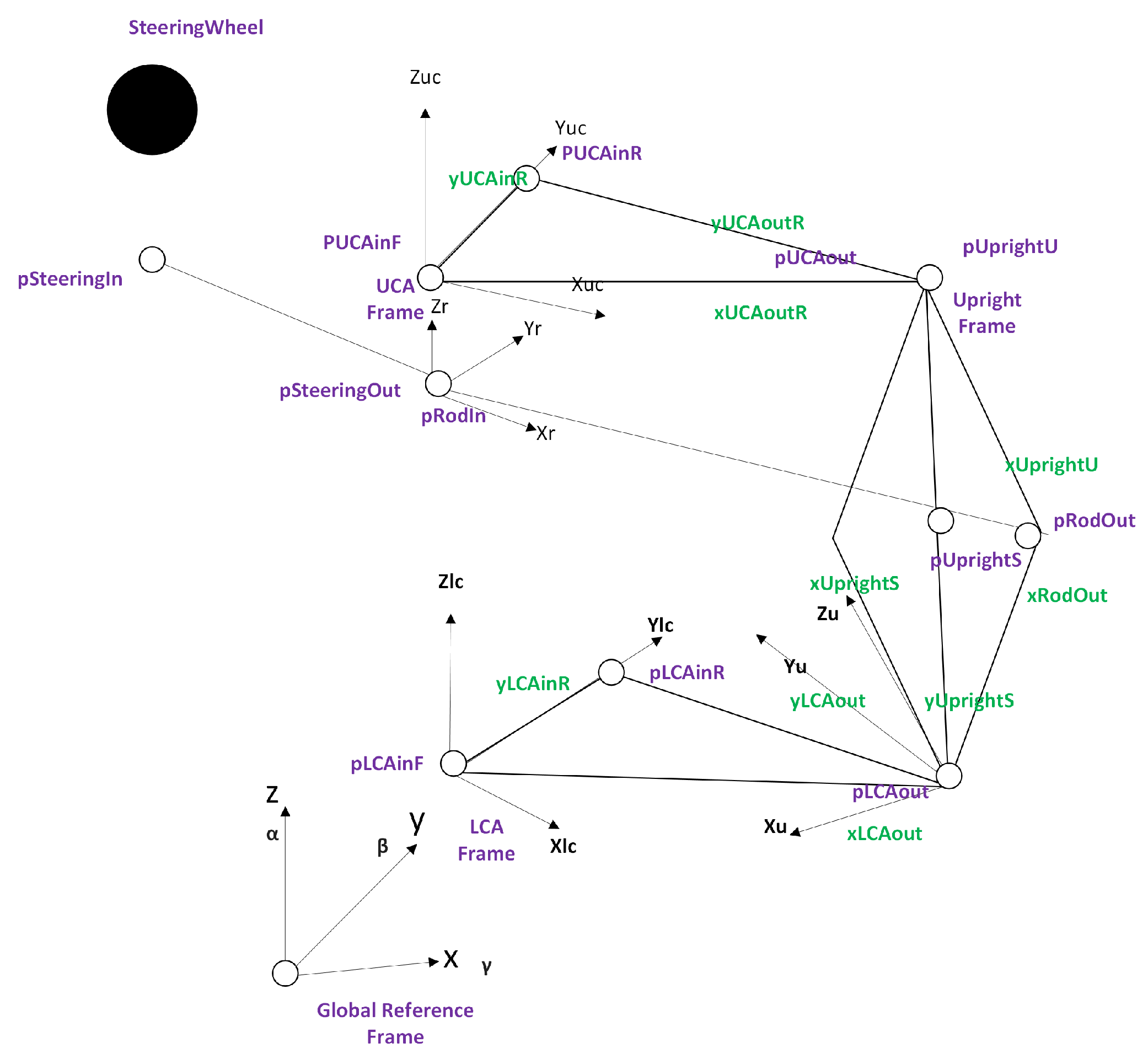
3.4. Global Transformation
3.4.1. Global Transformation of UCA Points
- pUCAinFglobal[…] computes the global coordinates of the UCA’s inboard frame mount, i.e., where the UCA attaches to the chassis. ACUCA[…] is the transformation from the chassis frame to the UCA frame. pUCAinF[] is the local point . Their matrix product yields the global position of the UCA’s inboard frame point.
- pUCAinRglobal[…] is a parameterized inboard point that might slide along a rail (e.g., an adjustable mount position on the chassis). pUCAinR[yUCAinR] introduces a Y-axis offset for the inboard mount. The results give the real-time global position based on chassis parameters and input angle.
- pUCAoutglobal[…] gives the global coordinates of the UCA’s outboard end, where it connects to the upright. The point pUCAout[xUCAout, yUCAout] defines this connection in local frame coordinates. After applying the chassis → UCA transformation, the returned position can be used to define the upright’s upper ball joint position, measure kinematic variables such as camber change or virtual swing arm length and visualize the actual suspension arm position in space.
3.4.2. Global Transformation of LCA Points
- pLCAinFglobal[…] calculation determines the global (chassis-relative) location of the lower control arm’s (LCA) inboard mount, which serves as the chassis-side pivot point. The transformation applies the origin point of the LCA frame through the LCA-to-chassis transformation matrix.
- pLCAinRglobal[…] is a parameterized inboard mount located along the Y-axis, offset from the LCA’s local origin. The parameter allows users to model different LCA pivot positions, which is useful to create adjustable or performance-optimized suspension geometries.
- pLCAoutglobal[…] defines the outer pivot point of the LCA in global space. The simulation becomes easier to modify using the inputs and , which control the LCA’s length and orientation in space. The actual spatial position of the lower ball joint becomes available through this function, enabling upright motion analysis, camber studies, and suspension force line calculations.
3.4.3. Global Transformation of Rod Points
- pRodinglobal[…] is the base of the rod that undergoes transformation into the global frame during this operation. The point pRodin[] has coordinates in the local coordinate system of the rod. The transformation matrix performs spatial orientation through yaw () and roll () and applies a spatial offset to describe the positioning of the rod and its angular orientation in space.
- pRodoutglobal[…] explain the calculation of this endpoint represents the outer end of the rod, which could potentially connect to the upright. The input specifies the extent and orientation of the rod in its local coordinate system along the X-axis. The output provides the actual global coordinates of this endpoint, allowing calculations for steering angle effects, change in tie rod length during articulation, and tracking of the contact point with the upright.
3.4.4. Transformations Chaining to Global Upright
4. Constraint
4.1. Upright Constraint Equations
- leftHandSideU: The global position of the upper joint on the upright is defined by this expression. The computation uses pUprightUglobal[…] which internally applies the transformation ACUpright[…] to the local point pUprightU[]. The inputs specify the upright’s orientation and translation through its linkage connection to the LCA.
- rightHandSideU: The global position of the outboard end of the UCA is represented by this expression. The transformation of a local point through the relative transformation of the UCA’s is calculated by pUCAoutglobal[…]. This result represents the expected global position where the UCA connects to the upright.
- equationsU = Thread[…]: The Thread function applies element-wise equality to create:This results in three scalar equations: one for the X-coordinate match, one for the Y-coordinate match, and one for the Z-coordinate match.
4.2. Constraint Equation for Upright–Rod Connection
- leftHandSideS: Determines the absolute (global) coordinates of a specific upright point that typically hosts rod connections. The local point pUprightS is defined within the upright’s local coordinate system at coordinates and . The transformation ACUpright is applied in the function pUprightSglobal to convert points from the upright’s frame to the global frame. This point dynamically tracks upright movement, as the upright adjusts its position based on lower control arm (LCA) motion and orientation.
- rightHandSideS: This represents the end of the rod outboard, the point that connects to the upright. The function pRodout(x_Rodout) determines the endpoint’s coordinates in the rod’s local reference system. The transformation pRodoutglobal applies rod-specific rotation and translation data relative to the chassis, converting the local coordinates into global space. This transformation enables the system take into account the steering angle, the position for mounting, and suspension travel when evaluating the rod position.
- equationsS = Thread[…]: The system generates three individual scalar equations that maintain the spatial relationship between the two global points:This constraint ensures that the upright side point precisely matches the spatial position of the rod’s outboard end.
4.3. Challenges in Solving Constraint Equations
- Multiple Solutions: For a given set of input parameters, the equations can yield multiple mathematically valid solutions. However, only one of these typically corresponds to the physically correct and intended assembly of the suspension.
- Convergence Issues: The numerical solver’s ability to converge to a solution can be sensitive to the initial guess and the domain constraints provided. If the input parameters define a geometrically impossible configuration (e.g., control arms are too short to connect), the solver will fail to find a solution.
- Singular Configurations: At the physical limits of motion, such as when two links become collinear, the system can approach a singularity. At these points, the solution may become unstable or non-unique, reflecting a real mechanical binding or toggle point.
5. Visualization Framework
5.1. Position Points for Visualization
- For the upper control arm (UCA):
- –
- posUCAinF[, , , tx, ty, tz];
- –
- posUCAinR[, , , tx, ty, tz, yUCAinR];
- –
- posUCAout[, , , tx, ty, tz, xUCAout, yUCAout].
These return the 3D positions of- –
- The inboard fixed and inboard rail-mounted chassis pivots of the UCA;
- –
- The outboard end of the UCA, where it connects to the upright.
- For the lower control arm (LCA):
- –
- posLCAinF[, , , tx, ty, tz];
- –
- posLCAinR[, , , tx, ty, tz, yLCAinR];
- –
- posLCAout[, , , tx, ty, tz, xLCAout, yLCAout].
These return the 3D coordinates of- –
- Inboard fixed and adjustable LCA pivots;
- –
- The upright-side joint on the LCA.
- For the upright,
- –
- posUprightS[, , , txu, tyu, xUprightS, yUprightS];
- –
- posUprightU[, , , txu, tyu, xUprightU].
These return- –
- posUprightS: The side attachment point (e.g., tie rod or damper mount);
- –
- posUprightU: The upper attachment point for the UCA.
These functions rely on the composite transformation from chassis → LCA → upright. - For the rod (tie rod or pushrod),
- –
- posRodin[, , txr, tyr, tzr];
- –
- posRodout[, , txr, tyr, tzr, xRodout].
These compute- –
- The rod’s chassis-side mounting (e.g., steering rack connection);
- –
- The rod’s upright-side endpoint.
5.2. Rendering of Suspension System
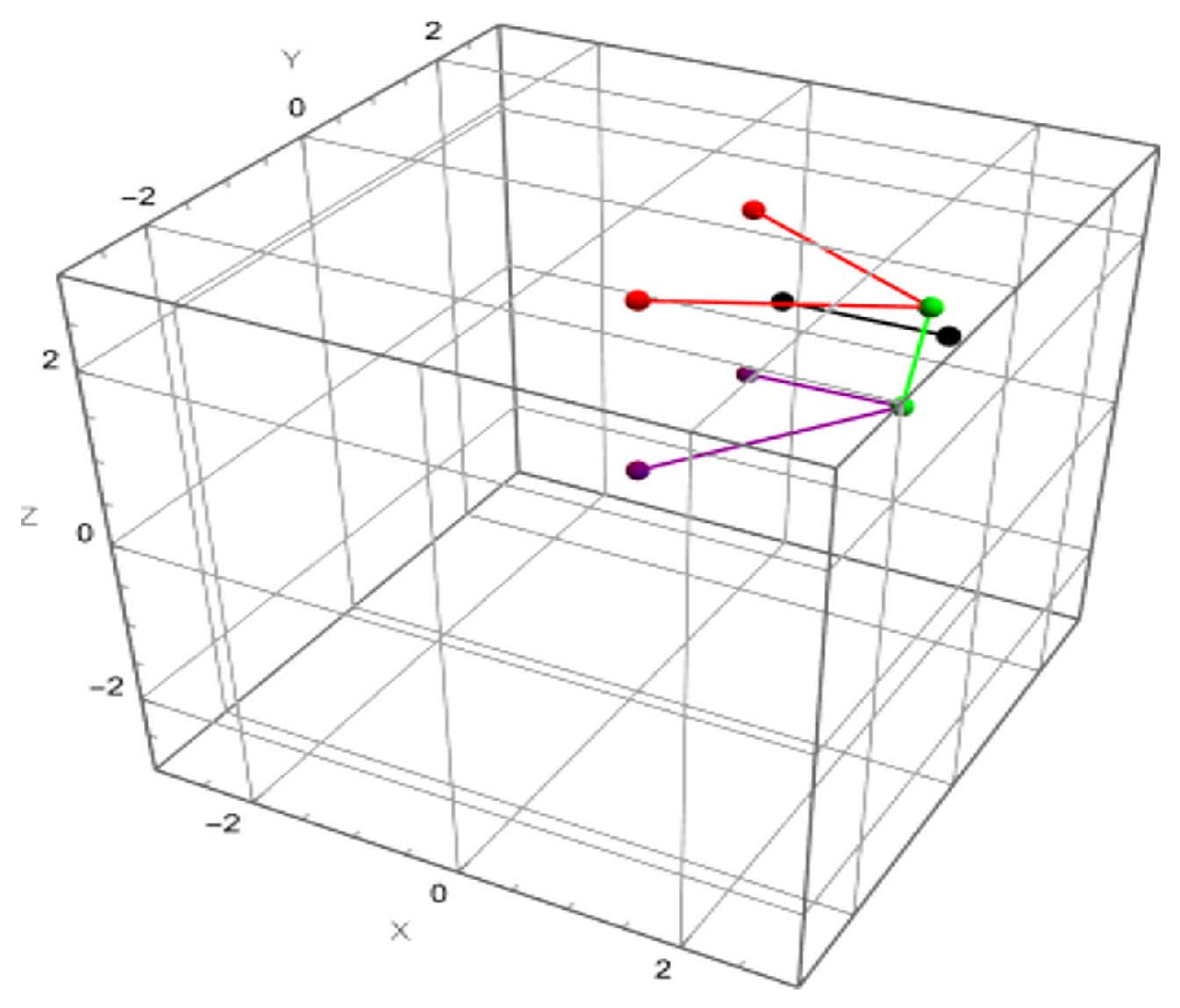
Graphics3D[{
(* Upper Control Arm *)
Red, Line[{pUCAinFglobalPos, pUCAoutglobalPos}],
Red, Line[{pUCAinRglobalPos, pUCAoutglobalPos}],
Red, Sphere[pUCAinFglobalPos, 0.1],
Red, Sphere[pUCAinRglobalPos, 0.1],
Red, Sphere[pUCAoutglobalPos, 0.1],
(* Lower Control Arm *)
Purple, Line[{pLCAinFglobalPos, pLCAoutglobalPos}],
Purple, Line[{pLCAinRglobalPos, pLCAoutglobalPos}],
Purple, Sphere[pLCAinFglobalPos, 0.1],
Purple, Sphere[pLCAinRglobalPos, 0.1],
Purple, Sphere[pLCAoutglobalPos, 0.1],
(* Upright vertical connection *)
Green, Line[{pUCAoutglobalPos, pLCAoutglobalPos}],
Green, Sphere[pUCAoutglobalPos, 0.1],
Green, Sphere[pLCAoutglobalPos, 0.1],
(* Rod (tie rod / pushrod) *)
Black, Line[{pRodinglobalPos, pRodoutglobalPos}],
Black, Sphere[pRodinglobalPos, 0.1],
Black, Sphere[pRodoutglobalPos, 0.1]\
}
]
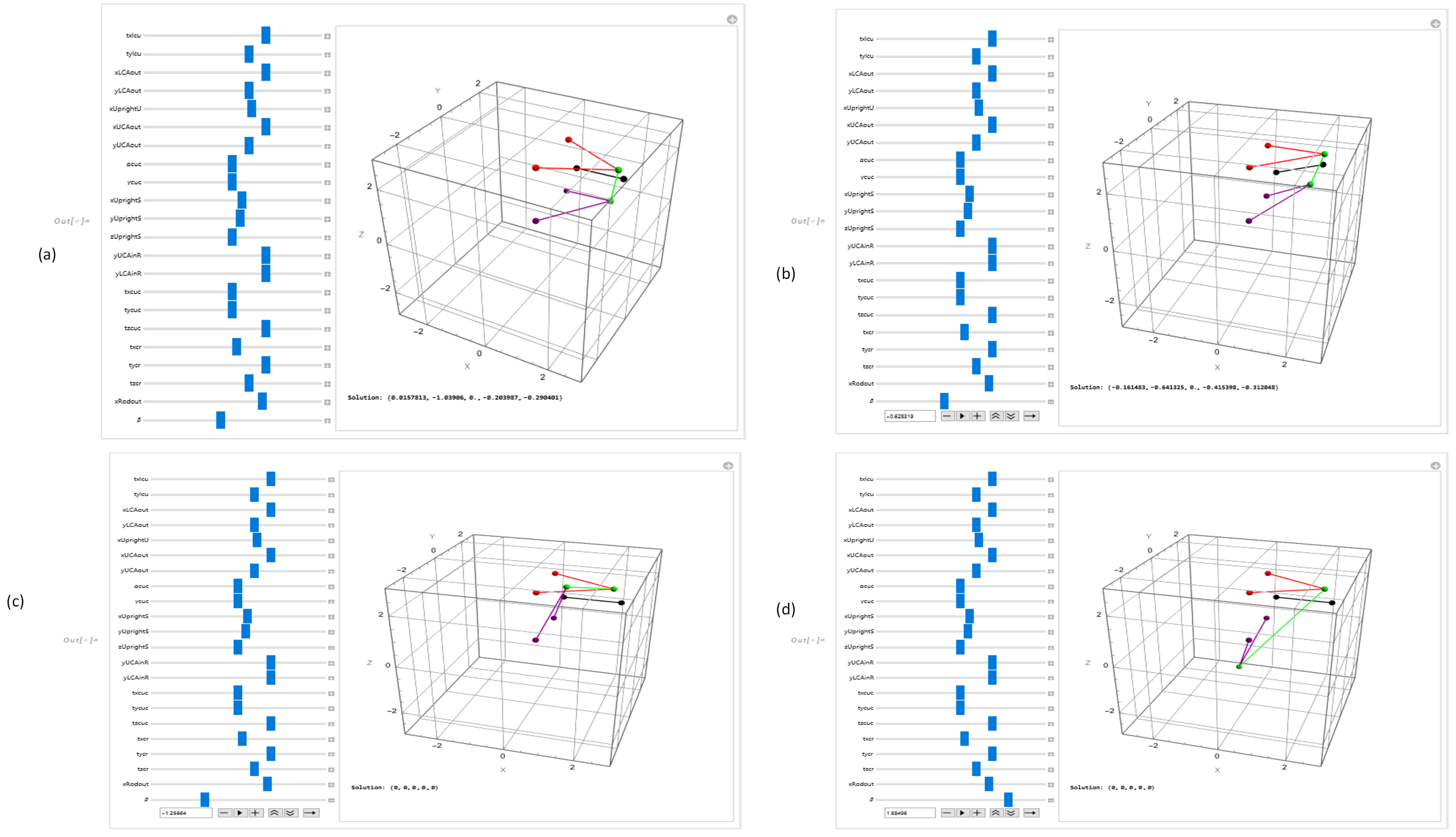
In color coding, red indicates the upper control arm, purple represents the lower control arm, green is used for the vertical upright connection, and black corresponds to the rod (such as a steering link or pushrod). The elements with a line[…] denotes mechanical links between components, while sphere[…, 0.1] is used to visualize joints or mounting points in the 3D suspension model.6. Dynamic Kinematic Solver
6.1. Performance and Computational Cost
6.2. Analysis of Computational Complexity
- Problem Complexity and Size: The dominant factor is the size of the equation system, which is a function of the number of independent loops and constrained degrees of freedom in the mechanism. As more components or constraints are added (e.g., modeling both sides of the vehicle or adding complex anti-roll bar linkages), the number of simultaneous equations and variables grows, which can lead to a non-polynomial increase in the time required to find a solution.
- Constraint Nonlinearity: The constraint equations are highly nonlinear, involving trigonometric functions (from the rotation matrices) and polynomial terms. The complexity of these equations directly impacts the difficulty of finding the roots of the system, which is the core task of the numerical solver.
- Parameter Dimensionality: While the dimensionality of the user-controlled parameters (the sliders in Manipulate) does not increase the complexity of a single solution, it expands the solution space that can be explored. As noted previously, navigating to regions of this space corresponding to singular or near-singular configurations can significantly increase the time to convergence for the solver.
6.3. Interactive Sensitivity Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Symbol | Description | Type/Unit |
| Rotation angle (pitch) of upper control arm (UCA) in chassis frame | Angle (radians) | |
| Rotation angle (yaw) of UCA in chassis frame, solved dynamically | Angle (radians) | |
| Rotation angle (roll) of UCA in chassis frame | Angle (radians) | |
| Rotation angle (pitch) of Upright in LCA frame, solved dynamically | Angle (radians) | |
| Rotation angle (yaw) of Upright in LCA frame, solved dynamically | Angle (radians) | |
| Rotation angle (roll) of Upright in LCA frame, solved dynamically | Angle (radians) | |
| Yaw angle of tie rod (rod) in chassis frame, solved dynamically | Angle (radians) | |
| Roll angle of tie rod (rod) in chassis frame, solved dynamically | Angle (radians) | |
| Suspension bump angle/deflection used to drive motion | ||
| (applies to LCA) | Angle (radians) | |
| X-coordinate of the UCA outboard connection in its local frame | Distance (units) | |
| Y-coordinate of the UCA outboard connection in its local frame | Distance (units) | |
| X-coordinate of the LCA outboard connection in its local frame | Distance (units) | |
| Y-coordinate of the LCA outboard connection in its local frame | Distance (units) | |
| X-offset of upright’s upper ball joint in upright local frame | Distance (units) | |
| X-offset of upright’s side connection (tie rod or damper) | Distance (units) | |
| Y-offset of upright’s side connection (tie rod or damper) | Distance (units) | |
| Z-offset of upright’s side connection (if used in 3D placement) | Distance (units) | |
| Y-offset of UCA inboard mount (rail variant) | Distance (units) | |
| Y-offset of LCA inboard mount (rail variant) | Distance (units) | |
| X-translation of UCA frame relative to chassis | Distance (units) | |
| Y-translation of UCA frame relative to chassis | Distance (units) | |
| Z-translation of UCA frame relative to chassis | Distance (units) | |
| X-translation of LCA-to-upright joint in chassis (manipulated input) | Distance (units) | |
| Y-translation of LCA-to-upright joint in chassis | Distance (units) | |
| X-offset of rod mount point in chassis | Distance (units) | |
| Y-offset of rod mount point in chassis | Distance (units) | |
| Z-offset of rod mount point in chassis | Distance (units) | |
| X-length of rod (from inboard to outboard tip) | Distance (units) | |
| pUCAinF[…] | Inboard frame-side point of upper control arm (global) | 3D Position |
| pUCAout[…] | Outboard point of UCA, connects to upright | 3D Position |
| pLCAinF[…] | Inboard chassis-side point of lower control arm (global) | 3D Position |
| pLCAout[…] | Outboard point of LCA, connects to upright | 3D Position |
| pUprightU[…] | Upper upright point where UCA connects | 3D Position |
| pUprightS[…] | Side upright point (tie rod or damper connection) | 3D Position |
| pRodinglobal[…] | Inboard (chassis-mounted) end of rod | 3D Position |
| pRodoutglobal[…] | Outboard (upright-connected) end of rod | 3D Position |
| drawSuspension[…] | Visualization function to render the entire suspension | |
| system using all calculated points | Graphics3D | |
| solution | Output of NSolve used to extract valid joint angles | List |
| equationsU, equationsS | Constraint equations that ensure connected | |
| parts meet at a common point | Equation Set | |
| deqs | Merged constraint equations from both UCA and tie rod systems | Equation Set |
| cons | Constraints on angle ranges for physically plausible behavior | Inequality Set |
| NSolve[…] | Numerical solver used to solve nonlinear constraint system | Solver Output |
References
- Dubey, A.D.; Verma, S.; Kumar, P. Analysis of Double Wishbone Suspension System Using MechAnalyzer. In Advances in Mechanical and Energy Technology; Yadav, S., Jain, P.K., Kankar, P.K., Shrivastava, Y., Eds.; Springer: Singapore, 2022; pp. 245–255. [Google Scholar] [CrossRef]
- Park, H.; Langari, R.; Yi, H. Design and testing of double-wishbone suspension for enhanced outdoor maneuver stability of a six-wheeled mobile robot. Mechatronics 2024, 103, 103237. [Google Scholar] [CrossRef]
- Taneva, S.; Ambarev, K.; Penchev, S. Strength and Frequency Analysis of the Lower Arm of a Double Wishbone Suspension of a Passenger Car. ETR 2024, 1, 352–357. [Google Scholar] [CrossRef]
- Sharma, R. Design and Optimisation of Double Wishbone Suspension for High Performance Vehicles. Int. J. Veh. Syst. Model. Test. 2023, 17, 185–195. [Google Scholar] [CrossRef] [PubMed]
- Niu, Z.; Jin, S.; Wang, R.; Zhang, Y. Geometry Optimization of a Planar Double Wishbone Suspension Based on Whole-Range Nonlinear Dynamic Model. Proc. Inst. Mech. Eng. Part D J. Automob. Eng. 2022, 236, 3–14. [Google Scholar] [CrossRef]
- Avi, A.G.; Carboni, A.P.; Stella Costa, P.H. Multi-Objective Optimization of the Kinematic Behaviour in Double Wishbone Suspension Systems Using Genetic Algorithm; SAE Technical Paper 2020-36-0154; SAE: Warrendale, PA, USA, 2021. [Google Scholar] [CrossRef]
- Shao, Y.; Li, G.; Wang, J. Optimization Design of Double Wishbone Front Suspension Based on Dynamic Simulation. Appl. Sci. 2023, 14, 1812. [Google Scholar] [CrossRef]
- Arshad, M.W.; Lodi, S.; Liu, D.Q. Multi-Objective Optimization of Independent Automotive Suspension by AI and Quantum Approaches: A Systematic Review. Machines 2025, 13, 204. [Google Scholar] [CrossRef]
- Arshad, M.W.; Lodi, S. Quantum computing in the automotive industry: Survey, challenges, and perspectives. J. Supercomput. 2025, 81, 1093. [Google Scholar] [CrossRef]
- Upadhyay, P.; Deep, M.; Dwivedi, A.; Agarwal, A.; Bansal, P.; Sharma, P. Design and analysis of double wishbone suspension system. IOP Conf. Ser. Mater. Sci. Eng. 2020, 748, 012020. [Google Scholar] [CrossRef]
- Golightly, D.; Pierce, K.; Palacin, R.; Gamble, C. A feasibility assessment of multi-modelling approaches for rail decarbonisation systems simulation. Proc. Inst. Mech. Eng. Part F J. Rail Rapid Transit. 2021, 236, 115–126. [Google Scholar] [CrossRef]
- Simpack Multibody Simulation Software. (n.d.). SIMULIA. Available online: https://www.3ds.com/products/simulia/simpack (accessed on 1 March 2025).
- Wang, J.; Zhao, Y. A repelling-screw-based approach for the construction of Jacobian matrices in parallel manipulators. Mech. Mach. Theory 2022, 170, 104726. [Google Scholar] [CrossRef]
- Guo, M.; De Persis, C.; Tesi, P. Data-Driven Stabilization of Nonlinear Systems via Taylor’s Expansion. In Lecture Notes in Control and Information Science; Postoyan, R., Frasca, P., Panteley, E., Zaccarian, L., Eds.; Springer: Cham, Switzerland, 2024; pp. 299–315. [Google Scholar] [CrossRef]
- Ashtekar, V.; Bandyopadhyay, S. Forward Dynamics of the Double-Wishbone Suspension Mechanism Using the Embedded Lagrangian Formulation. In Mechanism and Machine Science; Sen, D., Mohan, S., Ananthasuresh, G.K., Eds.; Springer: Singapore, 2021; pp. 843–859. [Google Scholar] [CrossRef]
- Zhang, B.; Li, Z. Mathematical modeling and nonlinear analysis of stiffness of double wishbone independent suspension. J. Mech. Sci. Technol. 2021, 35, 5671–5680. [Google Scholar] [CrossRef]
- Adams: The Multibody Dynamics Simulation Solution. (n.d.). Enteknograte. Available online: https://enteknograte.com/adams-multibody-dynamics-simulation-solution/ (accessed on 1 February 2025).
- Wolfram Research. (n.d.). Symbolic and Numeric Computation. Wolfram U. Available online: https://www.wolfram.com/wolfram-u/courses/mathematics/symbolic-numeric-computation-math915/ (accessed on 18 February 2025).
- Wolfram Research. (n.d.). Advanced Manipulate Functionality. Wolfram Language Documentation. Available online: https://reference.wolfram.com/language/tutorial/AdvancedManipulateFunctionality.html (accessed on 18 February 2025).
- Larcher, M.; Stocco, D.; Tomasi, M.; Biral, F. A Symbolic-Numerical Approach to Suspension Kinematics and Compliance Analysis. In Proceedings of the ASME 2024 International Mechanical Engineering Congress and Exposition. Volume 5: Dynamics, Vibration, and Control, Portland, OR, USA, 17–21 November 2024; p. V005T07A049. [Google Scholar] [CrossRef]
- Uchida, T.; McPhee, J. Driving Simulator with Double-Wishbone Suspension Using Efficient Block-Triangularized Kinematic Equations. Multibody Syst. Dyn. 2012, 28, 331–347. [Google Scholar] [CrossRef]
- Chun, H.-H.; Tak, T.-O. Sensitivity Analysis Using a Symbolic Computation Technique and Optimal Design of Suspension Hard Points. J. Korean Soc. Precis. Eng. 1999, 16, 26–36. [Google Scholar]
- Makita, M. An Application of Suspension Kinematics fMontreal, Quebec H3G 1M8, Canadaor Intermediate Level Vehicle Handling Simulation. JSAE Rev. 1999, 20, 471–477. [Google Scholar] [CrossRef]
- Balike, K.P. Kineto-Dynamic Analyses of Vehicle Suspension for Optimal Synthesis. Ph.D. Thesis, Concordia University, Montreal, QC, Canada, 2010. [Google Scholar]
| Parameter | Baseline Value | Range |
|---|---|---|
| 2.0 | ||
| 1.0 | ||
| 2.0 | ||
| 1.0 | ||
| 1.2 | ||
| 2.0 | ||
| 1.0 | ||
| 0.0 | ||
| 0.0 | ||
| 0.6 | ||
| 0.5 | ||
| 0.0 | ||
| 2.0 | ||
| 2.0 | ||
| 0.0 | ||
| 0.0 | ||
| 2.0 | ||
| 0.3 | ||
| 2.0 | ||
| 1.0 | ||
| 1.8 | ||
| −0.4 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arshad, M.W.; Lodi, S.; Liu, D.Q. Double Wishbone Suspension: A Computational Framework for Parametric 3D Kinematic Modeling and Simulation Using Mathematica. Technologies 2025, 13, 332. https://doi.org/10.3390/technologies13080332
Arshad MW, Lodi S, Liu DQ. Double Wishbone Suspension: A Computational Framework for Parametric 3D Kinematic Modeling and Simulation Using Mathematica. Technologies. 2025; 13(8):332. https://doi.org/10.3390/technologies13080332
Chicago/Turabian StyleArshad, Muhammad Waqas, Stefano Lodi, and David Q. Liu. 2025. "Double Wishbone Suspension: A Computational Framework for Parametric 3D Kinematic Modeling and Simulation Using Mathematica" Technologies 13, no. 8: 332. https://doi.org/10.3390/technologies13080332
APA StyleArshad, M. W., Lodi, S., & Liu, D. Q. (2025). Double Wishbone Suspension: A Computational Framework for Parametric 3D Kinematic Modeling and Simulation Using Mathematica. Technologies, 13(8), 332. https://doi.org/10.3390/technologies13080332








