New Approach to Dominant and Prominent Color Extraction in Images with a Wide Range of Hues

Abstract

Dominant colors significantly influence visual image perception and are widely used in computer vision and design. Traditional extraction methods often neglect visually salient colors that occupy small areas yet possess high aesthetic relevance. This study introduces a method for detecting both dominant and visually prominent colors in a wide range of hues and images. We analyzed the color gamut of images in the CIE L^*a^*b^* color space and concluded that it is difficult to identify the dominant and prominent colors due to high color variability. To address these challenges, the proposed approach transforms images into the orthogonal ICaS color space, integrating the properties of RGB and CMYK models, followed by K-means clustering. A spectral residual saliency map is applied to exclude background regions and emphasize perceptually significant objects. Experimental evaluation on an image database shows that the proposed method yields color palettes with broader gamut coverage, preserved luminance, and visually balanced combinations. A comparative analysis was conducted using the ΔE₀₀ metric, which accounts not only for differences in lightness, chroma, and hue but also for the perceptual interactions between colors, based on their proximity in the color space. The results confirm that the proposed method exhibits greater color stability and aesthetic coherence than existing approaches. These findings highlight the effectiveness of the orthogonal saliency mean method for delivering a more perceptually accurate and visually consistent representation of the dominant colors in an image. This outcome validates the method’s applicability for image analysis and design.

1. Introduction

Color determines consumers’ cognitive and emotional perceptions; it influences their behavioral responses and decisions. In his work, Johannes Itten defines color harmony as the basis of aesthetic perception and emphasizes the psychological and physiological aspects of color [1]. Color is one of the key factors in creating a recognizable brand. It creates first impressions and evokes associations in consumers. Color is a powerful marketing and branding tool: studies show that up to 90% of product perception decisions depend on color [2]. In addition, a scientific analysis of the color selection process in design confirms that 75% of designers struggle to select the right color scheme [3].

The dominant colors in an image are those primary colors that are most prevalent in its color distribution. They form the overall perception of the scene. This set of dominant colors is called a color palette. It is an important area of research in computer vision [4] and image processing, with a wide range of applications in image retrieval [5], image segmentation [6], and image compression [7]. Extracting color palettes from images is one of the research areas popular in computer graphics and design. It provides the ability to systematically analyze harmonious color combinations and adapt them for visual compositions. Scientific research confirms that the optimal color combinations are most often found in the natural environment. This is due to the evolutionary characteristics of human color perception [8]. The cognitive comfort of users can be increased by taking into account the peculiarities of natural color balance when creating graphic compositions.

The main goal of the study is to develop a new method for determining the dominant colors in an image using the ICaS color space [9,10], which we have used in previous studies to recalculate colors. In accordance with this goal, the following tasks were formulated: to analyze existing methods for determining dominant colors and formulate the requirements that the developed method must meet, and to implement an algorithm using the proposed method for the practical extraction of dominant and prominent colors in images.

This study is organized in the following way. Section 2 discusses related works on determining dominant colors in images. Section 3 is a description of the method of image color analysis and an explanation of the proposed method. The authors present the results of the method in detail in Section 4. A discussion of the study findings and future work is presented in Section 5.

2. Related Works

Automated color extraction from images has become increasingly popular, due to the development of computational methods. Various image analysis methods can identify key color combinations and create palettes that elicit certain emotional responses, such as the techniques of color clustering, spectral analysis, and statistical models [11]. The extraction of dominant and prominent colors from images is an important aspect of image analysis. It has a significant impact on processes such as image retrieval, processing, and sentiment analysis [12]. Traditional methods of dominant color extraction focus on those colors that occur frequently. Smaller, but visually important areas are often neglected. Traditional methods of dominant color extraction primarily focus on frequently occurring colors, often neglecting smaller but visually significant areas. Recent studies have addressed these limitations by incorporating salient object detection technologies to identify the important colors in smaller regions [13], analyzing chromatic diversity and attention-attracting colors in natural images [14], and proposing geometric approaches for creating harmonious palettes based on hue and saturation distributions [15]. Advances in image processing have also introduced machine learning models that analyze key colors, considering luminance, chromaticity, and human visual system characteristics [16], as well as flexible neural models that adapt palettes to the color gamut of images [17]. Deep learning and semantic segmentation techniques have been applied to assess image quality based on color features, demonstrating the broad applicability of dominant color detection methods [18]. The evaluation of visual color similarity has further progressed through palette comparison techniques utilizing Pearson’s coefficient [19], the analysis of palette color differences using the ΔE₀₀ formula [20], and pixel-weighted clustering methods for identifying key colors in mood boards [21]. Additionally, the efficiency of AI-generated color compositions has been explored, revealing that AI can replicate basic color schemes but lacks the diversity of human-designed compositions [22]. Emerging research on image sentiment analysis underscores the critical role of color palettes in conveying emotional signals and highlights the need for systematic approaches to understanding color-induced mood effects [12,23,24].

The selection of dominant and prominent colors is, therefore, a multifaceted task. It requires novel methodologies to accurately reflect the visual and color essence of images. An important area of research is the development of new techniques and the improvement of existing methods for determining the dominant and prominent colors in images. Visually important but less common color areas are often neglected by existing approaches. It is worthwhile to focus on the development of neural network analysis methods, improve the assessment of visual color similarity, and ensure the integration of emotional perception analysis into color palette detection systems.

Modern methods of determining dominant and prominent colors are ineffective for images with a wide range of colors. Therefore, new approaches are needed to solve this problem. This paper builds on existing research to propose a novel method for identifying the dominant and prominent colors in images with a wide range of hues. It achieves this by transforming and processing the colors in an orthogonal color space using a spectral saliency map and a K-means algorithm. Our approach aims to improve the accuracy of determining the dominant and prominent colors in an image by addressing domain-specific problems, such as images with extended color coverage. A new approach for image color processing in the orthogonal ICaS color space is developed in this study. Spectral residual saliency (SR) is used to detect salient objects with colors that attract the observer’s attention.

3. Materials and Methods

3.1. Image Database

For this study, 50 images were selected from open-access image libraries, licensed under Creative Commons Zero (CC0). These images represented real-world scenes. They were selected for their diversity of content, including both low-level features (color, contrast, frequency, and gradients) and high-level features [16]. Based on these features, the images were grouped into five categories: birds, fish, flowers, landscapes, architecture, and buildings, as shown in Figure 1. Each category presented a combination of color variety, complex details, contrast, and characteristic patterns. This affected the accuracy and speed of the algorithms when determining dominant and prominent colors. This approach ensures a representative sample for testing and evaluating the effectiveness of the algorithms under different conditions.

Many species of birds are distinguished by their bright and contrasting coloration, which complicates the identification of dominant colors due to high color saturation and fine morphological details, including plumage structure [25]. These features indicate substantial natural color variation that is contingent on species, habitat, and lighting conditions. Representatives of coral reef fish fauna demonstrate a wide variety of colors and textures. The morphology of flowers is characterized by a high degree of complexity, manifesting in the structural intricacies of petals, the vividness of coloration, and the pronounced contrast between primary hues and background colors. Natural landscapes are marked by numerous color gradients and multilayered compositions, exemplified by elements such as vegetation, sky, and water. The architecture and buildings category features geometric shapes and repeating structures that are painted in rich and varied colors. The high contrast between architectural elements and their surroundings poses challenges in identifying the dominant colors.

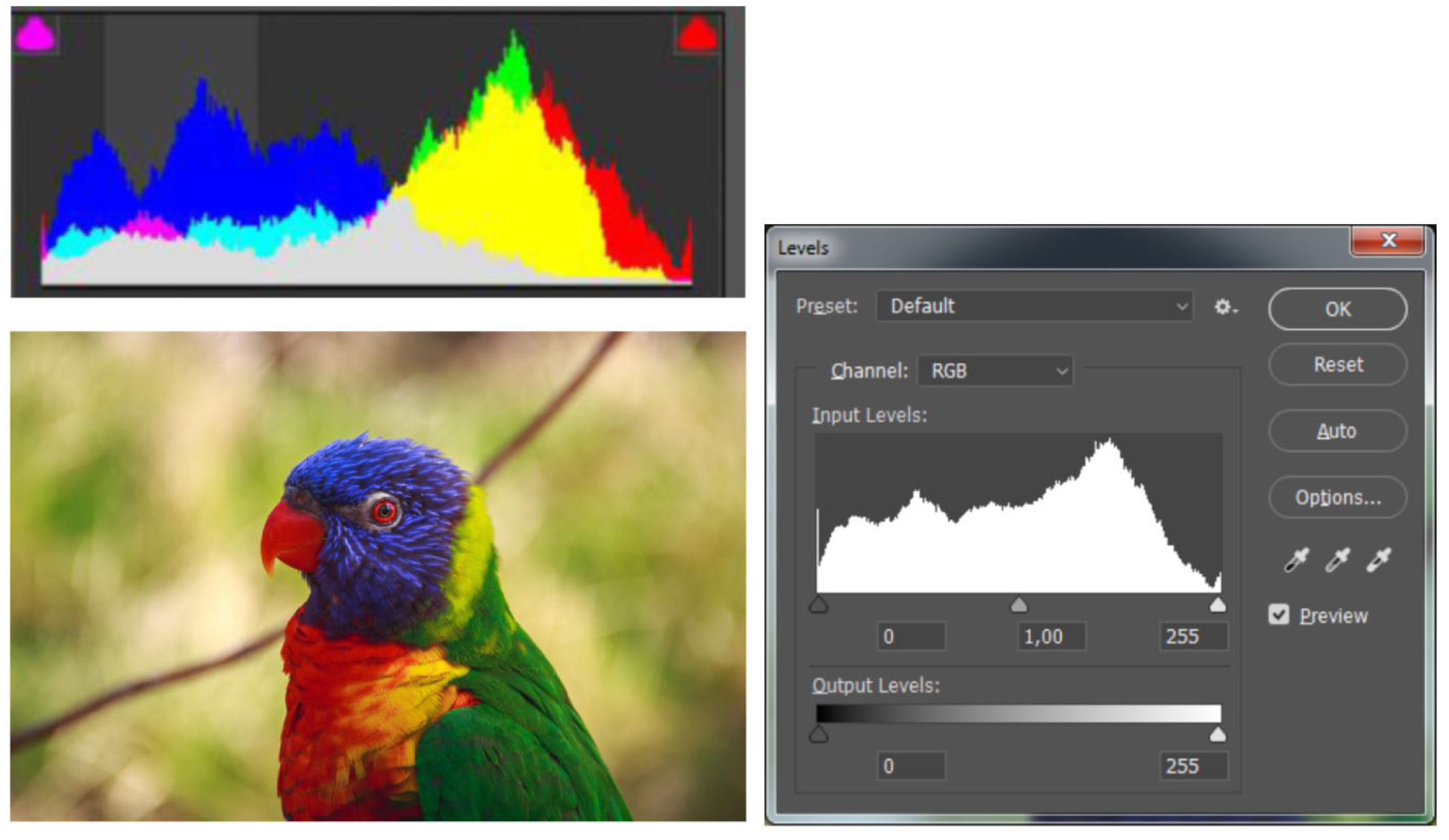
3.2. Color Gamut Analysis of an Image in the CIE L^*a^*b^* Color Space

The brightness distribution of pixels in the image was studied using a brightness histogram (linear histogram), which displays the ratio of dark to light areas (see Figure 2). The distribution of image brightness values is a key factor in determining the image’s chromaticity. An image with a uniform distribution of brightness values indicates a wide range of colors. The assessment of color saturation was conducted with a histogram, a statistical tool that is used to analyze the distribution of values within a dataset. A saturated color palette is characterized by the uniformity of its values across the entire range of the histogram, whereas a less saturated palette exhibits a concentration of values within a limited spectrum.

The chromaticity diagram in the CIE L^*a^*b^* space can be used to visualize the color distribution on the a^*b^* plane, where each point corresponds to a specific color in the image. A thorough examination of the distribution of points on the chart enables visualization of the predominant shades, as well as estimation of the color coverage of the image. The construction of the chromatic diagram was achieved through the implementation of the RGB to CIE L^*a^*b^* conversion algorithm. Initially, each of the red, green, and blue channels undergoes nonlinear correction due to gamma correction. Subsequently, the values are converted from the nonlinear space to the linear space (r, g, b) [26]:

$$v=V^{\gamma },$$

(1)

where V ∈ {R, G, B}—channel values in nonlinear form,

v ∈ {r, g, b}—channel values in linear form, and

γ is an indicator depending on the color model (e.g., γ = 2.2 for sRGB).

The conversion matrix into XYZ coordinates takes the following form [26]:

$$\left[\begin{array}{c}X\\ Y\\ Z\end{array}\right]=\left[\begin{array}{ccc}0.4124564& 0.3575761& 0.1804375Y\\ 0.2126729& 0.7151522& 0.0721750\\ 0.0193339& 0.1191920& 0.9503041\end{array}\right]\left[\begin{array}{c}r\\ g\\ b\end{array}\right]$$

(2)

The following equations are used for this calculation [26]:

$$X=x_r\times X_r; Y=y_r\times Y_r; Z=z_r\times Z_r$$

(3)

where X_rY_rZ_r—reference white D65: X_r = 0.9505; Y_r = 1; Z_r = 1.0891.

The following equations are used to calculate the coefficients x_r, y_r, and z_r [26]:

$$x_r=\left\{\begin{array}{c}{f}_x^3\\ \left(116f_x-16\right)/\kappa \end{array}\right. \begin{array}{c}if f_x^3>\epsilon \\ \mathrm{otherwise}\end{array}$$

(4)

$$y_r=\left\{\begin{array}{c}{\left(\left(L+16\right)/116\right)}^3\\ L/\kappa \end{array}\right. \begin{array}{c}if L>\kappa \epsilon \\ \mathrm{otherwise}\end{array}$$

(5)

$$z_r=\left\{\begin{array}{c}{f}_z^3\\ \left(116f_z-16\right)/\kappa \end{array}\right. \begin{array}{c}if f_z^3>\epsilon \\ \mathrm{otherwise}\end{array}$$

(6)

$$f_x={\displaystyle \frac{a}{500}}+f_y; f_z=f_y-{\displaystyle \frac{b}{200}}; f_y=\left(L+16\right)/116$$

(7)

where ε = 0.008856 and κ = 903.3.

A chromaticity diagram was used to evaluate the color gamut of the images. Images of painted buildings (as shown in Figure 3a) and aquarium fish (as shown in Figure 3b) had the highest level of color coverage. In the first case, this is due to the presence of bright and saturated colors that are typical of building facades. In the second case, this is due to the natural diversity of the fish’s colors, which covers a wide range of shades, from bright reds and yellows to deep blues and greens, thereby generally increasing the color variability of the image.

An image of flowers (see Figure 4a) also has a wide range of hues, due to the natural richness of floral coloration, while the landscape image (see Figure 4b) has a slightly narrower gamut dominated by darker tones.

We used the convex hull equation for a set of points in the CIE L^*a^*b^* three-dimensional color space [27] to quantify the volume of the image’s gamut. The volume of the corresponding convex hull is determined by the resulting expression. The gamut in CIE L^*a^*b^* space is modeled as a set of tetrahedra, with the common surface divided into these tetrahedra. The total volume is defined as the sum of the volumes of each tetrahedron. The volume of each tetrahedron is calculated using the following equation [28]:

$$V={\displaystyle \frac{1}{6}}\left[\begin{array}{cccc}1& 1& 1& 1\\ L_0^{*}& L_1^{*}& L_2^{*}& L_3^{*}\\ a_0^{*}& a_1^{*}& a_2^{*}& a_3^{*}\\ b_0^{*}& b_1^{*}& b_2^{*}& b_3^{*}\end{array}\right]$$

(8)

where $L_0^{*}{a}_0^{*}{b}_0^{*}$ is the center point in the CIE L^*a^*b^* color space; $L_1^{*}{a}_1^{*}{b}_1^{*}$, $L_2^{*}{a}_2^{*}{b}_2^{*}$, and $L_3^{*}{a}_3^{*}{b}_3^{*}$ are the three vertices on the surface of the tetrahedron.

Images with a wide range of L values but low saturation will have a large volume but a small chromatic projection. The latter is a better indicator of color saturation. Unsaturated colors (gray) tend to cluster near the origin of the a^*b^* plane coordinates. If an image contains many colors with low saturation, its palette volume may appear large due to changes in illumination. However, the projected color space will be small. Projection on the a^*b^* plane isolates the chromatic components but does not take into account variations in brightness. A similar method, which is conducted in two-dimensional space, is used to calculate the projection area on the a^*b^* plane. As a result, it is difficult to identify the dominant and prominent colors in images due to such color variability. It is possible to estimate volume but not hue by analyzing images in the CIE L^*a^*b^* space. The CIE L^*a^*b^* color space corresponds to human visual perception. However, it has a number of disadvantages related to the complex conversion process from RGB to XYZ to CIE L^*a^*b^*.

3.3. Image Processing Using Orthogonal ICaS Color Space

Color spaces determine how colors are represented and interpreted in a digital format. Different color spaces are used for different tasks, and their choice can affect the accuracy and perception of dominant colors. The ICaS color space simplifies and speeds up the conversion of color data, generalizes the properties of known spaces, and combines the two systems of color representation, RGB and CMYK, into one color space [23,24]. Considering the advantages of the ICaS color space, we will use it to determine the dominant colors in an image. The mathematical definition of the new ICaS color space is given in the form of a matrix of the canonical representation of the orthogonal color space, which is a matrix of the discrete Hartley transform with a dimension of 3 × 3 [29]:

$$\left[\begin{array}{c}I\\ C\\ S\end{array}\right]={\displaystyle \frac{1}{\sqrt{3}}}\left[\begin{array}{ccc}1& 1& 1\\ 1& H_1& H_2\\ 1& H_2& H_1\end{array}\right]\left[\begin{array}{c}r\\ g\\ b\end{array}\right], H_1={\displaystyle \frac{\sqrt{3}-1}{2}}; H_2=-{\displaystyle \frac{\sqrt{3}+1}{2}},$$

(9)

In the ICaS color space, three main coordinates are used to describe color: the achromatic coordinate I, which accurately describes the neutral grey component of the color, and the two chromatic coordinates C and S. These coordinates fully describe the chromatic properties of the color, including saturation (Cr_i) and hue (H_i), which are calculated using the corresponding equation:

$$C{r}_i=\sqrt{C_i^2+S_i^2}; H_i=\arctan \left({\displaystyle \frac{S}{C}}\right), {H^{\prime }}_i=H_i+{360}^{\circ }, \mathrm{if} H_i<0$$

(10)

To compare the color coverage of the ICaS and CIE L^*a^*b^* color spaces, two-dimensional color grids were constructed with a fixed achromatic component, namely, I = 0.866 in ICaS and L = 53.19 in CIE L^*a^*b^*. The values were both equivalent to the average grey color (RGB: 0.5, 0.5, 0.5). The colors on the planes (Figure 5a,b) have the same brightness (I or L), but different chromatic coordinates. The results visually demonstrate the wider color gamut of ICaS. The colors are evenly distributed in the shape of a hexagon. Previous studies have considered planes of constant brightness that are shifted relative to the origin. The orthogonality of the space was proven by determining the right angle between the axes [30].

It should be noted that a direct comparison of these spaces is difficult due to their different coordinate systems and scales. In the CIE L^*a^*b^* color space, the a and b coordinates vary from −128 to 128 and the L coordinate is in the range [0, 100]. In the ICaS space, the C and S coordinates are limited to the range [−0.78867, 0.78867], and the I coordinate ranges from 0 to √3 ≈ 1.73205.

To make a correct comparison, grid step normalization was used. It was determined that the step size of 0.5 in the CIE L^*a^*b^* space equated to 0.39% of the a and b coordinate range (0.5/128 ≈ 0.0039). Accordingly, the normalized step for the C and S coordinates in ICaS was calculated by proportion:

$$ste{p}_{ICaS}={\displaystyle \frac{0.78867\cdot 0.39}{100}}\approx 0.00308$$

(11)

The grids were constructed with the same normalized step of 0.195% of the range of the corresponding coordinates, which ensures proportional coverage of the space. The number of valid colors was calculated after the ICaS and Lab coordinates were converted to the sRGB space and the colors were checked (all the components of r, g, and b should be in the range [0 ... 1]). The CIE L^*a^*b^* space contains 59,679 valid colors on the ab plane and 136,829 valid colors on the CS plane. These data quantitatively demonstrate the advantage of ICaS for color coverage at a fixed achromatic coordinate, compared to CIE L^*a^*b^*.

Table 1. Quantifying the sRGB colors on constant luminance planes.

No	Fixed I (ICaS)	Number of sRGB Colors on CS Plane	Fixed L (CIE L*a*b*)	Number of sRGB Colors on ab Plane
1	1.299038	49,966	77.93	39,455
2	0.866025	136,829	53.77	60,053
3	0.433013	49,980	25.97	25,955

shows the results of a similar analysis that was performed for other values of I and L coordinates.

Two quantitative clustering metrics were calculated: the silhouette score and the Davies–Bouldin index. The silhouette score is a metric that quantifies the separation between clusters by comparing the average intra-cluster distance to the average inter-cluster distance. A value of −1 indicates incorrect clustering and 1 indicates well-separated clusters, while a score close to 0 suggests that the clusters are separated but have adjacent or overlapping boundaries [31].

The Davies–Bouldin index (DBI) reflects the ratio between intra-cluster and inter-cluster distances in the solution space. This metric measures the compactness and separation of clusters, with lower DBI values indicating tighter intra-cluster grouping and greater separation between clusters [32]. Both metrics were implemented in Google Colab, using the following functions: sil_score = silhouette_score (points, labels); db_index = davies_bouldin_score (points, labels). The metrics were applied to the color planes of fixed lightness in the ICaS and CIE L^*a^*b^* color spaces. Figure 6 presents a visualization of the clustering results, while the numerical data are provided in

Table 2. A quantitative assessment of color clustering in the constant luminance planes of the CIE L^*a^*b^* and ICaS spaces.

Clustering Metrics	CaS-Plane of Constant Brightness (I = 0.866) in ICaS Color Space	a*b*-Plane of Constant Brightness (L = 53.77) in CIE L*a*b* Color Space
Silhouette Score	0.342	0.378
Davies–Bouldin Index	0.872	0.835

. The results obtained by both metrics are consistent with each other, which confirms the possibility of using the ICaS space in clustering.

3.4. Proposed Method

In order to develop an effective method for detecting dominant and visually salient colors in images, we analyzed the generated palettes for 50 images studied using the methods described in a previous review article [11], as well as in tools for designers such as Coolors [33], Adobe Color Wheel [34], Image Color Picker [35], and Palette Generator [36]. Based on this analysis, the following generalizations are made:

• In most cases, the number of dominant colors varies from 4 to 10;
• The palette usually includes the color that occupies the largest area in the image, regardless of its visual expressiveness;
• The palette is usually based on the colors of the background, not the object of the image;
• Despite the wide range of colors, there is a limited variety of shades.

The following steps should be taken to develop an algorithm for detecting dominant and visually distinguishable colors in images with an extended color gamut that meets these requirements:

• Use of the visual salience model, which takes into account the contrast of the color relative to the surrounding background;
• Achromatic color filtering;
• Performing color segmentation in the orthogonal ICaS color space;
• Performing clustering in the ICaS color space, using the KM method to identify the most common color groups in the image;
• Performing the final selection of the dominant colors.

The selection of the final dominant colors from the preliminary set of candidates is based on the following criteria:

• Cluster size, which reflects the number of pixels of a particular color;
• Color saturation, which correlates with the probability of inclusion in the final palette;
• Contrast with the environment, which favors more visually expressive colors.

A general overview of the algorithm is shown in Figure 7. First, the image is transformed into the ICaS color space. In parallel, the color saliency is analyzed. Then, the colors are clustered using the KM method. Finally, the most expressive dominant colors are selected from the candidates. The SR method is used to analyze the saliency of colors. SR is an effective and rapid tool for detecting salient objects in images. It is based on an analysis of the image spectrum. It focuses on the extraction of high-frequency components that are responsible for the visual saliency of objects [37].

In this study, the threshold value of 24 was empirically determined, based on the characteristics of the target palettes and a visual analysis of various images. To illustrate the impact of this parameter, we present images with various visibility thresholds (Figure 8). Our analysis revealed that a threshold of 24 in the spectral saliency map method optimizes object selection in an image.

Color characteristics that influence the determination of dominant and prominent colors in ICaS color space fall into three main categories: chromatic saliency, color dominance, and spatial color segmentation. A transformation to the orthogonal ICaS color space was applied to evaluate the visual saliency of colors in an image. Chromaticity (Cr) is the key indicator of saliency. Colors with low chromaticity (Cr < 0.1), as well as high or low luminance (I > 1.15 or I < 0.2), are considered achromatic and are excluded from further analysis. The dominant colors are determined by KM clustering in the ICaS space. First, the image is divided into six color sectors according to the H_i angle. The H_i angle determines the hue. A separate clustering procedure is performed for each sector. The selection of six sectors is based on the number of primary colors in the additive (RGB) and subtractive (CMY) color models, which provide the greatest color coverage in digital images. In the ICaS space, the vectors of these six colors form a hexagon reflecting the boundaries of color coverage. This structure enables effective segmentation of the color space. As a result, a main centroid is selected. A set of six dominant colors is formed from the set of these centroids. The described approach takes into account the spatial structure of colors in the image. It reduces the influence of color mixing and provides more accurate detection of both the dominant and visually significant colors.

4. Results

4.1. Developed Algorithm and Experimental Environment

The experimental hardware platform was set up as follows: operating system—Windows 10-64bit, CPU—Intel(R) Core™ i5-7600U 3.50 GHz, and NVIDIA GeForce GTX 650. The software platform used Python 3.11.11 (64-bit) in the Google Colab environment; the preinstalled libraries NumPy 1.24.4, OpenCV (opencv-contrib-python 4.5.5.62), scikit-learn 1.2.2, Matplotlib 3.10.0, and Pillow 11.1.0 were used to implement the algorithm for detecting visually dominant colors in images. The OpenCV saliency module was used to create a saliency map, using the SR algorithm. For color analysis, we used our own implementation of the transformation into the orthogonal ICaS color space. The color pixels were then clustered using the KM method. The images were uploaded and processed in the Google Colaboratory environment. This environment provides interactive code execution, visualization of the results, and integration with cloud services.

We summarize the solution in Algorithm 1.

Algorithm 1 Determining Dominant and Prominent Colors of an Image Using Orthogonal ICaS color space

Require: input_image—input image

Ensure: dominant_colors—dominant colors in each color sector

1:  image_rgb ← load and convert input_image to RGB

2:  normalize image_rgb to [0, 1]

3:  compute I, C, S from RGB channels

4:  Cr ← sqrt(C2 + S2)

5:  Hi ← arctangent(S/C) in degrees, range [0, 360]

6:  alid_pixels ← (Cr > 0.1) ∧ ((I > 1.15) ∨ (I < 0.2))

7:  saliency_map ← compute spectral residual saliency from image

8:  binary_map ← threshold saliency_map at 24 to get salient areas

9:  salient_mask ← binary_map = 255 ∧ valid_pixels

10: define hue_sectors as named angle ranges

11: initialize sector_colors ← empty list for each sector

12: for each pixel in salient_mask do

13:   hi ← Hi at pixel

14:   assign pixel color to matching hue_sector by hi

15: end for

16: dominant_colors ← empty dict

17: for each sector in hue_sectors do

18:   if sector_colors not empty then

19:     apply k-means (k = 1) to pixel colors

20:     center ← cluster centroid

21:     store rounded center as RGB in dominant_colors

22:   end if

23: end for

24: visualize dominant_colors as a horizontal palette

25: return dominant_colors

Algorithm 1 implements the logic of the actions: determining the dominant and prominent colors of the image by transforming to the orthogonal ICaS color space, the spatial distribution of colors by hue, saturation analysis (Cr), and saliency map, followed by the clustering of colors within each sector.

4.2. Image Gamut Volume Calculating

We determined the color coverage indicators of the studied images in the CIE L^*a^*b^* color space using Equations (1)–(8). According to the calculations presented in

Table 3. Determining the color gamut of images.

Image Category	Average Value of Gamut Volume, Cubic CIE L*a*b* Units	Maximum Value of Gamut Volume, Cubic CIE L*a*b* Units
Birds	378,161.05	562,533.38
Fish	538,639.22	694,086.66
Flowers	514,948.65	671,420.25
Landscape	323,726.40	538,613.75
Buildings	589,373.96	729,224.01

, the largest average color coverage is observed in images of architectural objects—representing 589,374 cubic units in the CIE L^*a^*b^* space. This is due to the wide range of colors that are characteristic of bright facades and variable lighting. High values were also recorded for images of fish (538,639) and flowers (514,948), which can be explained by their natural color saturation in sufficient lighting conditions. Images of birds are characterized by a lower average gamma volume (378,161), although the maximum value (562,533) indicates the presence of individual examples of high color saturation. This is probably due to the predominance of neutral or natural tones in some images, which limits the overall color gamut. The lowest average color coverage is observed in landscape images (323,726), which are dominated by natural colors that rarely reach high levels of saturation.

It is a difficult task to determine the dominant colors of the studied images, taking into account the volume of their color space. The developed method allows the system to take into account the spectral complexity of the image and to select only the most visually significant colors. This reduces the influence of background or subtle pixels on the formation of the color palette.

4.3. Determination of Dominant and Prominent Colors

Using the proposed method, as well as the popular clustering methods described in the review [11], the dominant and visually distinguishable colors were identified. The results are shown in Figure 9. The arrangement of colors in each palette was ordered according to the saliency map and the binary map (see Figure 9a). The binary map was constructed using the SR method. To the right of the saliency map images are the input images and the corresponding color sets (see Figure 9b) obtained using K-means (KM), K-means in CIE L^*a^*b^* color space (KML, according to [38]), fuzzy C-means (FCM), mean shift (MS), and our orthogonal saliency mean (OSM) method.

The palette generated by OSM already contains colors sorted by saturation at the extraction stage. It automatically excludes the background because it is filtered by the saliency map. The first example shows that only our method extracts the two saturated colors of the bird’s feathers, which are the most visually salient. The palette obtained by the OSM method covers a wider range of colors than other methods for the second image of aquarium fish. In the image of flowers, our palette is characterized by a wider range of colors and higher saturation, including the blue color. This color is absent from palettes created with the other methods.

In the fourth example, the colors of the foreground objects are more distinct. The color of the sky is excluded. At the same time, in the image with colored buildings, we were able to accurately identify the foreground colors, as well as the visually distinct lilac color of the central building. Although it is not in the foreground, it attracts attention. The color palette obtained with our method (OSM) is visually perceived as darker than the color palettes obtained with the other methods (KM, KML, FCM, MS). However, the colors presented in the palette are characterized by a wider range of colors.

We selected the most colorful images from the MIT dataset and applied the method developed in this study for determining the dominant and prominent colors.

The developed method effectively identifies the prominent and dominant colors in the image. It sorts them according to their position on the color wheel. Sorting the selected colors allows us to compare the dominant colors of the palette with each other.

4.4. Evaluating the Color Diversity in Palettes

Comparing the dominant colors in a palette is necessary to quantify its diversity. Because observers tend to select colors from different color categories, palettes with greater color variations are usually perceived as more attractive [16].

Table 4. Color differences ΔE₀₀ between the colors of palettes generated by different methods.

Method	ΔE00 (CIE L*a*b*)
	Min	Mean	Max
KM	15.8	36.6	64.4
KML	15.4	37.2	58.9
FCM	14.3	36.1	67.1
MS	14.8	37.5	65.4
OSM	15.3	36.4	56.6

shows the comparative values of the color variability of palettes generated using the methods for determining the dominant colors of an image. The ΔE₀₀ metric (CIEDE2000) was used as a generalized indicator of variability, which allows us to estimate color differences in the CIE L^*a^*b^* space [28], taking into account the peculiarities of human perception. The presented minimum, average, and maximum values of color difference make it possible to analyze the degree of contrast and color variety within each of the obtained palettes.

Our analysis of these results shows that the developed OSM method provides a relatively stable level of color differences. Although the average value of ΔE₀₀ for OSM is close to other methods, its maximum value is the lowest among all studied approaches (56.6), which indicates a more balanced distribution of colors without excessive contrast combinations.

The obtained colors are represented in the CIE L^*a^*b^* color space, which was chosen for its correspondence to the peculiarities of human color perception. The points corresponding to the colors of the palette generated by the proposed method are evenly distributed on the color wheel, which indicates sufficient diversity and balance of the palette (see Figure 10). The position of the point in the center of the diagram indicates a low level of chromaticity, i.e., a weakly expressed chromaticity. A substantial number of color points are concentrated near the center of the color chart, indicating the predominance of colors with low chromaticity.

A histogram was constructed of the brightness of the colors of the palette generated from the test image using the studied methods (KM, KML, FCM, MS) and the developed method (OSM). The visualization of the results is shown in Figure 11. The average value of the luminance component for the dominant colors is L = 52. While most methods show an uneven distribution of brightness, the developed method provides more stable indicators, contributing to a holistic and visually pleasing perception of the palette.

Table 5. The L coordinate value in the CIE L^*a^*b^* space: color lightness characteristic.

Method	CIE L Value
	Min	Mean	Max
KM	12	54.3	88
KML	11	53.6	83
FCM	6	54.2	89
MS	7	55.3	87
OSM	32	52.3	73

shows the brightness values of the palette colors identified in the test images. The minimum, average, and maximum lightness values are shown. For example, with the FCM method, the range of L values is from 6 to 89, indicating the presence of both too-dark and too-light colors. A similar trend is observed for the KM (12 to 88), MS (7 to 87), and KML (11 to 83) methods. Instead, according to the results of the developed OSM method, the color brightness values are in a narrower range—from 32 to 73. This indicates a well-balanced distribution of luminance components without sharp drops, which ensures the consistency of colors in terms of brightness.

4.5. Visual Assessment of the Quality of Generated Palettes

We conducted a visual experiment in which users evaluated the aesthetic quality of color palettes generated by the OSM method and other comparable algorithms, such as KM, FCM, KML, and SM. The experiment took place in a training laboratory. It used a 27-inch LG IPS full HD monitor with a spatial resolution of 1920 × 1080 pixels. The monitor was calibrated to a white point of D65 and a gamma value of 2.2. The viewing distance was set to 40 cm [39]. The background of the images was neutral gray. The left side of the monitor displayed images, and the right side displayed five types of elongated color palettes, as shown in Figure 12. The order of the color palettes was shuffled for each image, and the method for selecting them was not disclosed.

The participants in the visual experiment were UI/UX design students from the Institute of Computer Science and Information Technology. Fourteen people took part in the experiment, including nine women and five men between the ages of 18 and 21. All observers had normal or corrected-to-normal visual acuity. To identify observers with color vision deficiencies, the Ishihara [40] online vision test was conducted on the Colorlite website. All participants passed the test.

The instructions given to the participants were as follows: “Five different color palettes will be shown on the monitor. Please rate each palette on a scale of 1 to 5 according to the following criteria: harmonious color combination, attractiveness, and relevance (i.e., the colors in the palette are dominant and prominent in the image)”.

Each score indicates the following grades:

5: Suitable.

4: Fairly suitable.

3: Moderately suitable.

2: Needs modification.

1: Not suitable at all.

Each participant spent approximately ten minutes evaluating five images.

Table 6. Total summary scores given in the expert assessments for five images.

Method	Harmony, Total Points	Appeal, Total Points	Relevance, Total Points
KM	279	274	283
KML	272	269	286
FCM	276	278	251
OSM	286	287	287
SM	272	272	262

shows the total scores obtained after evaluating each method for each criterion. The scores show that OSM performed best in terms of harmony and relevance, KM performed best in terms of attractiveness, and FCM performed best in terms of harmony. Thus, the developed OSM method demonstrated the highest consistency of ratings across all three criteria: harmony, attractiveness, and relevance.

We constructed histograms of the expert assessments according to the criteria of harmony, attractiveness, and relevance for each of the five images (see Figure 13). This approach allows us to observe how the nature of an image affects the effectiveness of the clustering methods. Among all categories, the proposed OSM method received the lowest user rating for images from the landscape group. This can be explained by the absence of a clearly defined object and the limited color range in such images.

4.6. Comparison of the Performance of the Developed Method with Other Methods

To evaluate performance, we measured the execution time of the various clustering algorithms used to identify the dominant colors. The testing procedure was performed in Google Colab using the start_time = time.time() and corresponding end_time commands. Although the absolute execution time varied slightly when the same image was processed multiple times (due to the specifics of the cloud environment), the relative performance between the methods remained consistent. OSM was the fastest algorithm. FCM was slower, due to its iterative process and the need to compute membership degrees. KM and KML demonstrated similar execution times. The results for the ten images are presented in

Table 7. A comparison of the execution times of methods for determining the dominant and prominent colors in ten images.

Number of Image	KM	KML	FCM	OSM	SM
1	1.74	2	29.25	0.62	1.94
2	1.31	1.02	80.29	0.5	2.36
3	1.64	1.87	79.71	0.54	2.22
4	0.95	0.65	30.58	0.45	1.49
5	0.86	0.98	24.31	0.31	2.46
6	1.33	2	115.63	0.47	2.08
7	2.03	1.12	119.27	0.9	4.13
8	1.57	1.46	67.23	0.46	9.96
9	4.23	2.09	94.95	0.49	2.46
10	2.43	1.52	75.32	0.47	6.24

.

5. Discussion and Conclusions

In this paper, we present a method for extracting dominant and salient colors from an image. To the best of our knowledge, this is the first study of images with a wide color gamut and the first attempt to extract their dominant and prominent colors using a method that utilizes the orthogonal ICaS color space. A comparison of color coverage in the ICaS and CIE L^*a^*b^* spaces at a fixed brightness revealed a wider color range in the ICaS space. This confirms its potential for processing images with a wide color range. The consistent results obtained using different metrics confirm the feasibility of using the ICaS space for image clustering.

For the purposes of this study, we created a database of images and analyzed their color coverage in the CIE L^*a^*b^* space. In addition, we identified the key factors that affect the extraction of dominant and prominent colors from an image. According to our results, the most influential factors are related to the color properties—hue and chromaticity, which are uniquely described by two coordinates of the ICaS space, C and S, and lightness, which corresponds to the achromatic component of color, coordinate I. A feature of the ICaS color space application is the use of an orthogonal transformation from the RGB digital image space, which allows for more efficient extraction of dominant and visually salient colors. The SR method, which is based on spectral analysis of the image, was used to assess the visual saliency of colors.

The effectiveness of the proposed method was verified by comparing the extracted dominant and prominent colors of the images with other known methods. For some images, the proposed method successfully identified dominant and visually salient colors that were not identified by other methods. The palette generated by the OSM method covered a wider range of colors compared to other approaches. The average value of the color difference metric ΔE₀₀ for all approaches obtained in this work was in the range of 36.1–37.2, which indicates a sufficient degree of contrast between the colors generated by each method. However, the developed orthogonal saliency mean method shows the lowest maximum value of ΔE₀₀ = 56.6, which indicates the absence of excessively contrasting combinations and a more balanced palette structure. In addition to color distance, the OSM method also ensures the consistency of luminance characteristics. Unlike KM, KML, FCM, and MS, where there is a significant variation in color lightness (L ranging from 6 to 89), the palettes created using OSM are characterized by the stability of the lightness values (L ranging from 32 to 73), which ensured holistic and harmonious visual perception. A visual experiment involving an expert evaluation of the palettes generated by the OSM method and comparable methods demonstrated that clustering effectiveness depends on image type. The evaluation was carried out according to three criteria—harmony, appeal, and relevance—which confirmed the advantages of using the developed OSM method. A comparison of the methods’ performance in terms of execution speed demonstrated the superiority of the OSM method, which had the shortest processing time among the tested approaches.

Although the results show the variety of colors obtained and their stable brightness, a number of limitations must be taken into account. Some salient colors were not extracted. Hence, further work on this topic should include the investigation of other methods for selecting salient colors. For example, instead of using a method based on a spectral analysis of the image, other approaches, such as machine learning models, could be implemented. It is advisable to consider the possibility of using alternative clustering methods that are better at taking into account the specifics of color data and the peculiarities of perceptual space. In addition, the method is currently limited to the extraction of a fixed number of colors, which should be expanded in future work.