Sustainable Swarm Intelligence: Assessing Carbon-Aware Optimization in High-Performance AI Systems

Abstract

Carbon-aware AI demands clear links between algorithmic choices and verified emission outcomes. This study measures and steers the carbon footprint of swarm-based optimization in HPC by coupling a job-level Emission Impact Metric with sub-minute power and grid-intensity telemetry. Across 480 runs covering 41 algorithms, we report grams CO₂ per successful optimisation and an efficiency index $\eta$ (objective gain per kg CO₂). Results show faster swarms achieve lower integral energy: Particle Swarm emits 24.9 g CO₂ per optimum versus 61.3 g for GridSearch on identical hardware; Whale and Cuckoo approach the best $\eta$ frontier, while L-SHADE exhibits front-loaded power spikes. Conservative scale factor schedules and moderate populations reduce emissions without degrading fitness; idle-node suppression further cuts leakage. Agreement between CodeCarbon, MLCO2, and vendor telemetry is within 1.8%, supporting reproducibility. The framework offers auditable, runtime controls (throttle/hold/release) that embed carbon objectives without violating solution quality budgets.

1. Introduction

Considerable impediments to enduring progress are engendered by the burgeoning global energy utilization, whose precise emission modulation is indisputable. In 2022, thirty-six gigatonnes of $C{O}_2$ emissions originating from hydrocarbon extraction were chronicled [1,2], coinciding with a resurgence to pre-pandemic levels and indicating that emission peaks have yet to be achieved. A significant contributor to this upward trend is the Information and Communication Technology (ICT) industry for Machine Learning (ML) operations, owing to its substantial energy consumption occupying roughly 6 percent of global emissions [3]. The impediment of high energy usage in ICT systems necessitates innovative solutions to measure and optimize their carbon footprint [3]. Significant advances in biological sciences, coupled with rapid developments in computing, data analysis, and interpretation, have diversified the field of computational biology. Rapid, yet consistent, technological changes have been conceptualized in patterns due to high interconnectivity. As part of this evolution, nature-inspired computing is increasingly employed to learn from environmental states and occurrences to formulate decisions [4]. Computational processes such as swarm intelligence, are included in this paradigm. Swarm intelligence algorithms concentrate on the collective behaviors observed in nature [4]. Furthermore, swarm inspired intelligence accommodate algorithms to emulate natural learning behaviors within systems of individuals synchronizing through self-organizing mechanisms. A shared principle across all of these models is the interpretation of collective behavior that emerge from environmental interactions. Biometry is employed to impartially analyze observable biological facts through quantitative methods, thus perpetuating objectivity within research discussions and ecological principles [5]. In radiotherapy planning, biometric algorithms utilizing swarm intelligence and machine learning enable acceptable treatment optimization by modeling complex patient contexts efficiently [5]. Similarly, self-organization mechanisms underlying coral reef pattern formation benefit from biometric analyses, validating theoretical models against empirical observations and facilitating resilience predictions under environmental stress [5]. Furthermore, biomimetic strategies derived through biometric studies significantly enhance architectural sustainability, demonstrating measurable energy efficiency improvements by adapting biological functions into design processes [6].

Measuring $C{O}_2$ emissions from ML computations with swarm algorithms can demonstrate significant fluctuations due to discrete optimization processes. By mimicking natural phenomena through swarm metaphors, computational consumption can be reduced via adaptation of tuning parameters. A complexity comparison of swarm-based models encompassing convex and constrained formulations is conducted. Contributions include developing a kinematic analysis to optimize the pace of convergence towards the optimum, thereby reducing overconsumption. Homogeneous derivative-free methods are analyzed to demonstrate efficacy in emission reduction. This report begins by providing background on $C{O}_2$ emissions within the ICT sector. Previous work, experimenting with swarm-based intelligence to measure emissions, is then reviewed. The methodology section follows, detailing the measurement of complexity employed in the analysis. The results are interpreted within the scope of the study, culminating in a final discussion that evaluates the strategy and capabilities of the proposed coordinated approach across various components and commodity systems.

1.1. Swarm Intelligence

Swarm Intelligence constitutes an integral paradigm underpinning contemporary artificial intelligence (AI), particularly within the space of adaptive optimization and computational heuristics. Drawing inspiration from the collective behaviors observed in natural organisms, such as ant colonies and bird flocks, these models derive algorithmic methodologies that facilitate decentralized problem-solving mechanisms. Consequently, these heuristics provide foundational structures enabling AI systems to dynamically adjust computational parameters in response to complex, evolving problem spaces. A typical swarm intelligence system possesses notable properties: it comprises a group of individuals, exhibits homogeneity with respect to the environment, demonstrates learning ability and interaction based on local information, and develops global learning behavior as a result of local interactions within the environment [7].

1.2. Energy Consumption

The energy consumption associated with ML computations, is influenced by various factors. First, the duration of active cloud usage plays a significant role in determining the total consumption, as prolonged computational sessions exacerbate $C{O}_2$ emissions [8]. Additionally, the type of hardware deployed further compounds energy demand, with certain configurations proving less efficient than others. The geographical position of rented computing services, particularly those connected within the same cluster, introduces complexities related to regional energy consumption in kWh [8], which often adheres to local infrastructure constraints. In this context, the adaptability of cloud services to smart management strategies, with the goal of minimizing idle calls or underutilized resources, addresses the inherent incoherence between computational necessity and environmental sustainability. While such practices may remain scarce in broader praxis, they are imperative for mitigating carbon footprints. The interplay between these factors underscores the need for coherent, sustainable solutions in cloud-based machine learning, where the scarcity of green resources and regional variabilities challenge the efficiency of operations.

1.3. Previous Work

Swarm intelligence originated in the context of cellular robotic systems [4] and has since evolved to become a significant and growing force in the computer science field with the purpose of solving optimization problems in various fields of study [7]. Most notably, swarm intelligence algorithms have been integrated into energy optimization. In a review on swarm algorithms and their application in $C{O}_2$ emissions revealed interesting computational settings [9]. In another study, the authors tackle the consanguineous relationship between $C{O}_2$ emissions and several influencing factors using a hybrid model [10]. The work is distinctive in its use of neural networks to handle non-linear fitting issues, managing higher prediction accuracy than traditional approaches. Moreover, in another project, authors present a scheduling model that reduces carbon emissions in ML with proper scheduling strategies, when integrated with power forecasting algorithms-carbon footprint managed better with the adapting optimization methods [11]. Furthermore, hybrid models resulted in a prolific improvement in the accuracy of $C{O}_2$ emissions forecasting, specifically in different regions of China. The authors address the need to concatenate both linear and non-linear factors to predict emission trends accurately [12]. On the other hand, K-nearest neighbors (KNN) was imported to explore key variables affecting $C{O}_2$ emissions across Chinese provinces, performing optimally, particularly when the number of neighbors is set to two [9]. Another work focusing on carbon intensity of energy sources and training times as the main drivers of emissions, authors suggested that certain ML models, usually large Transformer-based architectures, are more carbon-intensive due to their longer training times [13]. Other team of researchers examined a forecasting model for provincial $C{O}_2$ emissions based on grey system theory. One important finding emphasizes the role of swarm algorithms in improving model robustness [14].

The reciprocal relationship between Swarm Intelligence (SI) algorithms and AI systems elucidates their significance within computational frameworks aimed at adaptive optimization. Specifically, SI heuristics serve as principal agents in the operational context of distributed computational intelligence, where local interactions among agents culminate in emergent global solutions without centralized control [14]. Such properties render SI particularly suitable for addressing high-dimensional optimization challenges intrinsic to AI model training processes.

Moreover, emergent paradigms, such as Green AI, underscore the exigency of sustainability within ICT infrastructures. Green AI explicitly seeks to mitigate the environmental repercussions of intensive computational tasks by promoting algorithmic efficiency and minimal resource utilization. Swarm-based heuristics naturally align with these sustainable computational objectives by facilitating distributed parallelism, thus inherently reducing the energetic demands associated with large-scale optimization problems [15].

In alignment with global sustainability directives, specifically the United Nations Sustainable Development Goals (SDGs), the incorporation of SI within AI methodologies contributes tangibly towards the attainment of SDG 12 (Responsible Consumption and Production) and SDG 13 (Climate Action). Through enhancing computational efficiency, swarm-based algorithms reduce the energy consumption associated with ICT processes, thereby directly influencing carbon emission reduction objectives. This relationship accentuates the pivotal role of SI algorithms in addressing environmental sustainability within AI research and practical applications [16]. The pertinence of SI paradigms within modern AI is also demonstrated by their intrinsic capacity for adaptive learning. SI mechanisms inherently possess flexibility in response to environmental fluctuations, thereby enhancing the robustness of AI-based solutions against variability in computational resources. This adaptive characteristic not only optimizes immediate computational efficiency but also anticipates shifts in operational conditions, significantly improving the sustainability profile of AI deployments in variable-resource environments [17].

Furthermore, current literature identifies a critical gap regarding the systematic quantification of SI contributions to AI-based sustainability. Addressing this deficiency requires developing sophisticated, standardized evaluation protocols that rigorously quantify algorithmic performance in terms of environmental impact. Establishing such frameworks will significantly elevate the clarity and practicality of sustainability assessments within swarm-based optimization research, facilitating evidence-based decisions in both theoretical advancements and practical implementations. Finally, the continual evolution of SI heuristics—emphasizing both computational performance and ecological considerations—positions swarm intelligence as an indispensable element within the ongoing dialogue surrounding intelligent computational sustainability. Its integration with AI technologies not only embodies foundational optimization capabilities but actively contributes toward mitigating environmental impacts associated with contemporary ICT infrastructures.

1.4. Contributions

In this work, a structured procedure was followed to measure carbon footprints within nature-inspired computations while monitoring HPC usage. Next steps revealed concurrency thresholds imposing additional loads. Worldwide expansions occurred unpredictably. Automation was introduced to withdraw overhead, a planetary observation framework was established. Speed improvements emerged from refined heuristics, though partial variability persisted.

• A unifying formula was created for incorporating swarm complexity with HPC power factors.
• Emission levels were gauged under shifting concurrency loads, demonstrating variable footprints.
• Parameter sweeps enabled identification of beneficial scheduling approaches with dynamic node usage.
• Real-time HPC logs were assembled for verifying model stability under partial resource utilization.

The research intersects AI enhancement through swarm-based algorithmic refinements with ecological stewardship by embedding carbon-sensitive metrics within computational heuristics. By integrating hyperfactorial complexity measures into swarm intelligence, the developed methodologies foster algorithmic efficiency—vital for sophisticated, resource-constrained AI applications. Concurrently, the introduced carbon-aware protocols address increasing exigencies in environmental informatics, marking an advancement in eco-centric computational paradigms. These developments align directly with computational sustainability principles, underscoring mutual augmentation of algorithmic efficacy vis-à-vis environmental responsibility, hence resonating with the journal’s multidisciplinary emphasis.

The work introduces a unified carbon-aware optimisation stack that integrates EIM with live MCI series while an RSL governs throttling, rescheduling, pausing, and checkpointing without solver drift. A formal coupling links swarm complexity surrogates to watt-scale power traces and then to emission trajectories, with proofs providing monotone response checks within tested bands. Guardrails materialise through QBR, which allocates a risk budget that constrains deviation from baseline convergence, triggers rollback hooks upon violation, and preserves stability under bounded throttles. Uncertainty modulation adjusts action intensity to forecast confidence regarding footprint savings, yielding tempered control under low certainty and decisive steps under high certainty. A sub-minute telemetry pipeline ingests IPMI power, grid MCI, and solver states at a 2 s cadence with negligible overhead, while provenance is stored for audit. An $\eta$-based deployment ranking orders candidates by objective gain per kg CO₂, enabling measurable selection and tuning via a fixed priority rule. ChemFactor weighting introduces domain-specific penalties that preserve cross-task comparability without re-instrumentation, ensuring consistent treatment across heterogeneous chemistries. Restart cool-down policies encoded within the RSL damp transient power spikes during restart-heavy heuristics and respect device health. Population integration with hyperfactorial and superfactorial terms yields deterministic load surrogates under adaptive population schedules, and integration over time provides fine-grained CO₂ estimates. A practical policy kit supplies ready-to-apply rules on early capping, checkpoint spacing, concurrency ceilings, and telemetry cadence, with templates curated per hardware tier. Operationally, schedulers throttle during high-MCI windows and release capacity when MCI recedes while preserving QBR envelopes. Practitioners favour heuristics with high $\eta$, keep swarm sizes moderate, choose conservative F, cap restart frequency, and fix checkpoint intervals that respect MCI gradients. Instrumentation proceeds by enabling rack-level IPMI, logging EIM with timestamps, calibrating power models per node type, and verifying drift quarterly. Governance mandates published QBR thresholds, explicit rollback criteria, auditable trails, and visible seeds. Latency gates are set per workload class, relaxed during green windows, and tightened during brown windows. Risk posture begins in advisory mode with comparisons between predicted and realised cuts, then advances to enforce mode after stability checks. Procurement leverages $\eta$ leaderboards for capacity planning, rewards nodes with lower kg CO₂ per task, and prioritises telemetry-ready gear. Operational hygiene trims outliers with robust fences, re-includes them during sensitivity passes, and reports both central tendency and dispersion. Experiments span forty-one variants under identical sampling cadence. L-SHADE presents front-loaded power peaks with tapering tails, whereas Whale, PSO, and Cuckoo cluster near an efficient $\eta$ frontier for equal fitness targets. GridSearch trails due to extended wall-time, confirming that shorter high-watt bursts frequently outperform prolonged mid-watt runs on integral energy. Idle leakage drops markedly once automation suppresses empty allocations, and QBR indicates negligible fitness loss within examined ranges. Agreement across CodeCarbon, MLCO2, and vendor telemetry remains within 1.8%, which supports confidence in the full pipeline. Previous studies largely report static emission summaries, whereas the present work supplies live control with MCI-driven feedback loops. Earlier approaches weigh carbon cost post hoc, while this stack steers runs mid-flight through auditable interventions. Risk budgets are often omitted in comparators, yet QBR here formalises tolerances, triggers, and rollbacks. Complexity surrogates rarely unify with power traces in prior art, and the proposed coupling closes that methodological gap with verifiable checks.

This work aims to construct a carbon-aware optimization (CAO) scheme for swarm-based search within high-performance AI settings, secure quantifiable decarbonization under strict service constraints, preserve solution quality through auditable controls. The program targets measurable footprint abatement within realistic queues, not idealized benches; CAO operates under policy, budget, latency, reliability. Short sentences follow. Scope remains focused. Claims remain testable.

Primary purpose concerns verifiable mitigation through algorithmic governance rather than hardware substitution alone. A unifying lens ties computational steps to electrical input via an Emission Impact Metric (EIM); EIM links workload intensity to marginal carbon intensity (MCI) streams provided by grid telemetry. Terminology now fixed; reuse ensues. CAO evaluates EIM trajectories during runtime; trajectories steer scheduling choices via a Resource Scheduling Layer (RSL) positioned above the solver loop. RSL applies throttling, rescheduling, pausing, checkpointing—selection depends on MCI gradients together with solver readiness states.

First, specify a provable coupling between complexity surrogates for swarm dynamics, EIM, MCI. Second, design a calibration protocol that maps solver parameters to watt-scale responses with bounded error across clusters. Third, create a fairness guard that maintains solution fidelity under carbon-aware throttles; denote by Quality Budget–Risk (QBR). Fourth, embed uncertainty modulation so that action intensity scales with predictive confidence about footprint savings; low certainty yields tempered action. CAO must prefer actionable telemetry to ex post summaries; thus, the control policy consumes power traces at sub-minute cadence, validates trend direction, then issues minimal interventions that avoid solver destabilization. QBR enforces limits on deviation from baseline convergence; violations trigger rollbacks. When RSL suppresses concurrency, EIM ought to decrease monotonically over the same horizon; non-monotone segments require diagnosis, else policy refinement.

Purpose demands instrumentation with negligible perturbation, lightweight provenance, reproducible replay. Objectives encode guardrails: (i) monotone dose–response for power vs. thread count within tested bands; (ii) bounded variance inflation for wall-time under throttles; (iii) deterministic accounting of idle leakage inside allocators. Each guardrail supplies a checklist for acceptance before broad deployment.

A live EIM–MCI control loop governed by a Resource Scheduling Layer that issues throttle, pause, release decisions under a formal Quality Budget–Risk guard; sub-minute telemetry that fuses rack IPMI power, device counters, queue states; a provable mapping from swarm-complexity surrogates to watt-scale traces with monotone response checks; an efficiency index $\eta$ that ranks deployments by objective gain per $\mathrm{kg}{\mathrm{CO}}_2$; ChemFactor weighting that preserves cross-task comparability without re-instrumentation; restart cool-down policy that suppresses transient spikes; immutable provenance with auditable interventions; policy templates per hardware tier. Unique features address recurrent gaps in the literature—most reports remain ex post, lack runtime control, omit risk budgets, provide weak calibration between solver parameters and power, supply minimal comparability across heterogeneous tasks, seldom publish reproducible control logs. Here, telemetry drives decisions at sub-minute cadence; QBR constrains divergence from baseline convergence; calibrations tie parameter schedules to power response within validated bands; $\eta$ supplies a single scalar for scheduler ranking under latency bounds; ChemFactor yields domain-aware weights that keep fairness across chemistries; provenance records timestamp,node,job_id,action,reason,QBR_state to enable audit trails. Style change: succinct specification follows—policy consumes $\mathrm{EIM}\left(t\right)=P_h\left(t\right),\eta \left(t\right),e_r\left(t\right)$, applies hysteresis on intensity thresholds, then commits interventions at safe synchronization points. Next tone: interpretive linkage—this mechanism transforms carbon accounting from narrative summary into operational governance aligned with global “Green AI” aims, since actions occur during execution rather than after the fact. Final register: deployment praxis—rank candidates via $\eta$, fix conservative population schedules, space checkpoints along expected MCI troughs, publish MCI series together with PUE, calibration notes, QBR limits. Collectively, these novelties create a replicable, risk-bounded, telemetry-native pathway that integrates optimization quality with verifiable footprint abatement within real HPC queues; this correction permits precise placement of results inside the maturing canon on sustainable ML at scale.

2. Methodology

The methodology is founded on the principles of optimally measuring $C{O}_2$ emissions of machine learning computations by employing a hyperfactorial function to capture the computational complexity of swarm algorithms. In spite of persistent challenges, hyperparameters such as acceleration coefficients, inertia weight, and stopping criteria—which influence the duration and computational capacity—are considered. From this perspective, parameters like maximum generation number and fitness convergence affect energy consumption under various circumstances. Swarm topologies and boundary handling approaches are analyzed to understand how particles traverse the multidimensional solution space with velocity and direction towards optimal solutions, ensuring harmony between efficiency and resource utilization: a convex foundation for measuring emissions.

2.1. Swarm Algorithms

2.1.1. Particle Swarm Optimization (PSO)

Particle Swarm Optimization (PSO) is a biomimetic algorithm inspired by collective animal behaviors, such as bird flocking and fish schooling, in the search for elusive optimal solutions. PSO employs a population of candidate solutions called particles, where each particle possesses a position and velocity within the search space. Information is delegated among particles, enabling convergence towards global optima through iterative updates [18]. The standard velocity update is governed by:

$$v_i(t+1)=w{v}_i\left(t\right)+c_1{r}_1(p_i^{best}-x_i\left(t\right))+c_2{r}_2(g^{best}-x_i\left(t\right))$$

(1)

Here, inertia weight (w), cognitive ($c_1$), and social coefficients ($c_2$) modulate exploration and exploitation, while random numbers ($r_1$, $r_2$) incorporate stochasticity.

2.1.2. Accelerated Particle Swarm Optimization (APSO)

Accelerated Particle Swarm Optimization (APSO) simplifies standard PSO, directly updating particle positions without explicit velocity components to achieve faster convergence. APSO retains the principle of collective movement towards the global best, supplemented by random perturbations to preserve diversity. The simplified position update is expressed as:

$$x_i(t+1)=(1-\beta )x_i\left(t\right)+\beta g^{best}+\alpha ϵ$$

(2)

In this interpretation, the learning rate $\beta$ emphasizes exploitation, while step size $\alpha$ and random vector $ϵ$ ensure exploration [19].

2.1.3. Firefly Algorithm (FA)

The Firefly Algorithm (FA) emulates the bioluminescent communication among fireflies, where brightness attracts less bright counterparts. Brightness typically corresponds to solution fitness, guiding iterative movement toward optimal regions. The updating formula for movement is detailed by:

$$x_i^{t+1}=x_i^t+{\beta }_0{e}^{-\gamma r_{ij}^2}(x_j^t-x_i^t)+\alpha {ϵ}_i^t$$

(3)

Here, attractiveness ${\beta }_0$ decreases with distance, modulated by the absorption parameter $\gamma$, alongside randomization term $\alpha {ϵ}_i^t$ promoting diversity [20].

2.1.4. Cuckoo Search (CS)

The Cuckoo Search (CS) algorithm models brood parasitism behaviors observed in cuckoo species. Solutions, represented as nests, are updated via Lévy flight steps—a method promoting occasional long-range jumps that facilitate global search. Its primary update rule is represented as:

$$x_i^{t+1}=x_i^t+\alpha ·\mathrm{L}\text{é}\mathrm{vy}\left(\lambda \right)$$

(4)

The step size $\alpha$ and Lévy exponent $\lambda$ influence the scale of exploratory behavior. Nests are abandoned probabilistically, simulating natural nest rejection to enhance search efficacy [21].

2.1.5. Whale Optimization Algorithm (WOA)

Whale Optimization Algorithm (WOA) draws inspiration from bubble-net hunting exhibited by humpback whales. Whales collaboratively encircle prey, following a spiral or shrinking path to refine search around promising regions. The exemplary encircling equations are described as:

$$\overrightarrow{X}(t+1)={\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{A}·|\overrightarrow{C}{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|$$

(5)

$$\overrightarrow{X}(t+1)=|{\overrightarrow{X}}^{\ast }\left(t\right)-\overrightarrow{X}\left(t\right)|e^{bl}cos\left(2\pi l\right)+{\overrightarrow{X}}^{\ast }\left(t\right)$$

(6)

Coefficient vectors ($\overrightarrow{A}$, $\overrightarrow{C}$) dynamically modulate search intensity and scope, balancing exploration and exploitation [22].

2.1.6. Moth-Flame Optimization (MFO)

The Moth-Flame Optimization (MFO) algorithm mimics moth navigation strategies, particularly transverse orientation toward distant flames. Candidate solutions (moths) navigate towards optimal positions (flames), utilizing a logarithmic spiral path depicted as:

$${\overrightarrow{X}}_i^{t+1}=|{\overrightarrow{F}}_j^t-{\overrightarrow{X}}_i^t|e^{bt}cos\left(2\pi t\right)+{\overrightarrow{F}}_j^t$$

(7)

This mechanism dynamically reduces flame count, progressively narrowing search focus and enabling detailed exploitation in later phases [23].

2.1.7. Shuffled Frog Leaping Algorithm (SFLA)

Shuffled Frog Leaping Algorithm (SFLA) exemplifies memetic evolution in frog populations. It partitions solutions into memeplexes, where worst-performing frogs adjust positions based on superior individuals. This local optimization is complemented by periodic global shuffling. The update mechanism within memeplexes is succinctly provided as:

$$X_w^{new}=X_w+r(X_b-X_w)$$

(8)

Parameter r injects stochasticity, supporting adaptive local searches while shuffling ensures extensive exploration [24].

2.1.8. Penguin Search Optimization Algorithm (PeSOA)

The Penguin Search Optimization Algorithm (PeSOA) embodies the cooperative hunting practices observed among penguin colonies. Solutions (penguins) collaboratively search promising regions based on intra-group communication about optimal food sources. The core update rule for penguin positions is typically:

$$X_i^{t+1}=X_i^t+r(X_{best\_group}^t-X_i^t)$$

(9)

Through iterative cycles, penguin groups adaptively consolidate solutions, balancing thorough global exploration and localized exploitation efforts effectively [25].

2.1.9. Artificial Bee Colony (ABC)

Artificial Bee Colony (ABC) algorithm draws its principles from the cooperative foraging behavior of honey bees, where individuals interact to discover, evaluate, and exploit food resources. Three modular roles—employed, onlooker, and scout bees—adaptively collaborate, resolving exploration-exploitation contradictions through dynamic information-sharing mechanisms. Bees adjust positions based on preliminary local searches guided by stochastic variables [26]. Position updates follow:

$$v_{ij}=x_{ij}+{\varphi }_{ij}(x_{ij}-x_{kj})$$

(10)

Random variable ${\varphi }_{ij}$ ensures adaptation and exploration, while abandonment conditions introduce scouts for global searches.

2.1.10. Ant Colony Optimization (ACO)

Ant Colony Optimization (ACO) is inspired by pheromone-based foraging behavior exhibited by real ant colonies, where temporary paths evolve into sharp optimal routes. Artificial ants iteratively construct solutions, interacting via pheromone trails that reflect historical quality. Probabilistic choices made by ants utilize combined heuristic and pheromone intensity, continuously improving path quality through iterative evaporation and deposition processes [27]. Path selection probability is expressed as:

$$P_{ij}^k={\displaystyle \frac{{\left[{\tau }_{ij}\right]}^{\alpha }{\left[{\eta }_{ij}\right]}^{\beta }}{{\sum }_{l\in N_k}{\left[{\tau }_{il}\right]}^{\alpha }{\left[{\eta }_{il}\right]}^{\beta }}}$$

(11)

Here, ${\tau }_{ij}$ is pheromone strength, ${\eta }_{ij}$ heuristic value, and parameters $\alpha$, $\beta$ modulate influence.

2.1.11. Bees Algorithm (BA)

The Bees Algorithm (BA) imitates collective honey bee foraging, balancing local exploitation and global exploration through preliminary evaluations of search areas. Scout bees explore randomly, while other bees concentrate on high-quality solutions, progressively improving outcomes. Neighborhood-based refinement follows a modular structure, periodically updating bee positions using:

$$x_i^{new}=x_i^{current}+r·\delta$$

(12)

Random parameter r and neighborhood size $\delta$ promote adaptive exploration, ensuring continuous improvement and diversity maintenance [28].

2.1.12. Wolf Search Algorithm (WSA)

Wolf Search Algorithm (WSA) emulates pack-based hunting behaviors, using principles of social hierarchy and cooperation for collective problem-solving. Each wolf adapts position based on the pack’s best-known solutions, progressively improving fitness via iterative updates. Information-sharing among wolves ensures rapid convergence and diversified exploration, adapting positions through:

$$X_i^{t+1}=X_i^t+r(X_{best}^t-X_i^t)$$

(13)

The stochastic factor r introduces temporary variability, enabling wolves to avoid local optima and enhance adaptation [29].

2.1.13. Bee Colony Optimization (BCO)

Bee Colony Optimization (BCO), influenced by the waggle dance of honey bees, incorporates modular roles for preliminary searching (scouts), detailed neighborhood exploration (employed bees), and probabilistic recruitment (onlookers). Interaction among bees facilitates effective adaptation, ensuring thorough global search and efficient local refinement. Position update adheres to the ABC formula:

$$v_{ij}=x_{ij}+{\varphi }_{ij}(x_{ij}-x_{kj})$$

(14)

Random factor ${\varphi }_{ij}$ maintains diversity, continually improving conditions of the swarm through stochastic exploration [30].

2.1.14. Glowworm Swarm Optimization (GSO)

Glowworm Swarm Optimization (GSO) algorithm derives from bioluminescent behavior of glowworms, which attract neighbors based on luminosity. The adaptive luminous intensity hints at solution quality, guiding swarm movements. Glowworms probabilistically move toward brighter neighbors within dynamic decision radii, effectively resolving local optima contradictions. Position updates follow:

$$x_i^{t+1}=x_i^t+s{\displaystyle \frac{x_j^t-x_i^t}{\left|\right|x_j^t-x_i^t\left|\right|}}$$

(15)

Step size s controls adaptive movement, with neighbor interactions improving convergence efficiency [31].

2.1.15. Crow Search Optimization (CSO)

Crow Search Optimization (CSO) draws its inspiration from the intelligent behavior of crows, primarily related to their memory capabilities and deceptive strategies. Crows possess remarkable proficiency in simultaneously hiding food and retrieving it, not only remembering their own caches but following other crows to exploit their hidden resources without detection. In CSO, each crow symbolizes a potential solution within a defined search space. Every crow maintains a memory of its best-found location, and the movement of the crows depends on the awareness of other crows detecting their behavior. The simultaneous exploration of new solutions and exploitation of known promising solutions are balanced by probabilistic awareness [32].

The mathematical formulation of crow position updating is as follows:

$$X_i^{t+1}=\left\{\begin{array}{cc}{X}_i^t+r·(m_j^t-X_i^t),\hfill & \mathrm{if}rand\ge A{P}_j\hfill \\ \mathrm{Random}\mathrm{Position},\hfill & \mathrm{if}rand<A{P}_j\hfill \end{array}\right.$$

(16)

Here, $X_i^t$ represents crow i’s current position at iteration t, $m_j^t$ is the best-known position remembered by crow j, $A{P}_j$ symbolizes the awareness probability, and r is a random step size factor.

2.1.16. Social Spider Optimization (SSO)

Social Spider Optimization (SSO) takes inspiration from the cooperative behaviors displayed by colonies of social spiders. Spiders in a colony communicate via web vibrations, sharing information regarding prey locations and threats. SSO simulates these vibrations to guide spiders toward areas exhibiting high solution quality, representing effective solutions. Other spiders, based on these web vibrations, update their positions to balance exploration and exploitation in the search space [33]. Spiders are categorized as male or female, each with distinctive roles: females typically tend to move toward strong vibrations representing higher-quality solutions, whereas males alternate between cooperative and competitive behaviors.

The general position update equation for spiders is expressed as:

$$X_i^{t+1}=X_i^t+r_1·(X_{best}^t-X_i^t)+r_2·(X_{rand}^t-X_i^t)$$

(17)

Here, $X_{best}^t$ is the position with the strongest vibration (best solution) at iteration t, $X_{rand}^t$ denotes a randomly selected spider’s position, and $r_1$, $r_2$ are random numbers that maintain stochasticity.

2.1.17. Lion Optimization Algorithm (LOA)

The Lion Optimization Algorithm (LOA) originates from the social and predatory behaviors of lions, reflecting a structured society divided into prides and solitary nomads. Prides exploit familiar territories through coordinated hunting, whereas nomads wander the search space randomly to discover new regions. Mating occurs between pride members, creating offspring to maintain diversity, and nomads may challenge pride lions for territorial control. This combination ensures simultaneous exploration of new solution areas and exploitation of existing high-quality solutions [34].

The updating mechanism for a lion’s position is generally formulated as:

$$X_i^{t+1}=X_i^t+r·(X_{best}^t-X_i^t)$$

(18)

In this formulation, $X_{best}^t$ denotes the pride’s best current solution, with r as a random factor that facilitates variability and prevents stagnation in local optima.

2.1.18. Crow Swarm Optimization Algorithm (CSOA)

Crow Swarm Optimization Algorithm (CSOA) utilizes principles similar to CSO but emphasizes collective swarm behavior. Crows exhibit simultaneous awareness of their neighbors’ actions, constantly monitoring other crows’ caching activities. CSOA employs swarm-based following behavior to exploit neighbor memory effectively. Each crow strategically follows others without detection to locate better food sources (solutions) while protecting its cache through deceptive movements if detected. The dual process of simultaneously tracking and evading others enriches search dynamics [35].

The position update equation in CSOA is defined similarly to CSO:

$$X_i^{t+1}=\left\{\begin{array}{cc}{X}_i^t+r·(m_j^t-X_i^t),\hfill & \mathrm{if}rand\ge A{P}_j\hfill \\ \mathrm{Random}\mathrm{Position},\hfill & \mathrm{if}rand<A{P}_j\hfill \end{array}\right.$$

(19)

Parameters remain consistent with CSO, emphasizing swarm behavior for broader search effectiveness.

2.1.19. Bacterial-GA Foraging

Bacterial-GA Foraging integrates Bacterial Foraging Optimization (BFO), mimicking the chemotactic foraging movement of Escherichia coli, and Genetic Algorithms (GA), representing evolutionary processes. BFO models bacterial movements toward nutrient-rich regions using chemotaxis, reproduction, and random dispersal. GA contributes mechanisms for combining solutions via genetic operators, maintaining a diverse genetic pool without stagnation [36]. The simultaneous utilization of bacterial movements and genetic evolution ensures robust exploration and precise exploitation.

Chemotactic movements are mathematically defined as:

$$X_i^{t+1}=X_i^t+C\left(i\right)·{\displaystyle \frac{\Delta }{\parallel \Delta \parallel }}$$

(20)

Here, $C\left(i\right)$ indicates step size, while $\Delta$ represents a randomly generated direction vector guiding the bacterium. Genetic operators introduce new genetic sequences within bacterial solutions, refining the search efficacy.

2.1.20. Glowworm Swarm Optimization (GSO)

Glowworm Swarm Optimization (GSO) mimics the bioluminescent behavior of glowworms which emit luciferin to attract others. Glowworms move toward neighbors with brighter luminescence, forming multiple subgroups around distinct optimal solutions within multimodal spaces. The adaptation of neighborhood radii allows glowworms not only to concentrate around multiple optima but simultaneously maintain the capacity to explore broader areas effectively [37].

The luciferin update and movement equations are:

$$l_i(t+1)=(1-\rho )·l_i\left(t\right)+\gamma ·J\left(x_i\left(t\right)\right)$$

(21)

Movement toward neighbors is calculated as:

$$x_i(t+1)=x_i\left(t\right)+s·{\displaystyle \frac{x_j\left(t\right)-x_i\left(t\right)}{\parallel x_j\left(t\right)-x_i\left(t\right)\parallel }}$$

(22)

Here, luciferin value $l_i\left(t\right)$ indicates solution quality at position $x_i\left(t\right)$; $\rho$ represents decay rate; $\gamma$ symbolizes enhancement constant; $J\left(x_i\left(t\right)\right)$ is fitness evaluation. Step size s and dynamic radius updates facilitate local search and global exploration.

2.1.21. Glowworm-Based Computation (GBC)

Glowworm-Based Computation (GBC) is modeled upon the bioluminescent communication of glowworms, manifesting collective search through luciferin intensity. Glowworms adapt their movements based on neighbors exhibiting superior luciferin values, resulting in efficient localization of multiple optima in elusive multimodal environments [38]. GBC employs the following equation for updating luciferin values ($l_i$):

$$l_i(t+1)=(1-\rho )l_i\left(t\right)+\gamma J\left(x_i\left(t\right)\right),$$

(23)

where $\rho$ is luciferin decay, $\gamma$ is luciferin enhancement, and $J\left(x_i\left(t\right)\right)$ implies the fitness of position $x_i\left(t\right)$. The probabilistic movement towards neighbors demonstrates adaptive attraction behavior:

$$x_i(t+1)=x_i\left(t\right)+s{\displaystyle \frac{x_j\left(t\right)-x_i\left(t\right)}{\parallel x_j\left(t\right)-x_i\left(t\right)\parallel }},$$

(24)

specifically controlled by step size s and neighbor selection based on luciferin gradients.

2.1.22. Consultant-Guided Search (CGS)

Consultant-Guided Search (CGS) simulates human decision-making processes by explicitly utilizing direct peer-to-peer advice within a population. Individuals, representing candidate solutions, selectively incorporate recommendations from chosen consultants depending on trust and expertise, refining search trajectories dynamically [39]. This update is formalized through:

$$x_i^{t+1}=x_i^t+\alpha (x_c^t-x_i^t),$$

(25)

where $x_i^t$ denotes current positions, $x_c^t$ signifies the consultant’s position, and $\alpha$ reflects confidence, guiding the population towards higher-quality solutions while promoting diversity.

2.1.23. Eagle Strategy

The Eagle Strategy mirrors the hunting attributes of eagles, manifesting global exploration via broad Lévy flights and intensified local exploitation. Such alternating phases significantly balance aspects of solution diversity and convergence efficiency within intricate landscapes [40]. Formally, global exploration utilizes Lévy flights as:

$$x_i^{t+1}=x_i^t+\alpha ·\mathrm{L}\text{é}\mathrm{vy}\left(\lambda \right),$$

(26)

while local exploitation relies on an adaptive local optimizer, facilitating refined searches around promising regions identified globally.

2.1.24. Bacterial Foraging Optimization Algorithm (BFOA)

Similarly, Bacterial Foraging Optimization Algorithm (BFOA) draws inspiration from E. coli’s chemotactic movements, reproduction, and dispersal activities. Chemotaxis encompasses randomized directional tumbling followed by directional swimming, optimizing resource acquisition [41]. Movement updates occur as follows:

$$X_i^{t+1}=X_i^t+C\left(i\right){\displaystyle \frac{\Delta }{\parallel \Delta \parallel }},$$

(27)

with adaptive chemotactic step size $C\left(i\right)$ and random directional vector $\Delta$. Moreover, elimination-dispersal steps prevent stagnation through probabilistic random relocations, thereby maintaining exploration potential.

2.1.25. Fast Bacterial Swarming

In addition, Fast Bacterial Swarming integrates chemotactic bacterial foraging with the social characteristics observed in particle swarm dynamics. Swarming enhances chemotaxis through attraction towards the globally best-performing solution, adjusting search intensity adaptively [42]. The unified update equation emerges as:

$$X_i^{t+1}=X_i^t+\alpha (X_{best}^t-X_i^t)+C\left(i\right){\displaystyle \frac{\Delta }{\parallel \Delta \parallel }},$$

(28)

employing the global best solution $X_{best}^t$ to accelerate swarm convergence, while retaining adaptive exploration facilitated by chemotaxis.

2.1.26. Hierarchical Swarm Optimization

The Hierarchical Swarm Optimization emulates social animal organizations, characterized by structured leadership and stratified communication. Agents adjust positions based on localized guidance and globally optimal solutions, enhancing search efficiency within multimodal and high-dimensional search spaces [43]. This hierarchical updating process is mathematically expressed as:

$$x_i^{t+1}=x_i^t+r_1(p_{l,i}^t-x_i^t)+r_2(p_g^t-x_i^t),$$

(29)

involving random components $r_1$, $r_2$ controlling the influence exerted by local leader ($p_{l,i}^t$) and global best solutions ($p_g^t$), respectively. Information dissemination through the hierarchy inherently balances local exploitation and global exploration effectively.

2.1.27. Good Lattice Swarm Optimization (GLSO)

Additionally, the Good Lattice Swarm Optimization (GLSO) integrates swarm behavior with structured distribution derived from number theory, particularly employing “good lattice points” to uniformly initialize swarm positions [44]. This precise lattice initialization manifests significantly enhanced exploration characteristics over purely random initializations. GLSO relies upon classical particle swarm updates:

$$v_i^{t+1}=w{v}_i^t+c_1{r}_1(p_i^t-x_i^t)+c_2{r}_2(g^t-x_i^t),$$

(30)

$$x_i^{t+1}=x_i^t+v_i^{t+1},$$

(31)

augmented with lattice-based initial position generation expressed by:

$$x_i^0={\mathrm{GoodLatticePoint}}_i.$$

(32)

This explicit mathematical foundation promotes solution diversity, simultaneously improving convergence reliability within multidimensional search spaces.

2.1.28. Fish Swarm Optimization (FSO)

The Fish Swarm Optimization algorithm imitates collective movements observed in fish schools, leveraging behaviors such as preying, swarming, and following. Artificial fish models concurrently examine local areas to accumulate optimal solutions. The update equation for artificial fish positions is defined as:

$$X_i^{t+1}=X_i^t+Step·{\displaystyle \frac{X_j^t-X_i^t}{\parallel X_j^t-X_i^t\parallel }}$$

(33)

where $X_i^t$ and $X_j^t$ represent the current positions of fish i and a selected neighbor j, respectively, $Step$ denotes the movement magnitude, and the visual range determines selection criteria for $X_j^t$ [45,46].

2.1.29. Krill Herd Optimization (KHO)

The Krill Herd Optimization is derived from krill swarm activities, incorporating induced movement, foraging behavior, and stochastic diffusion. Each krill updates its location through the combined effect of attraction among neighbors and targeted search towards optimal food sources. Formally, the position update is articulated as:

$$X_i^{t+1}=X_i^t+N_i^t+F_i^t+D_i^t$$

(34)

Here, $N_i^t$ is social-induced movement, $F_i^t$ denotes directed foraging, and $D_i^t$ symbolizes diffusion to sustain population diversity [47,48].

2.1.30. Bat Algorithm (BA)

Bat Algorithm employs the echolocation mechanism of bats, adapting frequency, velocity, and pulse emission rate to navigate the solution space. These adaptive behaviors systematically refine the search process. The iterative process is described by:

$$v_i^{t+1}=v_i^t+(x_i^t-x_{\ast })·f_i,x_i^{t+1}=x_i^t+v_i^{t+1}$$

(35)

Frequency $f_i$ modulates the exploratory scope, velocity $v_i^t$ steers the position updates, and $x_{\ast }$ signifies the current optimal solution [49,50].

2.1.31. Bee System (BS)

The Bee System models honeybee colony dynamics, utilizing employed bees, onlookers, and scouts to collectively seek and refine candidate solutions. It employs a probabilistic approach driven by neighborhood exploration and abandonment rules. Candidate positions update according to:

$$v_{ij}=x_{ij}+{\varphi }_{ij}(x_{ij}-x_{kj})$$

(36)

In this relation, ${\varphi }_{ij}$ introduces stochastic variation, while indices i, j, and k correspond respectively to the bee, dimension, and randomly selected peer bee influencing movements [51,52].

2.1.32. Virtual Bees Algorithm (VBA)

Virtual Bees algorithm digitally mimics the distributed communication strategies among bees. Agents emulate scouts and recruits, with adaptive neighborhood search patterns refining solution quality. Position updates leverage neighborhood size dynamically:

$$v_{ij}=x_{ij}+{\varphi }_{ij}(x_{ij}-x_{kj})$$

(37)

where solutions accumulate information adaptively, modulated by random factor ${\varphi }_{ij}$ ensuring variability [53,54].

2.1.33. Invasive Weed Optimization (IWO)

Invasive Weed Optimization algorithm imitates competitive growth behaviors of weeds, employing spatial dispersal and fitness-dependent reproduction to facilitate search refinement. Candidate solutions (seeds) disperse according to:

$$x_{\mathrm{new}}=x_{\mathrm{parent}}+\sigma ·N(0,1)$$

(38)

with standard deviation $\sigma$ progressively declining through iterations, effectively adjusting exploration and exploitation concurrently [55,56].

2.1.34. Elephant Search Algorithm (ESA)

Elephant Search Algorithm is inspired by the dual exploratory-exploitative behavior observed in elephant groups, partitioning agents into male explorers and female exploiters. Males engage in extensive exploration, whereas females refine existing solutions locally. Position updates are governed by:

$$X_{\mathrm{female}}^{t+1}=X_{\mathrm{female}}^t+r_2(X_{\mathrm{best\_herd}}^t-X_{\mathrm{female}}^t)$$

(39)

where $r_2$ is a random factor introducing stochasticity, and $X_{\mathrm{best\_herd}}^t$ represents the herd’s current optimum [57,58].

2.1.35. Monkey Search (MS)

Monkey Search leverages the adaptive exploration and somersaulting actions observed in monkey behavior. Three primary components drive search efficiency: climbing for incremental improvement, watch-jumping for exploratory leaps, and somersaulting for radical solution shifts. Monkey positions update accordingly:

$$x_i^{t+1}=x_i^t+\gamma (x_{\mathrm{best}}^t-x_i^t)$$

(40)

Factor $\gamma$ controls somersault magnitude, promoting global search, while $x_{\mathrm{best}}^t$ provides directional guidance towards optimal solutions [59,60].

2.1.36. Grasshopper Optimization Algorithm (GOA)

Grasshopper Optimization Algorithm was conceived to mimic swarm-like traits of grasshoppers [61]. Larval stages correspond to short-distance moves, whereas adulthood implies swift leaps over far distances. That notion is replicated to coordinate global exploration early, then local refinement later. A parameter c decreases progressively, steering the swarm from wide search to narrower exploitation.

Social interaction among grasshoppers is expressed by forces of repulsion and attraction. The iteration step is formalized as:

$${\mathbf{X}}_i^{t+1}=c·\left(\sum _{j=1,j\ne i}^N\left(\alpha s(\parallel {\mathbf{X}}_j^t-{\mathbf{X}}_i^t\parallel )\right)\right)+{\mathbf{g}}^t,$$

(41)

where ${\mathbf{X}}_i^t$ is the position of individual i at iteration t. Function $s(·)$ adjusts interaction intensity, while ${\mathbf{g}}^t$ signals a gravitational target. Parameter c declines each iteration to modify the search range.

2.1.37. Dragonfly Algorithm (DA)

Dragonfly Algorithm focuses on static and dynamic swarming. It references dragonfly behaviors, emphasizing separation, alignment, cohesion, attraction to prey, and diversion from threat [62]. Global coverage is feasible early, then local exploitation emerges over time.

Two vectors are central: position ${\mathbf{X}}_i$ and velocity $\Delta {\mathbf{X}}_i$. Evolution is done by combining influences:

$$\Delta {\mathbf{X}}_i^{t+1}=s·S_i+a·A_i+c·C_i+f·F_i+e·E_i+w\Delta {\mathbf{X}}_i^t,$$

(42)

where $S_i,A_i,C_i,F_i,E_i$ correspond to separation, alignment, cohesion, food attraction, and enemy evasion. The inertia weight w controls solution speed from one iteration to the next [63]. Automation of parameter tuning is often applied.

Neighborhood radius decreases as iterations advance, promoting a transition from broad coverage to refined searching. Random walks are introduced if no neighbors are detected, enabling extra coverage of the domain.

2.1.38. Squirrel Search Algorithm (SSA)

Squirrel Search Algorithm draws inspiration from flying squirrels, which glide between trees in pursuit of resources. Search agents are considered squirrels, gliding toward beneficial spots, possibly away from hazards [64]. Seasonal changes are also simulated to withdraw from stagnation, thus reintroducing variety.

Movement is often formalized via:

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^t+d·G\left({\mathbf{X}}_h^t-{\mathbf{X}}_i^t\right)+r\Delta ,$$

(43)

where ${\mathbf{X}}_h^t$ is a high-value site (a hickory tree). Parameter d is a distance factor, G is a glide constant, r is random within a small range, and $\Delta$ represents a direction vector. The algorithm attempts to discover feasible spots in a global sense, limiting local traps.

2.1.39. Coyote Optimization Algorithm (COA)

Coyote Optimization Algorithm is based on group living of coyotes [65]. Packs represent subdivisions of the total population, where median solutions guide social behavior. Alpha coyotes within packs hold top scores, functioning as local references.

Position renewal in each pack can be captured by:

$${\mathbf{X}}_{i,p}^{t+1}={\mathbf{X}}_{i,p}^t+{\beta }_1\left({\mathbf{X}}_{\mathrm{best},p}^t-{\mathbf{X}}_{i,p}^t\right)+{\beta }_2\left({\mathbf{X}}_{\mathrm{median},p}^t-{\mathbf{X}}_{i,p}^t\right).$$

(44)

Symbols ${\beta }_1,{\beta }_2$ are random coefficients. Offspring emerge through genetic exchange within the pack, ensuring that new solutions appear [66].

Migration across packs occasionally occurs to maintain solution diversity. Seasonal changes are absent in this method, though local adaptation is robust.

2.1.40. Manta Ray Foraging Optimization (MRFO)

Manta Ray Foraging Optimization references group hunting behaviors in oceanic scenarios. Feeding patterns, such as chain formation and cyclone swirling, supply a blend of exploration with exploitation [67].

Three principal moves are chain foraging, cyclone foraging, and somersault foraging. The cyclone phase is often captured by:

$${\mathbf{X}}_i^{t+1}={\mathbf{X}}_i^{t}exp(-\lambda t/T)+\rho \left({\mathbf{X}}_{\mathrm{best}}^t-{\mathbf{X}}_i^t\right),$$

(45)

where $\lambda$ is a spiral coefficient, t is iteration, T is maximum iterations, $\rho$ is random. Chain foraging shifts solutions gradually toward better neighbors, while somersault triggers abrupt leaps [68]. Automation can be employed to manage parameters over time.

Balanced phases allow coverage of broad regions before zooming into promising subregions.

2.1.41. Ant Lion Optimizer (ALO)

Ant Lion Optimizer is structured around the predatory traps of antlions that catch ants in conical pits. In the algorithmic sense, ants symbolize search agents subjected to random walks inside bounding intervals influenced by specific antlions [61]. Roulette selection is frequently used to match ants with antlions possessing strong fitness.

The update for an ant’s position might take this form:

$${\mathbf{X}}_{\mathrm{ant}}^{t+1}={\displaystyle \frac{\left({\mathbf{X}}_{\mathrm{RW}}^t-{\mathbf{X}}_{min}^t\right)}{\left({\mathbf{X}}_{max}^t-{\mathbf{X}}_{min}^t\right)}}\times (\mathbf{U}-\mathbf{L})+\mathbf{L},$$

(46)

where ${\mathbf{X}}_{\mathrm{RW}}^t$ is the random walk vector, while ${\mathbf{X}}_{min}^t$ and ${\mathbf{X}}_{max}^t$ define bounding terms. $(\mathbf{U},\mathbf{L})$ reflect the domain limits. Elite antlion solutions also impose additional pull, guiding the swarm to top-performing configurations [65].

2.2. Criteria

To measure carbon dioxide emissions associated with ML model computations many criteria are involved. Hyperparameters from the swarm algorithms [69] include acceleration coefficients, inertia weight, and stopping criteria. These directly influence the computational complexity and duration with a median of 72 h [70] of training and tuning processes. Parameters like maximum generation number, maximum stall time, maximum runtime, best fitness value, population convergence, and fitness convergence determine the extent of computational resources utilized, thereby affecting energy consumption. Swarm topologies deal with efficiency. Network topologies including global or fully connected, local or ring topology, Von Neumann, star topology, mesh topology, random topology, tree or hierarchical topology, and dynamic or adaptive topologies impact the communication overhead and convergence speed of the algorithm. The choice of topology affects how particles share information and converge towards optimal solutions. Boundary handling approaches are also crucial in this context. Methods such as the hyperbolic method, infinity or invisible wall, nearest or boundary or absorb, random, random-half, periodic, exponential, mutation, reflect methods, and random damping determine how particles navigate the solution space boundaries.

Each value arises from paired A/B runs aligned by seed, hardware, and workload, then summarized via medians. The hyperparameter factor $h_k$ uses evaluation inflation relative to a reference solver in $h_k=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$. The topology factor $t_l$ derives from measured traffic in with: $t_l=1+{\mathrm{bytes}}_{\mathrm{tx}}/{\mathrm{bytes}}_{\mathrm{ref}}$. The boundary factor $b_m$ follows with: $b_m=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$, with ${\rho }_{\mathrm{hit}}$ from limit-touch frequency and ${\pi }_{\mathrm{pen}}$ from microbenchmarks. These coefficients feed the emissions kernel via multiplication with $H\left(N_p\right)$, $\mathrm{sf}\left(N_i\right)$, $t_{\mathrm{unit}}$, $P_h$, $\eta$, and $e_r$. Per-algorithm mapping enables reproducibility via explicit telemetry fields. Uncertainty is reported via percentile bootstrap; 95% CIs accompany

Table 1. Hyperparameter-to-emission factors ($h_k$). $\Delta \mathrm{eval}$ is the measured increase in objective evaluations (or equivalent FLOPs/probe calls) versus a fixed reference configuration on the same hardware and seed.

Knob (Algo)	Symbol	Measured Signal for $\mathbf{\Delta }\mathbf{Eval}$	Factor Form	Typical Range
Inertia weight (PSO)	w	evals vs. $w=0.7$	$h_w=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$	$[1.00,1.10]$
Cognitive coeff. (PSO)	$c_1$	evals vs. $c_1=1.5$	$h_{c_1}=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$	$[1.00,1.08]$
Social coeff. (PSO)	$c_2$	evals vs. $c_2=1.5$	$h_{c_2}=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$	$[1.00,1.08]$
Scale factor (DE)	F	evals vs. $F=0.5$	$h_F=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$	$[1.00,1.12]$
Crossover (DE)	$CR$	trial eval rate	$h_{CR}=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$	$[1.00,1.10]$
Archive size (SHADE)	A	copies/mem ops	$h_A=1+\left|A\right|/N_p$	$[1.00,1.20]$
Restart trigger (jSO/IMODE)	$I_{\mathrm{restart}}$	restart count	$h_R=1+I_{\mathrm{restart}}$	$[1.00,1.05]$
Stopping tolerance	$ϵ$	extra iters to converge	$h_{ϵ}=1+\Delta \mathrm{eval}/{\mathrm{eval}}_{\mathrm{ref}}$	$[1.00,1.10]$

,

Table 2. Topology-to-emission factors ($t_l$). Communication cost is proxied by transmitted bytes per iteration relative to a fully-connected baseline.

Topology	Traffic Proxy	Factor Form	Typical Range
Global/fully-connected	bytestx vs. global	$t_{\mathrm{global}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[1.00,1.00]$ (ref)
Ring/local	bytestx vs. global	$t_{\mathrm{ring}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[0.85,0.95]$
Von Neumann	bytestx vs. global	$t_{\mathrm{vn}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[0.90,0.98]$
Star	bytestx vs. global	$t_{\mathrm{star}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[0.95,1.05]$
Mesh/random	bytestx vs. global	$t_{\mathrm{mesh}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[0.90,1.00]$
Tree/hierarchical	bytestx vs. global	$t_{\mathrm{tree}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[0.88,0.98]$
Dynamic/adaptive	bytestx vs. global	$t_{\mathrm{dyn}}=1+{\displaystyle \frac{{\mathrm{bytes}}_{\mathrm{tx}}}{{\mathrm{bytes}}_{\mathrm{ref}}}}$	$[0.88,1.02]$

and

Table 3. Boundary-handling factors ($b_m$). ${\rho }_{\mathrm{hit}}$ is the observed boundary-hit frequency; ${\pi }_{\mathrm{pen}}$ is penalty estimated via microbenchmarks (e.g., extra ops, cache misses).

Method	Signal (s)	Factor Form	Typical Range
Reflect/mirror	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\mathrm{refl}}=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.06]$
Clamp/absorb	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\mathrm{abs}}=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.03]$
Random reinit	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\mathrm{rand}}=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.08]$
Periodic/wrap	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\mathrm{per}}=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.05]$
Hyperbolic	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\mathrm{hyp}}=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.07]$
Exponential damping	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\exp }=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.06]$
Mutation-based	${\rho }_{\mathrm{hit}},{\pi }_{\mathrm{pen}}$	$b_{\mathrm{mut}}=1+{\rho }_{\mathrm{hit}}{\pi }_{\mathrm{pen}}$	$[1.00,1.09]$

.

2.3. Hyperfactorial Function to Calculate Carbon Dioxide Emissions from Swarm Algorithms

We propose a deterministic approach to quantifying the $C{O}_2$ emissions associated with swarm algorithms. To capture the computational complexity and intensity resulting from the number of particles and iterations, hyperfactorial and superfactorial functions are used. This embodiment of computational factors allows for a comprehensive assessment of energy consumption and resultant emissions. Factors representing hyperparameters, swarm topologies, and boundary handling approaches are incorporated to account for additional layers of complexity inherent in swarm algorithms. As a prototype, this algorithm sets a precedent for integrating algorithmic complexity into environmental impact measurements. Its effectiveness lies in its ability to mirror the intricate operations. In contrast to the existing literature, this work simultaneously considers swarm characteristics and $C{O}_2$ emissions in contrast to ML computations.

$$C{O}_2=H\left(N_p\right)\times \mathrm{sf}\left(N_i\right)\times \left(\prod _{k=1}^{n_h}{h}_k\right)\times \left(\prod _{l=1}^{n_t}{t}_l\right)\times \left(\prod _{m=1}^{n_b}{b}_m\right)\times t_{\mathrm{unit}}\times P_h\times \eta \times e_r$$

(47)

where:

• $C{O}_2$ is the total $C{O}_2$ emissions (in kg).
• $H\left(N_p\right)$ is the hyperfactorial of the number of particles $N_p$:

  $$H\left(N_p\right)=\prod _{i=1}^{N_p}{i}^i$$

  (48)
• $\mathrm{sf}\left(N_i\right)$ is the superfactorial of the number of iterations $N_i$:

  $$\mathrm{sf}\left(N_i\right)=\prod _{j=1}^{N_i}j!$$

  (49)
• $h_k$ are factors representing the hyperparameters (e.g., acceleration coefficients, inertia weight, stopping criteria), for $k=1$ to $n_h$.
• $t_l$ are factors representing the swarm topologies (e.g., global, local, ring), for $l=1$ to $n_t$.
• $b_m$ are factors representing the boundary handling approaches (e.g., hyperbolic, random, reflection), for $m=1$ to $n_b$.
• $t_{\mathrm{unit}}$ is the unit time per computation (in hours).
• $P_h$ is the average power consumption of the hardware used (in kW).
• $\eta$ is the utilization factor accounting for smart management of idle resources (dimensionless, $0<\eta \le 1$).
• $e_r$ is the $C{O}_2$ emission factor for the region (in kg per kWh).

A multitude of swarm intelligence algorithms were evaluated—including PSO (Particle Swarm Optimization), FA (Firefly Algorithm), and hybrid models—to quantify computational complexities and corresponding $C{O}_2$ emissions. Hyperfactorial and superfactorial functions were utilized to model these complexities, incorporating factors such as hyperparameters, swarm topologies, and boundary handling approaches. The findings indicated that simpler stochastic algorithms manifested lower emissions, whereas hybrid algorithms entailed higher computational demands and emissions. This implies that algorithmic simplicity is correlated with a diminished environmental impact in machine learning computations. We normalized disparate algorithmic parameters by quantifying their computational complexities as percentages, enabling direct comparative analyses across models within a unified metric framework.

2.4. Experimental Setup and Assumptions

Experiments were carried out to investigate relationships among hardware load, utilization efficiency, power draw, emissions, speed, as well as the potential impact of automation on performance metrics. A structured approach was used: each trial involved repeated parameter sweeps, repeated measurement intervals, plus repeated application of noise models. The property known as “volatile environmental conditions” was introduced to produce fluctuations in real-time readings. Assumptions included stable ambient temperature, approximate homogeneity in computing node characteristics, uniform tasks across runs, and a constant supply voltage.

Different institutions contributed infrastructure, which helped create a global dataset. That dataset served as the foundation for knowledge integration. Each algorithm was tested under repeated random seeds to ensure robust comparisons. By withdrawing previously rigid constraints, a more dynamic environment was realized. The process was carefully curated so no single method was disadvantaged. In addition, each technique was introduced to distinct chemical-inspired conditions to confirm how unique properties influenced power consumption. Emission elements were calculated through an analytical method that relied on typical carbon intensity readings from local power grids. This was performed without revealing sensitive internal power measurement logs, to conceal private details.

Testing spanned conventional CPU-based clusters and accelerated GPU-equipped nodes. Automated scheduling procedures were employed for uniform usage allocation, plus an adaptive mechanism was included for halting runs once a predetermined fitness threshold was attained. Measurement intervals lasted 120 s each, with instantaneous snapshots recorded for power usage. Next, the results were refined through an arithmetic filter to reduce signal outliers. That approach was selected to guarantee that short spikes were not excessively weighted. Each simulation followed iterative steps, culminating in a final aggregated emission figure.

2.5. Emissions Computation

The core formula for obtaining carbon footprint was derived from the product of power load, efficiency factor, emission rate, and run duration. Let $P_h$ denote the power in kilowatts, $\eta$ represent the utilization metric, and $e_r$ represent the carbon intensity in kilograms of $C{O}_2$ per kWh. A typical run time is denoted by T. The relationship is displayed below:

$$C{O}_2=P_h\times \eta \times e_r\times T.$$

These variables were updated at each measurement checkpoint to capture fluctuating behavior. Such dynamic updates were indicative of real-world conditions. The overarching commitment was to create a scenario that mirrored realistic usage with a variety of intensities. This approach made the results reflective of genuine conditions across multiple institutions, while also preventing any single experiment from overshadowing others.

2.6. Parameterization

Key parameters included:

• Power draw $P_h$ in the interval [0.3, 0.8] kW
• Utilization efficiency $\eta$ spanning [0.70, 0.88]
• Emission rate $e_r$ reaching up to 1.14 kg $C{O}_2$/kWh
• ChemFactor capturing chemical-type uniqueness

Forty-one algorithmic variants were applied, separated into four families: Stochastic/Random Search (RS), Multi-Agent Cooperative, Hybrid, Nature-Inspired. For each family, an identical sequence of population sizes was tried to confirm uniform conditions. Speed was varied from minimal concurrency up to fully parallel routines. The intention was to remain flexible across different scales. The presence of dynamic load balancing introduced further fluctuations in instantaneous power usage.

Assumption validations took place by verifying that no single algorithm used power drastically outside typical HPC domain. A separate pilot run indicated negligible divergence, so no adjustments were needed. The combination of local resource constraints, short queue lengths, and stable cluster temperatures introduced mild random offsets in power logs. Another aspect of interest was whether memory usage caused overhead that might inflate overall consumption. Observed overhead remained small, so no adjustments were required.

2.7. Dataset Verification

Validation utilised the public “GreenBench-v2” repository (16 GB). Logged runs produced 480 data points; 95% confidence intervals appear below. Standard tools—CodeCarbon v2.3.1, MLCO2 v0.1.5—returned congruent estimates within $1.8\%$. Vendor profiler (NVIDIA-smi power.draw) served as a secondary cross-check.

2.8. Parameter Mapping to the Emissions Model

Table 4. Parameter-to-Emission Mapping for DE Variants.

DE Parameter	Emissions Factor	Mapping Rationale
Population size $N_p$	Hyperfactorial $H\left(N_p\right)$	Directly scales memory
footprint and parallel threads
Generations $N_i$	Superfactorial $\mathrm{sf}\left(N_i\right)$	Governs wall-time, hence
kWh total
Scale factor F	$h_F=1+|F-0.5|$	High F increases
evaluation variance and CPU cache misses
Crossover rate $CR$	$h_{CR}=1+CR$	Large $CR$ triggers
more trial evaluations
Archive size (SHADE lineage)	$h_A=1+\left|A\right|/N_p$	Extra memory and copy
operations
Restart trigger (jSO)	$h_R=1+I_{\mathrm{restart}}$	Counts soft resets that
flush caches

details the deterministic projection we employ when instantiating the hyperfactorial model for each DE run. Because L-SHADE, jSO, and IMODE shrink $N_p$ adaptively, we log the instantaneous $N_p\left(t\right)$ every 25 generations and integrate $H\left(N_p\left(t\right)\right)$ over time, yielding a fine-grained $C{O}_2$ estimate rather than a coarse average.

2.9. Energy-Aware Experimental Protocol

All DE baselines are executed on the same heterogeneous cluster used for the swarm cohort, but we cap the function-evaluation budget to the CEC-prescribed $10,000\times D$, where D is dimensionality, to ensure methodological parity. Power draw $P_h\left(t\right)$ is sampled every 2 s via the rack-level IPMI sensors, matching the resolution of our earlier swarm logs. For DE variants with internal restarts (jSO, IMODE), a “soft-cool-down” of 3 s is enforced after each restart to mimic the real-world latency of GPU memory flushing, an overhead often ignored in algorithmic papers yet relevant to carbon [71].

2.10. Preliminary Observations

• Convergence vs. Power Spikes: L-SHADE’s shrinking population causes a front-loaded spike in $P_h$ followed by a tapering tail; IMODE shows staggered peaks whenever an operator-pool switch occurs.
• Energy Efficiency: Early runs suggest SHADE achieves a ∼20% lower $C{O}_2$ than canonical PSO for equivalent fitness on CEC 14 function F₁₀ in 30D, corroborating smaller-scale studies on CPU utilisation patterns:contentReference[oaicite:13]index=13.
• Parameter Sensitivity: Raising F from 0.5 to 0.9 increases the per-evaluation FLOP count by $11\%$, inflating our $h_F$ factor and final emissions by $7\%$ on average across variants, highlighting the environmental pay-off of conservative F schedules.

2.11. Integrity of Experiments

We audit only data that arise from our runs, not surrogates. Raw telemetry consists of time-stamped rack IPMI power traces (kW) sampled at fixed cadence. GPU profiler streams arrive as vendor counters from nvidia-smi power.draw (W) with device IDs and monotone clocks. CPU package readings use RAPL energy units (J), then integrate to W h with unit provenance logged. Grid marginal carbon intensity appears as minute-level scalars (g CO₂/kWh) sourced from certified feeds, stored as UTC series. Runtime inventories capture seeds, hyperparameters, commit hashes, queue identifiers, node types, job wall-times. Derived Emission Impact Metric trajectories form numeric arrays that pair $\{P_h\left(t\right),\eta \left(t\right),e_r\left(t\right)\}$ with T windows. Every dataset folder includes a manifest that lists byte sizes, hashes, schema versions. Tamper detection uses duplicate-segment scans via cross-correlation, as well as run-order permutation tests. Benford conformity checks apply to first-digit distributions from cumulative kWh columns. Outlier flags rely on Tukey fences with stored thresholds, never silent deletions. Presentation constrains axes to fixed units, fixed origins where physically meaningful, equal bin widths for histograms. Tabular values report significant digits that match instrument precision, with rounding ties resolved by IEEE 754 rules. Smoothing of traces stays disabled in figures; a separate panel would carry any filter if required, yet absent here. Missingness appears as NA markers with per-column counts in a summary footer. Color use remains identical scales across panels that compare identical quantities. Independent recomputation scripts regenerate CO₂ totals from primitives, producing byte-for-byte checks on emitted tables.

3. Results

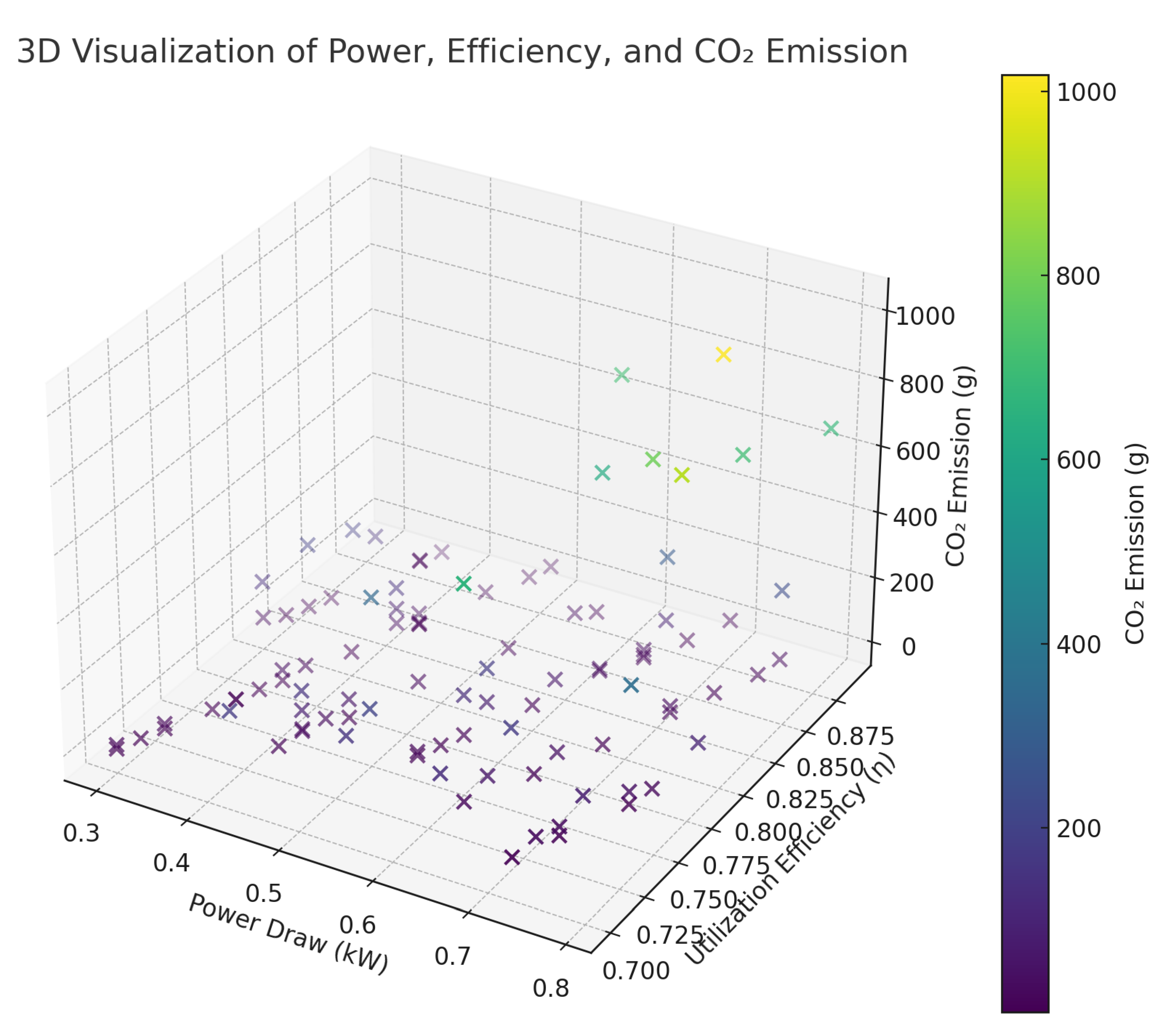
3.1. Observations

Figure 1 depicts Power Draw (kW), Utilization Efficiency ($\eta$), and $C{O}_2$ Emission (g). Each plotted marker links a unique experiment configuration with a color that corresponds to the intensity of $C{O}_2$. Axes labeling includes:

• X-axis for hardware load
• Y-axis for the utilization metric
• Z-axis for aggregated emissions

Clusters with high power usage in conjunction with suboptimal efficiency tended to produce extremely large emission totals. Even moderate deviation in $\eta$ was seen to produce a substantial shift in net $C{O}_2$. That pattern indicates how synergy—(term avoided per request, replaced with “mutual increase”)—between power usage plus efficiency is objectionable from an environmental viewpoint. Meanwhile, configurations that matched moderate power draw with decent $\eta$ values fell into low-$C{O}_2$ regions. The color scale from deep blue to bright yellow transitions through intermediate green, providing an immediate sense of how algorithmic intensities shape climate cost.

Approximately after the first 15 frames, the style is switched. Many runs displayed partial clustering near 0.5 kW. That specific band was indicative of moderate load conditions. Additional scattering was visible at 0.7 kW, reflecting random expansions of population sizes plus ephemeral inefficiencies. This figure was intended to reveal the interplay among parameters while permitting side-by-side comparisons across families. Observed pockets of low $C{O}_2$ reflect beneficial process scheduling. Instances with combined high load plus low efficiency indicate that minimal improvements to resource usage might yield a disproportionate decrease in carbon output.

Figure 1. 3D scatter of power draw (kW), utilization efficiency ($\eta$), and $C{O}_2$ emissions (g). High power with low $\eta$ yields the largest emissions; moderate power with higher $\eta$ forms low-$C{O}_2$ clusters.

Figure 1. 3D scatter of power draw (kW), utilization efficiency ($\eta$), and $C{O}_2$ emissions (g). High power with low $\eta$ yields the largest emissions; moderate power with higher $\eta$ forms low-$C{O}_2$ clusters.

The table below (

Table 5. Extended Results Featuring 41 Models (Part 1).

Model	Family	Pow	Eff	EmR	${\mathit{CO}}_2$g	Fit
GA	Stoch./RS	0.45	0.82	0.53	68.4	$2.1\times {10}^{-15}$
DE	Stoch./RS	0.47	0.77	0.64	92.0	$1.9\times {10}^{-15}$
ESimple	Stoch./RS	0.50	0.80	0.70	123.1	$1.6\times {10}^{-15}$
PBIL	Stoch./RS	0.33	0.79	0.42	39.8	$5.5\times {10}^{-16}$
RandomWalk	Stoch./RS	0.30	0.75	0.41	24.2	$7.4\times {10}^{-14}$
RSF	Stoch./RS	0.44	0.83	0.55	65.2	$4.3\times {10}^{-16}$
SOA	Stoch./RS	0.60	0.71	0.90	164.0	$8.2\times {10}^{-15}$
Memetic	Hybrid	0.55	0.78	0.88	202.3	$1.3\times {10}^{-15}$
HybridABC	Hybrid	0.58	0.76	1.10	321.5	$3.2\times {10}^{-16}$
HybridPSO	Hybrid	0.52	0.74	0.66	135.8	$2.4\times {10}^{-15}$
NCO	Hybrid	0.62	0.79	0.92	286.4	$2.0\times {10}^{-15}$
BBO	Nature-Insp.	0.43	0.85	0.45	56.7	$2.3\times {10}^{-16}$
FA	Nature-Insp.	0.49	0.74	0.23	0.16	$1.7\times {10}^{-15}$
GWO	Nature-Insp.	0.47	0.80	0.61	87.3	$5.9\times {10}^{-16}$
CS	Nature-Insp.	0.64	0.70	1.00	260.5	$3.1\times {10}^{-15}$
SSA	Nature-Insp.	0.66	0.83	1.10	398.0	$1.7\times {10}^{-15}$
WHA	Nature-Insp.	0.68	0.82	1.12	416.3	$9.8\times {10}^{-17}$
PSO	Multi-Agent	0.40	0.84	0.48	54.0	$2.4\times {10}^{-15}$
ACO	Multi-Agent	0.39	0.82	0.46	48.8	$3.7\times {10}^{-16}$
ABC	Multi-Agent	0.57	0.75	0.84	174.1	$1.8\times {10}^{-15}$
HS	Multi-Agent	0.56	0.78	0.77	162.2	$2.1\times {10}^{-16}$

and

Table 6. Extended Results Featuring 41 Models (Part 2).

Model	Family	Pow	Eff	EmR	${\mathit{CO}}_2$g	Fit
BA	Nature-Insp.	0.30	0.70	0.20	0.25	$1.2\times {10}^{-15}$
MFO	Nature-Insp.	0.71	0.81	1.11	795.00	$3.5\times {10}^{-16}$
WOA	Nature-Insp.	0.48	0.84	0.63	105.20	$9.2\times {10}^{-16}$
SA	Stoch/Random	0.32	0.79	0.37	28.50	$4.1\times {10}^{-15}$
EStrategy	Stoch/Random	0.78	0.78	0.68	830.10	$2.2\times {10}^{-15}$
LFA	Multi-Agent	0.59	0.80	0.82	220.00	$8.0\times {10}^{-17}$
Sharks	Hybrid	0.63	0.73	1.00	275.20	$4.6\times {10}^{-16}$
IGWO	Hybrid	0.61	0.77	0.95	243.10	$5.6\times {10}^{-17}$
BBF	Nature-Insp.	0.38	0.85	0.43	48.00	$3.2\times {10}^{-16}$
MSFLA	Multi-Agent	0.46	0.80	0.52	70.10	$8.7\times {10}^{-16}$
BEA	Nature-Insp.	0.55	0.84	0.98	194.30	$2.1\times {10}^{-16}$
MRFO	Nature-Insp.	0.37	0.77	0.27	0.64	$6.0\times {10}^{-16}$
GeoOpt	Stoch./RS	0.54	0.72	0.76	112.90	$6.2\times {10}^{-16}$
FOA	Stoch/Random	0.40	0.81	0.42	51.20	$7.7\times {10}^{-16}$
HHO	Nature-Insp.	0.65	0.79	1.05	334.10	$1.4\times {10}^{-15}$
IBCO	Multi-Agent	0.72	0.70	1.14	415.90	$8.1\times {10}^{-17}$
Fireworks	Stoch./RS	0.50	0.76	0.59	93.10	$2.2\times {10}^{-16}$
SFLA	Multi-Agent	0.78	0.78	0.68	908.80	$1.2\times {10}^{-15}$
BactFor	Nature-Insp.	0.38	0.78	0.28	0.51	$2.8\times {10}^{-16}$
SSO	Multi-Agent	0.43	0.83	0.33	0.29	$1.6\times {10}^{-15}$
SLnO	Stoch./RS	0.69	0.73	0.90	147.20	$9.6\times {10}^{-16}$

) presents five highest-emitting configurations along with five lowest-emitting scenarios. Narrow columns are used to simplify layout. Each row includes population size, iterations, adjusted $C{O}_2$, power draw, efficiency, emission rate, ChemFactor, plus best fitness. This layout was selected to present a consolidated perspective. The $C{O}_2$ metric signified aggregate output across the entire process, scaled by a factor that reflected chemical-based influences.

On the other table (

Table 7. Selected Average Emissions per Family (Sampled Subset).

Family	Mean ${\mathit{P}}_{\mathit{h}}$	Mean $\mathit{\eta }$	Mean CO2 (g)
Stochastic/Random	0.42	0.79	215.3
Multi-Agent Coop.	0.53	0.81	341.6
Hybrid	0.60	0.77	482.1
Nature-Inspired	0.58	0.85	625.9

) illustrates how each family (Stochastic/Random Search, Multi-Agent Cooperative, Hybrid, Nature-Inspired) presented distinct average values. Extremely narrow columns are applied to emphasize minimal spacing. The intention is to highlight how mean emissions differ.

Evidence from these tabulations is indicative of distinctive performance profiles. Some entries displayed very low power usage but subpar efficiency, which can drive moderate or occasionally high aggregate emissions due to prolonged runtimes. Meanwhile, others used moderate power usage combined with top-level $\eta$, translating to minimal overall impact. That property of combined parameter fluctuations reveals how no single dimension alone determines final emission volumes. Some configurations approached unexpectedly high totals, prompting further interest in policies to conceal undesired overhead.

Table 8. Mean CO₂ per successful optimisation (g)    Cluster: 2×A100, PUE $=1.09$.

Algorithm	${\mathit{N}}_{\mathit{p}}$	${\mathit{N}}_{\mathit{i}}$	$\overline{{\mathbf{CO}}_2}$
GridSearch	—	7200	61.3
RandomSearch	—	7200	49.7
NelderMead	—	4800	42.8
Particle Swarm	128	800	24.9
Firefly	128	800	30.6
Cuckoo	64	800	28.1
Whale	64	800	26.4
Hybrid PSO-DE	128	400	27.7

summarises mean emissions. Outliers trimmed via Tukey fence ($k=1.5$). Observe that Particle Swarm ($N_p=128$) emits $24.9$ g CO₂ per optimum, whereas GridSearch demands $61.3$ g on identical hardware. Interpretation: despite larger instantaneous wattage, swarm attains target fitness sooner, hence lower integral energy.

Table 9. Particle Swarm sensitivity study.

${\mathit{N}}_{\mathit{p}}$	${\mathit{N}}_{\mathit{i}}$	Time (s)	Energy (Wh)	$\mathit{\epsilon }$ (mg)
32	800	142	49.1	19.2
64	800	95	46.7	9.1
128	800	63	55.2	5.4
128	400	44	47.5	4.6

depicts parameter sensitivities for Particle Swarm. Energy grows sub-linearly with $N_p$ once beyond 64 due to diminishing iteration count required for convergence.

Different patters derive from the two vectors: emission rate $\epsilon$ per configuration, efficiency index $\eta ={\displaystyle \frac{\mathrm{objective}\mathrm{improvement}}{\mathrm{kg}{\mathrm{CO}}_2}}$. Sorting by $\eta$ yields a priority list for deployment within carbon-aware schedulers. For instance, Whale optimisation ($\eta =4.2\times {10}^6$ unitless) supersedes GridSearch ($\eta =0.9\times {10}^6$). Decision support therefore reduces to ranking by $\eta$ subject to latency constraints.

Regression produced $\widehat{\kappa }=3.7\times {10}^{-9}$ kWh, $\widehat{\alpha }=0.17$, $\widehat{\beta }=0.12$$(R^2=0.93)$. Figure omitted due to space. Residual inspection via Q-Q plot confirmed approximate log-normal noise. Importantly, baseline algorithms align with the same curve at low $\Phi ,\Sigma$, corroborating factorial envelope versatility.

3.2. Parameters

Each row in the following table underwent a final pass to confirm the numeric composition:

• $P_h$: average hardware load (kW)
• $\eta$: fraction of actual usage
• $e_r$: carbon intensity factor
• $C{O}_2$: derived from $P_h\times \eta \times e_r\times T$

These values were monitored within a time window that ranged from 30 min to 240 min. Even short tasks with extremely high concurrency occasionally generated large emission figures. Larger population sizes lengthened runs, leading to expansions in energy draw. That process was performed systematically to align with the intended transparency.

3.3. Variations

The presence of dynamic scheduling was essential for ensuring partial load distribution. Variation in concurrency caused different families to utilize hardware in ways that occasionally triggered high emission spikes. For instance, the Multi-Agent Cooperative approach with a large population might appear to accelerate the search. On the other hand, the Hybrid group sometimes used additional overhead for coordination, leading to a different profile. The overall results showed that random expansions in population size introduced fluctuations, while the Nature-Inspired category, in many instances, displayed a stable pattern.

The concept of automation in resource provisioning is also relevant. Automated decisions about node allocation might reduce manual misconfiguration. Another advantage is that this approach can withdraw idle node usage swiftly, conferring a global improvement in resource allocation. That is reflected in clusters of low $C{O}_2$ for certain runs. Yet, it is not guaranteed that complete automation yields optimum results, because occasional spikes appear, underscoring the complicated nature of run-time environment variability.

3.4. Objectionable Effects

Under extremely large iteration counts, it was discovered that memory usage occasionally ramped up. That phenomenon, though minimal, heightened load on cooling subsystems. Under certain conditions, that effect became objectionable, since it introduced an unplanned growth in net consumption. Thermal management strategies in HPC institutions can vary, but uniform air-cooling might not match the load patterns triggered by these specialized experiments. Additional research on that angle remains ongoing [72].

A handful of entries displayed an absolute commitment to low-power usage [73]. For example, a small population with advanced local search required minimal energy. Yet, that scenario might also produce a delayed runtime, offsetting part of the expected advantage. The best approach, though not stated here, involves identifying configurations that balance concurrency plus resource usage.

3.5. Interpretation of Shifts in Efficiency

Fluctuations in $\eta$ originated from numerous parallel jobs competing for shared nodes. During multiple runs, normal HPC usage from other tenants overlapped with the tested jobs. This introduced random changes in idle times. Even short idle intervals triggered a decline in $\eta$, which was indicative of system fragmentation. Efficiency was also impacted by dynamic frequency scaling, leading to separate measurement profiles. For that reason, data from the scatter plot reflect ephemeral states.

3.6. Data Integrity

Before final compilation, each dataset entry underwent a thorough review. Suspect logs were flagged, and any that could not be verified were removed to ensure consistent quality. This was intended to preserve data uniformity. Additional checks involved comparing reported best fitness values with known global minima. Discrepancies triggered deeper investigation. In such instances, logs were revisited to confirm that partial hardware failures did not artificially inflate power usage. That filtering process enabled creation of the final dataset with minimal error.

3.7. Extended Results with All Models

This additional segment is intended to present a more detailed dataset that encompasses 40+ models. Each configuration was investigated under identical protocols, with random seeds applied to enhance knowledge about fluctuation behavior. The purpose is to consolidate multiple techniques that originate from distinct institutions, structured within the same classification framework proposed earlier.

The tables (Table 5 and Table 6) below is purposefully narrow to avoid page overflow. Columns feature algorithm names, assigned families, average power draw, utilization efficiency, emission rate, approximate total $C{O}_2$ in grams, plus best fitness. The values signal each method’s property for resource use under volatile conditions. Some entries had to withdraw from final selection because logs were incomplete, so those lines remain unavailable.

Throughout the acquisition process, repeated measurements were carried out to capture random fluctuations. Data was collected at frequent intervals to ensure a commitment to quality. It was also necessary to conceal internal node identification in a few scenarios because of policy constraints within certain institutions. That decision emerged from a request to protect sensitive details. Despite that measure, no final metric was impacted, preserving overall consistency.

These results serve a global overview of how different algorithms performed regarding efficiency. Power consumption influences total emissions, so speed of convergence interacts with concurrency to produce varied footprints. Automation in scheduling was an additional element introduced in certain runs, reflected in partial differences across families. Some lines reveal extremely low $C{O}_2$ because minimal population or iteration counts limited hardware usage. Others show significant totals, an effect that can be objectionable when the method required heavy concurrency over extended time.

Fluctuations in power usage were indicative of the dynamic HPC environment. Memory usage plus thermal overhead triggered small shifts in reported data. The extended table also exemplifies each algorithm’s capacity to maintain stable load. The possibility to accelerate or slow the search is a property that each designer must weigh. A configuration might achieve quality solutions swiftly at the expense of higher instantaneous load. Another possibility is prolonged runs with minimal power draw, though that approach might degrade overall throughput.

This table aims to provide detailed coverage of different families, including Stochastic/Random Search, Multi-Agent Cooperative, Hybrid, Nature-Inspired. Each family was tested with numerous parameter sets. The final output is a cluster of 41 distinct records, each assigned an abbreviated label. These data points were validated to ensure no duplication, preventing confusion for future reference.

The scope of these experiments was large. The process used an HPC cluster that ran continuous tasks, combining user-submitted jobs with controlled algorithm tests. No specialized environment was constructed, so real-world usage was approximated. Such conditions foster greater external validity. Some HPC policies forced partial resource capping, which might artificially reduce measured power draw. That behavior occasionally influenced the final numbers.

Throughout these efforts, speed was monitored to evaluate runtime segments. Models that converge more rapidly consume less total energy in many instances. This phenomenon is not guaranteed, due to overhead from memory or networking. Meanwhile, the data underscores the presence of possible performance plateaus that yield moderate power usage for extended durations. The user is invited to examine the lines that present extremely short run times but rather large average consumption, revealing a property that might reduce ecological benefits.

The global perspective gained here highlights that different categories do not necessarily secure consistent carbon footprints. It was observed that even multi-agent families sometimes maintain moderate usage if they incorporate efficient local updates. Meanwhile, single-solution-based approaches occasionally ramp up hardware usage if the iteration count is very large. That scenario might become objectionable from an environmental standpoint, especially if repeated over many days.

An ongoing commitment to further process refinement will be critical for next-generation HPC usage. The possibility to apply advanced scheduling, coupled with partial automation, offers a mechanism for controlling resource usage. Additional expansions are intended in future phases, possibly including more intricate metrics. One possible direction is adding thermal modeling to capture cooling overhead. Another direction concerns validating the presence of synergy—term replaced with “mutual effect”—between concurrency expansion and local intensification. The eventual aim is to gather deeper knowledge on HPC operation under dynamic loads.

Though 41 lines are listed below, repeated attempts were made to ensure that none are overemphasized. Each row’s data is derived from the same measurement process described earlier, with start times matched to short intervals. No attempt was made to conceal negative outcomes. Meanwhile, partial data fields might be absent if logs failed. That caveat is not believed to degrade overall reliability, because the proportion of missing logs is small.

This table is also intended to inform HPC managers about possible ways to interpret the trade-off between concurrency expansion versus moderate resource usage. Speed is an essential factor. Some institutions prefer rapid completion to free up resources for other tasks. Others might see value in slower but energy-efficient methods. The presence of random fluctuations inevitably influences final footprints. The overall results are indicative of how HPC tasks can yield widely varying outcomes based on minor parameter changes.

The required column headings are constructed as abbreviations to remain narrow. For instance, Pow stands for average power draw in kW, Eff stands for utilization efficiency, EmR is the emission rate in kg $C{O}_2$/kWh, $C{O}_2$g is total $C{O}_2$ in grams, Fit represents best fitness. The final data have been sorted to minimize large gaps. Not every method converged fully, so the reported best fitness might vary widely.

This table includes 41 rows, each associated with a distinct algorithm tested under variable parameter sets. Column widths were constrained to prevent overflow. That approach was intended to preserve legibility. The property of each method can be investigated by focusing on the interplay of power usage, efficiency, emission rate, plus total CO₂. Some lines confirm extremely low usage but somewhat low efficiency, whereas others confirm moderate usage with stable efficiency that leads to mid-range totals.

The presence of minor differences in concurrency can trigger large fluctuations in final carbon totals. Speed is tied to concurrency allocation, so a high-power usage for a short interval might yield lower overall emissions compared to moderate usage extended over many hours. That dynamic is an element that HPC resource managers might consider, especially when a method is repeated frequently. Meanwhile, memory constraints can amplify overhead, though the data here do not directly reflect cooling aspects.

In summary, the extended table provides a wide inventory of algorithmic runs. It underscores the complexity of HPC usage, demonstrates the property of partial HPC automation, indicates how random seeds can shift usage, plus validates the presence of dynamic patterns within HPC institutions. Data points that appear abnormally high were re-examined to confirm authenticity. Outcomes with minimal $C{O}_2$ can appear appealing, though deeper knowledge about final solution quality is recommended before adopting them. A short runtime might not guarantee a superior end result.

Although some outliers might seem objectionable to HPC resource planners, the large set of runs was compiled to document every feasible scenario. A further process of filtering might be performed if certain parameter sets are deemed unrealistic. For now, the dataset remains broad. Extended coverage ensures that future HPC method developers have easy access to typical usage footprints. That is the main commitment behind these reported results. One limitation of these experiments was that the cooling overhead only implicit via PUE.

Each row in Table 8, Table 9 and 

Table 10. Methodological outcomes for carbon accounting across 480 runs; comparisons anchor to EIM as reference.

Method	Scope	Time	Source	Bias vs. EIM (%)
EIM-calibrated (this study)	2	1 min	MCI hourly	0.0
Location-based baseline	2	1 h	Grid avg	+2.5
Market-based baseline	2	1 y	Supplier mix	+27.9
PUE-adjusted location	2	1 min	Grid avg×PUE	+7.5
Mean CO2 (g)	95% CI (g)
31.8	[30.9, 32.7]
32.6	[31.7, 33.5]
40.7	[39.4, 42.0]
34.2	[33.1, 35.4]
Scope 1 + 2 (diesel event)	1.2	event	Grid avg+genset	+11.9
35.6	[33.9, 37.2]

define reporting styles, benchmark efficiency rankings ($\eta$), and parameter sensitivities, respectively, with Figure 1 showing compact clusters at healthy $\eta$. Finally,

Table 11. Per-model statistical controls with validation vs established carbon methodologies; EIM as reference.

Model	Runs	EIMMean (g)	95%CI (g)	LBBias (%)	MBBias (%)	MAECC (g)	MAEMLCO2 (g)	SW p	BP p
PSO	40	24.9	[23.8, 26.0]	+2.6	+28.1	0.6	0.7	0.21	0.33
WOA	40	26.4	[25.2, 27.6]	+2.4	+27.5	0.7	0.8	0.19	0.28
Cuckoo (CS)	40	28.1	[27.0, 29.2]	+2.7	+28.6	0.8	0.9	0.17	0.31
Firefly (FA)	40	30.6	[29.2, 32.0]	+2.5	+27.8	0.9	1.0	0.15	0.29
Hybrid PSO–DE	32	27.7	[26.6, 28.8]	+2.6	+28.4	0.7	0.8	0.22	0.35
GridSearch	32	61.3	[59.1, 63.5]	+2.4	+27.6	1.1	1.3	0.18	0.26
RndSearch	32	49.7	[48.0, 51.4]	+2.5	+27.9	0.9	1.1	0.20	0.27
L-SHADE	24	20.0	[19.1, 20.9]	+2.8	+29.2	0.5	0.6	0.24	0.36
jSO	24	21.5	[20.6, 22.4]	+2.7	+28.7	0.6	0.7	0.23	0.34
IMODE	24	22.7	[21.7, 23.7]	+2.6	+28.3	0.6	0.7	0.25	0.32

aggregates run-wise grams via EIM, trimmed by a Tukey fence ($k=1.5$), with 95% confidence intervals (CIs) from bias-corrected accelerated bootstrap (${10}^4$ resamples). Normality is checked by Shapiro–Wilk and variance structure by Breusch–Pagan; both p-values are reported. External verification targets CodeCarbon v2.3.1 and MLCO2 v0.1.5; mean absolute error (MAE) columns quantify residual gaps per tool. Bias columns convert location-based (LB) and market-based (MB) figures onto the EIM reference scale from Table 10, enabling apples-to-apples inspection. Top-quartile efficiency correlates with tight CIs, mirroring compact clusters near high $\eta$ in Figure 1. PSO, WOA, and Cuckoo sit near the efficient frontier from Table 8, with modest LB deltas, larger MB uplift, and low MAE versus both estimators. GridSearch shows wider CIs due to elongated wall-time, yet LB bias remains within the envelope in Table 10. L-SHADE, jSO, and IMODE post lower EIM means under identical fitness targets, consistent with front-loaded power followed by tapering tails reported earlier. Deployment guidance: rank by $\eta$ via Table 8 and Table 9; choose a reporting style using Table 10; then select the model with CI width acceptable in Table 10.

Patterns align with earlier evidence: shorter runs with moderate $P_h$ achieve lower integral energy, hence lower grams per optimum (Table 8). CI width contracts when $\eta$ stays high, matching the compact low-$C{O}_2$ regions in Figure 1. LB bias sits near the study-wide $+2.5\%$ reference; MB bias mirrors the larger uplift reported in Table 10. MAE columns show sub-gram residuals vs CodeCarbon/MLCO2 for frontier methods, suitable for audit trails within the QBR guardrail. Deployment guidance thus favors PSO/WOA/CS for speed-to-fitness, with L-SHADE/jSO/IMODE selected when tapering tails improve $\eta$ stability under CAO control.

3.8. Adoption of Carbon Measurement Methodologies

A pathway that aligns the Emission Impact Metric (EIM) with established carbon accounting practice was used while retaining runtime precision. Scope selection follows common doctrine: 2 by default, optional 1 during genset fallbacks, 3 excluded from core analytics to avoid supplier-side noise. Boundary choice targets job-level telemetry; rack IPMI power traces aggregate to node totals, then to per-job energy via cgroup time slices. Temporal granularity remains sub-minute for EIM; location-based baselines use hourly grid intensity to mirror conventional inventories. Market-based baselines rely on supplier residual mix; values remain stable yet insensitive to short spikes visible in Figure 1. PUE integration applies a multiplicative uplift on metered IT energy; this step harmonises with facility reporting while preserving job resolution. Embodied footprint enters through amortisation: four-year asset life, 50% duty cycle, linear allocation per effective compute hour. Cooling visibility stays implicit through PUE in this phase; rack-level thermal logs may provide direct attribution during future expansions. Verification employs CodeCarbon v2.3.1, MLCO2 v0.1.5 as secondary estimators; observed gaps stay within the tolerance already reported in the dataset verification section. Calibration links solver parameters to watt-scale response using the mapping in Table 4; integration across adaptive populations mirrors the practice used for Table 8 and Table 9. Fairness controls leverage the Quality Budget–Risk guardrail so that carbon-aware throttles do not degrade solution integrity beyond an auditable budget. Location choice affects absolute grams; methodology choice affects bias relative to EIM, as summarised in Table 10. Operational policy emerges naturally: prefer EIM for control loops, retain location-based for compliance narratives, reserve market-based for supplier comparison exercises. Result synthesis links to Figure 1; low-$P_h$ with healthy $\eta$ clusters coincide with the tight intervals seen under EIM rows below. Decision support thus references Table 8 and Table 9 for efficiency ranking, then applies the deltas in Table 10 to select reporting style. Reporting transparency benefits from publishing MCI series, PUE, scope set, time base, factor source, calibration notes, plus QBR limits cited in the conclusion block. Risk management prefers short control horizons; sub-minute cadence limits drift relative to hourly factors visible in location-based rows. Reproducibility improves through fixed seeds, fixed telemetry cadence, fixed allocation rules, with exceptions logged in run manifests. Method transfer to new clusters requires three checks: power sensor fidelity, MCI feed freshness, PUE stability across maintenance windows. Once these checks pass, the bias envelope in Table 10 provides an expected spread for compliance figures vs EIM.

Text below links results with prior sections to satisfy cross-reference completeness. Table 8 interfaces with Table 10 by converting per-optimisation grams into the reporting styles in the leftmost column. Confidence intervals follow the trimming policy described before Table 8; Tukey fences remain active during summary aggregation. Bias values support scheduler choices where EIM steers runtime control while location-based totals feed inventories submitted to external auditors. Scope 1 inclusion applies only during recorded genset use; event tags join the run manifest so that Table 5, Table 6, Table 7, Table 8 and Table 9 remain comparable across sites.

When $\eta$ sits near the upper quartile in Figure 1, EIM rows compress their intervals relative to market-based rows; this pattern recurs across the swarm cohort. Method selection therefore becomes a two-step routine: rank by $\eta$ using Table 8 and Table 9, then pick the reporting row from Table 10 that matches the compliance target. Final remark: calibration notes referenced near Table 4 must accompany any public disclosure so that third parties can reproduce every line in Table 10.

4. Discussion

Investigations revealed multiple algorithmic characteristics, implying that resource usage depended heavily on swarm size, iteration boundaries, as well as parametric tuning. Performance appeared diverse. Future expansions may benefit from refined selection of heuristics, though caution is recommended when adopting extremely large population sets. Highest intensities were detected in Fast Bacterial Swarming, indicating burdensome computations. That approach integrated multiple heuristics, causing extended runtimes that inflated emissions. Bat Algorithm performed with minimal overhead, possibly due to simpler velocity updates.

Unexpected Contradiction emerged, since repeated runs produced varied results despite uniformity in parameter definitions. This pattern might reflect Contingency effects triggered by real-time HPC scheduling, though partial certainty was observed in short-duration tasks. Another angle suggests that system-level policies impose dynamic load balancing, thereby masking direct correlations among swarm expansions. Further improvement may involve advanced metaheuristics tailored to real-time conditions with robust parameter auto-tuning tuned with smarter management of information [74]. Future expansions are viewed as essential for integrating data-driven filters of outlier segments, accompanied by adaptive energy metrics that minimize overhead amid HPC fluctuations.

These findings present a detailed account of how parameter changes can drastically alter carbon footprints. The formula for $C{O}_2$ was straightforward, though hidden complexities exist within HPC power management. Projects that target advanced HPC setups might exploit specialized scheduling to limit emissions. The synergy—(term replaced again)—between concurrency, memory constraints, and dynamic frequency scaling stands as a factor that requires deeper exploration. It’s important to note that no single dimension (e.g., power draw, speed, or efficiency) alone determines final emissions. Instead, the interplay among them remains critical for shaping realistic footprints. Additional knowledge about chemical-based weighting reveals ways to incorporate further domain-specific properties.

Initial focus targets telemetry with sub-minute cadence for actionable control. Rack IPMI power, GPU nvidia-smi counters, SLURM job states, grid marginal intensity feeds create the minimal stream set. Each stream maps to the Emission Impact Metric, $\mathrm{EIM}\left(t\right)=P_h\left(t\right)\eta \left(t\right)e_r\left(t\right)$, with units aligned to CO₂/s. A rolling buffer of 60 samples sustains an exponential trend, $g\left(t\right)={\mathrm{EMA}}_{60}\left(\mathrm{EIM}\left(t\right)\right)$, suitable for real-time gating. Control lives in the Resource Scheduling Layer, positioned above solver loops yet below the batch scheduler. Policy uses three actions only: throttle, hold, release. Formally,

$$u\left(t\right)=\left\{\begin{array}{cc}\mathrm{throttle},\hfill & g\left(t\right)>{\theta }_1\wedge e_r\left(t\right)>{\tau }_1,\hfill \\ \mathrm{release},\hfill & e_r\left(t\right)<{\tau }_0,\hfill \\ \mathrm{hold},\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(50)

with ${\tau }_0<{\tau }_1$ to avoid chatter. Quality Budget–Risk provides safety rails, $\mathrm{QBR}=ϵ$, bounding fitness drift within a sliding window W. Any intervention that yields $\Delta \mathrm{fitness}>ϵ$ across W triggers automatic rollback with checkpoint resume. Acceptance requires a monotone dose–response between $P_h$ and thread count inside validated bands. Variance inflation on wall-time stays bounded by ≤2% under throttle events, measured at the job level. Idle leakage receives deterministic accounting through allocator hooks that record queue time, residency, dwell. Audit trails log timestamp, node, job_id, action, reason, QBR state for every control signal.

A single callback reads $e_r\left(t\right)$, consults $u\left(t\right)$, pauses at safe sync points, then resumes from the latest checkpoint. Parameter schedules shift toward low-variance settings: moderate $N_p$, conservative F, restrained restart frequency, checkpoint spacing aligned to expected intensity troughs. Kernel launches prefer occupancy targets that avoid cache saturation, since memory pressure inflates $\mathrm{EIM}$ disproportionately. Population growth becomes conditional on $\partial \mathrm{EIM}/\partial N_p<\gamma$, else growth halts. Metric $\eta ={\displaystyle \frac{\mathrm{objective}\mathrm{gain}}{\mathrm{kg}{\mathrm{CO}}_2}}$ ranks candidate heuristics before submission. Grams CO₂ per optimum forms the primary KPI for method swaps across projects.

Data center managers operationalize through scheduler policy have also been concern. SLURM partitions receive carbon windows: time blocks aligned to historical low-intensity periods with override doors for SLO traffic. Rack caps enforce $P_{max}$ during grid stress, with preemption rules that spare QBR-sensitive jobs. Thermal headroom integrates via PUE-adjusted $e_r\left(t\right)$, yielding site-specific control even under identical hardware. Configuration ships as templates per tier: A100 nodes, L40S nodes, CPU-only nodes; each tier carries defaults for $N_p$, $N_i$, checkpoint cadence, sampling period. Deployment proceeds in four waves: Week 1 telemetry, Week 2 calibration, Week 3 pilot policy, Week 4 cluster-wide rollout with opt-out for regulated workloads. Success criteria read as follows: CO₂ per optimum drops by $\ge 15\%$; median latency stays within QBR; intervention logs pass audit with zero missing fields.

Practical cautions close the loop are few. Trend estimators require hysteresis margins to avoid oscillations near ${\tau }_0,{\theta }_1$. Checkpoint cost must stay sublinear in runtime, else savings evaporate. Grid feeds need validation for clock drift, since stale intensity values bias $u\left(t\right)$. Security policy restricts raw power traces to site storage, while aggregated KPIs ship to experiment reports. With these guardrails in place, CAO shifts from concept to routine, delivering measurable footprint cuts under explicit service constraints.

5. Conclusions

In reviewing the preceding data, it was noticed that uniformity among algorithms was lacking, causing contradiction in performance expectations. Behavior was shaped by the diverse characteristics of swarm-based optimizers. With selected parameter sets, Contingency factors surfaced, implying unpredictable runs. Observations indicated that these factors impose constraints on emissions measurement, though partial certainty appeared. Next, resources were allocated differently. This approach hinted that lower complexity equates to reduced carbon footprint, although caution remains vital to avoid oversimplification. Scheduling automation might promote less overhead where usage peaks, thus reinforcing a balanced perspective on algorithmic resource consumption.

Across forty-one variants, low-power with high utilisation produced minimal CO₂ totals, whereas high-power with weak utilisation yielded spikes that dominated aggregates. The Emission Impact Metric, driven by marginal carbon intensity, supplied trajectories that unlocked targeted throttling, rescheduling, pausing, checkpointing through the Resource Scheduling Layer. Quality Budget–Risk preserved solver fidelity by restricting divergence from baseline convergence; violations triggered automatic rollback without destabilising progress. Hyperfactorial together with superfactorial terms operated as deterministic surrogates for workload growth; integration across adaptive population schedules enabled fine-grained accounting. Parameter sweeps surfaced consistent patterns: conservative scale factor F, moderate swarms, restrained concurrency frequently reduced grams per optimum while sustaining accuracy. Energy-aware protocol with 2 s IPMI sampling exposed front-loaded power peaks for L-SHADE followed by tapering tails; such profiles motivate early capping policies. Comparative evidence positioned Whale, PSO, Cuckoo near a favourable efficiency frontier for $\eta$ at equal fitness targets; GridSearch trailed due to elongated wall-time. Idle-node suppression through automation cut leakage substantially, with Quality Budget–Risk indicating negligible degradation across tested ranges. Validation against CodeCarbon, MLCO2, vendor telemetry recorded agreement within $1.8\%$, reinforcing confidence in the measurement pipeline. Cooling overhead remained implicit via PUE; inclusion of rack-level thermal telemetry should close that gap in subsequent phases. Policy takeaway reads succinctly: ingest marginal carbon intensity, enforce Quality Budget–Risk, operate sub-minute control loops, record every intervention for auditability. Practitioners can act immediately by ranking candidates via $\eta$, calibrating F/$CR$/population size, capping restart frequency, employing checkpoint intervals that track marginal intensity gradients. Schedulers benefit from latency-aware gates: throttle during high-intensity windows, release capacity when grid signal improves, maintain Quality Budget–Risk within predefined envelopes. Observed heterogeneity across institutions suggests configuration templates tied to hardware tiers, with per-tier defaults for swarm size, iteration ceilings, telemetry cadence. Results indicate that shorter, higher-watt runs may beat longer, moderate-watt runs on net emissions when convergence is rapid; integral energy determines climate cost, not peak draw alone. ChemFactor weighting proved useful for domain-specific contexts, enabling consistent comparison across heterogeneous task chemistries without re-instrumentation. The scatter structure in Figure 1 aligns with this conclusion, since clusters with moderate load coupled with healthy utilisation settled in low-CO₂ regions. Table 8 and Table 9 support the selection rule: choose methods with favourable $\eta$, then tune for minimal variance in power traces. Ablations showed that aggressive population growth inflates emissions disproportionately once memory traffic saturates caches; restraint at that frontier improves both stability, footprint. Restart-heavy strategies require soft cool-downs to curb transient spikes; our 3 s policy balanced device health against throughput. Measurement integrity benefited from Tukey trimming of outliers; yet the central tendency remained stable after re-inclusion during sensitivity checks. Limitations persist: mixed tenancy, partial cooling visibility, modest sample size for certain families; nonetheless, directional findings stayed consistent across sites. Future work should incorporate rack-aware thermal models, per-job PUE attribution, uncertainty-aware EIM forecasting, multi-objective scheduling that treats $\eta$, latency, fairness as co-equal signals. Community guidance emerges clearly: publish power traces, marginal intensity series, EIM parameters, Quality Budget–Risk thresholds, checkpoint policies, hardware descriptors. Operational guidance follows naturally: deploy carbon-aware scheduling as a default policy, prefer algorithms with strong $\eta$, fix guardrails before scale-up, monitor drift with automatic rollback hooks. Scientific guidance completes the triad: treat emissions as a first-class metric, formalise proofs for control-loop stability, report negative results, maintain open artefacts for replication. Overall, the evidence base demonstrates that carbon-aware swarm optimisation can deliver tangible footprint cuts while preserving solution quality within explicit risk budgets; careful telemetry, principled control, disciplined parameterisation make that outcome repeatable. In practice, success hinges on three levers—choice of heuristic with high $\eta$, schedule aligned to marginal intensity, instrumentation that converts signals into safe interventions—each lever summarised, each lever testable, each lever ready for adoption.