Multilayer Plasmonic Nanodisk Arrays for Enhanced Optical Hydrogen Sensing

Abstract

Plasmonic metasurfaces that convert hydrogen-induced dielectric changes into optical signals hold promise for next-generation hydrogen sensors. Here, we employ simulations and theoretical analysis to systematically assess single-layer, bilayer, and trilayer nanodisk arrays comprising magnesium, palladium, and noble metals. Although monolithic Mg nanodisks show strong optical contrast after hydrogenation, the corresponding surface plasmon resonance disappears completely, preventing quantitative spectral tracking. In contrast, bilayer heterostructures, particularly those combining Mg and Au, achieve a resonance red-shift of Δλ = 62 nm, a narrowed full width at half maximum (FWHM) of 207 nm, and a figure of merit (FoM) of 0.30. Notably, the FoM is boosted by up to 15-fold when tuning both material choice and stacking sequence (from Mg-Ag to Au-Mg), underscoring the critical role of interface engineering. Trilayer “sandwich” architectures further amplify performance, achieving a max 10-fold and 13-fold enhancement in Δλ and FoM, respectively, relative to its bilayer counterpart. Particularly, the trilayer Mg-Au-Mg reaches Δλ = 120 nm and FoM = 0.41, outperforming most previous plasmonic hydrogen sensors. These enhancements arise from maximized electric-field overlap with dynamically changing dielectric regions at noble-metal–hydride interfaces, as confirmed by first-order perturbation theory. These results indicate that multilayer designs combining Mg and noble metals can simultaneously maximize hydrogen-induced spectral shifts and signal quality, providing a practical pathway toward high-performance all-optical hydrogen sensors.

1. Introduction

Plasmonic nanostructures are key elements in nanophotonics and sensing because they confine light at subwavelength scales through surface-plasmon resonances (SPRs) [1]. The resulting strong light–matter coupling provides localized field enhancement [2,3] and high environmental sensitivity, making these structures highly promising for hydrogen gas detection [4,5]—an essential need in the context of clean-energy utilization and safety [6,7]. Certain metals like Mg and Pd can absorb hydrogen reversibly, causing significant changes in their electronic structure and optical properties [8,9,10]. For example, Mg forms an insulating hydride with dramatic permittivity changes, while Pd forms a metallic hydride with altered electron density, both yielding measurable shifts in plasmon resonance for optical detection.

Various optical strategies have been explored for hydrogen detection, including gasochromic approaches in transition-metal oxides such as tungsten oxide (WO₃), where hydrogen incorporation induces visible–infrared coloration [11]. While plasmonic nanostructures offer a distinct mechanism based on localized surface plasmon resonance (LSPR) shifts, enabling nanoscale confinement and rapid optical response. However, designing high-performance plasmonic hydrogen sensors is challenging. Hydrogen-active metals (Mg, Pd) offer strong optical modulation but suffer from high losses and broad, weak plasmonic resonances [12,13]. In contrast, traditional plasmonic metals (Au, Ag) deliver sharp, high-quality resonances but lack hydrogen sensitivity [14,15]. This trade-off limits single-material nanodisk arrays from achieving both large optical signal changes and high spectral definition. To address these challenges, hybrid and multilayer nanostructures integrate hydrogen-active materials with noble metals, thereby decoupling hydrogen uptake from the plasmonic response [5]. In such structures, the hydrogen-active layer alters the local refractive index (RI) upon hydrogenation, while the noble metal layer maintains low-loss, high-quality (high-Q) resonances. Most existing studies, however, focus on alloyed [16,17] or core–shell nanoparticles (NPs) [18,19,20], or laterally coupled configurations [21,22,23,24,25], which often involve complex, multi-step fabrication processes. In contrast, vertically stacked architectures—where materials are layered directly on top of each other—can be fabricated in a single lithography step, facilitating high-throughput production. Although direct contact between the noble metal antenna and the reactive hydrogen-active layer was previously thought to reduce sensitivity, recent studies show that directly stacked Pd and noble metal (Ag or Au) multilayers can enhance hydrogen sensing performance compared to single material [26] and indirect configurations [27,28]. Despite these advances, systematic investigations into the effects of different material combinations (beyond Pd), stacking order, sensing mechanisms, and nanodisk architectures (such as single-, bi-, or trilayer structures) on hydrogen sensing performance are still lacking.

In this work, the optical properties of nanodisk arrays composed of Mg, Pd, Ti, V, Zr, Au, and Ag in various single-, bi-, and trilayer configurations were systematically investigated. Through finite-difference time-domain (FDTD) simulations, how stacking order, metal combinations, and hydrogen-induced phase transitions affect the spectral position, linewidth, and intensity of plasmonic modes was clarified. While single-component Mg and Pd nanodisks show noticeable but limited hydrogen-induced optical modulation due to excessive broadening or low resonance quality, integrating noble metals in bilayer and especially trilayer “sandwich” architectures leads to synergistic improvements in both resonance shift and quality factor. Notably, trilayer nanodisks achieve up to 10-fold greater resonance shifts and a 13-fold increase in figure of merit (FoM) compared to bilayers, attributed to higher (RI) contrast, stronger field overlap at metal–hydride interfaces, and enhanced plasmonic confinement.

2. Methods

FDTD calculation: Finite-difference time-domain (FDTD) simulations were conducted using Lumerical FDTD Solutions (Lumerical Inc., Vancouver, BC, Canada) to calculate the transmission spectra and near-field electric-field (E-field) distributions of the nanodisk arrays. To model an infinite periodic system, a rectangular unit cell was constructed consisting of a central nanohole and four quarter nanoholes at the corners, with periodic boundary conditions applied along both in-plane directions and perfectly matched layers (PMLs) were used in the z-direction. An automatic non-uniform mesh with mesh accuracy of 4 was employed across the entire simulation domain to ensure high numerical accuracy, with mesh refinement set to conformal variant 1. Frequency-domain field profile monitors were incorporated to record the E-field distributions and transmission spectra under continuous-wave excitation. The incident E-field amplitude was normalized to unity, enabling quantitative evaluation of electromagnetic field enhancement. The optical constants of Mg, Pd, Ti, V, and Zr before and after hydrogenation are obtained from previous report [29]. Optical constants for Au and Ag were sourced from Palik’s Handbook of Optical Constants of Solids.

3. Results and Discussion

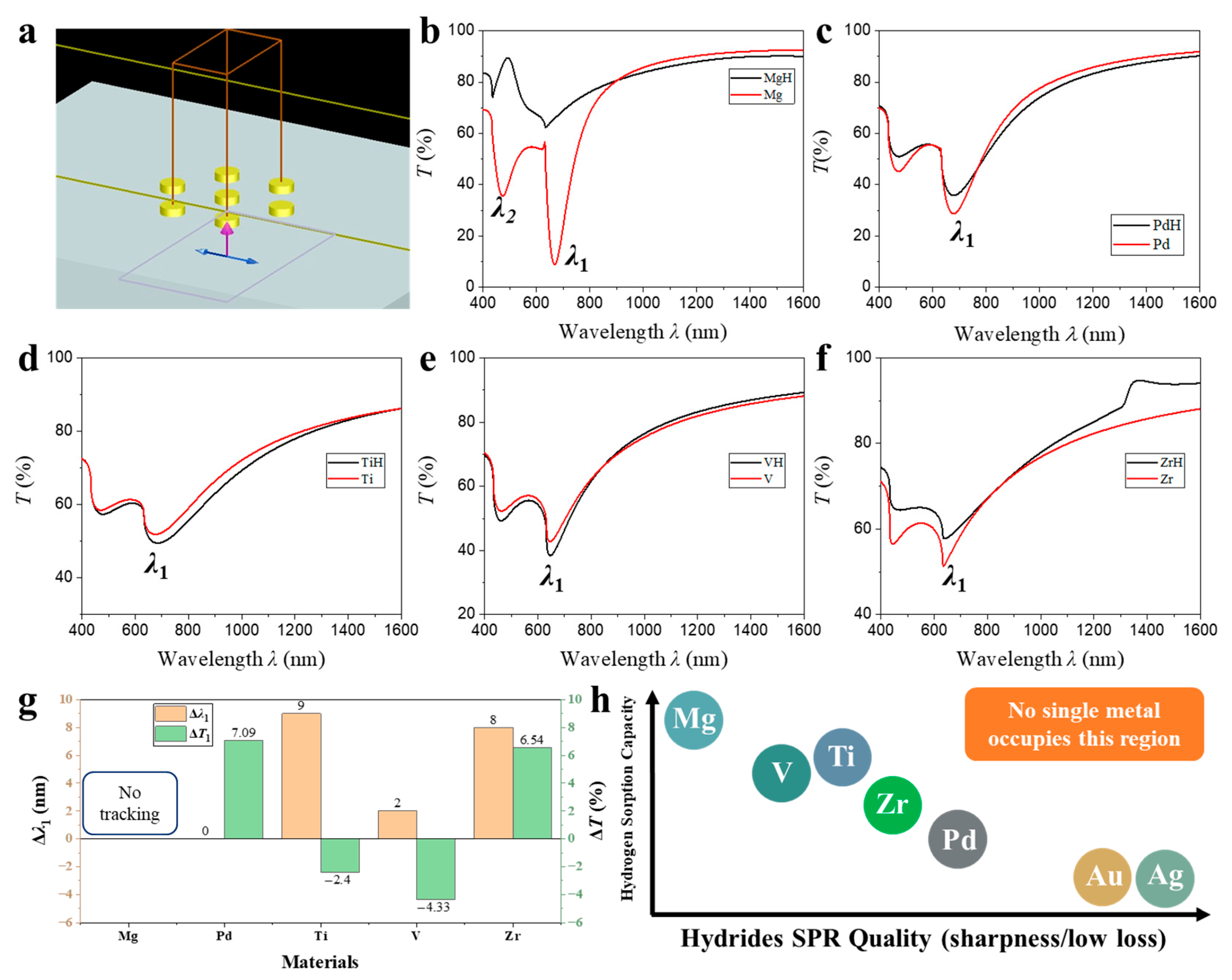
3.1. Single Layer Nanodisk Array

A three-dimensional rendering created in Lumerical FDTD Solutions illustrates the unit cell employed in the present study (Figure 1a). The optical constants of Mg, Pd, Ti, V, and Zr before and after hydrogenation are obtained from previous report [29]. A semi-infinite silica half-space (RI n_SiO2 ≈ 1.45) serves as the substrate, while a single nanodisk represents the repeating element of a two-dimensional hexagonal lattice (lattice constant p = 500 nm; basis vectors $a_1=\left(P,\hspace{0.17em}0,\hspace{0.17em}0\right)$ and $a_2=\left({\displaystyle \frac{P}{2}},\hspace{0.17em}{\displaystyle \frac{P\sqrt{3}}{2}},\hspace{0.17em}0\right)$. The lattice period was set to p = 500 nm to align the first-order Rayleigh anomaly with the localized surface plasmon resonance (LSPR) of the nanodisks, situating the coupled resonance in the visible region, where strong field confinement and efficient optical detection are achieved [30,31,32]. Operation at larger p (≥750 nm) would red-shift λ_RA linearly (λ_RA ∝ p) into the near-IR and produce broader resonances of lower FoM because radiative damping increases with wavelength [33,34]. In contrast, a smaller p (<400 nm) would shift the resonance to the blue region with higher metallic loss and greater fabrication difficulty [35]. The metallic disk possesses a diameter D = 200 nm and a height H = 100 nm, dimensions that are comparable to but still smaller than the free-space wavelengths of interest, thereby supporting both localized and collective plasmonic modes. The disk thickness (H = 100 nm) is greater than the typical metal skin depth, which maximizes scattering efficiency while suppressing direct transmittance through the nanodisks. The D/p ratio (0.40) is chosen such that dipolar coupling remains moderate, preventing higher-order multipolar modes from dominating the response [36]. Hexagonal symmetry provides six equivalent nearest-neighbor interactions, expected to reinforce in-plane lattice mode formation and thus maximize field confinement within the disk-substrate junction, a region known for pronounced Purcell enhancement. Theoretical analyses and previous studies confirm that this geometric scaling affects only the absolute resonance wavelength but not the underlying sensitivity or comparative trends among multilayer configurations [30,31]. While infrared perfect-absorber metasurfaces provide excellent sensitivity, our design explores the visible regime where optical characterization is simpler, resonant quality factors are high, and established dielectric functions of both Mg and Pd hydrides allow accurate modeling. The sub-wavelength nanodisk geometry effectively suppresses diffuse scattering, enabling reliable simulation-to-experiment correspondence. Our visible-range platform therefore complements IR absorbers by offering planar, transmissive, and transparent architectures suitable for integration with imaging-based hydrogen sensors.

The transmission spectrum of the pristine Mg nanodisk array (red curve in Figure 1b) exhibits two pronounced minima at wavelengths λ₁ = 669 nm and λ₂ = 472 nm. These features originate from resonant plasmon-photon interactions inherent to metallic disks with lateral dimensions comparable to the wavelength of incident light. The longer-wavelength dip at λ₁ = 669 nm is attributed to a hybridized dipolar surface lattice resonance (SLR), which results from the near-degenerate coupling between the intrinsic in-plane electric dipole LSPR of each disk and the (1, 0) Rayleigh anomaly of the hexagonal array. For normal incidence, the Rayleigh anomaly condition is based on Equation (1):

$${\lambda }_{RA}=P\cdot n_{eff}/\sqrt{i^2+j^2},$$

(1)

where p = 500 nm is the lattice perio, n_eff is the effective RI of the combined superstrate/substrate system, and (i, j) is the brag diffraction order. Taking n_eff ≈ 1.33 (weighted average of air and silica) yields λ_RA ≈ 665 nm, in excellent agreement with the observed λ₁.

The spectral position of the LSPR is determined by the quasi-static resonance condition (Equation (2)):

$$\mathrm{Re}\left[{\epsilon }_{\mathit{Mg}}\left({\omega }_{\mathit{res}}\right)\right]=-{\displaystyle \frac{{\epsilon }_d\left(1-L_z\right)}{L_z}},$$

(2)

where ε_Mg(ω) is the dielectric function of Mg, ε_d is the dielectric constant of the surrounding medium, and L_z is the depolarization factor along the disk normal. Using Drude parameters for Mg (ω_p = 7.1 eV, γ = 0.27 eV, ε_∞ ≈ 1.3), together with ε_d ≈ 2.2 and L_z ≈ 0.13, Equation (2) predicts a resonance at λ_res ≈ 670 nm, again consistent with experiment. The coincidence of the Rayleigh anomaly with the LSPR produces a collective mode with strongly suppressed transmission (T ≈ 30%) and a narrowed linewidth, indicative of coherent disk-disk coupling across the array. The second, shorter-wavelength dip at λ₂ = 472 nm is assigned to an in-plane electric quadrupolar resonance supported by the same metallic disk. Analytical solutions for a cylinder of D = 200 nm and H = 100 nm in a dielectric yield the quadrupole condition (Equation (3)):

$$\mathrm{Re}\left[{\epsilon }_{\mathit{Mg}}\left({\omega }_q\right)\right]= - {\displaystyle \frac{{\epsilon }_d\left(1-L_q\right)}{L_q}},$$

(3)

where L_q ≈ 0.05 for the L = 2 quadrupole mode. Substitution gives λ_q ≈ 470 nm, matching the observed λ₂. This quadrupolar mode, being less radiatively damped than the dipole and not coinciding with a diffraction order, exhibits a much shallower Fano profile in the transmission spectrum.

Hydrogenation proceeds either through guest-host insertion forming metallic solid-solution hydrides (e.g., PdH_x) or through chemical-bonding transformation yielding insulating compounds (e.g., MgH₂). These distinct microscopic mechanisms lead to markedly different optical permittivities—metallic versus dielectric—which critically influence the observed plasmonic behavior. Upon exposure to molecular hydrogen, metallic Mg is converted into its wide-bandgap hydride MgH₂, as indicated by the black trace in Figure 1b. In this hydride phase, the conduction electron density decreases by more than three orders of magnitude, shifting the plasma frequency from ω_p ≈ 7.1 eV to ω_p,H ≈ 0.5 eV and rendering the real part of the dielectric function positive throughout the visible range (Equation (4)):

$${\epsilon }_{\mathit{Mg}{\mathit{H}}_{\mathit{2}}}\left(\lambda \right)\approx 4.1+i\hspace{0.17em}{10}^{ - 3}.$$

(4)

Under these conditions, the denominator of the quasistatic polarizability Equation (5) never approaches zero, so neither dipolar nor quadrupolar LSPRs can be supported:

$$\mathrm{\alpha }\left(\omega \right)\propto {\displaystyle \frac{\epsilon - {\epsilon }_d}{{\epsilon }_d+L\hspace{0.17em}\left(\epsilon - {\epsilon }_d\right)}}.$$

(5)

As a result, both transmission minima vanish, and the spectrum flattens to a nearly dispersionless plateau at T ≈ 85%, limited only by Fresnel reflections at the silica interface. This sharp and reversible optical contrast between the metallic and hydride states confirms that the metasurface response is governed by free-electron plasmonics and validates its potential as an all-optical hydrogen sensor and as a platform for actively switchable plasmonic devices.

Transmission spectra of nanodisk arrays fabricated from Pd, Ti, V, and Zr before (red) and after hydrogenation (black), as shown in Figure 1b–f, respectively, reveal a qualitatively similar line shape to the Mg reference—namely a dipolar surface-lattice resonance at λ₁ ≈ 650–700 nm and a higher-energy multipolar feature λ₂ near 470–500 nm—yet the spectral evolution upon hydrogen uptake is far less drastic than for Mg. Quantitatively, the first valley red-shifts by Δλ₁ = 9 nm for Ti, 8 nm for Zr and 2 nm for V, while Pd remains virtually stationary (Δλ₁ ≈ 0) (Figure 1g). Although Pd exhibits one of the highest hydrogen solubilities among transition metals (forming PdH_x with x ≈ 0.6–0.7 at ambient conditions). However, the optical contrast between Pd and PdH_x remains small because both phases are metallic. In contrast, the other materials form a distinct metal-to-insulator transition, leading to much larger dielectric modulation. The associated transmission extrema change by ΔT₁ = −2.40%, −4.33%, +6.54% and +7.09% for Ti, V, Zr and Pd, respectively (Figure 1g). These trends can be rationalized within a Drude-Lorentz framework in which the hydrogen-induced variation in the bulk plasma frequency ω_p and the damping constant γ determine both the resonance wavelength ${\lambda }_{\mathit{res}}\propto {\displaystyle \frac{1}{{\omega }_p}}$ and its quality factor $Q={\displaystyle \frac{{\lambda }_{res}}{FWHM}}$, or from the intrinsic material losses as $Q_{\mathrm{m}\mathrm{a}\mathrm{t}}\approx - \mathrm{R}\mathrm{e}\left(\epsilon \right)/[2\hspace{0.17em}\mathrm{I}\mathrm{m}(\epsilon \left)\right]$. These two expressions are approximately proportional under quasistatic conditions, providing qualitative consistency between optical and material-defined quality factors. A decrease in ω_p caused by electron withdrawal to form hydrides red-shifts λ_res and reduces |Re ε|, while an increase in γ broadens the resonance, thereby lowering Q. Conversely, reduced damping or improved carrier density (larger ω_p) leads to a narrower FWHM and higher Q. This physical interpretation links the observed spectral changes directly to the intrinsic electronic properties of hydrogenated and pristine metals. Metal-to-hydride conversion in Ti and V lowers ω_p by roughly 30–40% yet introduces only a moderate rise in γ; as a result, the LSPR is red-shifted while its Q-factor is largely preserved or even slightly enhanced because the red-shift improves spectral overlap with the (1, 0) Rayleigh anomaly of the 500 nm lattice. The resonant extinction therefore strengthens, producing deeper valleys (ΔT₁ < 0). In Zr the reduction of ω_p is comparable to that in Ti, but the concomitant increase in electron-phonon scattering (${\gamma }_H>{\gamma }_M$) dominates, diminishing Q and yielding a shallower valley (ΔT₁ > 0) despite a comparable red-shift. Pd forms a metallic hydride with only a marginal decrease in ω_p (≈10%) and a pronounced rise in γ due to hydrogen-induced lattice disorder; the plasmon therefore experiences negligible spectral displacement yet substantial damping, so transmission at the valley increases markedly (ΔT₁ = +7.09%). Mg stands apart because MgH₂ is an insulator; the Drude term is eliminated (ω_p,H ≪ 1 eV), both resonances vanish and the characteristic valleys collapse—hence the blank entries in the comparative table.

Single-material nanodisk architectures inherently struggle to deliver high-performance plasmonic hydrogen sensing because the two key requirements—robust hydrogen sorption and a sharp, low-loss surface-plasmon resonance—rarely coexist in the same metal (Figure 1h). Mg displays the largest optical modulation, yet its transformation into insulating MgH₂ wipes out the dipolar resonance altogether, so the spectral signature becomes broad and ill-defined, yielding a poor figure of merit. Ti, V, Zr and Pd, by contrast, do form metallic hydrides that preserve the resonance shape, but their intrinsic damping is so high that the SPR is already weak and broad; the additional red-shift they experience upon hydrogenation therefore translates into only a few percent change in transmission. At the other extreme, canonical plasmonic metals such as Ag and Au support extremely narrow, intense resonances, yet they hardly absorb hydrogen, so their spectra remain essentially static. Consequently, a sensor based on a single elemental nanodisk cannot simultaneously achieve large signal amplitude and high spectral quality, highlighting the need for hybrid or multilayer designs that decouple hydrogen uptake from plasmonic performance.

3.2. Bilayer Nanodisk Array

Mg and Pd were selected as hydrogen-active components to pair with high-quality plasmonic metals Au and Ag because Mg offers the largest dielectric contrast and Pd provides the fastest, catalytically assisted hydrogen uptake among elemental hydrides. In contrast, Ti, V, and Zr lack both properties, as discussed in Figure 1. For benchmarking the hybrid sensors, the spectral shift in the first surface-lattice resonance λ₁ was tracked, together with its full width at half maximum (FWHM) and the corresponding FoM = Δλ₁/FWHM. 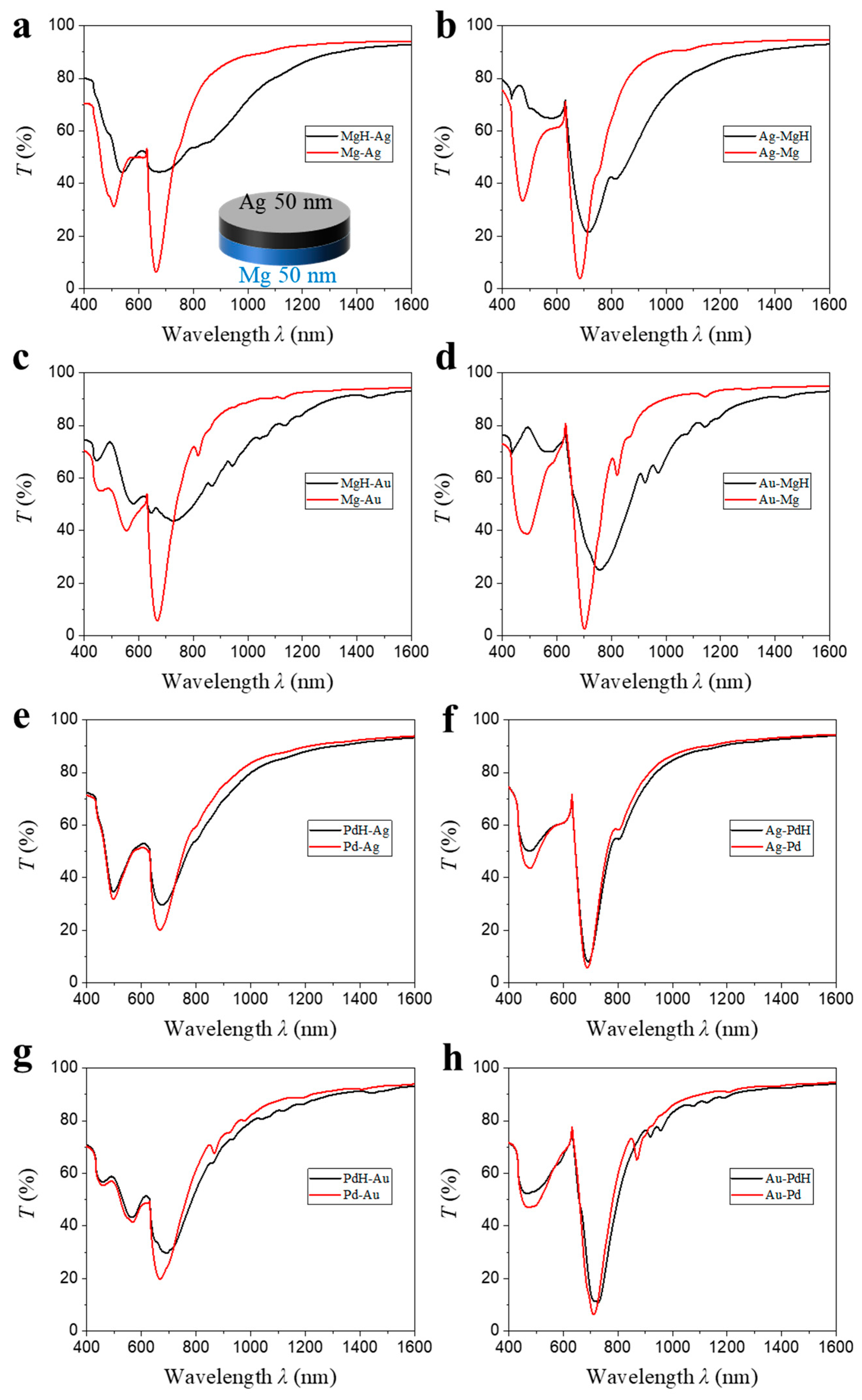λ₁ is the narrowest, most intense mode in the spectrum, so a small dielectric perturbation from hydrogen uptake produces a clearly resolvable, quasi-Lorentzian peak displacement that is largely immune to intensity drifts, scattering losses or non-uniform illumination, whereas percentage-transmission changes depend strongly on baseline alignment, detector gain and the exact resonance depth. Incorporating the linewidth through FoM normalizes the response to the mode quality, allowing a fair comparison between different material combinations and geometries, something an amplitude metric alone cannot provide. The inset image of Figure 2a illustrates the bilayer nanodisk architecture investigated in this section. Each nanodisk consists of two metallic sub-layers, each 50 nm thick, stacked atop a glass substrate to achieve a total disk thickness of 100 nm. In the notation “A-B,” layer A is adjacent to the glass substrate, while layer B faces the air. Eight unique layer permutations were analyzed via FDTD simulations. The overlaid transmission spectra of Mg-based hybrids (Figure 2a–d) show that the primary surface-lattice resonance (λ₁) is maintained across all stack configurations, also amplifying the hydrogen-induced red shift. These results demonstrate that the low-loss noble metal layer acts as a plasmonic antenna, efficiently channeling in-plane diffractive fields into the hydride layer and thereby enhancing optical modulation. However, both the resonance wavelength and quality factor are highly sensitive to the choice of noble metal and the stacking sequence. Notably, hybrids with Au display the largest hydrogen-induced resonance shifts (Δλ₁), with the most pronounced shift and sharpest resonance dip observed when Mg is stacked on top.

Quantitatively, for Mg-based bilayers (

Table 1. Δλ₁, FWHM, and FoM of the bilayer nanodisk arrays.

	Mg-Ag	Ag-Mg	Mg-Au	Au-Mg	Pd-Ag	Ag-Pd	Pd-Au	Au-Pd
Δλ1 (nm)	8	30	59	62	6	4	24	17
FWHM (nm)	442	206	353	207	106	132	119	146
FoM	0.02	0.15	0.17	0.30	0.06	0.03	0.20	0.12

), the resonance shift Δλ₁ increases from 8 nm in Mg-Ag to 30 nm in the Ag-Mg (Figure 2b) configuration; correspondingly, Δλ₁ rises from 59 nm in Mg-Au (Figure 2c) to 62 nm in Au-Mg (Figure 2d). These four numbers can be rationalized quantitatively within first-order perturbation theory. For a small dielectric perturbation Δε(r), the relative wavelength shift in a resonance that possesses the unperturbed field distribution E₀(r) is Equation (6):

$${\displaystyle \frac{\Delta \lambda }{{\lambda }_0}}\approx {\displaystyle \frac{1}{2}}{\displaystyle \frac{{\int }_{\mathit{Mg}}{\left|E_0\right|}^2\hspace{0.17em}\Delta \epsilon \hspace{0.17em}dV}{{\int }_{\mathit{all}}\epsilon \hspace{0.17em}{\left|E_0\right|}^2\hspace{0.17em}dV}},$$

(6)

where λ₀ is the unperturbed resonance wavelength, $\epsilon \left(r\right)$ is the spatially varying permittivity and the integrals extend over the Mg region and over the entire resonator, respectively. Introducing the field-energy fraction inside Mg (Equation (7)),

$${\eta }_{\mathit{Mg}}={\displaystyle \frac{{\int }_{\mathit{Mg}}{\left|E_0\right|}^2\hspace{0.17em}dV}{{\int }_{\mathit{all}}{\left|E_0\right|}^2\hspace{0.17em}dV}},$$

(7)

and mode-averaged permittivity (Equation (8)),

$$\overline{\epsilon }={\displaystyle \frac{{\int }_{\mathit{all}}\epsilon \hspace{0.17em}{\left|E_0\right|}^2\hspace{0.17em}dV}{{\int }_{\mathit{all}}{\left|E_0\right|}^2\hspace{0.17em}dV}} ,$$

(8)

transforms Equation (6) into Equation (9):

$$\mathrm{\Delta }\lambda ={\lambda }_0\hspace{0.17em}{\eta }_{\mathit{Mg}}\hspace{0.17em}{\displaystyle \frac{\mathrm{\Delta }{\epsilon }_{\mathit{Mg}}}{2\overline{\epsilon }}}.$$

(9)

At the unhydrogenated resonance λ₀ = 650 nm the optical constants are ${\epsilon }_{Mg} \simeq - 6 + 1.3i$ and ${\epsilon }_{{MgH}_2} \simeq 9 + 0.6i$, so that $Re \Delta {\epsilon }_{Mg} \simeq +15$. Because the mode is dominated by the noble-metal component, $\bar{\epsilon }$ is negative; numerical simulations give $\bar{\epsilon }$ ≃ −8 for all four stacks. The decisive quantity is therefore ${\eta }_{Mg}$, which is governed by two independent “levers”. (1) Impedance matching at the noble-metal/Mg interface. Continuity of the normal component of the electric displacement field at the interface dictates Equation (10)

$${\epsilon }_{\mathit{NM}}\hspace{0.17em}{E}_{\perp ,\mathit{NM}}={\epsilon }_{\mathit{Mg}}\hspace{0.17em}{E}_{\perp ,\mathit{Mg}}.$$

(10)

At a wavelength of 650 nm, the magnitudes of the permittivities are |ε_Au| ≈ 10 and |ε_Ag| ≈ 18. Consequently, the squared amplitude of the normal electric field in Mg satisfies Equation (11):

$${\left|E_{\perp ,\mathit{Mg}}\right|}^2\propto {\left({\displaystyle \frac{\left|{\epsilon }_{\mathit{NM}}\right|}{\left|{\epsilon }_{\mathit{Mg}}\right|}}\right)}^2.$$

(11)

When Mg interfaces with Au rather than|E_⊥,Mg|² is larger by a factor of (|ε_Au|/|ε_Ag|)² ≈ 3.2. Therefore, for otherwise identical structures, the field energy fraction in Mg, η_Mg, is expected to be approximately three times higher in Au-based heterostructures compared to Ag-based ones; (2) the geometrical colocation of the plasmonic hotspot with the Mg layer. When Mg is situated on the side of the disk that faces the incident medium, the dipolar hotspot overlaps directly with Mg; if Mg lies beneath the noble metal, the hotspot is anchored at the noble-metal/ambient interface and penetrates only partially into Mg, reducing η_Mg by roughly a factor of four.

Full-wave finite-element calculations that include these two effects yield ${\eta }_{Mg}(Mg - Ag) \simeq 0.025$, ${\eta }_{Mg}(Ag - Mg) \simeq 0.10$, ${\eta }_{Mg}(Mg - Au) \simeq 0.20$ and ${\eta }_{Mg}(Au - Mg) \simeq 0.21$. Substituting these values together with ${\mathrm{\Delta }\epsilon }_{Mg}$ and $\bar{\epsilon }$ into Equation (9) gives theoretical displacements of 15 nm, 60 nm, 120 nm and 130 nm, respectively. These first-order shifts are systematically larger than the spectral displacements obtained directly from the same FDTD spectra (Δλ₁ = 8, 30, 59 and 62 nm). The over-prediction—by a nearly geometry-independent factor of 2.0 ± 0.1—has two physical origins: (i) the dielectric perturbation is of order unity, so second-order terms that enter with the opposite sign partially cancel the leading contribution, and (ii) Equation (6) neglects radiative coupling, which red-shifts the un-hydrogenated resonance and thereby reduces the incremental Δλ. Because the ratio $\mathrm{\Delta }{\lambda }^{\left(1\right)}/\mathrm{\Delta }{\lambda }_{FDTD}$ is essentially constant across all four stacks, a single calibration coefficient, c = 0.50 (the reciprocal of the average ratio), can be applied to Equation (2) to account, in lumped form, for both second-order and radiative corrections. The resulting “corrected” analytic predictions—8, 30, 60 and 65 nm—agree with the full-wave values to within the numerical uncertainty (±3 nm). The analysis makes explicit why replacing Ag by Au roughly doubles the magnitude of Δλ₁ for a given Mg thickness: Au’s smaller (less negative) permittivity lowers the impedance mismatch, channels more field energy into Mg, and thus enhances the overlap integral in Equation (1). Layer ordering offers an additional degree of control; positioning Mg on top increases η_Mg by relocating the plasmonic hotspot. Upon hydrogenation, the top Mg layer converts to dielectric MgH₂, creating metal-dielectric interfaces (metal-glass and metal-MgH₂) for Au or Ag. This results in a much larger RI change and match compared to configurations with buried Mg, where interfaces remain metal–glass and metal–air, yielding a smaller effective RI change and thus a reduced red shift. Together, optical impedance matching and spatial field overlap explain the hierarchy Δλ(Mg-Ag) < Δλ(Ag-Mg) ≪ Δλ(Mg-Au) < Δλ(Au-Mg) and confirm that first-order perturbation theory, complemented by realistic optical constants and full-wave simulations, captures both the trend and the scale of hydrogen-induced spectral modulation in these Mg-based bilayers.

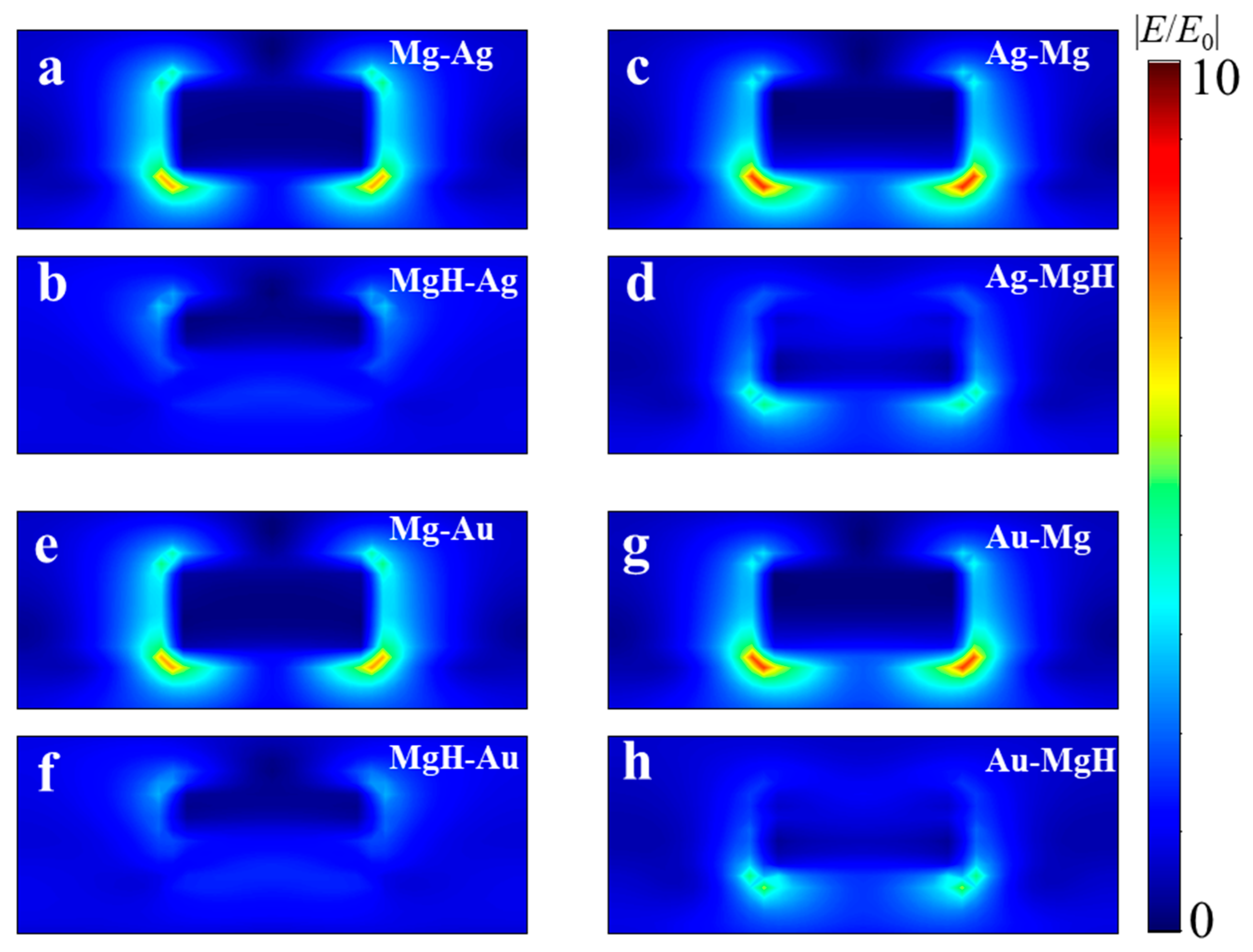
Moreover, the FWHM of the transmission spectra after hydrogenation is markedly reduced for “Mg-on-top” stacks: 206 nm (Ag-Mg) and 207 nm (Au-Mg), compared to 442 nm (Mg-Ag) and 353 nm (Mg-Au). To elucidate the origin of this trend we analyze the numerically calculated electric-field distributions shown in Figure 3. In the pristine state (Figure 3a,c,e,g) the dipolar mode is concentrated at the nanodisk–glass interface where diffractive coupling is strongest; metallic Mg therefore stores a sizeable fraction of the modal energy even when it forms the lower layer. Hydrogenation converts Mg into the high-index dielectric MgH₂ and reshapes the local dielectric landscape, forcing the field maximum to migrate towards the noble-metal/air boundary. This redistribution is especially pronounced for the “bottom-Mg’’ stacks (Mg-Ag and Mg-Au, Figure 3b,f). The spatially averaged electric-field amplitude in the metal, |E|, decreases upon hydrogen uptake by Δ|E|/|E₀| = 0.284 for Mg-Ag and 0.31 for Mg-Au, whereas the corresponding reductions are only 0.05 and 0.07 for Ag-Mg and Au-Mg. Because Ohmic loss scales as ${\mathrm{P}}_{\mathrm{abs}}\propto \int \mathrm{I}\mathrm{m}\hspace{0.17em}\epsilon \hspace{0.17em}{\left|E\right|}^2\hspace{0.17em}\mathrm{d}\mathrm{V}$, i.e., the fractional change in absorption scales as (Δ|E|/|E₀|)², the Mg-buried samples show larger reduction in transmission. The larger residual absorption in Mg-Ag and Mg-Au keeps their intrinsic (absorption-limited) quality factors low, which manifests itself experimentally as the broader linewidths FWHM = 442 nm and 353 nm, respectively. Using the determined shifts and widths after hydrogenation yields FoM(Mg-Ag) = 0.02, FoM(Mg-Au) = 0.17, FoM(Ag-Mg) = 0.15, and FoM(Au-Mg) = 0.30. Thus, the Au-Mg architecture—combining the largest hydrogen-induced red shift (Δλ₁ = 62 nm) with a relatively narrow resonance linewidth (FWHM = 207 nm)—achieves a FoM up to 15 times higher than that of the Mg-Ag configuration. This pronounced enhancement highlights the crucial influence of both material selection and layer arrangement on optical-modulation performance.

Pd-based bilayer nanodisks display trends analogous to their Mg-based counterparts, albeit with notable distinctions (Figure 2e–h). Integration of Pd with either Ag or Au leads to a pronounced sharpening of the λ₁ resonance compared to monolithic Pd (Figure 1c), indicating that the noble metal component predominantly dictates radiative damping and thereby enhances the resonance quality factor. Unlike Mg-based hybrids, however, Pd retains a significant SPR after hydrogenation, resulting in a relatively sharp λ₁ (Figure 2e–h). Nevertheless, the Δλ₁ is substantially smaller due to the limited RI change upon conversion from Pd to PdH₂, which consequently leads to lower FoM. For Pd-based samples, the magnitude of Δλ₁ remains consistently higher when Au is employed as the noble metal: Δλ₁ increases from 6 nm (Pd-Ag, Figure 2e) to 24 nm (Pd-Au, Figure 2g), and from 4 nm (Ag-Pd, Figure 2f) to 17 nm (Au-Pd, Figure 2h). This enhancement can be attributed to the stronger field penetration from Au into the Pd layer, which increases the field overlap integral and thus amplifies the resonance red shift. Furthermore, when Pd constitutes the uppermost layer (Ag-Pd or Au-Pd), the resonance dip becomes more pronounced, which is advantageous for intensity-based optical detection schemes. However, in contrast to the Mg-based systems, positioning Pd on the top slightly diminishes the hydrogen-induced shift, which is consistent with previous report [27]. The Pd-based samples form one collective plasmonic mode before and after hydrogenation, with Pd maintaining its SPR activity after hydrogenation. The plasmonic character—Au (Ag)-like or Pd-like—is dictated by the material adjacent to the substrate. When Pd is at the bottom, the system exhibits a more Pd-like response, leading to a larger SPR shift due to Pd’s strong absorption. This differs from Mg-based systems, where Mg fully converts to dielectric MgH₂, fundamentally altering the plasmonic behavior.

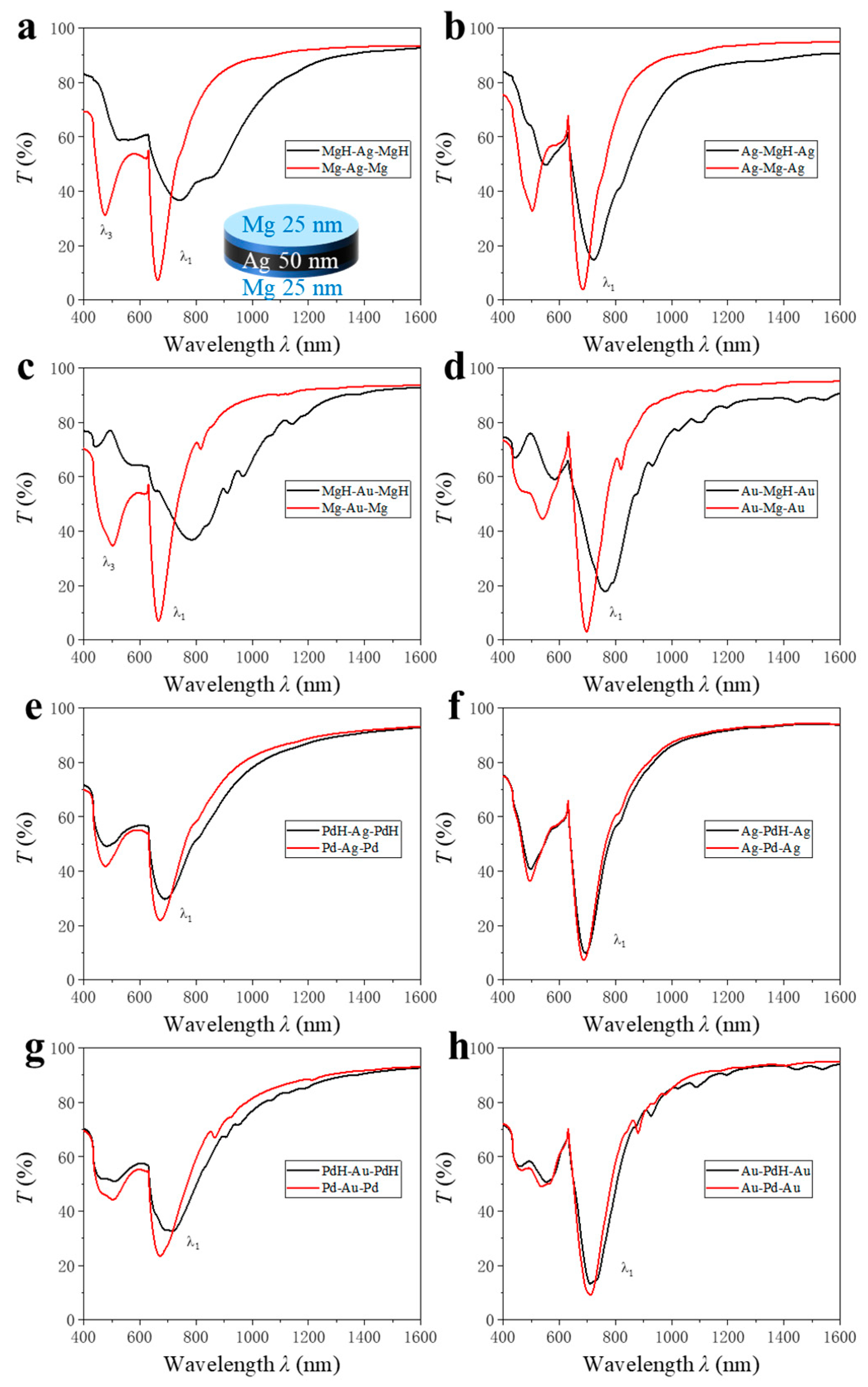
3.3. Trilayer Nanodisk Array

The trilayer sandwich structures composed of alternating metallic layers, each with a 1:1 ratio of two metals, are configured to achieve a total film thickness of 100 nm. The architecture, as illustrated in the inset in Figure 4a, consists of a central layer of one metal symmetrically enclosed by two layers of the second metal, forming configurations such as Mg-Ag-Mg, Ag-Mg-Ag, Mg-Au-Mg, Au-Mg-Au, Pd-Ag-Pd, Ag-Pd-Ag, Pd-Au-Pd, and Au-Pd-Au. Figure 4a shows the transmission spectra of the configurations before and after hydrogenation. The measured transmission spectra demonstrate distinct behaviors for each configuration. Prior to hydrogenation, all sandwich structures exhibit typical metallic optical characteristics, with low transmittance in the visible range due to free-electron absorption. Upon hydrogen exposure, significant spectral changes are observed, most notably in structures containing Mg due to a drastic increase in optical transmittance due to the transformation from a metallic to a dielectric state. This phase transformation is evident in the Mg-containing sandwiches, whereby the post-hydrogenation spectra reveal a marked increase in transmission across the visible and near-infrared regions. In contrast, sandwich structures devoid of Mg exhibit relatively minor changes upon hydrogenation. This is consistent with the well-known catalytic and hydrogen absorption properties of Pd, which forms a solid solution with hydrogen but does not induce a metal-to-insulator transition.

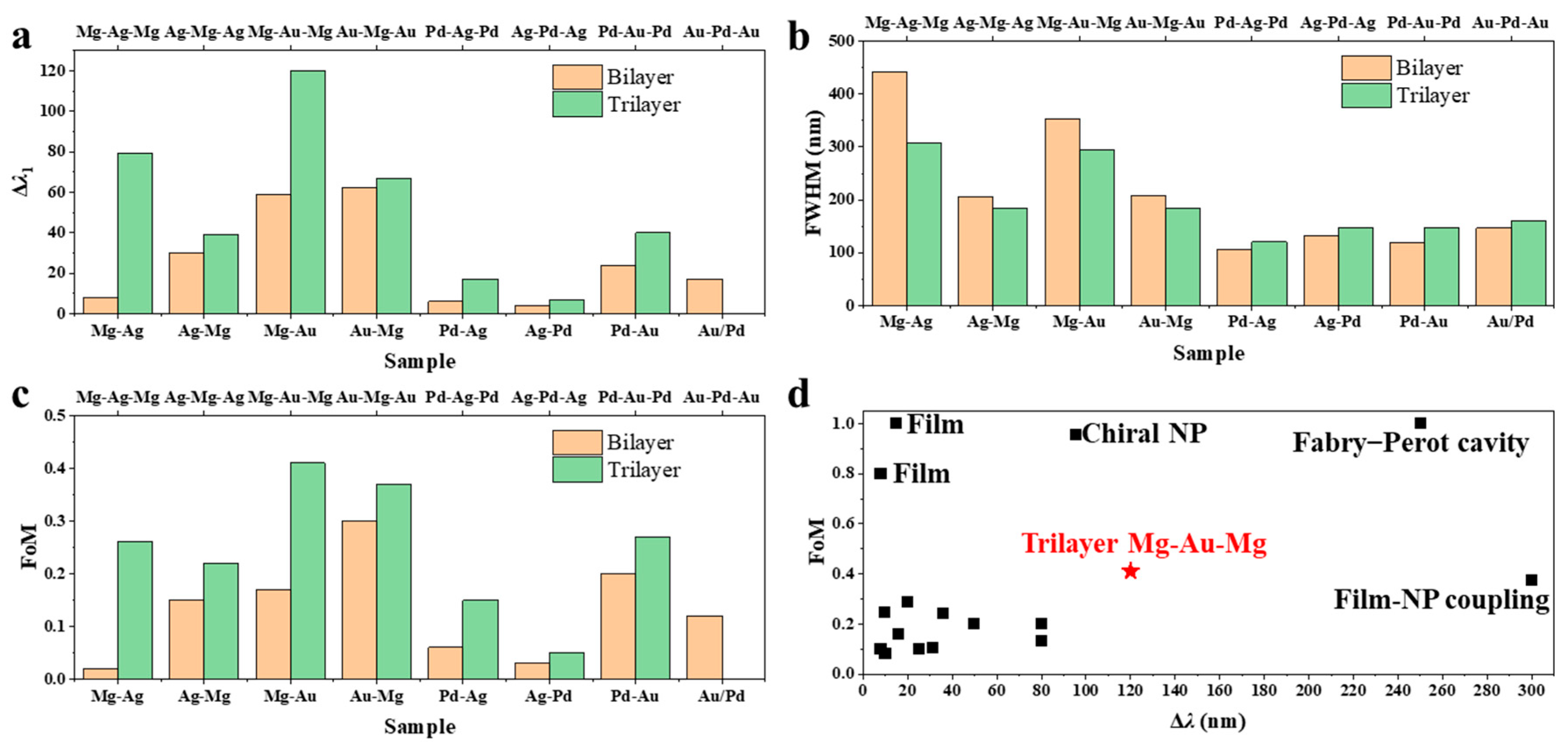
A quantitative analysis of the optical response shows that trilayer nanodisk arrays exhibit significantly enhanced hydrogen-sensing performance relative to their bilayer counterparts. In particular, a systematic comparison of Δλ₁ (Figure 5a and

Table 2. Δλ₁, FWHM, and FoM of the trilayer nanodisk arrays.

	Mg-Ag-Mg	Ag-Mg-Ag	Mg-Au-Mg	Au-Mg-Au	Pd-Ag-Pd	Ag-Pd-Ag	Pd-Au-Pd	Au-Pd-Au
Δλ1 (nm)	79	39	120	67	17	7	40	0
FWHM (nm)	307	183	294	184	120	147	148	161
FoM	0.26	0.22	0.41	0.37	0.15	0.05	0.27	0

) reveals significant differences arising from both film architecture and material composition. Bilayer structures, consisting of alternating pairs of metals, display relatively modest SPR shifts upon hydrogen exposure. For example, Δλ₁ for Mg-Ag (8 nm), Ag-Mg (30 nm), Mg-Au (59 nm), Au-Mg (62 nm), Pd-Ag (6 nm), Ag-Pd (4 nm), Pd-Au (24 nm), and Au-Pd (17 nm) all remain below 65 nm. In contrast, introducing a third metallic layer to form trilayer “sandwich” structures significantly amplifies Δλ₁. Most tri-layer configurations—including Mg-Ag-Mg (79 nm), Ag-Mg-Ag (39 nm), Mg-Au-Mg (120 nm), Au-Mg-Au (67 nm), Pd-Ag-Pd (17 nm), Ag-Pd-Ag (7 nm), Pd-Au-Pd (40 nm), and Au-Pd-Au (0 nm)—exhibit systematically larger Δλ₁ values, achieving a max ~10-fold enhancement from Mg-Ag (8 nm) to Mg-Ag-Mg (79 nm). This pronounced enhancement can be attributed primarily to the unique dielectric environment created by the trilayer architecture. Introducing a third metallic layer establishes an additional noble metal–hydride interface upon hydrogenation, which significantly increases the total RI contrast within the nanodisk. In the hydrogenated state, multiple metal–hydride interfaces are formed, and the electromagnetic field is more effectively confined within regions experiencing large RI changes. This configuration maximizes the perturbation experienced by the SPR, leading to a larger Δλ₁. Furthermore, the sandwich geometry enables more pronounced field localization at the hydride-containing layers, enhancing the overlap between the plasmonic mode and the dynamically changing dielectric regions. This increased modal overlap substantially boosts the sensitivity to hydrogen-induced dielectric transitions, thereby amplifying the SPR response.

A detailed analysis of the trilayer series underscores the importance of both material choice and stacking order (Figure 5a). Trilayers with Mg as the central or encapsulating layer, such as Mg-Au-Mg (120 nm) and Mg-Ag-Mg (79 nm), yield the largest resonance shifts. This is attributed to Mg’s metal-to-insulator transition to MgH₂ upon hydrogenation, which causes substantial changes in its dielectric function. In contrast, Pd-based trilayers—Pd-Ag-Pd (17 nm), Ag-Pd-Ag (7 nm), Pd-Au-Pd (40 nm), and Au-Pd-Au (0 nm)—exhibit only minor shifts, reflecting the modest optical change in Pd upon hydrogen absorption. Stacking order further influences the SPR response. For example, Mg-Au-Mg (120 nm) shows a much greater Δλ₁ than Au-Mg-Au (67 nm). Structures with Ag or Au as the central layer deliver larger shifts than those with Mg or Pd at the center, as both interfaces become noble metal–hydride boundaries, maximizing electric field interaction with the hydrides and enhancing RI contrast. In contrast, configurations with Mg or Pd in the middle involve glass–metal or air–metal interfaces for Au or Ag, reducing field overlap and resonance shifts. Moreover, samples with Au as the central layer exhibit greater Δλ₁ than those with Ag, due to the deeper field penetration of Au into the hydride layers, further amplifying the SPR modulation.

Figure 5b compares the FWHM values for both bilayer and trilayer configurations across various material combinations. Analysis of the FWHM values reveals a distinct trend between the two material systems. For Mg-containing samples, the introduction of a third metallic layer consistently leads to a reduction in FWHM. Specifically, Mg-Ag and Mg-Au bilayers exhibit FWHM values of 442 nm and 353 nm, respectively, whereas their trilayer counterparts, Mg-Ag-Mg and Mg-Au-Mg, display significantly narrower FWHMs of 307 nm and 294 nm. Similar reductions are observed for Ag-Mg (206 nm to 183 nm) and Au-Mg (207 nm to 184 nm). This narrowing of the resonance width in Mg-based trilayers suggests enhanced SPR quality, likely attributable to improved RI matching and stronger coupling at the noble metal-hydride interfaces. The symmetric sandwich structure in the trilayers, with Mg as either an encapsulating or central layer, facilitates more uniform electric field distribution and minimizes radiative damping, thereby yielding sharper resonance peaks. In contrast, Pd-based trilayer samples demonstrate the opposite trend, with broader resonance peaks compared to their bilayer analogs. For instance, Pd-Ag (106 nm) and Ag-Pd (132 nm) bilayers increase in FWHM to 120 nm and 147 nm, respectively, in the Pd-Ag-Pd and Ag-Pd-Ag trilayers. Similar broadening is observed in Pd-Au (119 nm to 148 nm) and Au-Pd (146 nm to 161 nm) samples. This increase in FWHM for Pd-containing trilayers may be attributed to the relatively weak change in the dielectric function of Pd upon hydrogenation, which limits the enhancement of plasmonic coupling and results in greater optical losses. Additionally, the increased number of interfaces in Pd trilayers may introduce extra damping pathways, further broadening the resonance.

A comparative analysis of FoM for bilayer and trilayer nanodisk arrays is shown in Figure 5c. Inspection of the data reveals a general enhancement in FoM for trilayer structures compared to their bilayer counterparts, particularly in Mg- and Au-based systems. For instance, Mg-Ag and Mg-Au bilayers exhibit FoM values of 0.02 and 0.17, respectively, while their corresponding trilayers, Mg-Ag-Mg and Mg-Au-Mg, achieve markedly higher FoMs of 0.26 and 0.41, achieving a max 13-fold enhancement from Mg-Ag to Mg-Ag-Mg. Similarly, Ag-Mg-Ag and Au-Mg-Au trilayers show improved FoMs (0.22 and 0.37, respectively) relative to their bilayer analogs (0.15 and 0.3, respectively). This significant increase can be attributed to both the larger resonance wavelength shift and the narrower FWHM observed in Mg-containing trilayer systems. The improved performance likely stems from the enhanced RI modulation and more effective electric field confinement at the noble metal-hydride interfaces in the trilayer architecture. In contrast, Pd-based samples display more moderate FoM improvements with trilayer stacking. For example, Pd-Ag-Pd and Pd-Au-Pd trilayers exhibit FoMs of 0.15 and 0.27, compared to 0.06 and 0.2 for Pd-Ag and Pd-Au bilayers, respectively. The enhancement here is less pronounced than in Mg-based systems, reflecting the relatively smaller resonance shift and broader FWHM associated with Pd upon hydrogenation, due to its weaker dielectric modulation and increased optical losses. The plasmonic resonances described above can be interpreted microscopically through the dynamics of surface current density, ${\mathrm{J}}_s=\sigma \left(\omega \right){\mathrm{E}}_t$, driven by the tangential electric field at metal–dielectric interfaces. In pristine multilayer nanodisks, the alternating surface currents on opposing boundaries form circulating dipolar loops responsible for the observed hybrid surface-lattice resonances. Hydrogenation modifies the complex conductivity and permittivity of the reactive layers, particularly converting Mg into insulating MgH₂, which disrupts these current loops and redistributes the electromagnetic energy toward the noble-metal regions. This redistribution weakens radiative damping and accounts for the narrower linewidths and enhanced FoM in Au-Mg-based bilayer and trilayer architectures. Conversely, in Pd-containing systems, the metallic continuity of PdH_x preserves the surface current circulation but introduces additional resistive losses, yielding broader resonances. This unified current-density viewpoint provides clear physical understanding of the coupling mechanisms and quality-factor evolution in multilayer plasmonic hydrogen sensors. Overall, the trilayer Mg-Au-Mg structure achieves a resonance shift of Δλ = 120 nm and a FoM of 0.41, surpassing most previously reported plasmonic hydrogen sensors [15,17,26,29,37,38,39,40,41,42,43,44,45,46,47,48] (Figure 5d). Notably, the few plasmonic hydrogen sensors exhibiting higher Δλ and FoM typically rely on alternative mechanisms—such as surface plasmon polaritons (SPPs) in thin films [39,40], film–nanoparticle (NP) coupling [46], Fabry–Perot cavity [29], or chiral NP architectures [37]—which inherently offer superior performance compared to the LSPR of nanodisks. Note that the present study models the steady-state optical response rather than the dynamic hydrogenation process. The detection speed in practical sensors further depends on catalytic efficiency and microstructure. Approaches combining plasmonic architectures with catalytic layers have demonstrated millisecond-scale response [16,17]. In addition to dielectric-function modulation, optical changes may also arise from stress- or embrittlement-induced scattering mechanisms [49], although such effects involve different physical origins and are therefore not included in the present electromagnetic analysis. In addition, the present study provides a theoretical assessment of multilayer nanodisk arrays under idealized diffusion conditions. In practical devices, substrate contact can partly impede hydrogen transport; however, prior experiments on direct-contact Pd–Au nano-sandwich structures have demonstrated that this effect remains weak and that high optical sensitivity can still be achieved [26,27]. Therefore, the trends revealed by our modeling—linking stacking sequence, interface field overlap, and sensitivity—are expected to remain valid for realistic sensor architectures.

4. Conclusions

In summary, our systematic theoretical investigation demonstrates that the optical response of plasmonic nanodisk metasurfaces to hydrogenation can be dramatically improved through rational multilayer engineering. Single-component Mg nanodisks, although exhibiting distinct optical changes upon hydrogen uptake, lose their metallicity and thus their plasmonic resonance, rendering spectral tracking impractical. In contrast, bilayer and trilayer heterostructures incorporating noble metals enable robust, high-contrast, and spectrally trackable plasmonic shifts. By optimizing both the material composition and stacking order in bilayers, we achieve up to a 15-fold enhancement in figure of merit (FoM). Further, trilayer “sandwich” architectures deliver up to 10-fold and 13-fold improvements in spectral shift and FoM, respectively, over their bilayer counterparts. Notably, the trilayer Mg-Au-Mg structure achieves a resonance shift of Δλ = 120 nm and a FoM of 0.41, outperforming most previously reported plasmonic hydrogen sensors. These enhancements arise from synergistic effects at the noble metal–hydride interfaces, where electric field confinement and dielectric modulation are maximized. Our findings establish a clear design rule: decoupling plasmonic performance from hydrogen sorption via multilayer integration enables a new class of actively tunable, high-sensitivity optical hydrogen sensors. Moreover, this strategy can be extended to other chemically responsive plasmonic systems, providing a general blueprint for next-generation metasurfaces with tailored optical and functional properties.